中学受験：脳科学をフル活用！偏差値を上げる４つの勉強法

偏差値を効率的に上げるために…先人の知恵を活用すべき

こんにちは。かるび勉強部屋 ゆずぱ です。

昔から多くの心理学者や脳科学者が様々な実験結果をもとに、”やる気” や “学習” に関する学説を立てています。偏差値をあげるために試行錯誤することも大切ですがゼロからでは大変でしょう。

先人達が積み上げたこれらの学説を使わない手は無い！

本記事では下の図の右側にある”学習に関する学説４つ”をまとめてみましたd(^_^o)

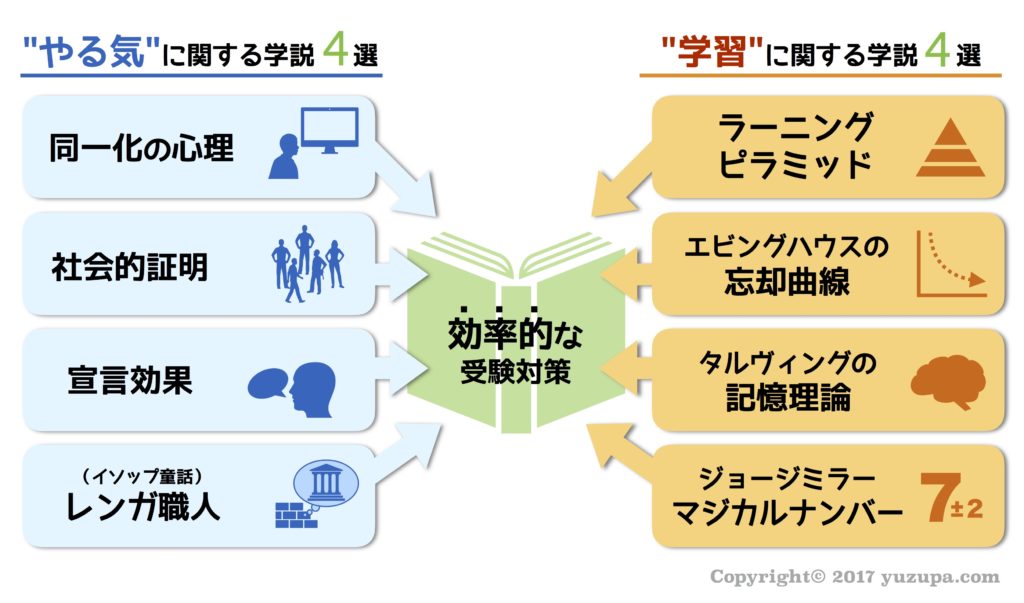
本記事は右側の”学習”…つまり勉強のやり方について書かれたものです。左側の”やる気”に関しては以下の記事で詳しく説明しておりますので合わせてお読みください。

中学受験：使える！やる気に関する学説４選

 

ラーニングピラミッド

人に教えるのがイチバン効果的

最近はアクティブラーニングという言葉が流行っています。アクディブラーニングとは、従来の講師から生徒への一方通行の受動的な学習法ではなく、生徒が能動的に参加する学習法のことです。今後、学校教育カリキュラムに取り入れられ、２０２０年度には大学入試もこちらに重きを置いたものに変わっていきます。

これらの世の中の流れの中でよく引用されるのが、アメリカ国立訓練研究所（National Training Laboratories）のラーニングピラミッドです。簡単に説明すると、講師から一方的に説明を受けるよりも、誰かに説明するなど能動的にアウトプットした方が学習の定着率は高いということを示した学説 です。学習の定着率順に７つの学習方法がランキングされています。

イチバン効果的な学習方法は 人に教える事 なのだそうです。

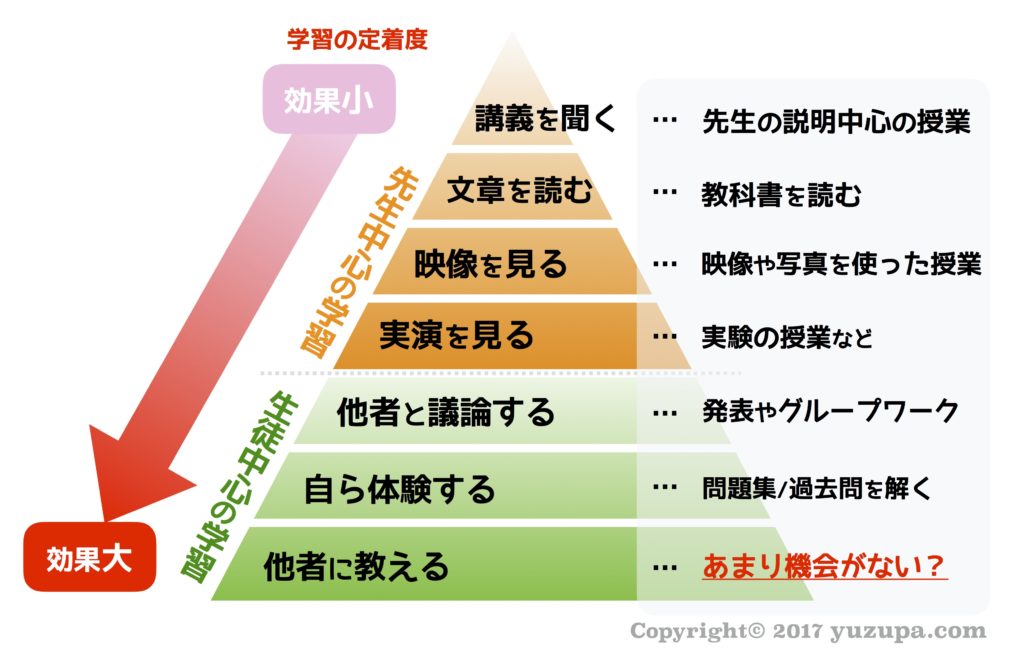
念のため…。このラーニングピラミッドには根拠となる数値データは無いそうです…。ずいぶんと古い学説ですしね。なぜ、根拠が無いのに市民権を得ているのでしょうか？ それは…、経験上まぁだいたい合ってるから…(^^;)  根拠が無かろうが役に立てば良いでしょう！

 

子供を “講師” に仕立て上げる

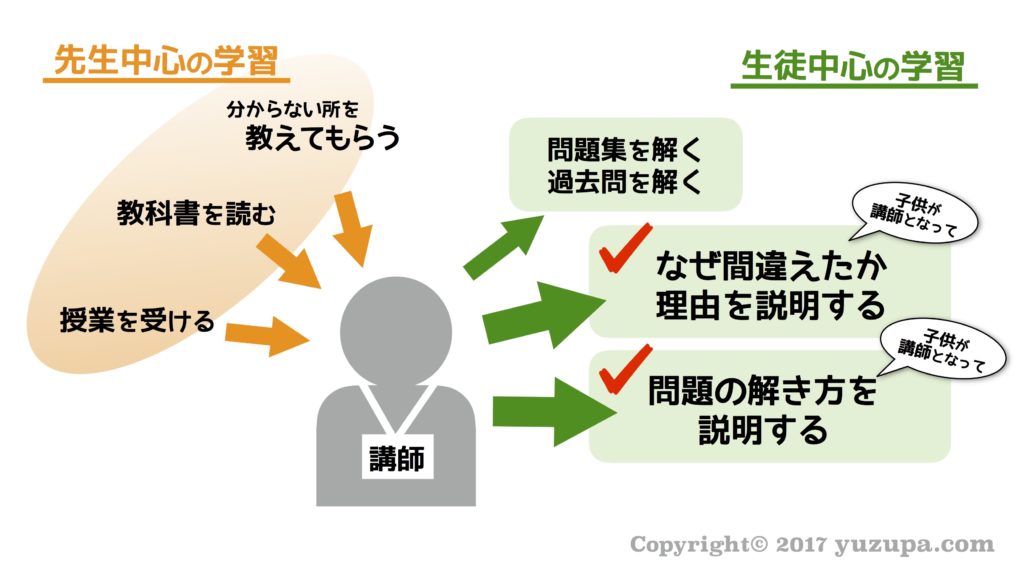
ラーニングピラミッドの学説では、受動的な学習よりも、能動的にアウトプットする学習の方が定着率が上がるとの事でした。であれば…。お子様自身が講師となって説明する場を作ってあげれば良いでしょう。普段の生活ではそんな機会は滅多に無いので、親が意識的に子供が講師となって説明する場を作れば良い のです。

我が家では休日にテストなどで間違えた所を親子２人で見直しをするサイクルを作っています。ひと通り見直しが終わった後に（1）なぜ間違えたかの解説 （2）問題の正解の解説 の２つの解説 を意識的に子供にしてもらうようにしています。まさにラーニングピラミッドの定着度ナンバーワンのやり方です。

過去の記事 で紹介したノートのまとめ方を実践していると、こんな解説をお子様から聞くことができるかもしれません。「聖徳太子について教えてくれる？」と問いかけると…。

「聖徳太子に関しては４つのポイントがあってね…、１つ目は推古天皇中心の政治を作ったということ、２つ目は役人の心得を書いた１７条の憲法を作ったこと、３つ目は役人の身分を定めた冠位十二階を作ったこと、最後は隋の文化を調べるために遣隋使を送ったこと。だから、正解は ＸＸＸ になるんだよ。」

これだけの説明の元となるバイブルは…、自分でまとめたノート（まとめノート作りも能動的な学習の一種）です。

 

エビングハウスの忘却曲線

人はとにかくモノを忘れる生き物

とてもとても有名な学説なのでご存知の方も多くいらっしゃるかと思いますが、人は…とにかくモノを忘れる生き物であるということを証明した学説 です。次の図があれば 説明も不要なくらいですね…。要は、いくら勉強をしても１日たったら７割は忘れてしまうという受験生にとって ちょっと ミもフタも無い話 です。

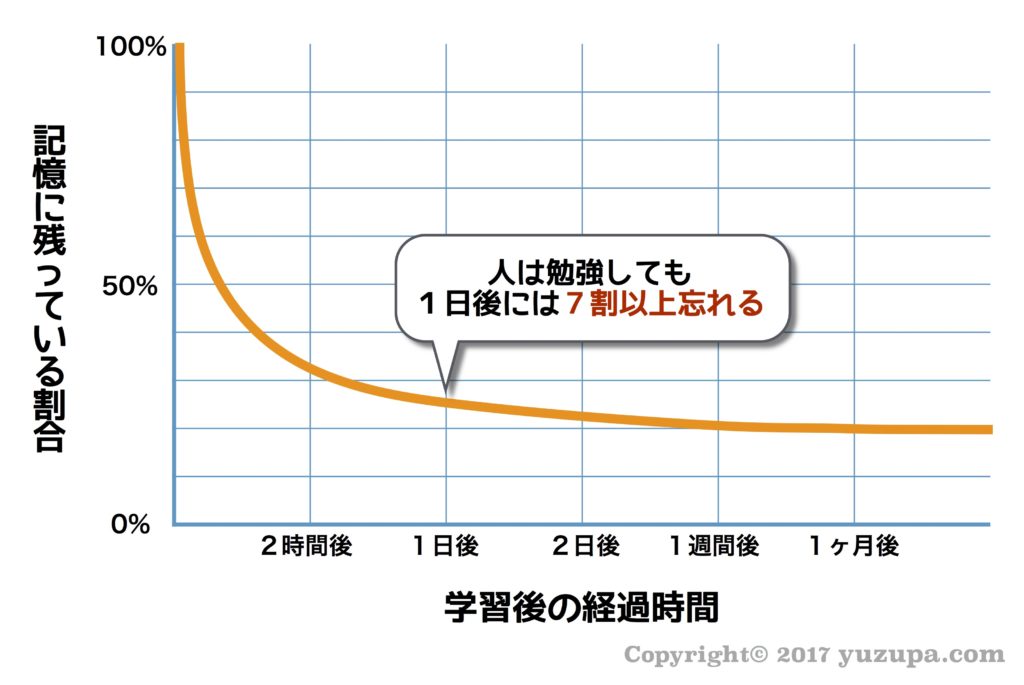
多くのサイトや受験指南書で推奨されているのが、このエビングハウスの忘却曲線を利用して１日後に復習して、２日後に復習して、１週間後に復習して…という提案です。確かにその通りなんですが… 多くのサイトで紹介されている何度も反復する手法は少なくともウチは無理でした。

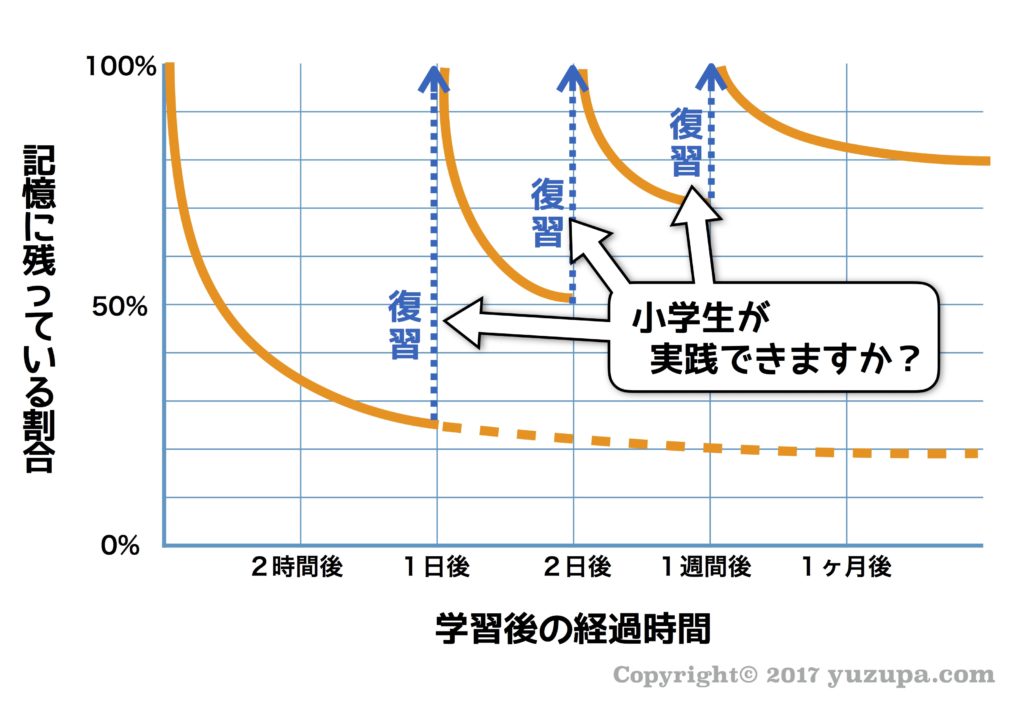
なぜ出来ないのか？ 理由はただ１つ… 小学生ひとりでは管理しきれない (*_*) 大人が学習するにはとてもよい提案だと思いますが、この記事 でも紹介したとおり自己管理が未熟な小学生にはちょっとハードルが高そうです。ではどのようにこの学説を活用するのでしょうか？

 

事実を知っているだけでも十分

ひとつは親子喧嘩の防止です… こんな経験ありませんか？ さっき教えた事をもう忘れている…(@_@) 。でも…ヒトは忘れる生き物だと親が割り切ることでイライラもなくなる でしょう。エビングハウスの忘却曲線を親が正しく理解することで不要な親子喧嘩の防止になるという事です。

 

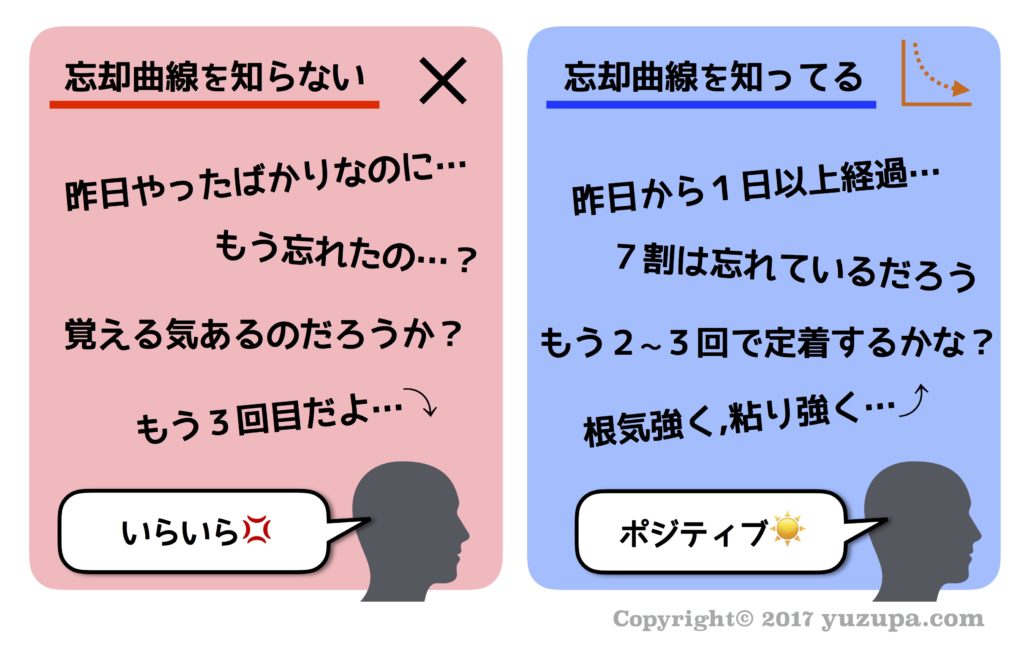
厳密すぎない忘却の管理

我が家の場合、親がサポートできるのは土日だけで…忘却曲線の時間軸と合わない んです。そうであれば、厳密に時間軸を管理しない程度に活用すればよい！ということで… 我が家流の忘却曲線の活用は、単純に忘却してしまった回数をシンプルにシールで印をつけて管理し、厳密すぎないタイミングで復習しています。

 

タルヴィングの記憶理論

頭に長く残る記憶、すぐ忘れる記憶

記憶には頭の中に長く残る記憶とすぐに忘れてしまう記憶があるという事実を数々の実験を元に体系化した学説です。この学説が正しい事を感覚的に実感できる質問があります。「あなたは小さな頃の記憶をどれくらい覚えていますか？ 」

私の昔話 その１

私は小さな頃 ソロバンをやっていました。１年生から始めて、３年生の終わりまで、だいたい３年くらいでしょうか…。 最近、小学校１年生の娘がソロバンをはじめたのですが、やはり ３０年以上ふれる事すらなかったソロバンの弾き方を覚えている んです。

私の昔話 その２

また、幼稚園の頃、園庭にあった塀から落下して頭を打ち、数時間の記憶喪失の後、病院に行った事を覚えています（記憶喪失した経験を覚えているというのも変な話ですが ^-^;）３０年も前の出来事なのに、病院の雰囲気、どんな検査か、保母さんの顔まで覚えてます。

私の昔話 その３

一方で、高校で授業を取っていた”世界史”…学校の学期末テストではそれなりの点数を取っていたはずなのですが、綺麗さっぱり覚えていないんです。ただ… ところどころ覚えている。覚えているのは自分でオリジナルの覚え方を作って覚えた部分 なんです。

私の昔話が長くなってしまいましたが、本題に入りましょう。記憶には長く頭に残る記憶と、すぐ忘れる記憶がある事を体系的にまとめたのがタルヴィングの記憶理論です。図で要点だけに絞って表すと以下のようになります。

 

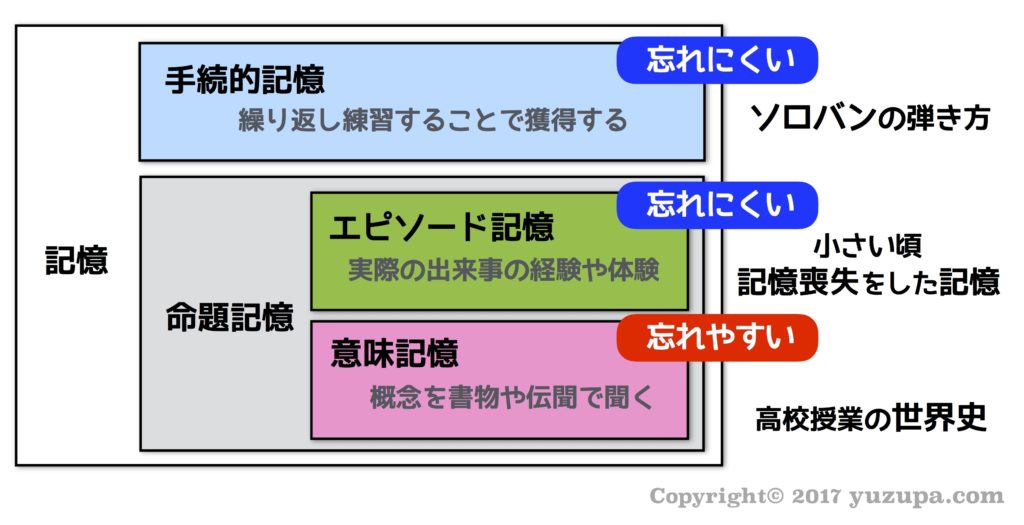
ただ分類する…それだけ！

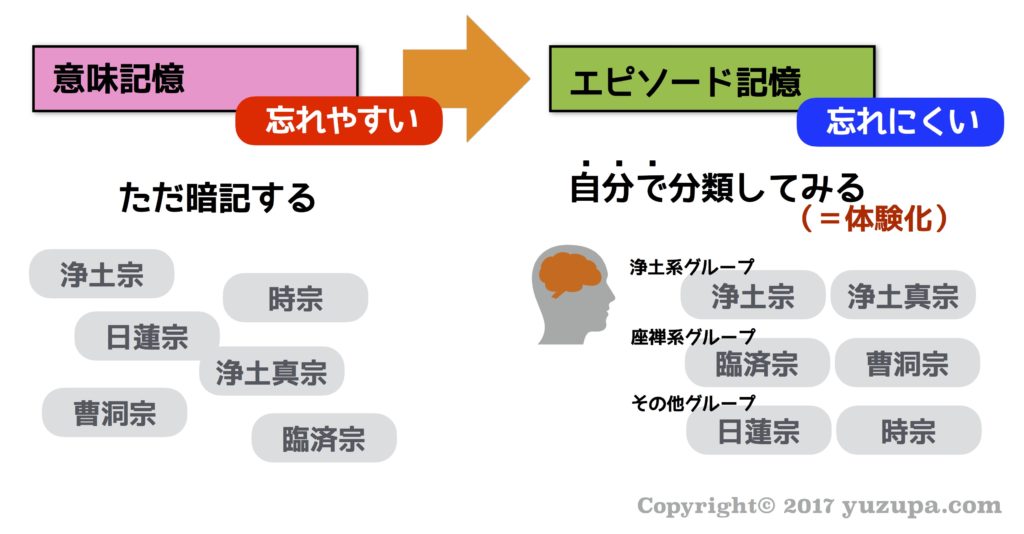
タルヴィングの記憶理論を受験に活用するのは、とてもシンプルです。すぐに忘れる”意味記憶”を減らして、頭に残る”エピソード記憶”を増やせば良いのです。具体的にはどんな方法があるのでしょうか？ タルヴィング博士は、とても面白い実験をしています。

１００枚のカードを、グループＡには 暗記するよう指示し、グループＢには分類するよう指示しました。実験後のテストで暗記の定着が高かったのは？ お察しの通り…ただ分類しただけのグループＢです。単なる暗記＝意味記憶 となるか、分類するという体験＝エピソード記憶 となるかは、ちょっとした工夫次第 なのです。

そうであれば、中学受験に活用するのは簡単です。あらゆる事柄を子供が自ら考えて分類するだけです！ これだけでだいぶ記憶の定着率が上がってきます。具体的なイメージを紹介しましょう。分類のやり方については こちらの記事 も参考にしてください。

 

毎日の音読、毎日の計算

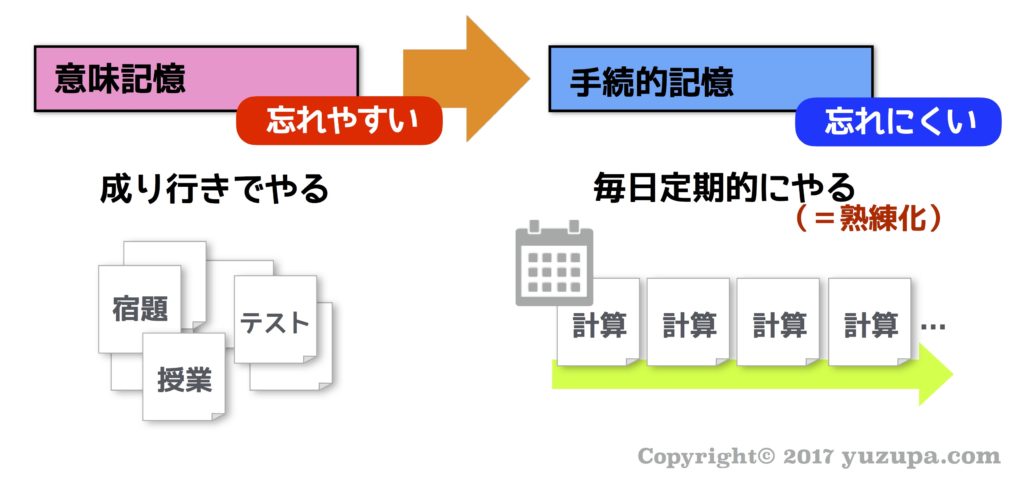
それでは、すぐに忘れる”意味記憶”を、頭に長く残る”手続的記憶”にするには…？ 残念ながら、これはテクニックなどありません。タルヴィング博士の理論にもある通り、練習…練習…練習…そして習熟を目指すのみ です。それでは、どんな事を練習すれば良いのか？

毎日の音読と、毎日の計算です。

音読と計算の効果は、受験業界の各所で主張されていますので、ぜひ実践してみてはいかがでしょうか？ タルヴィングの記憶理論の通り… いったん習得すれば、本当に忘れません。日本語を自由にあやつり…ちょっとした計算を無意識にこなせる… 小学生の大切な工程です。

 

ジョージミラーのマジカルナンバー

脳がぱっと記憶できる数は意外と少ない！

脳がぱっと記憶できる事柄の数は、意外と少ないという事を示した学説です。古くは心理学者のジョージミラー博士が提唱しました。７±２ つまり ５つ〜９つ と言われていますが、最新の研究では４±１ つまり ３つ〜５つと言われています。最大でも５つ… 意外と少ないと感じますが感覚的にも納得できます。

５つ以上の物事が、どれほど頭に入ってこないのか？ よくある実例で体感してみましょう！

 

数が少ない方がスッと頭に入ってくる

まずは以下の記事を見て下さい。

いかがでしょうか？ 頭に残るノートのまとめ方のコツを示したものです。３つのコツから成り立っており、シンプルでぱっと頭に入ってきて、簡単に暗記する事も出来るのでは無いでしょうか？ いっぽう… 以下もよく見かけるような記事ですが、どうでしょうか？

分かりやすいと感じた方もいるかもしれませんが、実際にご自分で文章を書くシーンを思い浮かべて下さい。頭の中で同時に、この10か条すべてに注意を払うことはできますでしょうか？ きっと難しいのではないでしょうか？ 私にはとても無理でした (^^ ;

マジカルナンバーである５つを超えると、頭がぱっと把握できなくなる。という事は、長期的にも記憶しにくいという事 です。よく円周率を何千桁も暗記している方がいらっしゃいますが、何千桁をまとまった数字ではなく、５桁ずつに区切って暗記している そうです。

 

５つ以下を目指して分類する！

そうであれば、円周率暗記の達人に習って、５つ以下を目指して分類すれば、頭にぱっと入り、記憶もしやすくなります。１つポイントがあります。”分割”するのでは無く ”分類”する こと。前述したタルヴィングの記憶理論で紹介した エピソード記憶 にする為です。

分類の仕方は人それぞれ異なるでしょう。重要なのは学習する本人が考えて分類する事です。実例として日本全国の伝統工芸品２４種類を、５つ以下を目指して分類してみましょう。繰り返しになりますが分類の仕方は自分で考えること。当然ながら無限に分類パターンがあります。

これは中学受験に登場する日本の伝統工芸品からよく出るもの２４種類を抜粋したものです。順番はランダムに並べてありますが、これを眺めていても覚えるのはとてもじゃありませんが至難の技でしょう。では５つ以下になるように分類してみましょう！まずは… シンプルに地域別で分類です。

これだけでもグッと頭に入りやすくなりましたね？ 次は、なんとなく似ている種類で分類してみましょう。

焼き物が６種類あるので５つを超えてしまいました。だったら…ええぃ！ 湯呑みのイメージが強いものとお皿のイメージが強いものにテキトーに分けてしまいましょう！ 専門家の方には怒られてしまうかもしれませんが… 目的は学会での発表ではなく自分の頭に残す事です。大事なのは分類の美しさよりも自分で考える事 なんです。

 

まとめ

中学受験に使える学説４つを選び、紹介しました。当ブログの他の記事で紹介しているノウハウやテクニックもこのような学説を参考にしたものが多いです。ゼロから試行錯誤するよりも先人の偉人たちが積み上げてきたものを使わない手は無いと考えています。