中学受験：面積図を使う問題は３ステップで解ける

面積図は掛け算を面積で表すもの…図形思考で方程式を解くための思考ツール

こんにちは。かるび勉強部屋 ゆずぱ です。

面積図…なんだそれ？ 私と同じように中学受験を経験していない親の方々はそう思われるでしょう。なぜなら…自らが小学生の時はそんなものは習わなかった上、中学高校と進学してもそんなツールは全く使わない からです(^^;  面積図とはナニモノなのでしょうか？

私も 面積図 について知識が全くなかったのですが… 息子と受験勉強を続けている中、問題を普通に解こうとすると、“方程式”を使わないと簡単には解けない問題がウジャウジャ出題されるんです。それを解決するのが  面積図 というツールというわけです。つまり面積図は方程式の代替手段であり、とても難しそうですが…

面積図を使う問題の多くは３つのステップで解けます

注釈： “方程式を教えてしまった方が早いのでは？” と思われる方もいらっしゃるかと思います。様々な受験関連のブログを読むと 稀に方程式を教えてしまったという記事も見つかります。ただ…マイナスの計算が出てくるなど結構ハードルが高いです(^-^; 

面積図とは

面積図とは何か？

面積図をひとことで説明すると…  掛け算「A x B = C」という数式を「縦=A、横=B、面積=C」の図形に変換したもの です。ちょっと言葉だけでは伝わりにくいところもあるかと思いますので、以下の図を見てください。考え方自体はとってもシンプルですね。

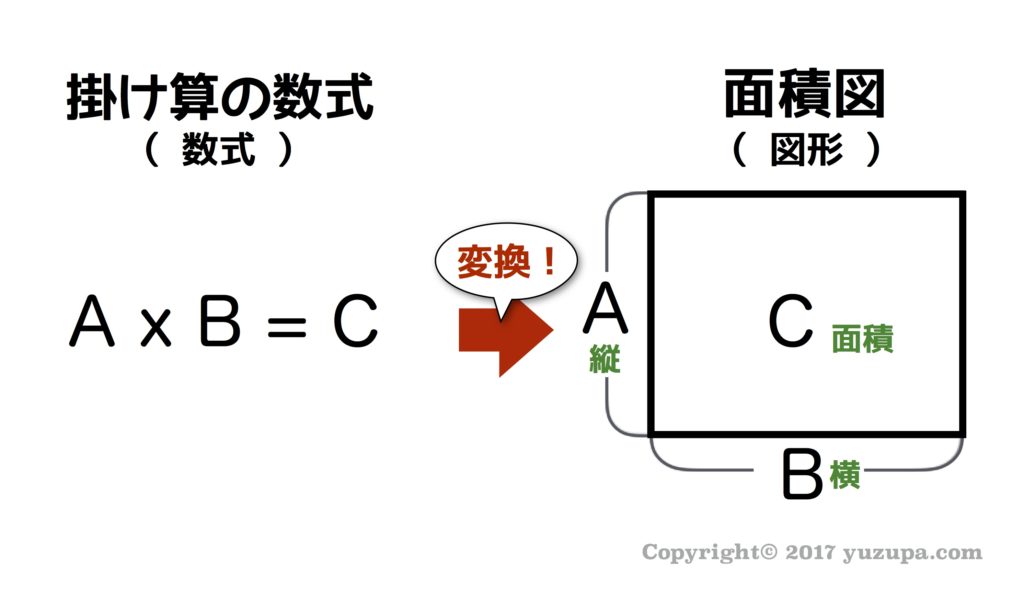
いくつか具体的な事例も紹介したいと思います。メジャーな掛け算の例だと…「単価 x 数量 = 合計金額」とか「速さ x 時間 = 道のり」あたりでしょうか？ 誰でも知っている掛け算の式なのですが、数式を面積図に変換すると以下の図ようになります。

面積図の利点は？

面積図がナニモノなのかは分かっていただけたかと思いますが、これって…何が嬉しいの？と思われる方がいらっしゃるかと思います…少なくとも私はそうでした(-.- )  面積図を使うと方程式を使わなくても問題を解けるというところ。つまり以下のようになります。

１つ目は、一般的には方程式を使って解く問題を シンプルな面積問題として扱う事できる 点です。面積が苦手だというお子様もいるかと思いますが、正方形や長方形の面積はできる子が多いでしょう。面積図さえ書けてしまえば単純な面積問題になるんです。

２つ目は、方程式に比べてダラダラとした計算を減らす事ができるという点です。方程式って…式を立てた後ダラダラ計算が続きますよね。一方、面積図は図に数値を書き入れていくという作業が中心となり計算はシンプルです。解く際のイメージで比較してみましょう。

面積図を使うべき４分野

面積図の仕組みとメリットは分かったけど…。使い方の詳しい説明前に、まずはどんな問題が出た時に使うべきかをハッキリさせないといけません。こんな問題が出たらこう解くという知識をどれだけ多く使いこなせるか が中学受験で偏差値を上げるキーポイントになります。

注釈：仕事算という分野があり旅人算と同様途中で仕事量が変化する問題があります。本記事は旅人算の一種として扱います。

最も重要なポイント

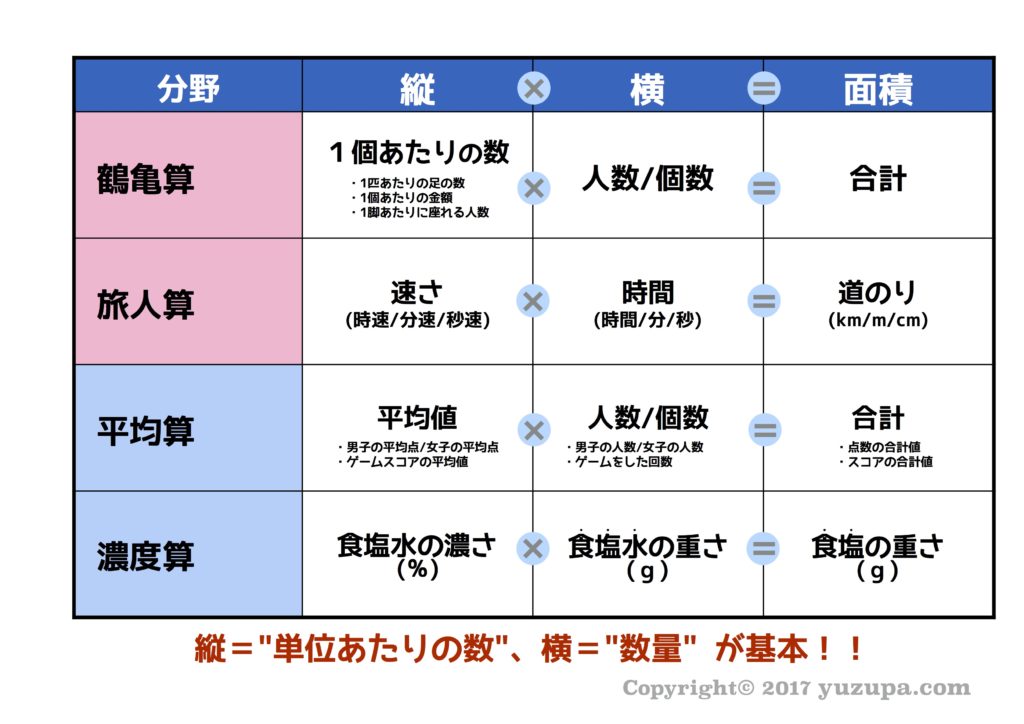
面積図で 最も重要なポイントが”縦”と”横” と”面積”に何を割り当てるかを固定する事 です。縦と横は逆にしても解けてしまいますが、決してキマグレで決めてはいけません。縦と横をひっくり返すと全く別の解き方になってしまい間違いなく混乱します。必ず固定しましょう。

以下は “縦” と “横” と “面積” に何を割り当てるかを表にまとめたもの「縦横面積の表」です。私の息子は割り当てを固定するために、この表を暗記というよりは、手が覚えてしまっています。計算や漢字のように無意識の領域まで持っていけるとベスト ですね！

面積図を使った問題の解き方

面積図問題の全体の流れ

いよいよ、面積図を使って問題を解くときの全体の流れを示したいと思います。実は どの問題もこの３つのステップで解く事ができます。最初にすべき重要な事は、”縦”と”横”と”面積”を最初に決めてしまう事。また問題文に出てくる数字を見逃さずに拾うと言う事です。

全体の流れを見てみましょう。

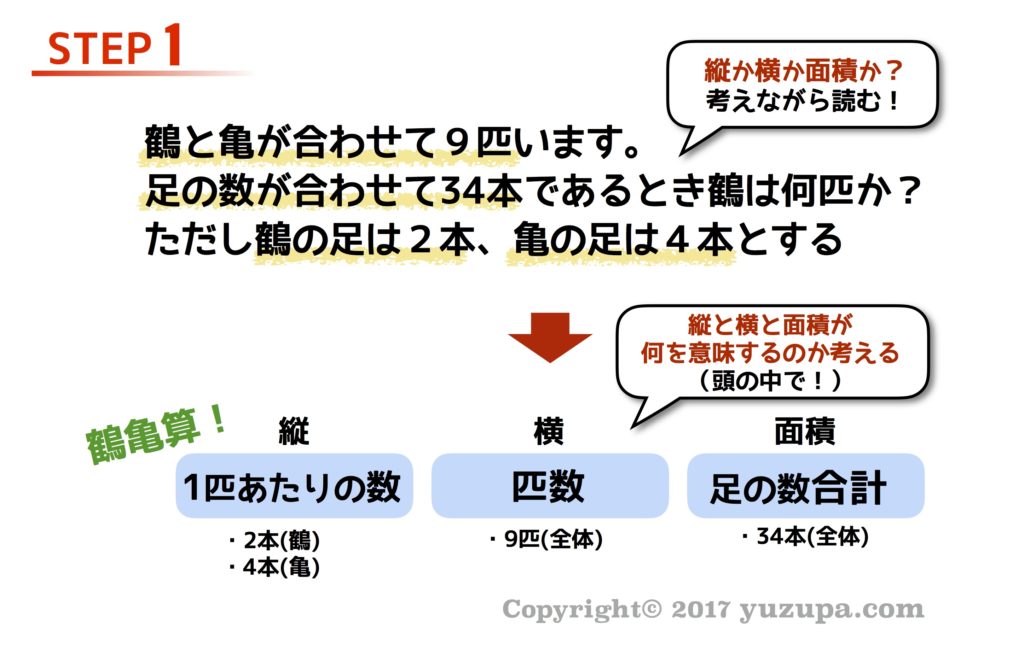
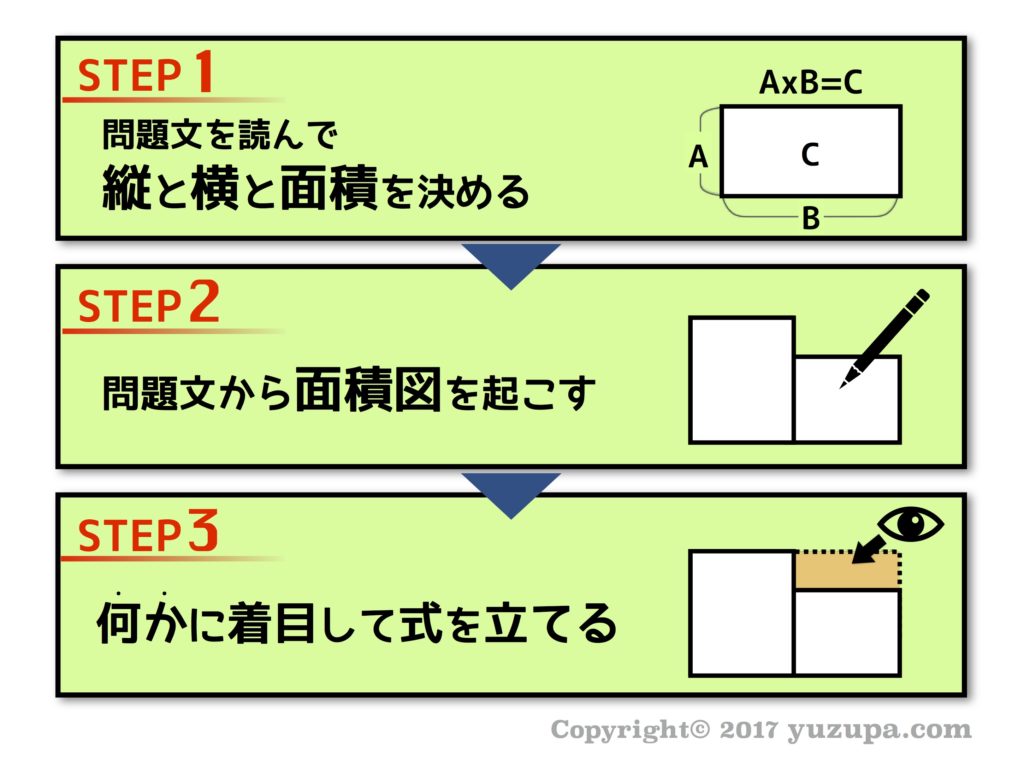STEP1：縦と横と面積を決める

もっとも重要なポイントは縦と横と面積を固定する事でしたね。問題文を読みながら 鶴亀算なのか旅人算なのか、平均算なのか濃度算なのかを判断し、縦と横と面積に何を割り当てるか決定しょう。先ほどの「縦横面積の表」を参考にしましょう。

ポイントは、問題文を読みながら出てくる数字が 縦か横か面積か…どこに当てはまる数字なのかを考える事なんですが、私の息子はよく問題文で出てくる数字を見落とす…(-_-) 出てくる数字は全部使わないと解けないように出来ていますから”見逃し”は命取りです！

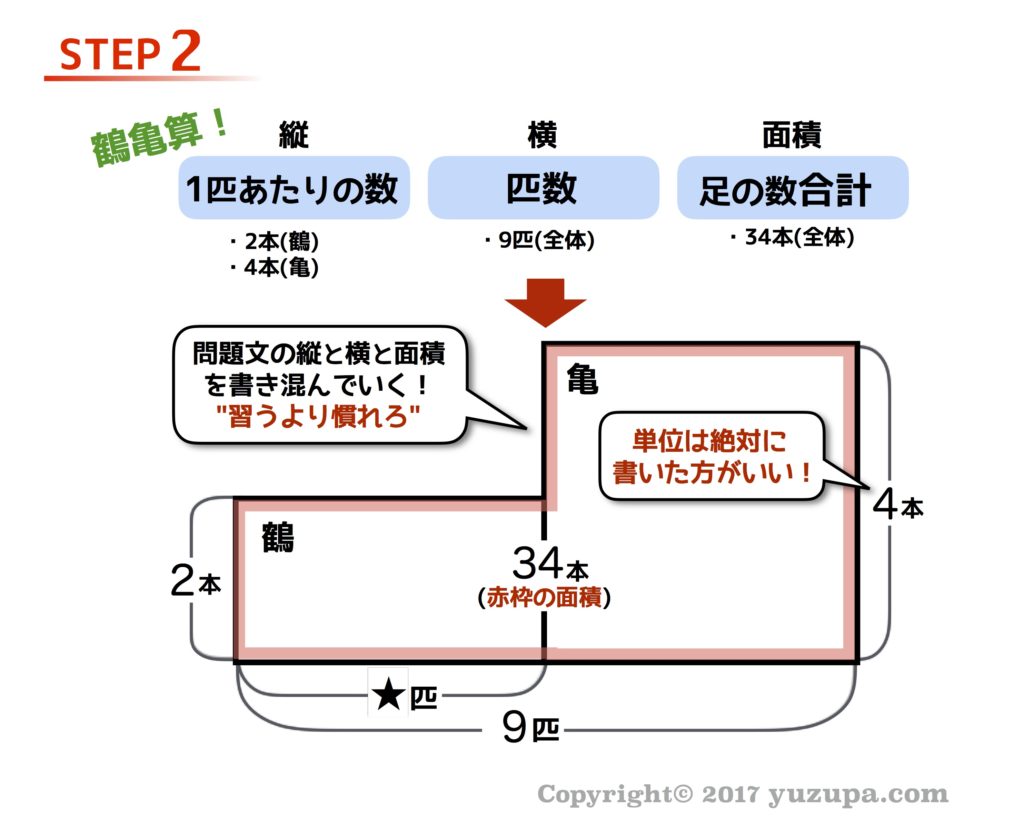
STEP2：面積図を起こす

思ったほど難しくはないのでしょうか…私の息子の場合は意外にもスンナリとマスターしてくれました。少しばかり慣れるための時間は必要かと思いますが、やはりポイントは”縦”と”横”と”面積”に何を割り当てるかをしっかり意識する事ではないかと思っています。

いくつかポイントを紹介します。まず…面積図には必ず単位を書く事です。面積図を作っているうちに縦や横や面積が何を意味しているかを忘れてしまうので意識を最後まで維持するために。。また何を求めているのか 忘れてしまうので★印をつけておくとよいです。 

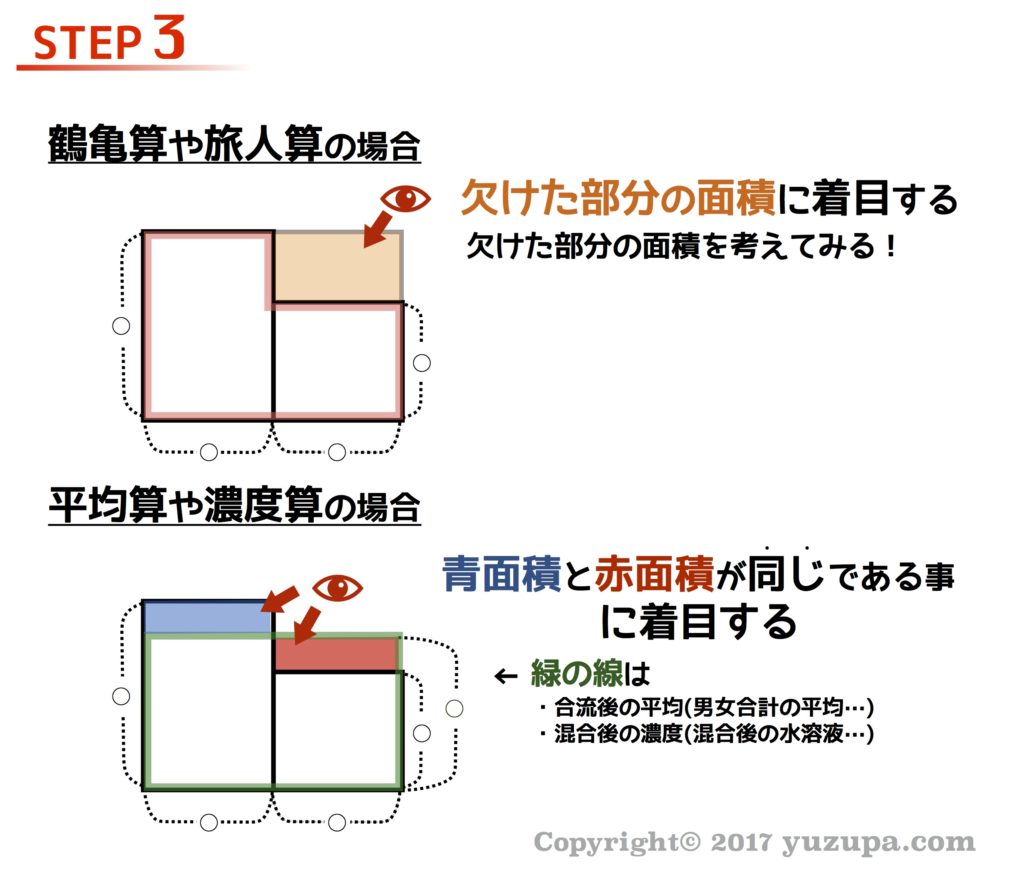
STEP3：何かに着目して式を立てる

実は面積図を使って問題を解く手順において もっとも苦労する点は面積図を書いた後 にあります。面積図を書いたはいいんだけど…次に何をすれば良いかわからなくなるんです。これでは便利な面積図も台無しですね。

しかしながら、着目するポイントが分かっていれば全く心配する必要はありません。なぜなら 実はとてもシンプルで２つのパターンしか無い からです。鶴亀算や旅人算の場合は欠けた部分の面積に着目し、平均算や濃度算の場合は赤と青の面積が同じであることに着目します。

具体的な解き方は実際の例題をじっくりやるのが最短の道ですが、ここではこの２つの図のイメージを目に焼きつけてください。

具体的な解き方の例

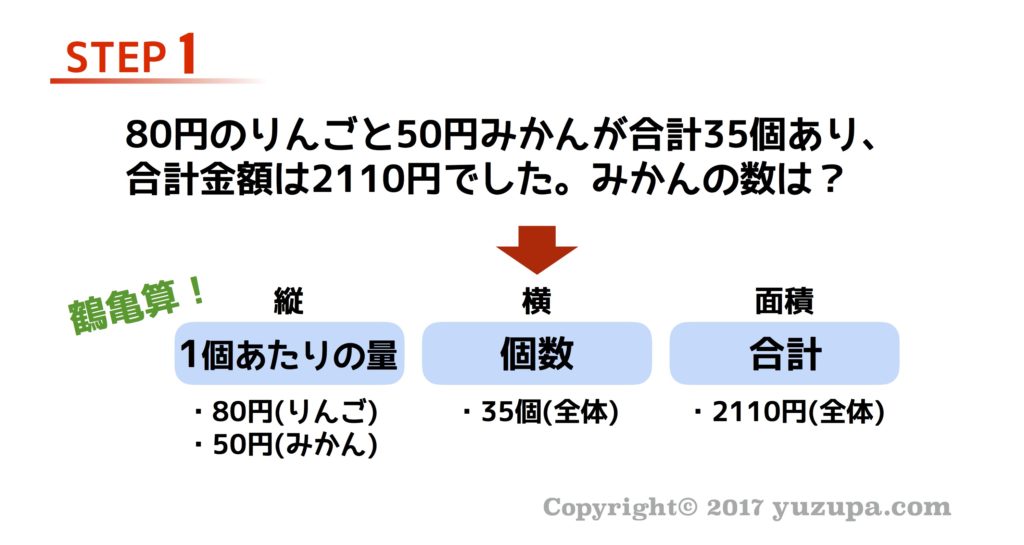
鶴亀算の例

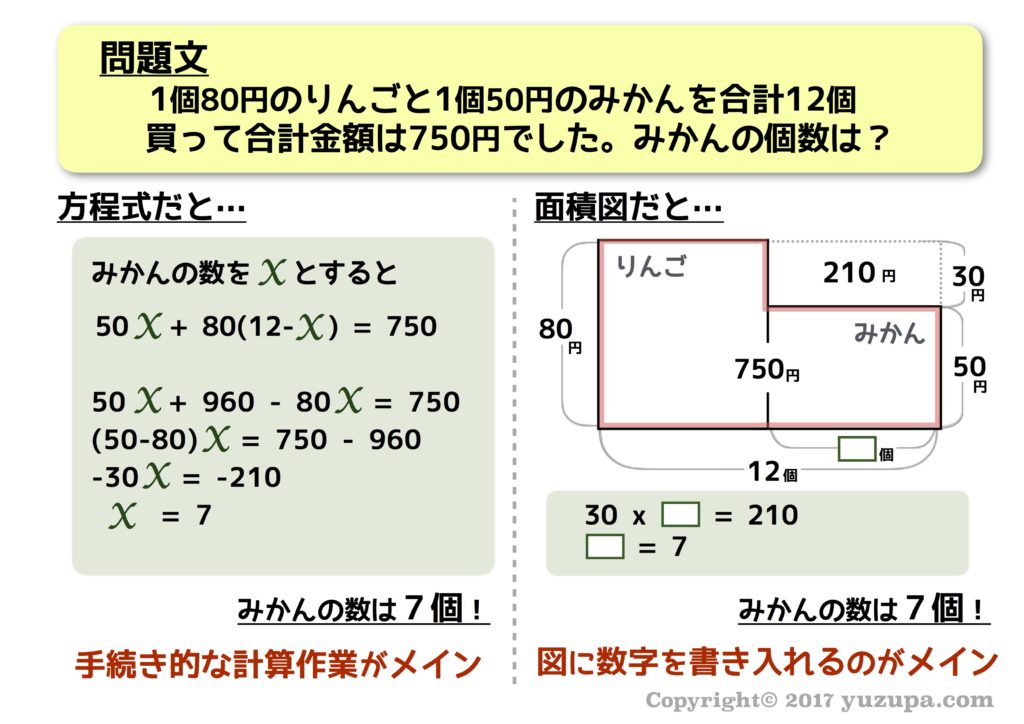
それでは、具体的な例題を通して 面積図の問題の解き方(３つのステップ)を見ていきましょう。まずは “鶴亀算” です。問題を読んで以下のように横が何で…縦が何で…面積が何であるかを頭の中でしっかり考えます。数字をひとつたりとも見逃さないのがポイント です！

次に面積図を書きます。ポイントは赤枠の面積 です。面積は合計金額を意味する のでしたね。りんごの合計金額やみかんの合計金額がわからなくても全体の合計金額がわかれば、図のように赤枠の面積が2110円 という事をしっかり書いておきます。

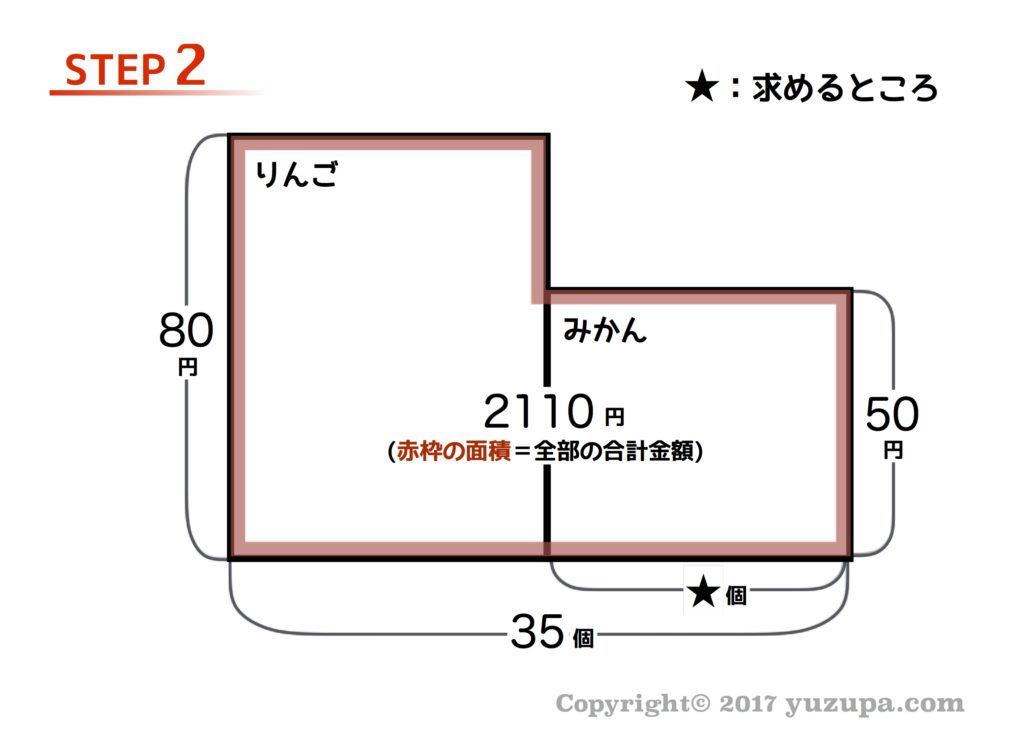
最後は面積図問題の難所… “何かに注目して式を立てる” です。鶴亀算ですので 欠けた部分の面積に着目 してみましょう。この欠けた部分の面積は690円になります。お子様はなぜ690円になるのか答えられないかもしれません…

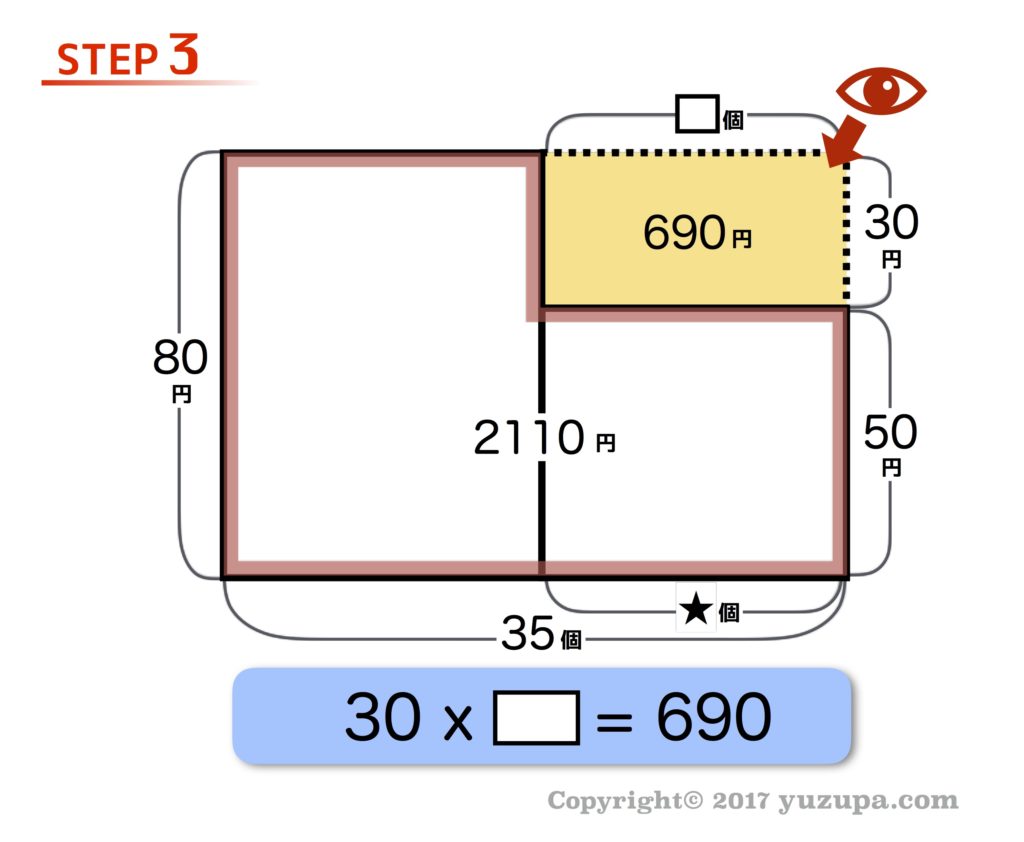
安心材料にはならないかもしれませんが…うちの息子も苦戦しました。冒頭で面積図の利点は “シンプルな面積問題として扱える” と紹介しました。では、シンプルな面積問題と捉えて”オレンジ部分の面積を求めなさい”という問題だったらいかがでしょう？

大きい四角形(80円x35個)の面積は80×35= 2800円なので、そこから赤枠の面積である2110円を引けばこの690円を出すことができます。まさにシンプルな面積の問題です。そこまでいければ後は簡単… 欠けた部分の面積に着目して式を立てるだけです。

後は計算間違いをしないように気をつけるだけ！ 図の□は23になりますが、求めるのは★の部分(みかんの数)ですので、そのまま答えになります… すなわち 答えは23個 です。

旅人算の例

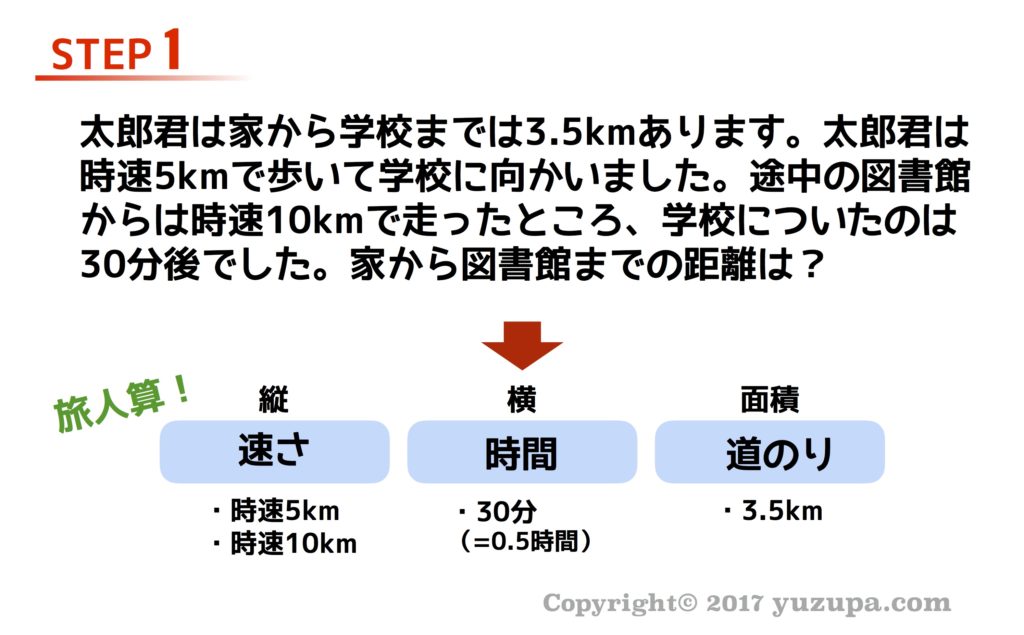
次は”旅人算(速さが途中で変わる問題)”です。先ほどの鶴亀算と同様に 数字の見逃しが無いように注意をしながら 縦と横と面積に割り当てる数字をひろっていきます。鶴亀算とまったく同じ考え方でとけちゃいます(^_^)

面積図を書くステップのポイントも鶴亀算と同様です。面積は道のりを意味しますから赤枠の面積は最初から最後までの道のり…つまり家から学校までの道のり3.5kmになりますね。今回は求めるものも家から図書館からの道のりになるので青枠の部分の面積になります。

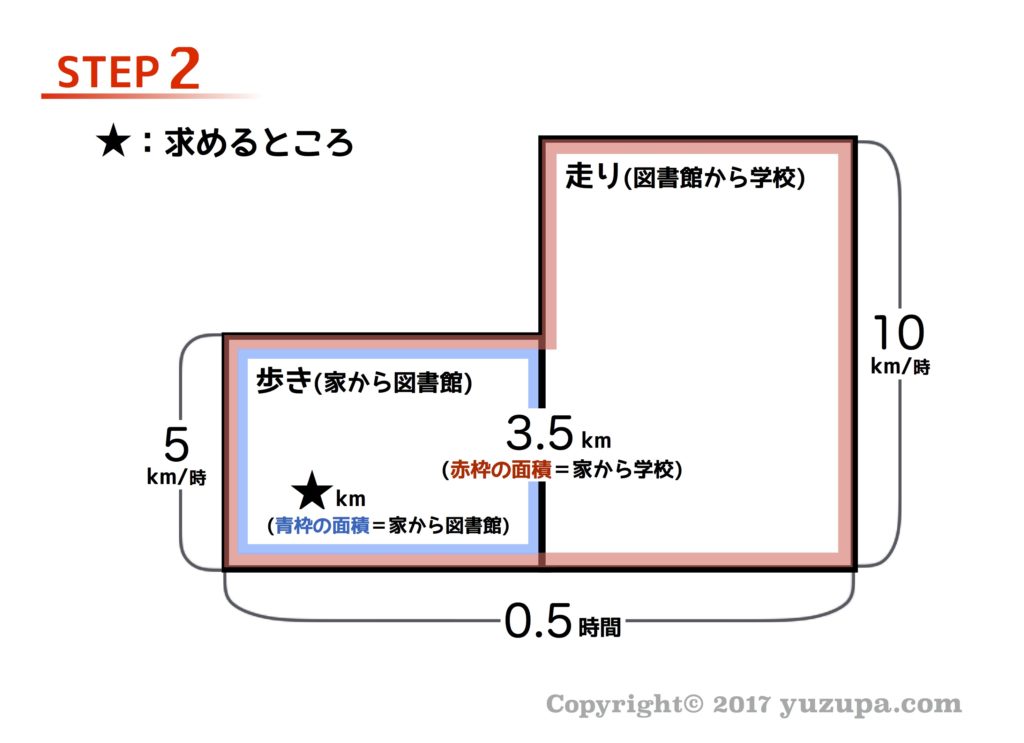
最後も同様、欠けた部分の面積に着目して式を立てます。

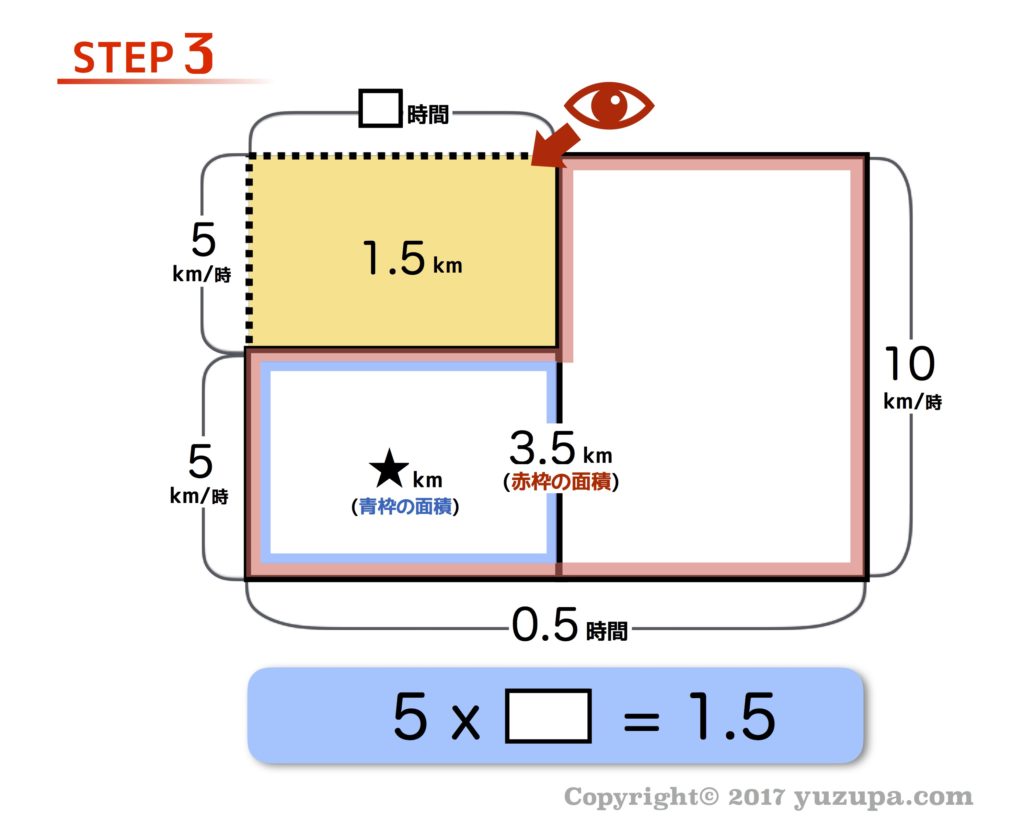
図の□は  0.3時間 になりますね。求めるのは★の部分の面積になりますので、5×0.3=1.5kmで 答えは1.5km になります。

平均算の例

次は”平均算”です。繰り返しで恐縮ですが…(^^;  数字の見逃しが無いように注意をしながら 縦と横と面積に割り当てる数字をひろっていきます。問題文から縦と横と面積に該当する数字を漏らさずにひろっている事がわかりますでしょうか？

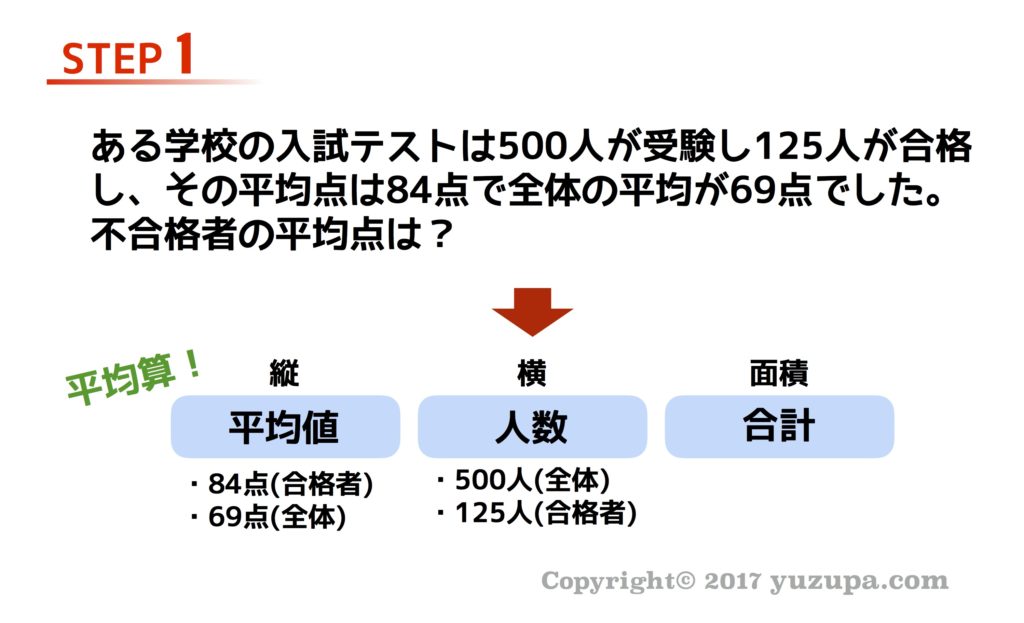
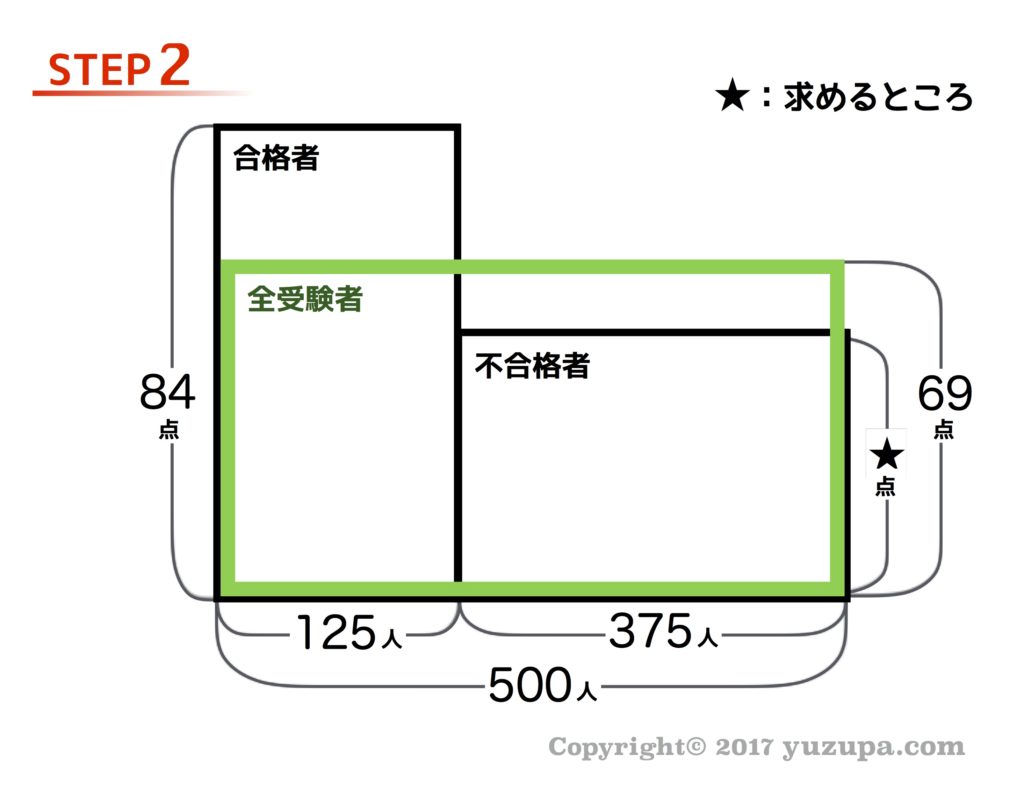
平均算の場合、鶴亀算や旅人算とは違ったポイントがあります。それが緑枠の部分です。緑枠は合格者と不合格者を足した全体の平均を表す面積図です。全体の平均は必ず合格者の平均と不合格者の平均の間にきます。このイメージを覚えましょう。

最後のステップは “何かに着目して式を立てる” です。着目点は青面積と赤面積が同じという事です。なぜ同じになるのでしょうか？平均とはデコボコしたものを平らにするという事ですので、でっぱった青い部分を赤い部分にならして平らにした という風に考えましょう。

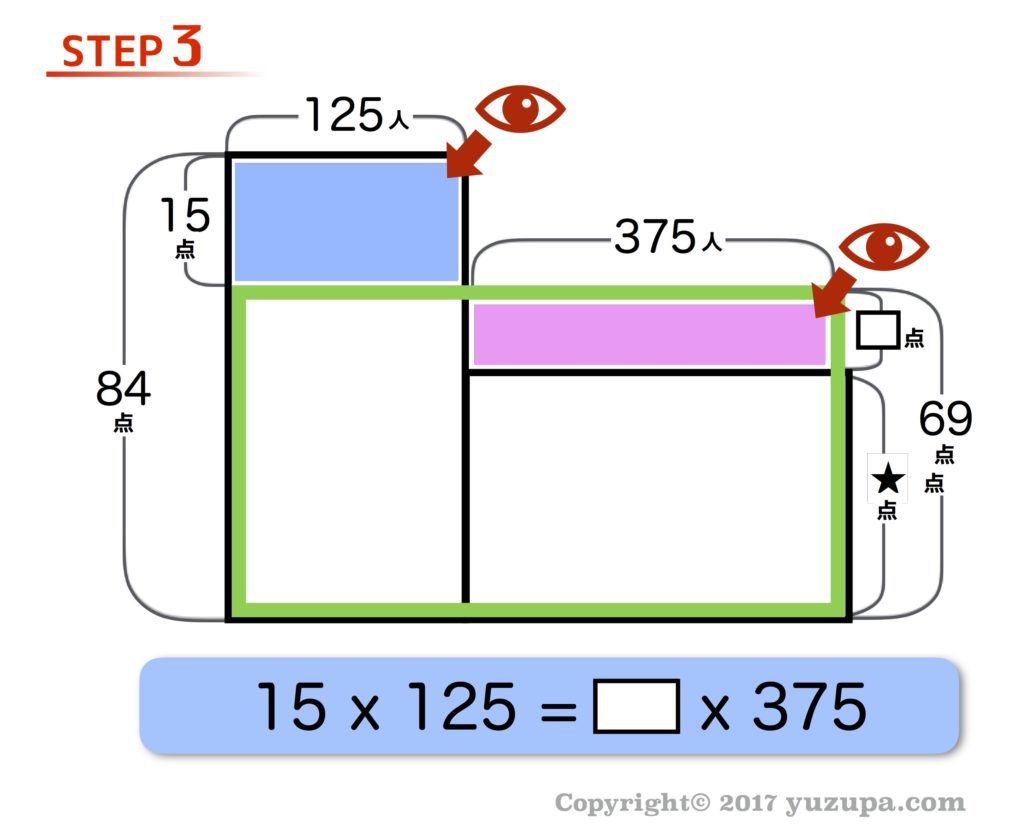
最後は計算に気をつけて… 図の□は5になります。求めるのは★の部分(不合格者の平均)ですので 69-5=64となり 答えは64点 です。

濃度算の例

最後は”濃度算”です。ほとんどが食塩水を混ぜる問題ですかね…(^^; 今までと同様に問題文からひとつ残らず数字をひろっては縦なのか横なのか面積なのかを考えます。

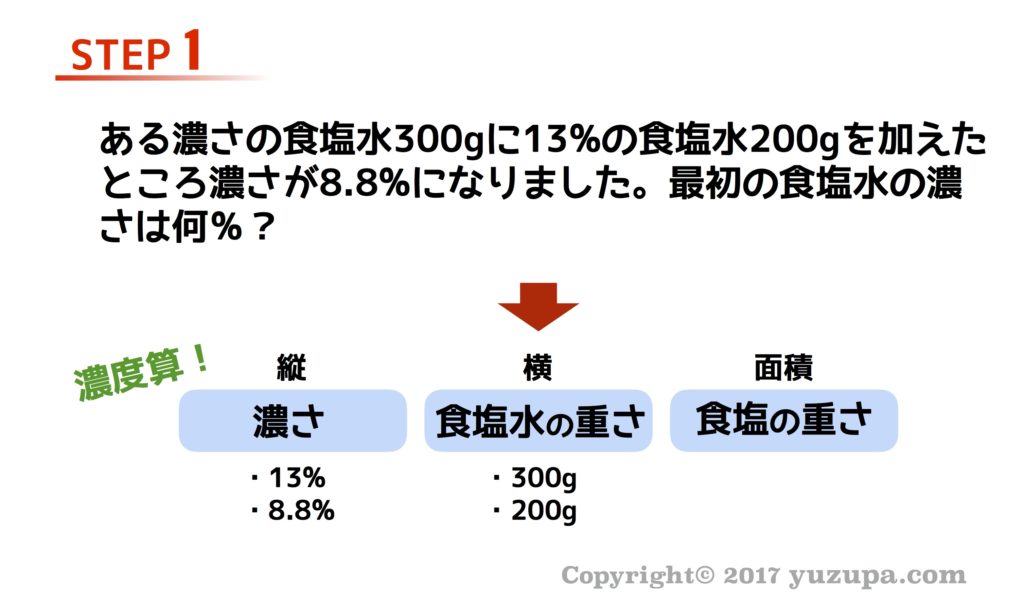
濃度算は平均算と同様、緑枠が登場します。ポイントは同様で、濃い食塩水と薄い食塩水を混ぜたら混ぜたあとの食塩水の濃度は当然、混ぜる前の２つの食塩水の間にきますよね (^_^) 濃度算の場合…濃度は計算しやすいように少数か分数で書きましょう。

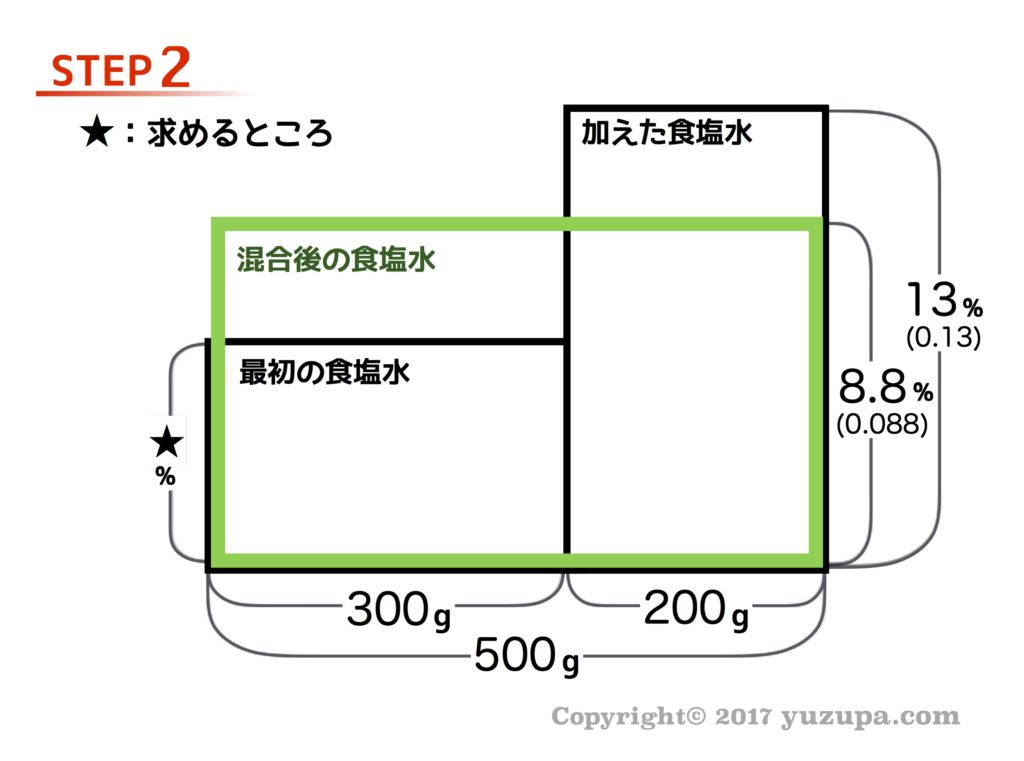
最後は青面積と青面積が同じことに着目して式を立てます。なぜ同じになるか？先ほどの平均算と同じです。混ぜる前と混ぜた後で食塩水に入っている食塩の合計は変わりませんので、でっぱった青い部分の食塩が赤い部分に移動したと考えましょう。

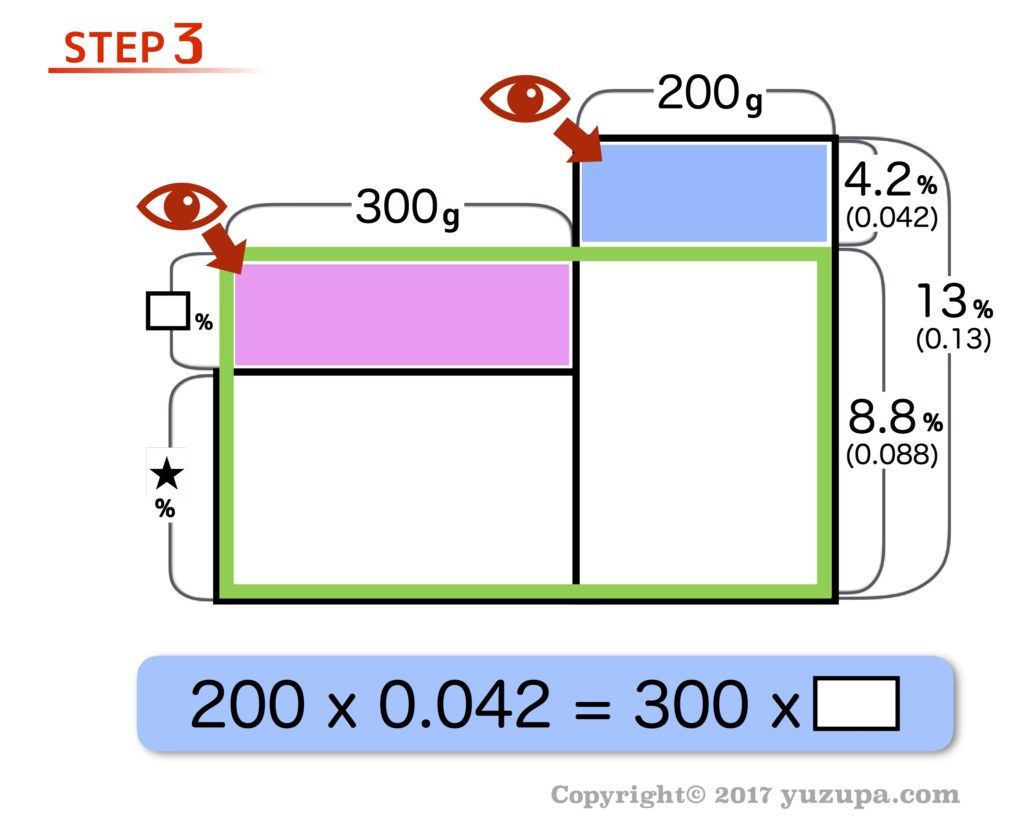
左辺は 8.4 になりますので、□は 8.4を300で割れば出てきます。

図の□は0.028になります。求めるのは★の部分(最初の食塩水の濃度)ですから 0.088-0.028 = 0.6 で 答えは6% になります。

まとめ

方程式がなくても問題がとけてしまう便利な面積図。大事なポイントとやり方を解説してきました。いかがだったでしょうか？

１）面積図で最も重要なポイント
・面積図の適用は 鶴亀算/旅人算/平均算/濃度算の４つ
・もっとも重要なのは 縦と横と面積に割り当てるものを固定する事

２）面積図の解き方３つのステップ
STEP1：縦と横と面積を決める
STEP2：面積図を起こす
STEP3：何かに着目して式を立てる

最後に…、面積図の基本はこの記事の内容で学習できるかと思います。一方、奥の深い中学受験…応用力が必要な問題も存在します。また”穴埋め計算問題”ができる事を前提にした記事になっています。食塩水の濃度問題(いわゆる濃度算)についてのコツをまとめた記事は以下のリンクからどうぞ！

中学受験：食塩水の問題…面積図のコツ

 

印刷用のPDFは以下からダウンロード可能ですd(^_^o)