中学受験：中学受験のキモ “逆比”… 掛け算の関係を探せ！

中学受験のキモとなる比の問題…”かけ算の関係”を探せすところから

こんにちは。かるび勉強部屋 ゆずぱ です。

我が息子は初めて逆比を使う問題を見た瞬間に固まってしまいました(/ _ ; ) 逆比を使う問題は一見すると答えが出せないのではないかと思ってしまうほどヒントが少ないと感じてしまうものが多いんです。中学受験のキモでありながら難問が多い (-_-;)

このような問題を攻略するためには、問題を見た瞬間に “この問題は逆比を使うのかもしれない” と気づくことが重要です。また比を使うんだと気付いても、逆比の関係にあるのか、同じ比の関係にあるのか、混乱してしまうお子様も多いのではないでしょうか？

逆比を使う問題だと気づくために… かけ算の関係をベースに思考することが必須です！

逆比とは何か？

“速さ”と”時間” の関係は逆比

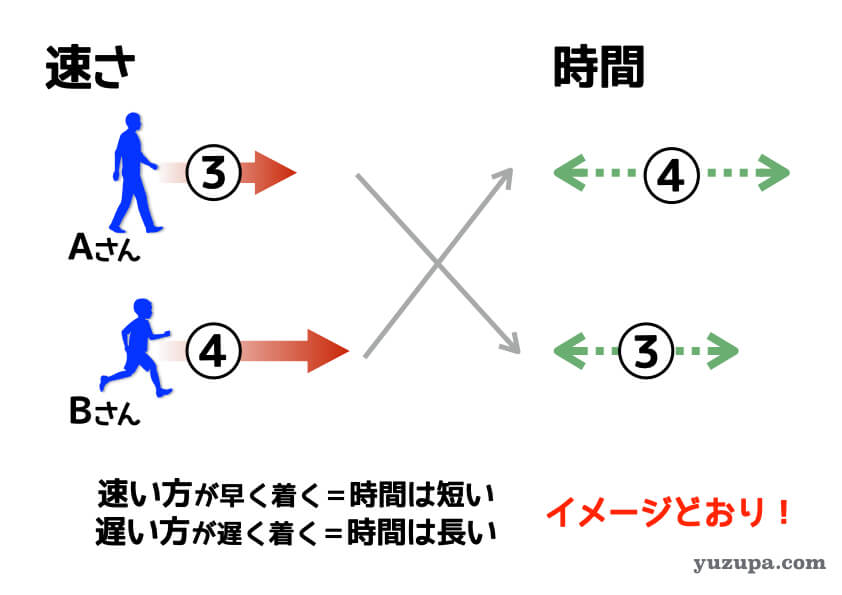
まずは感覚的に “逆比” を身につけましょう。家から学校まで行くのに、ＡさんとＢさんの速さの比が３：４であった場合、所要時間は数字が逆になって４：３になります。速さの比と時間の比は数字が逆になるので逆比と言います。

速い方が所要時間は短く…遅い方が所要時間は長い…イメージ通りですね d(^_^o)

逆比のポイントは”かけ算の関係”

逆比をもっと算数的に理解するために長方形の面積を考えてみましょうd(^_^o)

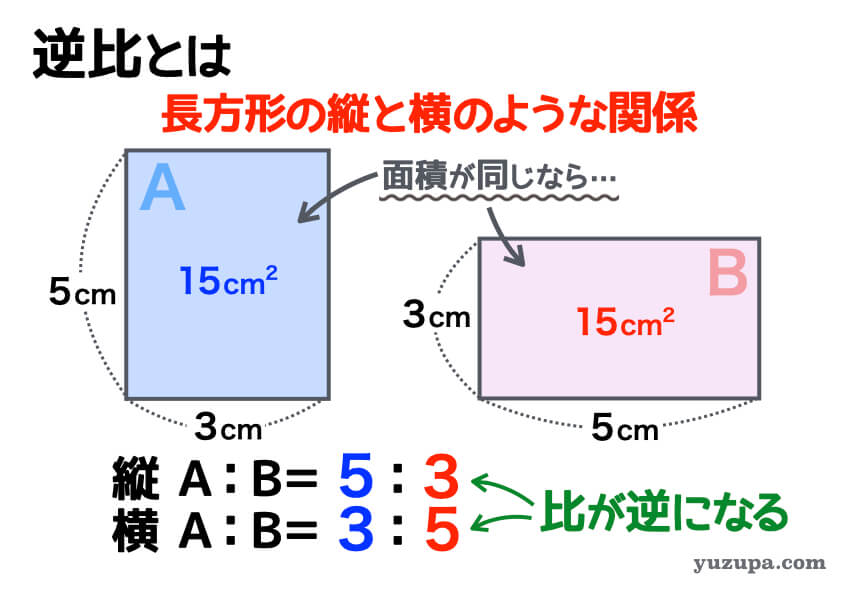
長方形の”縦の長さ”と”横の長さ”と”面積”はかけ算の関係になっています。縦×横＝面積 ですね。そこで面積が同じ長方形のパターンを考えると逆比がどういうものでかるか理解できます_φ(･_･

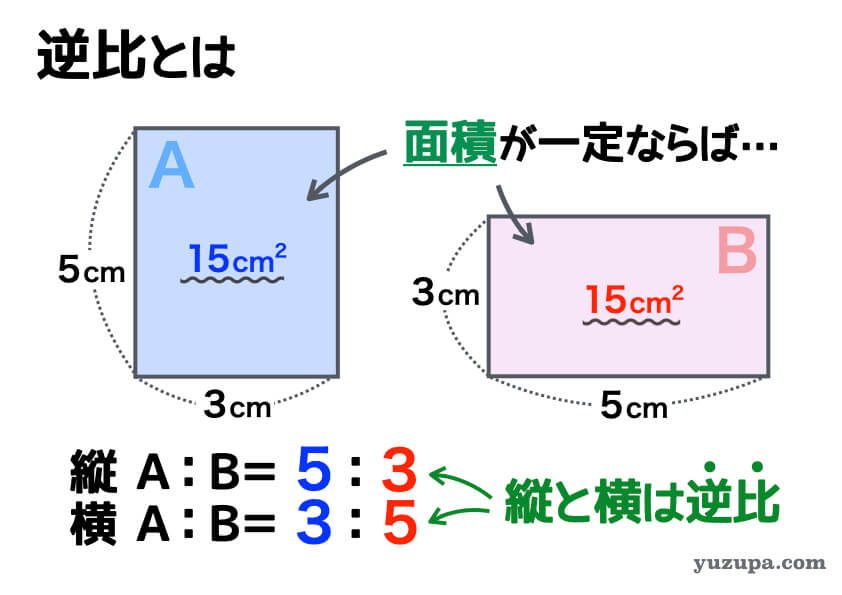
面積が同じであれば
縦の長さと横の長さは逆比の関係になります

大切なのは “面積が一定” であること！

中学受験の算数で全般的に言えることでもありますが、問題文の中には一定であるものがあったりします。一定であるものを見つけたら比が使える と考えましょう！

どんな時に逆比が使えるのか？

まずは例題をご覧ください。

太郎くんは普段、８時に家を出て分速５０ｍで学校に向かい始業時刻の１５分前に到着します。ところが今日は寝坊をしてしまい８時2０分に家を出て、分速８０ｍの早歩きで向かったところ始業時刻の１０分前に到着しました。この学校の始業時刻は何時でしょうか？

ヒントが少ないと感じる問題は注意！

この逆比(比も含む)を使った問題は、一見するとヒントが少なすぎて解けないのではと思ってしまうような問題が多いのが特徴です。何かの”比”とわずかなヒントだけが分かっている状態の問題です。

この問題から条件を拾ってみると…まさに”比”とわずかなヒントだけが分かっている状態です。”比”は速さの比(分速５０mと分速８０mで５：８ですね)。他にわずかなヒントとして普段と今日の所要時間の差がわかりますねd(^_^o)

ヒントが少ないと感じたら、まずは”比”を問題文から探して見ましょう。

比を使うには”一定なもの”が必要

比を見つけたらさっそく比を使いたくなりますが、ただ１つ条件があります。一定なものがあること。この問題の場合は ”道のり”が変わらない ですね。家と学校の道のりはいつも一緒なので d(^_^o)

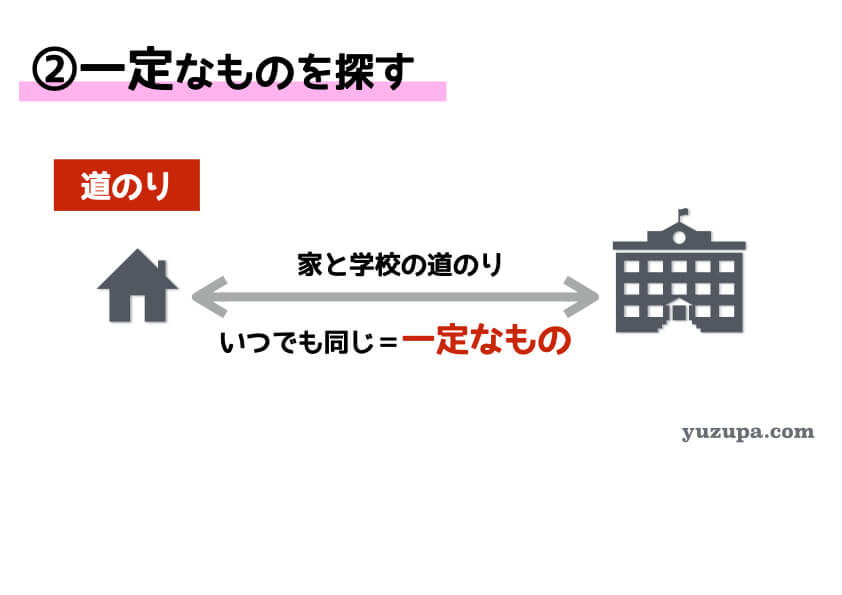
比を使う問題では必ず ”一定なもの” を探しましょう。速さが一定の場合もありますし、時間が一定の場合もあります。

 

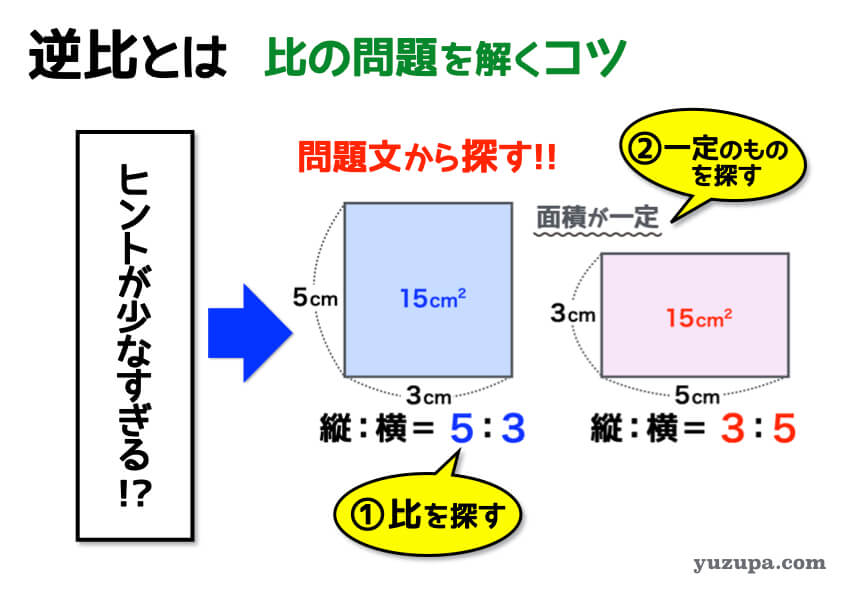
一定のものを見つけたら比の関係が分かる！

比と一定なものが分かったら 面積図で考えてみましょう… ”一定なもの” が分かれば 比の関係が見えてきます。面積が一定だったらもちろん縦と横は”逆比”の関係となります d(^_^o)

 

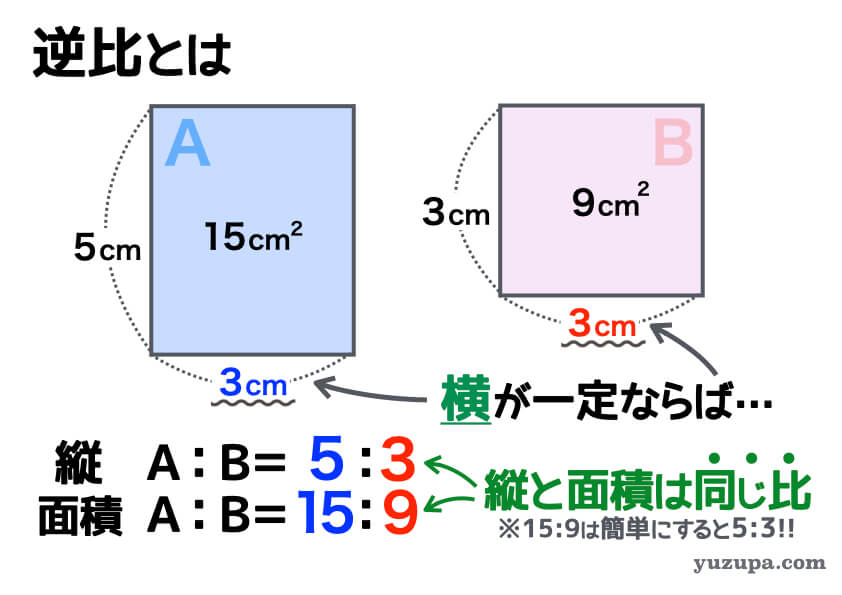
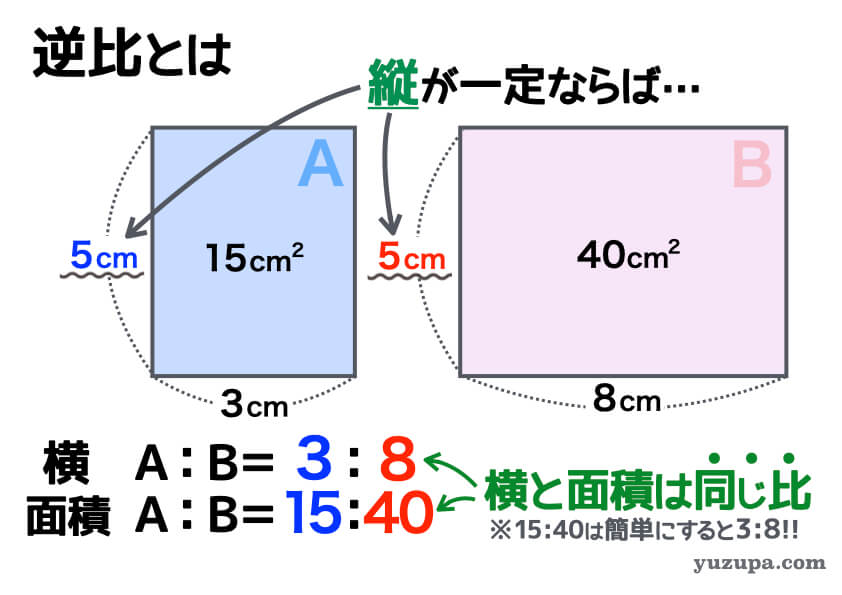
他のものが一定の場合も同様です。横が一定の場合はどうでしょうか？ また、縦が一定の場合はどうでしょうか？

 

速さの問題以外にはどんな分野があるの？

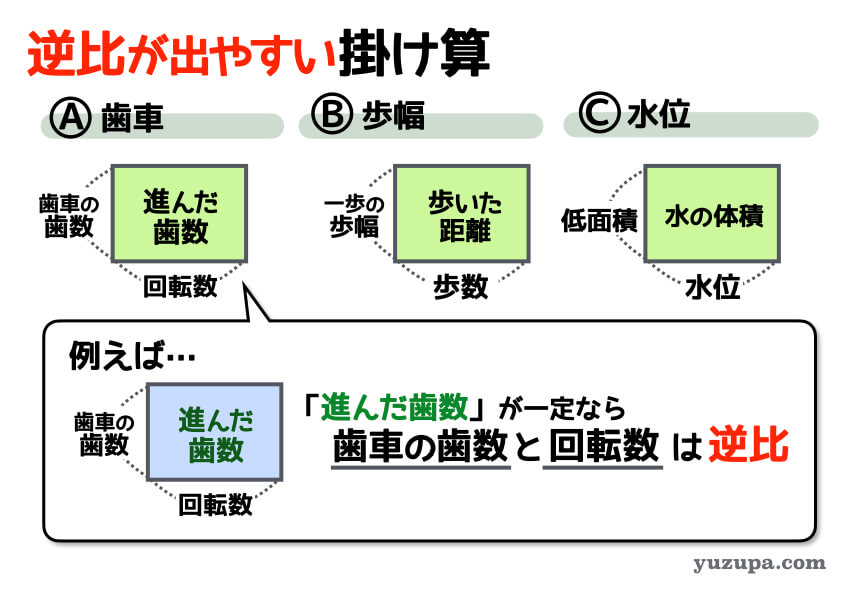
速さの問題以外に、比や逆比が使われるものにはどんなものがあるのでしょうか？ 中学受験でよく出題される “６つのかけ算” を紹介しましょう。かけ算の関係になっているものは全て比や逆比に応用されて出題される可能性があります。

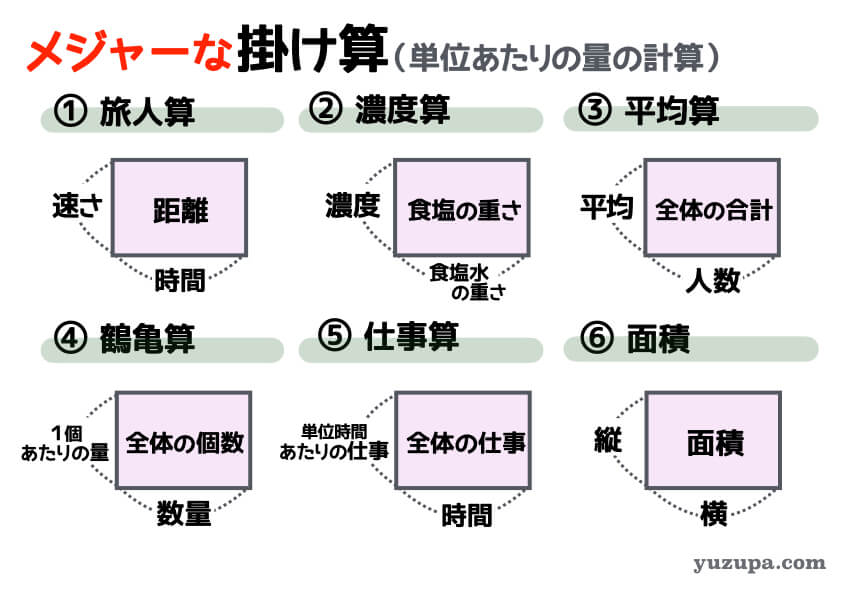
上記のメジャーなかけ算で、問題文から一見ヒントが少なそうでも”何か一定のもの”が読み取れたら比や逆比かもしれないと考えるようにしましょう。マイナーどころだと 歯車の問題や 歩幅の問題、水位の問題があります。

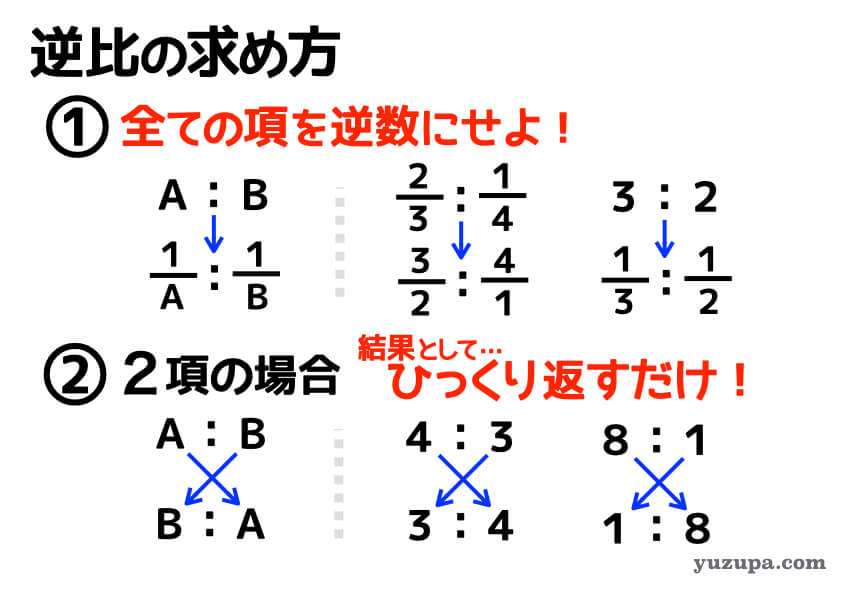
逆比の求め方

ひっくり返すだけではないので注意！

逆比とは数字をひっくり返すだけではありません。正確には各項の逆数をとるという行為です。比の項が３つにある場合は、ひっくり返す事は出来ませんので、各項の逆数を取るようにしましょう！

逆比を使った問題の例

前項で述べてきた通り逆比や比を使う問題は、一見ヒントが少なすぎる印象をを受けます。そんな時は落ち着いて ”比が分かっているもの”、”一定のもの” を問題文から探しましょう！

例題① 旅人算の問題

太郎くんは普段、８時に家を出て分速５０ｍで学校に向かい始業時刻の１５分前に到着します。ところが今日は寝坊をしてしまい８時2０分に家を出て、分速８０ｍの早歩きで向かったところ始業時刻の１０分前に到着しました。この学校の始業時刻は何時でしょうか？

ヒントが少なく単純な計算では解けないと感じたら”比”が無いか、そして”一定のもの”が無いか問題文をよく読んでみましょう。この問題の場合は、普段と寝坊をしてしまった今日の速さの比がわかります。また、学校までの道のりは一定ですね。

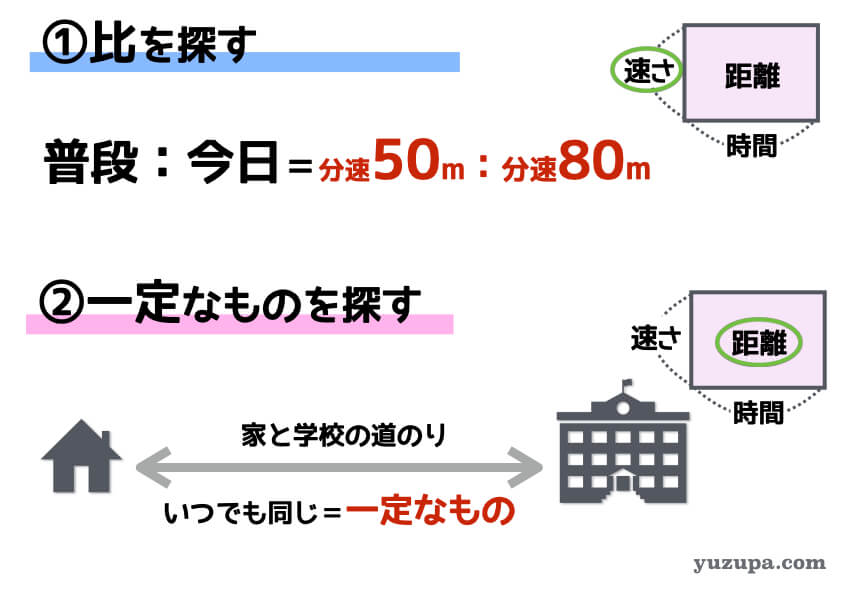
比と一定なものが見つかったら、面積図を使って逆比を使ってみましょう。一定なものである道のりを隠してみると、速さと時間が左右の関係で現れました。比の項の数は２つなので数字をひっくり返すだけで逆比を求めることができます。

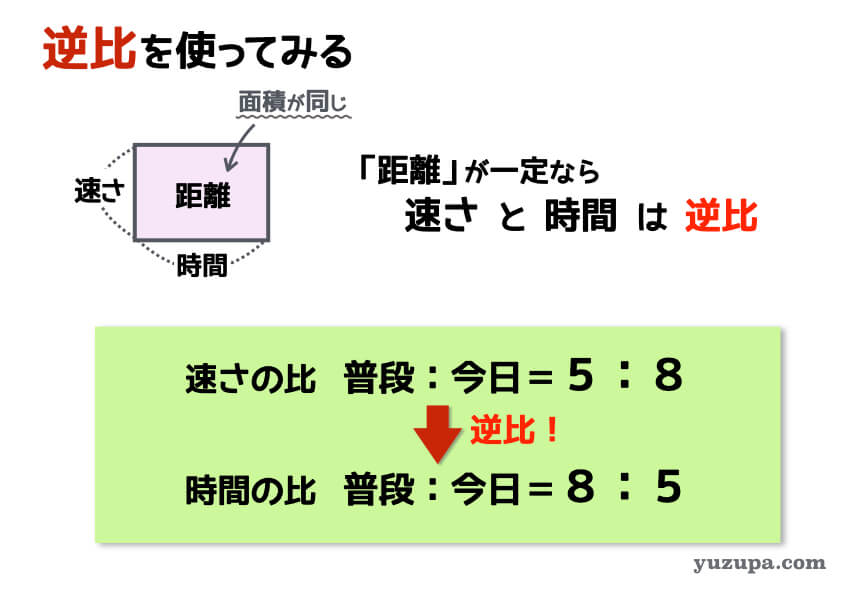
最後は比を使って値を求めていきます。この問題の場合は、線分図を使って求めるのが手っ取り早そうです。線分図に比が出てくる場合は、相当算というテクニックを使います。線分図の中で比と実数字のペアを見つけたら、他の比の部分の数字も計算することができます。

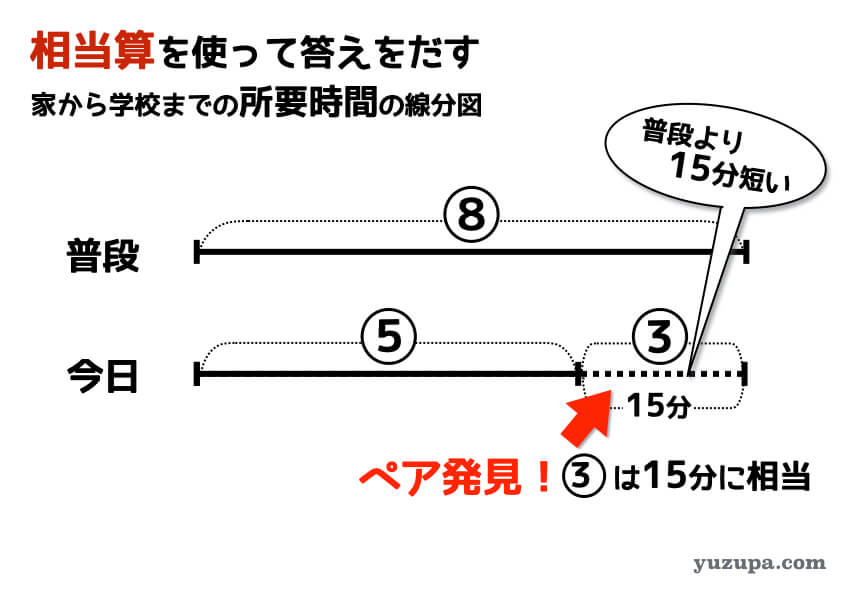
比の③が15分に相当するので、比の①は5分に相当します。そうならば⑧は40分になりますね(´ｰ｀) 太郎くんは普段８時に家を出て４０分掛けて学校に向かい始業の１５分前に着くのです。つまり始業時間は８時５５分となりますねo(^-^)o

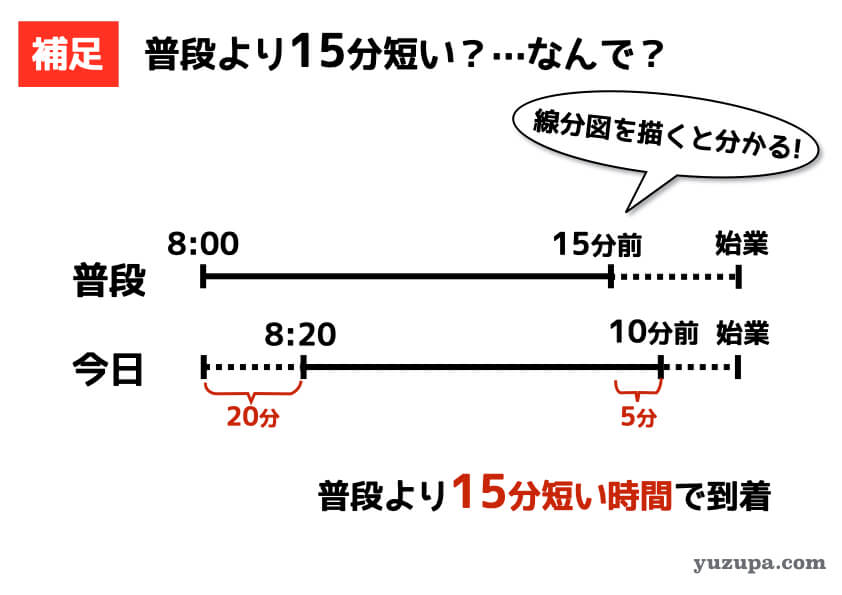
例題② 仕事算の問題

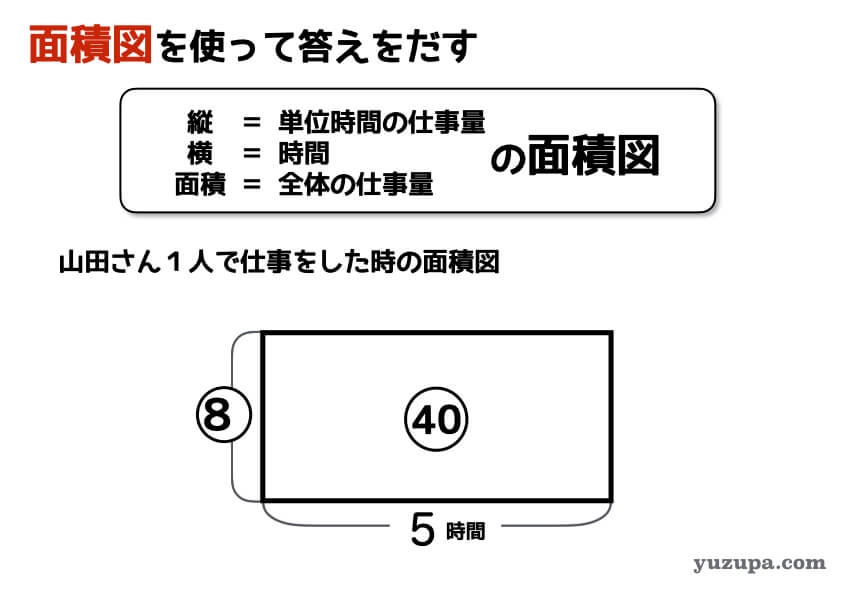
ある仕事を終わらせるのに山田さんは５時間かかり、佐藤さんは８時間かかります。この仕事を朝１０時に山田さんが開始し、途中で佐藤さんに引き継いだところ、佐藤さんがひとりでやるよりも１時間早く終わりました。山田さんが仕事を引き継いだ時刻は何時でしょうか？

例のごとく、ヒントが少ない… 比を探しましょう！

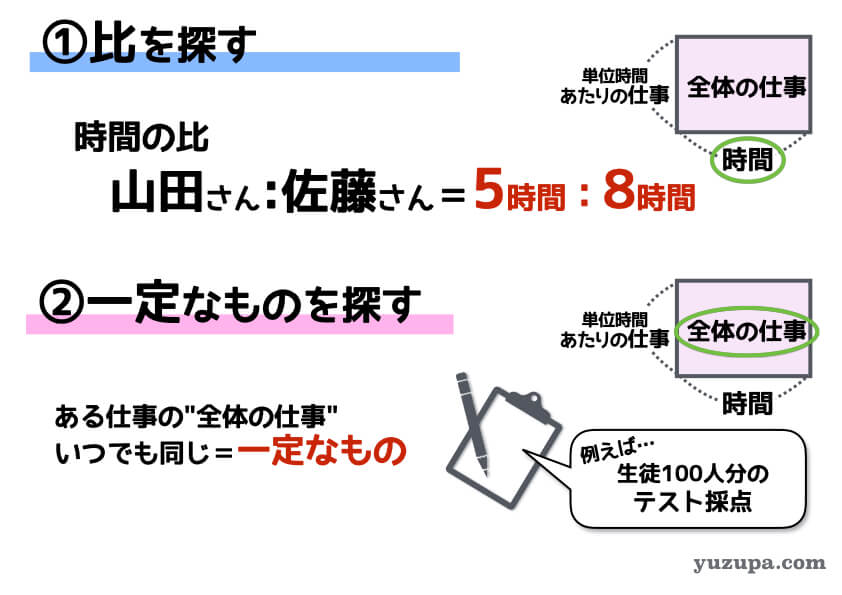
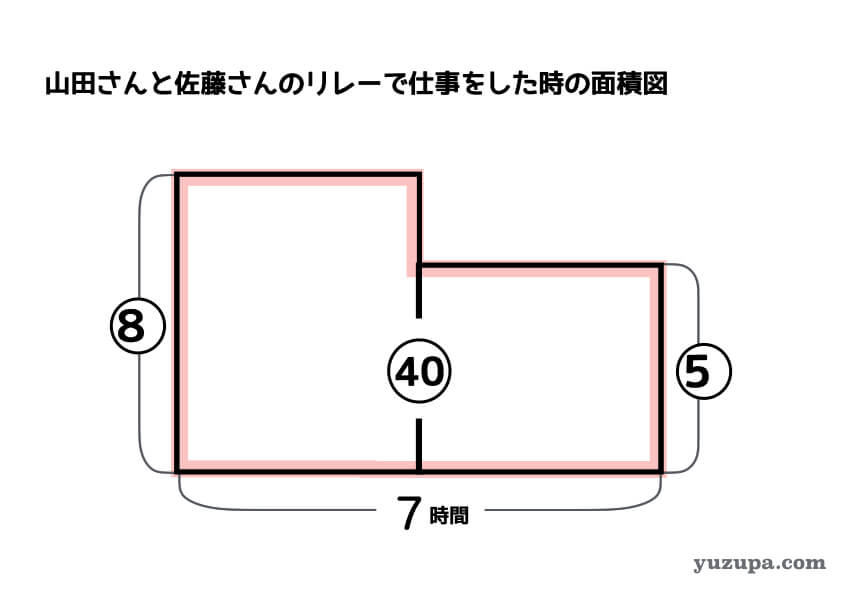
仕事算を解くためのメジャーな道具は面積図です。逆比で求めた山田さんと佐藤さんの単位時間あたりの仕事量の比を使って、面積図を描いてみます。

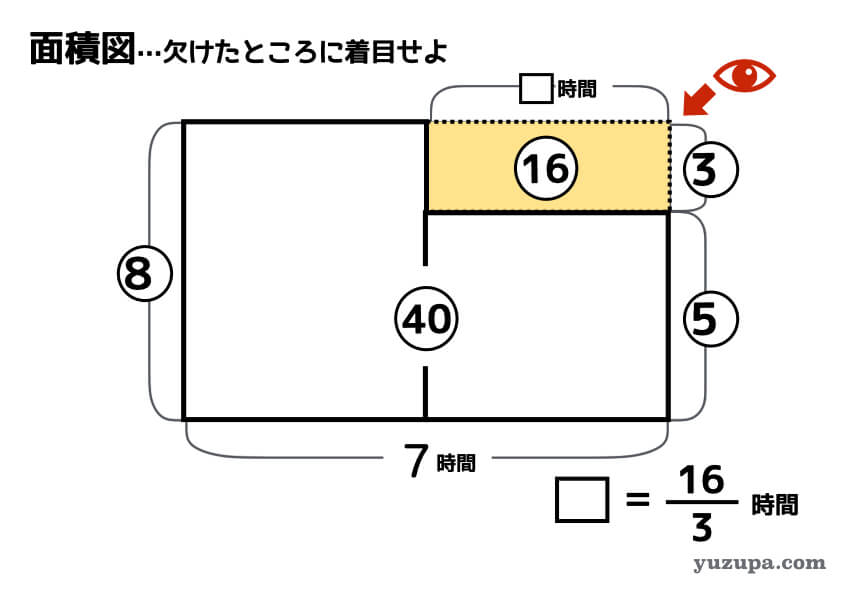
面積図の使い方が不安な方は以下の記事もご参照ください！
中学受験：面積図を使う問題は３ステップで解ける

 

例題③ 水量の問題

ある水槽に２０ｃｍの高さまで水が入っています。この水槽の底面積の３分の２の底面積を持つ棒をこの水槽に沈めたところ、水槽の水位は何ｃｍになるでしょうか？ただし、棒の長さは完全に沈んでしまわない十分な長さがあるものとします。

底面積の具体的な値が分からず… 普通の計算では解けないですね。そんな時は比と一定なものを探しましょう！

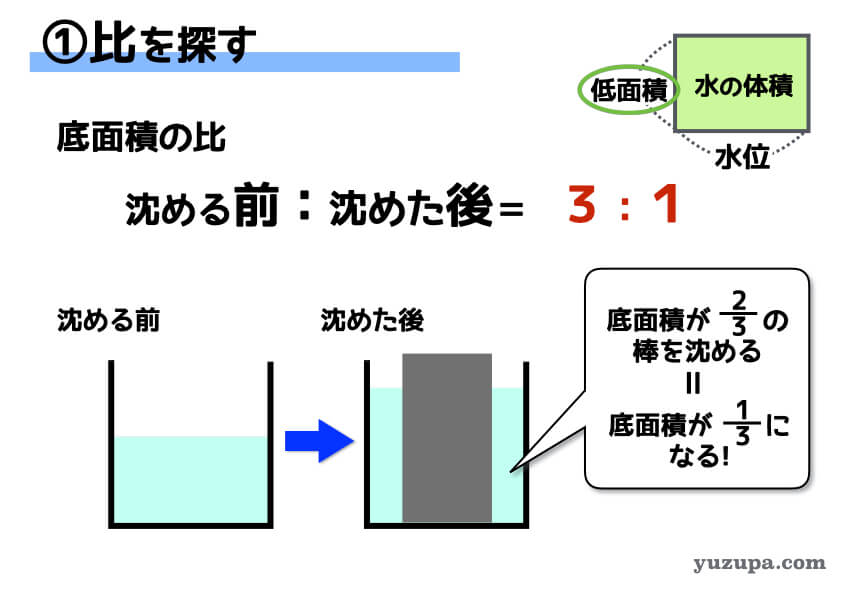
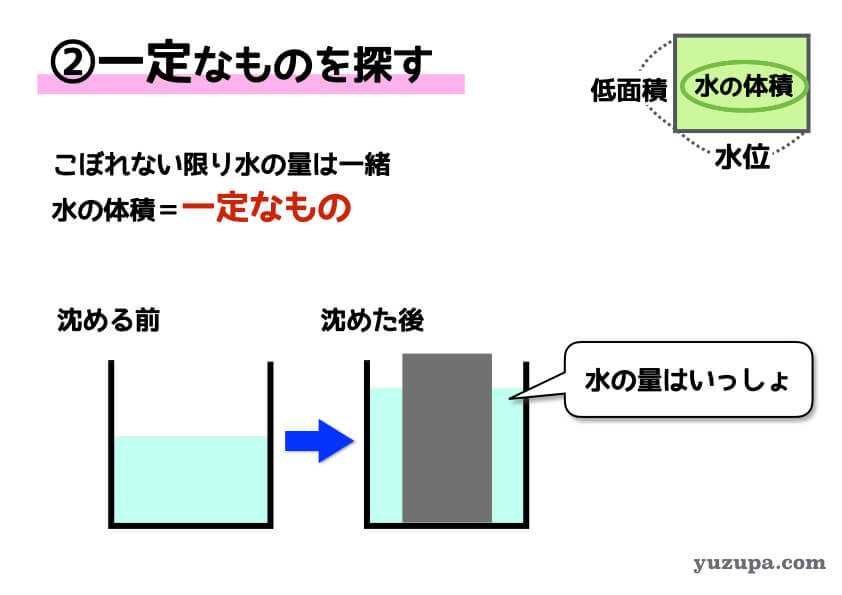
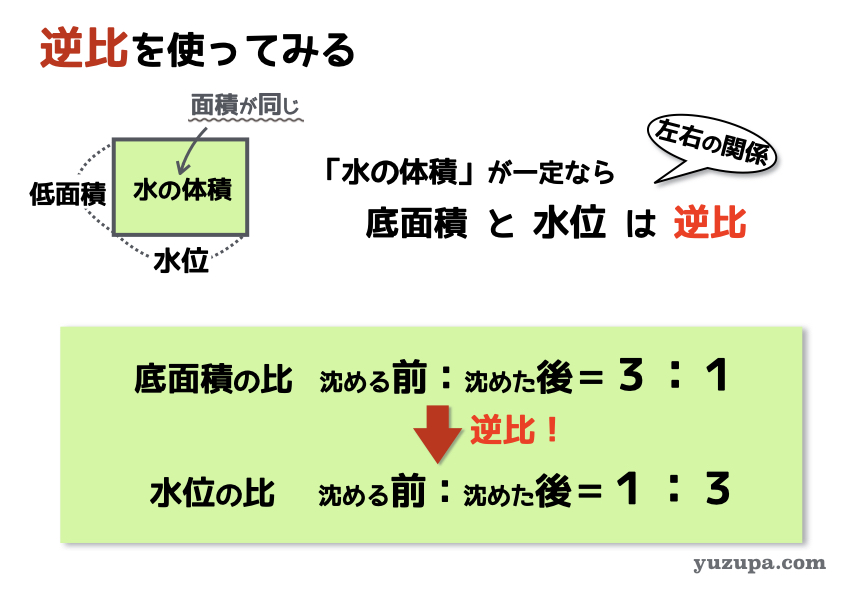
この問題の場合は、比例式がそのまま使えるので比較的難易度は低いですね！

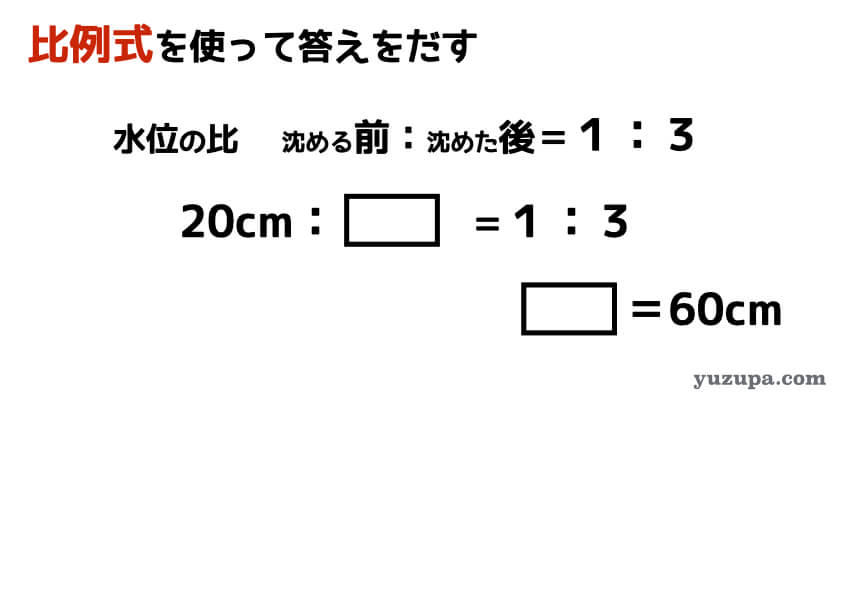
比例の計算に不安のある方は以下の記事もどうぞ！
中学受験：割合と比は”７つ道具”で克服

まとめ

比や逆比を使う問題は、ヒントが少なく一見解けないのではと思うような問題ばかりでした。もっとも重要なのは問題を見た瞬間に”この問題は比か逆比を使うかもしれない”と気づくことです。そのためのポイントをまとめてみると以下のようになります。

１）一見するとヒントが少なすぎる
２）”比”と”一定のもの”を探す
３）思考のベースは円形図！

難問と言われる逆比の問題、少しずつ慣れていきましょう！