中学受験：仕事算とは？分かりにくい”仕事”の概念からスッキリ理解

時間の経過で変化するモノはすべて”仕事”…同じ考え方で解く事ができる

こんにちは。かるび勉強部屋 ゆずぱ です。

中学受験の世界には ”仕事算” という単元があります… 小学生にとって最初に立ちはだかるのが “そもそも仕事ってナニモノ”という真っ当なギモン…　小学生はまずココからつまづきます(-_-;)

“仕事”の正体をシンプルに表現するならば…

時間と共に変化するモノなら
ぜんぶ ”仕事” です!!

１日あたり５００個の製品を作る工場も…１時間に５Ｌの水を汲み上げるポンプも…１分間に宿題を５問さばく小学生も…すべて”仕事”として同じ考え方で解いちゃいます∑(ﾟДﾟ)

 

仕事算で大切な”３つのポイント”

ポイント① 時間と共に変化するなら”仕事”

冒頭でご紹介したとおり、小学生が最初につまづくのは”仕事ってなんぞや？”というしごく真っ当なギモン。

シンプルに表現するならば、時間の経過と共に変化するものであれば全て ”仕事” ですd(^_^o)

水を汲み上げるポンプ…１時間あたり５リットルの水を汲み上げています。水を汲み上げるという”仕事”をしています。

牧草を食べ続ける牛…１時間あたり１平方メートルの草を食べてしまいます。これも草を食べるという”仕事”をしています。

モノを作る工場も、人を運ぶ電車も、チケットを売る販売員もみーんな”仕事” をしているワケです(^_^;)

共通点はたった１つ…
時間の経過とともに変化しているということ！

 

ポイント② 単位時間あたりとは

時間の経過と共に変化するモノを考える時…大人であれば当然 ”単位時間あたり” の変化量を意識 しますよね？

小学生はこの
単位時間あたりの変化量 が分からない

なにごとも基本が大切。”単位時間あたり”というものをシッカリとおさえることも大事ですd(^_^o) 

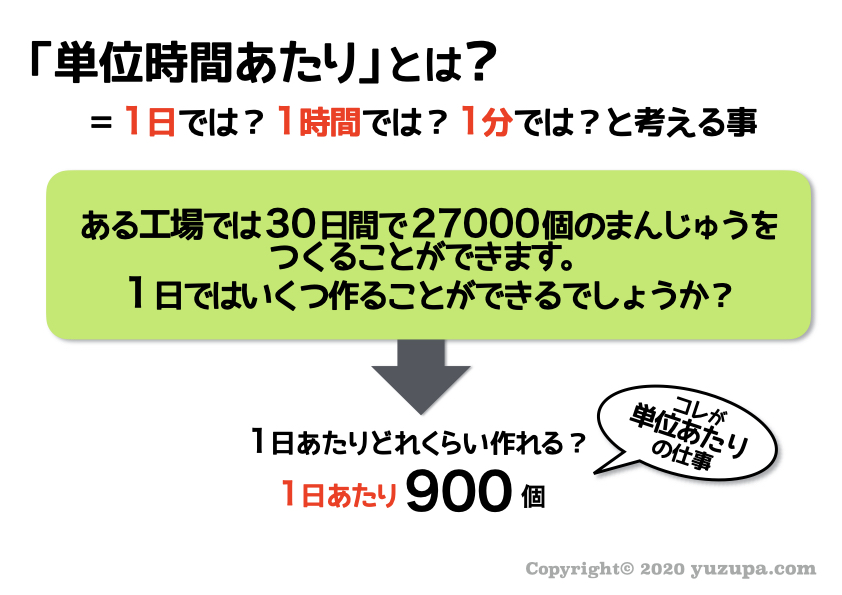
といっても超シンプルです。

単純化して表現するならば ”１日では？１時間では？１分では？と考えること” ですねd(^_^o)

 

ポイント③ 仕事算の本質は割合の公式

最後のポイントは ”仕事算の本質” ですd(^_^o)

いわゆる仕事算の公式というヤツです。速さの公式と同じように円形の図でおさえると良い でしょうd(^_^o) 

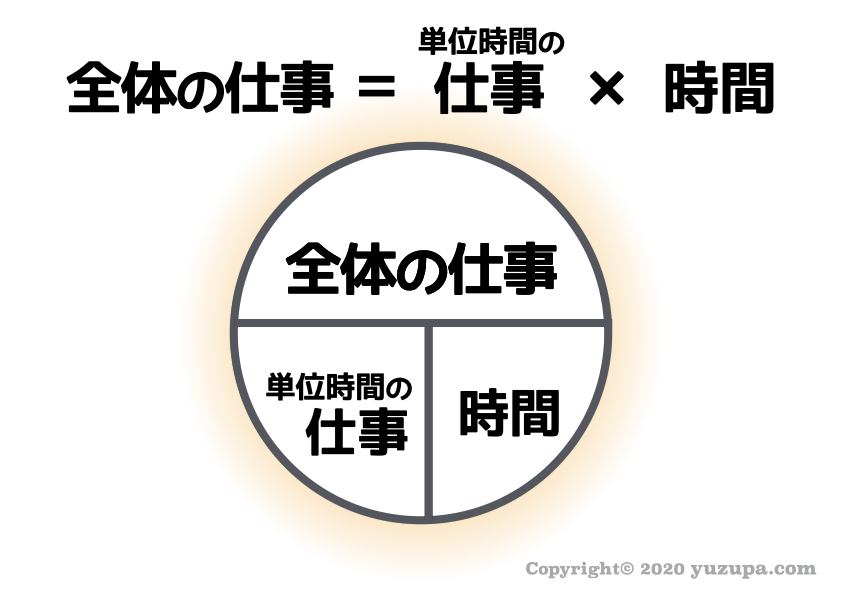
この公式を自在に使うことこそが仕事算の本質　です。

試しにさきほどのまんじゅう工場が１週間に何個のまんじゅうを作れるか計算をしてみましょう_φ(･_･

１日あたり９００個のまんじゅうを作れる工場ですので、７日間であれば６３００個のまんじゅうを作ることができます。

 

 

仕事算を解くための３ステップ

仕事算を理解するための３つのポイントをおさえることができましたでしょうか？ あとは問題を解くための練習のみです…。

練習といっても最初はどう解けばよいか分からない… ベースとなる３つのステップで考えるのがオススメ ですd(^_^o) 

まずは、問題文の中から全体の仕事量を見つけるところから始めます。具体的なモノがなければとりあえず①と置きます。

次は、単位時間あたりの仕事量を考えます。ポイントは“すべての”単位時間あたりの仕事量を準備しておくことです。

最後は、問題が求めるものに対して仕事算の公式を使う！

さっそく具体的な問題を通して、この３つのステップを体得していきましょう d(^_^o)

 

仕事算を実際に解いてみる

① もっともシンプルな仕事算

工場の機械が行う ”まんじゅうをつくる仕事” の問題 です。さっそく３つのステップを見てみましょうd(^_^o)

問題文をよく読みながら全体の仕事量を探します。この問題では３０日間に機械が行う具体的な仕事量が書かれています ね。

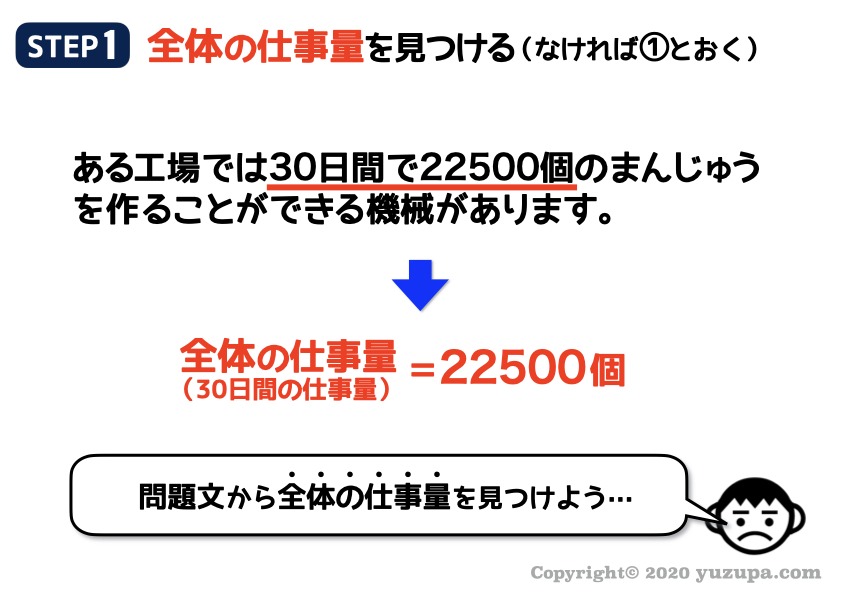
３０日間で２２５００個のまんじゅうです_φ(･_･

次は単位時間あたりの仕事を考えます。この問題の場合は”１日あたり”の仕事量 を求めてみましょう。

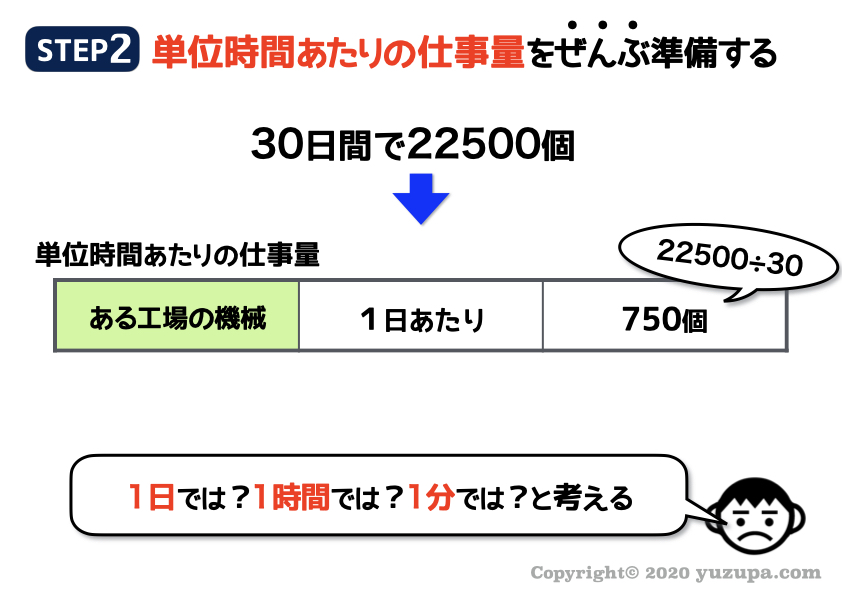
この工場の機械は１日あたり７５０個のまんじゅうを作るという仕事を行うということが分かりましたね！

最後は問題が求める１２日間の仕事量を求めるために、仕事算の本質である公式を駆使しますd(^_^o)

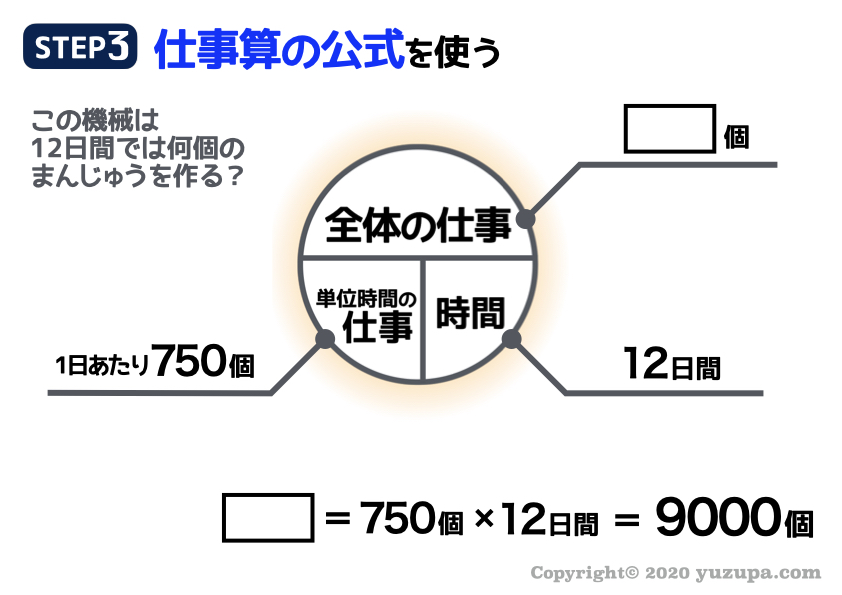
落ち着いて 仕事算の円形図を埋めていけば答えを導くことができます。答えは９０００個ですね_φ(･_･

 

② 全体の仕事量が分からない

この問題は “プールに貯められた水を汲み上げる仕事” です。

先ほどの問題は全体の仕事量が ”まんじゅうの個数” という形で具体的に見えていたのですが…今度は見えません∑(ﾟДﾟ)

仕事算の問題のほとんどが、この問題のように 仕事の具体的な姿が見えない形で出題 されます…d(^_^o)

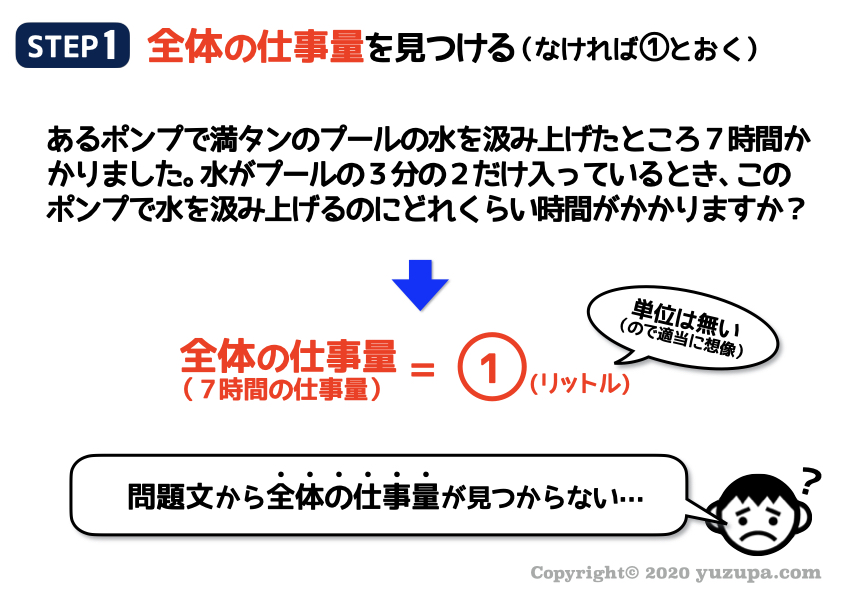
プールの水は何リットルなのでしょうか？具体的な仕事量が見えない…そんな時はどうすればよいでしょう？

比を使うんですd(^_^o)

全体の仕事量を①と置きましょう。単位は特にありません。なので適当に想像しておけばＯＫです(^_^;)

次は単位時間あたりの仕事量を考えてみましょう。

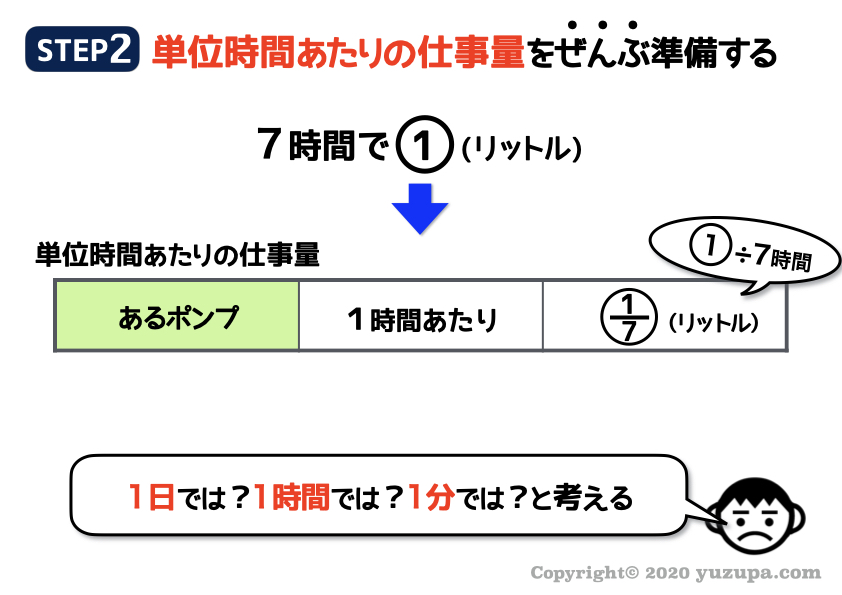
仕事量に 具体的な数字がなく比であっても考え方は同じ です。１時間あたりの仕事量を考えてみましょう。

最後は仕事算の公式です。

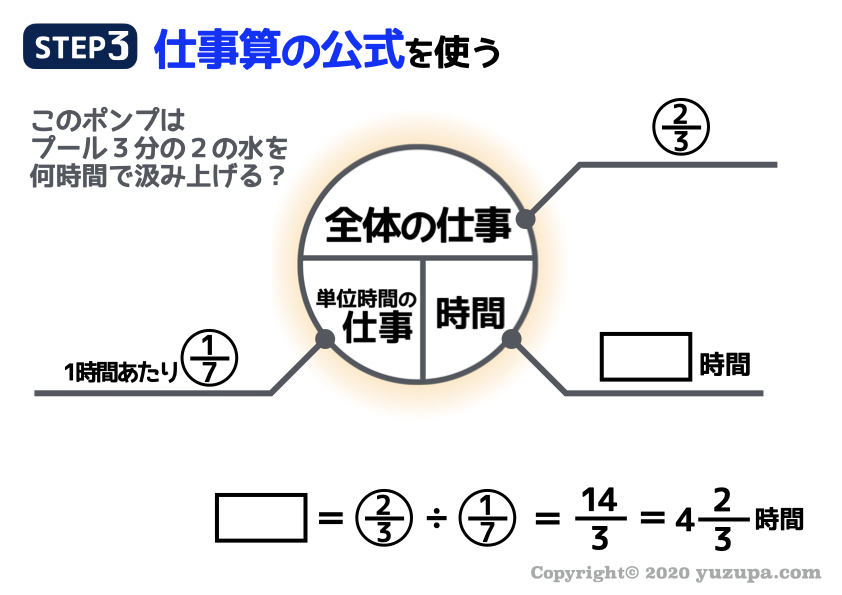
プールに３分の２の水があるので全体の仕事量は３分の２ですね。ポンプの１時間あたりの仕事は７分の１です。

あとは計算をすれば答えが出せますd(^_^o)

 

③ ふたりで協力して仕事をこなす

今度は学校でよくみられる ”校庭に白線を引くという仕事” です(^_^;) 太郎君と次郎君という２人の登場人物がいます。

さっそく全体の仕事量から探ってみましょう。

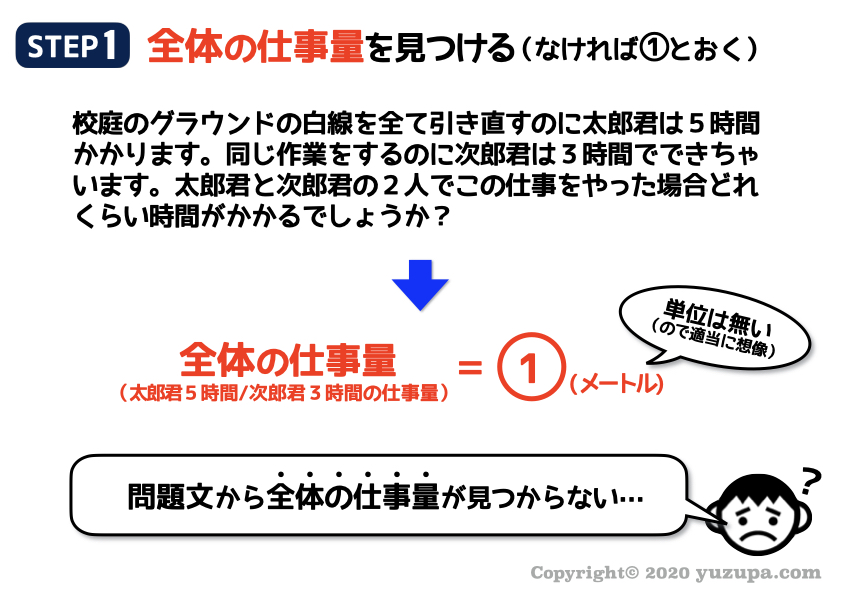
やっぱり具体的な仕事量が書かれていません。白線の長さを想像して…”メートル”をイメージ_φ(･_･

次は１時間あたりの仕事量を考えるのですが、ポイントは”ぜんぶ”という点。１つでは無いということですd(^_^o)

ここでは太郎君と次郎君では仕事をさばく速さが違うので、太郎君と次郎君のそれれぞれで考えます。

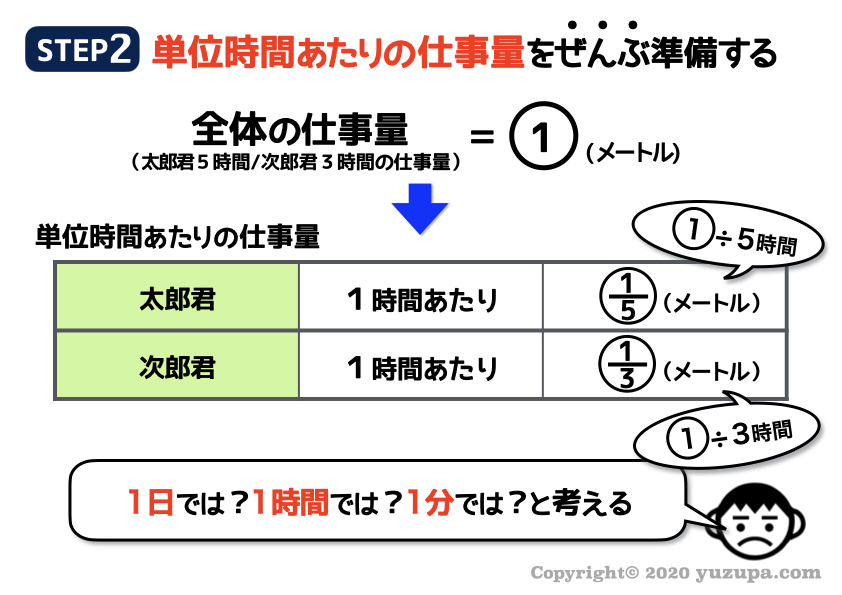
さて、単位時間あたりの仕事は太郎分と次郎分だけで良いでしょうか？ もうひとつ考える必要がありますd(^_^o)

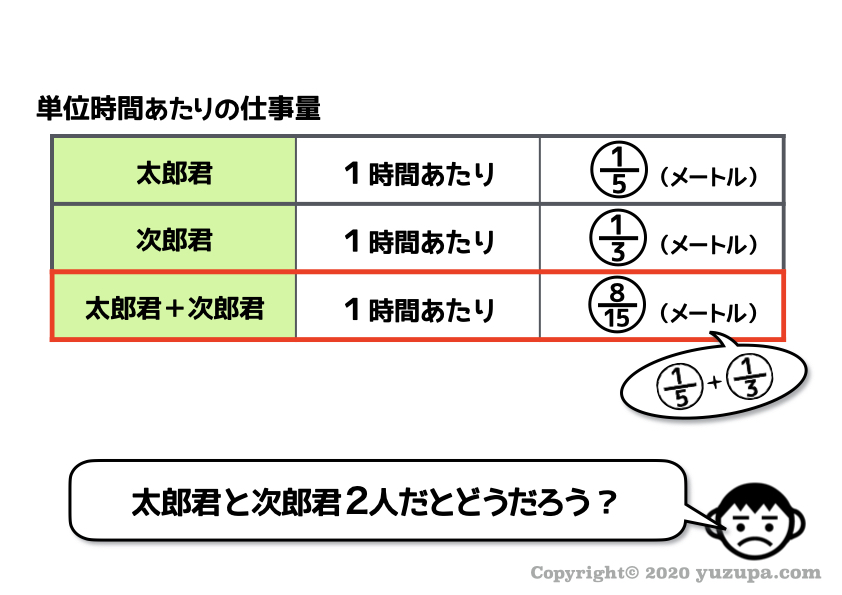
太郎君と次郎君のふたりで仕事をやった時の １時間あたりの仕事量もいっしょに考えておく必要があります。

出し方は簡単ですd(^_^o)

太郎君が１時間でできる仕事量と、次郎君が１時間でできる仕事量を足してあげればよい だけですね。

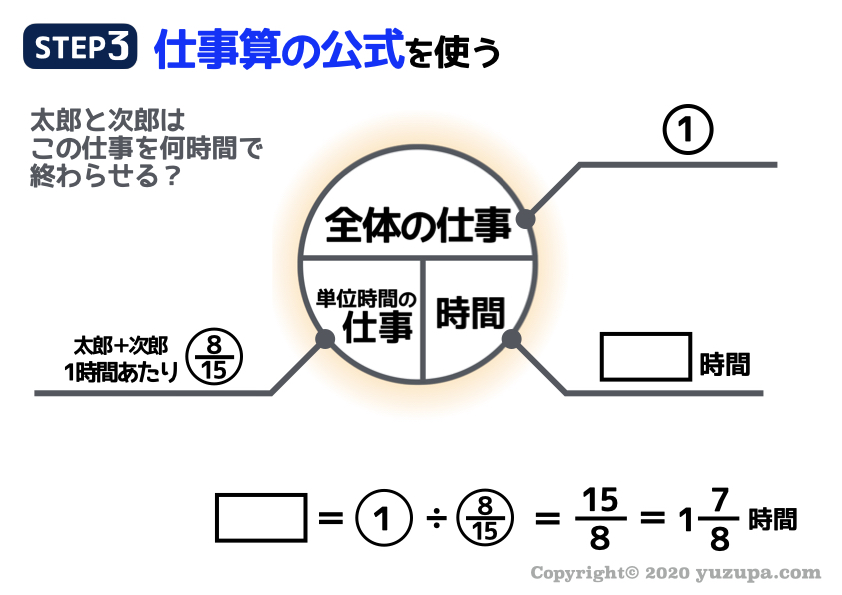
最後は仕事算の公式です。分数の計算を間違えないようにしましょうd(^_^o) 

 

 

④ ふたりで協力して仕事をこなす

同じ学校に存在する仕事ですが、今度は先生達の仕事 “テストの丸つけをする仕事” ですd(^_^o)

相変わらず具体的な仕事量は書かれていません…。単位も適当に想像しながら比である①とおきましょうd(^_^o)

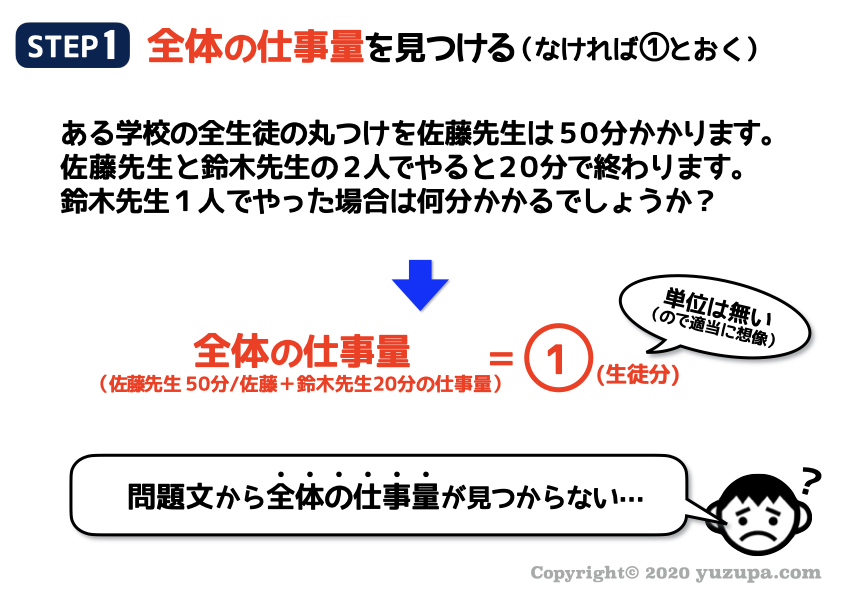
次は１分間あたりの仕事量を考えますが、佐藤先生、鈴木先生、佐藤＋鈴木先生 の３つのパターンですね_φ(･_･

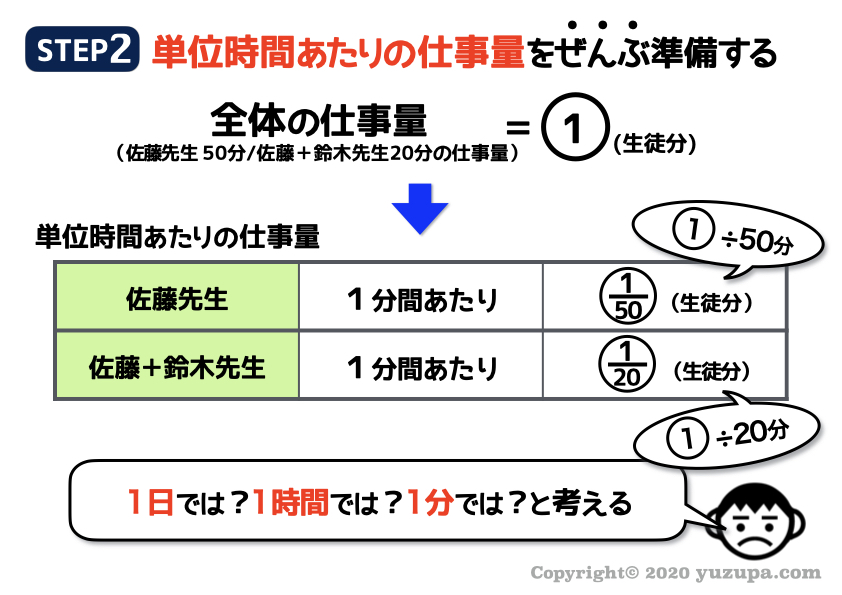
この問題の場合は、鈴木先生ひとりで仕事をした時の仕事量を求めるために引き算を使いますd(^_^o)

１分間あたりの仕事量が出そろったら、仕事算の公式を駆使して答えを出しましょうd(^_^o)

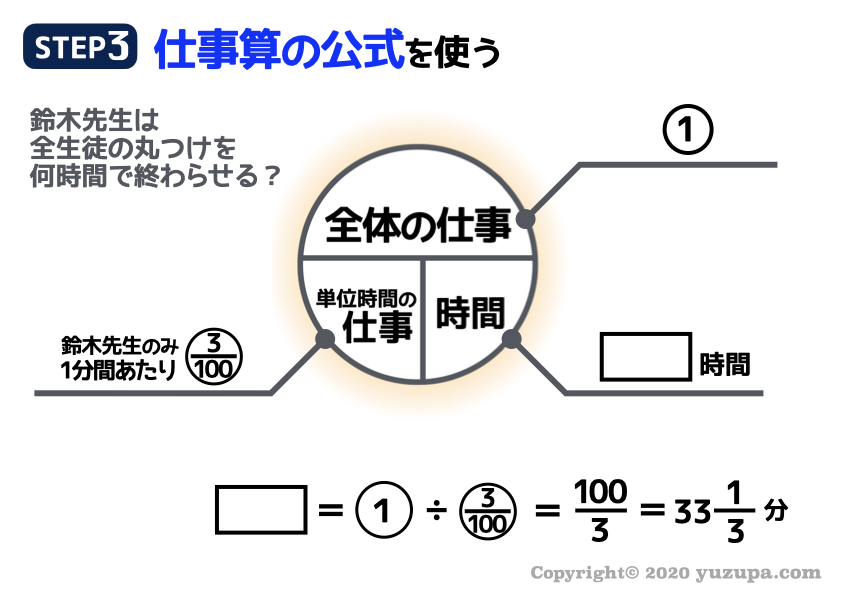
答えは分数になりますので注意をしましょうd(^_^o)

 

⑤ 途中で仕事の分担が変わる

最後はボブとアリスが ”何らかの仕事” をしています。もはやどんな仕事かの想像すらできません (-_-;)

気にせずさっそく全体の仕事量をさがしましょう！

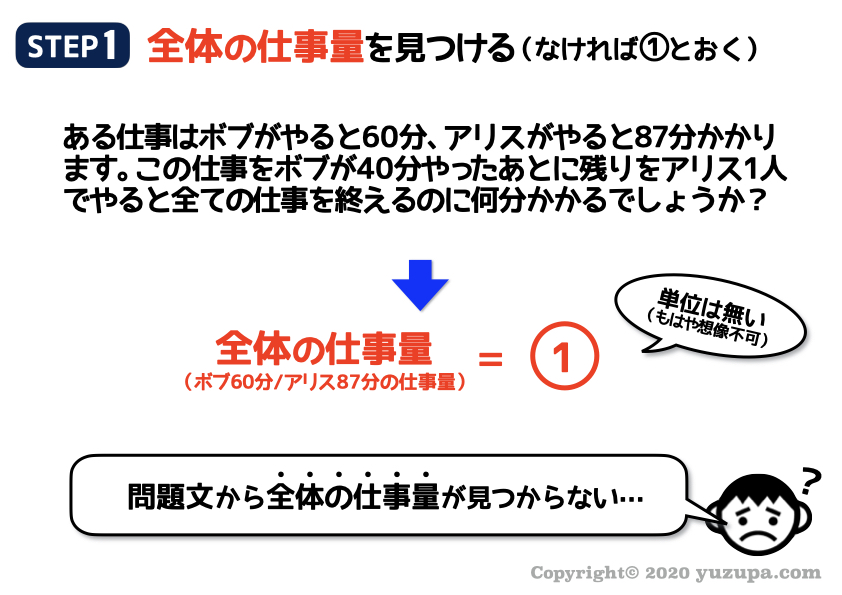
もちろん具体的な仕事量はありませんので、比である①とおきましょう。適当に想像しても構いません(^_^;)

次は単位時間あたりの仕事量を考えましょう。

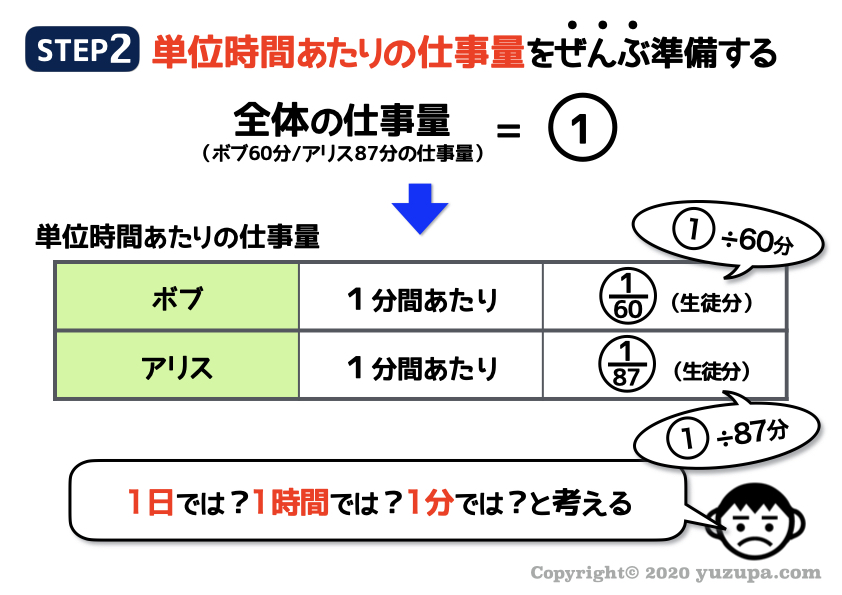
いつもどおりボブとアリスのそれぞれで１分間あたりの仕事量を準備します_φ(･_･

最後は仕事算の公式で仕上げに入ります。

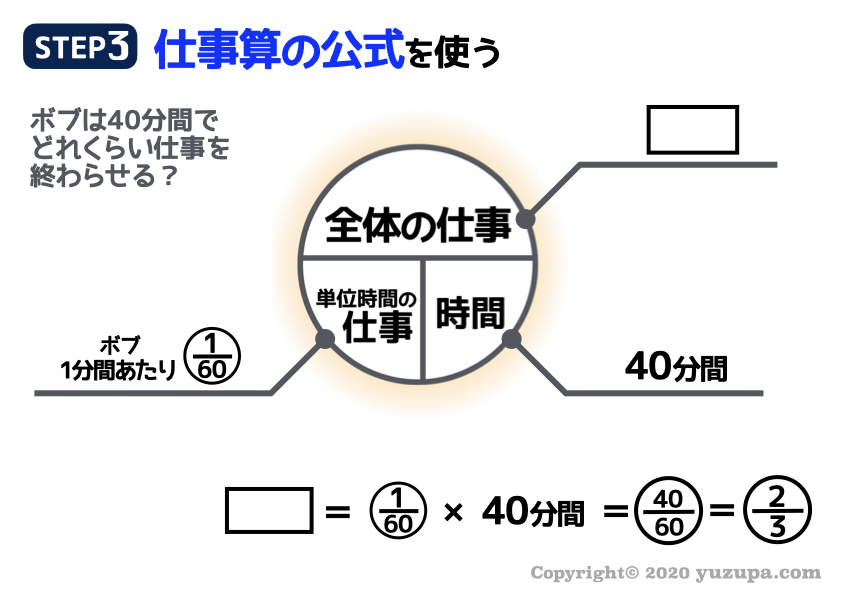
まず前半はボブが４０分の仕事を先に行うので、その部分で仕事の公式を当てはめてみます。ボブの仕事が終わった時点で仕事は３分の２が終わっていることが分かりますd(^_^o)

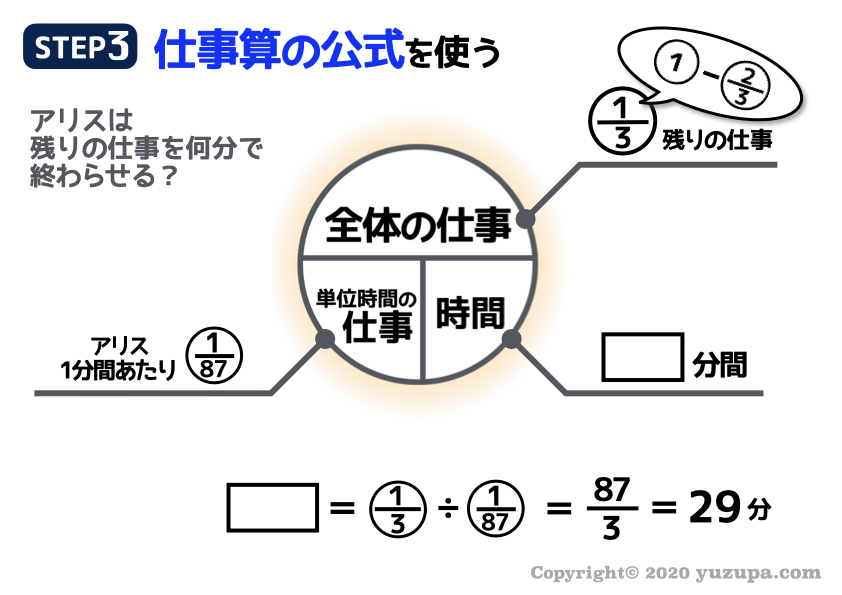
そして後半はアリスです。

ボブの仕事が終わった時点で、３分の２の仕事が終わっていますので残りの仕事は３分の１ですね_φ(･_･

後半のアリスの仕事は２９分かかる事がわかります。

答えは ボブの４０分とアリスの２９分を合わせて６９分となりますね_φ(･_･

 

 

以上が仕事算の５つの例題でしたd(^_^o) 

最後に仕事算について注意事項が… 実は今回紹介したのはシンプルな仕事算。いくつかバリエーションがあるのです…

 

仕事算のバリエーション

仕事を扱う問題の全体像

今回は ”仕事算” について３つのポイントと問題を解く時にベースとなる３ステップをご紹介しました。

が…仕事算って他にもあるんです ∑(ﾟДﾟ) 

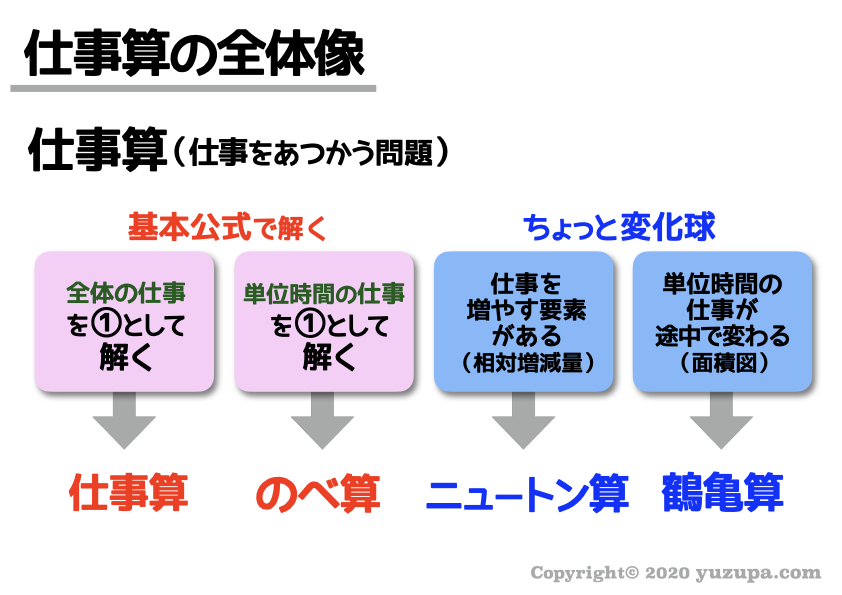
全体の仕事を①と置いて解いていくのが、今回解説をした最もシンプルな仕事算ですd(^_^o)

一方、単位時間あたりの仕事を①と考えて、全体の仕事を計算する解法を”のべ算” といいます。

さらには、仕事を邪魔する要素(仕事を増やす邪魔者)がある問題はニュートン算という解法があります。

さらには、単位時間あたりの仕事量がずっと同じではなく、途中で変わっちゃう問題まで出てきます(-_-;)

でも仕事算の本質は全て同じです！

 

今回ご紹介した３つのポイントを理解していれば、スンナリと理解できることでしょうd(^_^o)

参考：ニュートン算とは？ “３つの基本” だけで簡単に解ける！

 

まとめ

今回は ”仕事” という概念が小学生の理解をさまたげる仕事算について解説をしました d(^_^o)

まず大事なこと。仕事とはナニモノなのかという事。

時間と共に変化するモノなら
ぜんぶ ”仕事”!!

あとは…落ち着いて 全体の仕事量、単位時間あたりの仕事量を考え、最後に仕事算の公式を駆使することで多くの問題を解く事ができますd(^_^o)