中学受験：通過算は”走った距離”さえ分かれば 単なる基礎問題

通過算のポイントは”走った距離”…とにかく図を書いて”走った距離”を正確に把握

イキナリですが…まずは通過算の例題をd(^_^o)

長さ200mの列車が1.6kmのトンネルを通過するのに90秒掛かりました。この列車の速さは毎時何kmでしょうか？

これが通過算と呼ばれる問題の典型的な例です。その正体は速さの公式を使う基礎問題に他なりません…では通常の基礎問題と何が違うのか？　それは 問題文に”走った距離”が素直に書かれていないだけ ですd(^_^o)

つまり “走った距離” が問題文から読み取れるかがポイントとなります。”読み取る” という言葉を使いましたが… 通過算の唯一の攻略法は “図を書いて走った距離を把握する” です。とにかく図を書きましょう！

通過算はとにかく図を書くべし

通過算は”走った距離”の把握がポイント

通過算…本当に基礎問題なんですが “走った距離” が素直じゃありません(^_^;) 例えば冒頭の例題の走った距離はいくらでしょうか？1.6kmのトンネルを通過したのだから走った距離も1.6kmと考えてしまったらアウトです。

公式的なもので考えるのもキケンです。脳内で考えるのはやめてとにかく図を書きましょう！

始めと終わりの状態を書けば距離がわかる

ではさっそく図を書いてみましょう。

図を書くときのポイントは２つ…１つ目は “通過する”の意味を正しく理解する事です。”通過する”とは列車の先頭がトンネルに入った瞬間から列車のお尻がトンネルから出た瞬間までを意味します。

２つ目は “始めの状態”と”終わりの状態”を書く事です。この問題であれば “列車の先頭がトンネルに入った瞬間の図” と “列車のおしりがトンネルから出た瞬間の図” ですね d(^_^o)

注意：”通過する”以外にもいくつかバリエーションがあるので後ほど紹介します

長さ200mの列車が1.6kmのトンネルを通過するのに90秒掛かりました。この列車の速さは毎時何kmでしょうか？

“走った距離”の５つのパターン

走った距離を求めるためのいくつかのパターンがありますのでご紹介しますd(^_^o)

１）電柱や人を “通過する”

電柱や人とは…橋やトンネルと違い長さが無いものを意味します。電柱や人で無くても 長さのない１点 を通過する問題であれば、同様に考える事ができますね。

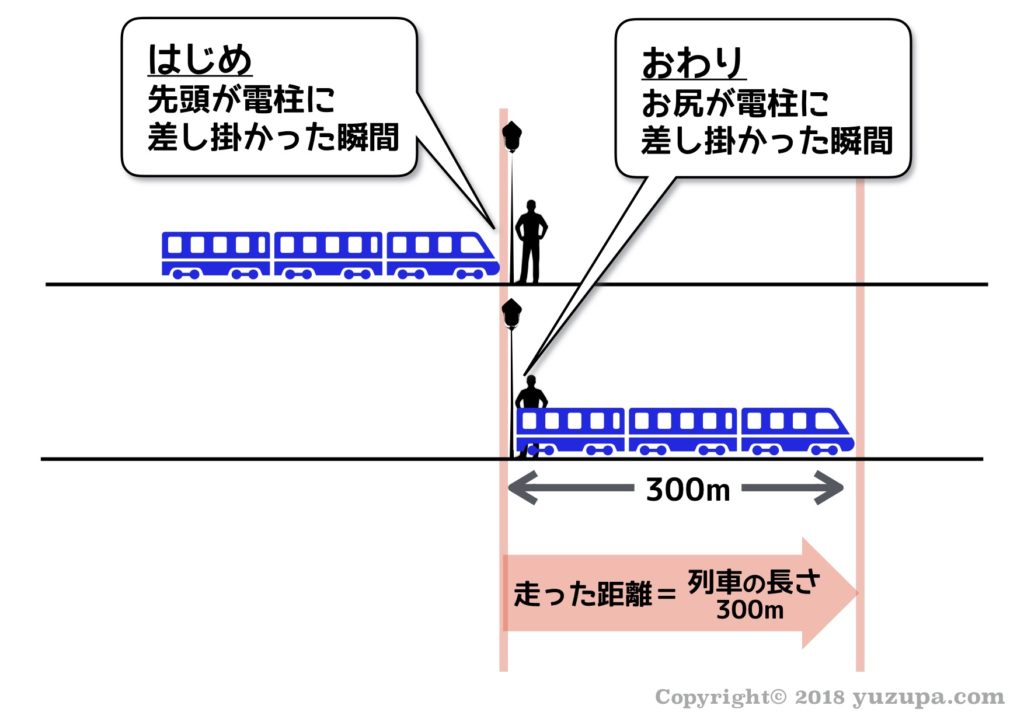
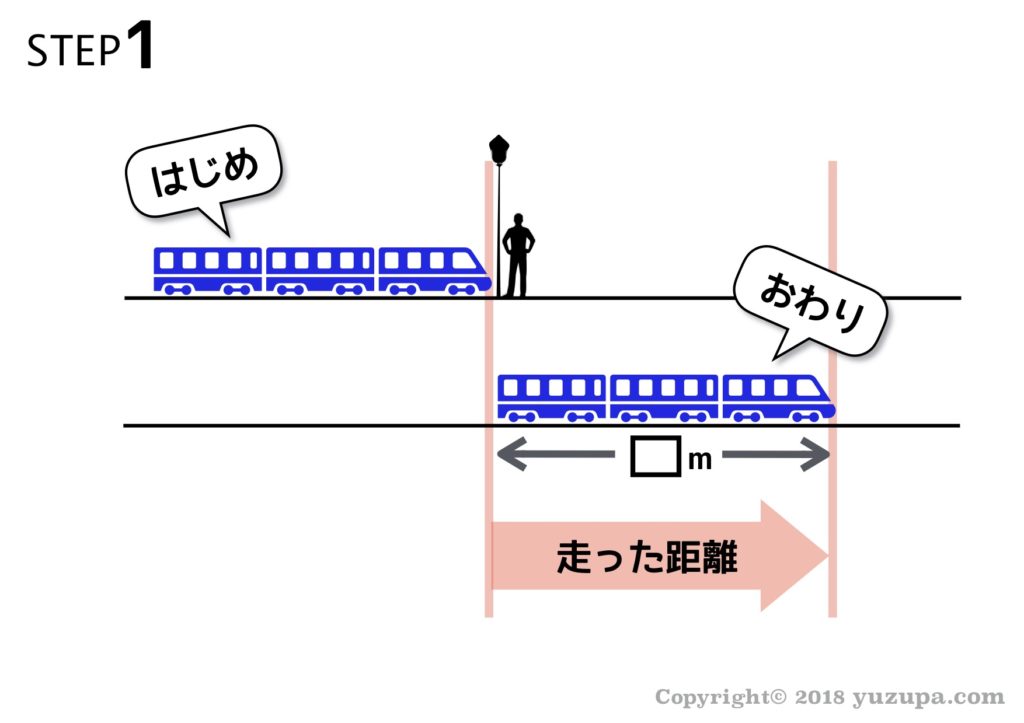
はじめの状態は… “列車の先頭が電柱に差し掛かった瞬間”
おわりの状態は… “列車のお尻が電柱に差し掛かった瞬間”
走った距離は　… “列車の長さ” と同じになります

２）橋やトンネルを “通過する”

橋やトンネルとは…電柱などと違い長さが有るものを意味します。例えば駅のホームなど 長さがあるもの を通過する問題であれば、同様に考える事ができますね。

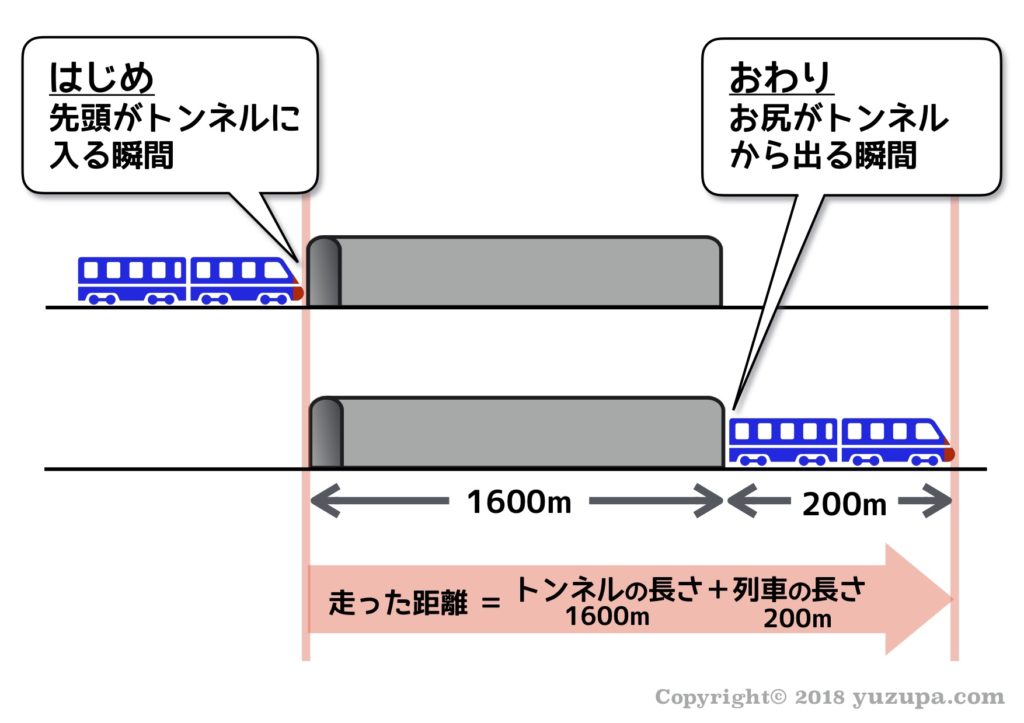
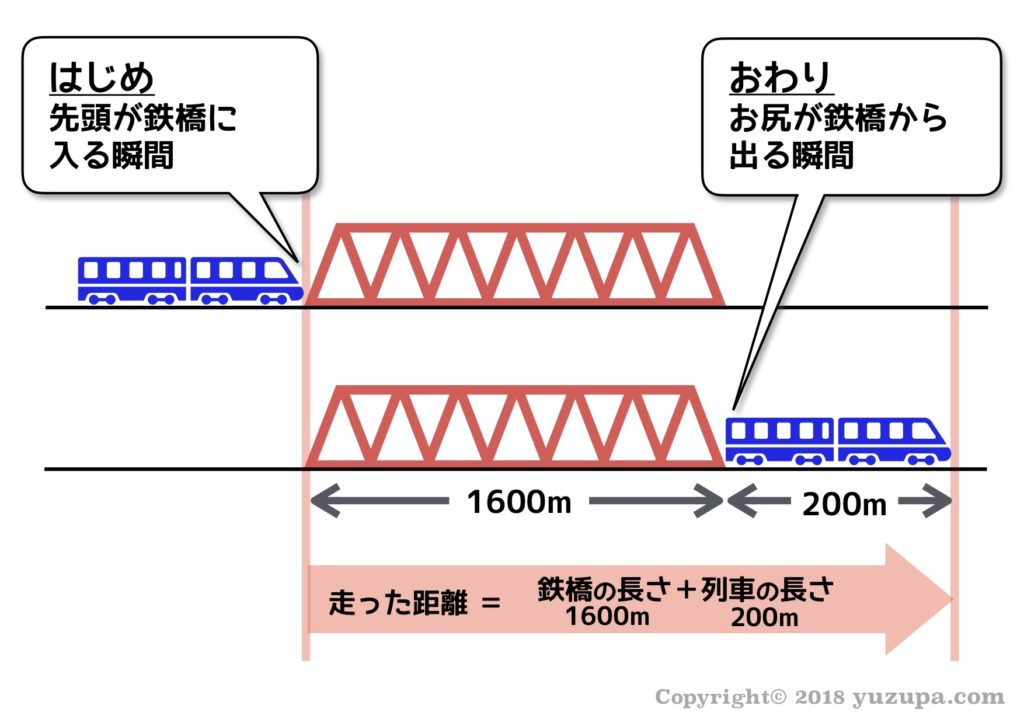
はじめの状態は… “列車の先頭が橋に入った瞬間”
おわりの状態は… “列車のお尻が橋から出た瞬間”
走った距離は　… “橋の長さ＋列車の長さ” と同じになります

３）トンネルに “完全に隠れる”

ちょっと変わり種です(^_^;)  単なる通過では無くひねった条件が出されます。その代表例がトンネルに完全に隠れる問題です。例えば…「ある列車がトンネルを通過する際に完全に隠れている時間が４０秒でした」という形で出題されます。

これも図を書いてしまえば “走った距離” がどうなるか見えてきます。

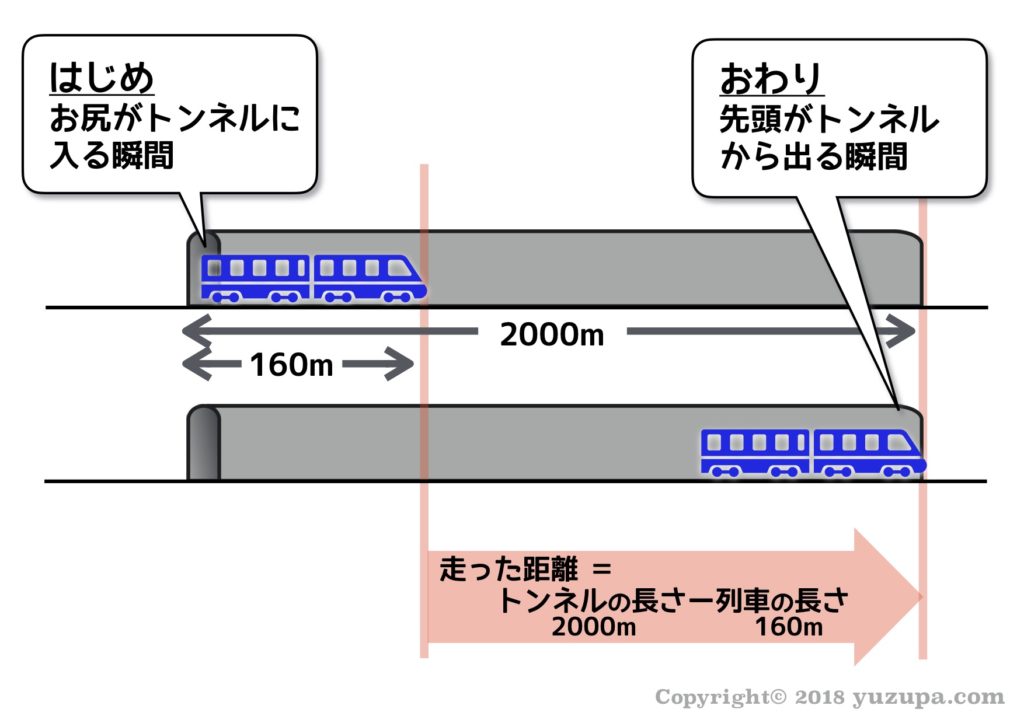
はじめの状態は… “列車のおしりがトンネルに入った瞬間”
おわりの状態は… “列車の先頭がトンネルから出た瞬間”
走った距離は　… “橋の長さー列車の長さ” と同じになります

４）列車と列車が “すれ違う”

列車と列車がすれ違う？これは旅人算の”出会いの式”ですね。旅人算の場合…速さは相対速度を使いますから、走った距離は２者の走った距離の合計です。片方の列車を止まったトンネルと考える のがポイントです。

はじめの状態は… “列車の先頭どうしが重なった瞬間”
おわりの状態は… “列車のお尻どうしが重なった瞬間”
走った距離は　… “２つの列車の長さの和” と同じになります

注意：”片方を止まったものと考える” 事ができるのは相対速度を使う場合のみです。相対速度を使うものとして旅人算の”出会いの式”や”追い越しの式”がありますねd(^_^o)

５）列車が列車を “追い越す”

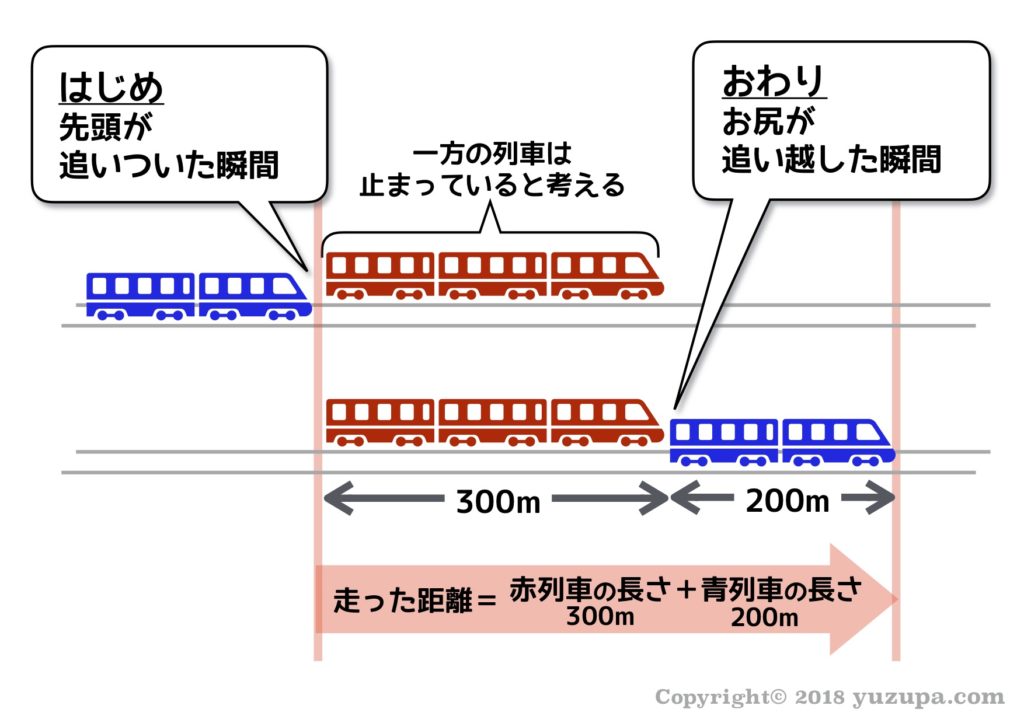
列車が列車を追い越す…これは当然、旅人算の”追い越しの式”ですね。同様に旅人算の場合、走った距離は２者の走った距離の合計となります。これも片方の列車が止まったものと考えましょう。

はじめの状態は… “先頭がお尻に追いついた瞬間”
おわりの状態は… “お尻が先頭を追い越した瞬間”
走った距離は　… “２つの列車の長さの和” と同じになります

“速さ” は相対速度に注意！

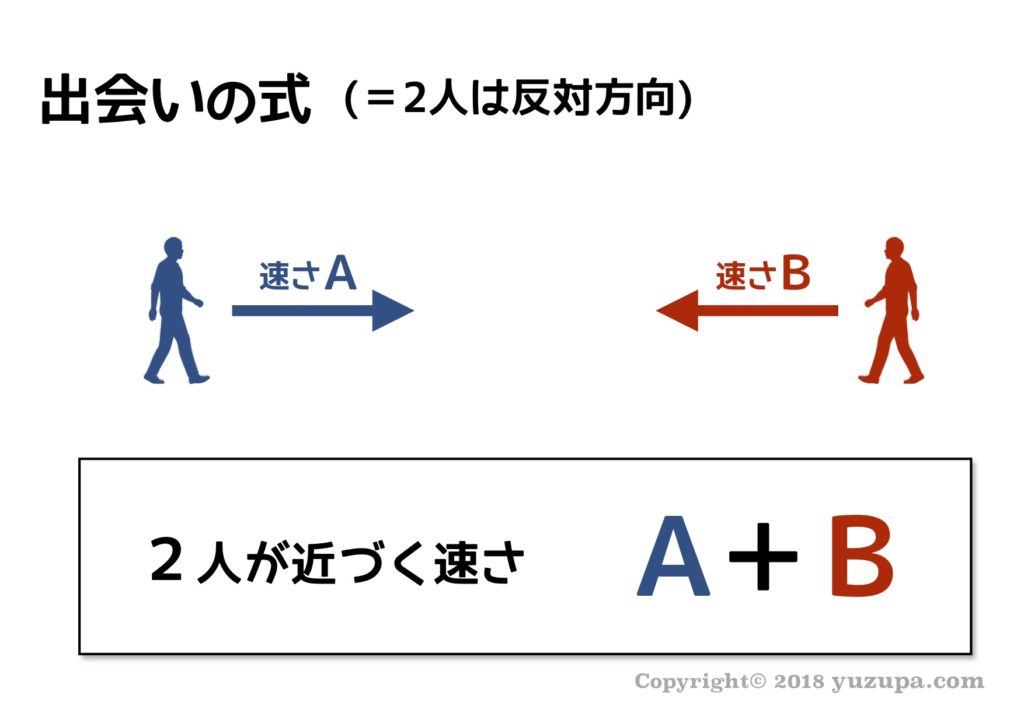
前項の”すれ違い”と”追い越し”の場合、相対速度を使う必要があります。相対速度とは…ある物体を別の観測者から観測したときの速度ですが中学受験では、かの有名な旅人算の”出会いの式”と”追い越しの式”です。

相対速度は、”すれ違い”の場合…２つの速さ和となり、”追い越し”の場合…２つの速さの差となるので注意しましょう！

通過算を解く３つのステップ

それでは冒頭にご紹介した例題を３つのステップにしたがって解いてみましょう！

長さ200mの列車が1.6kmのトンネルを通過するのに90秒掛かりました。この列車の速さは毎時何kmでしょうか？

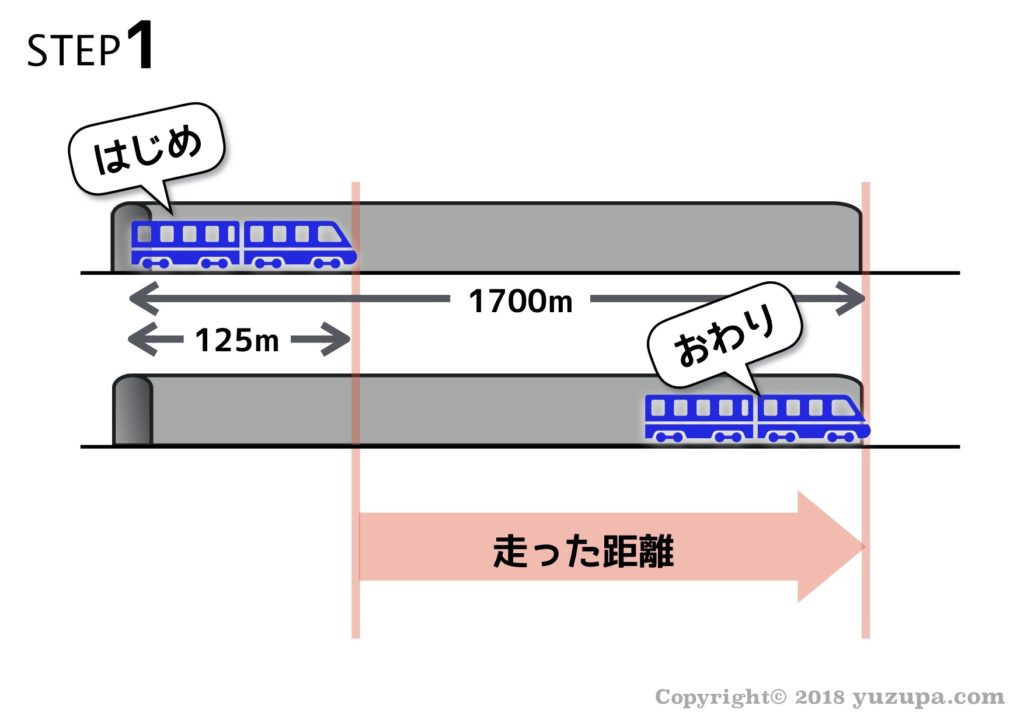
STEP1：とにかく図を書く

とにかくまずは図を書くことです。この問題の場合、はじめの状態はトンネルに入る瞬間。そしておわりの状態はトンネルから出る瞬間です。

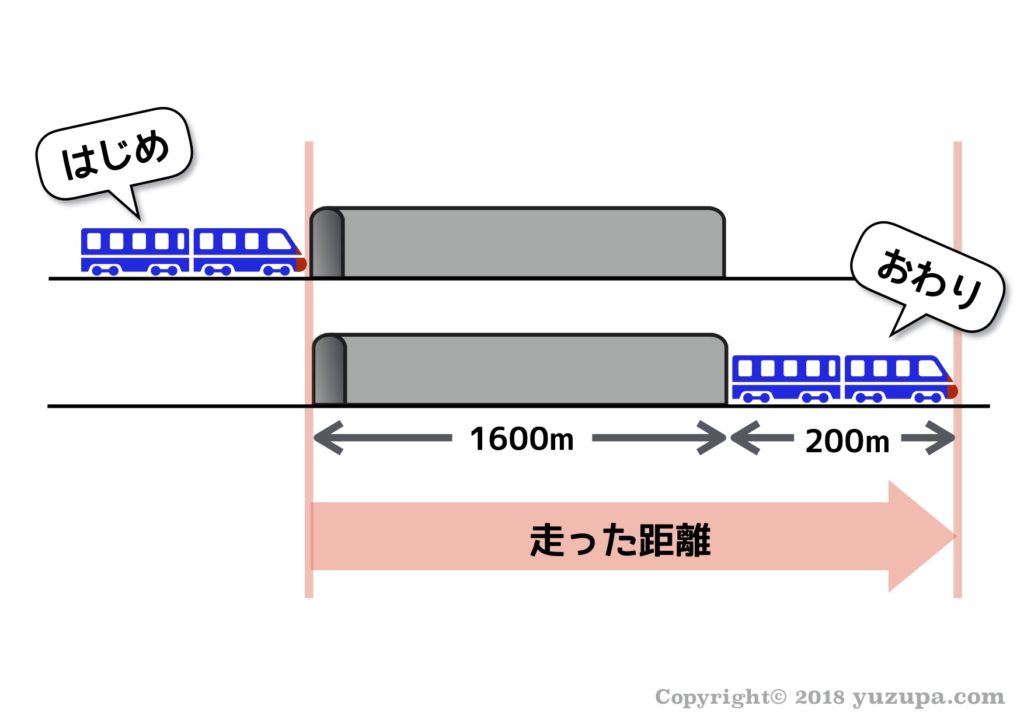
STEP2：”走った距離”を正確に把握する

STEP3：速さの公式で答えを導く

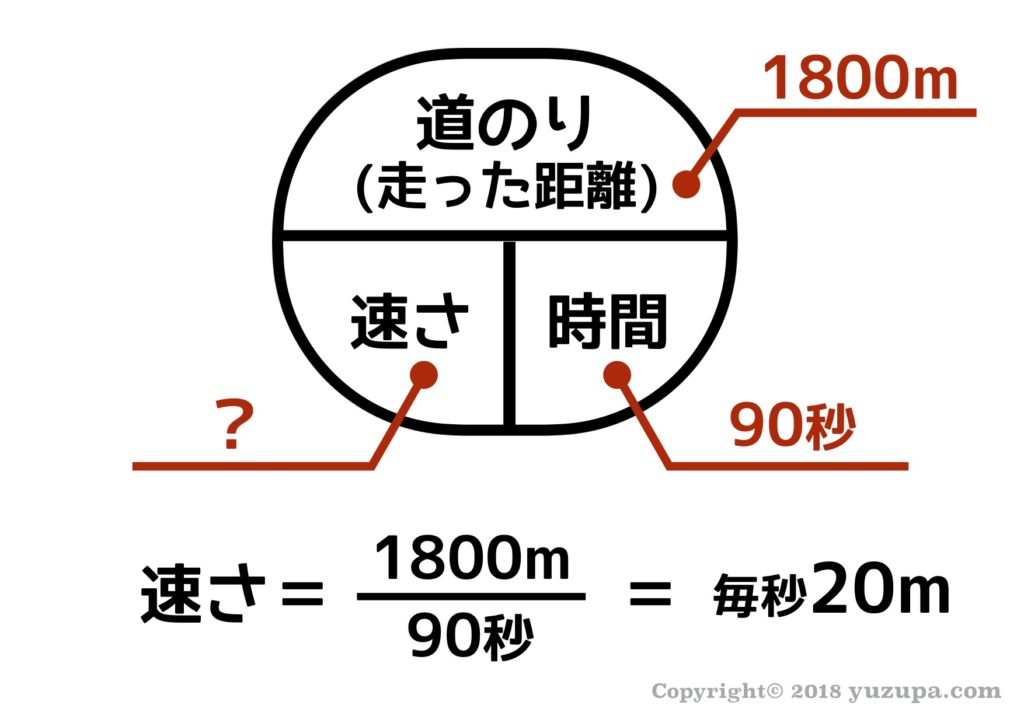
求められているのは毎時何kmですので単位変換をしてあげれば答えて出ますね。答えは毎時７２ｋｍ です。

通過算の練習問題

例題１：電柱を通過する問題の例

時速９０kmで走る列車があります。この列車が電柱を通過するのに５秒掛かりました。この列車の長さは何mでしょうか？

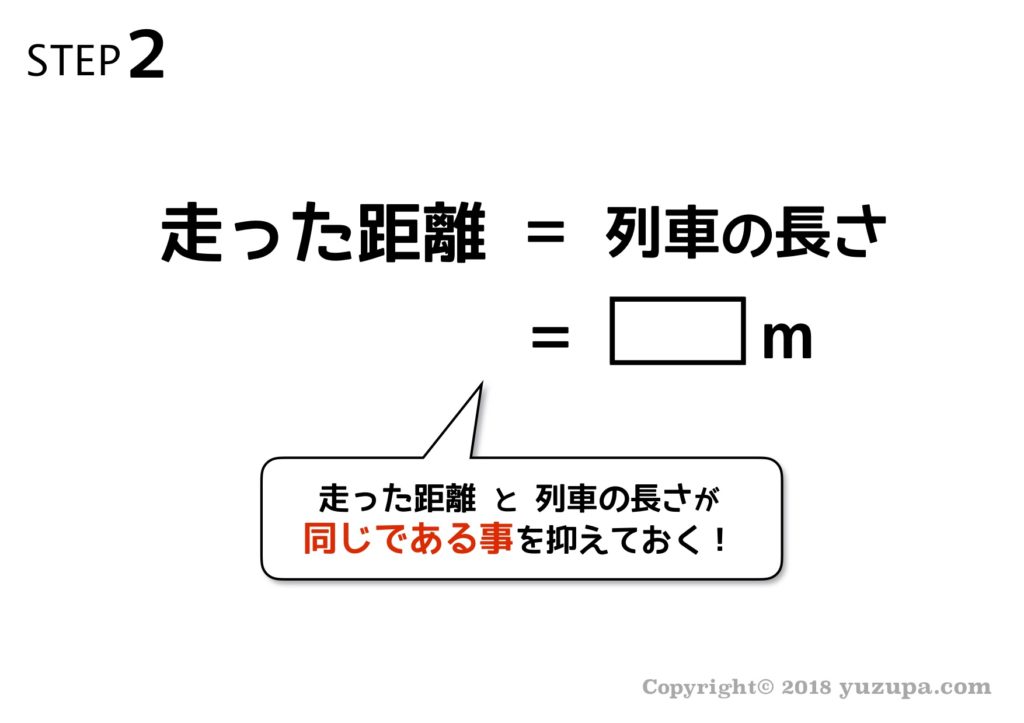
求められているのは列車の長さです。STEP2で確認したように 走った距離と列車の長さは同じ ですので、列車の長さは１２５ｍが答えとなります。

例題２：橋を通過する問題の例

長さ８２mの列車が、時速９３.６kmで走行しています。この列車がトンネルを通過するとき、トンネルに入り始めてから完全にトンネルを出るまでに５２秒かかりました。トンネルの長さは何mでしょうか？

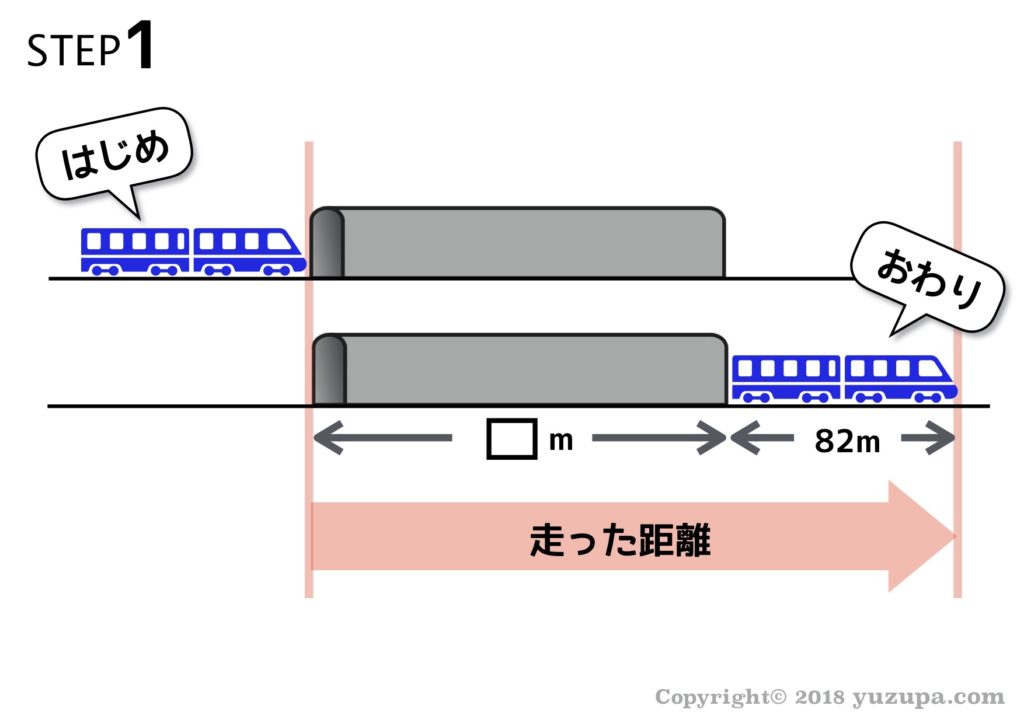
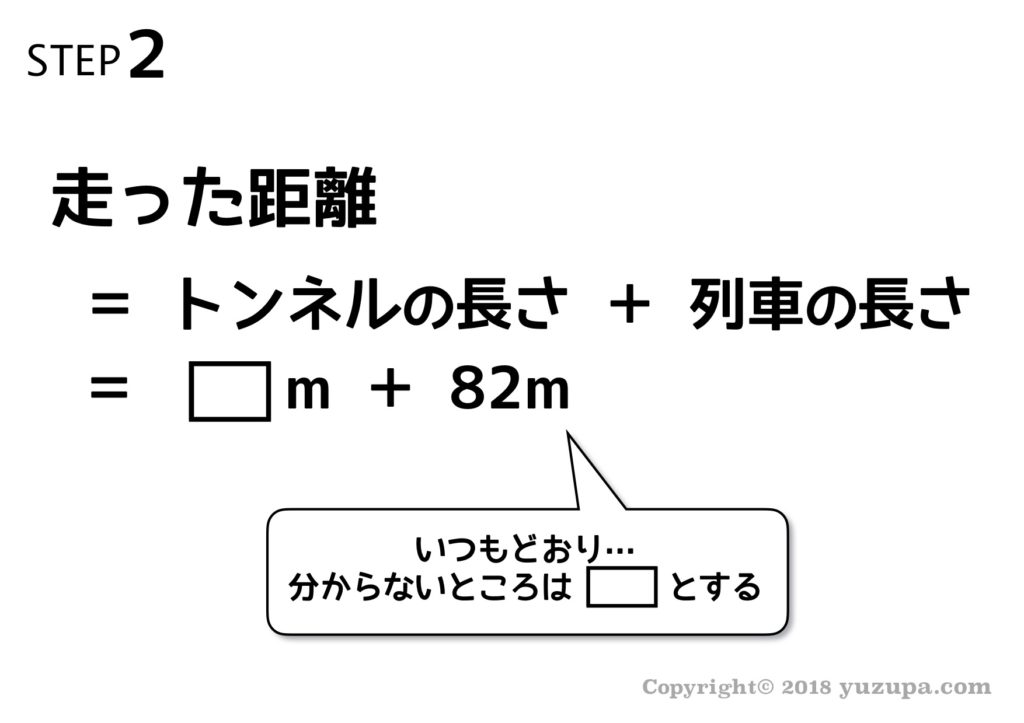
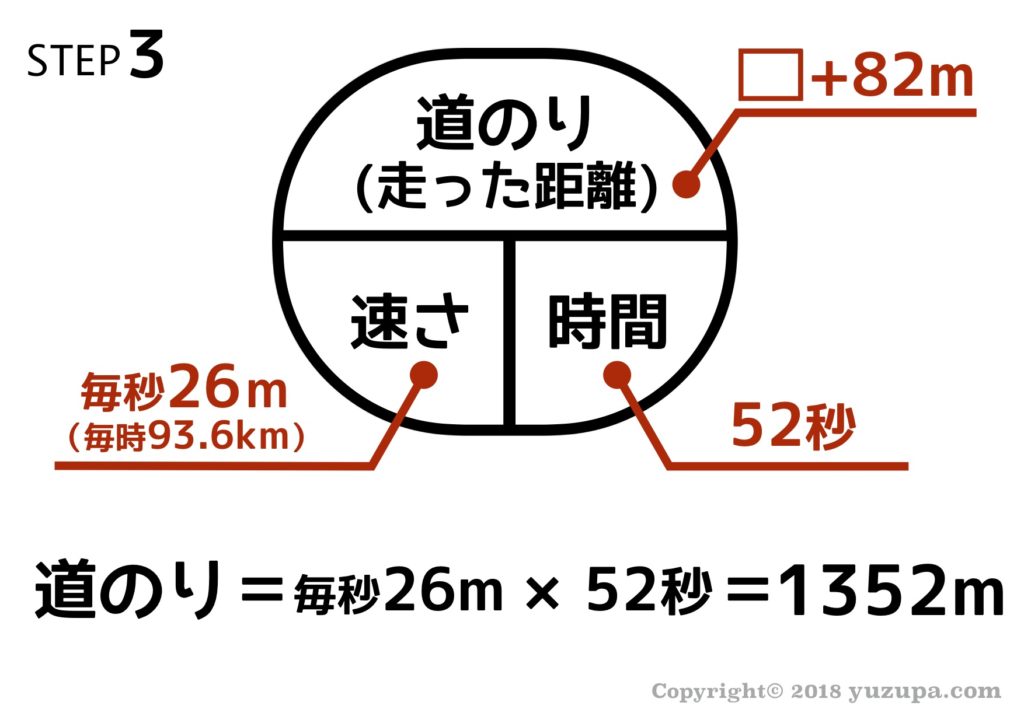
求められているのはトンネルの長さです。走った距離は１３５２ｍですが、これはSTEP2で確認したとおりトンネルの長さと列車の長さの合計です。列車の長さが８２ｍですから トンネルの長さは１２７０ｍ となります。

例題３：トンネルに隠れる問題の例

長さが１２５mある列車が、長さ１.７kmのトンネルを通過するときにトンネルに完全に隠れている時間が４５秒間でした。この列車の速さは毎時何kmでしょうか？

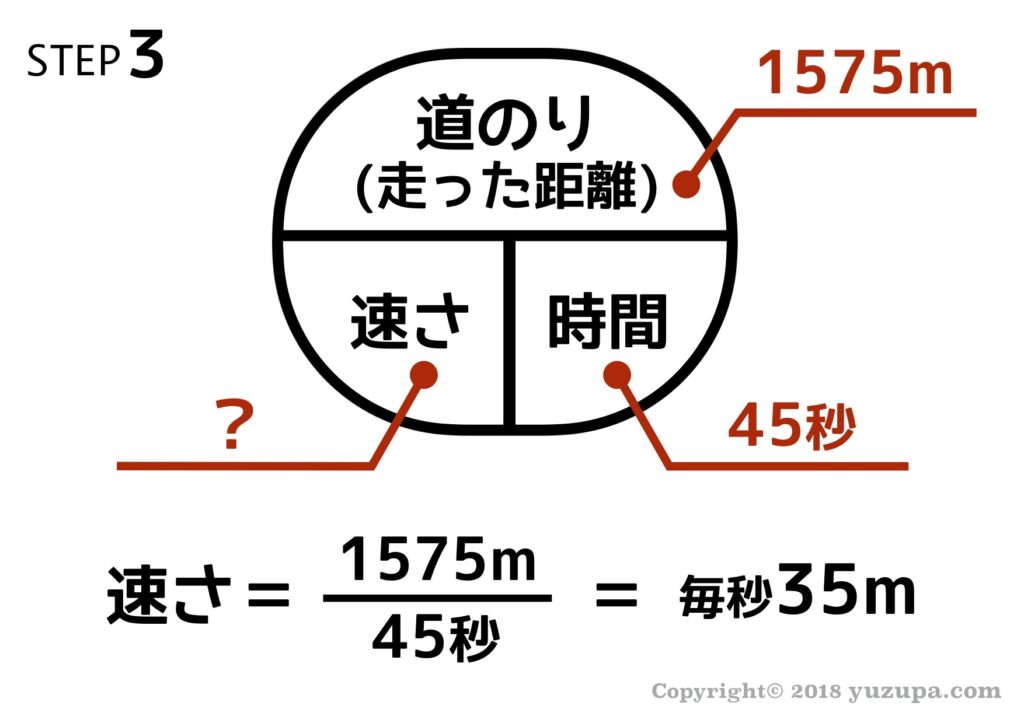
問われているのは毎時何ｋｍかなので、秒速３５ｍを変換すると…答えは毎時１２６ｋｍですね！

例題４：列車のすれ違い問題の例

長さ２００mで時速７２kmで走る列車と、長さ１６０mで時速９０kmで走る列車があります。この２つの列車がすれ違うのに何秒の時間を要するでしょうか？

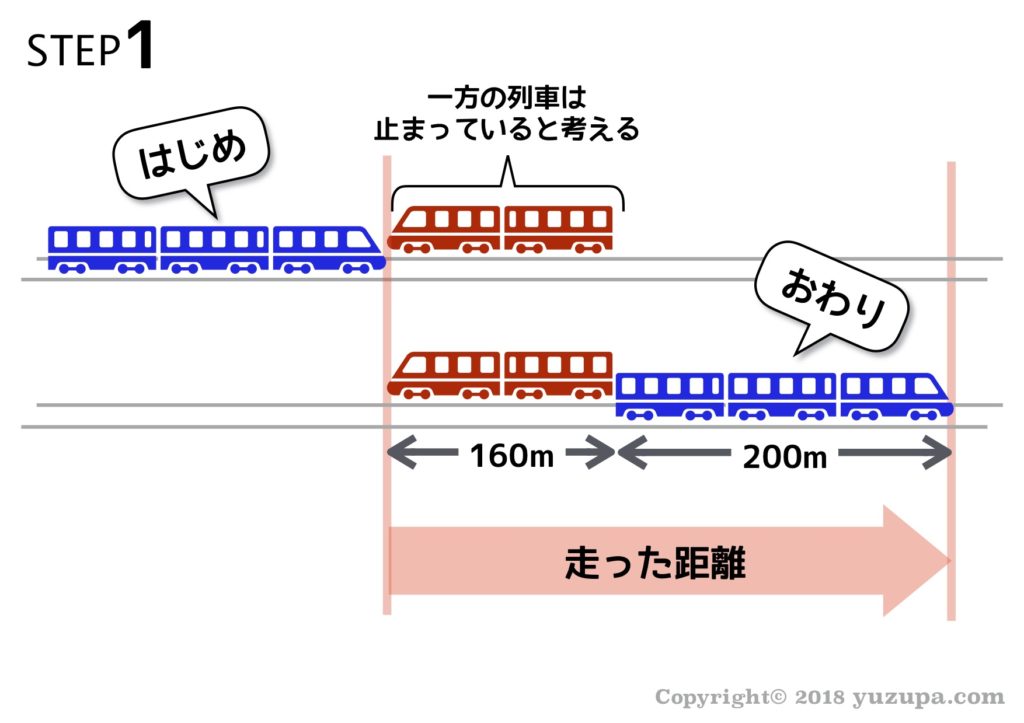
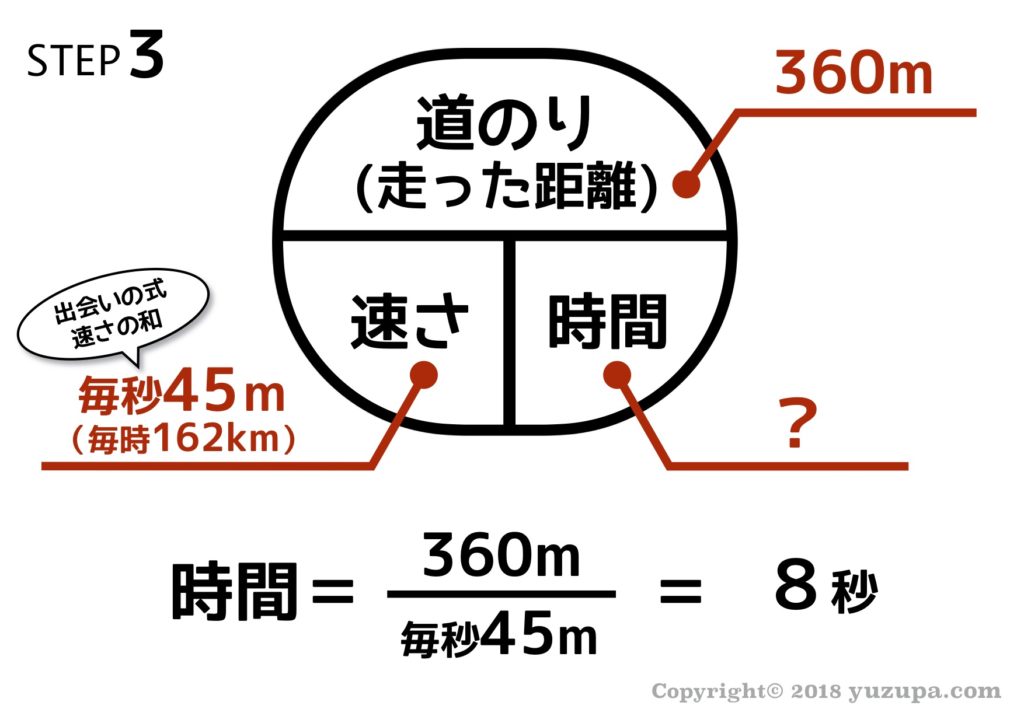
この問題の場合、所要した時間を求められていますので、答えはそのまま８秒となります。

例題５：列車の追い越し問題の例

長さ２００mで時速７２kmで走る列車と、長さ１６０mで時速９０kmで走る列車があります。時速９０kmの列車が時速７２kmの列車を追い越すのに何秒かかるでしょうか？

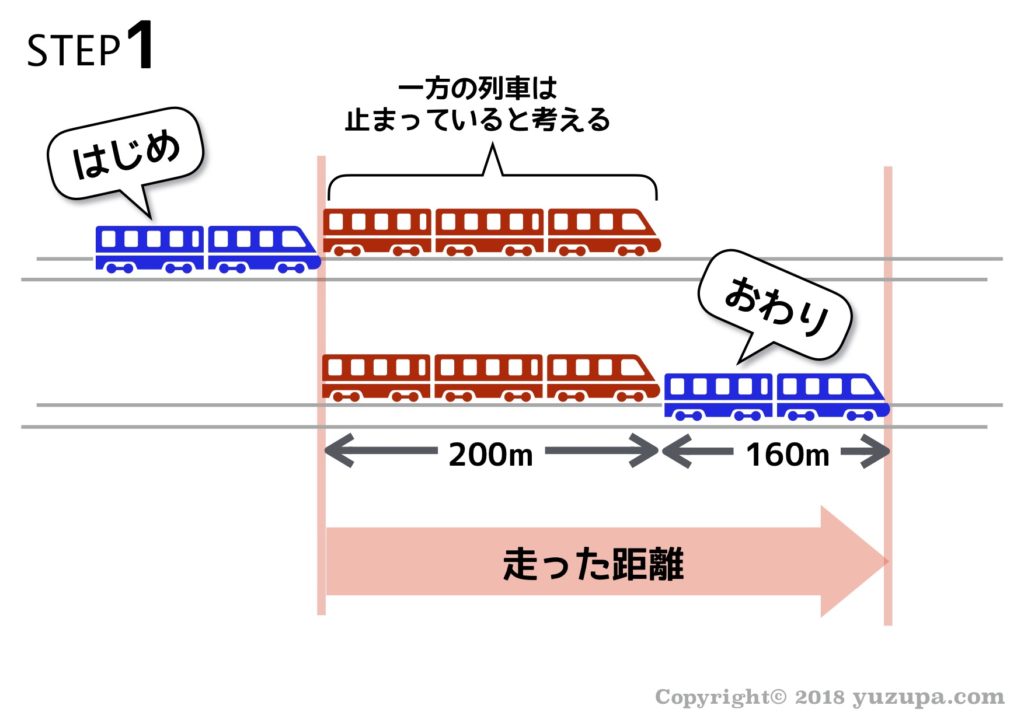
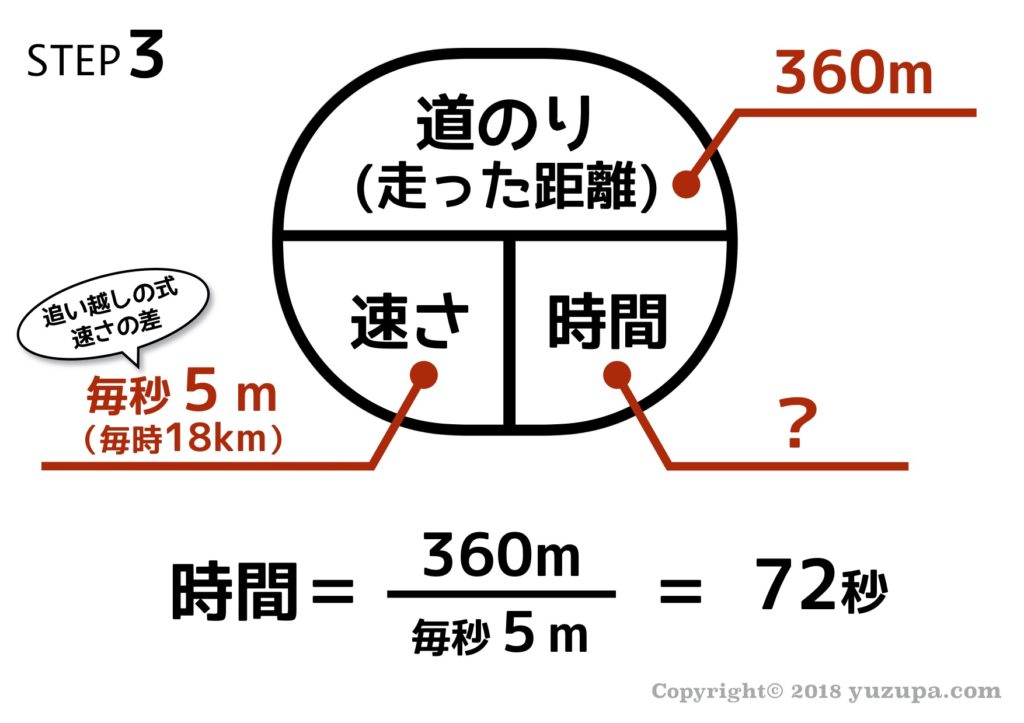
この問題も求められているのは所要時間ですので、答えはそのまま７２秒となります。

まとめ

通過算の正体は単純な速さの問題の基礎問題なんですが、問題文に”走った距離”が素直に書かれていないという特徴があります。問題文から無理に読み取ろうとせず、図を書いて着実に”走った距離”を把握しましょう。

そのあとは、速さの公式に従って落ち着いてとけば通過算は攻略できます！