中学受験:クセモノ”動く点P”問題はパターンを知れば怖くない
クセモノ”動く点P”…パターンを整理すれば意外に簡単!

こんにちは。かるび勉強部屋 ゆずぱ です。
図形の上を毎秒1cmの速さで動き回る謎の”点P”…。苦手だった方も多いのではないでしょうか(^_^;) 中学受験においてもこのクセモノ点Pはよく登場します。
ただ…中学受験においてこの”動く点P”問題
正体は”旅人算”と”図形問題”の複合問題
出題パターンが比較的限定されているので、旅人算と図形問題それぞれの単元の基本を抑えいくつかのパターンを学習すれば怖くありません!
目次
“動く点P”問題とは?
“動く点P”問題とは…
中学受験の算数ではよく出る単元となります。図形の上を一定の速さで点が動きまわっており ① ある瞬間の面積や長さを求めたり ②ある条件に合致するのが何秒後であるかを求める問題 です。圧倒的に出題頻度が高いのは後者の “何秒後” かを求める問題です。”動く点P”問題の全体像は以下のようになります。
本記事では 主に②のある条件に合致する状態が何秒後であるかの問題について解説します。
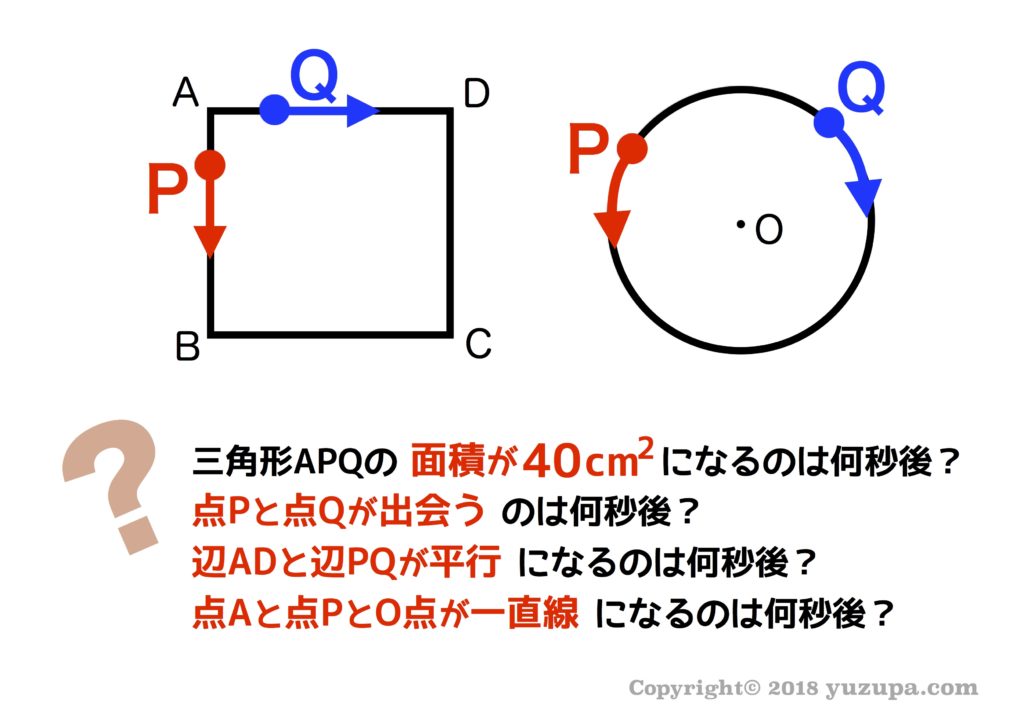
正体は”旅人算”と”図形問題”の複合問題
クセモノ”点P”は一定の速さで動きます。“速さ”が出てくるので解き方の基本は “旅人算” になります。ですので旅人算の基本を抑えている必要があります。また図形問題ですので面積の求め方など図形の基本も抑えている必要があります。まずはこれら”動く点P”問題で使う道具たちの復習から説明します d(^_^o)
必要な道具 [ 旅人算編 ]
1)基本3公式の円形図
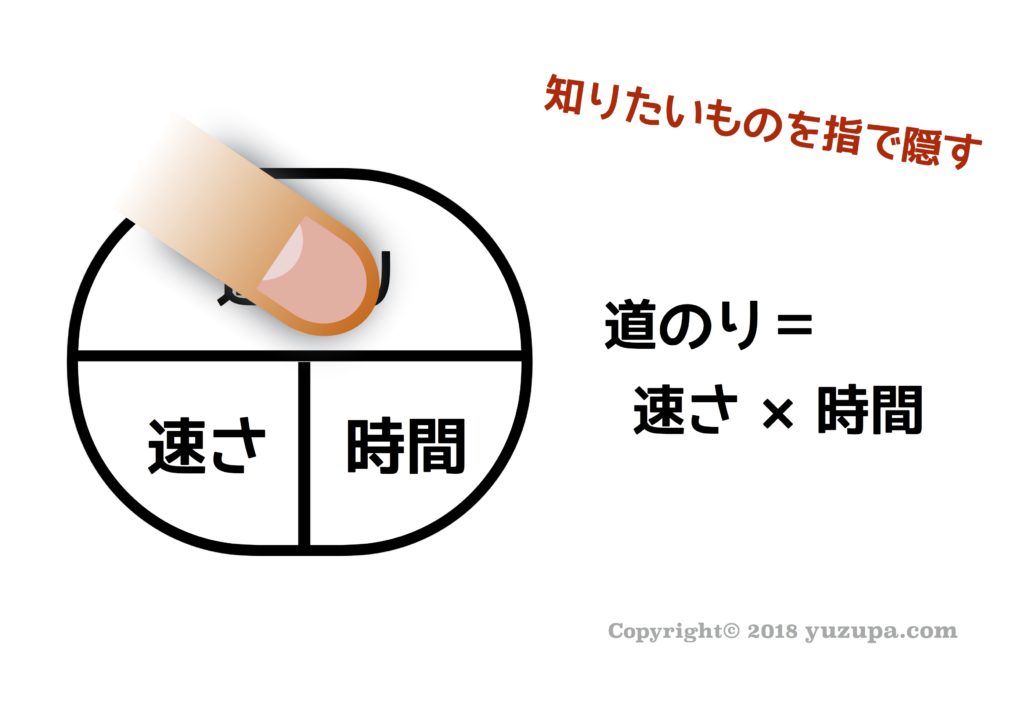
旅人算といえばコレです! “速さ”と”時間”と”道のり”のうち2つがわかっていればもう1つを求めることができます。”動く点P”問題では”速さ”と”道のり”が分かっていて “時間”を求めるシーンがとても多いです。速さの基本3公式を活用するのは円形図です。円形図の使い方を復習しましょう!
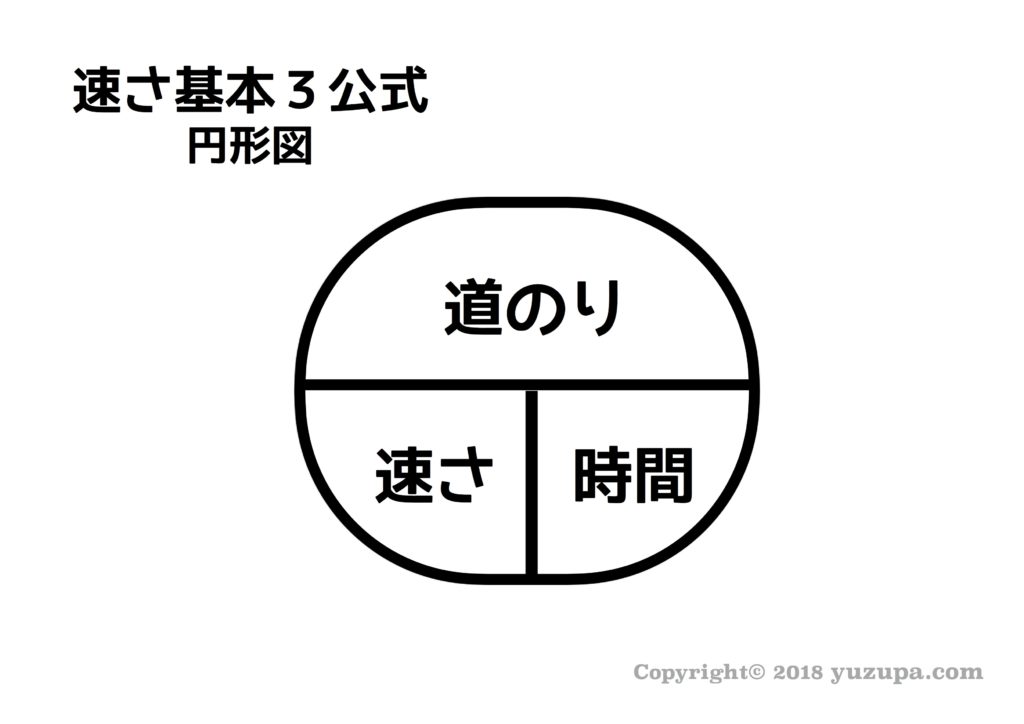
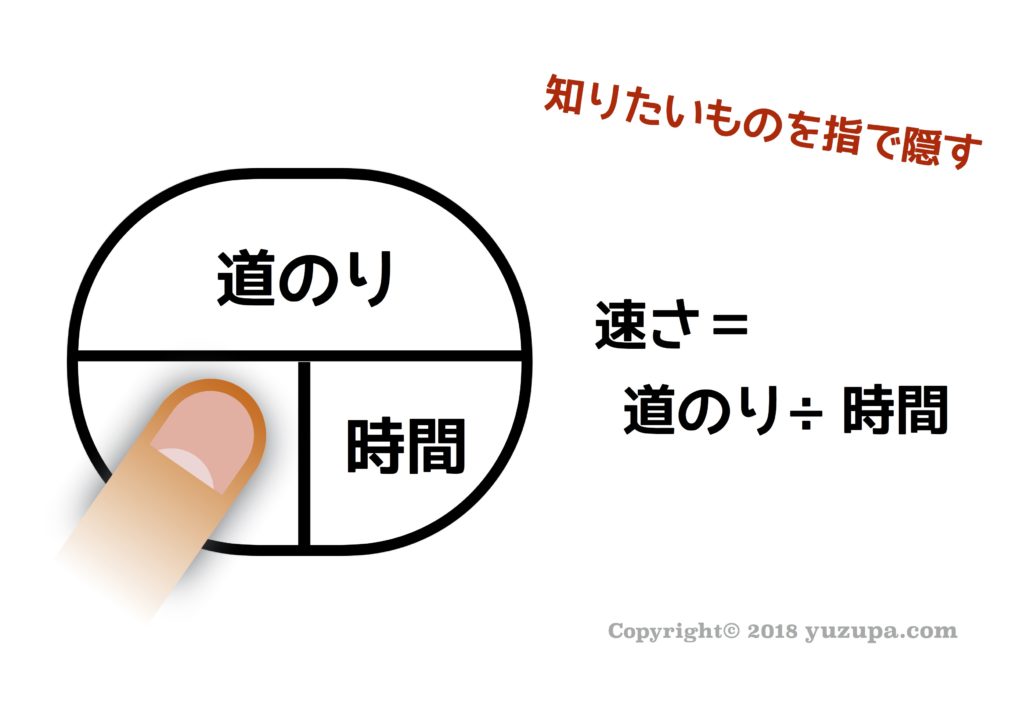
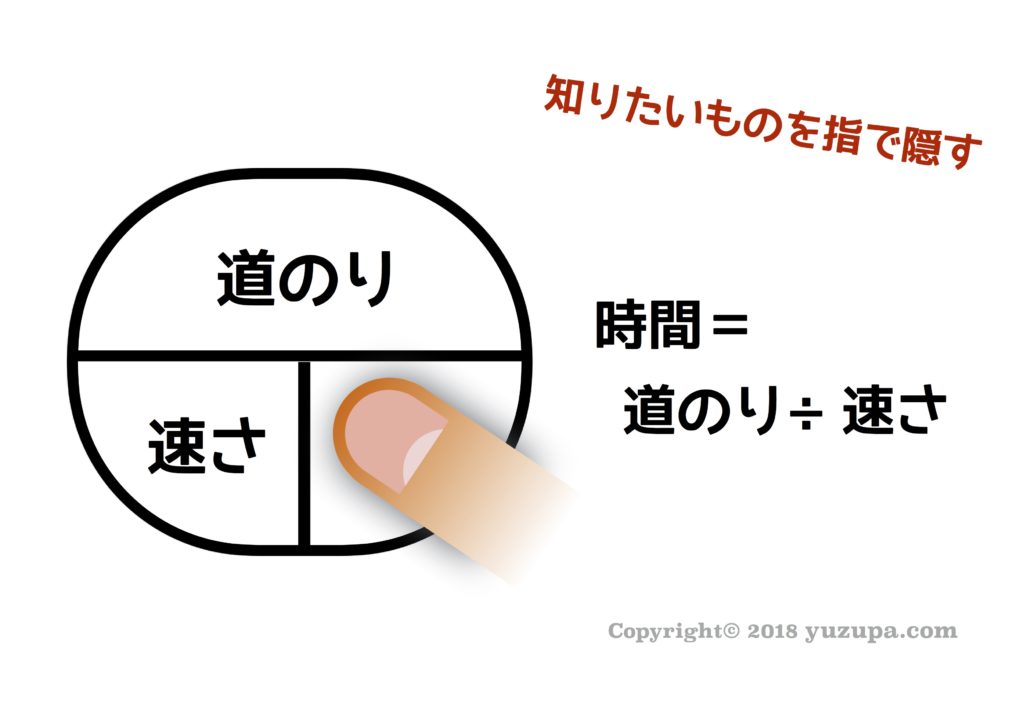
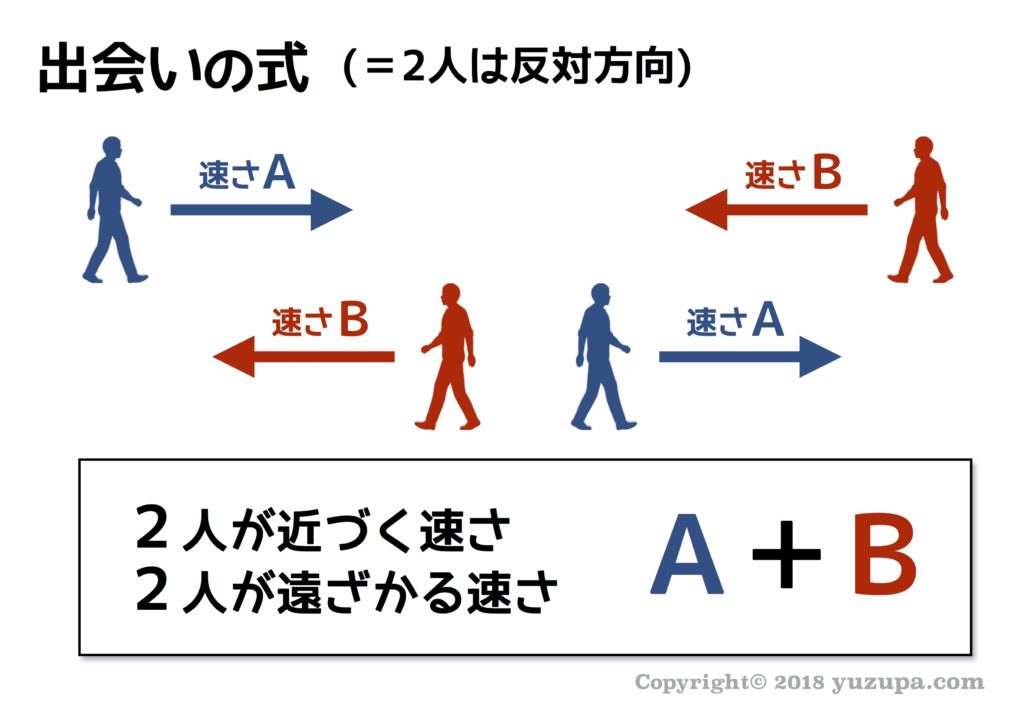
2)出会いの式と追いこしの式
そして、旅人算と言えば…! “出会いの式” と “追いつきの式” です。2人がお互いに近づいている場合は、2人の近くづく速さは2人の速さの和。2人が追いかけっこ状態の場合は、2人の近づく速さは2人の速さの差。この2つの式を使いこなすことが”動く点P”問題をとくキーとなります。しっかり抑えましょう!
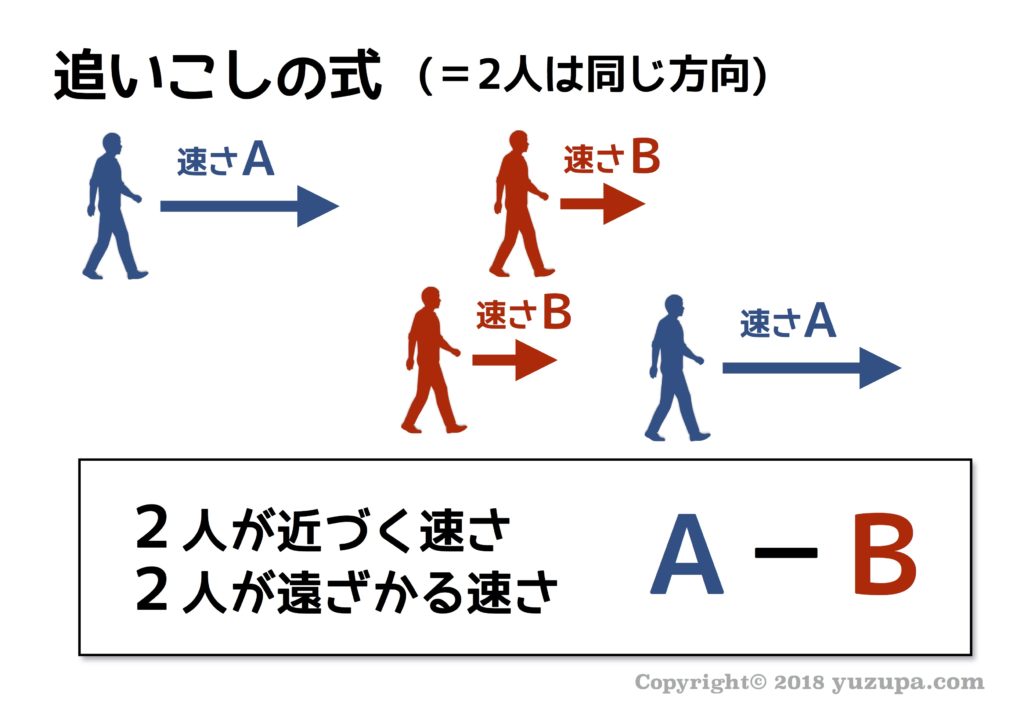
3)速さは”角度”にも!
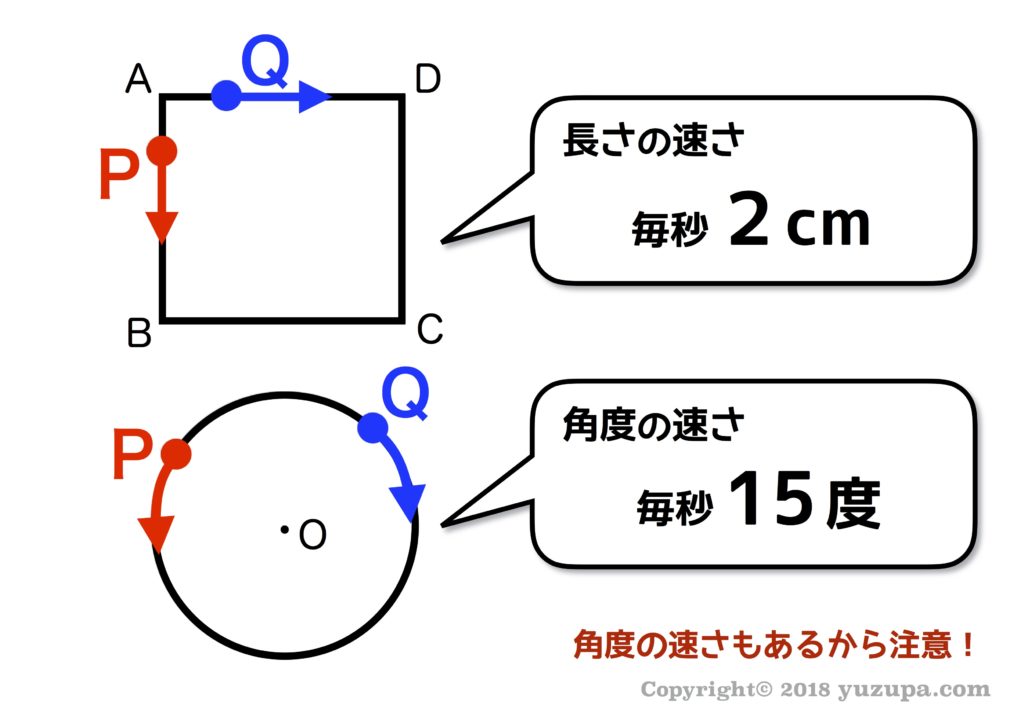
速さの問題と言えば “距離(長さ)” がメジャーですが、”動く点P”問題では角度の速さがよく出ます。”円の上を1秒間に15度すすむ点P”といった感じです。円の上を動く点Pが出てきたら下手に距離(長さ)に手を出さず、必ず “角度での速さ” を考えましょう。一応、長さの速さでも解くことはできますがちょっと大変です(^_^;)
旅人算についての詳しい記事もいずれまとめたいと思います(^_^;)
必要な道具 [ 図形問題編 ]
1)基本5図形の面積
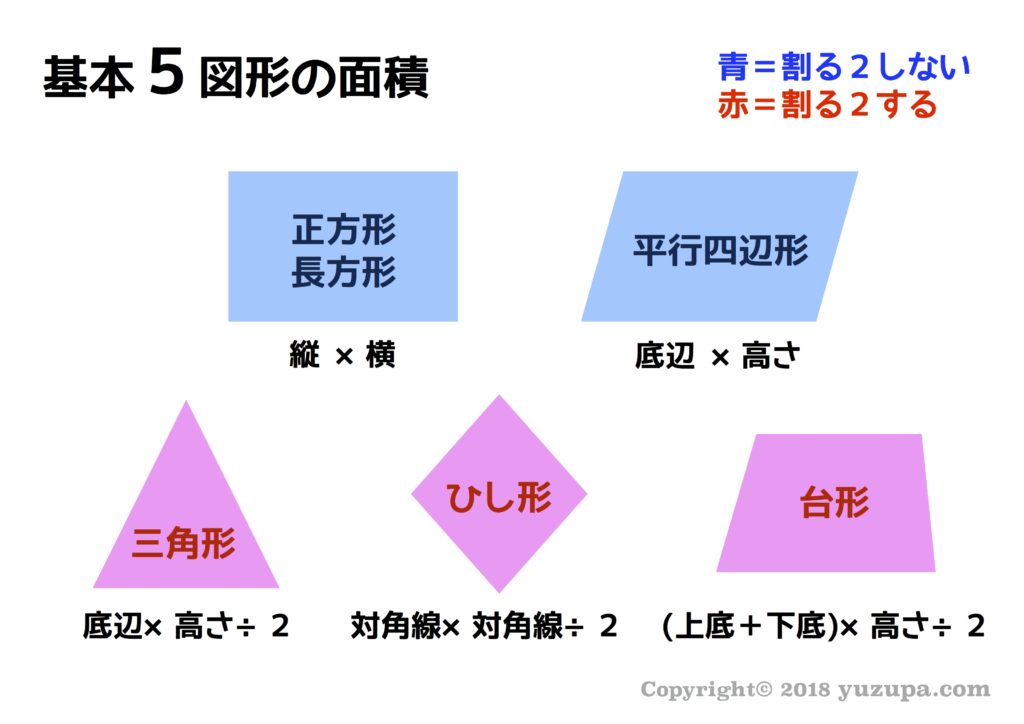
まずは基本5図形の面積はよく使います。四角形の面積、三角形の面積、平行四辺形の面積、台形の面積、ひし型の面積の5つの図形です。私の息子もよくあったのですが…(^_^;) 最後に2で割るのを忘れてしまう問題…。2で割るグループと、2で割らないグループに分けてこの基本5図形を覚えると良いですね!
2)円の基本4公式
円の上を動く点Pもあり… 円の公式も必須です。円の面積、円の周りの長さ、おうぎ形の面積、おうぎ形の弧の長さの4つの公式です。円周率3.14の計算が含まれるので計算ミスには気をつけましょうね。円周率の計算は最後の最後までしないのがコツです。小数のひっ算が最も計算ミスが発生しやすいので回数を減らす工夫です。

3)忘れてはいけない “パズル思考”
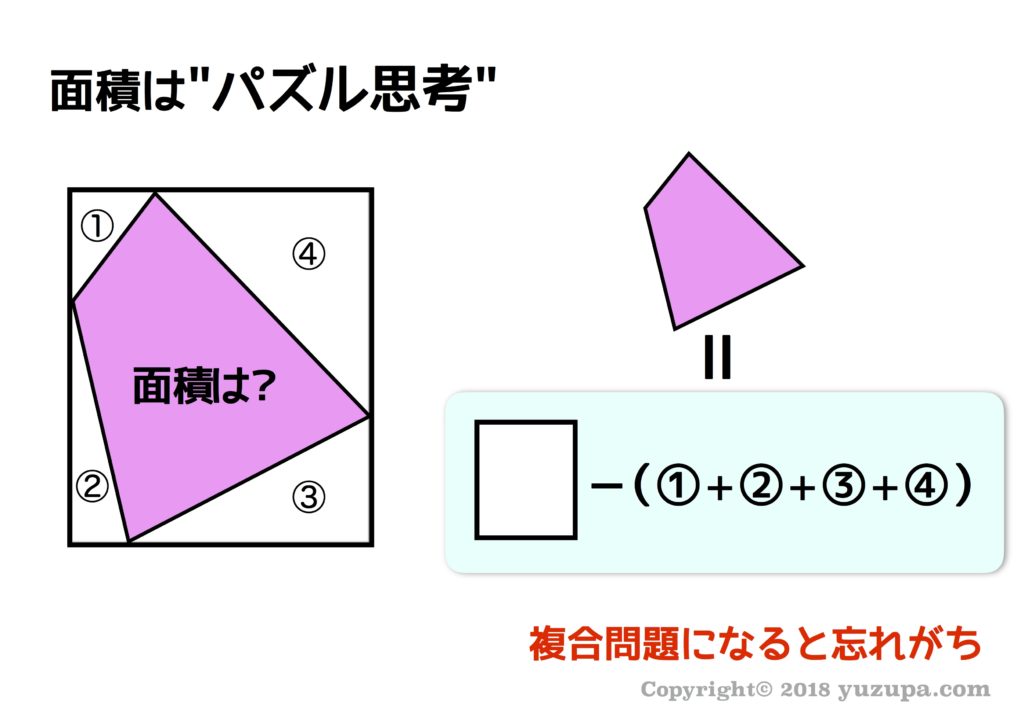
面積を求める時に、がっつり図形問題だと子供たちは試行錯誤で何とか面積を求めようと図形を足したり引いたり図形のパズルを始めます。ところが… “動く点P”問題などの複合問題だと、なぜかパズルする事を忘れてします…(^_^;) 複合問題であっても通常の図形問題と同様に”パズル思考”を忘れないようにしましょう!
動く点P問題は3ステップで解く
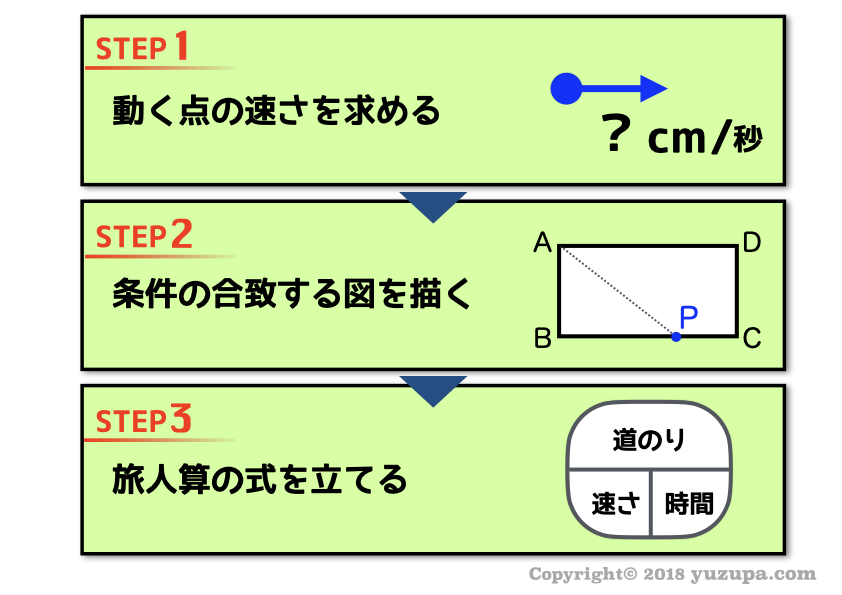
STEP1 動く点の速さを求める
まずは動く点の速さがいくつなのかを把握することが最初にやるべき事です。秒速1cm、秒速3cmと長さの場合もありますが、秒速5度や秒速20度といった角度の場合もあります。ほとんどの問題では問題文に書かれています。が…グラフから点Pの速さを読み取らなくてはならない場合もあるので注意深く読み取りましょう。
以下は例題ですが問題文に書いてありますね d(^_^o)
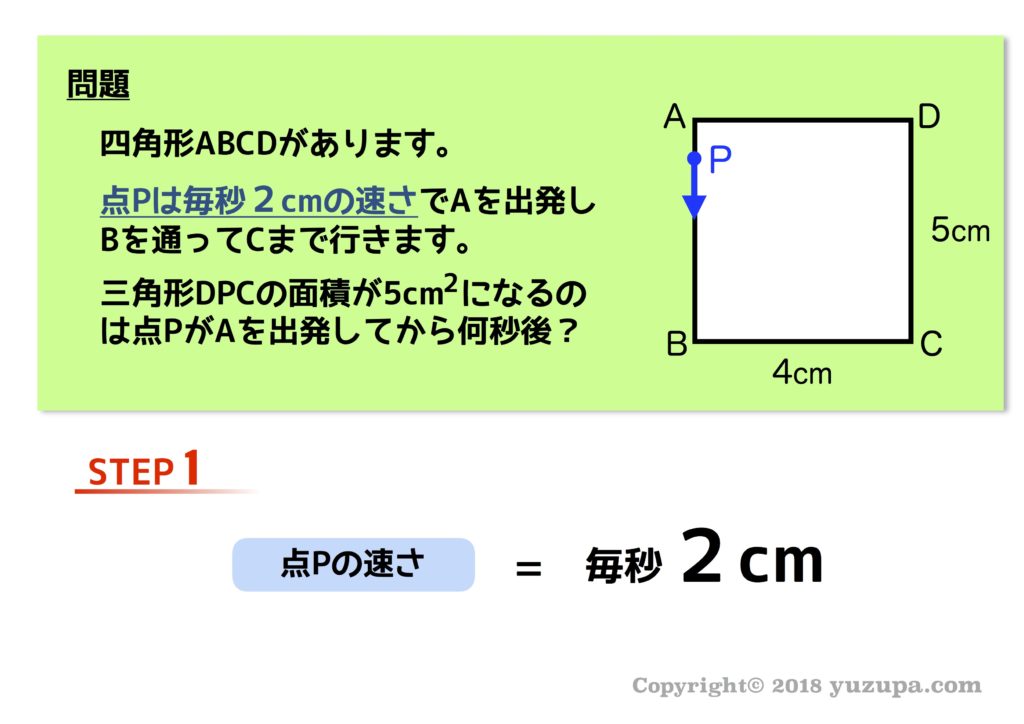
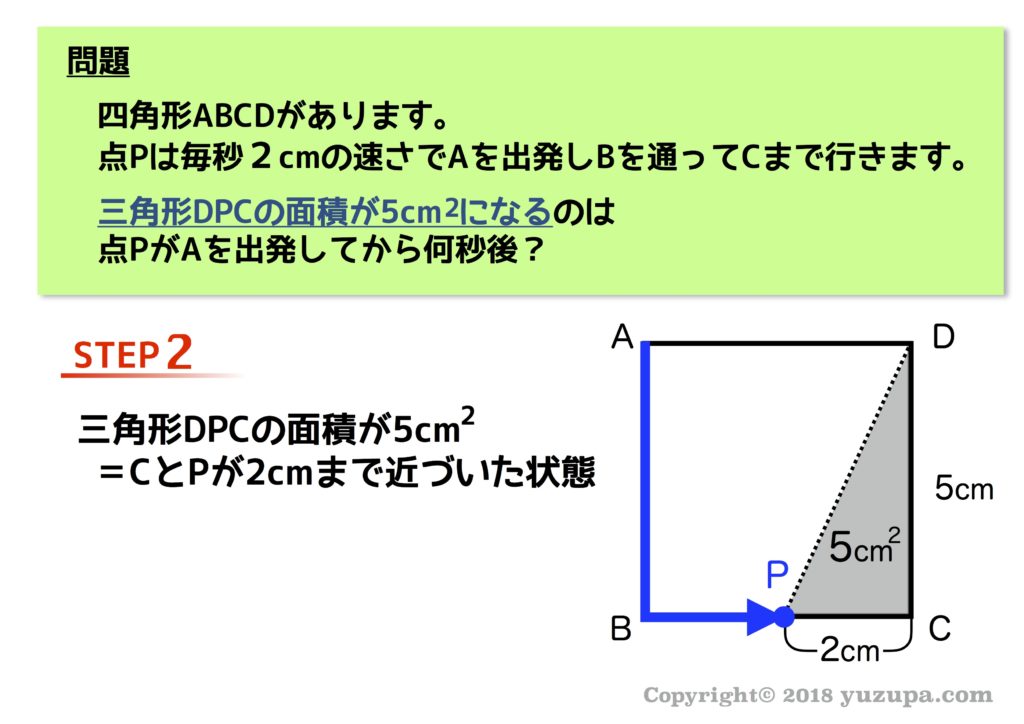
STEP2 条件に合致する図形を描く
次は条件に合致する図形を書く作業です。点Pと点Qが初めて重なる時…三角形OPQの面積が30cm2になる時…辺ABと辺CDが平行になる時…条件のパターンはたくさんありますが、図形を書く事がポイントです。シンプルな問題で慣れてくれば図を書かないでも解けますが、はじめは図を書く練習をする事をオススメします!
この問題の場合は三角形DPCの面積に条件があります。
STEP3 旅人算の式を立てる
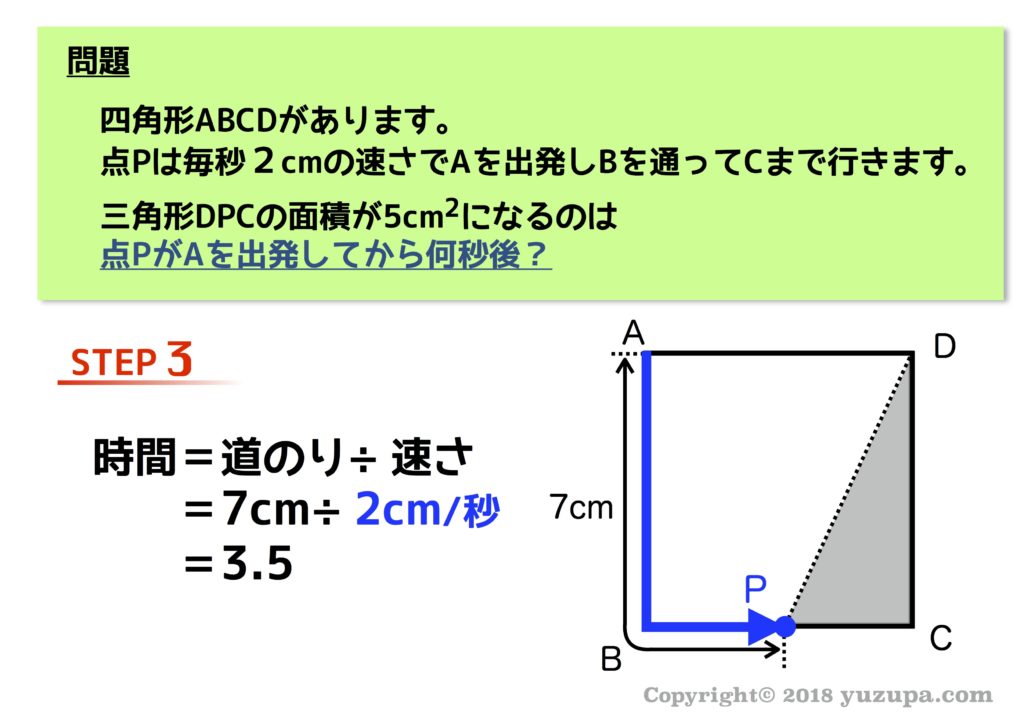
最後は旅人算の式を立てます。多くの問題では “時間” を求める事が多いです。STEP2で描いた図形から”速さ”と”長さ(道のり)”を取り出し、速さの基本3公式に当てはめていきましょう。2つの点がある場合は、出会いの式や追いこしの式が当てはまる場合もあります。式が立てられれば答えは出たようなものです!
点Pの速さと通ってきた長さ(距離)がわかるので時間が求められます。
いかがでしょうか? 条件部分は問題によってバリエーションがありますので3つほど紹介したいと思います。
動く点P問題のよく出る条件
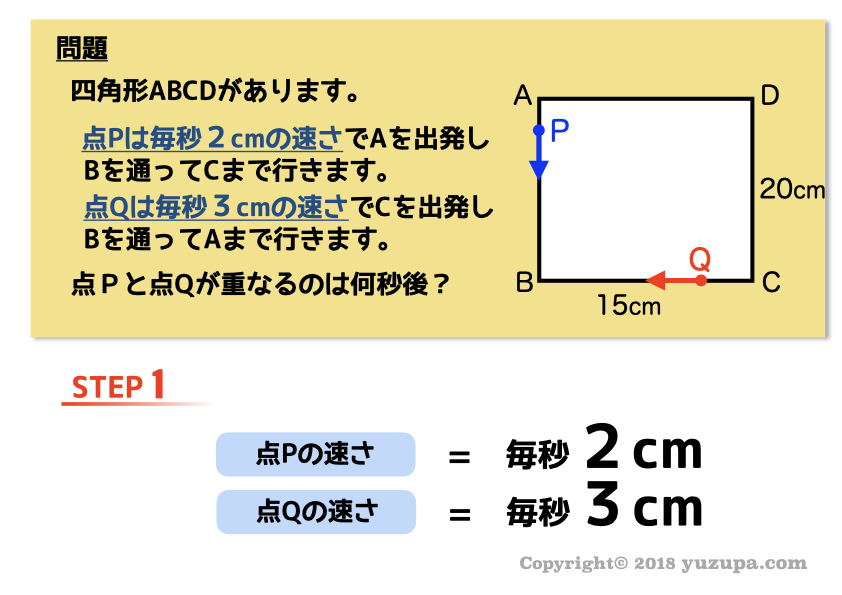
条件例① 点が重なるのは?
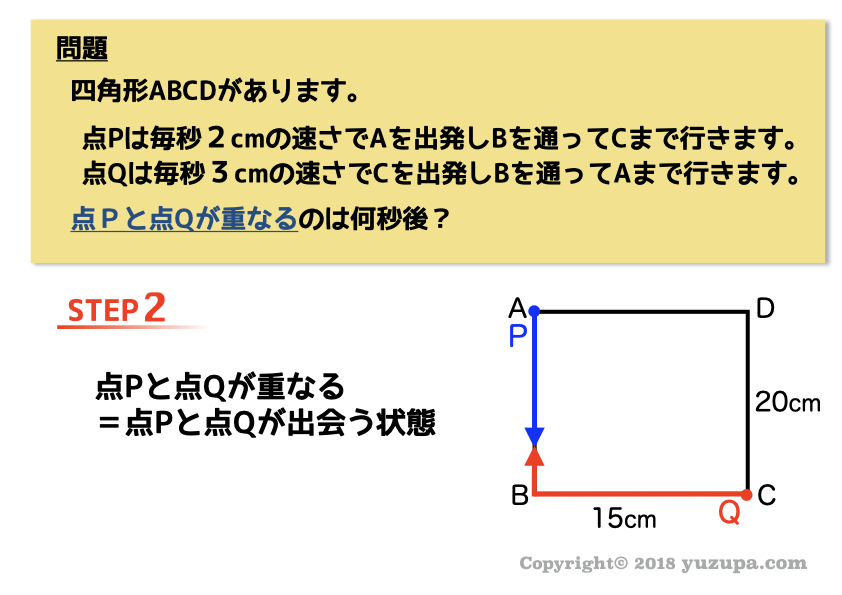
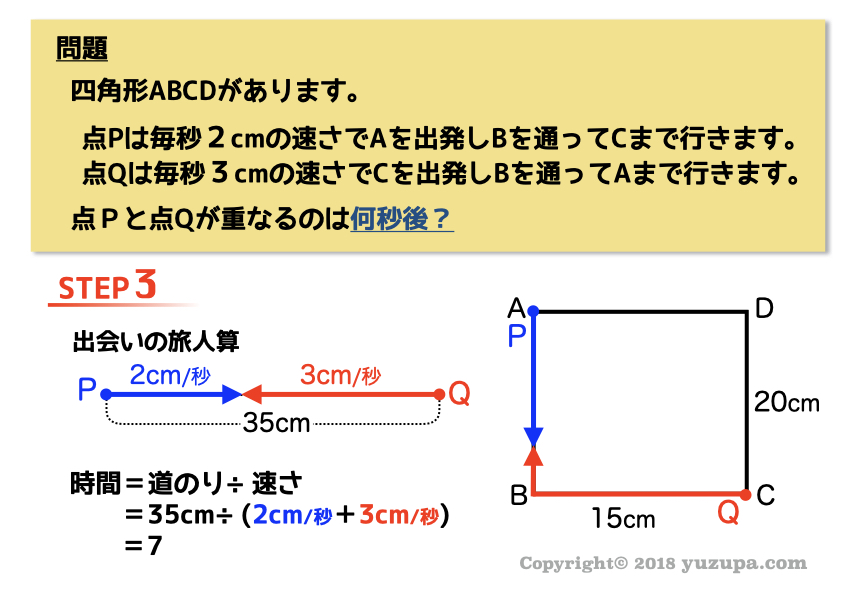
条件例② 平行になるのは?
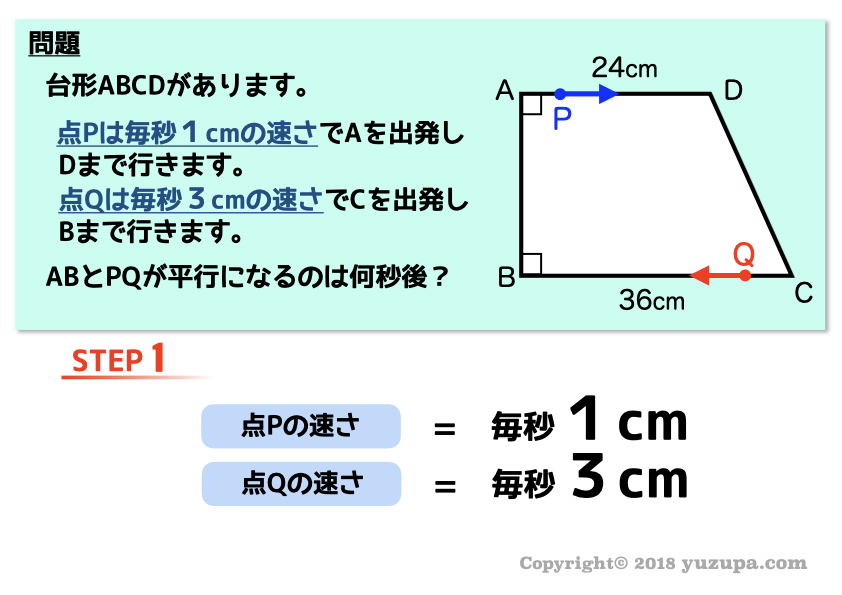
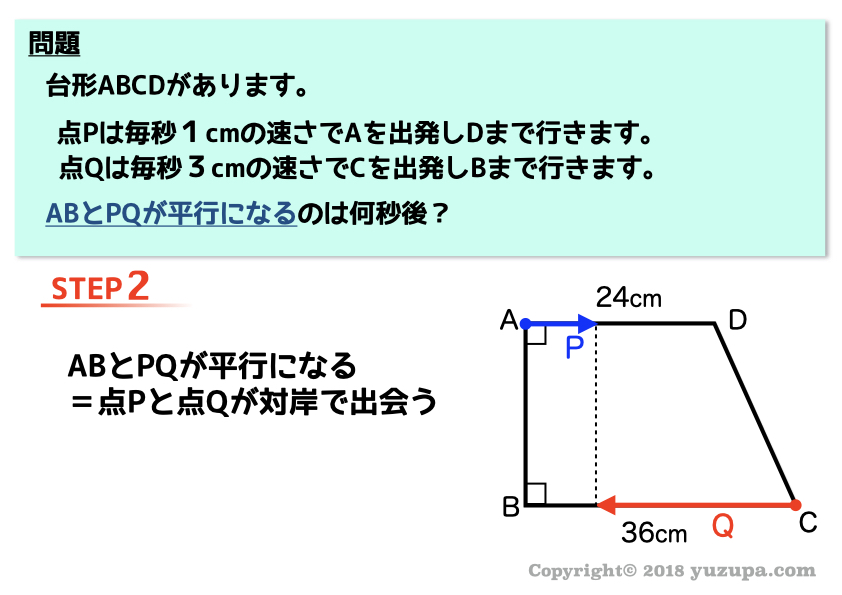
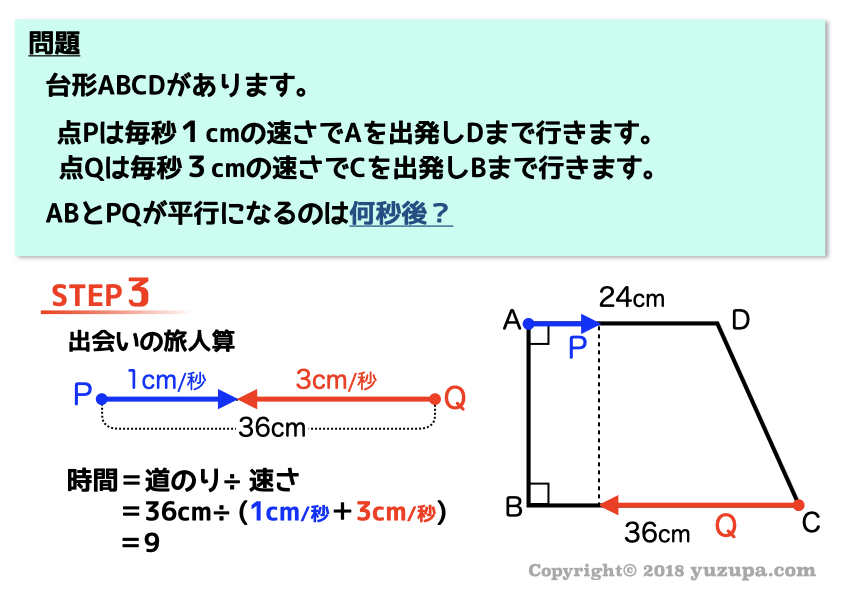
条件例③ 一直線になるのは?


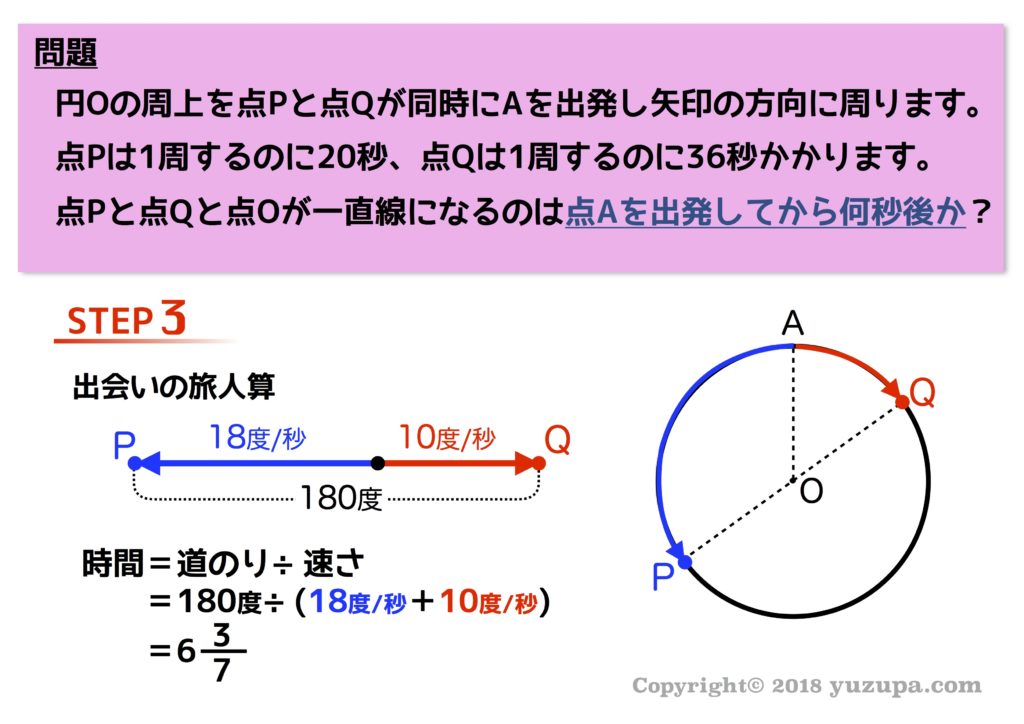
まとめ
苦手意識を持つ子供が多い”動く点P”問題ですが、正体は”旅人算”と”図形”の複合問題でした。3つのステップを踏めば多くの問題を解く事ができます。ちょっと難しいのがSTEP2の条件に合う図を描くところですね(^_^;) 本記事では4パターンの条件を掲載しました。この基本パターンをマスターすると応用がききますよ!










苦手な単元でしたが、とてもわかりやすくて、テストで点数がとれるようになりました!
これからも使わせていただきます(≧∇≦)
苦手な分野だったけれど、ゆずぱさんのおかげで、
テストもスムーズに解けそうです‼️
図も細かく書いていて、分かりやすかったです‼️
匿名さま
かるび勉強部屋 ゆずぱ です。
少しでもお役に立てたようであればよかったです!
テスト勉強、大変かと思いますが
ぜひ頑張ってくださいo(^-^)o
図がわかりやすすぎる‼️
匿名さま
かるび勉強部屋 ゆずぱ です!
コメントをいただきありがとうございます。
よかったです!!
凄いわかりやすかったです!!
条件②の「平行になるのは?」という問題がとても苦手だったんですけど、ゆずぱ様のおかげでしっかり分かりました!
ありがとうございます(人”▽`)
優彌さん
かるび勉強部屋 ゆずぱ です。
こちらこそありがたいコメントをいただき感謝いたします!
良かったです!!
すごい
ゆずぱぱ
神
わかりやす!
匿名さん
ゆずぱです。
ありがとうございます(^_^;)
匿名さま
ゆずぱです・・恐れ多いです(^_^;)
すごく分かりやすかったです
いつも点Pには苦戦していたのですが、このパターンを全部覚えたら、「ああ、この解き方ね」とすぐわかるようになったので嬉しいです
調べてよかったです
匿名さま
かるび勉強部屋 ゆずぱ です。
コメントをいただきありがとうございます!
少しでもお役に立てたのであれば嬉しく思います!
ゆずぱ
このサイトわかりやすくて毎日つかっています!ありがとう御座います!
受験生さま
かるび勉強部屋 ゆずぱ です。
ありがとうございます!少しでもお役に立てたならば嬉しく思います!