中学受験：図形の角度問題は “７つ道具” で攻略

図形問題はパズルで “試行錯誤”と”ヒラメキ”が必要…ヒラメキが思いつかずに苦労していませんか？

こんにちは！かるび勉強部屋 ゆずぱ です。

算数における図形問題はよく”パズル”に例えられます。私も息子と図形問題を解いていると 複雑な問題であればあるほど試行錯誤やヒラメキが必要 だと感じます(>_<)

どうやったら効率よくヒラメく事ができるのでしょうか？

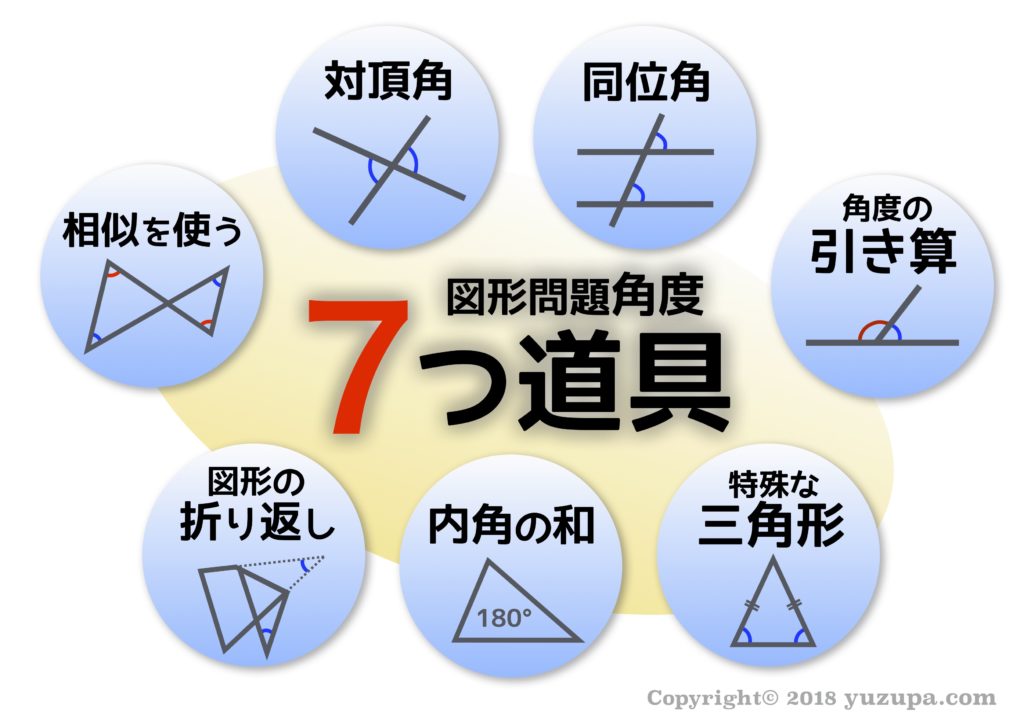
ヒラメくためには “使える知識の全体像” を知ることが大切 d(^_^o)

自分がどんな道具を持っているのかも知らずに図形問題に挑むことは、回復の呪文を知りながらも全く使わずにラスボスに挑むゲームのようなもの(￣^￣) 分かりにくい例えですみません…。

注釈：いわゆる基礎問題を解くために必要な知識を”道具”として表現しています。入試の応用問題は基礎問題の組み合わせで解ける…まさにこれらの知識は”道具”のイメージですd(^_^o)

自分の使える道具(定理や定義)を持って図形問題に取り組んでいれば、いざという時は総当たりで考えることもできますので何とか正解にたどり着けることもある でしょうd(^_^o)

 

道具① 基本中の基本…対頂角

まずは基本中の基本となる “対頂角” からです。２本の直線が交わる図形で向かいあう角は等しい というものですねd(^_^o)　この道具は小学生でもスンナリ受け入れられます。

そして、あくまで感覚ですが… 一番よく使う道具なんじゃないか と思います。

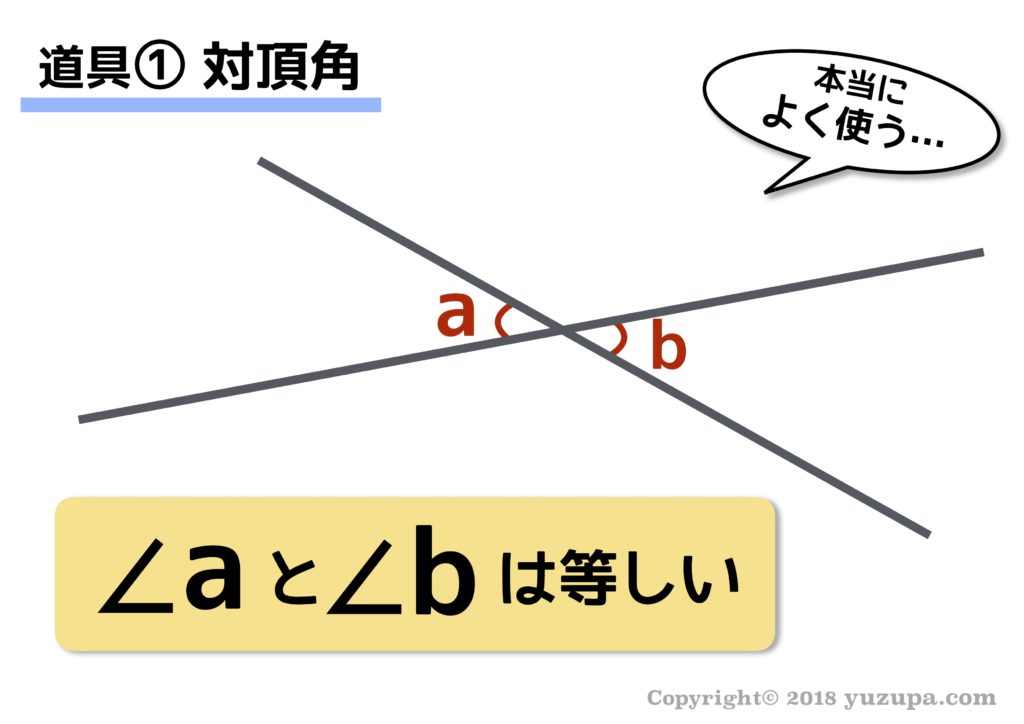
図形問題で 対頂角を見つけたらガンガン書いてしまう のが良いですね。

道具② 平行があれば…同位角

２つ目の道具は “同位角” です。２本の平行な直線において同位角は等しい というものです。平行じゃない場合も同位角と言いますが、図形問題では全く使いません！あくまで平行であることが条件です。

“平行な線があったら同位角”という感じで条件反射的に！

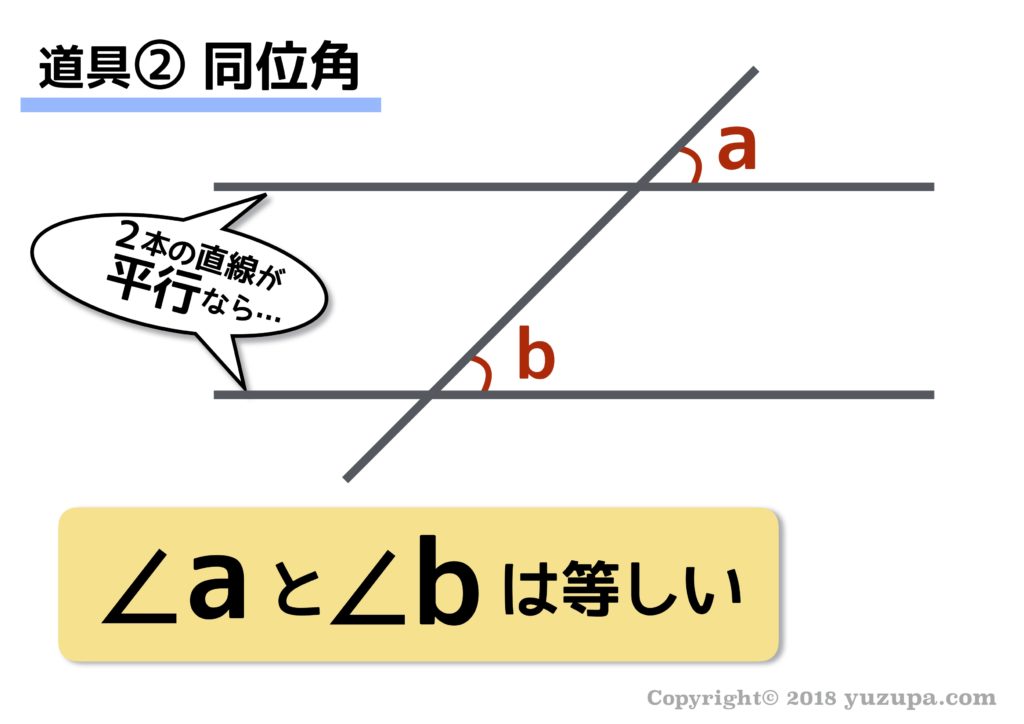
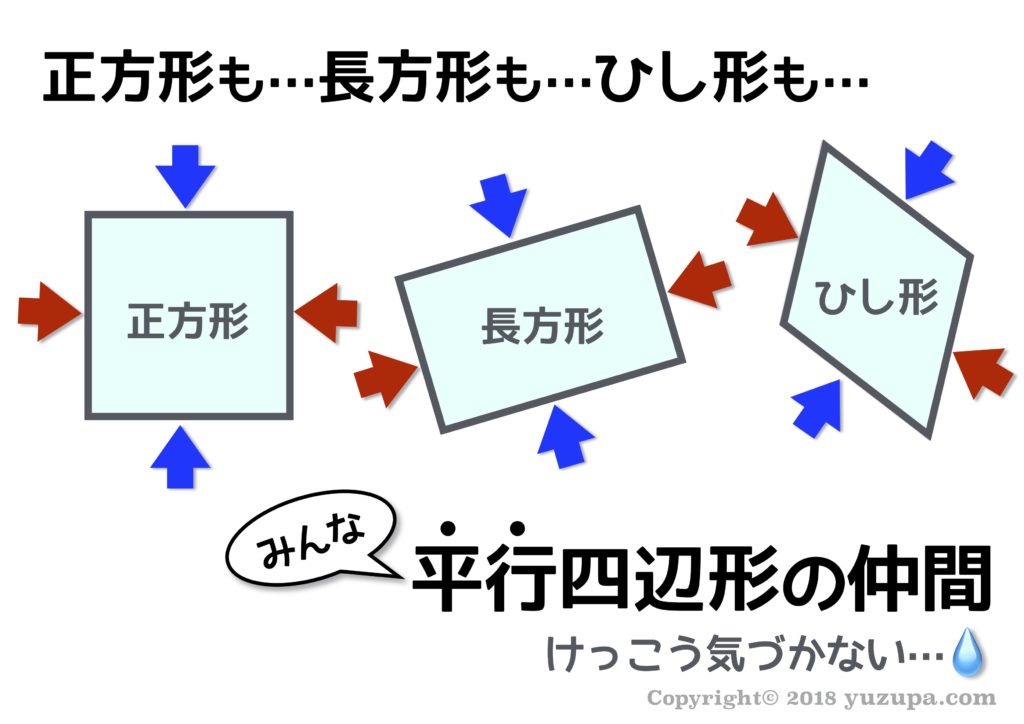
この同位角… 明らかな平行線がある場合、同位角の存在に気づくのですが、隠れた平行線だと結構気づきません(-_-;)　例えば “平行四辺形” といったその名のとおりの平行はすぐ気づきます。

ところが正方形が出てくる問題だと気づかなかったりします… 当然ですが ひし形も正方形も長方形も向かい合う辺は平行です…私の娘はなぜかよく見落とします(-_-;)

あとは 問題文を読まずに見落とすパターン…(-_-;) 問題をよく読めっ！と言いたくなります… 算数の図形問題においては問題文をよく読んで条件を図に書き入れていく作業は慎重に…丁寧に…。

 

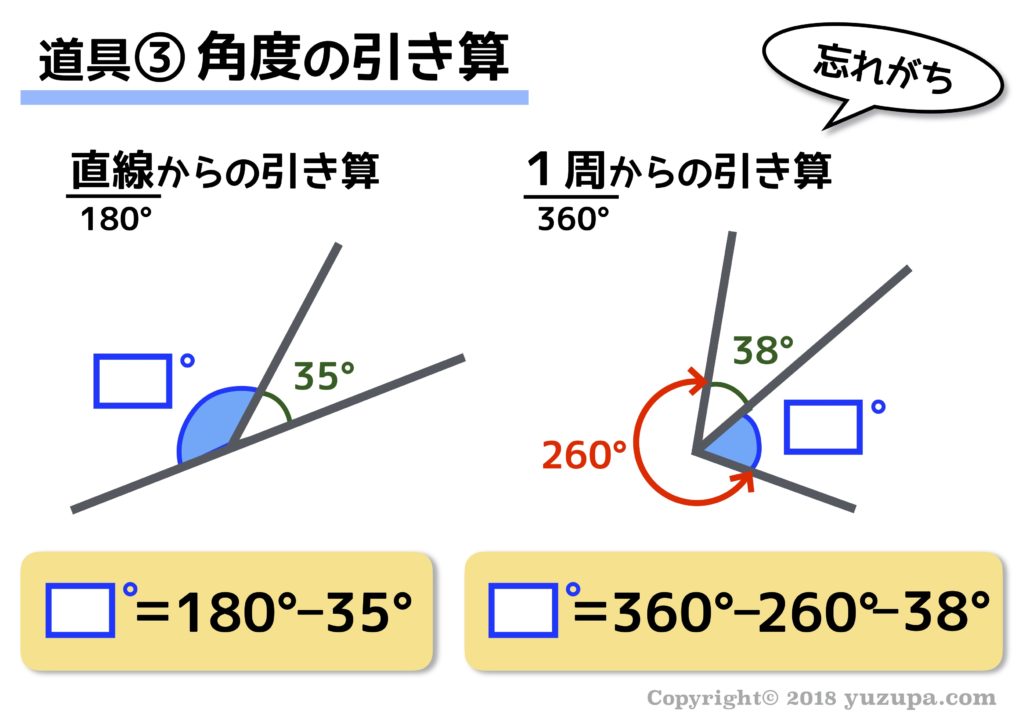
　道具③ 忘れがち! 角度の引き算

意外にも忘れがちなのが…この “角度の引き算” です。息子や娘があまりにも気づかないのであえて道具として定義してみました… ７つ道具の１つとして君臨していれば気づくでしょう(^_^;)

よく見落とすのは… 直線＝180度からの引き算、１周＝360度からの引き算 です。正方形や長方形の角は90度なのでその引き算を見つけられない事もよくありますね。

道具④ 二等辺三角形と正三角形を探せ

４つ目の道具は、特殊な三角形… 二等辺三角形や正三角形を利用したもの です。二等辺三角形の底辺にある２つの角は等しいですし、正三角形の角はどれも60度ですねd(^_^o)

なぜ、この道具が使えないのか？それはシンプルに二等辺三角形や正三角形を見つけられないからです(-_-;) 特に気づかないパターンは、我が家の実績では以下の２つのパターンでした。

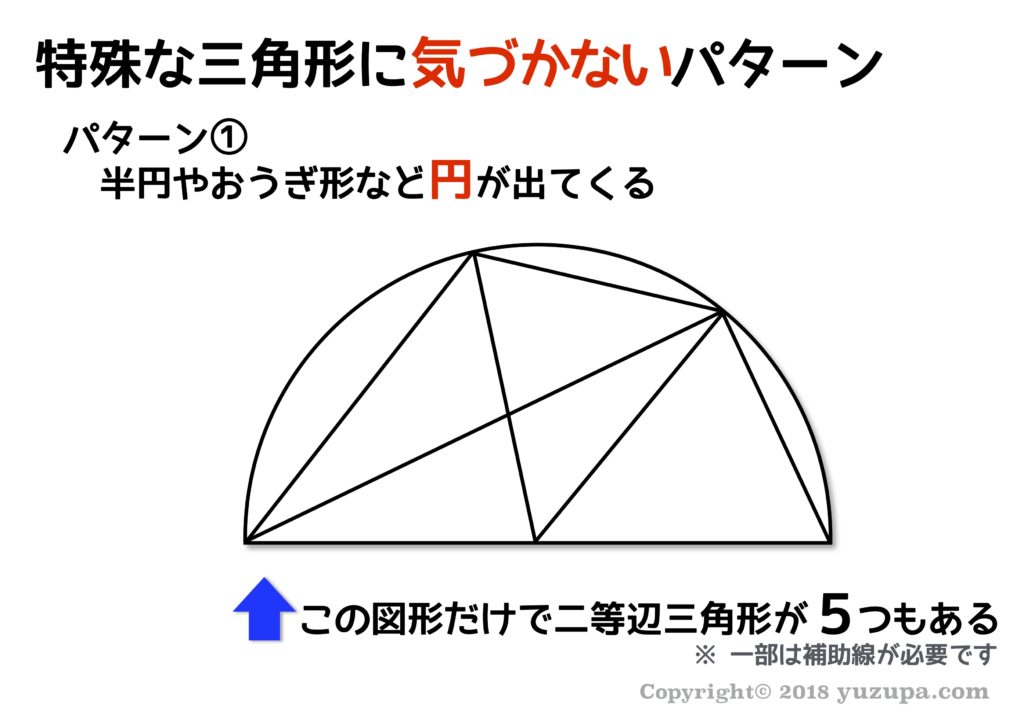
(1) 円の半径がどこも同じという事に気づかない
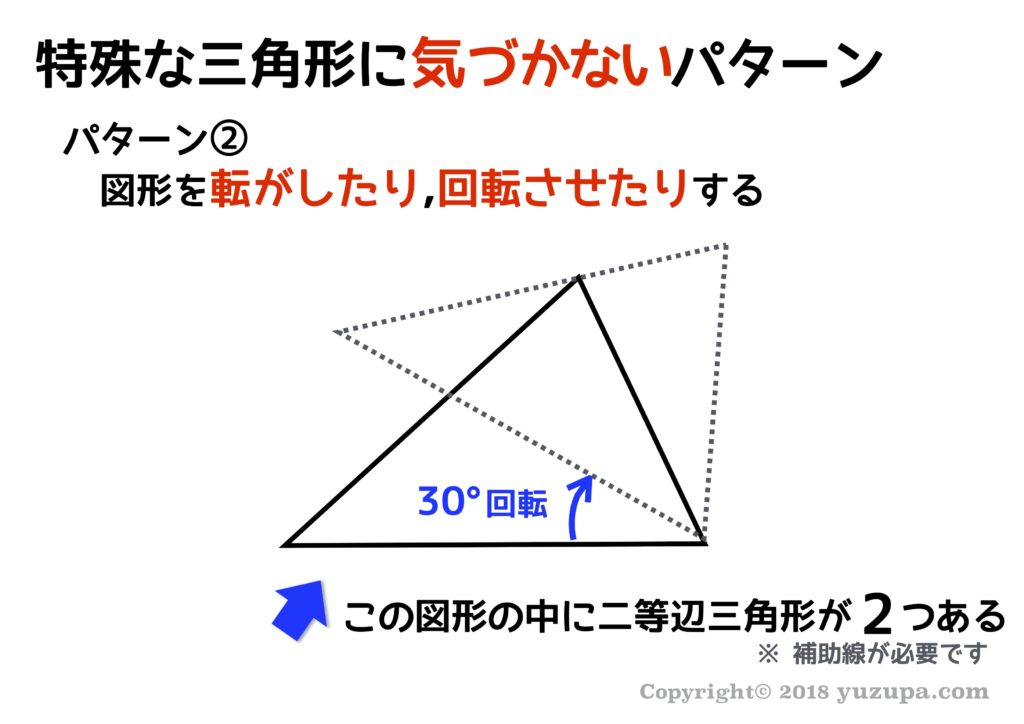
(2) 図形の回転でできる同じ長さの辺に気づかない

半円でもおうぎ形でも…とにかく円が出てきたら半径は全て等しいので二等辺三角形や正三角形が現れる確率がグンと上がります。円が出てきたら”特殊な三角形”の道具が使えるかもと意識するのが大切ですね。

半円やおうぎ形などの円が出てくるパターンと同等なのですが、図形がある点を軸にして何度か回転したり、図形が転がる問題 でも “特殊な三角形” が使える確率が高いと言えるでしょうd(^_^o)

 

道具⑤ 必ず使う!? 内角の和

必ず使うのでは無いかと錯覚するほどよく使うのが “内角の和” です。三角形であれば180度、四角形であれば360度、五角形であれば540度です_φ(･_･

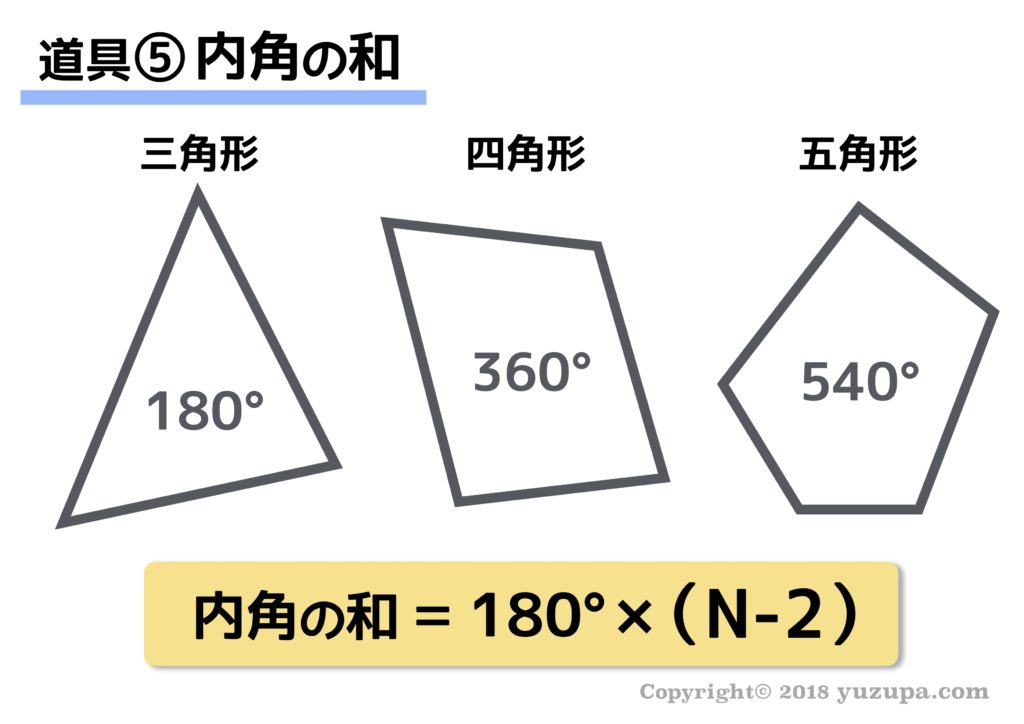
公式もありますが角度を求める図形問題で使うのは三角形と四角形がほとんどです。課題は、複雑な図形になると三角形や四角形を見つけられないということです(-_-;)

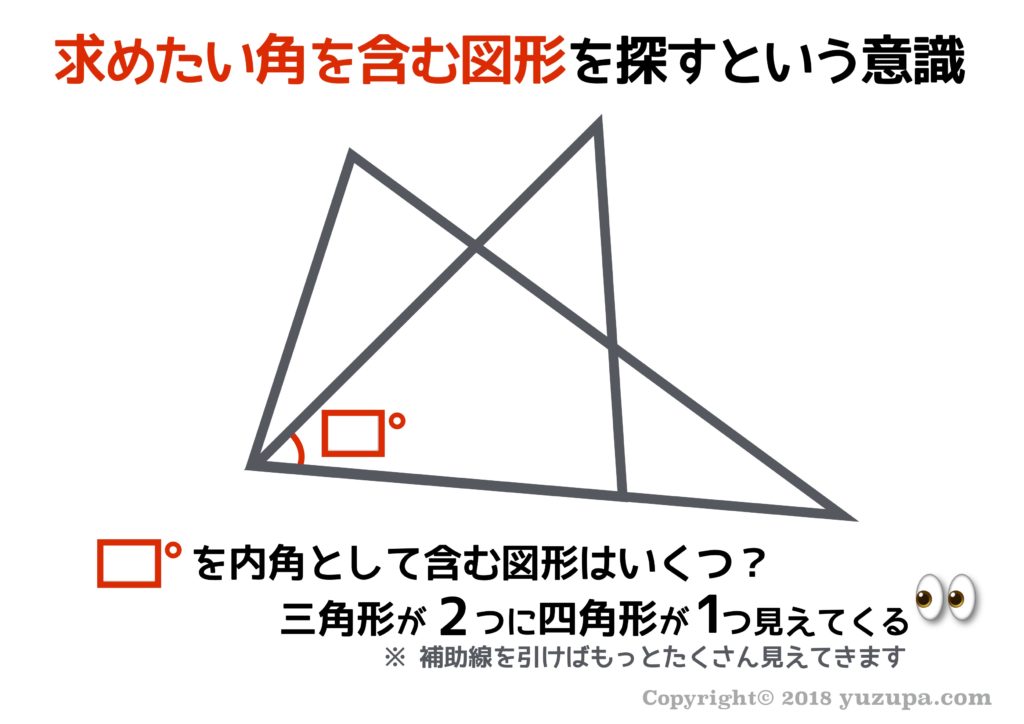
なかなかうまく使えない時は… “求めたい角が含まれる三角形や四角形を探す” という意識を持ってもらうと効果があるかもしれませんd(^_^o) うちはこの “意識” だけで改善しました。

道具⑥ 図形の折り返しに注意

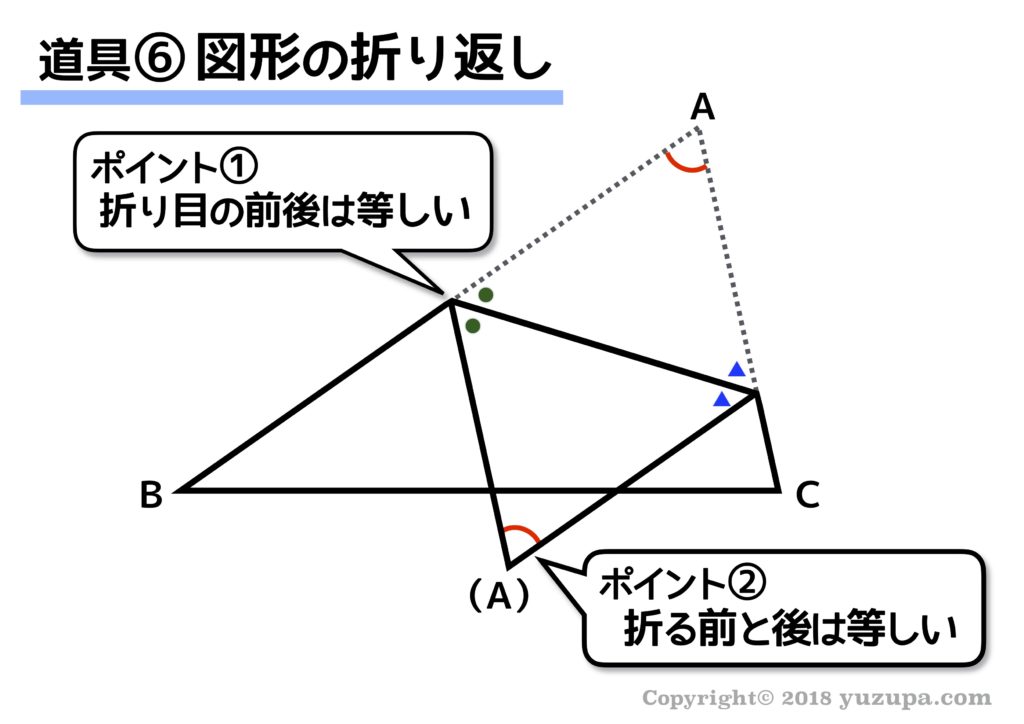
６つ目の道具は、私の娘がどハマりした “図形の折り返し” です(^_^;) 図形を折り返すと同じ大きさ角が結構たくさん出てくる 事に気づかないんですね…

元の図形と折り返した後の図形で対応する角が同じ大きさである事に加え、折り目のところにも同じ大きさの角があるのですが…とにかく忘れてしまう(-_-;)

図形を折り返した時…同じ大きさの角は２ポイント あります

道具⑦ 相似であれば角度は同じ

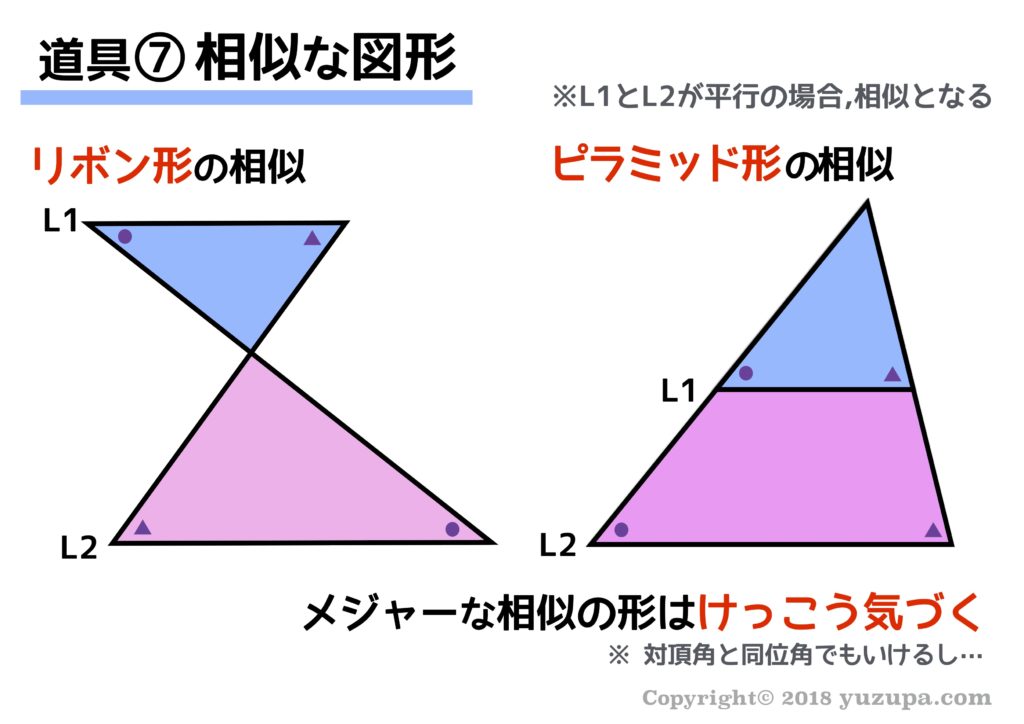
いよいよ最後の道具… 小学生には、けっこうな嫌われモノの相似 です(^_^;) もちろん使う道具は 相似の図形は対応する角の大きさが等しい というものですね。

相似といえば… “リボン形の相似” と “ピラミッド形の相似” です。が…この２つのタイプの相似は子供はけっこうちゃんと発見してくれます ( ２本の平行があるので同位角＋対頂角でもイケちゃいますしね… )

見落とすのは…問題文にサラっと書かれる”相似” です

問題文にサラっと書かれる「三角形ABCと三角形DEFは相似です」は本当にクセモノです(-_-;) 当然対応する角は同じ大きさなんですが…気づかない。道具の１つとして挙げたのはそんな理由からです。

補足：円周角は道具じゃない？

受験サイトや受験ブログでちょっと話題になった入試問題があります。２０１７年の渋谷教育学園幕張中学校の算数の問題で “円周角の定理” が出た というもの。

なぜ話題になったかというと 円周角の定理 は小学生の教育過程には無く中学３年生で習得する範囲だからです…。えっ…中学３年生の範囲 ∑(ﾟДﾟ)

でも実際は、円周角の定理を使わなくても解ける(小学生の学習範囲だけで解ける)ものでした(^_^;) でも多くの人が円周角の定理を使った方がすぐに解けると思ったようです。

結果として…円周角は道具としては不要 と考えています

が、もう…図形問題なんて余裕だぜっ！というお子様であれば８つ目の道具として覚えておくと、２０１７年の渋幕の問題もサクッと解けるかもしれません(^_^;)

まとめ

以前公開して読者の方からコメントやご意見が多かった “割合と比の７つ道具” に続き、図形問題で角度を求める時に使う定理や定義を道具としてまとめてみましたd(^_^o)

算数の問題…特に図形問題は、使える道具の全体像を知ることで”試行錯誤”や”ヒラメキ”が有利 に動き出します。図形問題が苦手なお子様はぜひお試しを！

 

７つ道具のプリントは以下からダウンロードできます！印刷してご活用くださいd(^_^o)

 

比と割合でも７つ道具の記事を公開しています。以下からどうぞ！
参考リンク：割合と比は “７つ道具” で克服