中学受験:年齢算は “線分図の伸び縮み” を体得してスッキリ理解
年齢算を解くためには”線分図を伸ばしたり縮めたり”する
 こんにちは。かるび勉強部屋 ゆずぱ です。
こんにちは。かるび勉強部屋 ゆずぱ です。
あなたとお子様の年齢差は何歳でしょうか? 35歳だったり… 30歳だったりしますよね? では、あなたが80歳になった時はどうでしょうか? 当たり前ですが…あなたとお子様の年齢差はいつになっても変わらないですね(^_^;)
年齢差というものはいつまでたっても変わらない。当たり前の事ですが この条件を利用した算数の問題が年齢算と呼ばれる算数の特殊算です。年齢を扱うから年齢算…そのまんまですね (^_^;)
多くの受験サイトでは”年齢差が変わらない事がポイントだ!”とありますが、これを抑えただけではうちの息子はダメでした…(@_@) ではどうすれば良いか… 線分図を伸ばしたり縮めたりするという考え方をするだけで改善した んです。
目次
線分図の伸び縮みとは?
多くの受験サイトでは冒頭でご紹介した ”年齢の差はいつまでたっても同じ” という条件を線分図に描けば解けると解説されています。息子もこれで基礎問題は解けたのですが、複数人が出てくる応用っぽい問題になるとダメでした(T_T)
息子の場合、むしろ線分図を描くところに苦労していたのです。試行錯誤の結果…線分図を描く時に”何年後”とか”何年前”のような時間の流れを線分図の伸び縮みであると意識する事で線分図が描けるようになりましたd(^_^o)
未来だったら線分図を伸ばす
まずはシンプルな線分図を描いてみます。例えば… ”38歳の母親と11歳の息子” の線分図を描いてみます。 年齢算の場合、年齢の大きさを線分図の長さにして描くだけです。左端を揃えるのがポイントですd(^_^o)
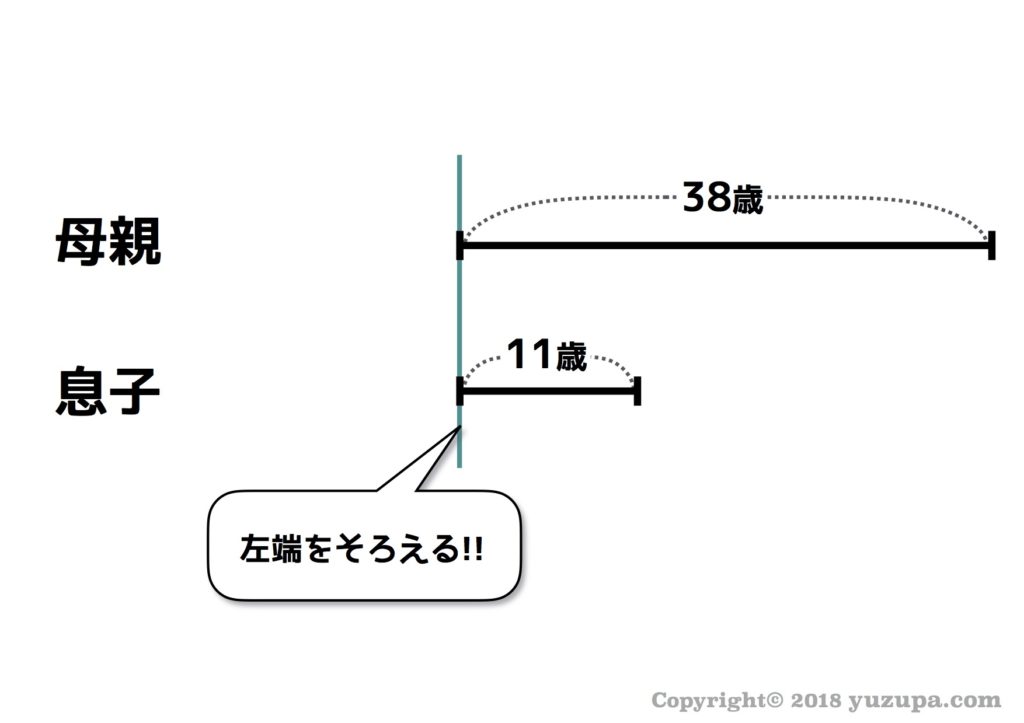
この親子ですが…15年後はどうなっているでしょうか? 今から年齢をさらに15歳とる事になるので…15年分だけ線分図を伸ばしましょう。これまたシンプルですね。ただ…ひとつだけコツがあります。
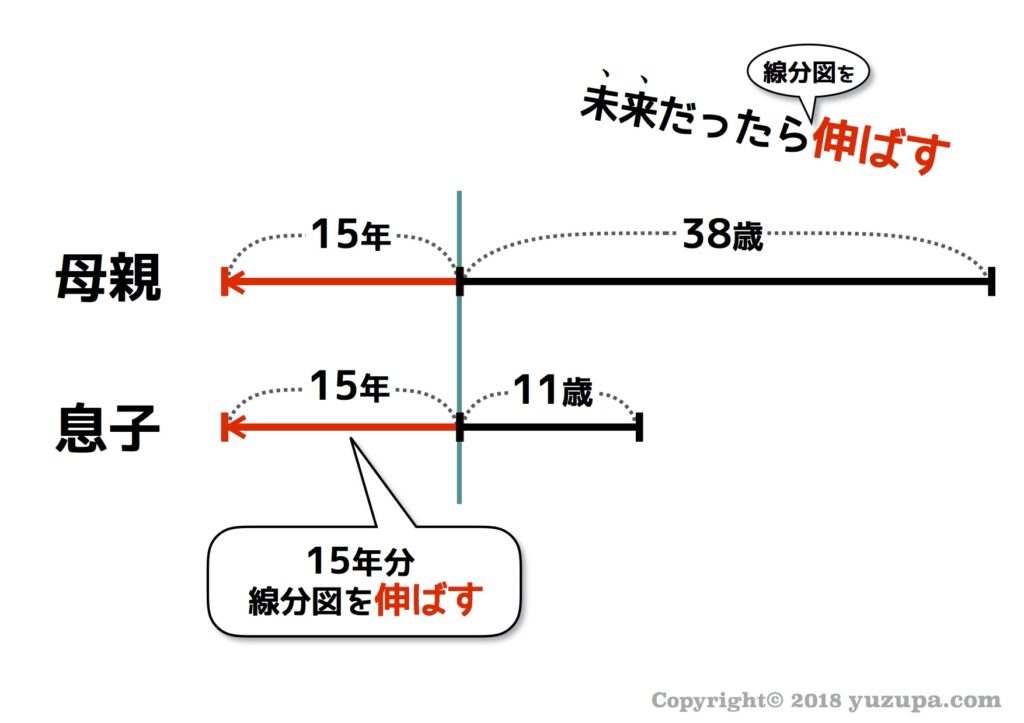
コツは左端を起点として左側へ伸ばすという事です。右側でも良いのですが…右へ伸ばすと比較しづらい…。また親子の年齢の差は27歳差ですが、左側に伸ばすと何も意識しなくても線分図に年齢差が自然と現れるんです _φ(・_・
過去だったら線分図を縮める
今度は過去です。先ほどの27歳の差がある親子…5年前はどんな感じだったでしょうか? 今よりも5歳年齢が少なかったので…5年分だけ線分図を縮めてみましょう。コツは同様に左端を起点とする事ですd(^_^o)
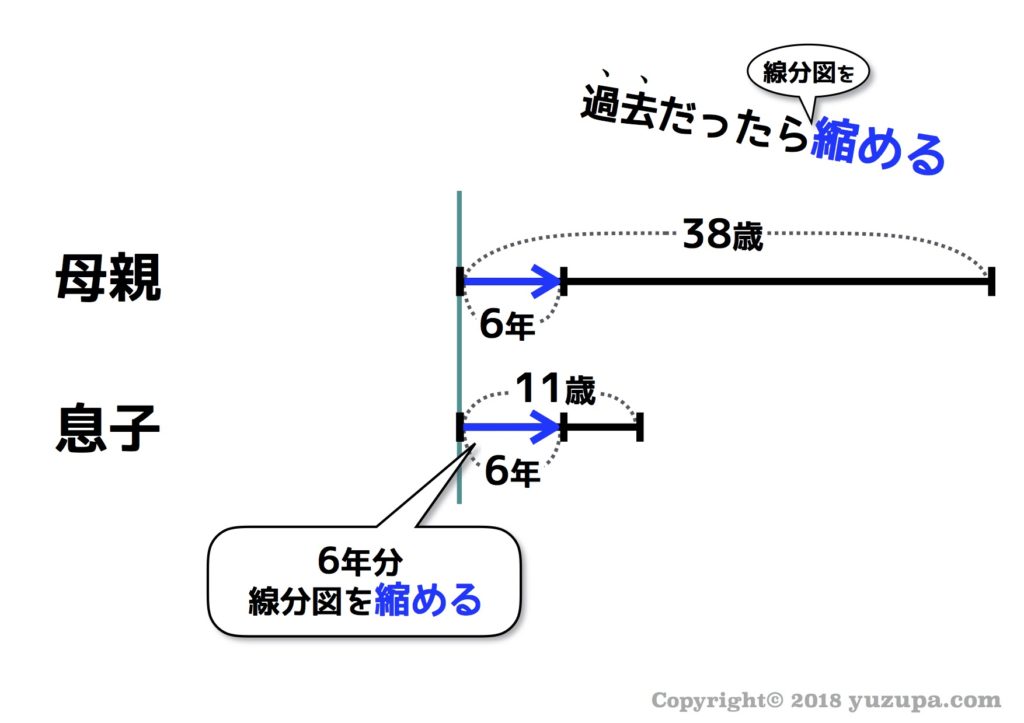
平等に年をとる=伸び縮みはみな同じ
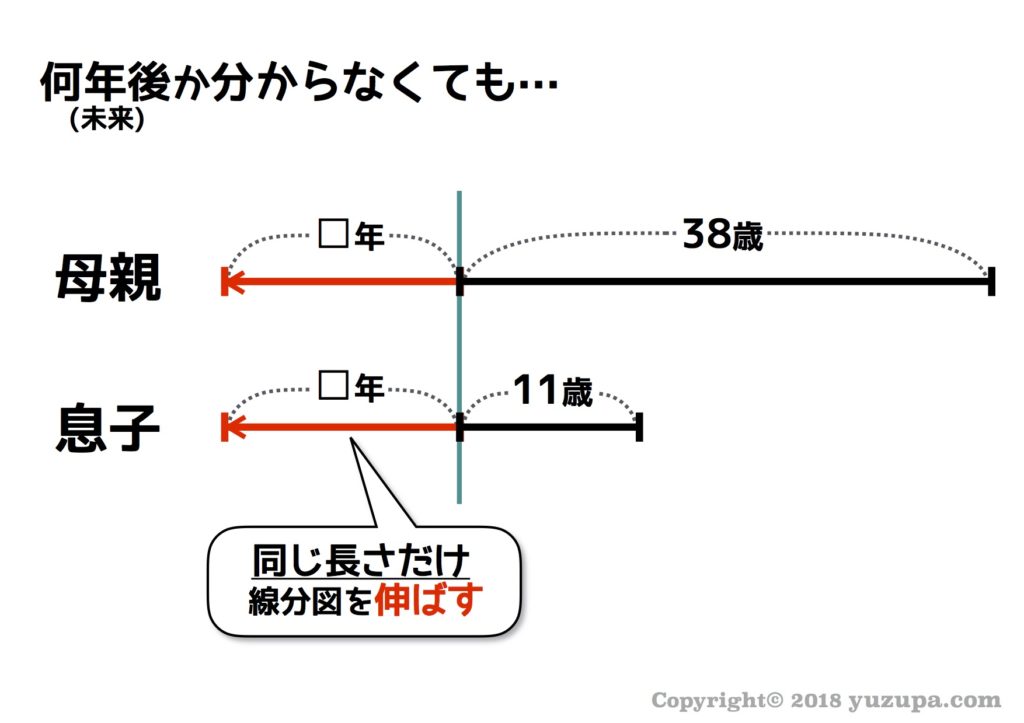
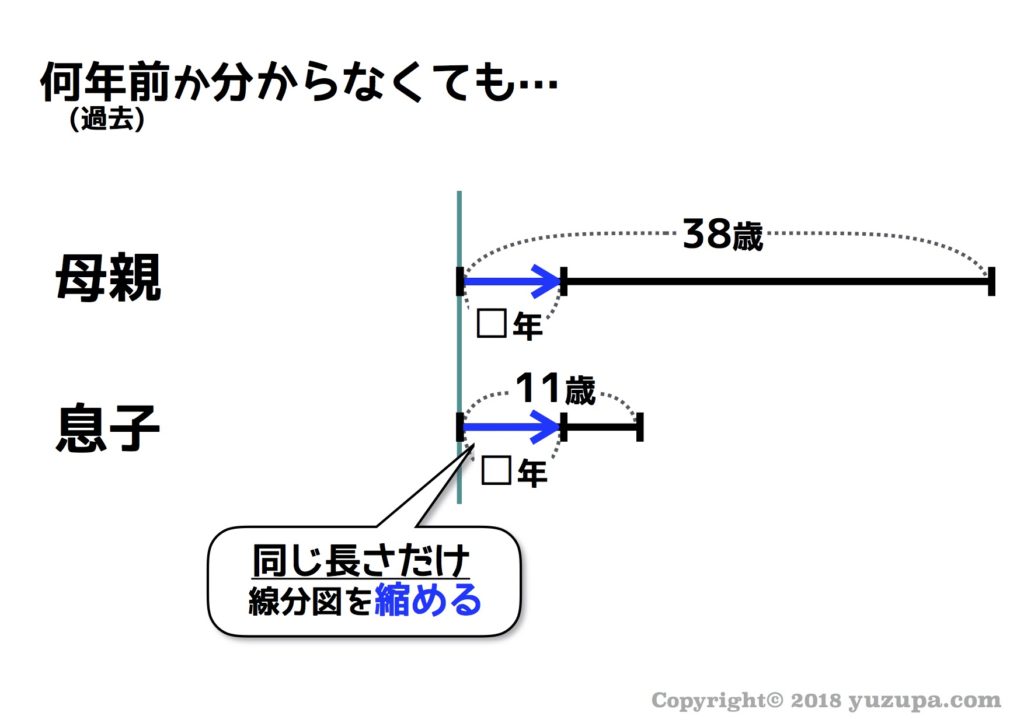
つぎは”何年後かの未来の姿”や”何年前か過去の姿”を線分図に描いてみましょう。何年か分からないので長さは適当に書くことになりますが、ひとつだけ気をつける事、それは…母も子も同じ長さの伸び縮みをさせる事ですd(^_^o)
年齢算を解くための3ステップ
線分図の伸びと縮みを意識して正しい線分図が描けたら8割は解けたようなものですが… 最後に比のテクニックが必要です。具体的な問題を元に年齢算を解くための3つのステップをご説明したいと思います (^-^)
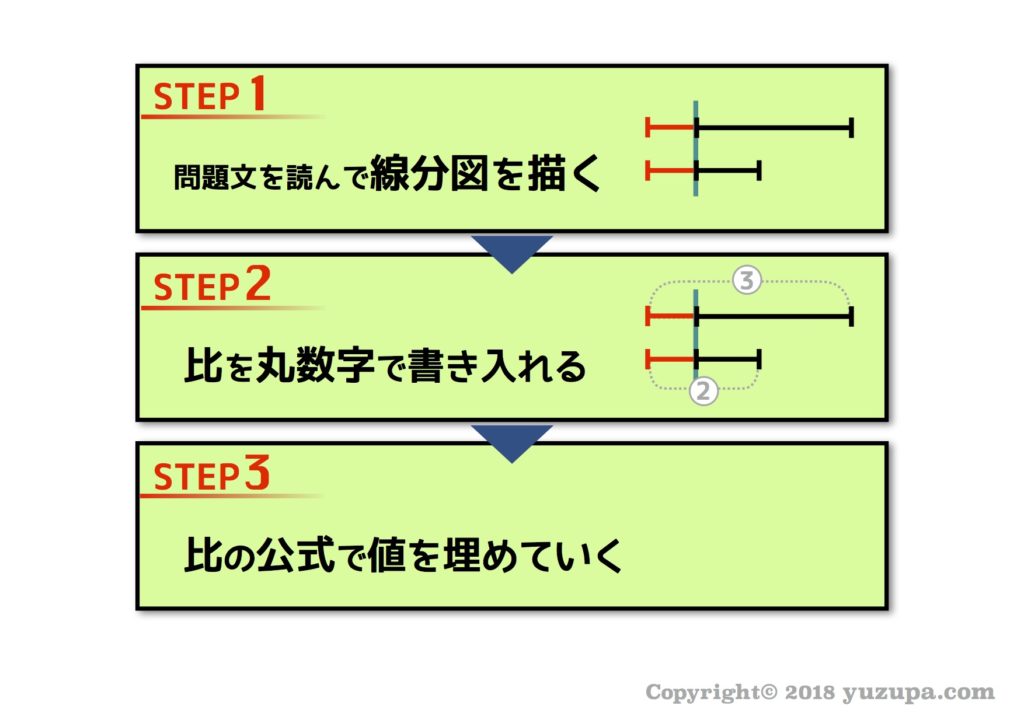
STEP1 線分図を書く
アキラさんは8歳で、ヒロシくんという5歳の弟がいます。2人の年齢の比が5:4になるのは今から何年後でしょうか?
それでは線分図を描いてみましょう。まずはシンプルにアキラさん(8歳)とヒロシくん(5歳)の線分図を書きます。左端は揃えておきましょう。フリーハンドなので長さはだいたい合っていれば良いですね。
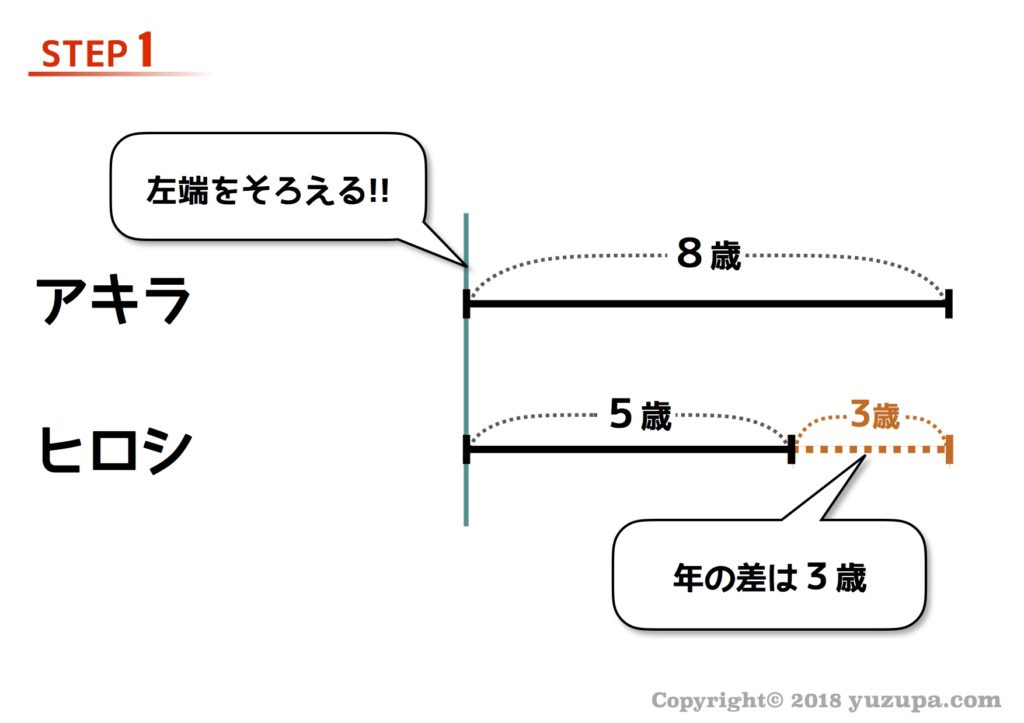
問題文では”何年後か”を求めさせようとしているので、描く線分図は”未来”ですねd(^_^o) 左端を起点として線分図を伸ばしましょう! 何年後かは分からないので□年として、長さは2人とも同じ長さにするのがポイントです。
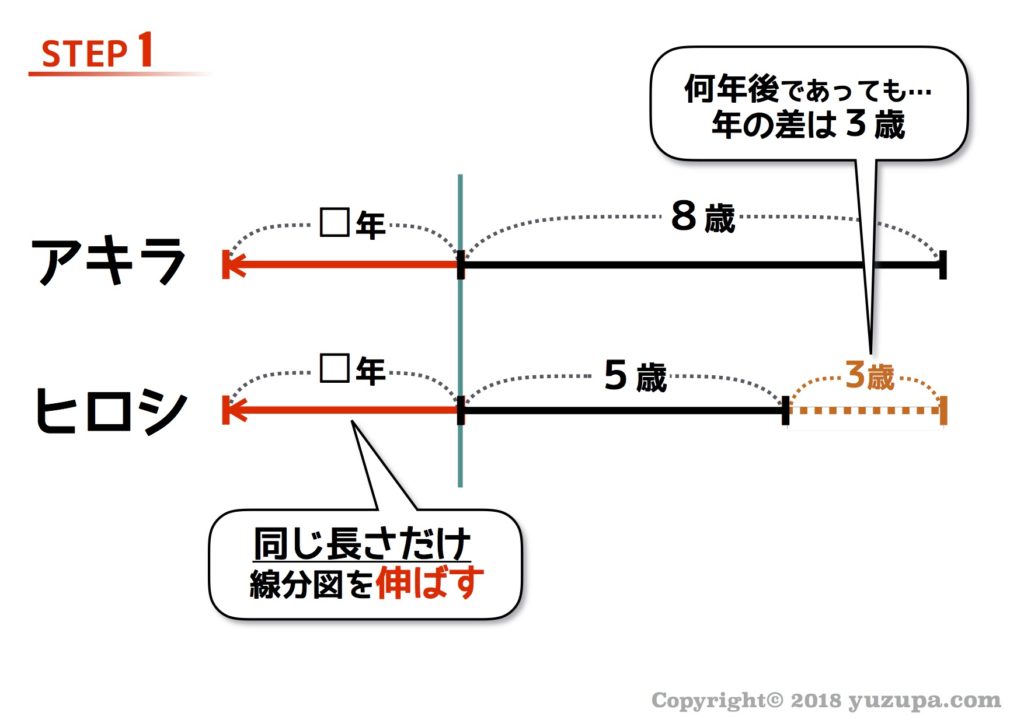
たったこれだけで 線分図は完成 です!
STEP2 比を丸数字で書く
アキラさんは8歳で、ヒロシくんという5歳の弟がいます。2人の年齢の比が5:4になるのは今から何年後でしょうか?
次に比を丸数字で書いてみます。これもシンプルに描く事ができますね…”比”ですので必ず丸数字を使いましょう。また何が5:4なのかに気を付けましょう。この問題の場合は…ふたりの何年後かの年齢が5:4ですね!
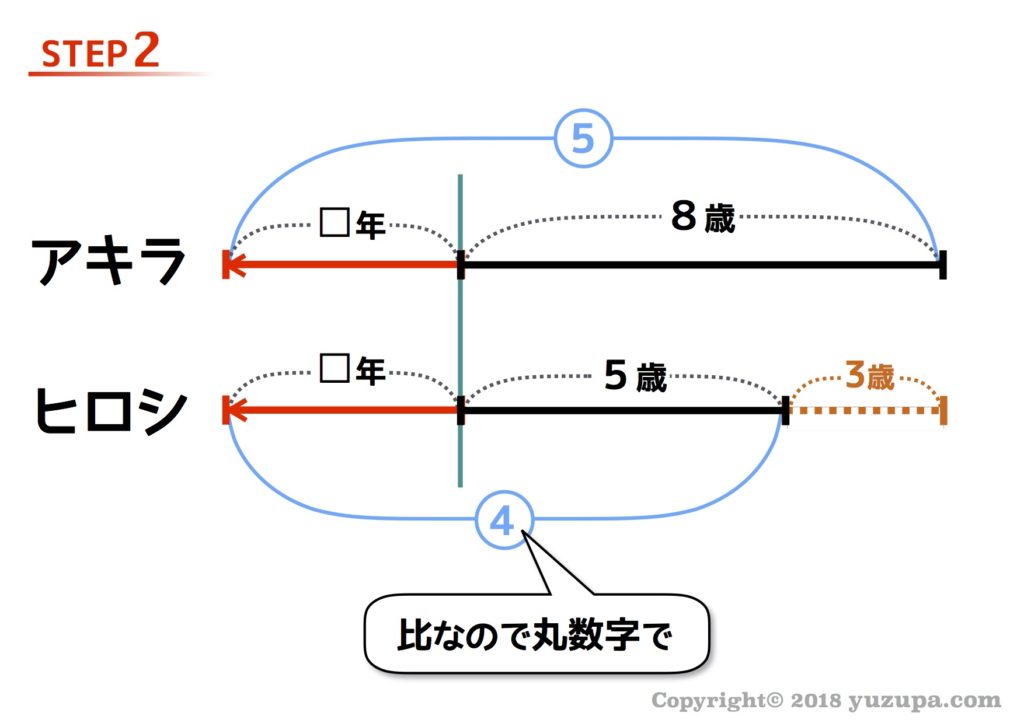
STEP3 比の公式で値を出す
アキラさんは8歳で、ヒロシくんという5歳の弟がいます。2人の年齢の比が5:4になるのは今から何年後でしょうか?
最後は比を使って値を求めていきます。実はここで相当算というテクニックを使います。詳細の解説は割愛しますが、線分図で丸数字と実際の数字のペアを見つけて丸数字ひとつ分の値を求める テクニックです。
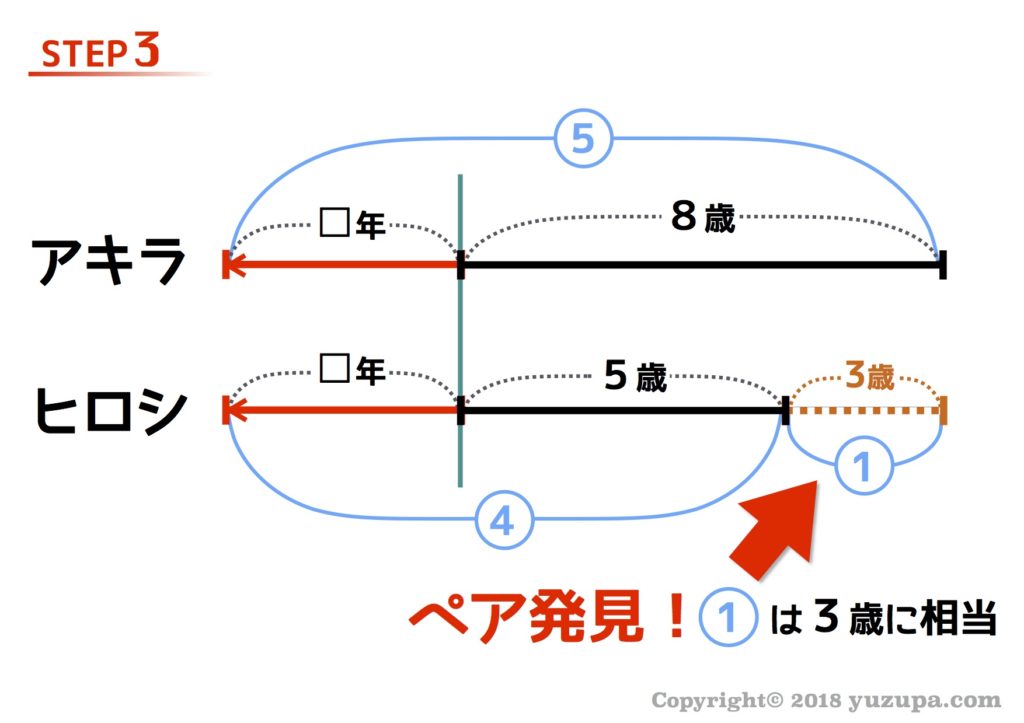
この問題の場合は、ちょうど兄弟の年齢差のところが①と3歳でペアになってますね。丸数字ひとつ分は3歳ということが分かります。最後に丸数字を実際の年齢に変換すれば答えが導き出せますd(^_^o)
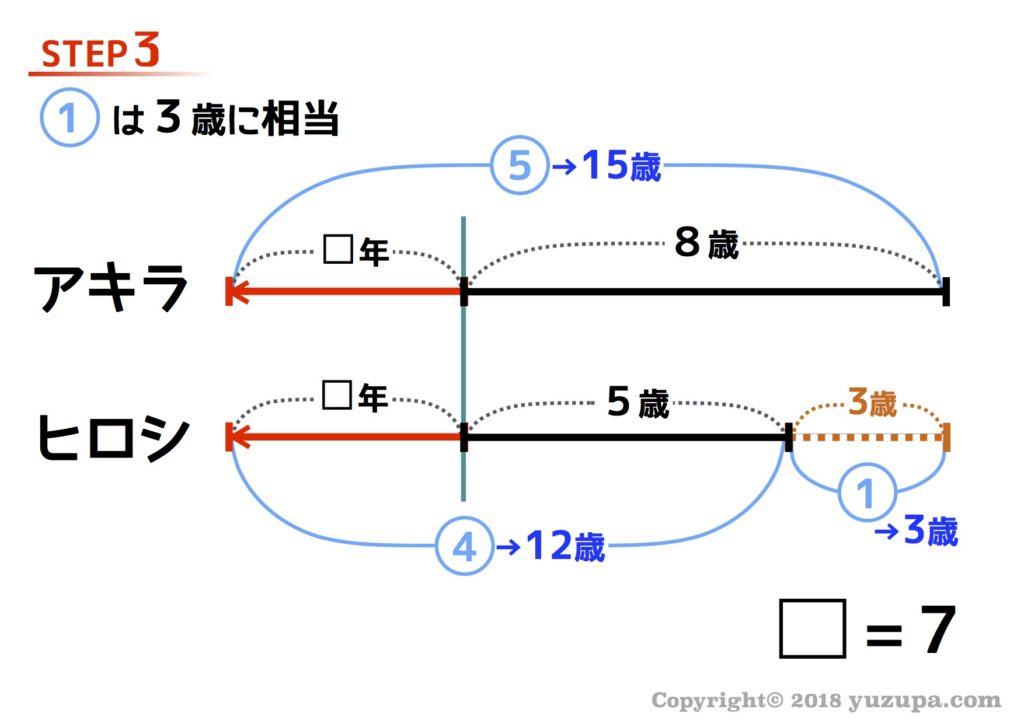
この問題で問われているのは ”何年後でしょうか?” なので… 答えは7年後 になります。
年齢算の練習問題
実際の3題の例題を元に年齢算の3ステップを問題のパターンを意識しながらやってみたいと思います(^_^*)
未来を想像する問題
アキラさんは8歳で、ヒロシくんという5歳の弟がいます。2人の年齢の比が5:4になるのは今から何年後でしょうか?
未来を想像する問題は…上記のように2人の年齢の関係が条件に当てはまるのは何年後か?といった未来にフォーカスされた問題です。アキラさんとヒロシくんの問題と同等ですので本項での説明は割愛いたします。
過去を振り返る問題
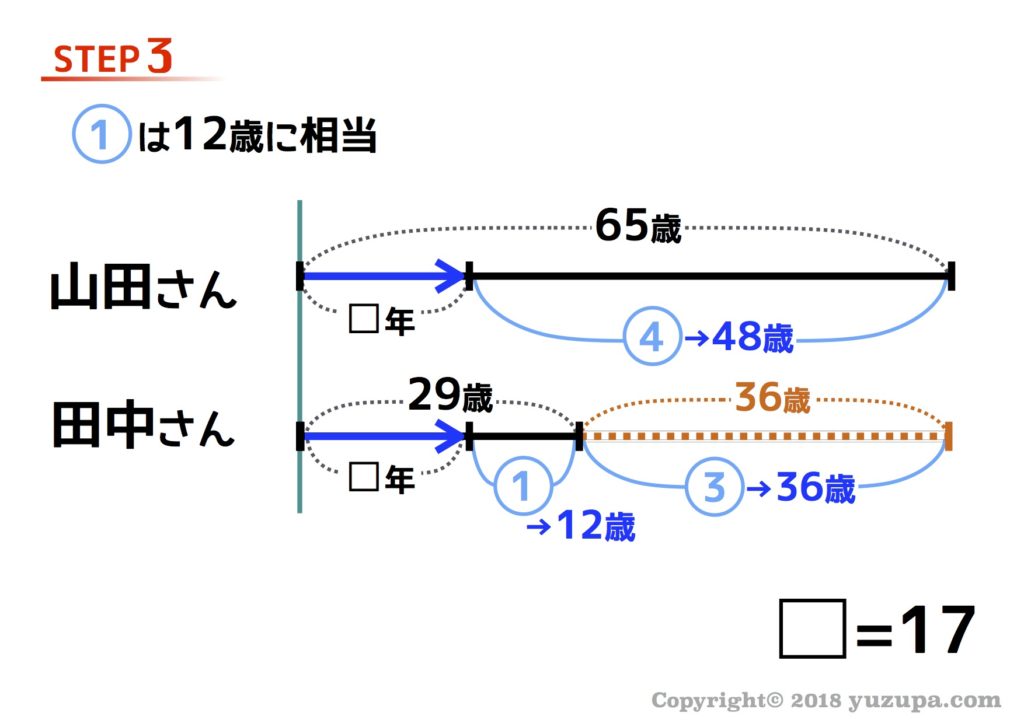
いま山田さんは65歳で田中さんは29歳です。2人が出会った時…山田さんの年齢は田中さんの4倍でした。2人が出会ったのは何年前でしょうか?
まずは線分図を描いてみましょう… 長さにこだわりすぎないように!
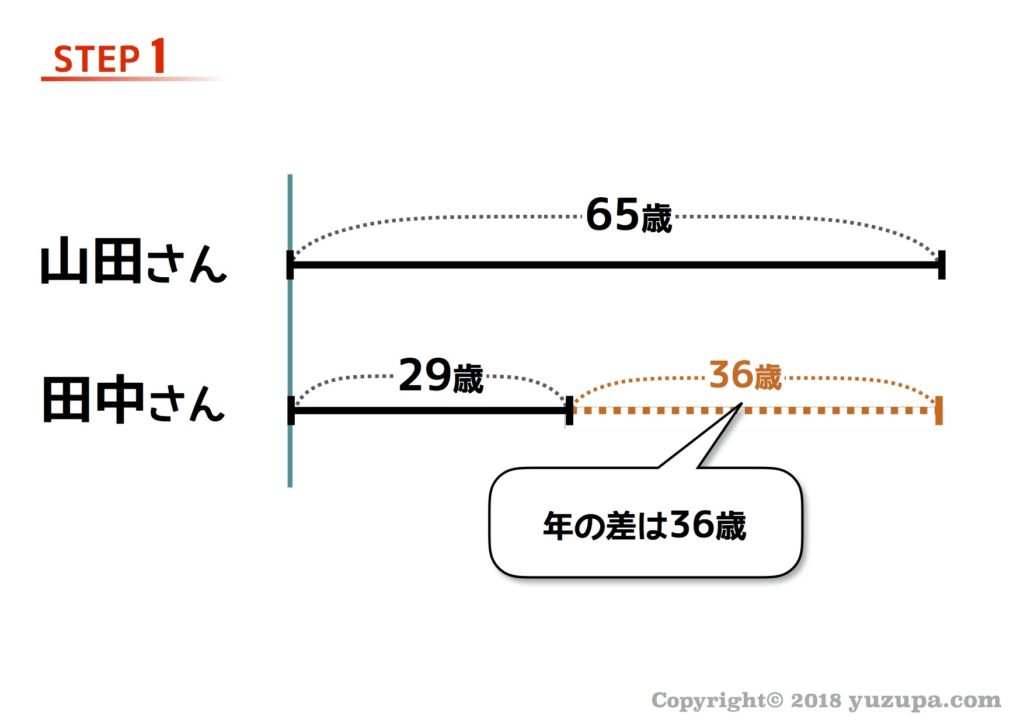
これは 過去を振り返る問題なので線分図を縮める ですね d(^_^o)
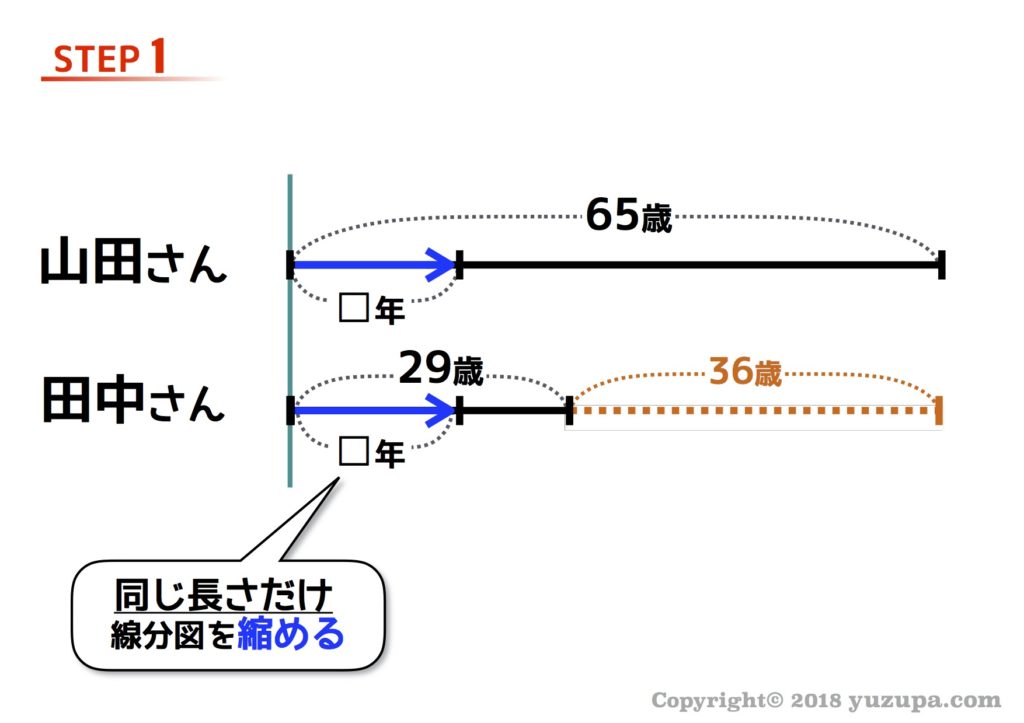
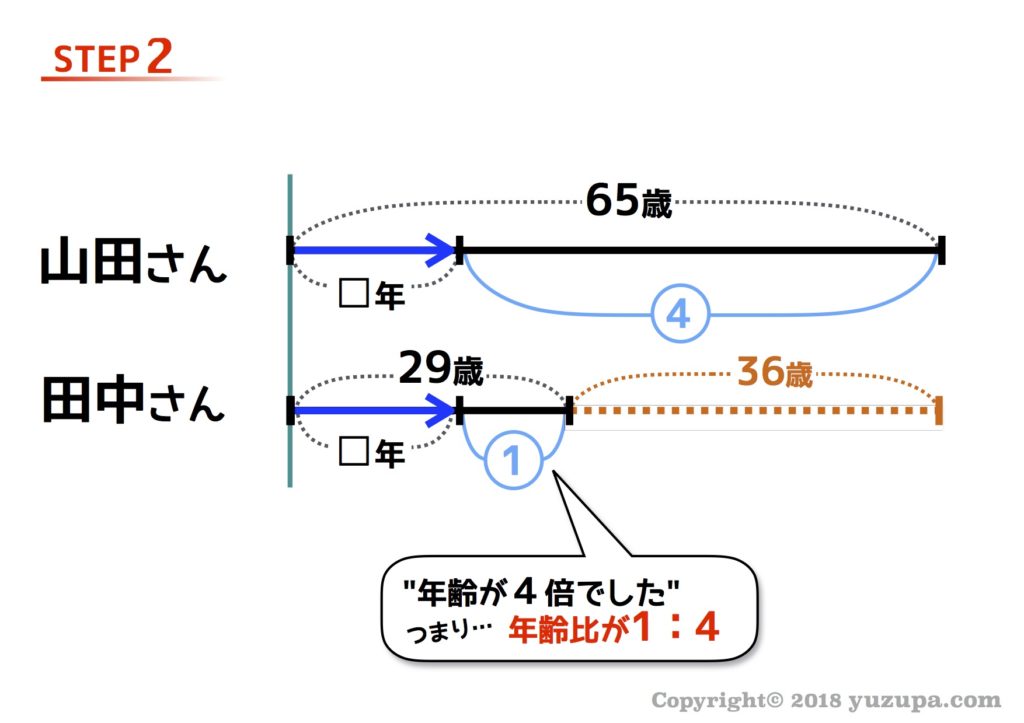
STEP2は比を丸数字で書き入れます。”山田さんの年齢が田中さんの年齢の4倍” という事は…田中さんが①のとき山田さんは④になりますね。線分図に書き加えましょう_φ(・_・
最後はSTEP3です。山田さんと田中さんの年齢差の部分に比の丸数字と実際の数字のペアを見つける事ができます。③が36歳分に相当するという事がわかります。
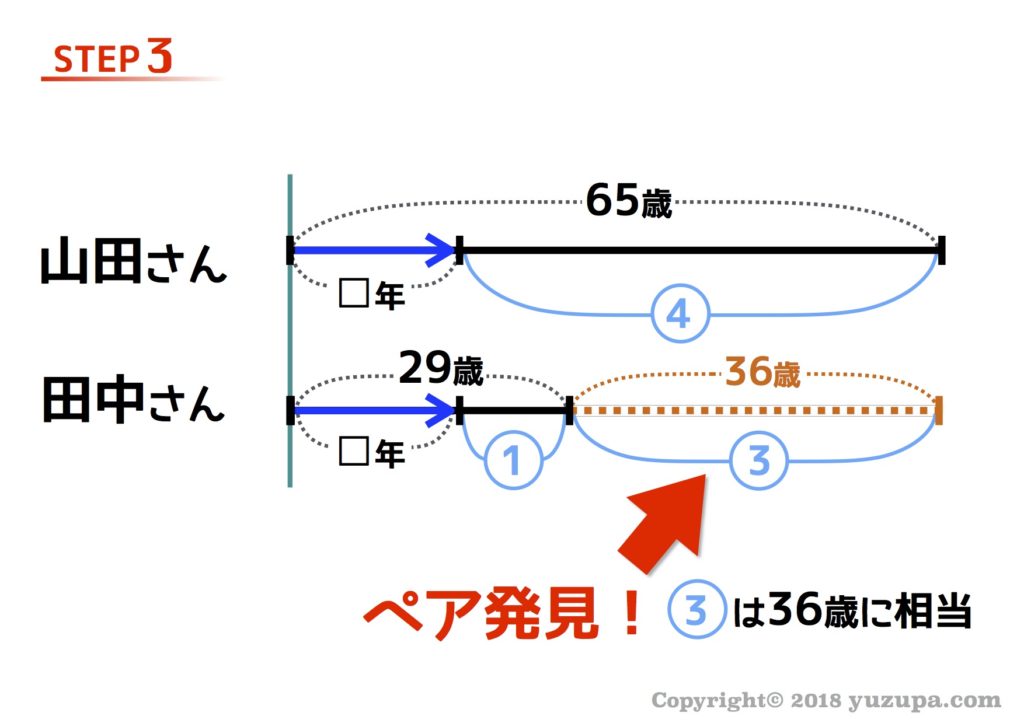
最後はひたすら比で分かった数字を線分図に埋めていきます…。この問題で問われているのは”ふたりが出会ったのは何年前” ですから、答えは17年前 となります。
年齢の和が出てくる問題
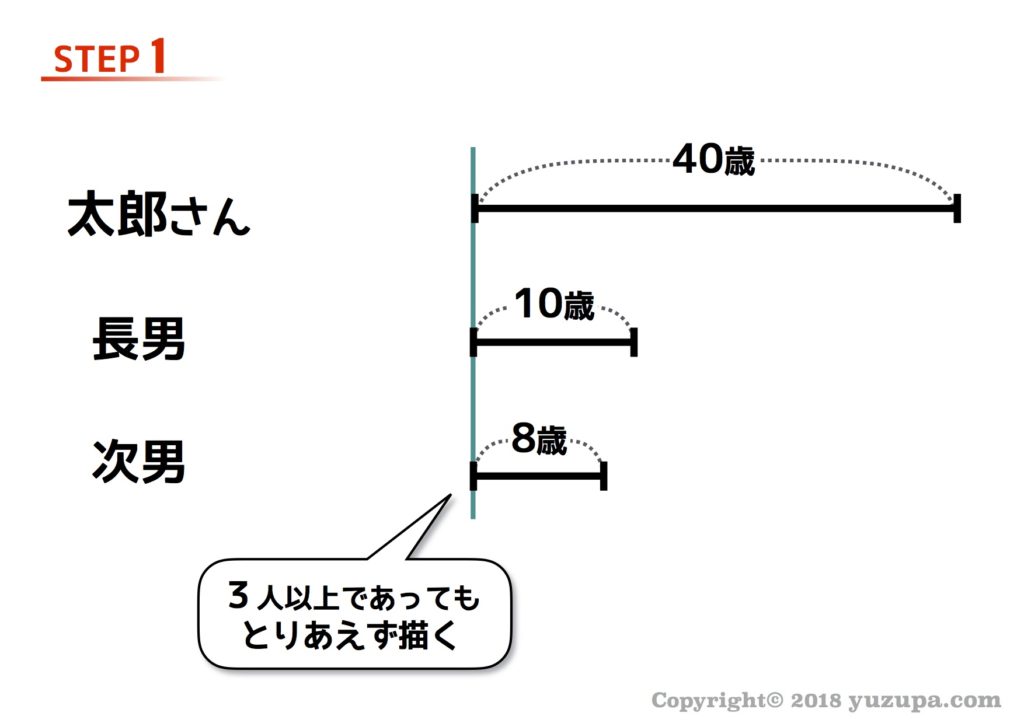
太郎さんは現在40歳で、長男が10歳、次男が8歳です。長男と次男の年齢の和が太郎さんと同じになるのは何年後でしょうか?
STEP1はいつものように年齢を線分図に落としていきます。3人であっても4人であっても気にしない!とにかく線分図を描いてみるところから着手しましょう!
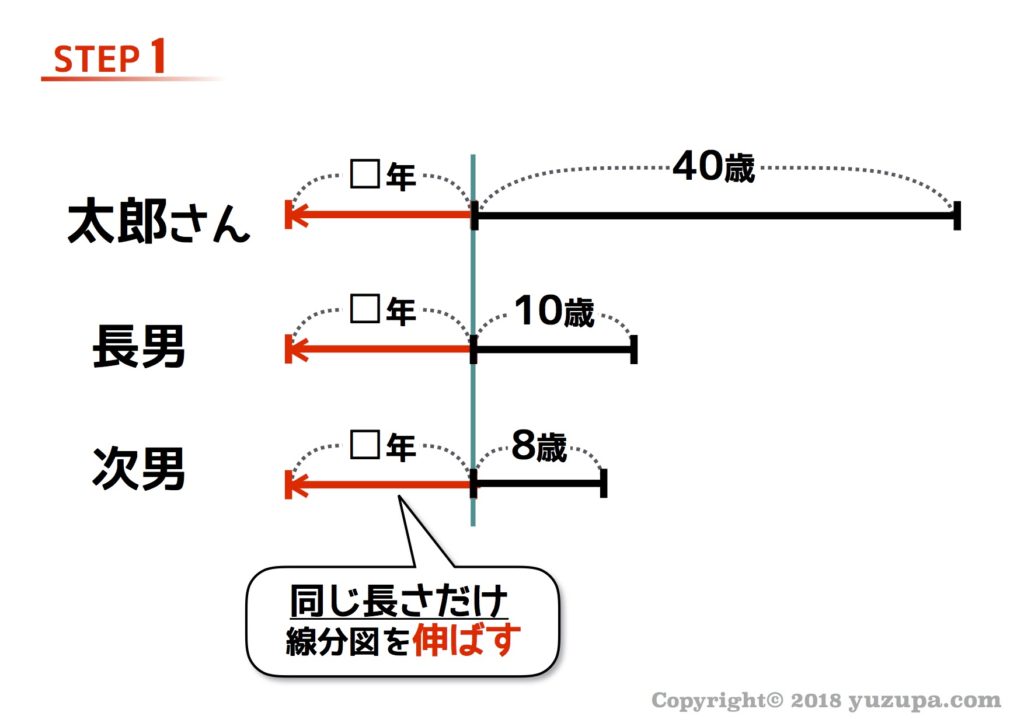
この問題はどうも未来を想像する問題のようなので線分図は伸ばすです!子供であっても大人であっても歳をとる速度は同じなので伸ばす線分図は同じ長さで!
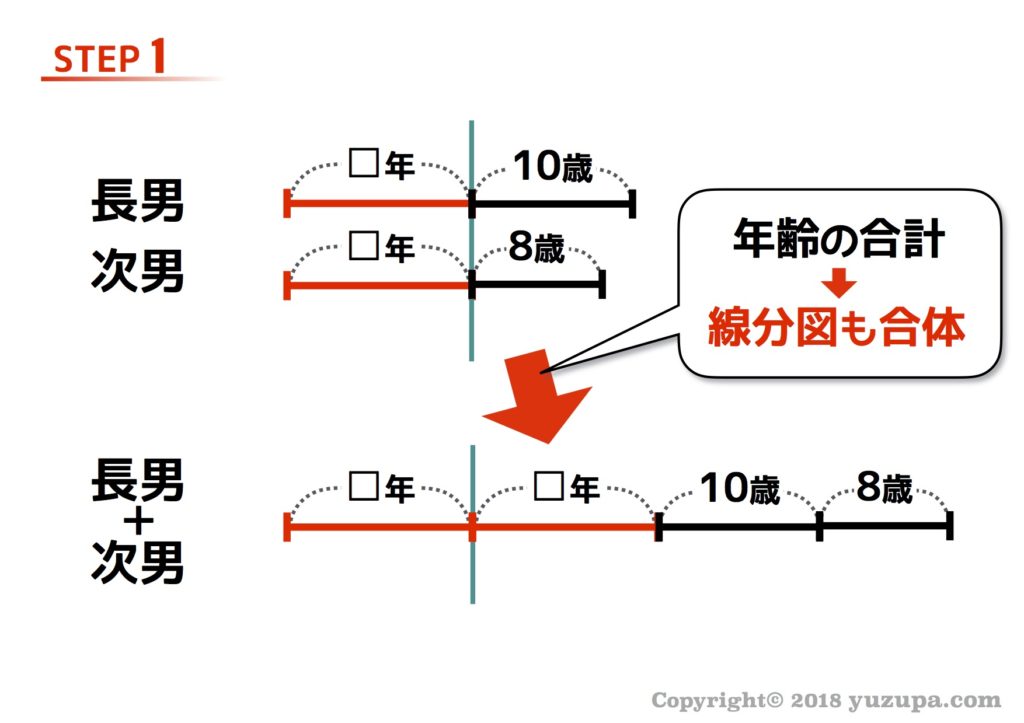
さて…今までの問題と違い “2人の年齢の合計” という条件が出てきます。でも…年齢の合計と言われているので言われたとおり線分図も合計に…つまり合体させればよいと考えます。
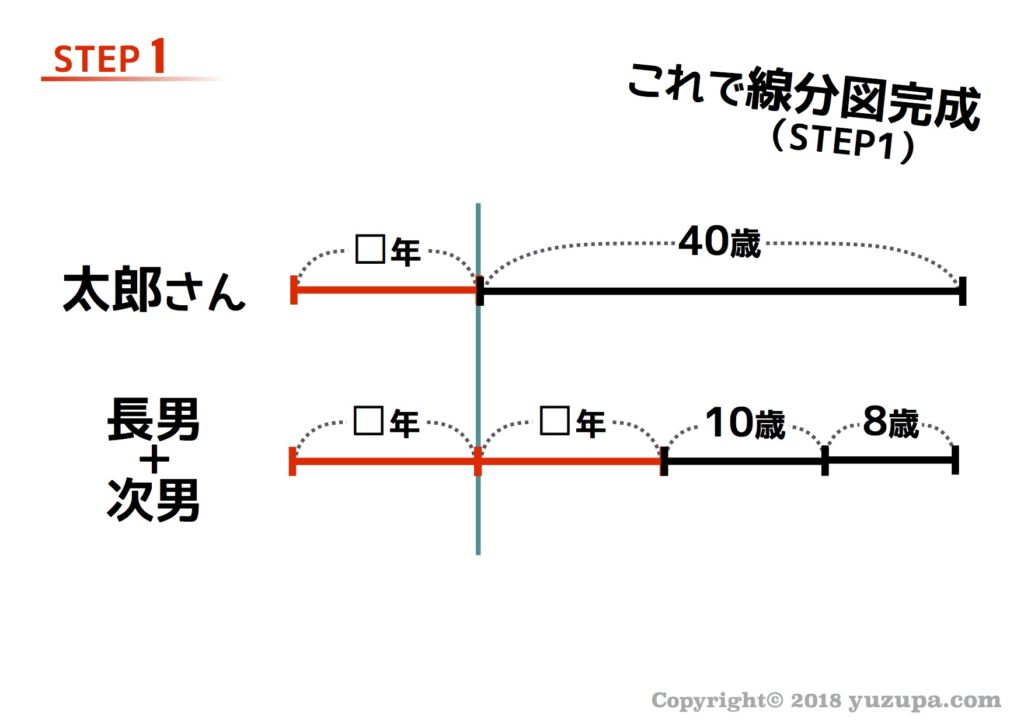
STEP2は比を丸数字で描き入れる作業です。 “年齢が同じになる”という条件は 年齢の比が1:1になるという事ですので、線分図にそれを描きいれます。
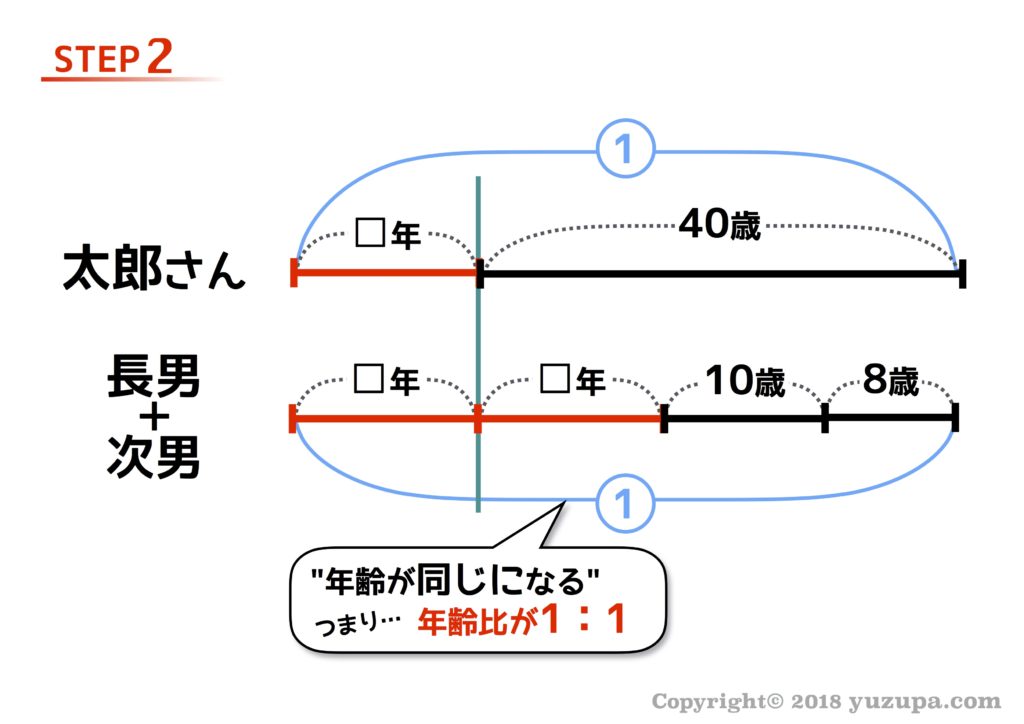
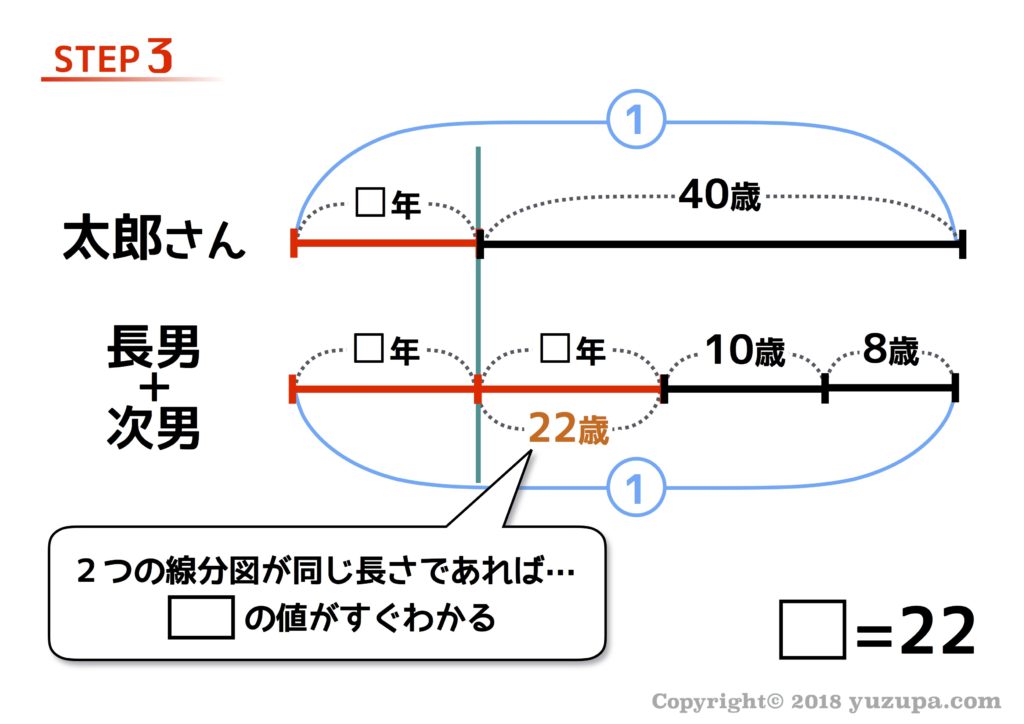
STEP3では値をどんどん埋めていきますが、この問題の場合…2つの線分図の長さが同じと分かった時点でもとめるべき値が分かってしまいます。求めているのは”何年後”の部分ですので 答えは22年後 になります。
まとめ
今回の記事では年齢算を解説しましたが、きっかけは私の息子が応用問題に太刀打ちできなかったからです(T_T) 応用問題を解くには年齢差がいつも同じという事よりも線分図の書き方を復習した方が良さそうです。
線分図を描くときのコツ3つです。
1)未来は左端を起点に伸ばす!
2)過去は左端を起点に縮める!
3)伸び縮み長さはみんな同じ!