中学受験:線分図はいつ使う? たった3つの本質で解ける
中学受験の世界の謎のツール”線分図”…実はたった”3つの本質”で解ける超シンプルなもの
 こんにちは。かるび勉強部屋 ゆずぱ です。
こんにちは。かるび勉強部屋 ゆずぱ です。
娘が新しく4年生になり改めて感じた中学受験の独特な世界観… 江戸時代の鶴亀算からはじまり塾の先生方が作り上げた ナントカ算(別名:特殊算)という算数問題を解くための体系… そこで使うツールが “線分図” です。
“線分図”という名前がついてはいますが…実は単なる棒グラフです(^_^;) それでも色々な問題で使われるので子供達は “どんな時に使ったらよいのか?どうやって使ったらよいのか?” 混乱している模様(@_@)
でも問題を子供と多数といていると
実はとってもシンプルなものであることが分かりますd(^_^o)
① 線分図はどんな時に使う?
和差算・分配算・年齢算・相当算・倍数算・損益算の6つの特殊算② 線分図のたった3つの本質
1. 差に着目して数字を埋める
2. 背の高さをそろえて割る
3. 数字と割合のペアを見つける
ちなみに… こちらの記事 でも紹介しておりますが、”特殊算” とは塾の先生を中心とした有識者が算数の解法を考案しては名前をつけ…浸透したもの。実はバラバラで体系的ではありません(^_^;)
目次
線分図とは?
線分図とは何か?
線分図とは… 数字を横軸にとった模式図です。左端をそろえて描くことが一般的ですので 複数の棒グラフが並んでいると思ってしまって差し支えありません(^_^;) 実際の例題で簡単な線分図を描いてみましょう。
太郎くんの所持金は1200円で、二郎くんの所持金は500円、三郎くんの所持金は二郎くんの2倍です。この線分図を描いてみると以下のようになります。ほら…とてもシンプルな棒グラフですねd(^_^o)
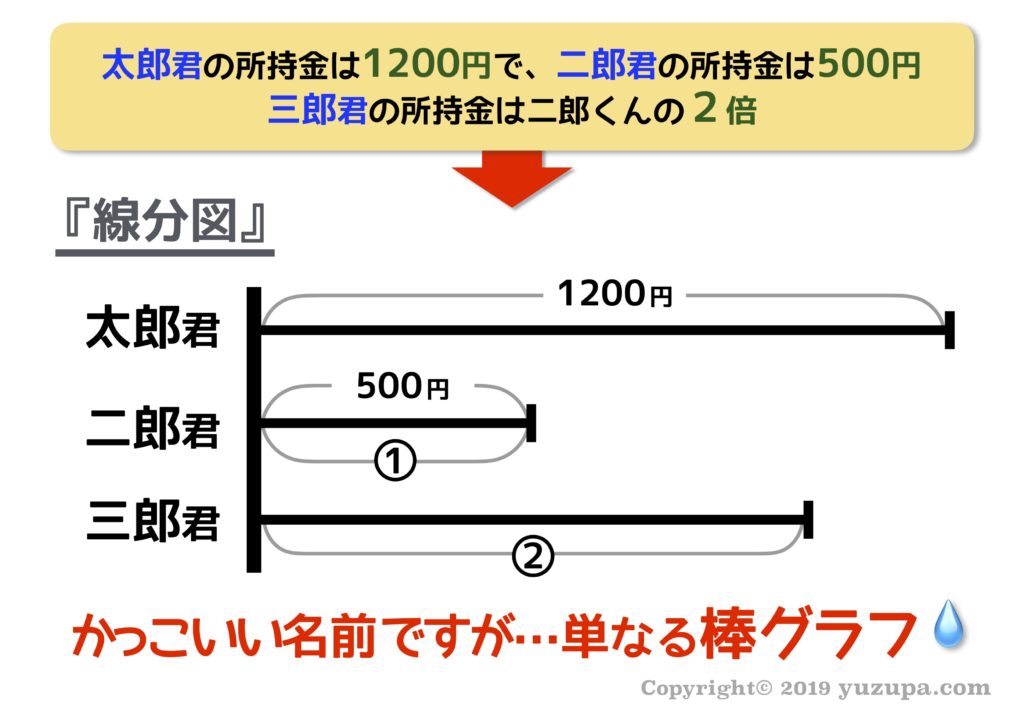
線分図の利点は?
さて線分図というものは シンプルな棒グラフ であることが分かりましたが…これって何が嬉しいのでしょうか? 面積図の記事でも同様の事をお伝えしましたが 方程式を使わなくても問題が解けてしまう事…
えぇ…こんなもの覚えるより、小学生と言えども1次方程式くらいなら教えてしまった方が良いのでは?と…思いますよね (^_^;) ただ方程式を教えずに敢えて “線分図” を使うことには以下のメリットがあります。

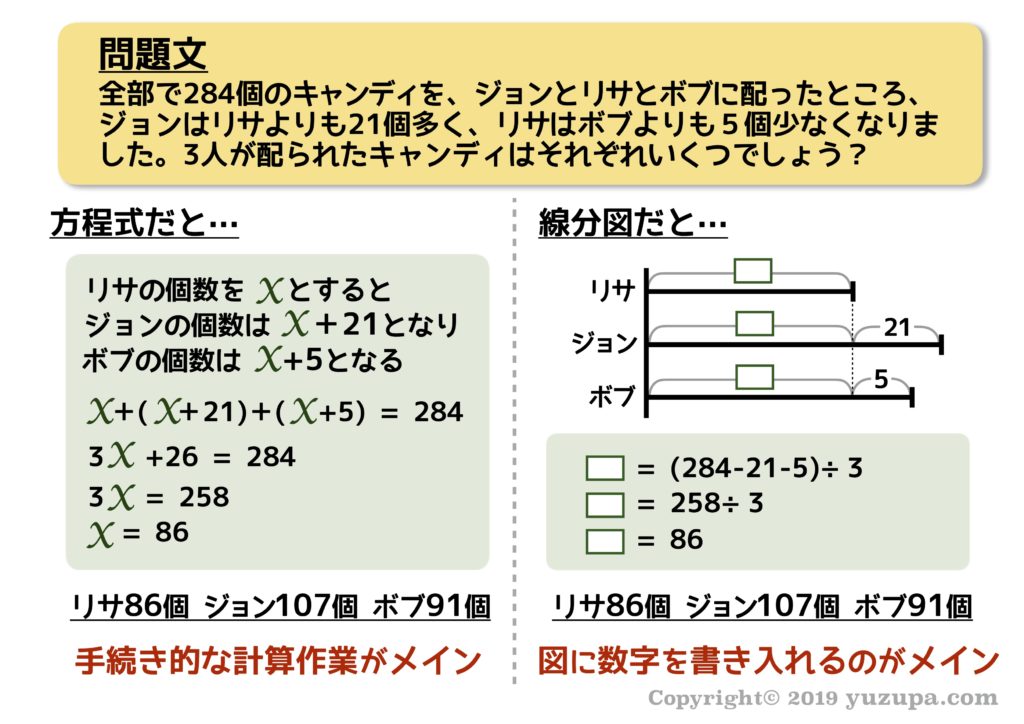
方程式であっても式を立てるところまでは小学生でも簡単にできるんです。でも… “負の数”が出てきたり…”文字式”の計算が出てきたり… 方程式は結構な ”計算力” が必要なため思った以上にハードルは高い です ∑(゚Д゚)
ためしに…簡単な例題を “方程式” と “線分図” で解いて比較してみましょう。式は立てられても方程式を計算ミスなく解けるように練習するのは骨が折れそうです。
線分図を使うべき6分野
小学生に方程式を教えるのはハードルが高いから…といって多くの特殊算が考え出された結果、どんな時に線分図を使うと便利なのかを判別できなくなるという課題 が出てきました…∑(゚Д゚)
パーフェクトな答えはありませんが、以下の6つの特殊算は線分図を使うと概ねうまく解けますd(^_^o) 問題を多くこなせば “こういう問題は線分図だ” という感覚ができあがりますが、まずはこの6つを線分図で!

線分図を使うための “3つの本質”
さて…最後は線分図を使う事の本質に触れたいと思います。線分図を描いた後に… この3つの本質を使って数字を埋める事こそが線分図を使った解法の全て なんです d(^_^o)

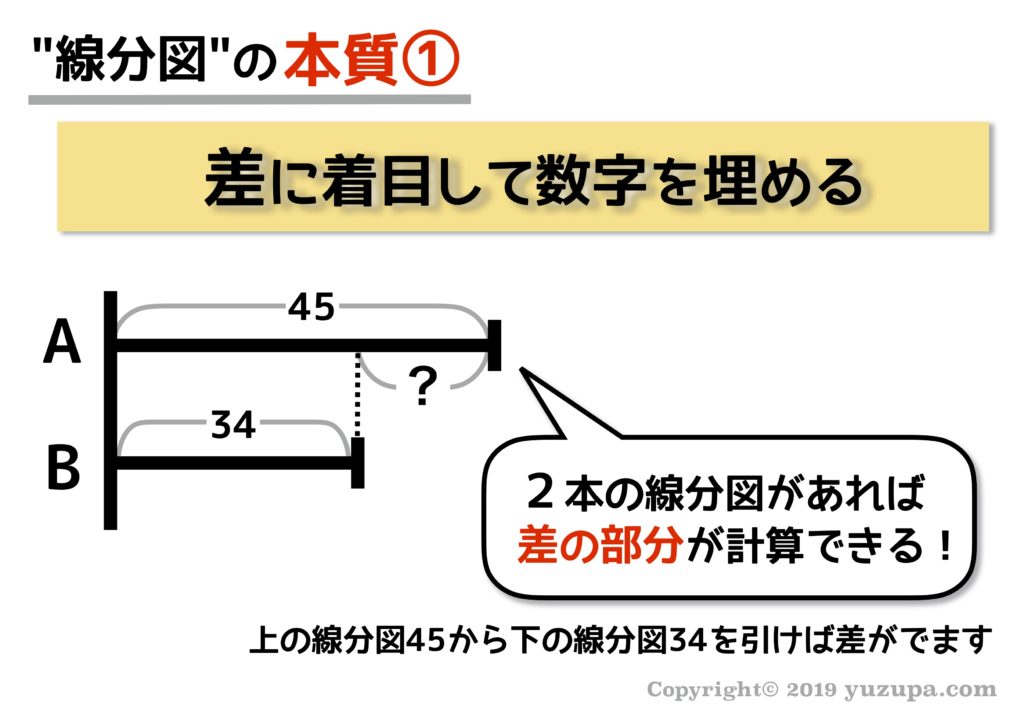
本質①: 差に着目して数字を埋める
線分図の正体は棒グラフでしたね? 棒グラフで最も視覚的にわかるのは “差” です。線分図を描けば いろんな値の差が手に取るように分かりますよね。これこそが線分図を描く事のメインの目的です。
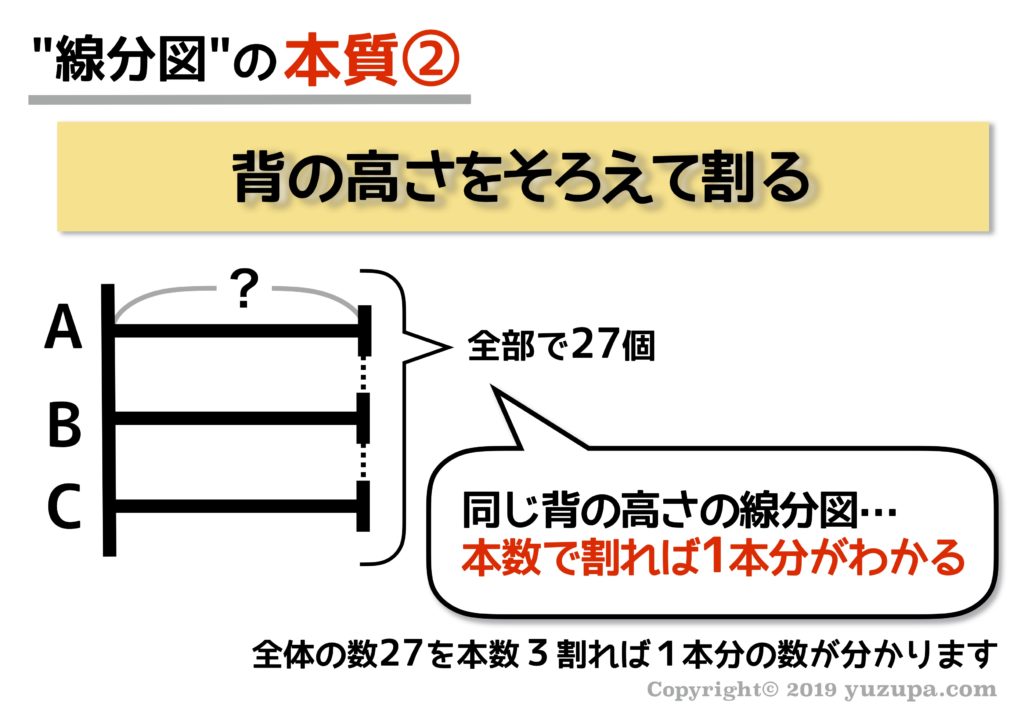
本質②: 背の高さをそろえて割る
線分図の高さをそろえる事ができれば割り算をすることができるという点が2つ目の本質です。ちょっとイメージしにくいかと思いますので例をもとに見てみましょう。
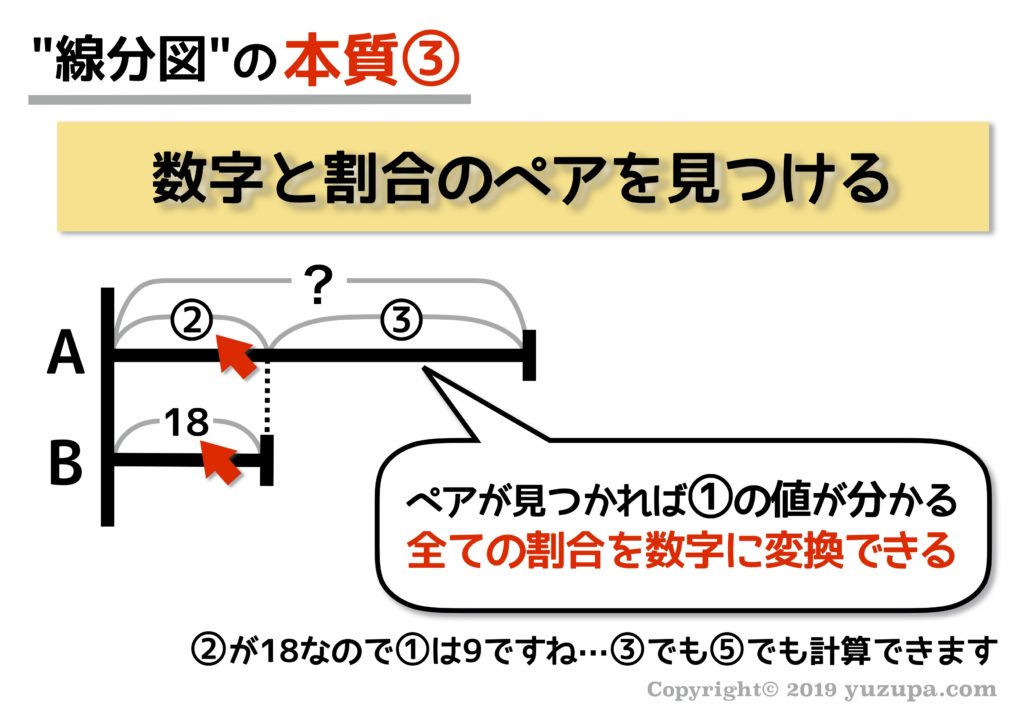
本質③: 数字と割合のペアを見つける
こちらの記事 でも紹介しましたが、割合と数字のペアが1組でも見つかると一気にゴールに近づく事ができます。あらゆる割合の実際の数字を求めることができます。線分図でも同様ですねd(^_^o)
線分図を使った問題の解き方
問題を解くための全体の流れ
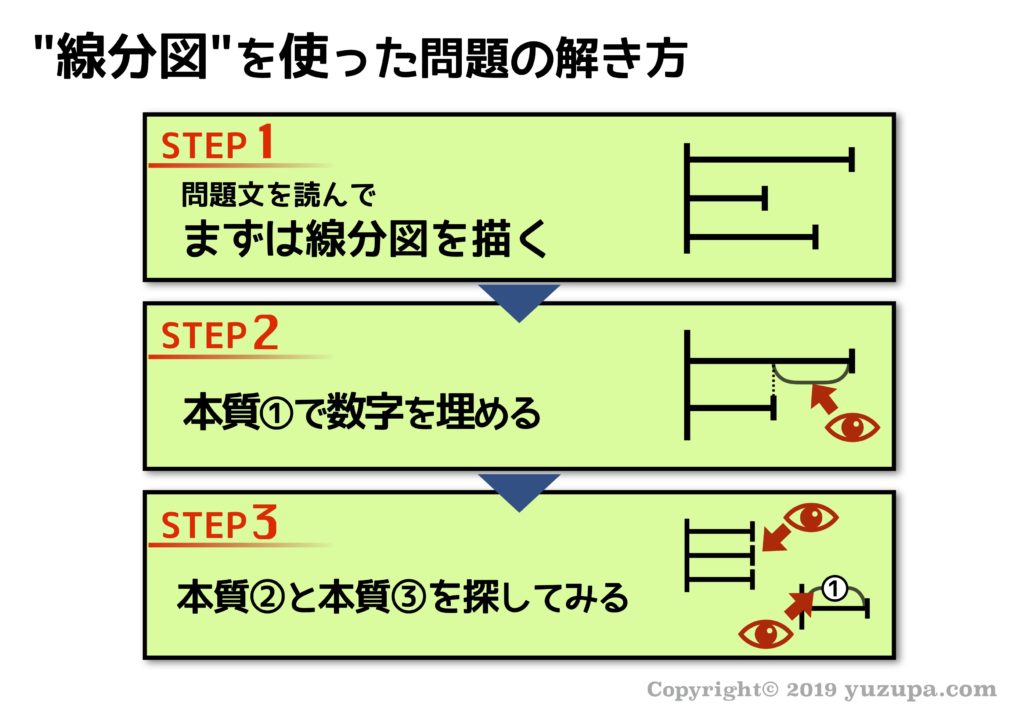
線分図を使って問題を解く場合、3つのステップで解いていくのが良い でしょう。最初のステップは、問題文をよく読みながら線分図を描く事。次に”本質①”を使って埋められる数字をトコトン埋める事。最後は”本質②”と”本質③”を使えないか試行錯誤する事です。
それでは順番に見てみましょう
STEP1:問題を読み線分図を描く
まずは問題文をよく読みながら、線分図を描きます。問題文に使われている数字は問題を解くために必ず必要になる数字ですので、もっとも注意すべきことは数字の見逃しですd(^_^o)
ただ… 問題によって線分図を描くためのちょっとしたコツが必要です(-_-;) 特に年齢を扱う年齢算や、商売を扱う損益算は線分図を書く練習が必要 です。こちらについては過去の記事でも詳しく解説していますd(^_^o)
STEP2:本質①に注目して値を埋める
何本かの線分図を並べて描くと、必然的に”差”が浮き彫りになりますね!2つ目のステップは ”差”に着目してひたすら数字を埋めること です。これは本質①ですねd(^_^o)
ここで注意すべきことは 実際の数値だけでなく割合も差を求めることができる という事です。そして割合は実際の数字と区別するために丸数字で書くということもポイントです!
STEP3:本質②と本質③を探してみる
最後はSTEP2までに出来上がった線分図を眺めて、本質②と本質③を使えるところがないか探してみます。背の高さを合わせられるところは無いか?丸数字と実数字がペアになっているところが無いか?
ここで 本質②や本質③を見つけることが出来れば解けたも同然 です!
ちなみに… STEP2とSTEP3は順不同 です。簡単なヒントから埋めていくのが一般的なので敢えて順序を描いてみました。当然、簡単な問題だとSTEP2までで解けてしまうこともあります(^_^;)
具体的な解き方の例
和差算の例
まずは和差算です。和差算とは2つの値の和と差が与えられている問題 です。解説サイトによっては不親切にも公式だけがポツンと書かれている場合がありますが、その公式は線分図を描かいて導き出した公式です(^_^;)
公式の暗記はその公式がなぜそんな式になっているか? を理解しているのが大前提!公式の元ネタが分かっていれば応用問題が出されても対応できますd(^_^o) 逆に…単なる公式の丸暗記は応用が効かなくなるので注意を!
それでは問題をどうぞd(^_^o)
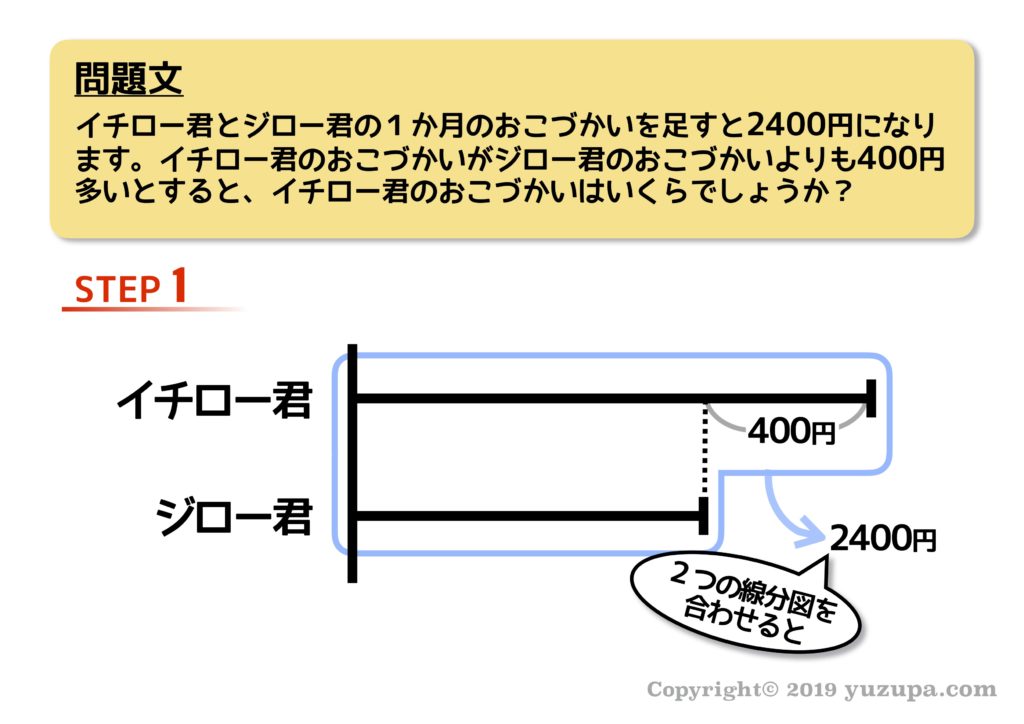
STEP1では問題文をよく読みながら線分図のベースを描きます。この問題の場合とてもシンプルですね! 和の部分はこんな感じで線で囲んで描くのが良いでしょうd(^_^o)
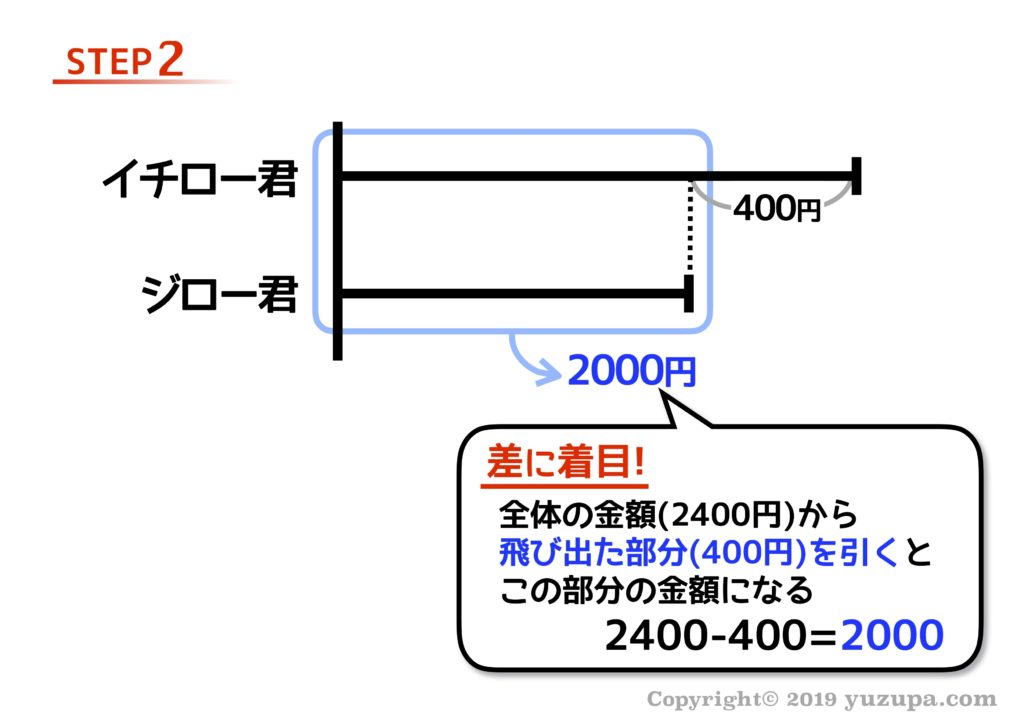
線分図に現れる”差”に着目 すると飛び出た部分以外の数字を出すことができますねd(^_^o)
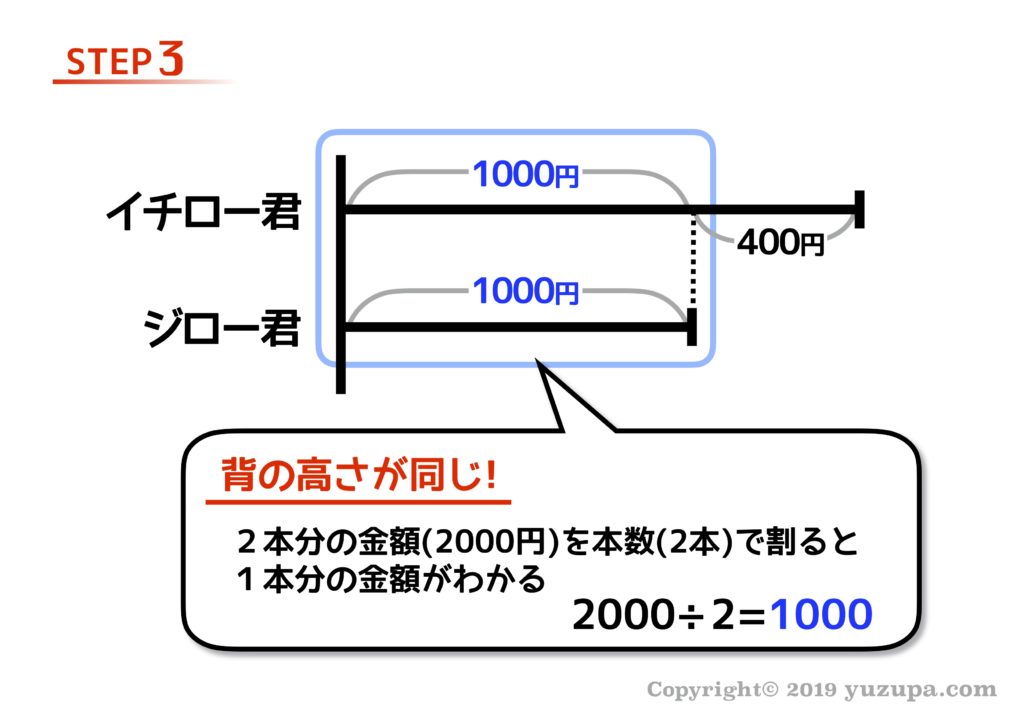
和差算ではだいたい本質②を使います。2つの線分図の高さをそろえてあげて2で割れば1本分の高さが分かりますねd(^_^o) ここまで来れば答えが出ます。イチロー君のおこづかいは、1,400円ですね! ちょっと安い…。
分配算の例
次は分配算です。分配算とはアメ玉を複数の人に分配したり… お金をみんなで分けたり… 何かを複数の人に分配するときの条件が与えられている問題 です。せっかくなので今度は線分図が3本になる問題をd(^_^o)
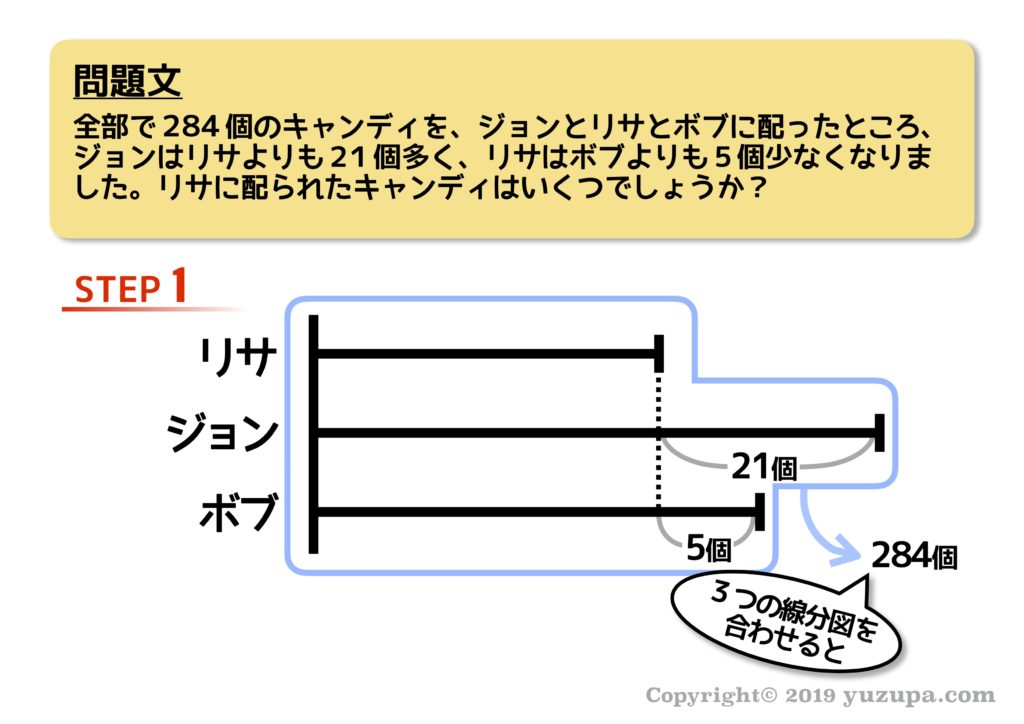
ここまでは問題文を読むことができれば描けるはずです。もし間違ってしまう場合は問題文を読むための国語力や、慌てず落ち着いて問題文を読む注意力の問題かもしれません。ちなみに我が家の場合… ”よーく問題を読め!”と何度も息子に注意しました(-_-;)
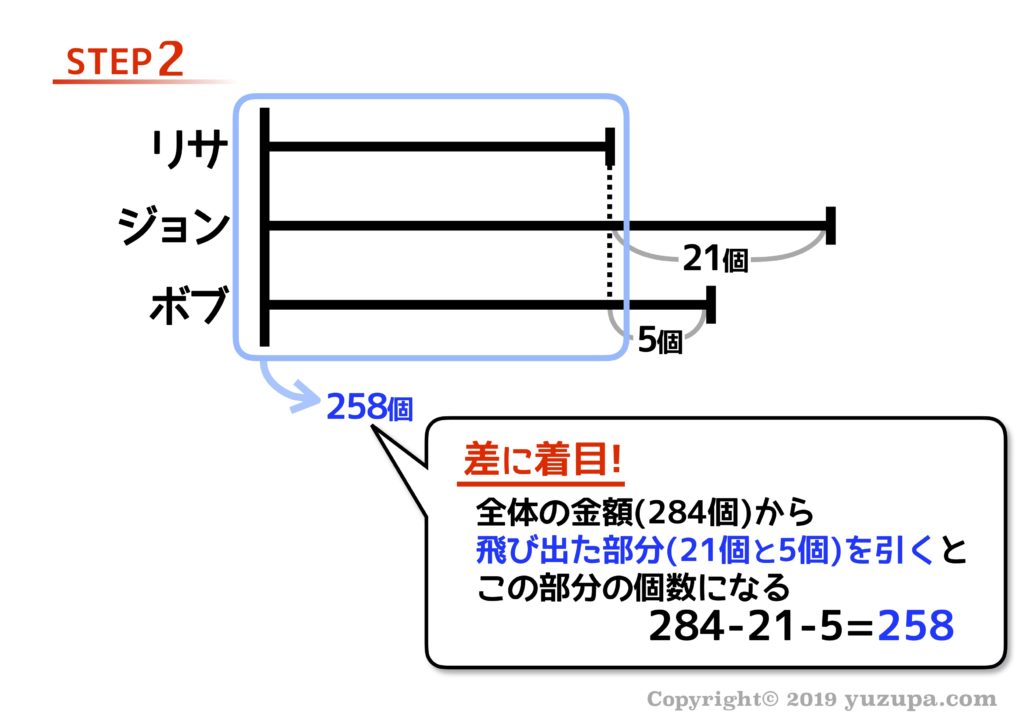
和差算とほぼ同様… 線分図を眺めながら”差”に着目する と出っ張った以外の部分の数字が分かりますd(^_^o)
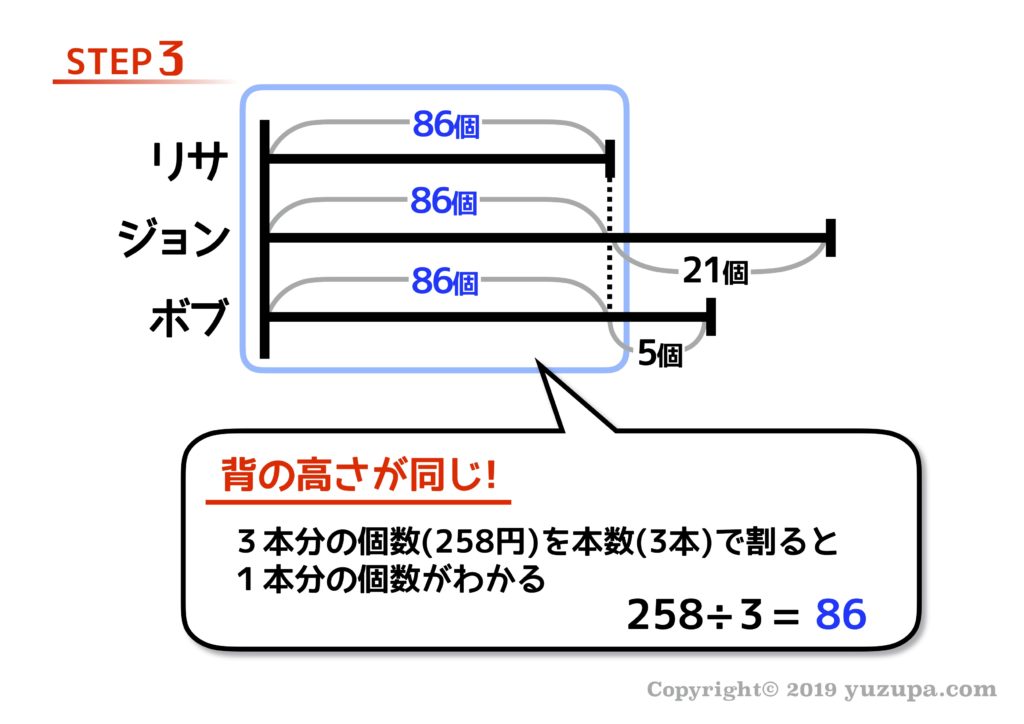
そうすると… 同じ高さの線分図3本が見つかりました! 今度は線分図の数は3本ですので、3で割ってあげれば1本分の値を出すことができますねd(^_^o)
リサに配られたキャンディーは86個です!
年齢算の例
次は年齢算です。年齢算とは年齢を扱う問題です。年齢算も線分図の本質を使って難なく解けるのですが、ベースの線分図を描くのに、ちょっとコツが必要です。詳しくは こちらの記事 で解説していますのでご参照を!
それでは問題です。
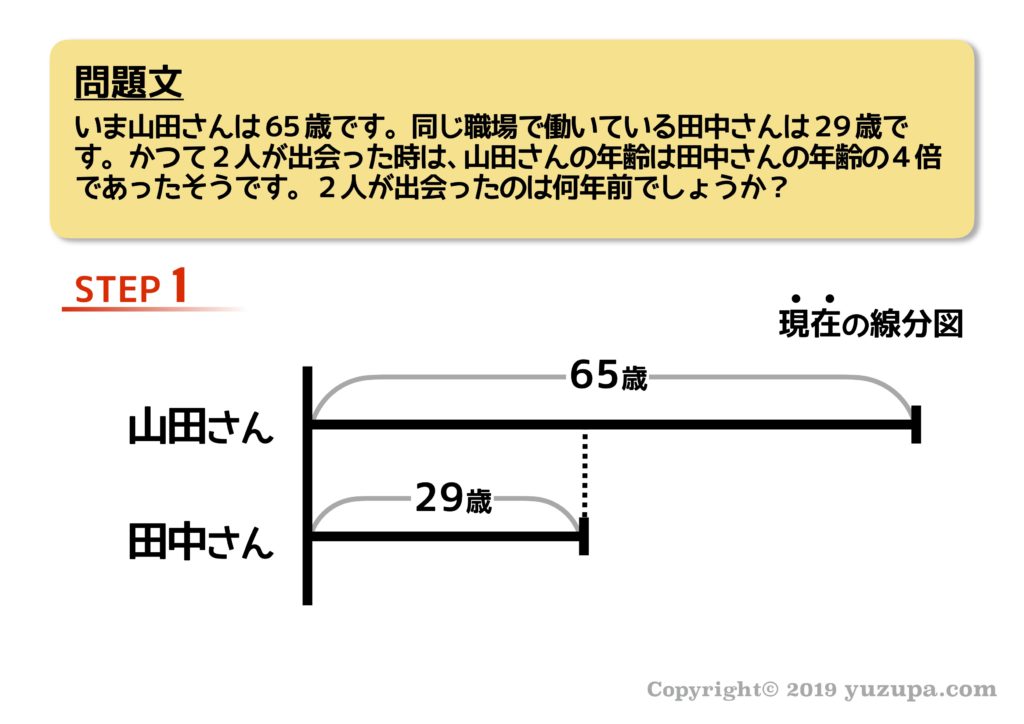
ここまでは問題を読めば誰でも線分図を描けますね。線分図を描く上での ポイントは “出会った頃”の線分図を描かなくてはならない事 です。こう描きます。
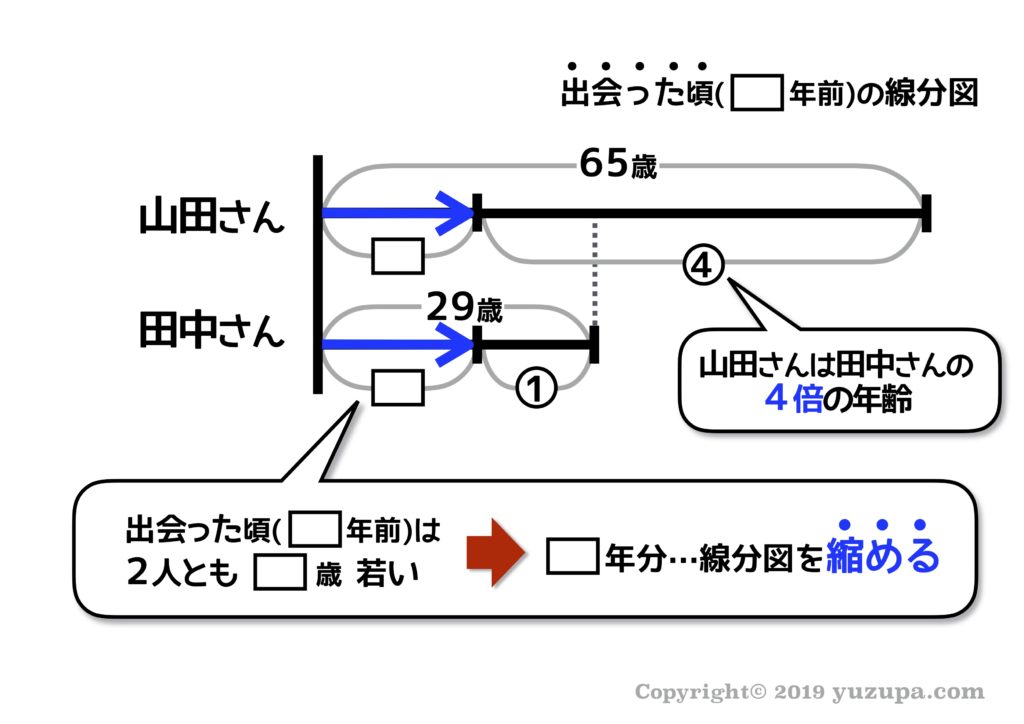
何年前か分かりませんが、過去の線分図を描く場合は同じ長さだけ線分図を縮める事でキレイな線分図を描くことができます。
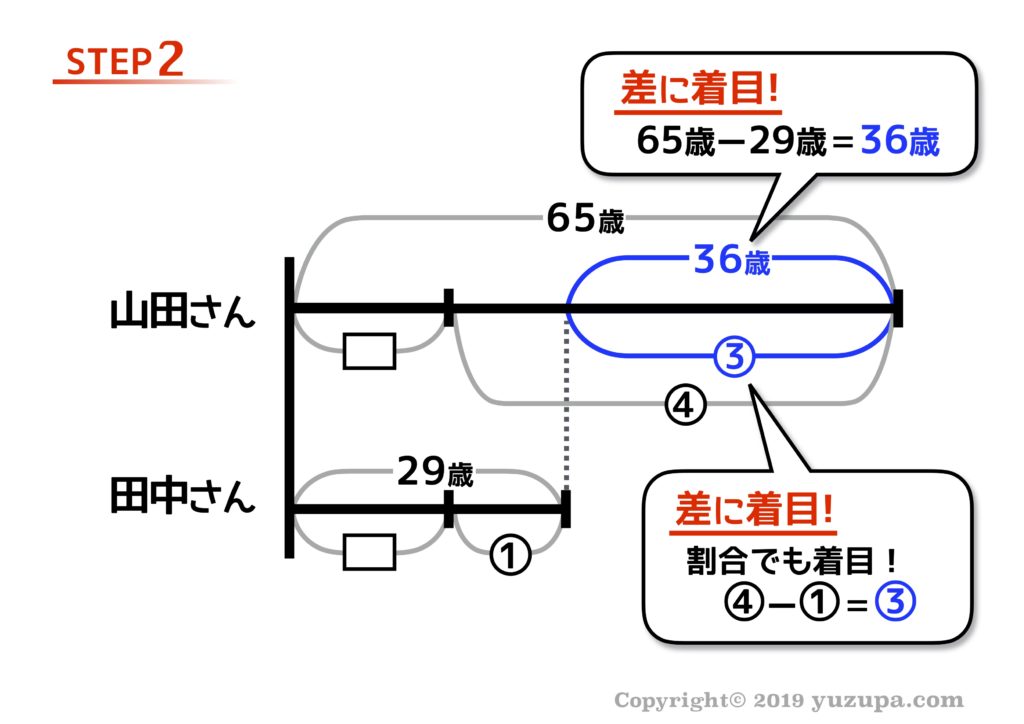
STEP2とSTEP3では、セオリー通り“差”が分かるところを片っ端から埋めてみましょうd(^_^o)
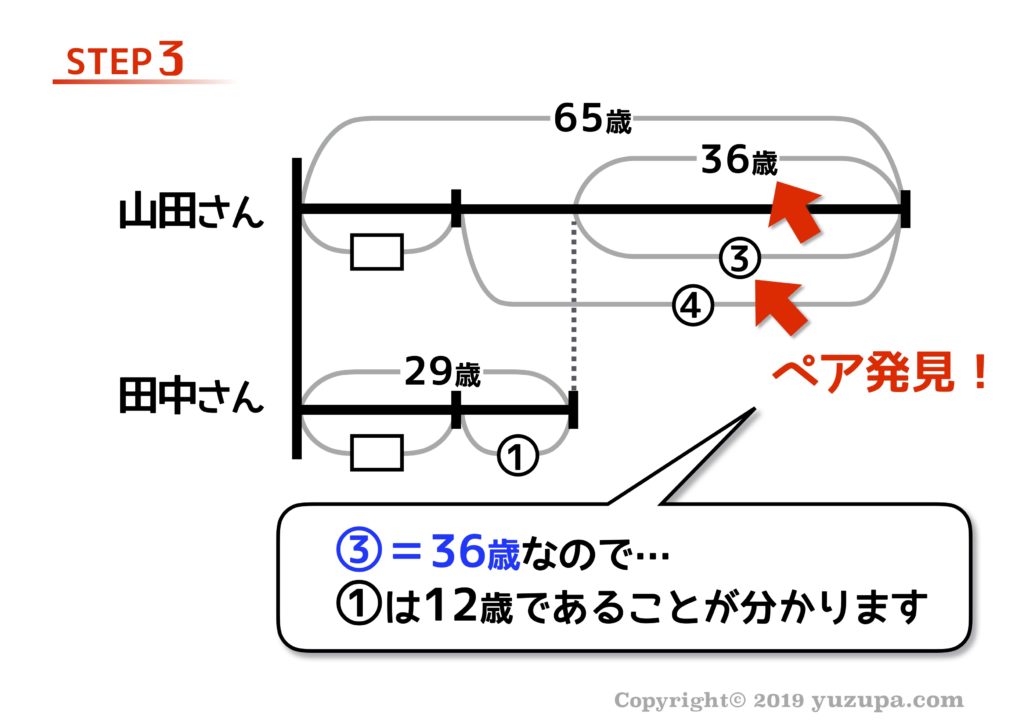
そうすると本質③の割合と数字のペアが見つかりますね∑(゚Д゚) 割合と数字のペアが見つかったら、丸数字1つ分がいくつなのか計算をします。この問題の場合は①は12歳分ですね!
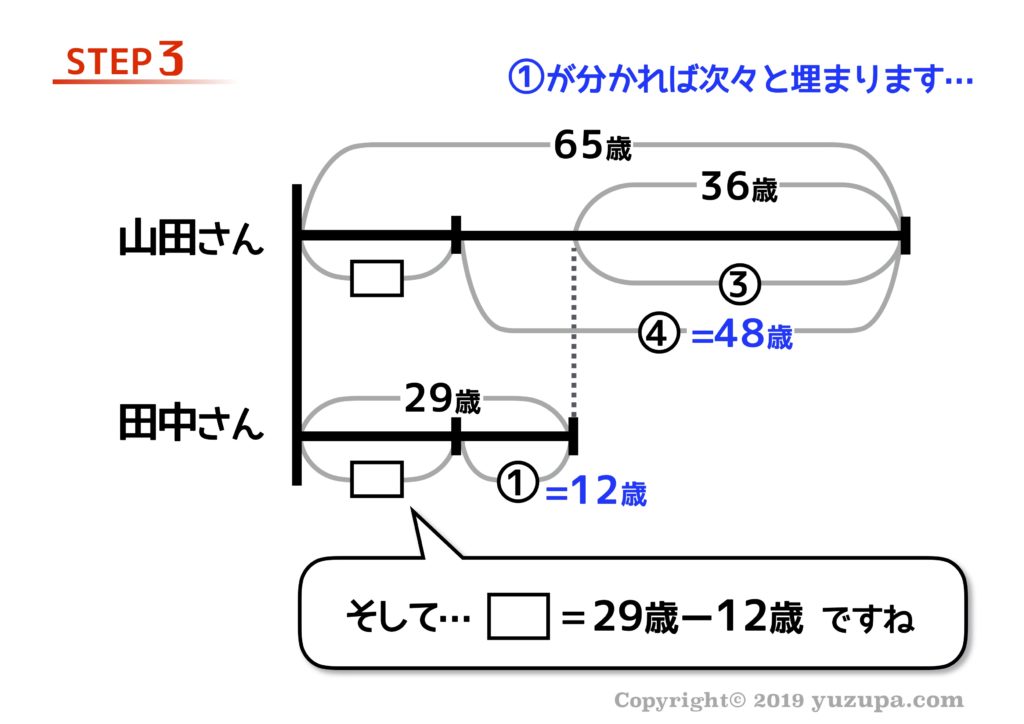
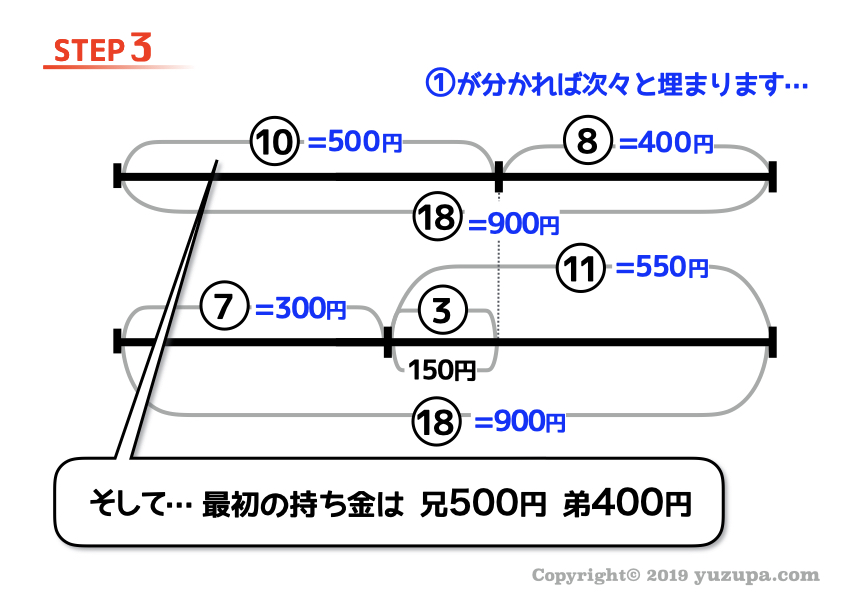
割合と数字のペアさえ見つかってしまえば 線分図の数字は一気に埋まります。出会ったのは田中さんが12歳の時。今から17年前ですね d(^_^o)
相当算の例
お次は相当算なるものです。相当算とは割合や比が登場すると同時に、いつくかの実数値が出る問題を総称して、そう呼ぶそうです(^_^;) 割合が出てくるので実数値とのペアを見つけることが出来れば、割合を一気に実数値に変えることができます。
それでは例題をどうぞ。
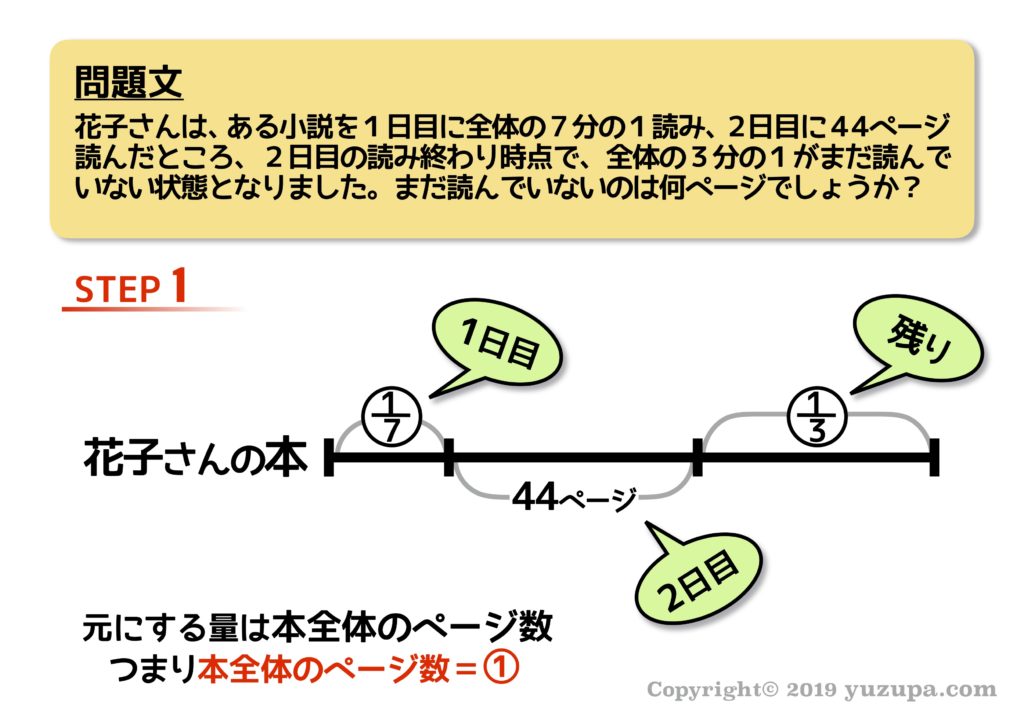
問題文を読みながらベースとなる線分図を書いていきますが、注意すべきは割合の”元になる数” です。何の7分の1なのか? 何の3分の1なのか?しっかり意識しましょう。
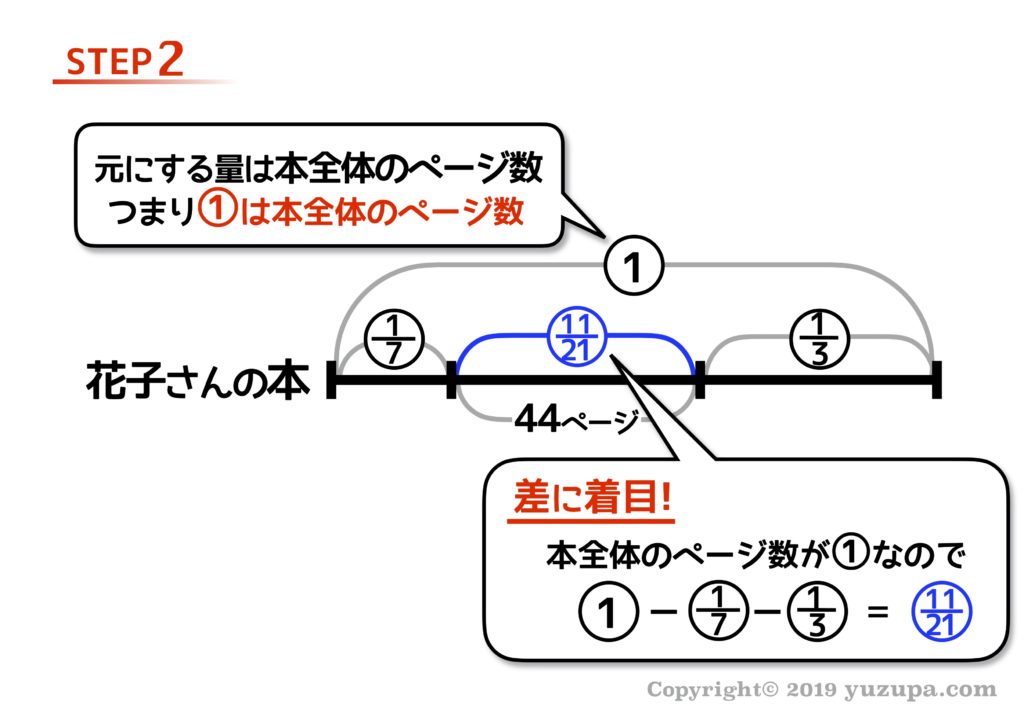
差に着目すると、2日目に読んだ部分の、割合が分かりますね。
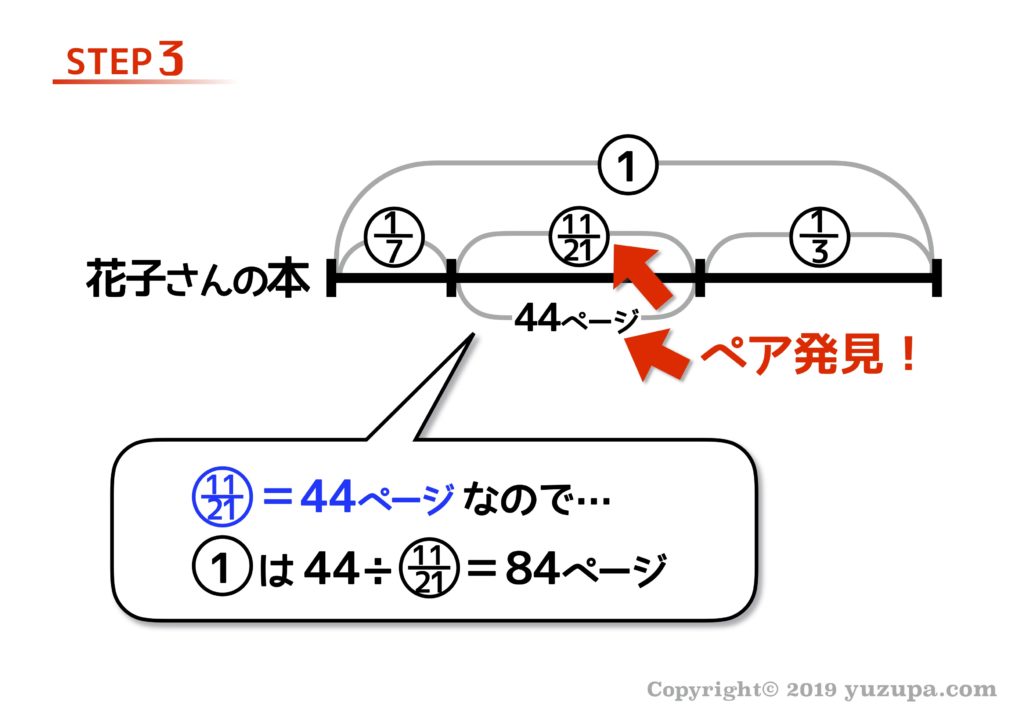
そして割合と数字のペアが見つかりましたd(^_^o) あとは割合をジャンジャカ実際の数字に変換させましょう!
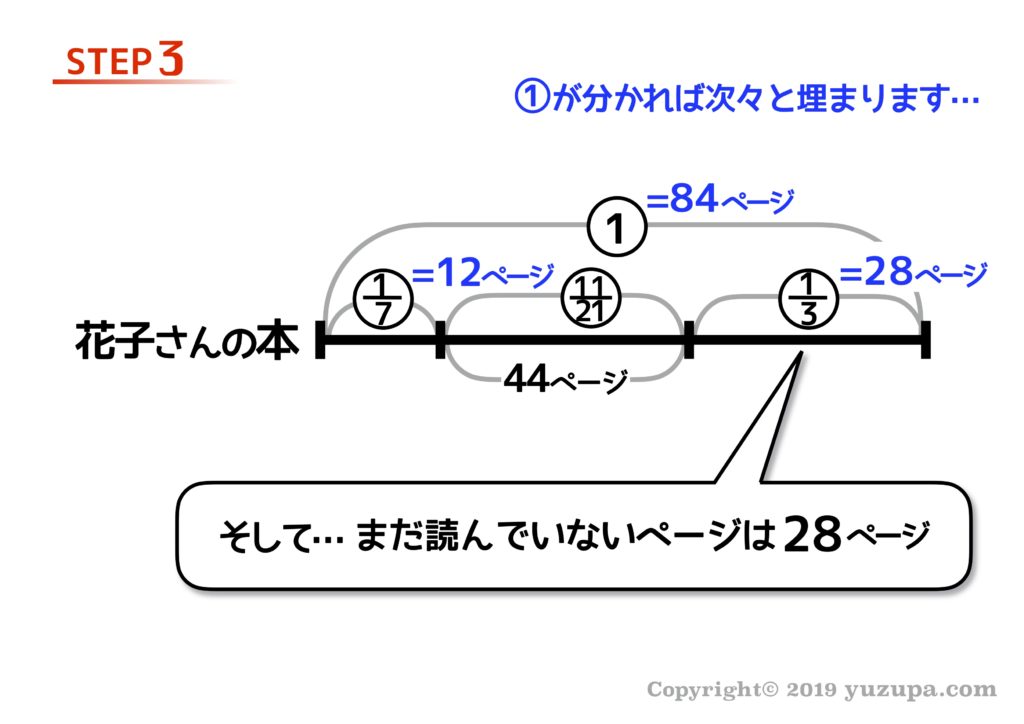
おのずと答えが導き出されます。この本のまだ読んでいないページ数は28ページですねd(^_^o)
倍数算の例
次は倍数算です。同じモノに対して複数の異なる比が登場する問題 です。相当算の仲間ですが、たったひとつだけコツが必要 になりますd(^_^o)
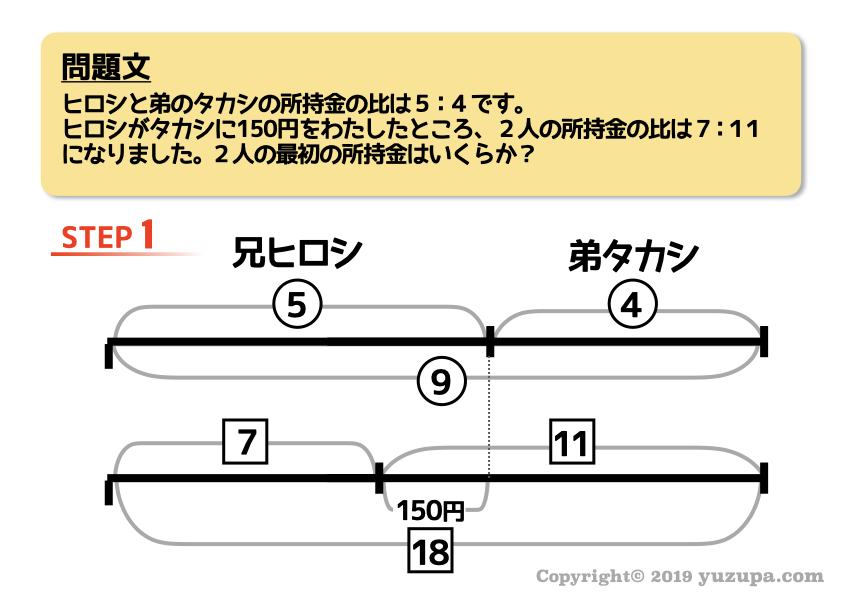
ひとつのモノに対して比が複数でてきましたね… どうすれば良いでしょうか?
ここでコツが必要になりますd(^_^o)
丸数字の比 と 四角数字の比 の結合です。割合と比の知識なので詳細の説明は割愛しますが、比どうしのペアを見つけて数字を合わせる作業をしてあげます。
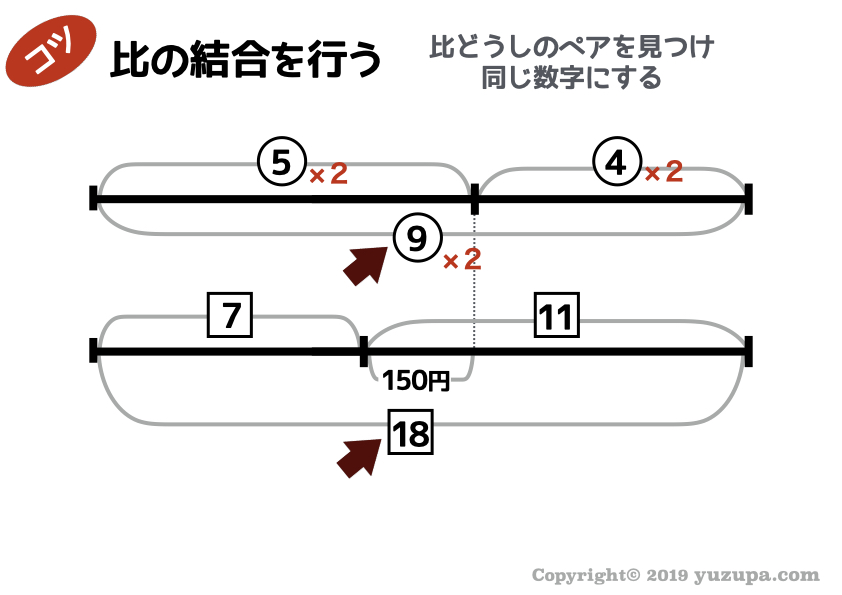
丸数字の比すべてに2をかけてあげます。
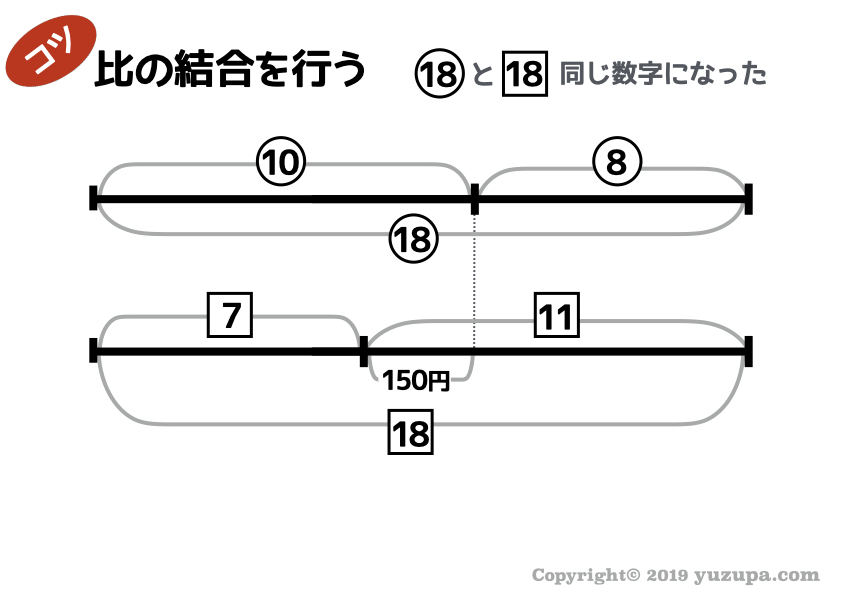
無事、丸数字の比と四角数字の比 で18の部分が一致しましたd(^_^o)
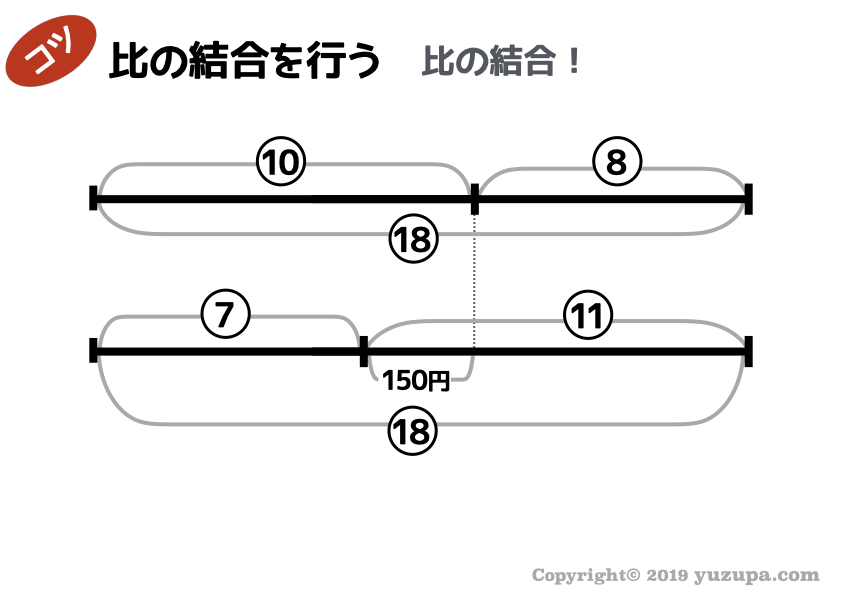
めでたく、全て丸数字の比にすることができました。
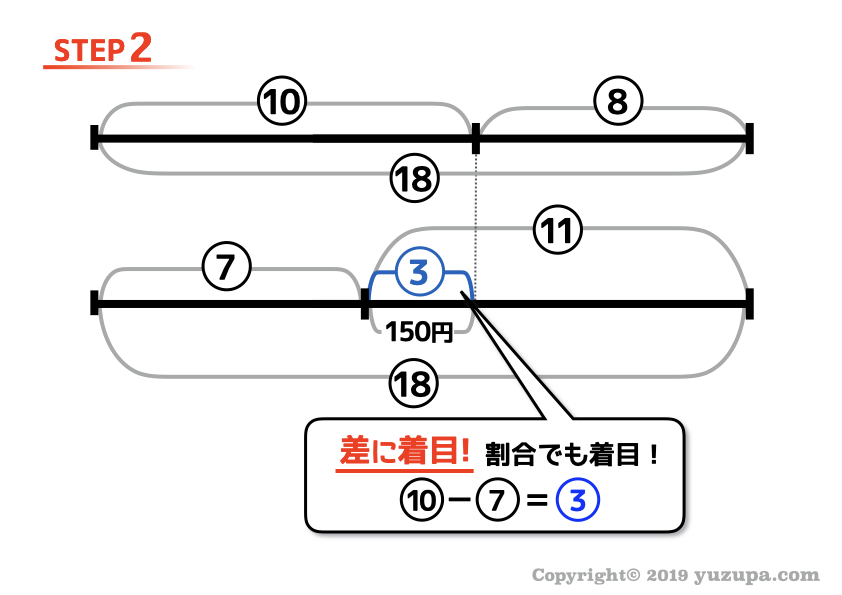
STEP2で差に着目。
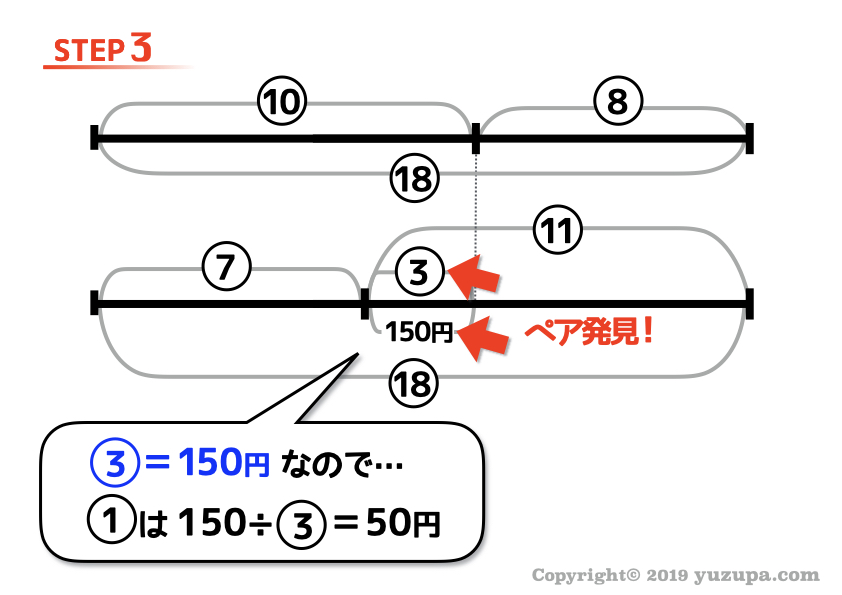
そうすると、ペアを発見することができます!
損益算の例
最後は損益算です。損益算というたいそうな名前がついていますが、売上や原価や利益を計算する問題を総称してそう呼んでいるようです(^_^;) さっそく例題を見てみましょう。
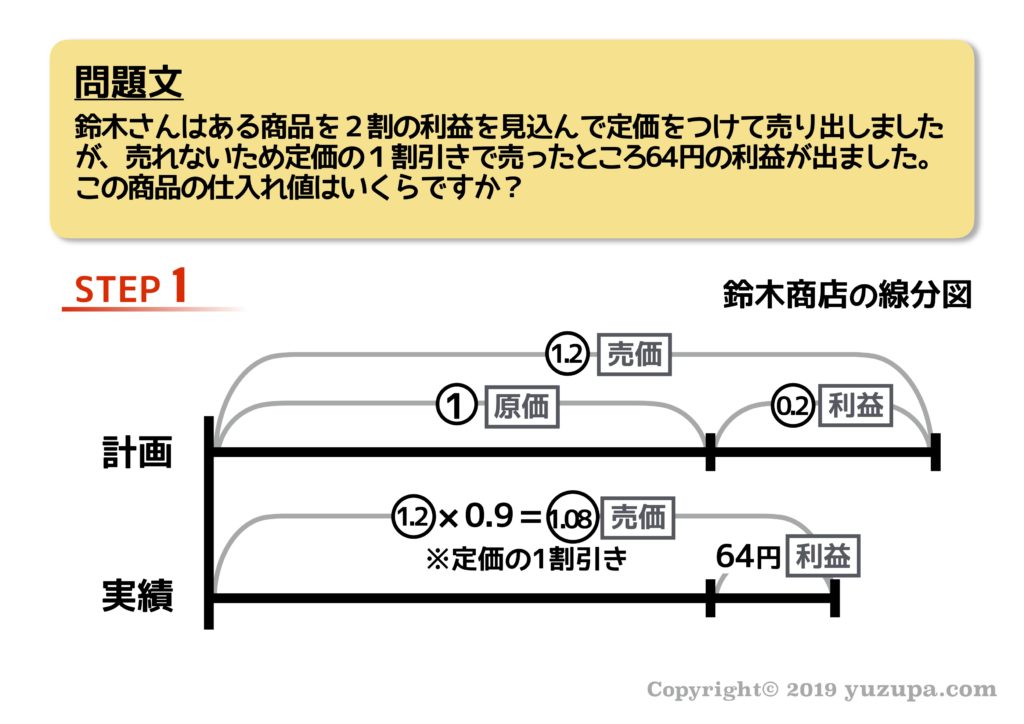
問題を読んで大人はこの線分図をスンナリ描けるのですが、子供は苦戦したりします(@_@) 私の息子の場合、原因は言葉の定義がイマイチだったためでした_φ(・_・
もしこの例題の線分図が描けない場合は、損益算で使ういわゆる”商売用語”を先に学習した方が良いかもしれません。こちらの記事 で詳しく解説していますd(^_^o)
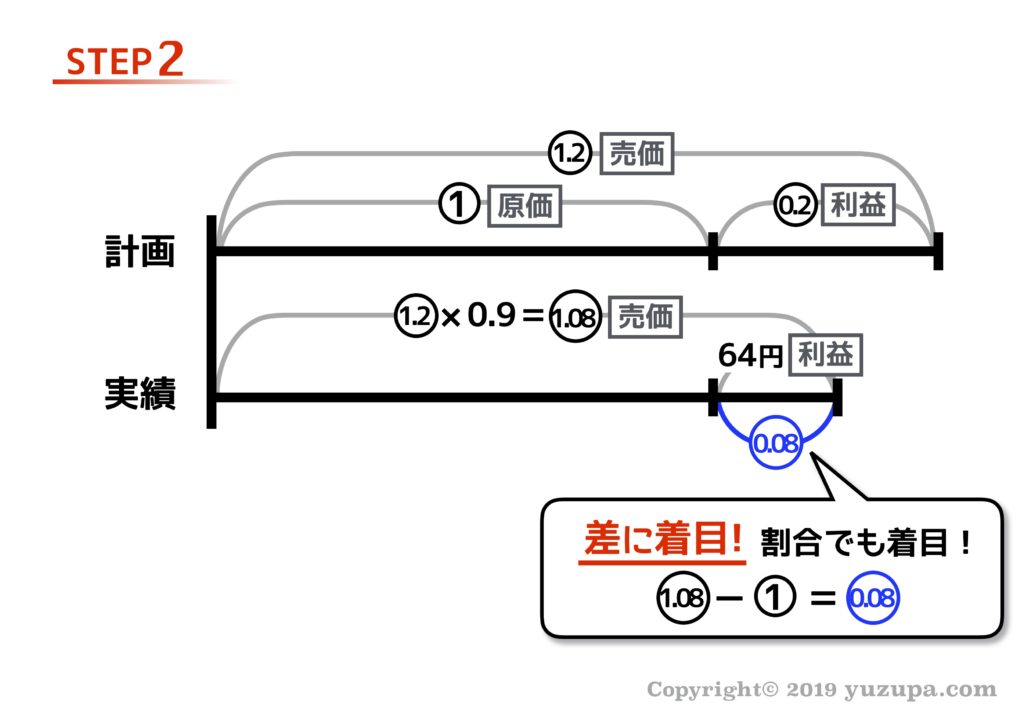
いつもどおり”差”に着目すると、割合と数字のペアが見つかりますねd(^_^o)
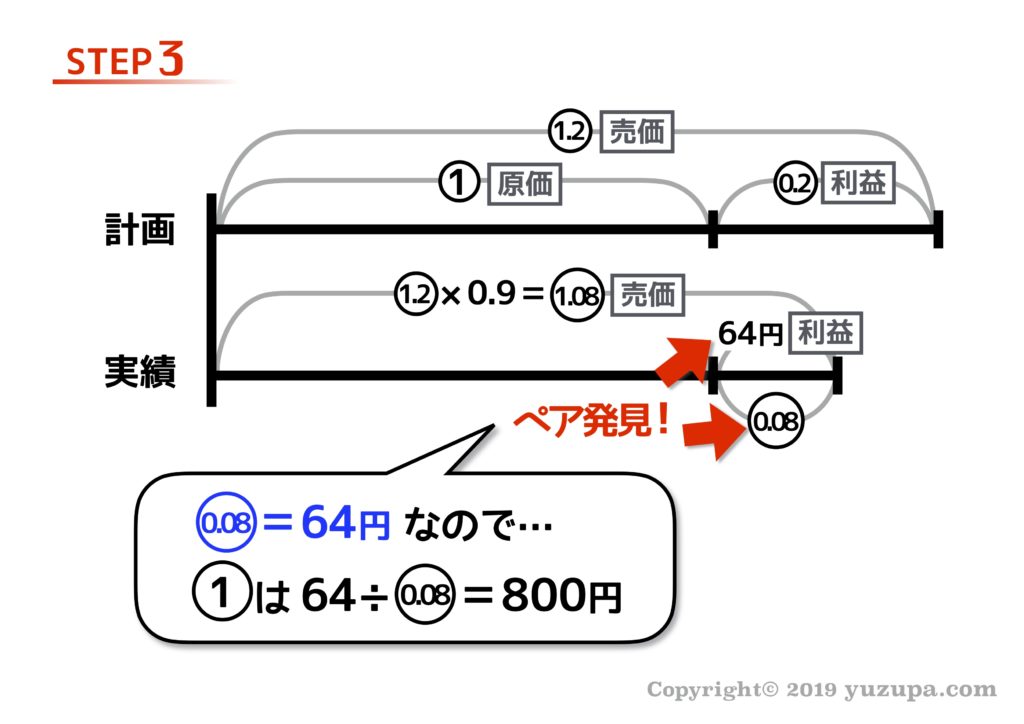
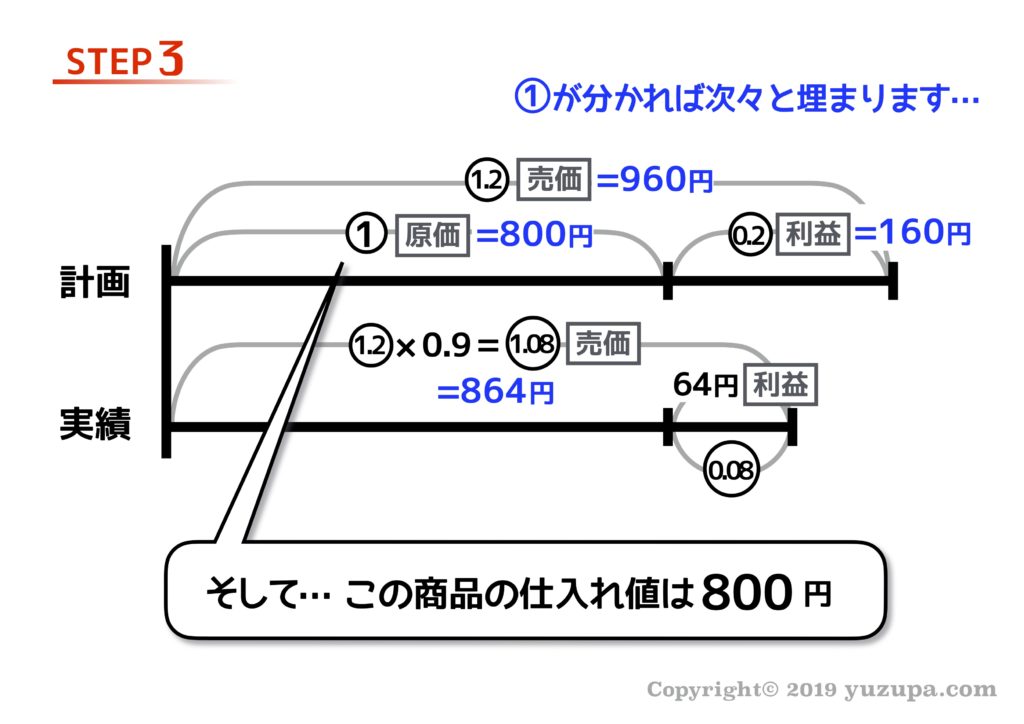
繰り返しとなりますが、ペアさえ見つかってしまえば線分図の大部分を埋めることができるようになりますd(^_^o)
まとめ
中学受験で登場する”線分図”という謎のツールの基本から、実際の例題を通して使い方をまとめてみました。例題も全て読んでいただいた方は お気づきかと思いますが実は超シンプルです…
言い換えると、たった3つの本質をビジュアルにとらえるために線分図があるようなものですd(^_^o) 6つの特殊算の解法としてご紹介しましたが大切なのは 3つの本質を意識して線分図を眺めることです!
① 線分図はどんな時に使う?
和差算・分配算・年齢算・相当算・倍数算・損益算の6つの特殊算② 線分図のたった3つの本質
1. 差に着目して数字を埋める
2. 背の高さをそろえて割る
3. 数字と割合のペアを見つける
印刷用のPDFは以下からダウンロードをd(^_^o)











