中学受験:割合と比は”7つ道具”で克服
割合や比は基本的な7つ道具の体得で苦手意識を無くす!!
※ 2019年1月3日 ご要望のあった 印刷用プリントのダウンロードを追加 …詳細は記事の末尾へ!
 こんにちは。かるび勉強部屋 ゆずぱ です!
こんにちは。かるび勉強部屋 ゆずぱ です!
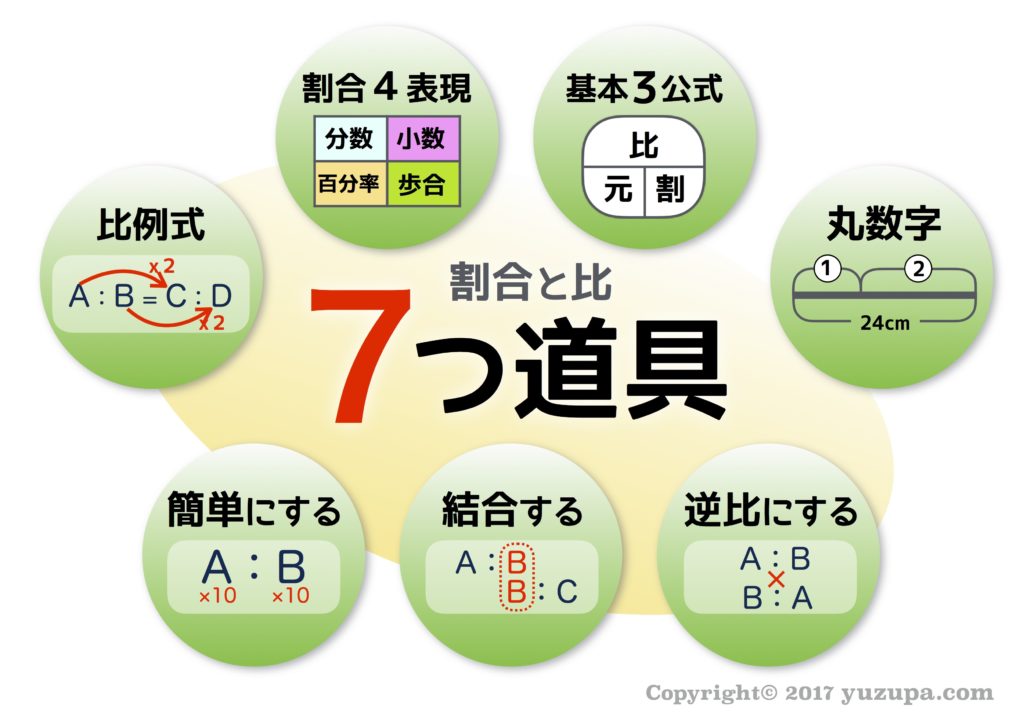
中学受験では地獄の領域と言われる”割合と比”…なぜ、地獄の領域と言われるか? それは言わずもがな…ここでつまづいてしまう小学生がとても多いからです(><) 克服するためには、割合や比の概念を理解する事が大切ですが、これらの問題を解く為に使う道具類をマスターする事も必要 です。メジャーな道具は7つです。
注釈:いわゆる基礎問題を解くために必要な知識を”道具”と表現しています。入試の応用問題は基礎問題の組み合わせで解ける… まさにこれらの知識は”道具”のイメージです(^-^)
これらの道具は基礎問題に相当し、この7つの道具を学習していくうちに割合や比の概念が頭に入ってきます。もし、お子様が苦戦しているようであれば、いまいちど初心にかえり、この7つ道具を復習してみるのはいかがでしょうか?道具を使いこなせるからこそ問題が解ける…最大の武器になります!
目次
道具① 割合の3公式は円形図!
まずは割合の基本3公式です。公式を学ぶ前に割合の概念から復習しましょう。お子様は ”元にする量”、”比べる量”、”割合”という3つの言葉を正しく理解していますでしょうか? 基本の3公式を練習する前に絶対に抑えておくべき事… 割合で出てくる3つの言葉を頭に浸透させる事こそ最初にやる事です!
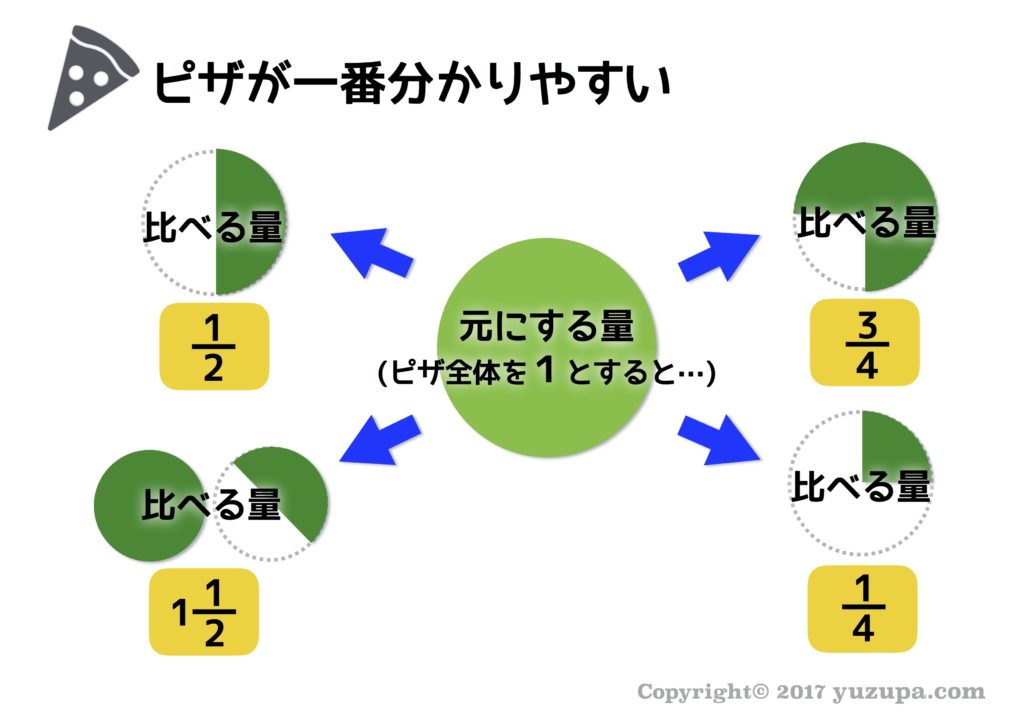
割合を考える上で合言葉のような文章があります。『元にする量(基準にする量)を1とすると、比べる量はいくつだ? 』割合の3公式を日本語にした時に最もシックリくるのがこの文章です。実は式よりも大事かもしれません…(^_^;) 合言葉を心の中でブツブツ唱えながら次の線分図を見てみましょう。
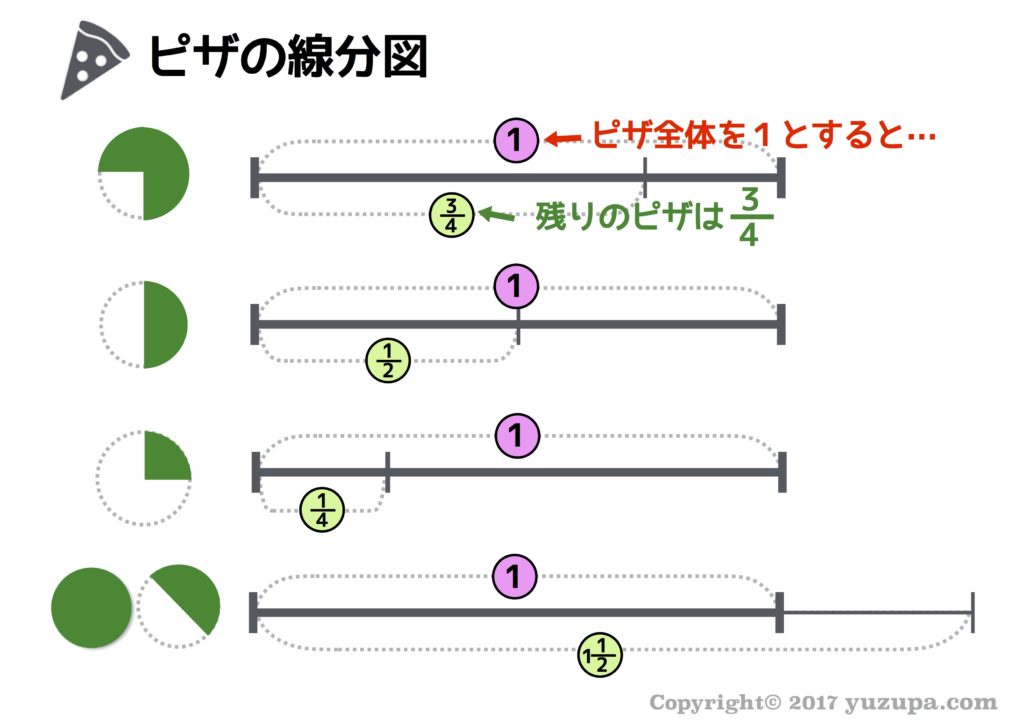
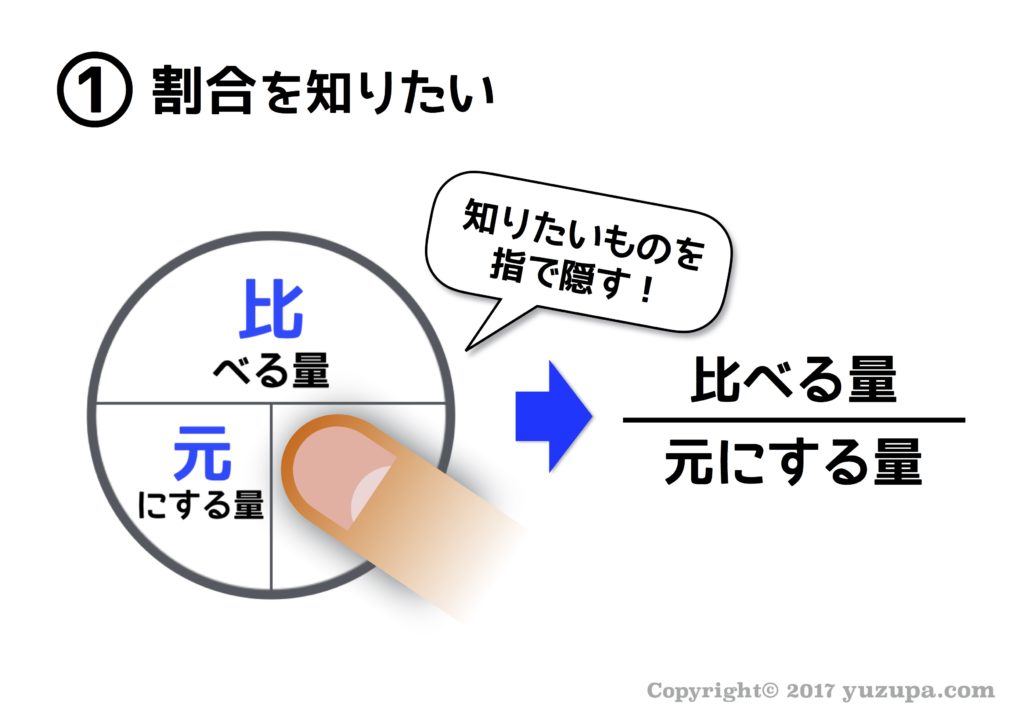
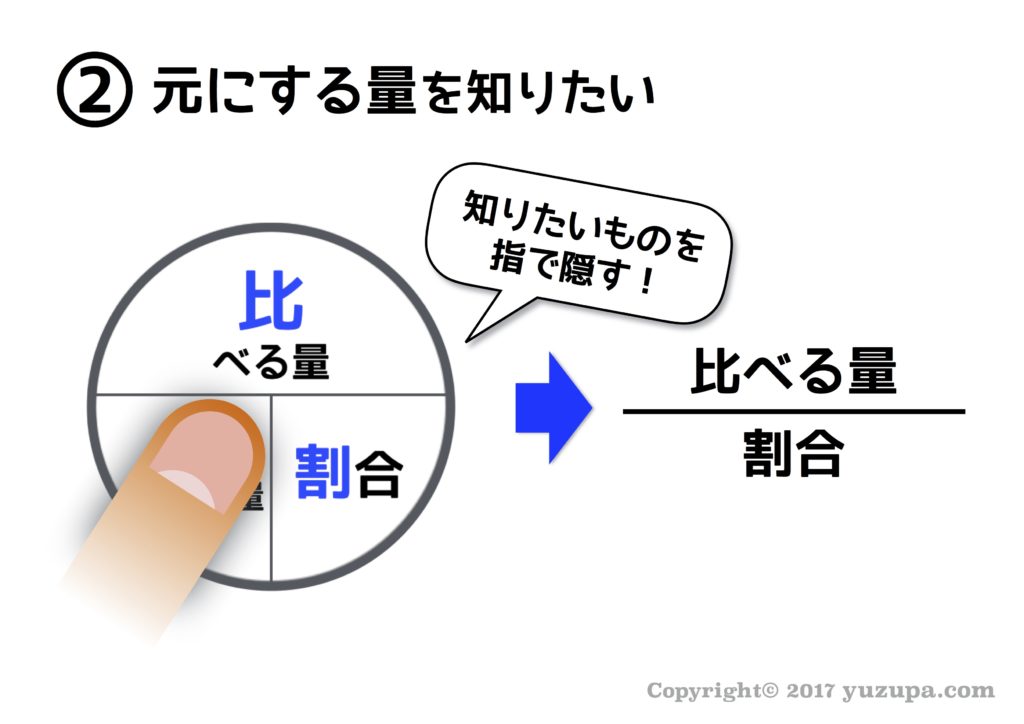
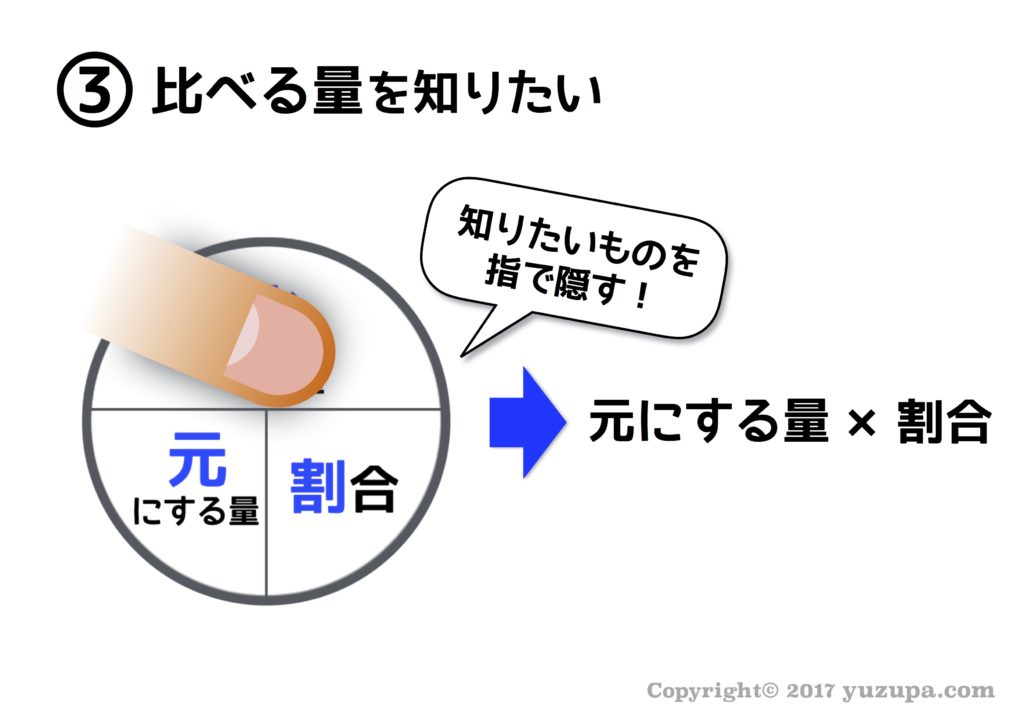
元にする量と比べる量のイメージが定着してきたら、本題の基本3公式です。教科書などでは3つの公式がズラっと書かれているのですが他の表現方法があります。速さと時間と道のりの関係を円形の図を使って覚えた記憶はありませんか? この手の公式にはこの円形図が使えるんです…使わない手はないでしょう!
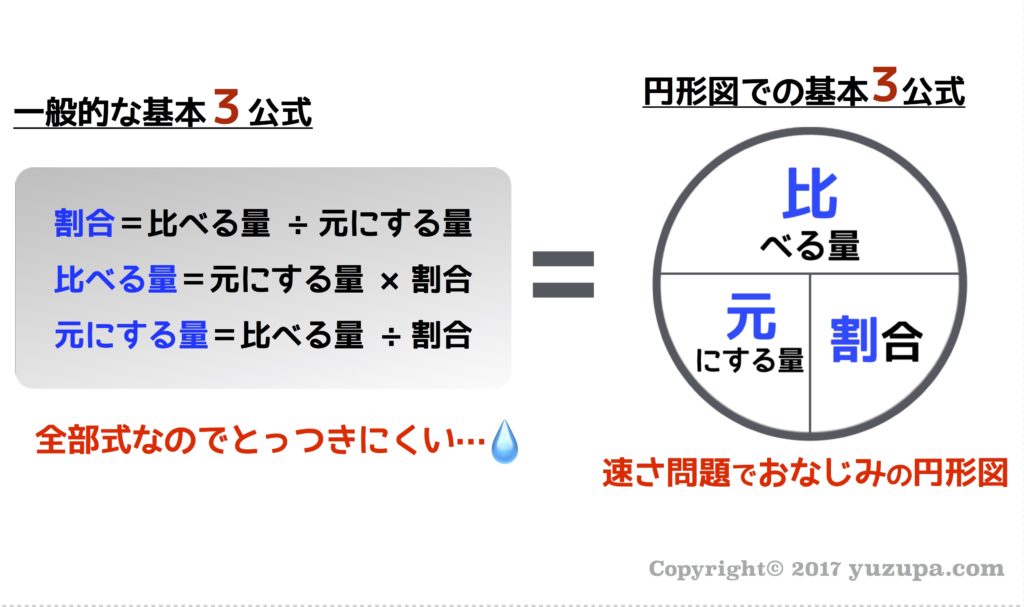
この円形図の使い方もおさらいしておきましょう。知りたいモノを指で隠すと式が出てきます!” 割合”を知りたければ”割合”を指で隠すと…割合を表す式が出てきますね。”比べる量”を知りたければ”比べる量”を指で隠しましょう。ほら… 公式が出てきます!割合や比の問題ではこの円形図を意識する癖をつけましょう!
道具② 割合の4つの表現
割合の表し方は4種類ありますが…お子様によっては苦戦するかもしれません…(*_*) でも世の中には割合が溢れかえっています! スーパーのお刺身の3割引きのシール…野球が好きなお子様は打率ですね…テレビではカロリー80%オフをうたうコマーシャル…割合を見つけたら、お子様と一緒に意味を考えてみましょう!
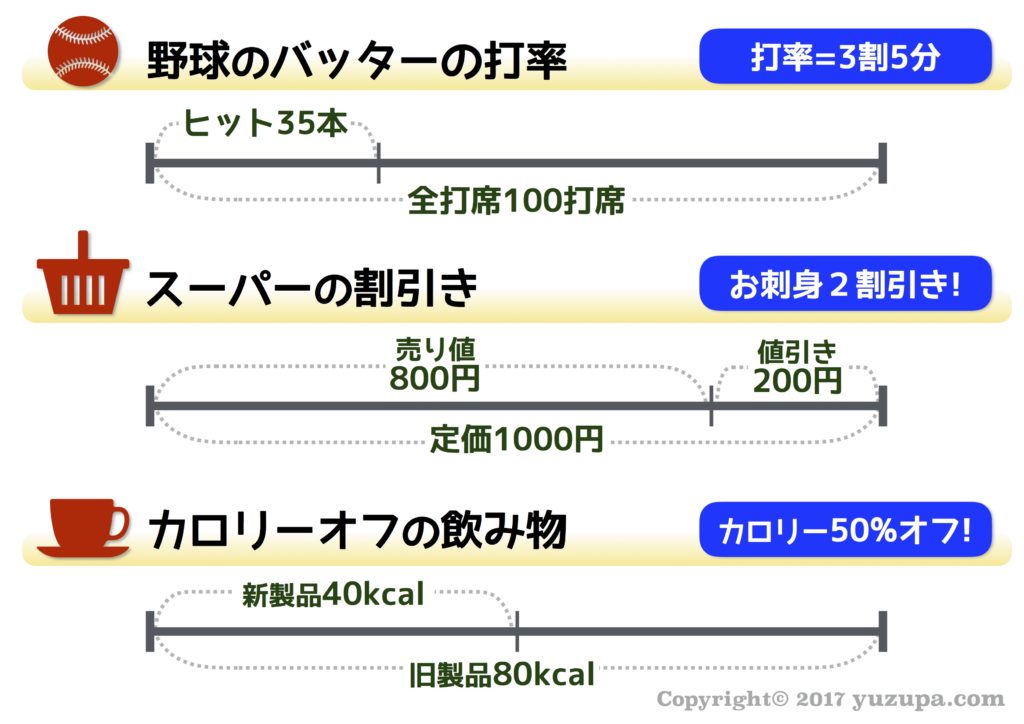
実生活で割合の色々な表現方法を考えるための前提となるのが、割合の表現4種類の表です。この表に関しては、覚えるための特別なテクニックはありません(O_O) 10%が1割に相当したり、0.1が10分の1に相当したり…。私の息子も苦労せず習得しました。実生活で見つけた時に意識するというのが唯一のポイントです!
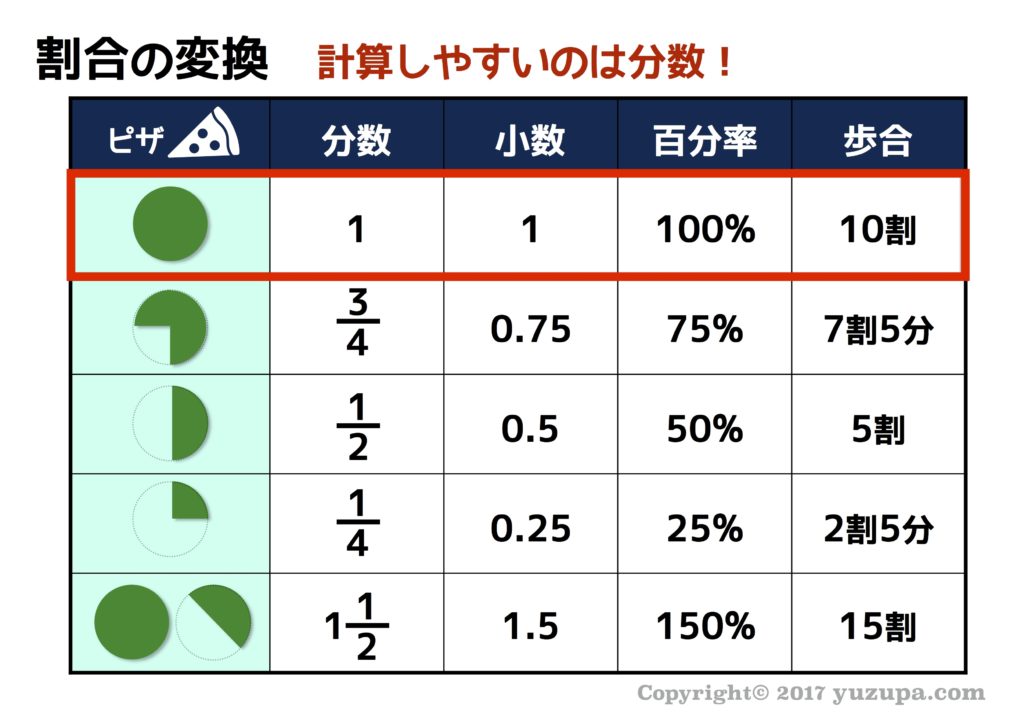
計算をする時に最もミスが少なく、計算のスピードも確保できるのは分数です。少数はどうしてもひっ算を書かなくてはならず、狭い計算スペースに書いている間にミスが発生するようなんです。最終的に計算式を作る時は分数を使うように心がけましょう。なぜ分数が良いかは別の記事で詳しく紹介したいと思います(o^^o)
道具③ 比を簡単に!
割合と比は小学算数の単元では別扱いとなっていますが、割合は元にする量(基準にする量)を1に固定しただけで比の一種です。比の単元では元にする量(基準にする量)が1ではなく…2だったり…3だったり…時には少数だったり…分数だったりします。先ほどと全く同じ例で比の概念を表すと以下のようになります。
注釈:比の単元では”元にする量”という言葉は出てきません。比べるもの全てが対等に扱われます。でも頭の中では『こっちが4だとすると…あっちは3だ』というように… 無意識のうちに割合と同じ考え方をしてるのです。
 比を使うときは割合と同様に合言葉があります。『こちら(基準にする量)が600とすると、こちらの量は?』頭のなかでブツブツつぶやきながら線分図などを眺めるのです。ピザの例であれば…グラムやキログラムといった重さで比を作っても良いし、枚数で作っても良い… 比較できる数字であれば何でも良いんです!
比を使うときは割合と同様に合言葉があります。『こちら(基準にする量)が600とすると、こちらの量は?』頭のなかでブツブツつぶやきながら線分図などを眺めるのです。ピザの例であれば…グラムやキログラムといった重さで比を作っても良いし、枚数で作っても良い… 比較できる数字であれば何でも良いんです!
もちろん、図形であれば長さでも良いし、お金であれば金額でも良いです。分厚い本であればページ数でも良いですね!さぁ、比の概念を復習したところで本題です。比は全ての要素に同じ数を掛けたり同じ数で割ったりすることが出来ます。その目的は主に3つあります。先ほどのピザの比を簡単にしてみましょう。

中学受験の比を答える問題は “最も簡単な整数の比” で回答しないと不正解になります。分数や少数があったら迷わず整数に。そして最後は出来るだけ小さい整数にするクセをつけましょう!実際の中学入試では、部分点をくれる学校もありますが、勿体ないですよね?普段からクセをつける事をお勧めいたします。

道具④ 比は丸数字を使う
比の問題で私の息子が最初にぶつかったのが長さなどの数字と比の数字が混同してやってはいけない計算をしてしまうという間違いです(T_T) 辺の長さの”比”が1:3だったはずなのに、いつのまにか1cmや3cmとして計算してしまってる…(>_>) 原因は単純です。実際の数字と比の数字を区別しないで書くので混同するのです。
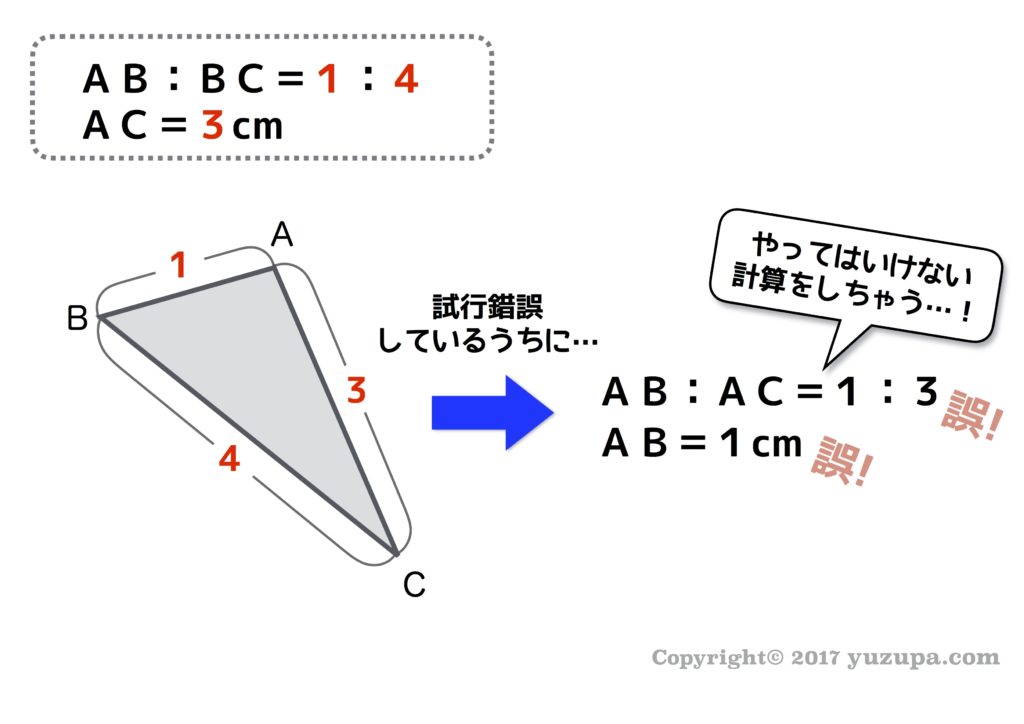
原因が単純であれば対策もシンプルです。長さなど実際の数字には単位をつけ、比の数字には丸数字を使うだけです。これで一安心…と思いきや、複数の比が出てくる問題で2つ目の間違いにぶつかります(T_T) 複数の比が出てきても全部丸数字にしてしまうと、やってはいけない計算をしてしまうのです。
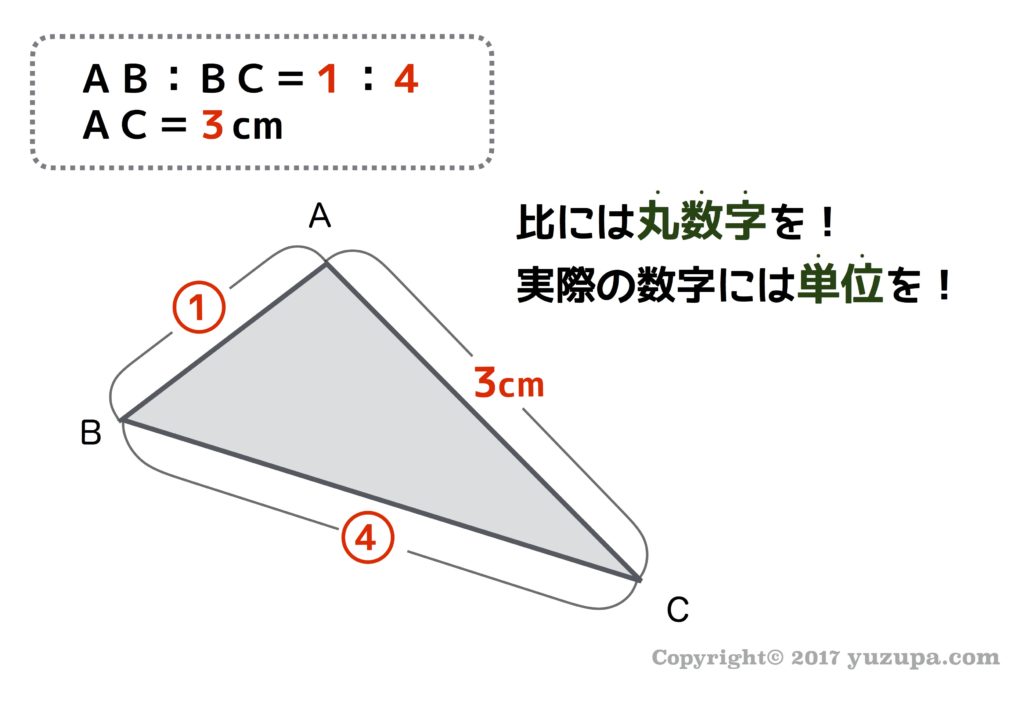
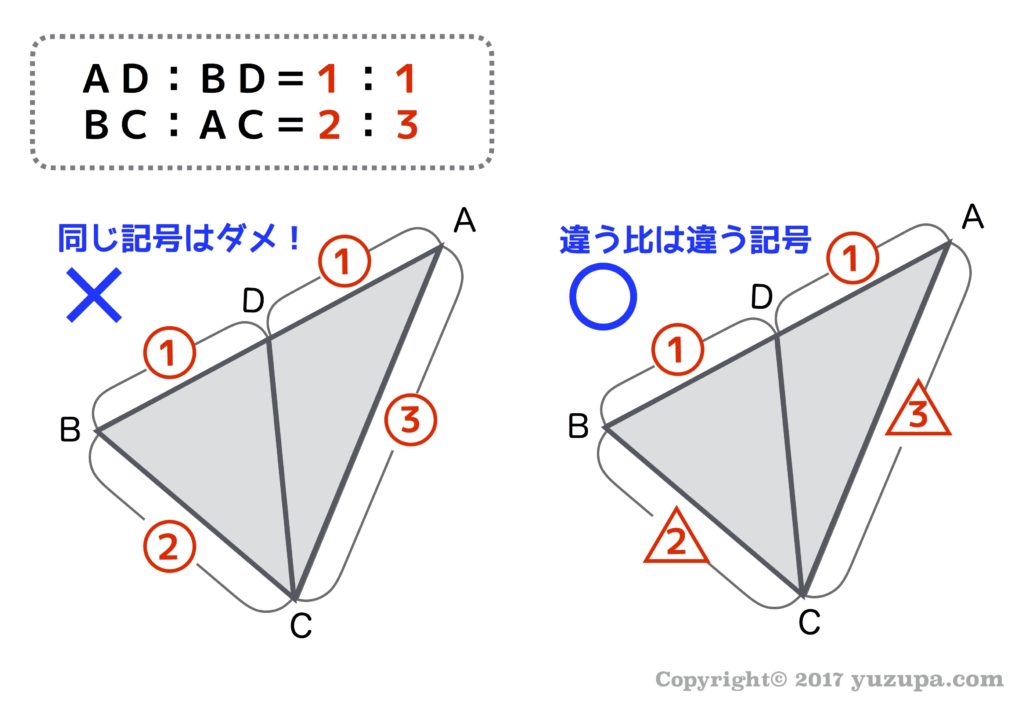
複数の比が出てきたら記号を変えましょう!
道具⑤ 比を結合する
丸数字と三角数字と四角数字と…それぞれ違う比なので、そのまま一緒に扱うことは出来ません。ところが初心者小学生はおかまいなしでバンバン計算し始めます。へんなクセが付く前に… 複数出てきた比をくっつける方法をお子様と頭に入れましょう。それが比の結合…連比(れんぴ)という方法を使います!
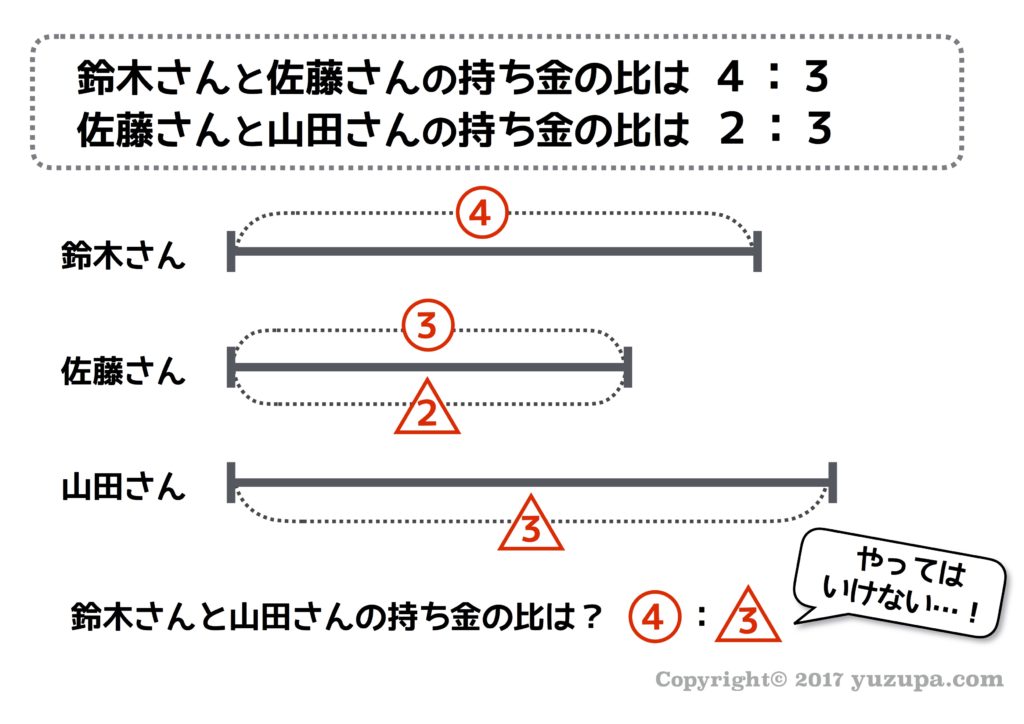
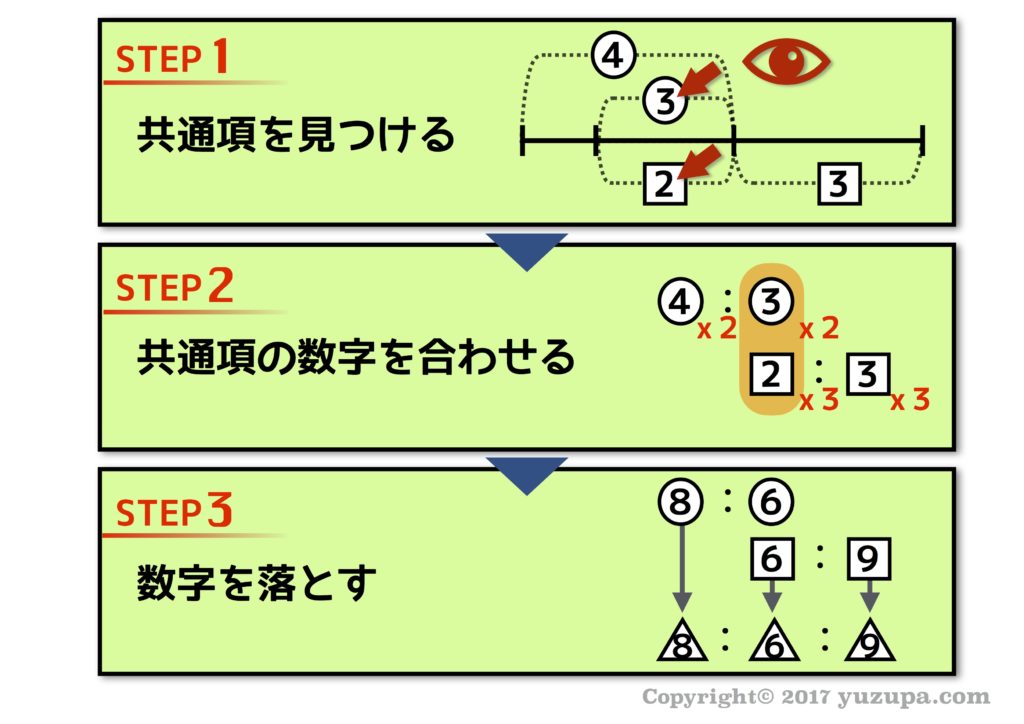
手順は3ステップです。共通項を見つけて、共通項の数字を合わせて、数字を落とす…です。見つけて… 合わせて… 落とす! の3ステップです。テンポの良いフレーズですので覚えやすいかと思います。比を結合することができたら、同じ基準での比例式になりますので、お子様には思う存分、計算してもらいましょう!
道具⑥ 逆比を使う
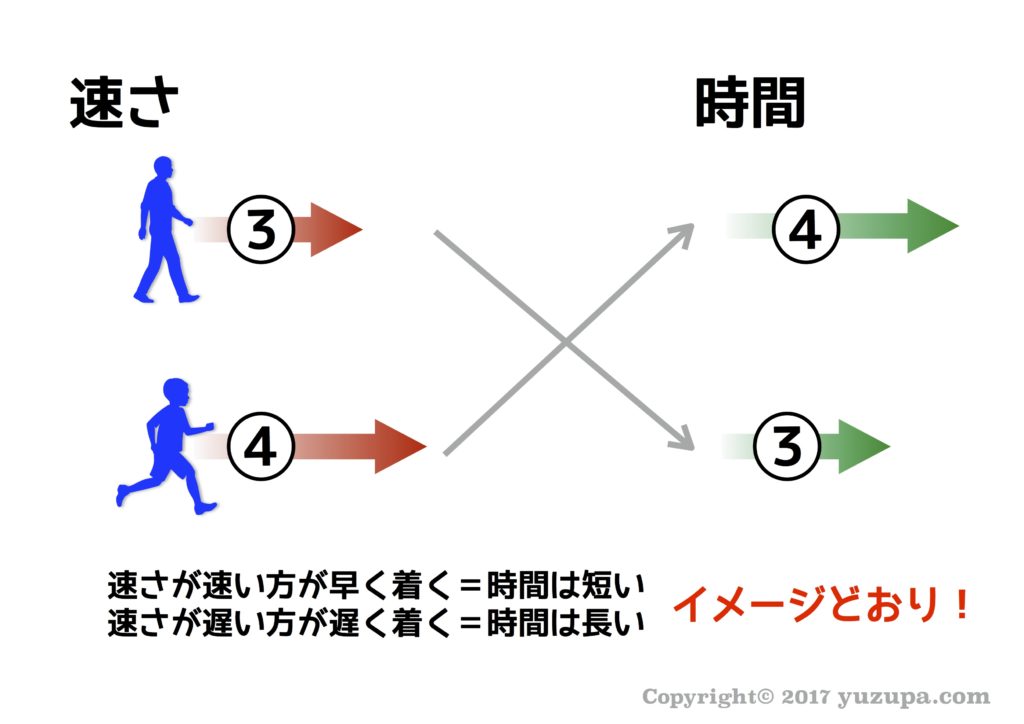
逆比も中学入試では頻出です… 必ずマスターしましょう!まずは逆比の概念を頭に入れるために逆比の例からご紹介します。太郎君と花子さんの歩く速さの比が4:3である時、2人が図書館から学校まで歩くのに掛かる時間の比は? 答えは3:4です。速さの比と時間の比がひっくり返ってますよね? これが逆比というものです。
逆比の詳しい説明は以下の記事でも紹介しています!
中学受験:逆比をいつ使って良いのか分からない…円形図を使え!
先ほどの例は速さと時間の関係でしたが、逆比は算数のあらゆる単元で出てきます。つまり…逆比を使って解くことが出来る問題は無数にあるという事です。どんな問題で逆比を使うのでしょうか? 大雑把にいうと…面積図や円形図で表すことが出来る式は全て逆比の問題が出る可能性があると言えます_φ(・_・
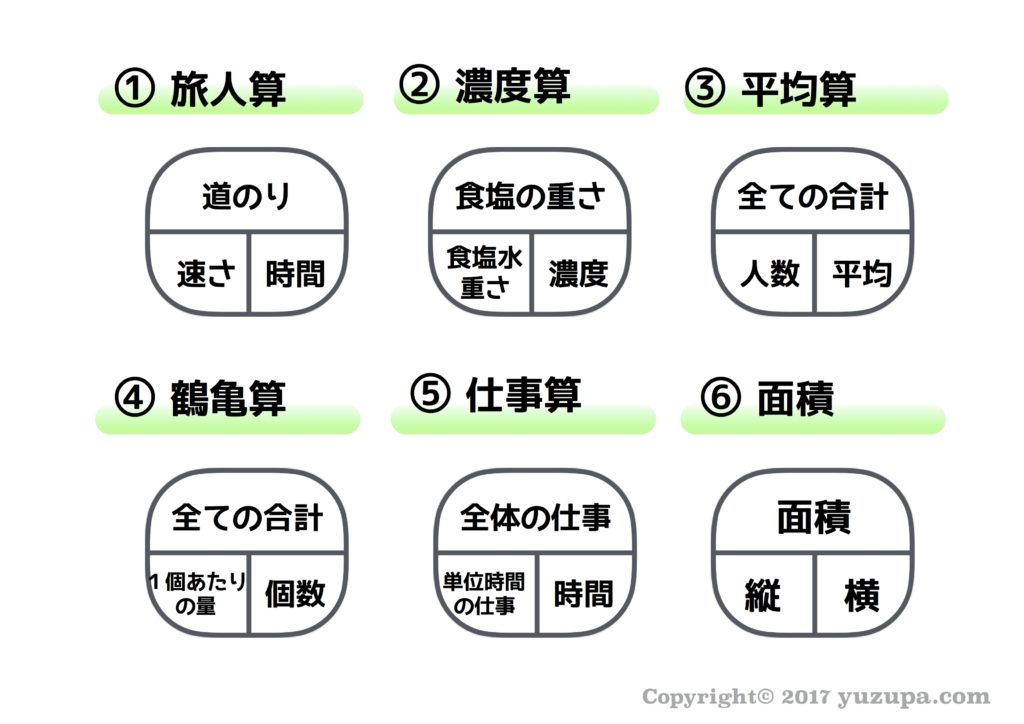
この円形図において上半円の値が同じ時、下半円に左右に並んでいる値が逆比の関係にあります。道のりが同じなら、速さと時間は逆比の関係です。食塩の重さが同じなら、食塩水の重さと濃度が逆比の関係です。面積が同じなら縦と横の長さは逆比の関係にあります。具体例を見ていきましょう。
食塩水AとBの濃度の比が4:5で、両食塩水に入っている食塩の量が同じ時、食塩水の重さの比は? 濃度の逆比で5:4です! リンゴ1個の値段とミカン1個の値段の比が8:7で、リンゴもミカンも合計額がいっしょだった時、リンゴとミカンの個数の比は? 1つあたりの価格の逆比で7:8になります!
では、逆比はどう作れば良いのでしょうか?ひっくり返すだけでしょう…簡単簡単? ちょっと待ってください!3つ以上の項がある比は、ひっくり返せないですよ。3つ以上の項がある比の場合…全ての項を逆数にしましょう。これで逆比の出来上がりです。これで3つ以上の項がある比でも大丈夫ですね!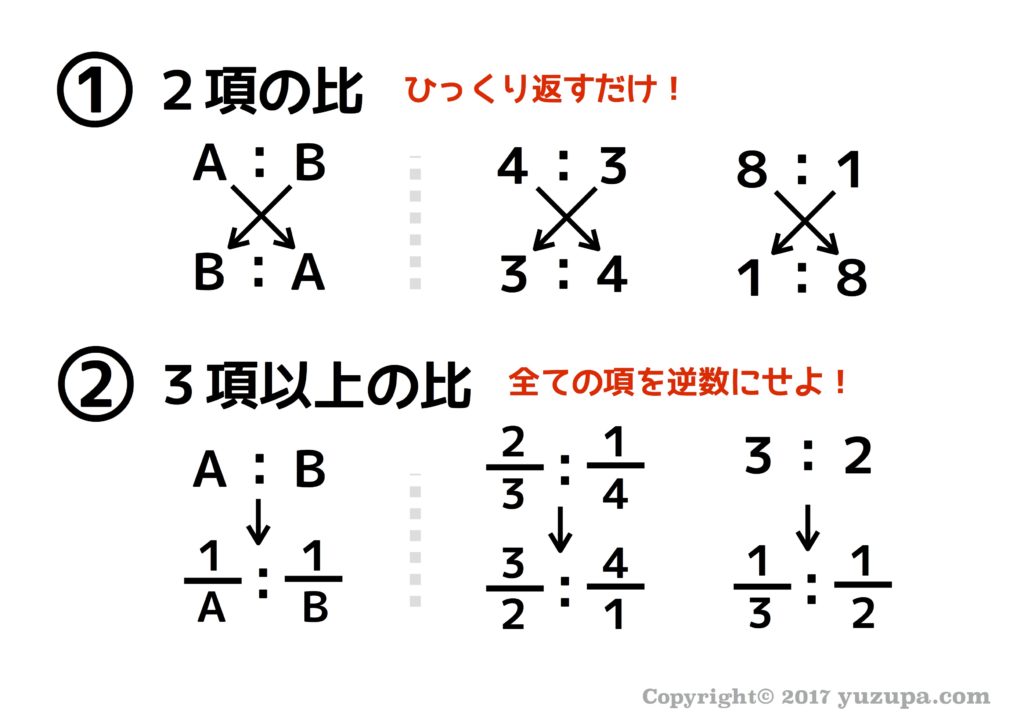
道具⑦ 比の穴埋めは”比例式”
7つ道具の最後は”比例式の穴埋め計算”です。比の問題では比例式という式を立てて答えを出す問題が頻出しています。比例式とは”A:B=C:D”というように2つの比がイコールで結ばれた式です。A,B,C,Dの中に分からない所があっても求める事ができます。比例式でも実際の数字には単位をつけ、比の数字には丸数字を使うように!

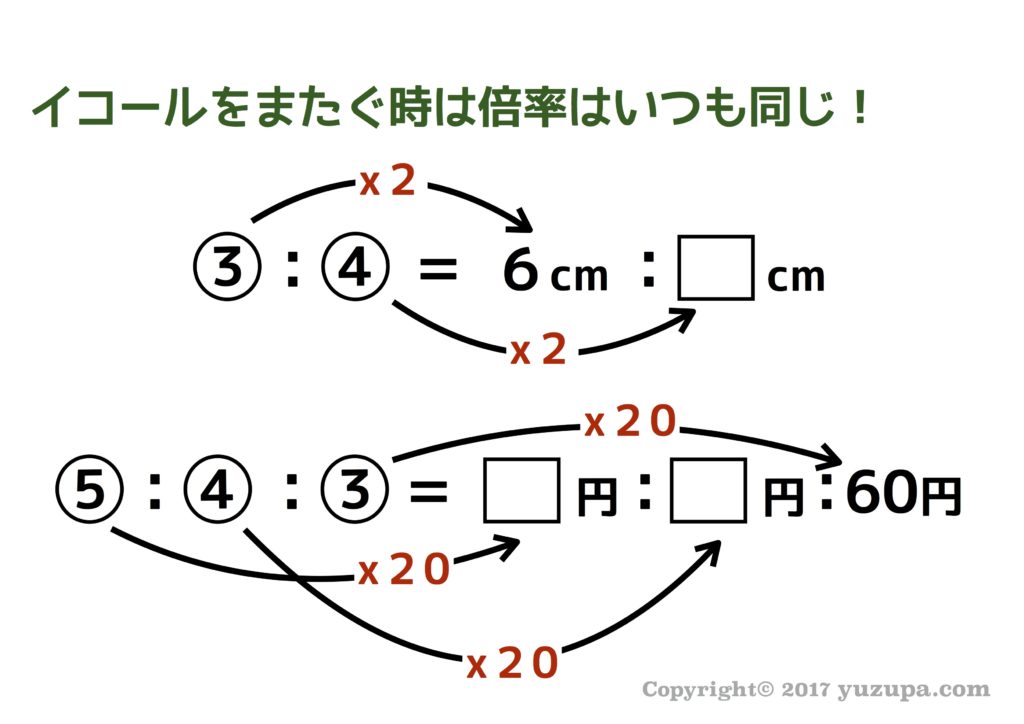
分からないところを埋めるためには”イコールをまたぐ時には同じ倍率”という比例式の性質を利用します。ある項でイコールの左から右にまたぐ時に数字が2倍になっていたとしたら、他のどの項でも同じように2倍であるという性質です。イコールの右から左にまたぐ時も同様に同じ倍率になります。
多くの受験サイトでは”内側の積=外側の積”という公式が紹介されています。ただ3つ以上の項を持つ比例式が出てくると焦ってしまいどうすれば良いか分からなくなる。普段から3つ以上の項を持つ比にも耐えうる練習をしておくべきですね。これは私の息子が混乱して鉛筆が止まってしまったという実体験からの考えです(´-`)
まとめ
中学受験の算数という科目は、2つの力が試されます。1つ目は問題文を読んで解釈する力。2つ目は早く正確に処理をする力。いずれの力を発揮するのにも共通的に必要となるものが、問題を解くための道具類です。この道具だけで解ける問題がいわゆる基礎問題です。
基礎問題は中学入試の本番でも出題されますので、割合や比の分野での7つの道具類をしっかりと復習しましょう!
印刷用プリントのダウンロードは以下からどうぞ!

7つ道具シリーズ…図形問題の7つ道具は以下のリンクから!
参考リンク:図形問題の角度は “7つ道具” で攻略
参考リンク:図形問題の面積は ”7つ道具” で攻略











めっちゃわかりやすい!!!
ありがとうございます!
ところで 「ものの燃え方と気体」、「生命の誕生」と「植物の増え方
」の単元はありますか?今年中によろしくお願いします!
匿名さま
かるび勉強部屋 ゆずぱ です。
コメントをいただきありがとうございます!
ヒトの体 生命の誕生は近いうちに後悔予定です。
ものの燃え方と気体、植物の増え方
については、可能な限りご希望にお応えできるよう
頑張ってまいりますm(_ _)m
めっちゃわかりやすいです!速さと比もやってくれたら嬉しいです
ゆきさん
かるび勉強部屋 ゆずぱ です。
コメントをいただきありがとうございます!
速さと比ですが↓こちらの記事が参考になるかと思います。
ぜひご参照ください!
https://yuzupa.com/gyakuhi/
分かりやすいです。もっと書いてくれたらyoutubeもチャンネル登録するし、グットボタン押します。
受験生さん
ゆずぱです!コンテンツは順次公開していきます!
受験頑張ってください!
わかりやすスギィ 娘です
匿名さま
ゆずぱです!ありがとうございますっ
濃度の問題もよろしく
ソウカナさん
かるび勉強部屋 ゆずぱ です。
コメントをいただきありがとうございます!
いろいろリクエストをいただき感謝いたしますo(^-^)o
可能な限りリクエストに応えられるようなコンテンツ拡充に
努めてまいります!
貴重なリクエスト、感謝いたします!
濃度はこちらも参照してみてください_φ(・_・
https://yuzupa.com/mensekizu-shokuen/
割合や比の問題を入れてその様な問題を解くコツを書いて‼️‼️❗️してくれたらYouTuberもチャンネル登録するから