中学受験：場合の数の基本パターンを全網羅！ サイコロ問題編

サイコロ問題…樹形図をベースに条件に合わないものを排除せよ

こんにちは。かるび勉強部屋 ゆずぱ です。

読者の方々からもリクエストの多い場合の数… この場合の数が苦手な小学生が多いようです (-_-;) 場合の数の問題は、ありうるパターンをただ数えるだけなのに苦手なのはなぜでしょうか？

それは数え方があまりにも多すぎるので
全体像が見えずにモヤモヤするから

塾や学校の授業では次から次へと数え方のパターンが出てきてわからなくなってしまう。まずは基本となる１０のパターンを仮の全体像としてとらえることが大事です。

今回は１０のうちの６つ目の出題パターン…サイコロ問題のパターンです。サイコロ問題は計算できそうですが、あわてずに樹形図をベースにかぞえることで攻略できます。

本題のサイコロ問題の前に、場合の数の全体像をオサライします。具体的な問題の解説は第２項へお進みください d(^_^o)

 

おさらい：場合の数には３つの道具がある

道具を使い”全ての可能性を数える”こと

”場合の数問題” の全体像をご覧ください。

場合の数の問題というのは、ズバリ”全ての可能性を数え上げなさい”という問題 のこと。正しく問題を解くには以下の３つのステップを着実にこなすことが最も近道です。

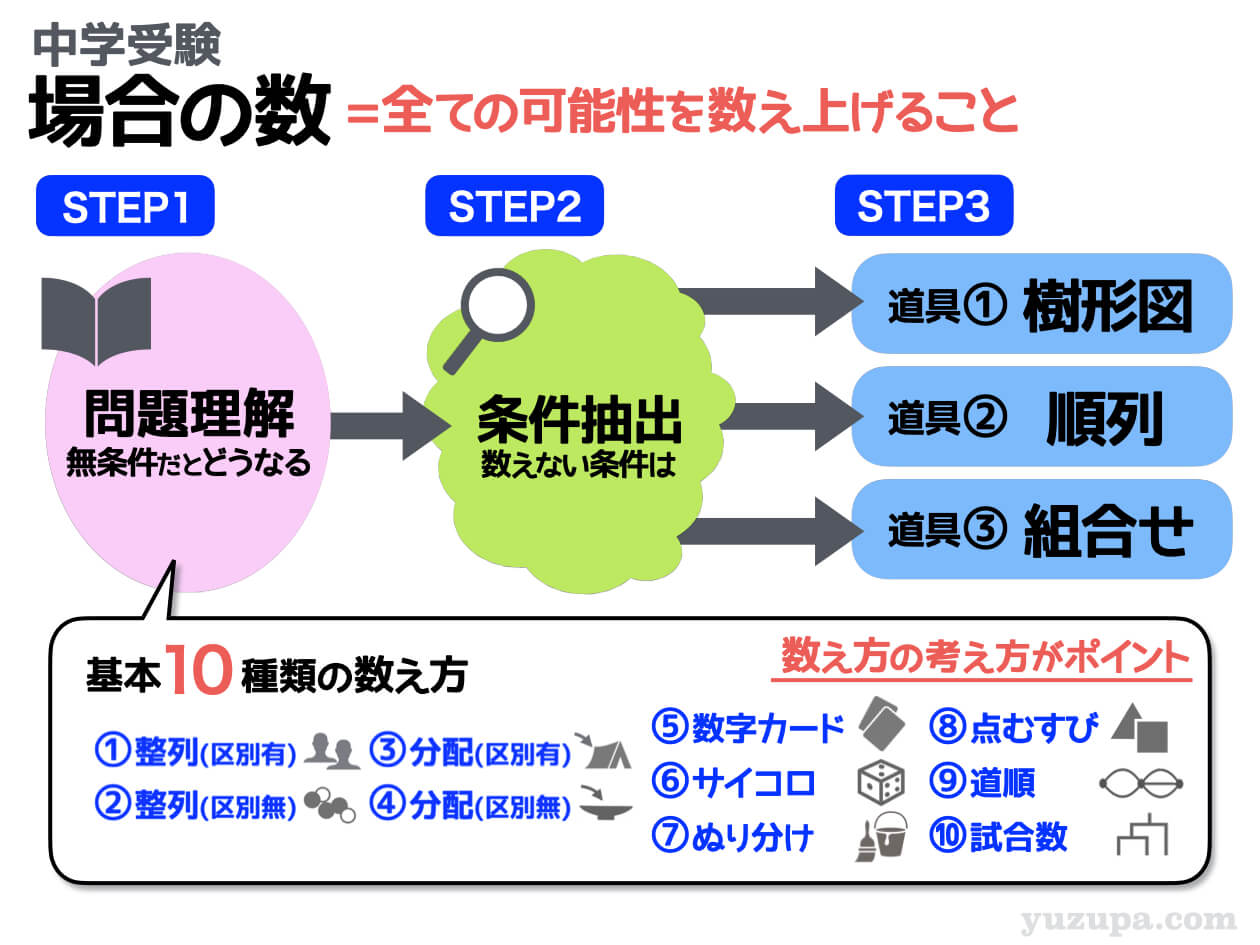
STEP1では、問題文を読んで”いったい何を数えたらよいのか”をしっかり把握します。その際に役に立つのが”基本的な１０種類の数え方”です。まずは基本パターンを考えましょう。

STEP2では、条件を理解します。偶数”だけ”数えなくてはいけなかったり、男子が両端にくる並び方”だけ”数えなくてはいけなかったり、入試の問題には必ず条件がついてきます(^_^;)

STEP3でいよいよ数えます。数えるには必ず道具を使います。樹形図はオールマイティですが、通り数の多い問題には使えません。樹形図をサボる道具として”順列”と”組合せ”があります。

 

３種類の道具を使って数える

３つの道具とは”樹形図”と”順列”と”組合せ”のことです。

樹形図はオールマイティな道具です。どうやって数えたら良いか迷ったらまずは樹形図で数え始めてみてもよいでしょう。書いていているうちに数え方のヒラメキがあることもあります。

順列は並べ方が何通りあるか数える道具です。シンプルに何かを並べる場合の数を求める問題の他に、並べること以外の題材を並べる行為に置き換えて数えることもよくあります。

組合せは選び方が何通りあるか数える道具です。例えば１０種類のケーキがあり、３つだけ食べて良いと言われたら何を選びますか？ この道具を使えば選び方が何種類あるか分かります。

場合の数の全体像を確認したい場合は、ぜひ以下の記事をご参照してみてください。スッキリしますd(^_^o)

参考：場合の数が苦手…３つの道具を使い10種の数え方をマスターせよ

 

サイコロを使った場合の数の問題を全網羅

サイコロ問題の全体像

サイコロを使った問題とは サイコロをいくつか振ってその目の出方の場合の数を数える問題です。まず基本パターンとしてサイコロに区別の有無で２種類が存在します。

そして 出た目がの条件が必ず つきます！

出た目が全て異なるとか１つが偶数であるとか…出た目についてシンプルに条件を指定してくる問題、そして出た目を足した数字がどうなるか？出た目を掛けた数字がどうなるか？の条件も∑(ﾟДﾟ)

 

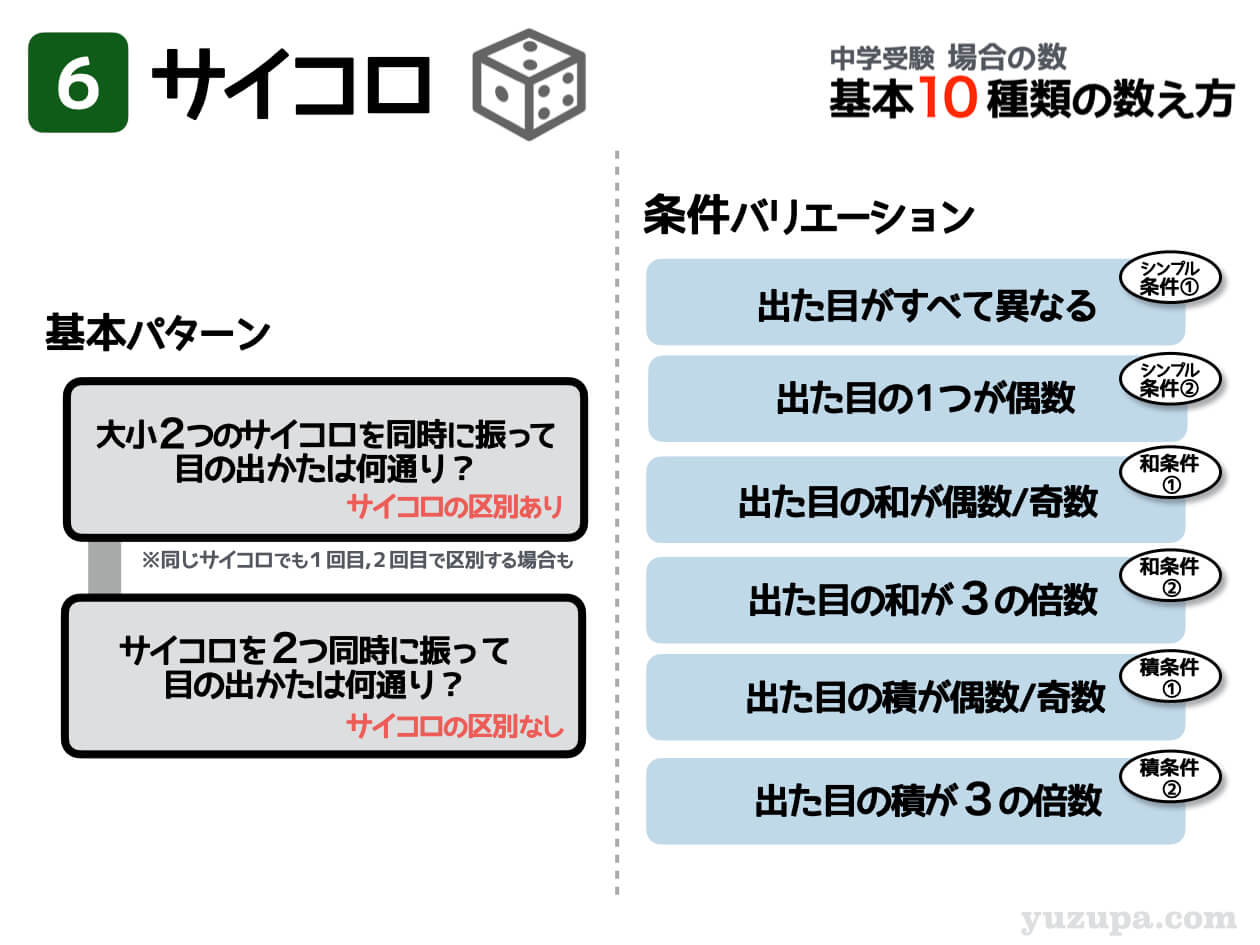
基本パターン２種

サイコロに区別がある場合とサイコロに区別が無い場合の２つの基本パターンがあります。気をつけるのは区別の無い場合です。サイコロ問題で 最初に確認すべきは区別の有無 ですd(^_^o)

 

(1) サイコロに区別があるパターン

大小２つのサイコロを投げる…同じサイコロを２回投げる…これらは大や小だったり、１回目や２回目だったり出た目に区別があります。最もシンプルなパターンです。

(2) サイコロに区別がないパターン

では…形も大きさも全く同じサイコロを同じに投げた場合はどうでしょうか？これは投げた後にどのサイコロであるか区別がつきません_φ(･_･ これが２つ目の基本パターンです。 

 

条件バリエーション６種

そして受験問題ではサイコロの出た目に必ずと言ってよいほど条件がつきます(-_-;) シンプルな条件の時もありますが、よく出題されるのが出た目の和や出た目の積に条件がつくパターン∑(ﾟДﾟ)

・シンプルに出た目に条件がつく×２題
・出た目の和に条件がつく×２題
・出た目の積に条件がつく×２題

本記事では代表的な６つのパターンを掲載しますが、その条件は無数にあります∑(ﾟДﾟ) ただし、この６つの条件を理解できればほとんどの条件に対応することができます_φ(･_･

頭の中は以下のように理解します
数え方は何パターンあるのか
＝ 基本パターン２種 × 条件バリエーション６種

サイコロ問題では２つの基本パターンと６つの条件バリエーションをご紹介します。これで１２パターンですねd(^_^o) 条件は無数にあるので、数え方のパターンも無数ということです_φ(･_･

でも安心してください

２つの基本パターンと条件バリエーションを掛け合わせるという意識を持っていれば、どんな問題にも対応できます。未知の条件が出てきたら数え方のレパートリーを追加していきましょう。

それではまずは基本パターンです。

 

サイコロ問題…２つの基本パターン

基本① サイコロに区別があるパターン

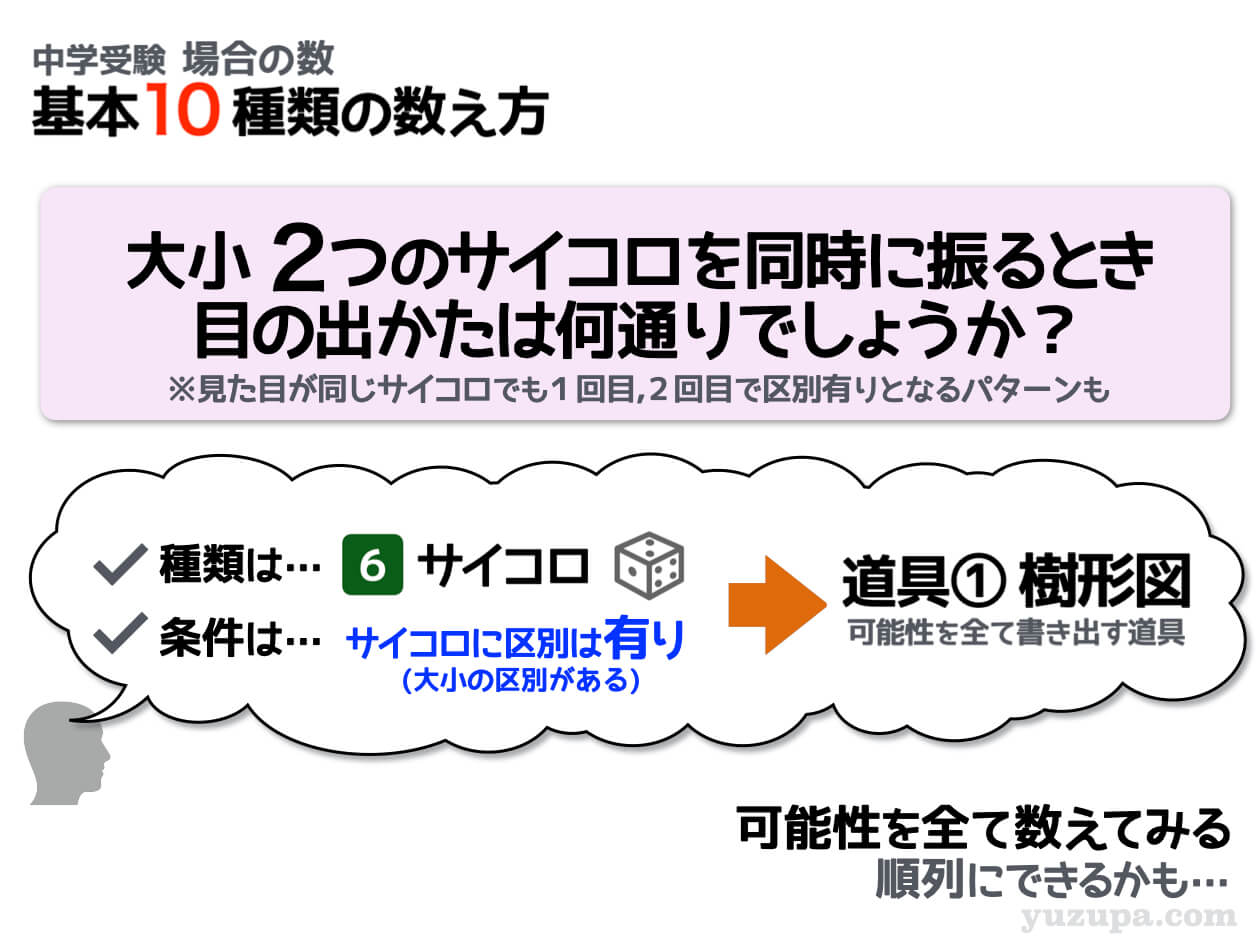
問題を読むと大小２つのサイコロを振ると言っておりサイコロに区別があるということが分かりますね！それ以外に出た目の条件は記載されていないので最もシンプルな区別ありのパターンです。

条件が無いので全てのパターンを数えます

サイコロ問題では 樹形図を描いているうちにパターンに気づくというやり方が王道の解き方 です。パターンに気づくというのはどういうことでしょうか？

樹形図をすべて書かかずに計算しちゃうということですd(^_^o) では実際に樹形図を書いてみましょう。

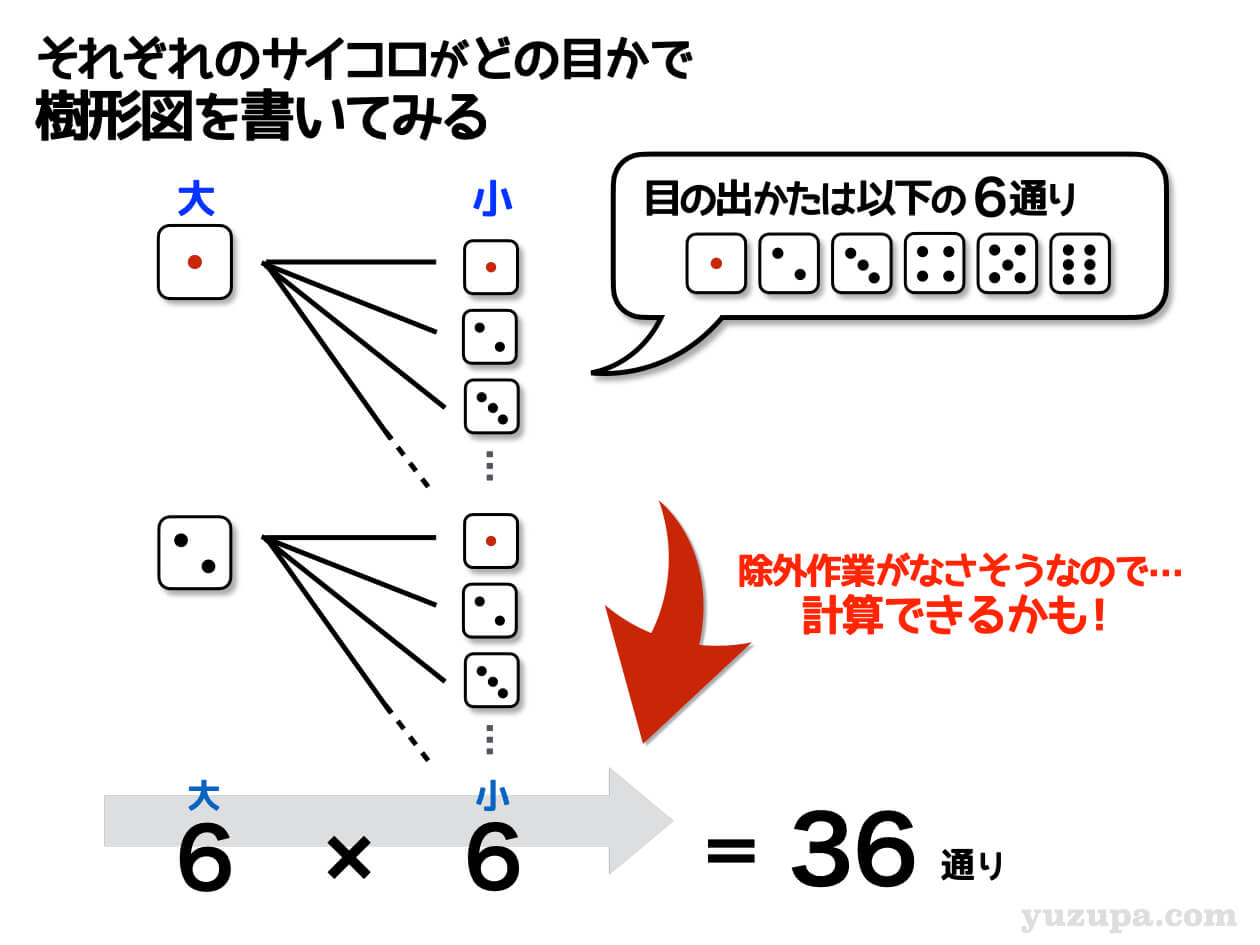
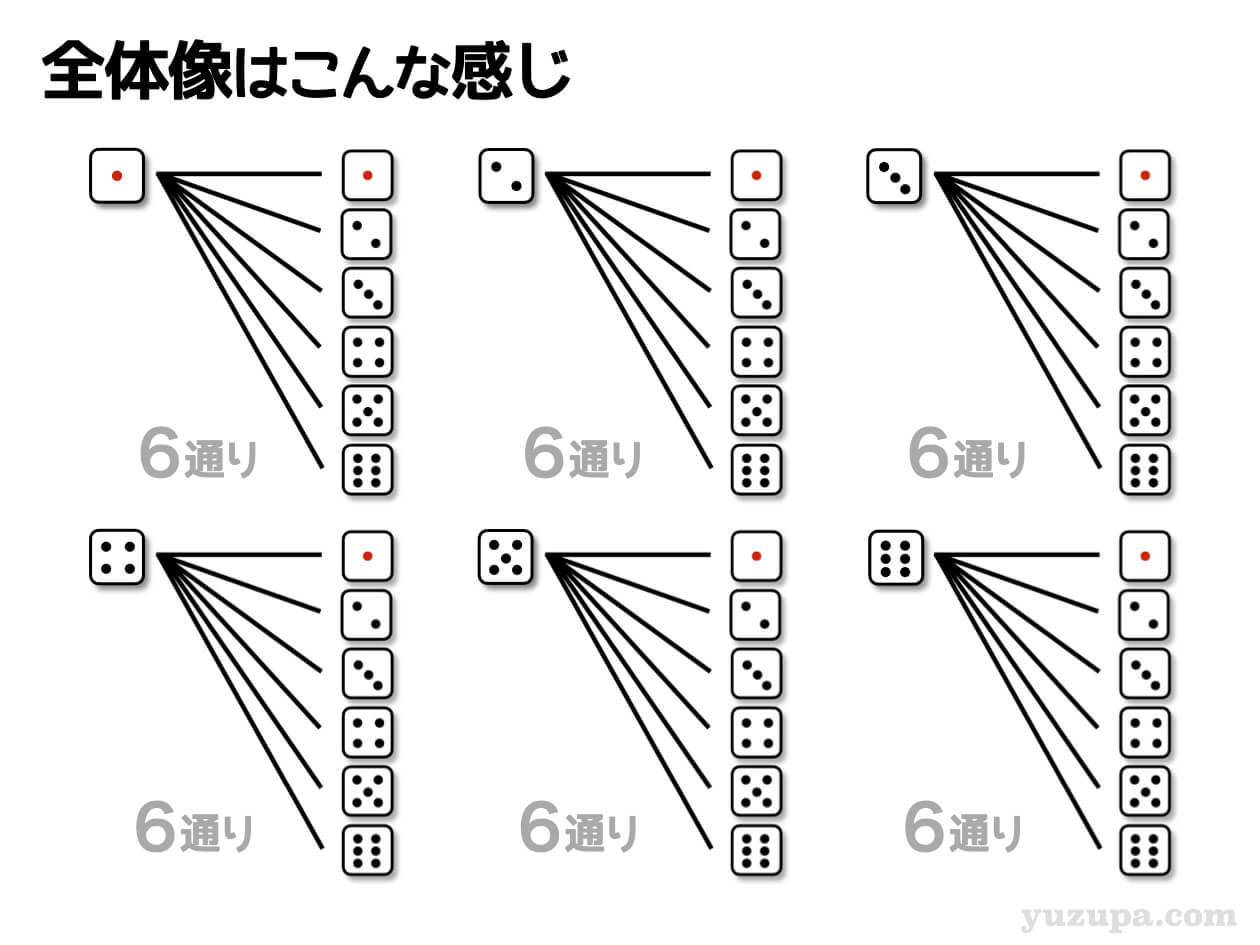
大小２つのサイコロでどんな目が出るかを樹形図で描いていきます。サイコロの目は１～６の６通りですので、樹形図をすべて書かなくても計算して出せそうですd(^_^o)

大＝１のとき…小は６通り
大＝２のとき…小は同じく６通り
大＝３のとき…小はまた同じく６通り
大＝４のとき…小はまたまた同じく６通り
…

大のサイコロも１～６なので、このような樹形図が６つあることになります。すべての樹形図をかかずとも６×６＝３６通りと計算で求めることができます。これは順列の考え方ですね。

順列の使い方が怪しい方は、以下の記事に戻って道具の使い方をおさらいしてから戻ってきましょうd(^_^o)

参考：場合の数が苦手…３つの道具を使い10種の数え方をマスターせよ

 

基本② サイコロに区別がないパターン

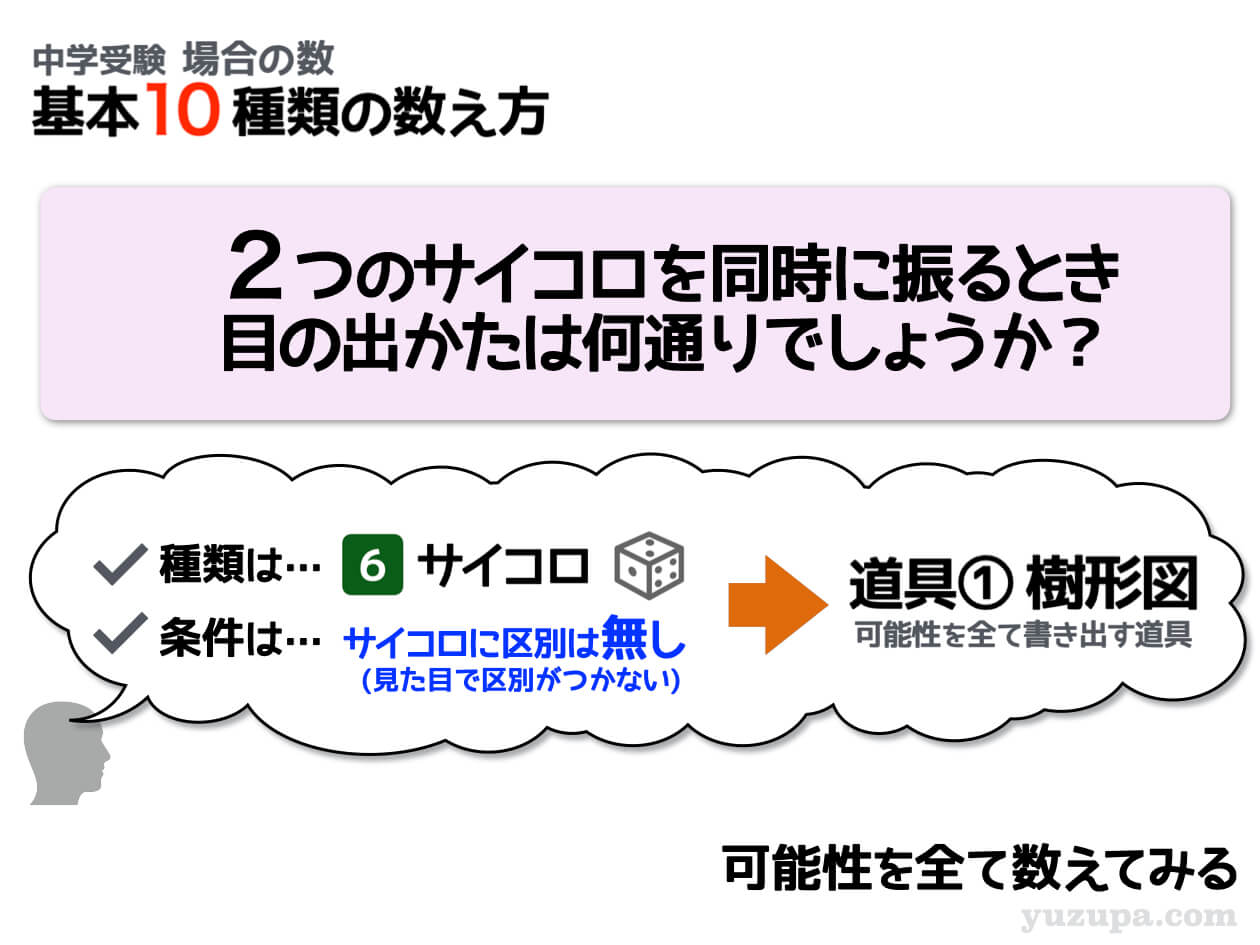
今回の問題文は”２つのサイコロを同じに振る”と書かれています…２つ同時にサイコロを振った場合、よっぽど動体視力が優れていなければどっちがどっちのサイコロか分かりませんよねd(^_^o)

区別がないときの重要ポイント
樹形図で同じものが登場するので注意が必要 

 

 

例えば樹形図で出てくる１ー２と２－１は同じパターンとなり、数えてはいけません_φ(･_･ ちょっと大変ですが、同じものを数えないように樹形図をすべて描き終えてみましょう。

同じものを数えないようにする工夫があります…

それは 右に行くほど数字が大きくなるものを数える という意識！

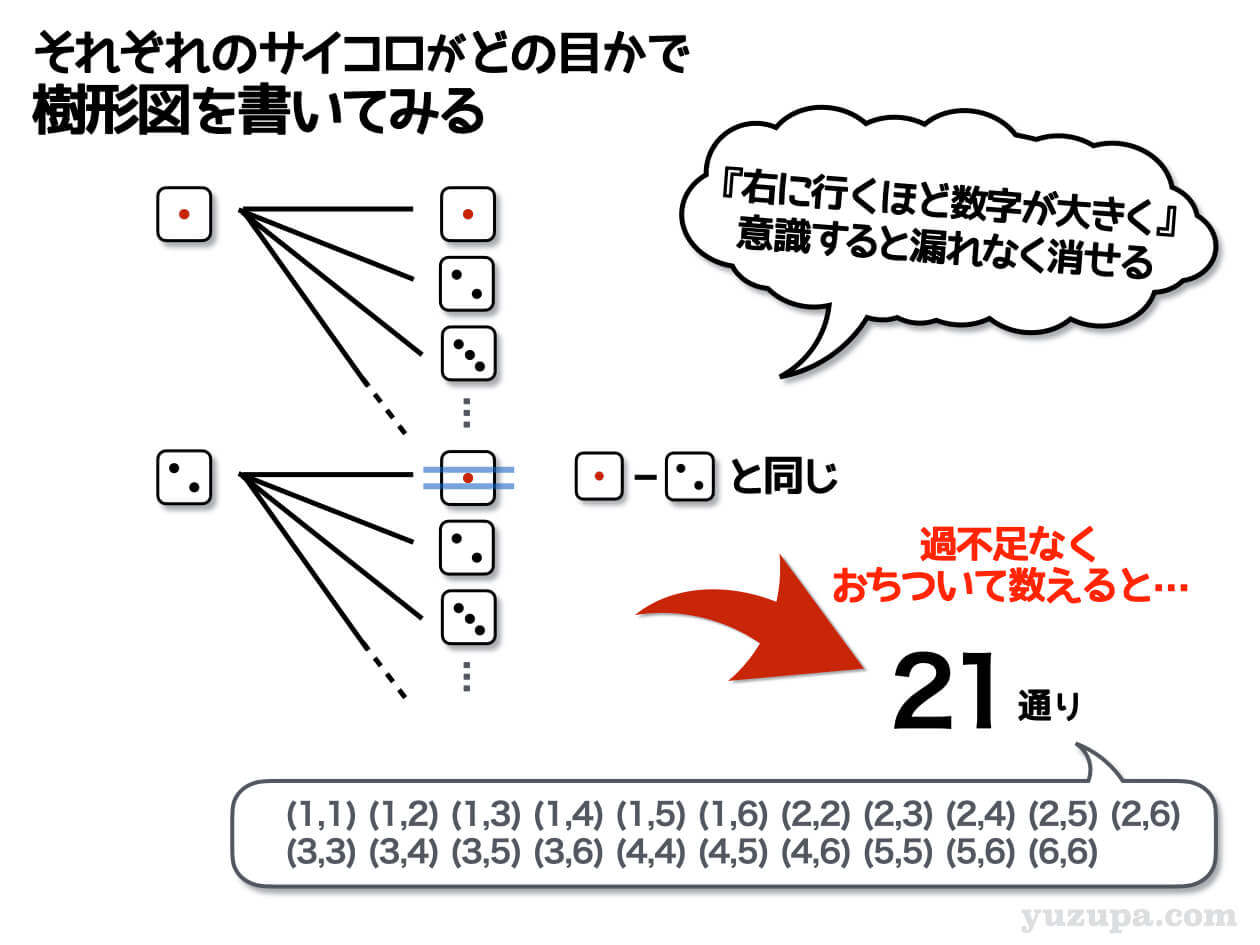
たとえば１－２は右の数字の方が大きいので初めて登場した組み合わせと判断できます。ところが２－１は右の数字の方が小さいので以前にも登場しているので数えてはいけませんd(^_^o)

すべて数えると２１通りになります。

 

補足：サイコロの区別について

ちなみに…”サイコロを２つ同じに振る”とにている文章で”サイコロを２回振る”というのがあります。サイコロを同じに２つ振った場合は区別がつきませんが、２回振る場合はどうでしょう？

１回目を振って出た目を確認し、２回目を振って出た目を確認し…という感じで区別がついちゃいます∑(ﾟДﾟ)

大小２つのサイコロを同時に振る → 区別がつく(大と小)
サイコロを２つ同じに振る → 区別がつかない
サイコロを２回振る → 区別がつく(１回目と２回目)

となりますので気をつけましょうd(^_^o)

 

サイコロ問題…６つの条件バリエーション

出た目に条件がなければ前項の基本２パターンで全て数えることができます。問題例ではサイコロの数は共に２つでしたが、３つだろうが１００個だろうが考え方は同じですd(^_^o)

出た目に条件があったらどうすれば良いでしょうか？

・出た目が全て異なる
・出た目の和が偶数になる
・出た目の積が３の倍数になる

たとえば上記のような条件です…

樹形図を描きながら漏れなく落ち着いて数えていきますが意識することは１つです。条件に合わないパターンは数えない。条件に合わなかったら取り消し線で消すのでも良いでしょうd(^_^o)

それでは６つの条件バリエーションで練習しましょう。

 

条件バリエーション① シンプル条件(1)

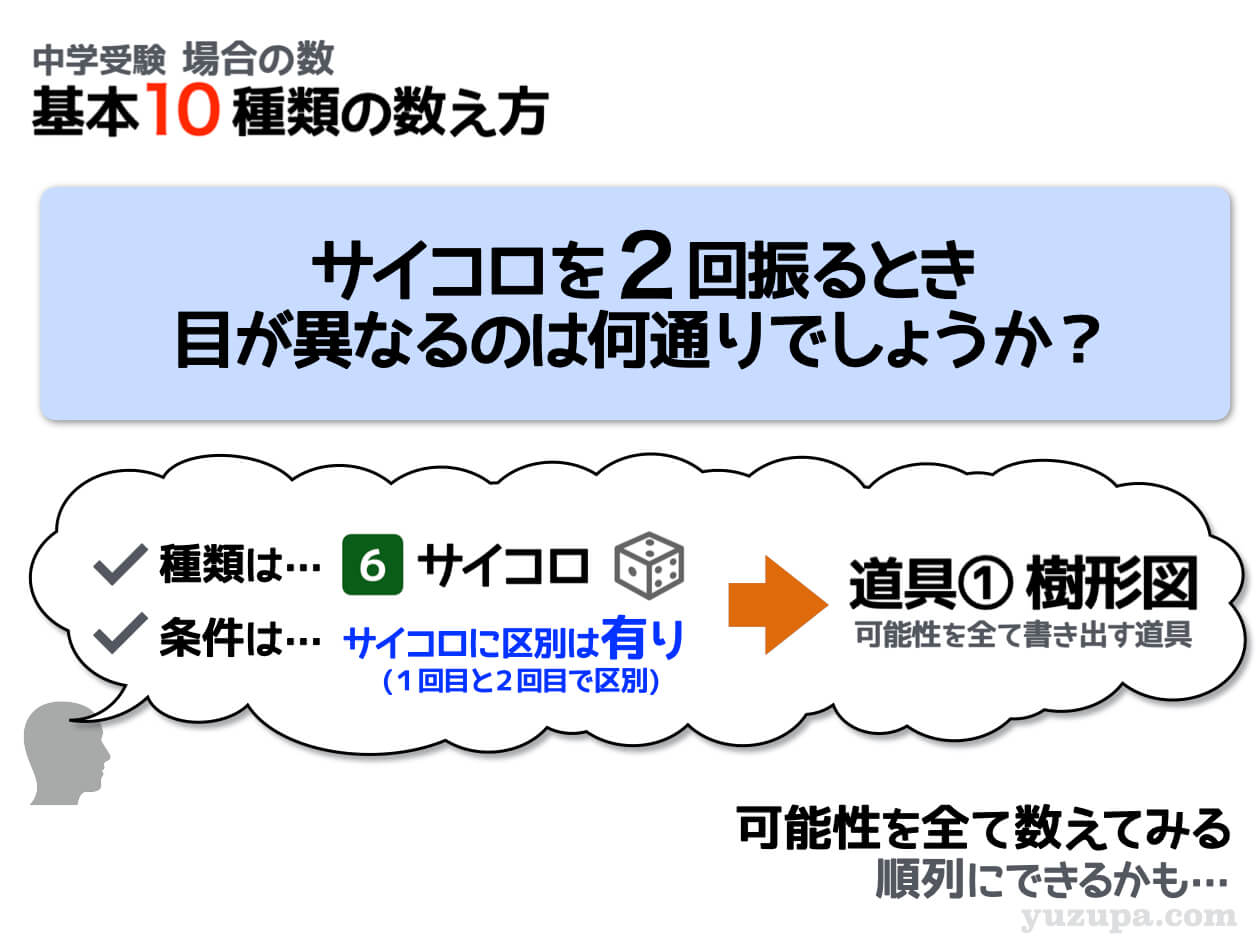
この問題の場合は”サイコロを２回振る”のでサイコロに区別が有ります。そして 出た目がすべて異なるという条件 がついていますね。この条件に合わないものは数えてはいけません d(^_^o)

条件外のものをカウントしたらアウトです(>_<)
間違えないために条件をかみ砕いてみましょう

すべて異なるという条件を”かみ砕く”とどうなるでしょう？言い換えると ２つのサイコロの目が同じでは無い ということです。 つまり…同じ目のものは数えてはいけません d(^_^o)

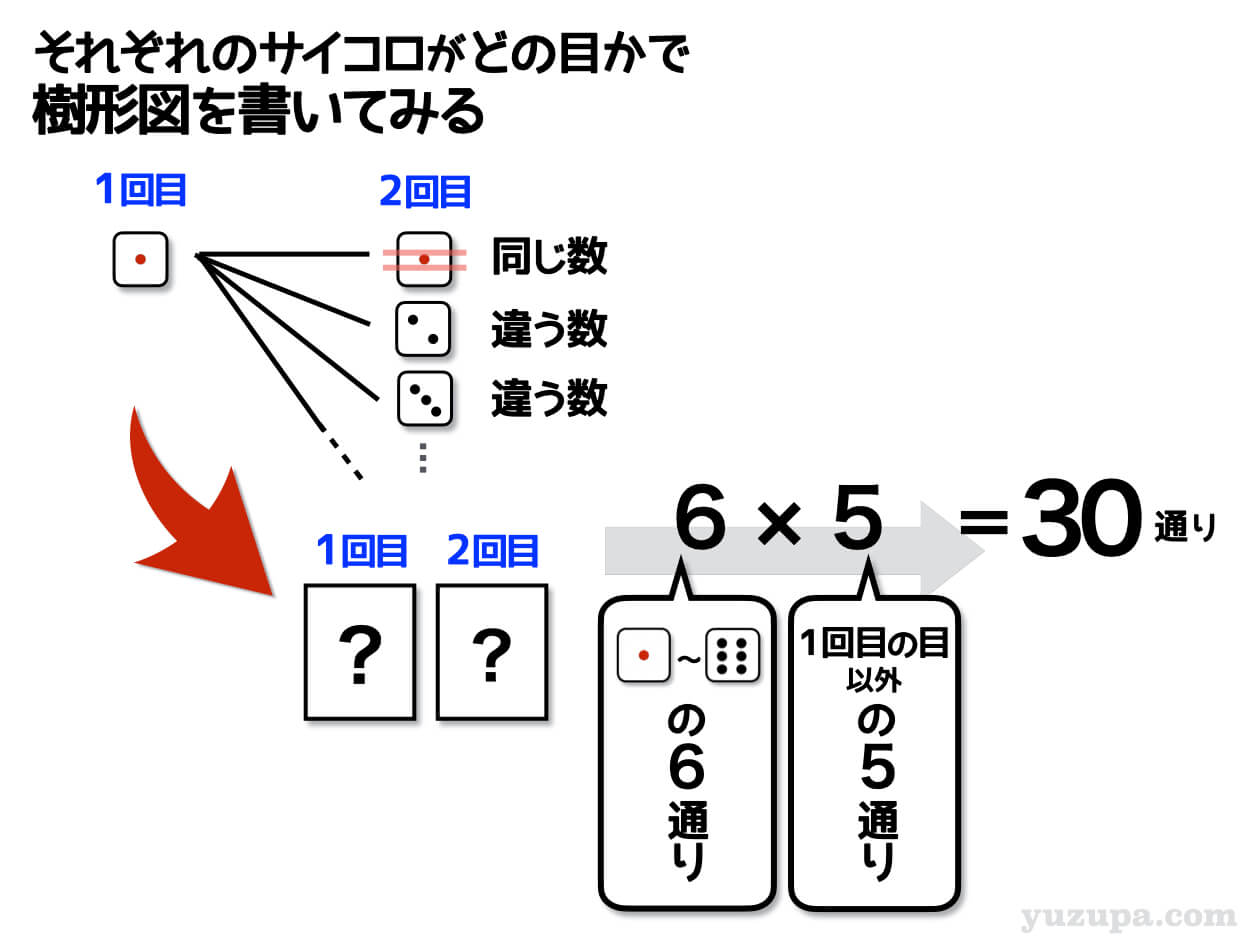
それでは…同じ数になるパターンを数えないように気をつけながら樹形図を描いてみましょう_φ(･_･ ちょっと樹形図を描くと、すべての樹形図を書かなくても計算できそうなことに気づきます d(^_^o)

１回目の目は１～６の６通りですが、２回目は１回目に出た目と同じ場合は数えてはいけません。つまり上記のように、６×５＝３０通りという具合に数えることができますd(^_^o)

全体像は以下のようになります。

 

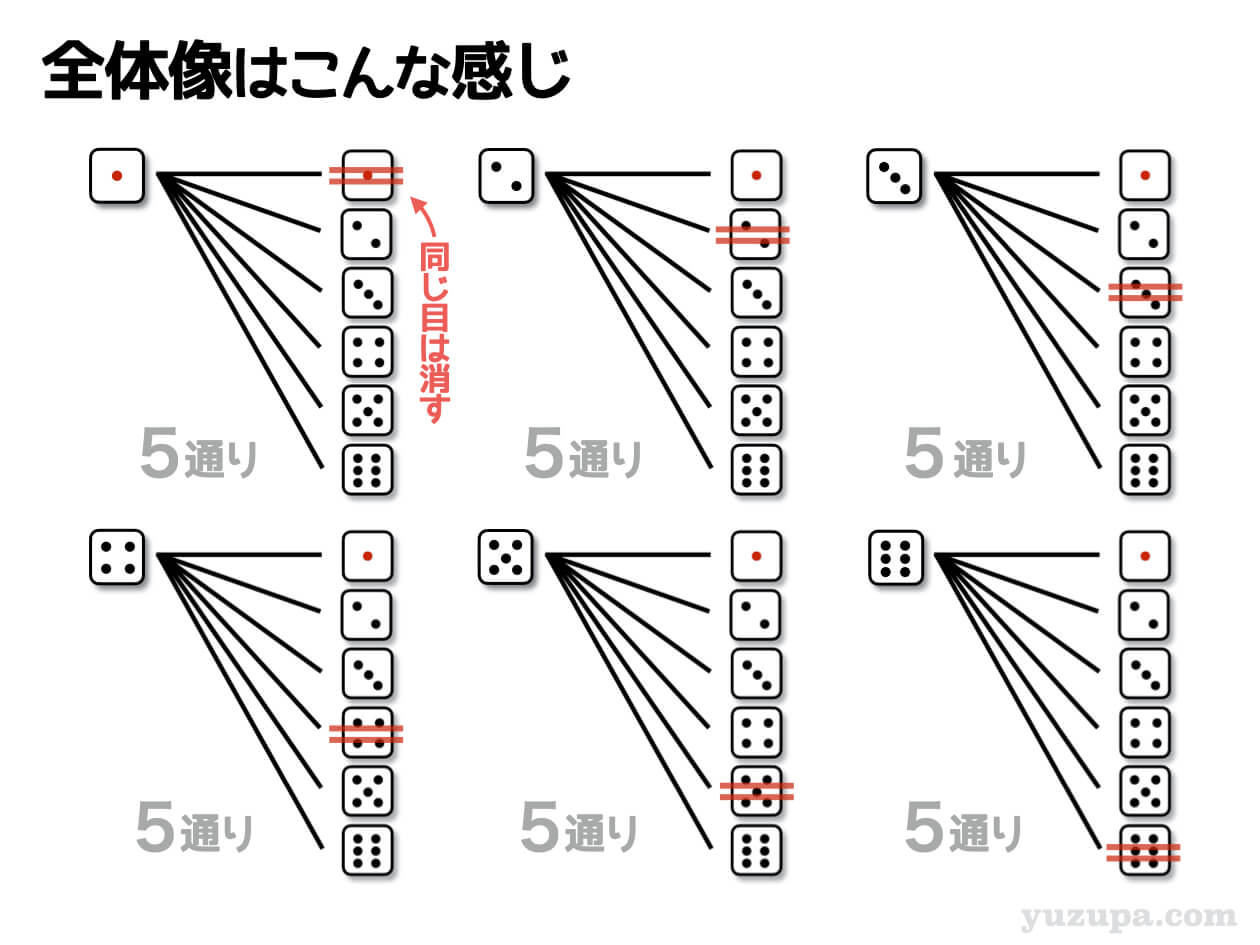
条件バリエーション② シンプル条件(2)

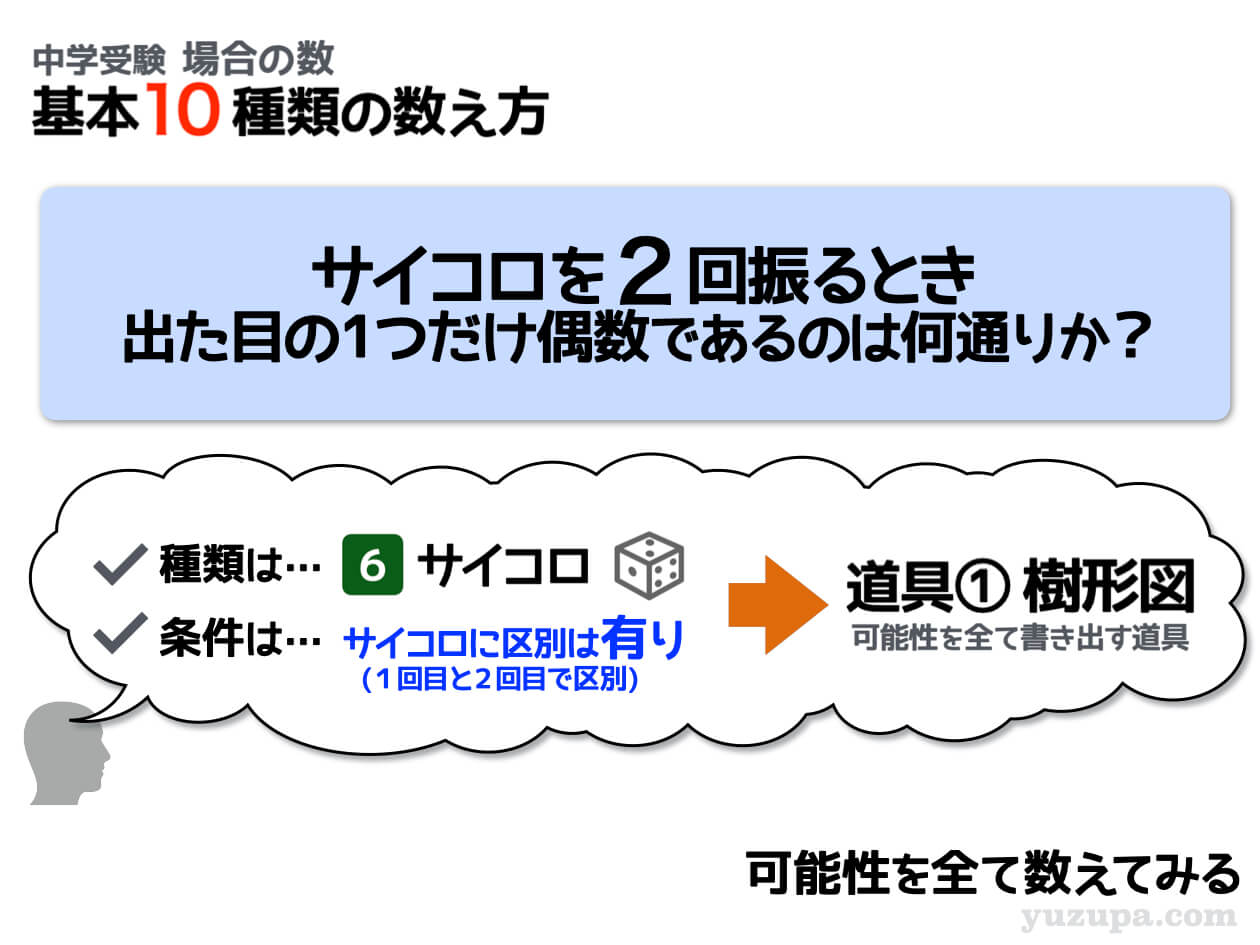
この問題も”サイコロを２回振る”…つまり１回目と２回目で区別が有ります。そして 出た目の１つだけが偶数という条件 がついていますね。この条件に合わないものは数えてはいけません d(^_^o

もちろん条件外のものを数えたらダメ(>_<)
間違えないために条件をかみ砕いてみましょう

出た目の１つだけが偶数…この条件をいつもどおり“噛み砕いて“みましょう。 サイコロを２回振るのだから偶数が出る回数は３パターンしかありません。みてみましょう。

・偶数が０個 … 数えちゃダメ
・偶数が１個 … 数えろ！
・偶数が２個 … 数えちゃダメ

この３つのパターンしか無いことを意識しながら樹形図を描いていきましょう。樹形図を２つか３つ描いたあたりで、なんとなく法則性があることに気づきますでしょうか？

１回目が奇数のときは２回目が偶数の場合だけ数える… １回目が偶数のときは２回目が奇数の場合だけ数える… これはひとつの樹形図につき３通りだ！ということに気づきますねd(^_^o)

結果として答えは１８通りになります_φ(･_･

 

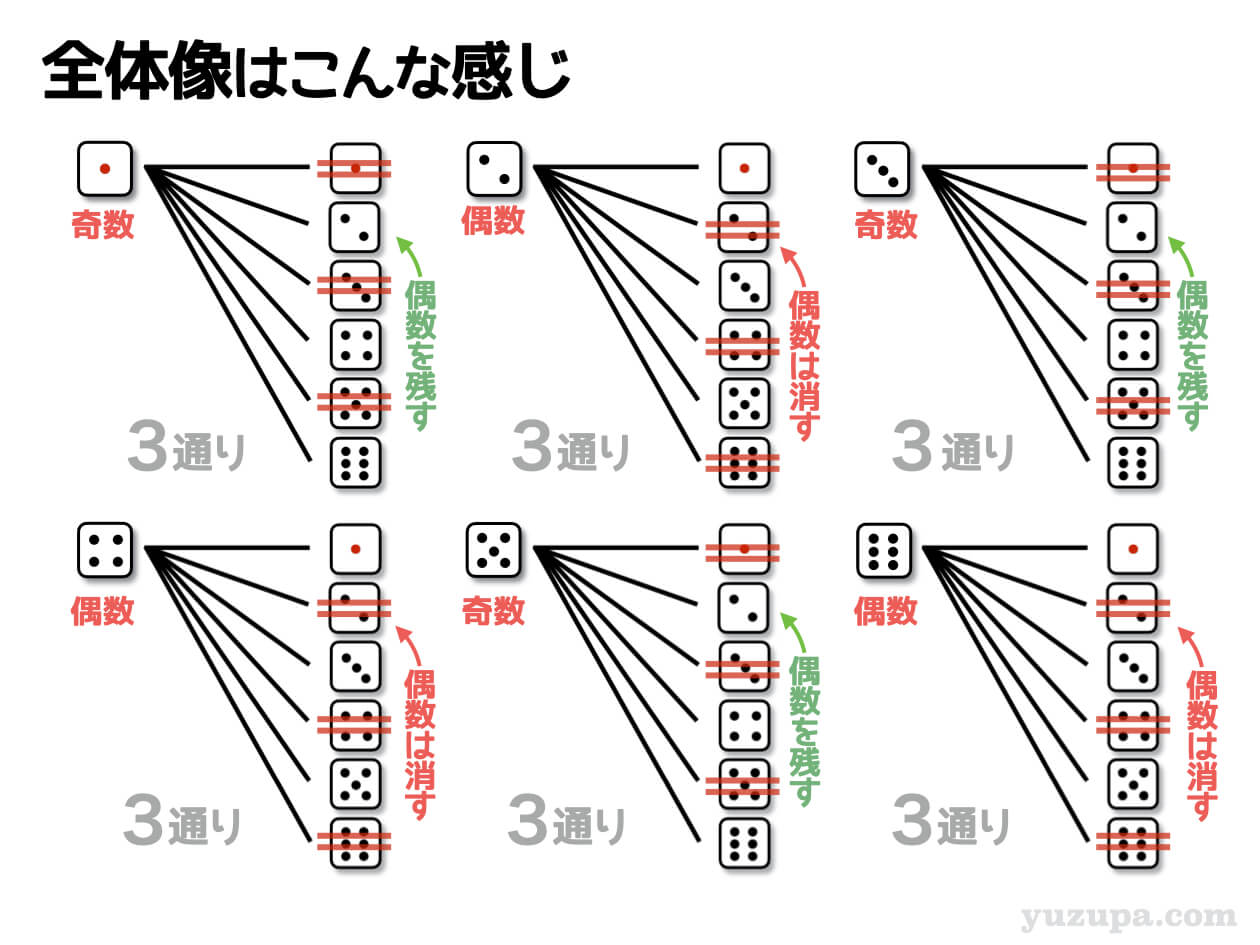
条件バリエーション③ 和の条件(1)

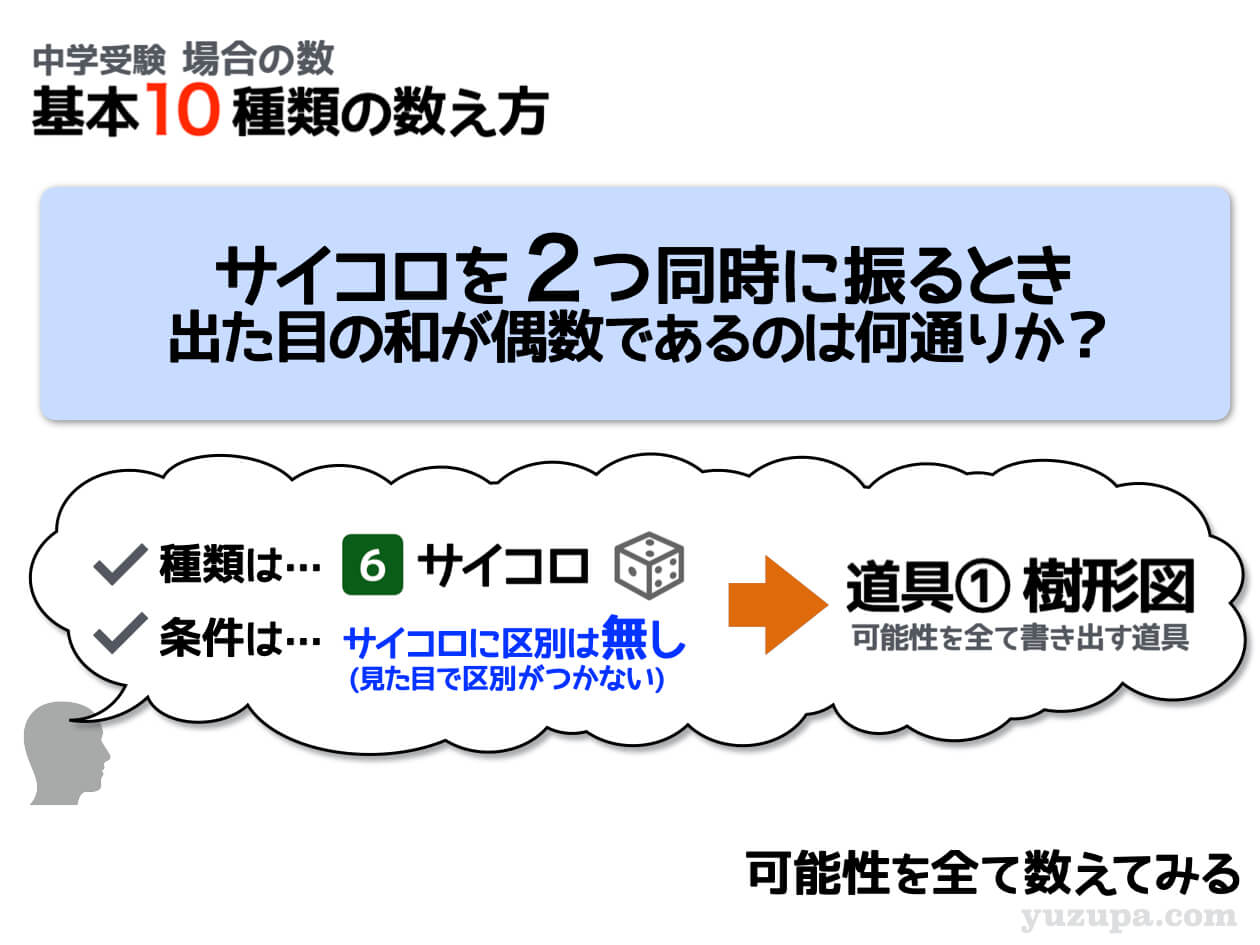
まずはいつもどおり基本パターンがどちらかを読み取りましょうd(^_^o) “サイコロを２つ同時に振る“とありますね。これは２つのサイコロの区別がつかないパターンですね。

そして数えていけない条件は…出た目の和が偶数ということ。出タ目の和が奇数の場合は数えてはダメです_φ(･_･

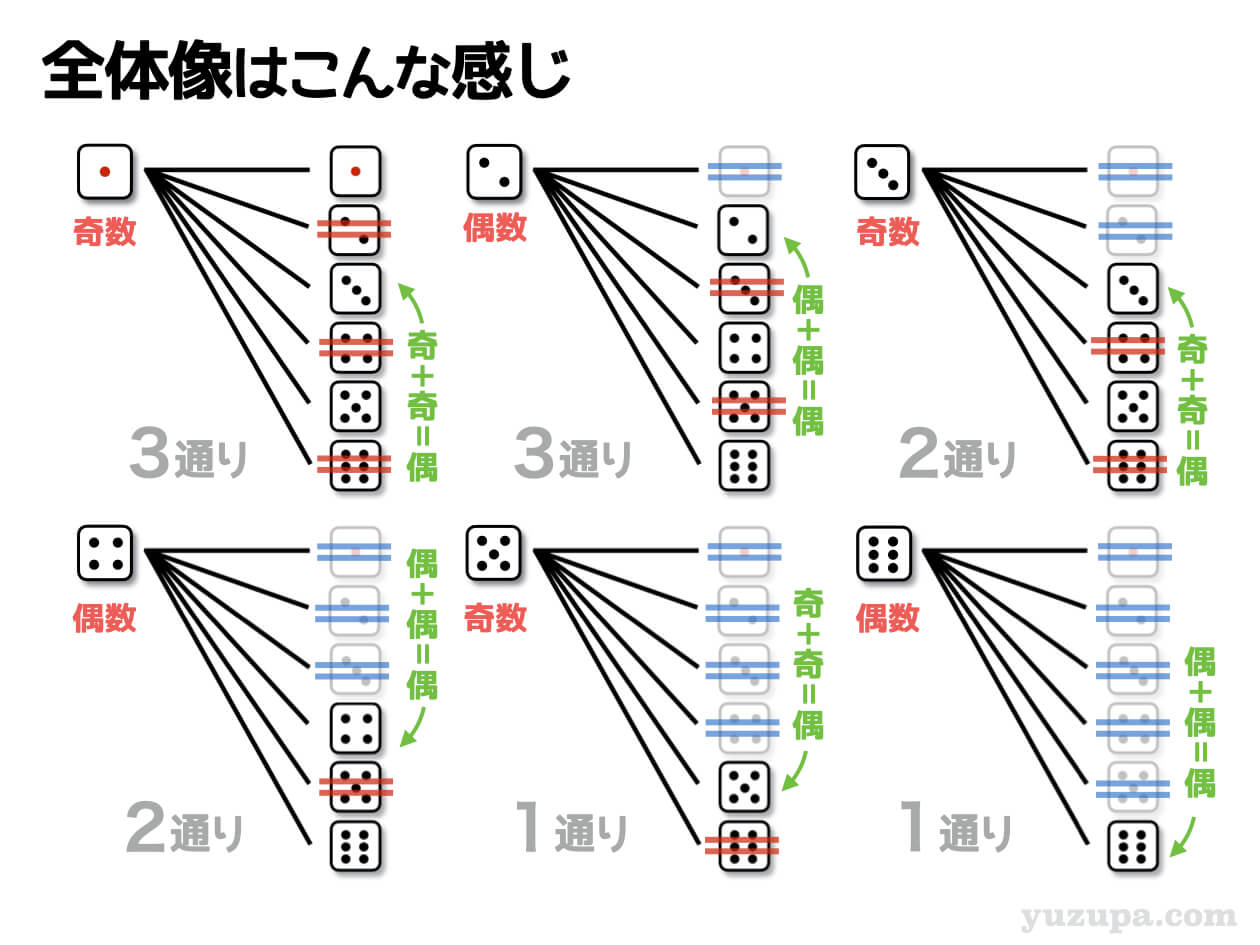
そして和が偶数になるか奇数になるかのパターンは以下です。

・偶数＋偶数＝偶数 　 数える
・偶数＋奇数＝奇数 　 数えちゃダメ！
・奇数＋偶数＝奇数　  数えちゃダメ！
・奇数＋奇数＝偶数　  数える！

上記の４つのパターンを意識しながら、樹形図を落ち着いて描いてみましょう。２つのサイコロに区別が無い場合は、同じものを消さなくてはいけないので細心の注意で数えていきましょう！

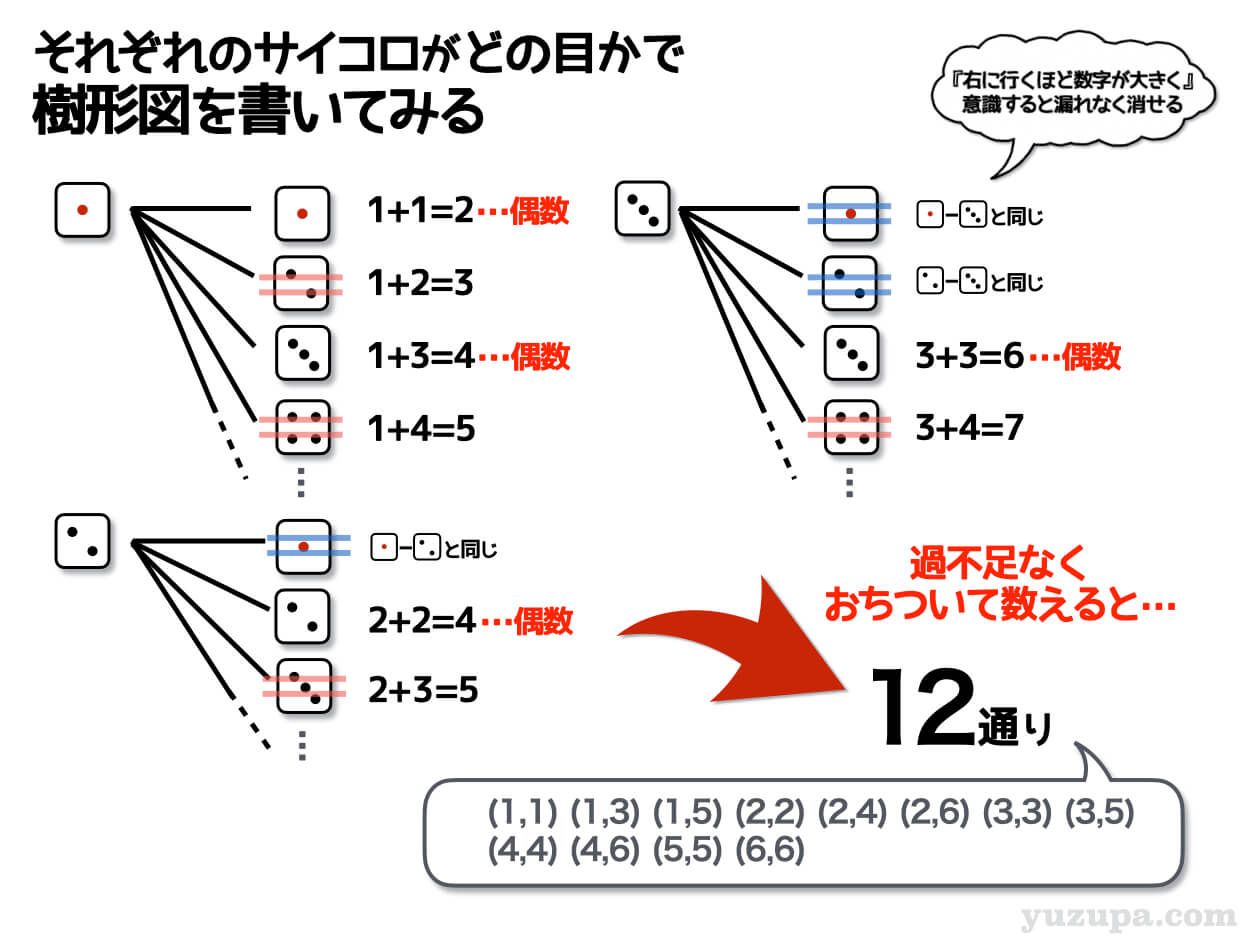
落ち着いて数えることができましたでしょうか？ 上記のように１２通りになります _φ(･_･

 

条件バリエーション④ 和の条件(2)

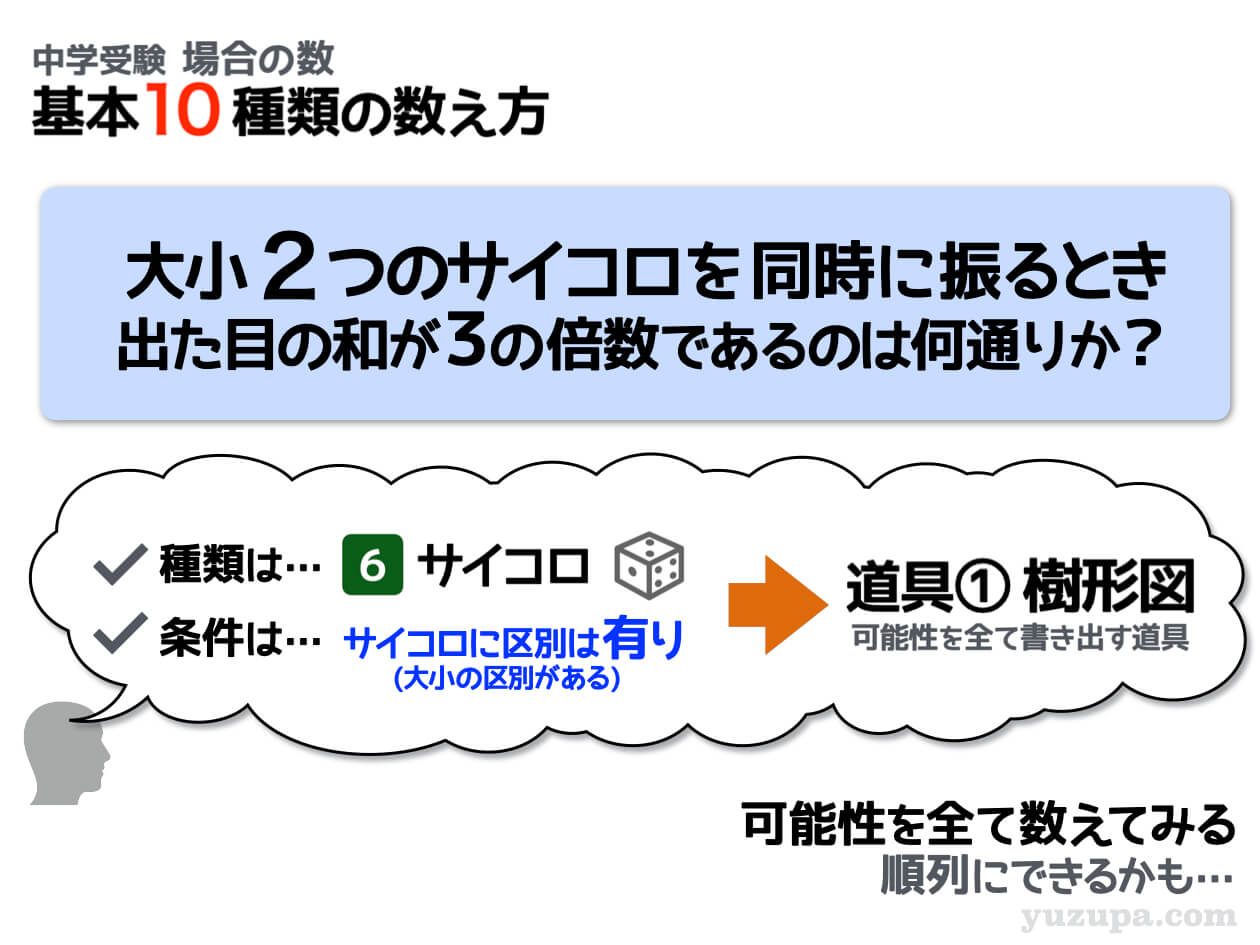
大小２つのサイコロを振ると書かれているので２つのサイコロには区別があるパターンです。そして条件は…出た目の和が３の倍数となっています。

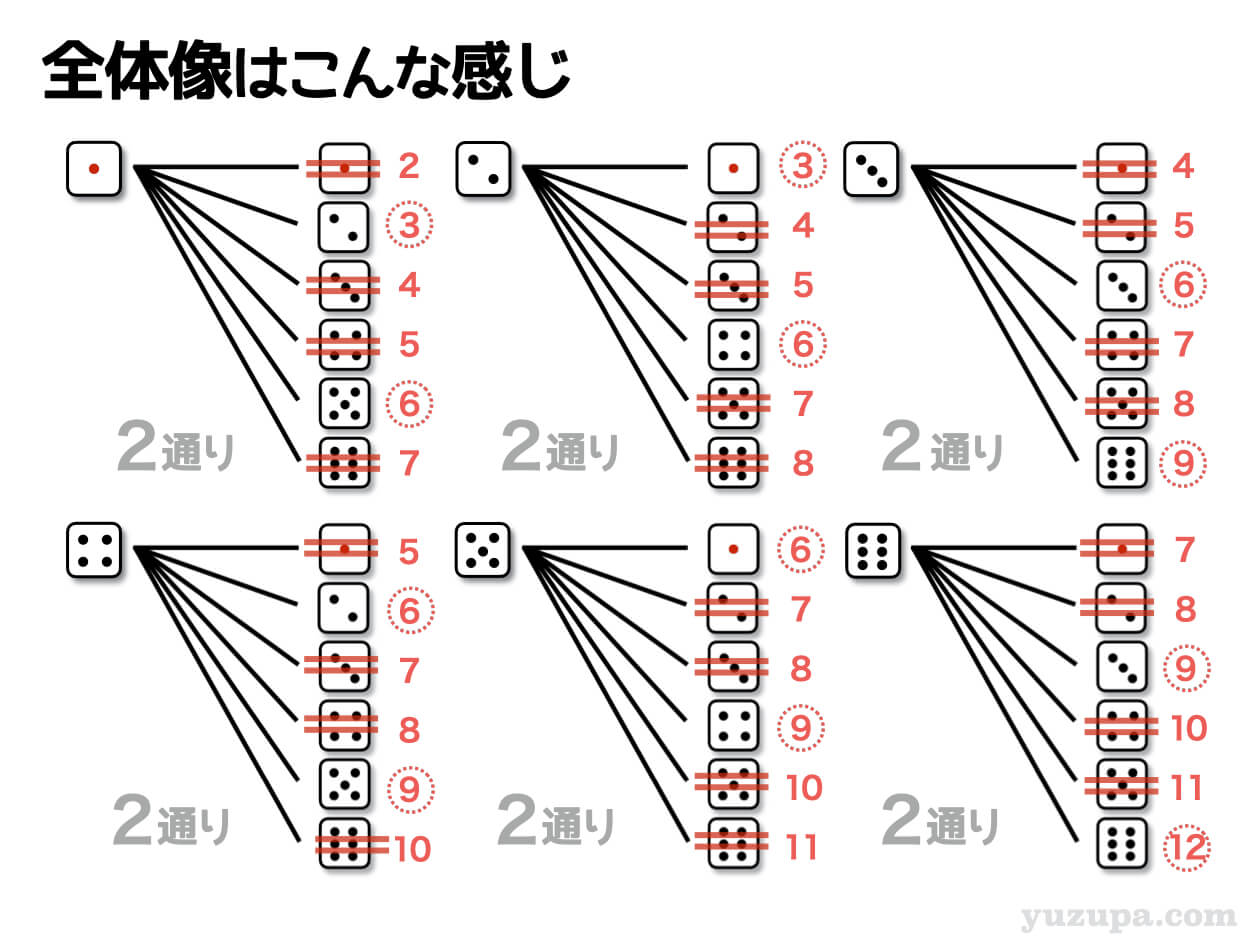
３の倍数は ３、６、９、１２、１５、１８…ですね。

サイコロの目は最大６ですので、２つのサイコロの和は最も大きくても１２です。２つのサイコロの出た目の和が３、６、９、１２のパターンを数えればよさそうですd(^_^o)

落ち着いて樹形図を描いてみましょう。出た目の和が３、６、９、１２にならないパターンは数えてはいけません！

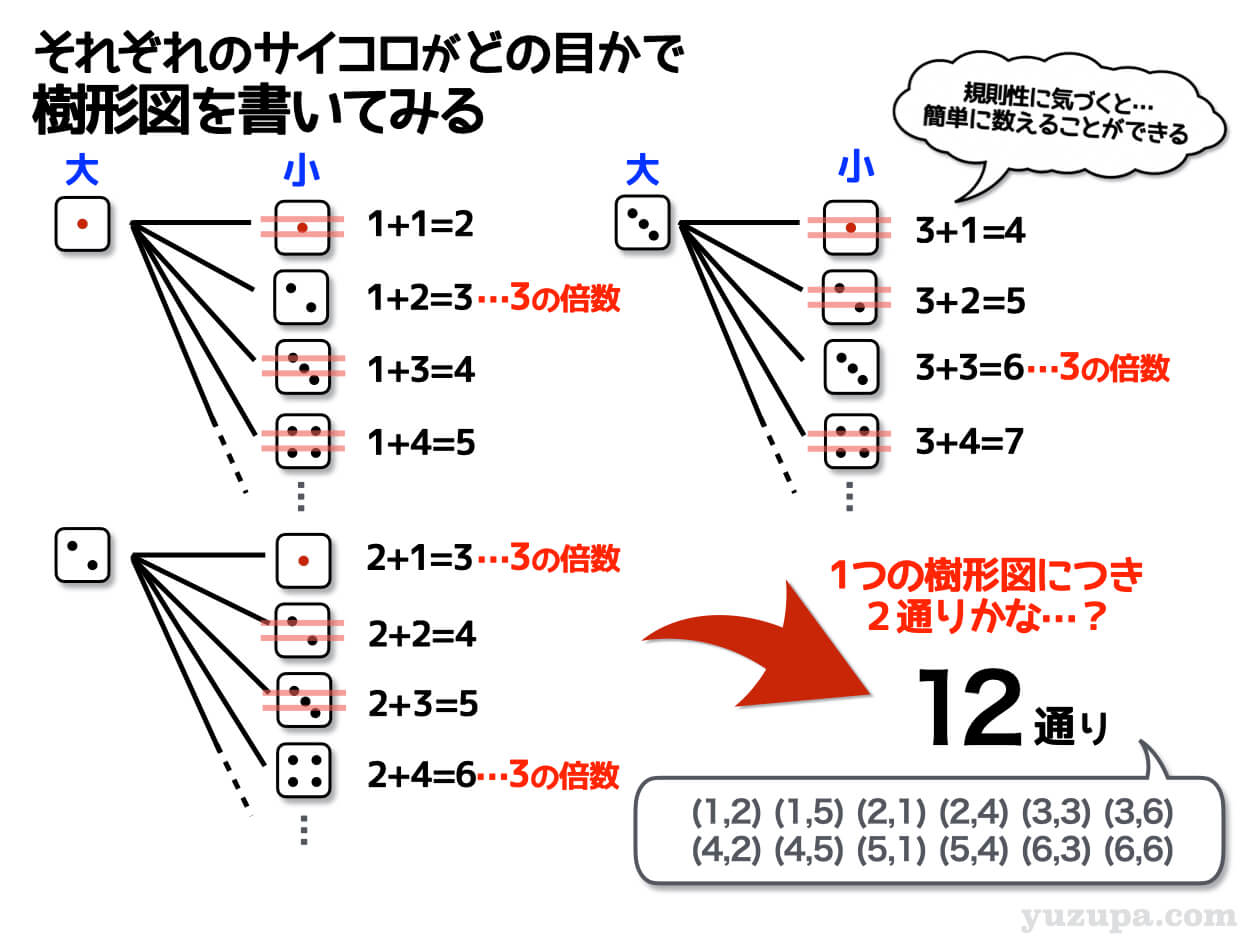
樹形図をいくつか描くと気づくことがあります。１つの樹形図には６本の枝ができますが ひとつの樹形図につき３の倍数は必ず２つ登場するということ。そこに気づいてしまえば簡単ですねd(^_^o)

答えは１２通りですd(^_^o)

 

条件バリエーション⑤ 積の条件(1)

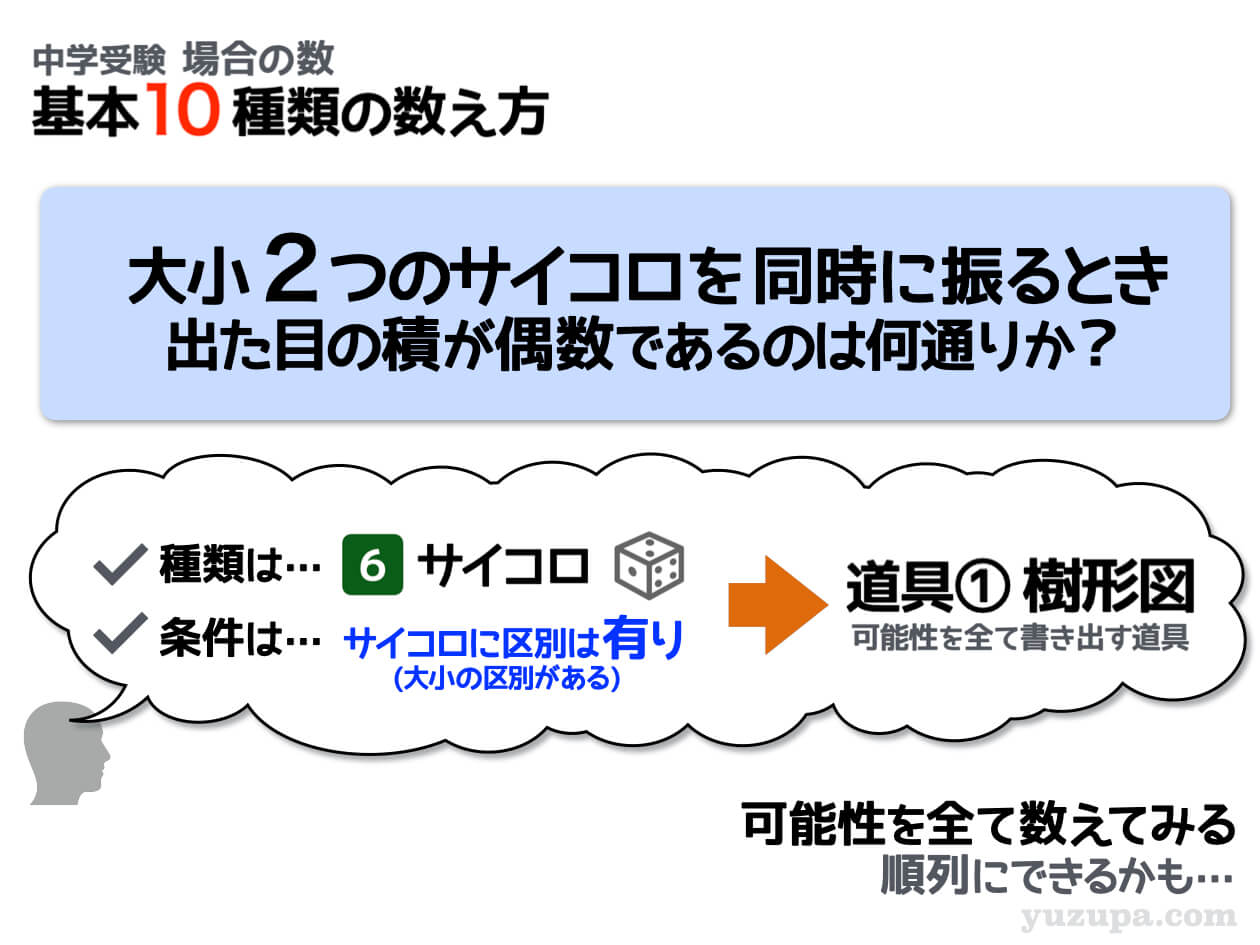
サイコロの区別はもう大丈夫ですか？ 大小２つのサイコロを振るので２つのサイコロには区別があります。同じものを消す必要がないので条件に合致したものをガンガン数えましょう！

そして今度の条件は 出た目の和ではなく出た目の積 です。

出た目の和のときと同様、どのようなパターンがあるかあらかじめ整理してから樹形図を描くと最小限の労力で数えることができます。パターンを整理すると以下のようになります。

・偶数×偶数＝偶数　数える
・偶数×奇数＝偶数　数える
・奇数×偶数＝偶数　数える
・奇数×奇数＝奇数　数えちゃダメ！

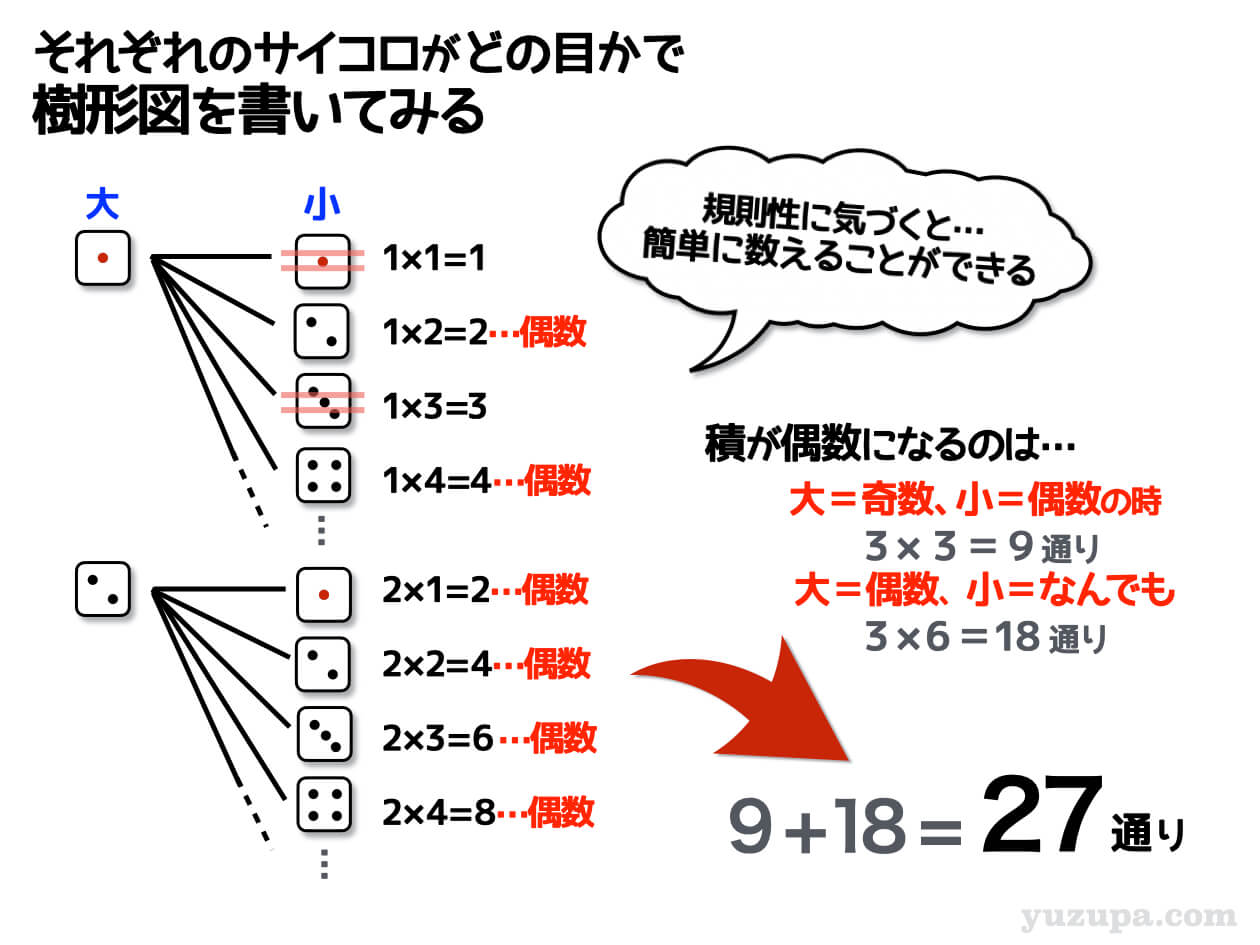
どのような時に条件合致となるか見えてきましたでしょうか？

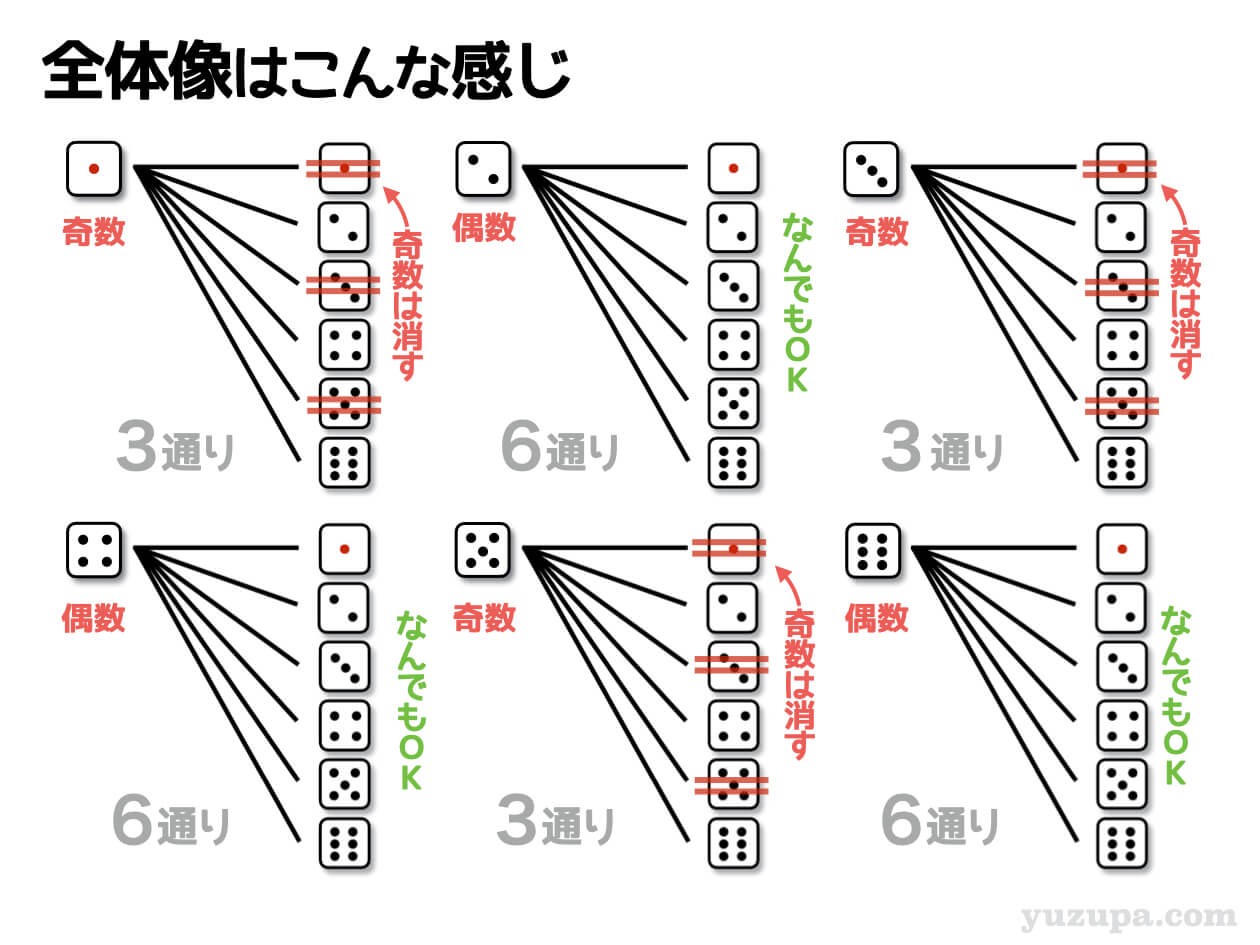
大きいサイコロが奇数の時は、小さいサイコロが偶数のときのみ出た目の積が偶数になることがわかりますね？小さいサイコロが２、４、６の時の３パターンですd(^_^o)

大きいサイコロがぐうすの時は、小さいサイコロがどんな数であっても偶数になりますね ∑(ﾟДﾟ) 小さいサイコロの目は１～６まであるので６パターンです_φ(･_･

それぞれを足し合わせると２７通りになります。

ここで別解を紹介します。

実はこの問題… 出た目の積が偶数になる場合の数を数えるよりも、出た目の積が奇数になる場合の数を数える方が圧倒的に楽チンです。出た目の積が奇数になるのは奇数×奇数の時だけだから！

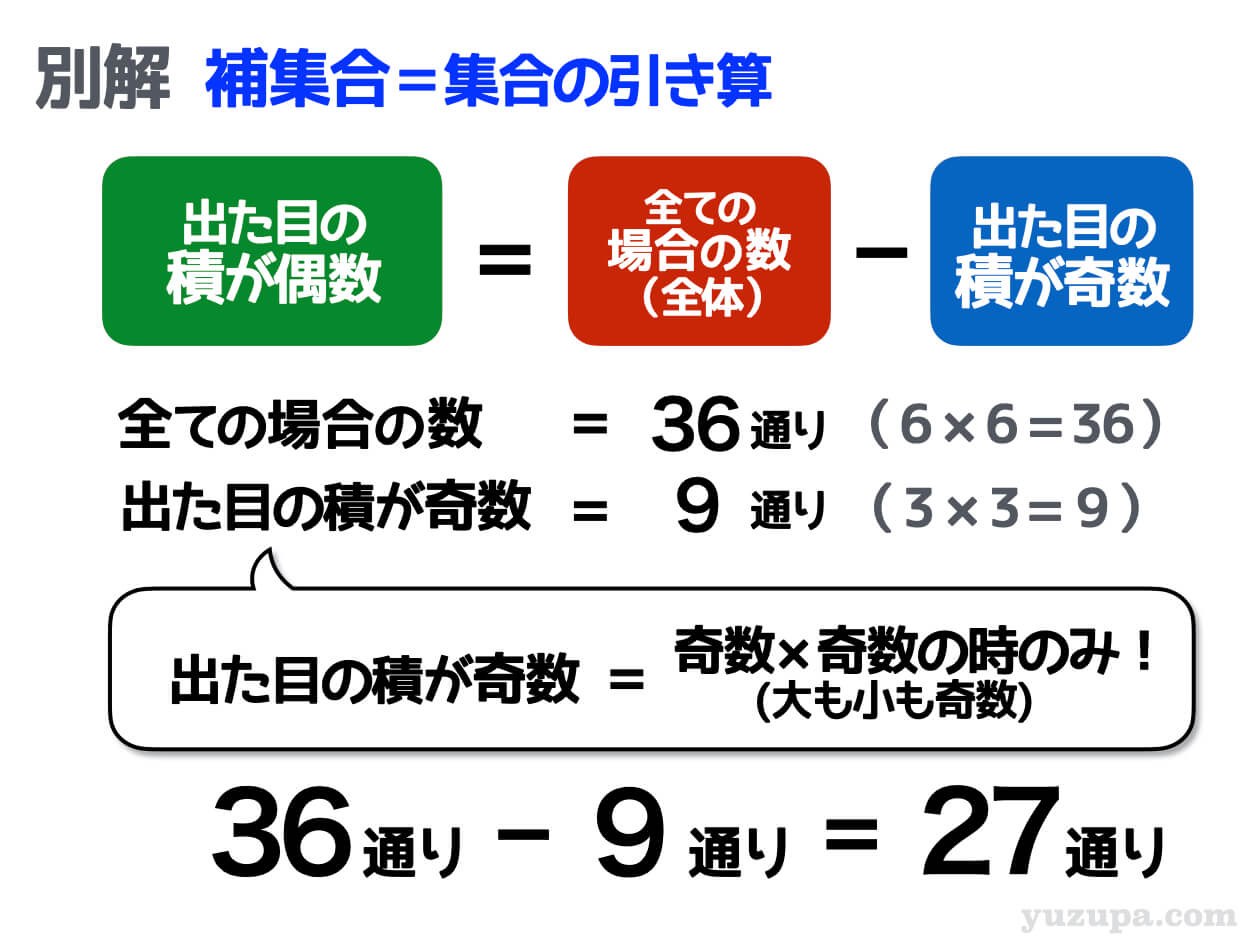
そんな時は ”補集合の考え方”が便利 ですd(^_^o)

数というのは偶数と奇数しかないわけですから、数えるのが楽な出た目の積が奇数の方を数えて、全ての場合の数から引いてあげるという考え方ですねd(^_^o)

上記のとおり２７通りが簡単に出せます∑(ﾟДﾟ)

 

条件バリエーション⑥ 積の条件(2)

いよいよ最後の問題ですd(^_^o)

もう基本パターンは大丈夫ですね！大小２つのサイコロと書かれているので、サイコロに区別はあります。つまり同じものを消すという面倒臭い確認は不要です_φ(･_･

条件は出た目の積が３の倍数というもの…こう考えましょう。かけ算を構成する数のどこか１つでも３の倍数が入っていればそのかけ算の答えも３の倍数になる！

つまり… 出た目の中に３か６が１つでも含まれていれば出た目の積は３の倍数になるということですd(^_^o) これを意識しながら樹形図を描いて条件に合うものを数えていきましょう！

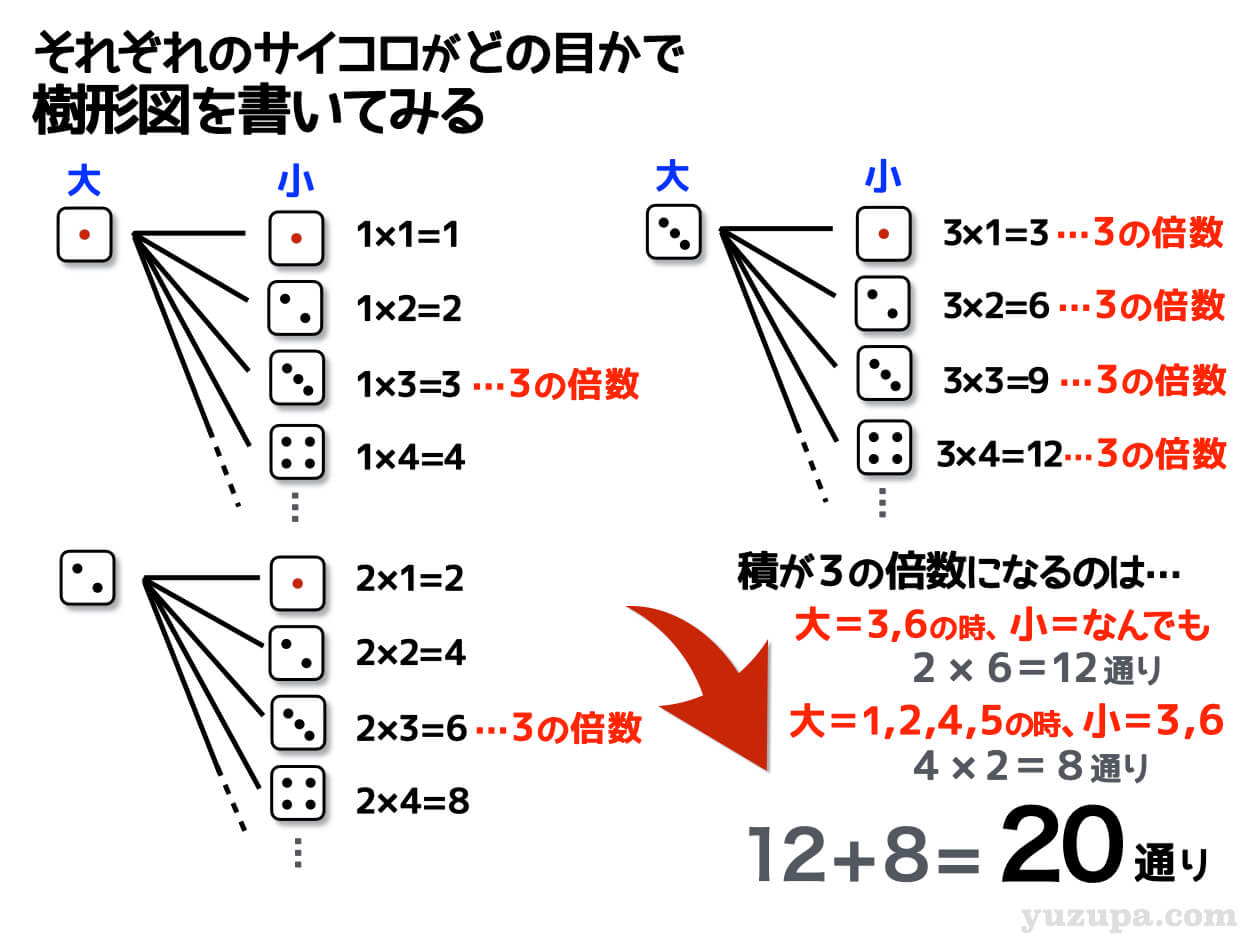
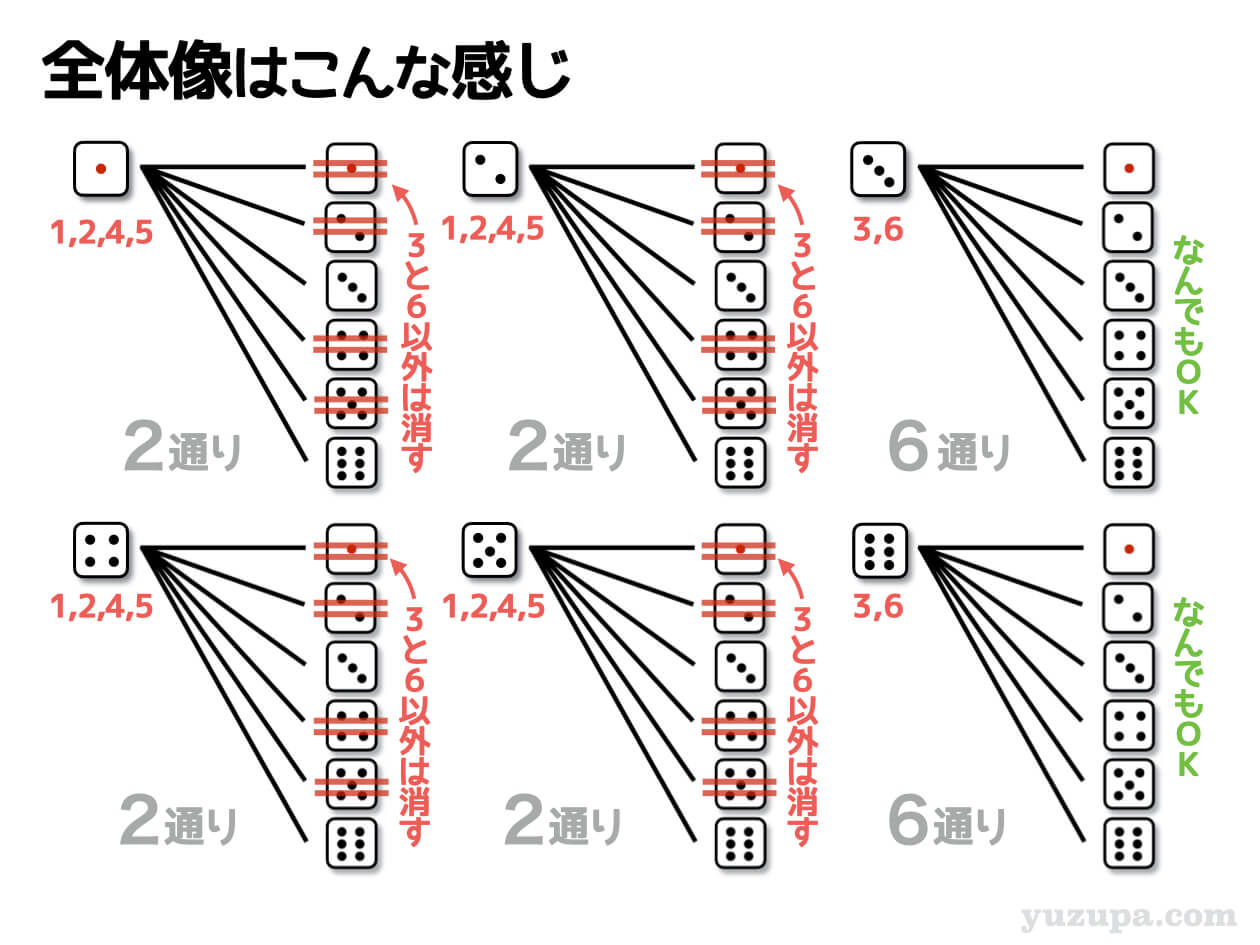
大きいサイコロが３の時は、小さいサイコロがどんな数であっても積は３の倍数になります。同じく大きいサイコロが６の時も小さいサイコロがどんな数であっても積は３の倍数になります。

大きいサイコロが３でも６でもない時…つまり１か２か４か５の時は、小さいサイコロが３か６の時に積も３の倍数になります。

落ち着いて数えると…全部で２０通りになります_φ(･_･

 

まとめ

今回は無数にあるように思われる、場合の数の問題の中からサイコロをフル問題にフォーカスして解説をしてまいりました。ポイントはサイコロに区別があるのか？区別がないのか？を最初に問題文から見極めることd(^_^o) サイコロに区別が無い場合には、順番違いの同じパターンを数えないようにしなければなりません_φ(･_･

サイコロの区別の有無がわかったら、落ち着いて樹形図をベースに条件に合致するパターンを数えていきます。ほとんどの問題が出た目に条件がついています(^_^;)

しかし数え方の考えをじっくりおさえれば怖くありません！

参考：場合の数が苦手…３つの道具を使い10種の数え方をマスターせよ

参考：場合の数の基本パターンを全網羅！ 整列と分配問題編

参考：場合の数の基本パターンを全網羅！ カード問題編