中学受験：場合の数の基本パターンを全網羅！ カード問題編

カード問題は基本パターン３種と条件バリエーション６種のかけ合わせ

こんにちは。かるび勉強部屋 ゆずぱ です。

場合の数が超苦手な子供が本当に多い (-_-;) 場合の数の問題というものは、可能性のあるパターンを数えるだけ… なぜそんなに苦手と感じる小学生が多いのでしょうか？

それは数え方があまりにも多すぎるので
全体像が見えずにモヤモヤするから…

確かに色んなパターンがあります ∑(ﾟДﾟ) しかし、実際の入試問題を分析してみると、無数にあるように見える場合の数の問題も、その出題パターンは１０種類であることが分かります。

参考：場合の数が苦手…３つの道具を使い10種の数え方をマスターせよ

この１０種類の出題パターンのうち、今回はカードを使った場合の数の問題について解説いたしますd(^_^o) カード問題とは、何枚かのカードを並べて整数を作る場合の数を数えるという問題です。

まずは場合の数の全体像を解説いたします。具体的な問題の解説は第２項へお進みください d(^_^o)

 

おさらい…場合の数には３つの道具がある

道具を使い”全ての可能性を数える”こと

”場合の数問題” の全体像をご覧ください。

場合の数の問題というのは、ズバリ”全ての可能性を数え上げなさい” という問題のこと。正しく問題を解くには以下の３つのステップを着実にこなすことが最も近道です。 

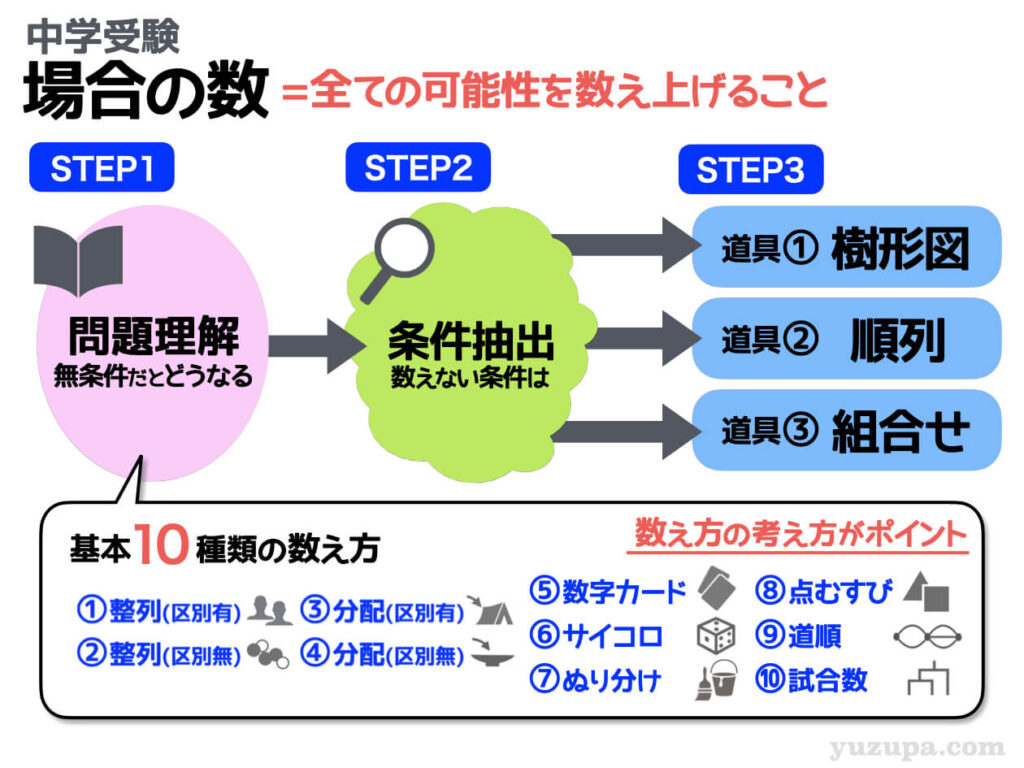
STEP1では、問題文を読んで”いったい何を数えたらよいのか”をしっかり把握します。その際に役に立つのが”基本的な１０種類の数え方”です。まずは基本パターンを考えましょう。

STEP2では、条件を理解します。偶数”だけ”数えなくてはいけなかったり、男子が両端にくる並び方”だけ”数えなくてはいけなかったり、入試の問題には必ず条件がついてきます(^_^;)

STEP3でいよいよ数えます。数えるには必ず道具を使います。樹形図はオールマイティですが、通り数の多い問題には使えません。樹形図をサボる道具として”順列”と”組合せ”があります。

 

３種類の道具を使って数える

３つの道具とは”樹形図”と”順列”と”組合せ”のことです。 

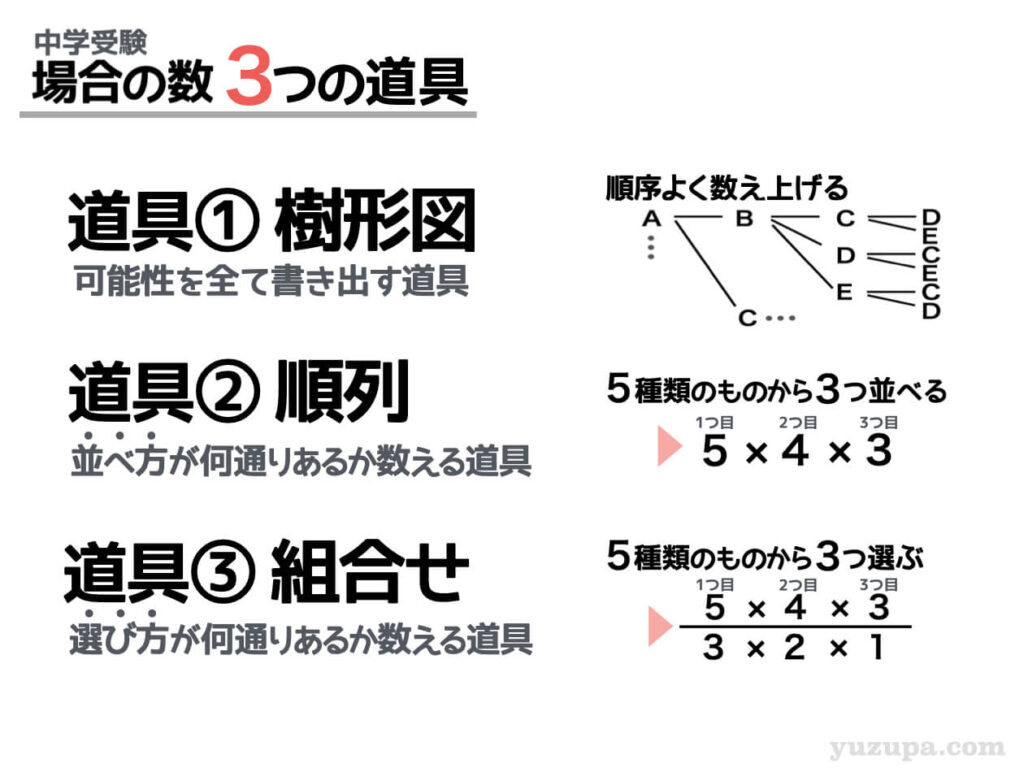
樹形図はオールマイティな道具です。どうやって数えたら良いか迷ったらまずは樹形図で数え始めてみてもよいでしょう。書いていているうちに数え方のヒラメキがあることもあります。

順列は並べ方が何通りあるか数える道具です。シンプルに何かを並べる場合の数を求める問題の他に、並べること以外の題材を並べる行為に置き換えて数えることもよくあります。

組合せは選び方が何通りあるか数える道具です。例えば１０種類のケーキがあり、３つだけ食べて良いと言われたら何を選びますか？ この道具を使えば選び方が何種類あるか分かります。

場合の数の全体像を確認したい場合は、ぜひ以下の記事をご参照してみてください。スッキリしますd(^_^o)

参考：場合の数が苦手…３つの道具を使い10種の数え方をマスターせよ

 

カードを使った場合の数の問題を全網羅

数字カード問題の全体像

カードを使った問題とは、何枚かのカードが配られて、そのカードを使って何ケタかの整数を作るという問題です。何種類の整数を作ることができるかを数えなければいけません (-_-;) 

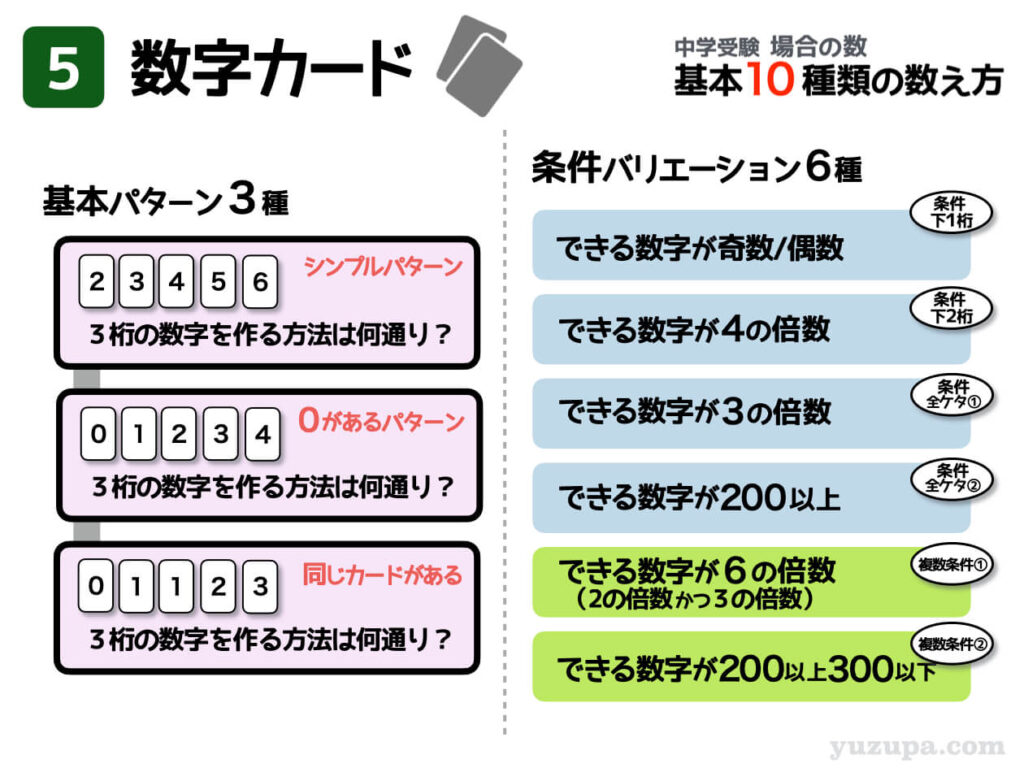
ただ整数を作るというのであれば簡単ですが、もちろんそんなに甘くはありません(-_-;) 配られるカードにバリエーションがあったり、できあがる整数に条件がつけられたりします。

 

基本パターン３種

なんの条件もない３桁の整数を作る問題です。できあがる整数には何も条件がありませんd(^_^o) パッと見では、シンプルな問題で簡単だろうと思われますが…配られるカードにパターンがあります。

(1) シンプル(バラバラのカード)パターン
　１枚も被っていないバラバラのカードが配られる。これが最もシンプルな出題パターンです。

(2) ０のカードが紛れているパターン
　シンプルパターンと同様にバラバラのカードですが、配られたカードの中に「０」のカードが紛れています。

(3) 同じ数のカードが複数枚あるパターン
　シンプルパターンと異なり全く同じ数が書かれたカードが存在します。ちょっと複雑なパターンですね。

 

条件バリエーション６種

できあがる整数に条件がつけられていることがあります。できあがる整数が偶数でなくてはいけないとか… できあがる整数が１００以上でなくてはいけないとか…

これが条件バリエーションですd(^_^o)

ここには代表的な６つのパターンを掲載しましたが、その条件は無数にあります∑(ﾟДﾟ) ただし、この６つの条件を理解できればほとんどの条件に対応することができます_φ(･_･

そしてこう考えましょう…
数え方は何パターンあるのか
＝ 基本パターン３種 × 条件バリエーション

ここでは３つの基本パターンと６つの条件バリエーションですので少なくとも１８種類はあります。他にも似た条件が無数にあるので、数え方のパターンも無数にあることになります_φ(･_･

でも安心してくださいd(^_^o)

３つの基本パターンを条件を掛け合わせるという意識さえもっていれば、どんな問題にも対応できます。未知の条件が出てきたらその解法を条件バリエーションに加えてあげればよいのです。

それではまずは基本パターンから見ていきましょう！

 

カード問題：基本パターン３種

基本① シンプル(バラバラのカード)パターン 

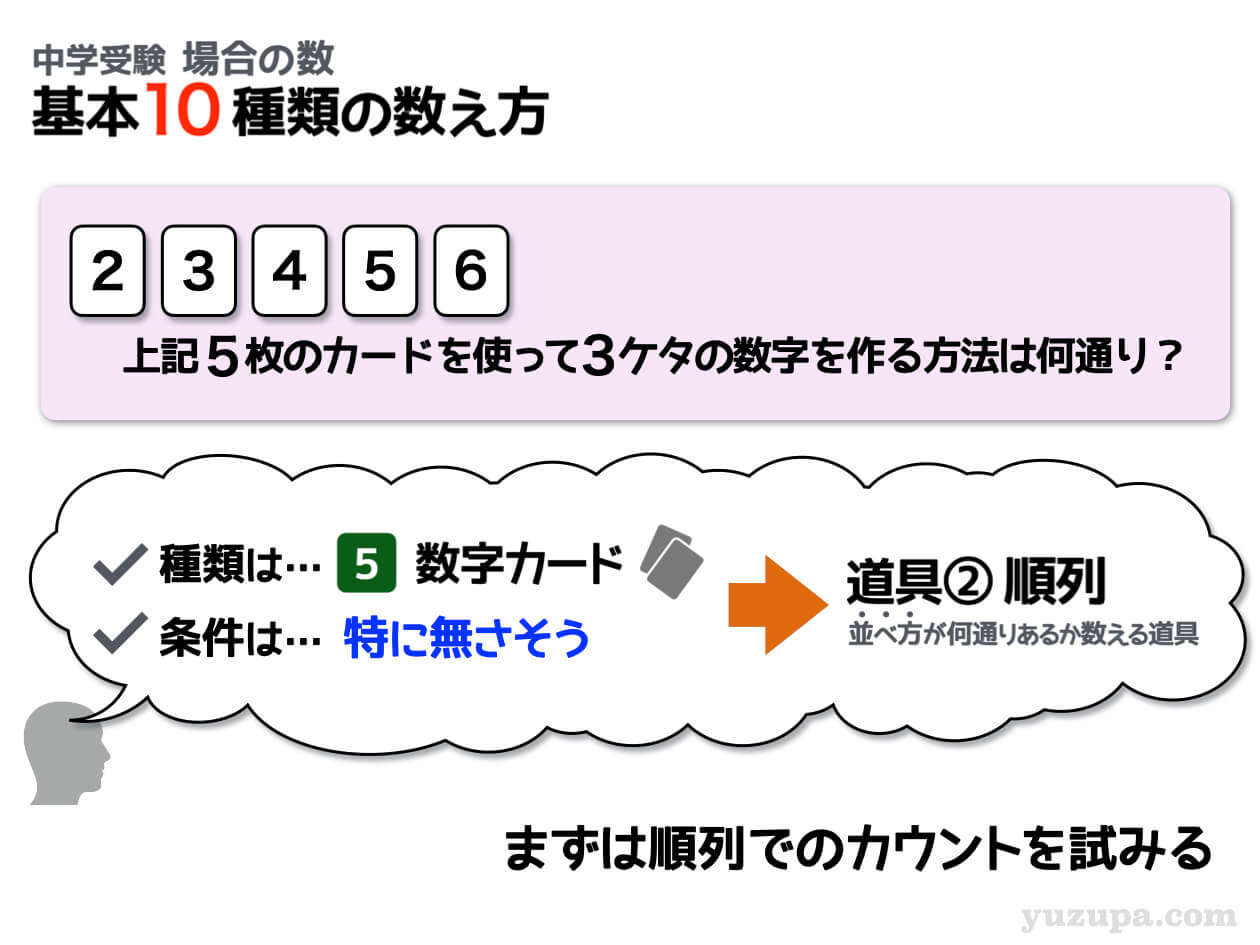
配られる数字カードにはバラバラで、できあがる整数に３ケタであるということ以外には条件はなさそうです。数字カードの問題では最もシンプルな基本的な問題ですd(^_^o)

つまり…何も考えずに並べれば良いのです

並べ方の数え方といえば、便利な道具がありました。そう…順列ですね。では順列を使って数えることを試みてみましょう！

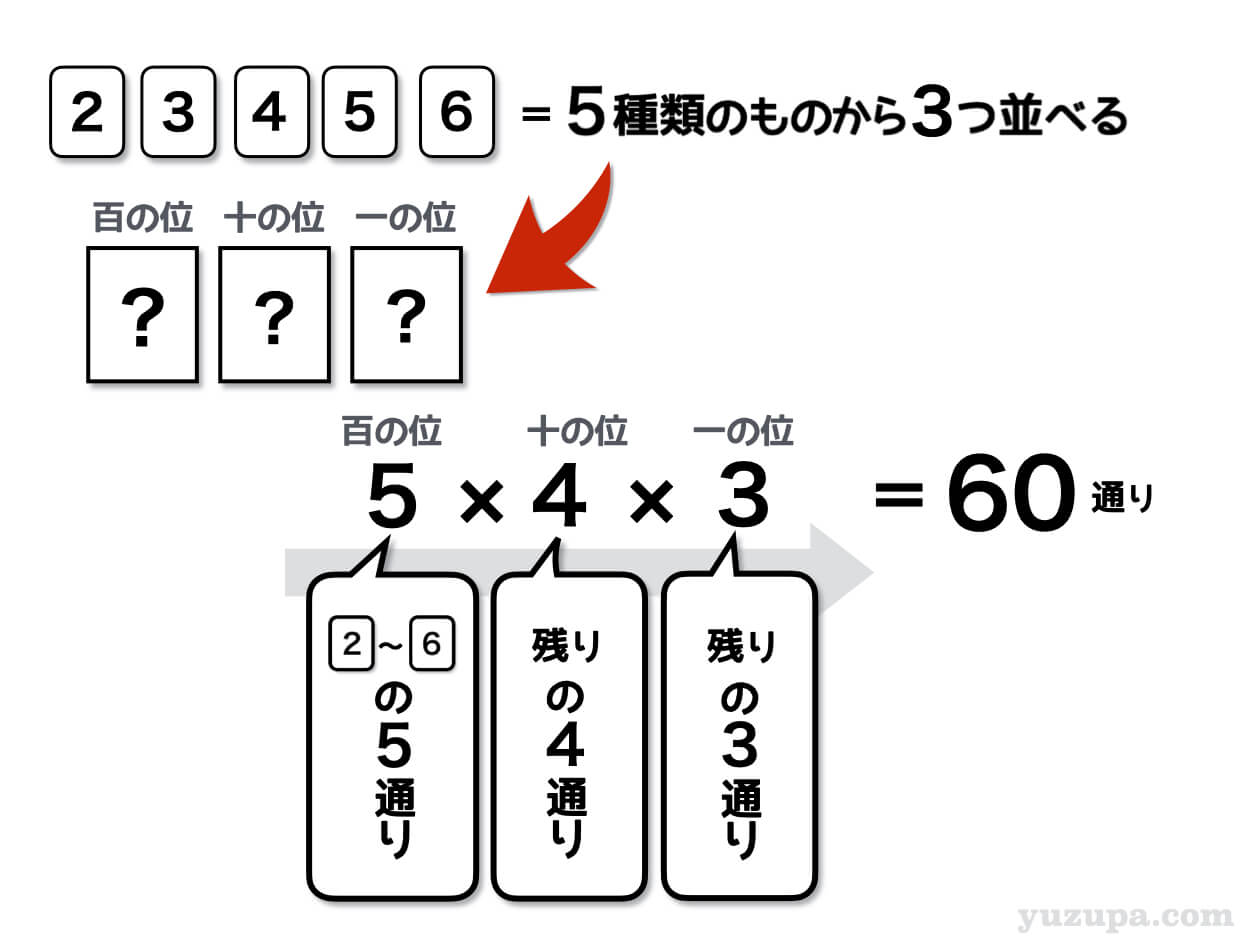
５種類のカードから３つを取り出して並べる方法を数えれば良いのです。百の位には５枚のカードが入る可能性があります。十の位は百の位に入れたカード以外の４枚のカードです。さらに一の位には、十の位に入れたカードを除く３枚が入る可能性がありますね。

このように計算すると答えは６０通りとなりますo(^-^)o

順列の使い方が怪しい方は、以下の記事に戻って道具の使い方をおさらいしてから戻ってきましょうd(^_^o)

参考：場合の数が苦手…３つの道具を使い10種の数え方をマスターせよ

 

基本② ０のカードが紛れているパターン

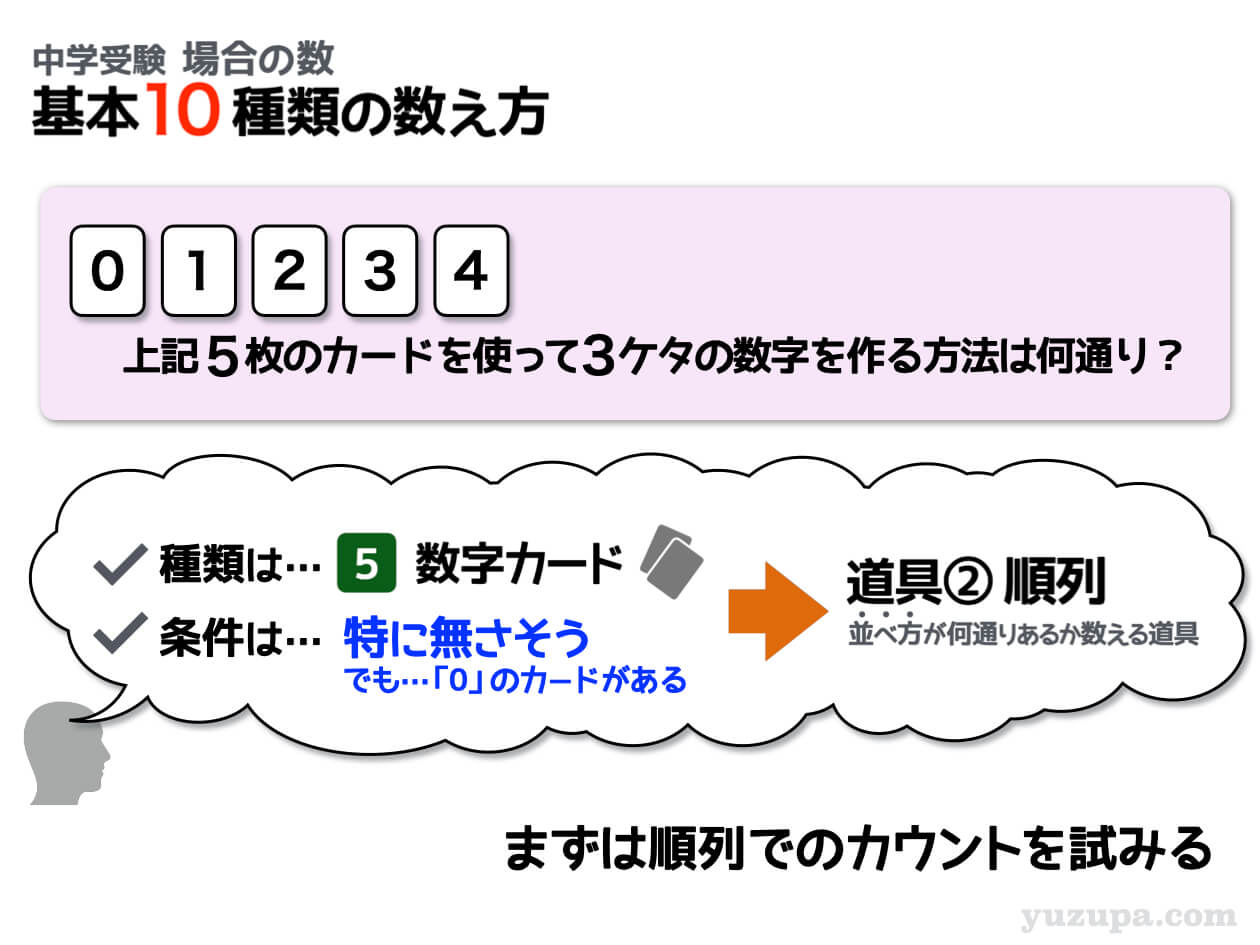
配られる数字カードにはバラバラで、できあがる整数に３ケタであるということ以外には条件はなさそうです。が…配られるカードに０の数字カードが含まれていたら要注意です∑(ﾟДﾟ)

なぜなら…０は百の位には使えないから！

もし百の位が０だったらどうでしょう？ ３ケタの整数ではなく２ケタの整数になってしまいます(>_<) ３ケタの整数に限らず０のカードはイチバン上の位には使えない ということです。 

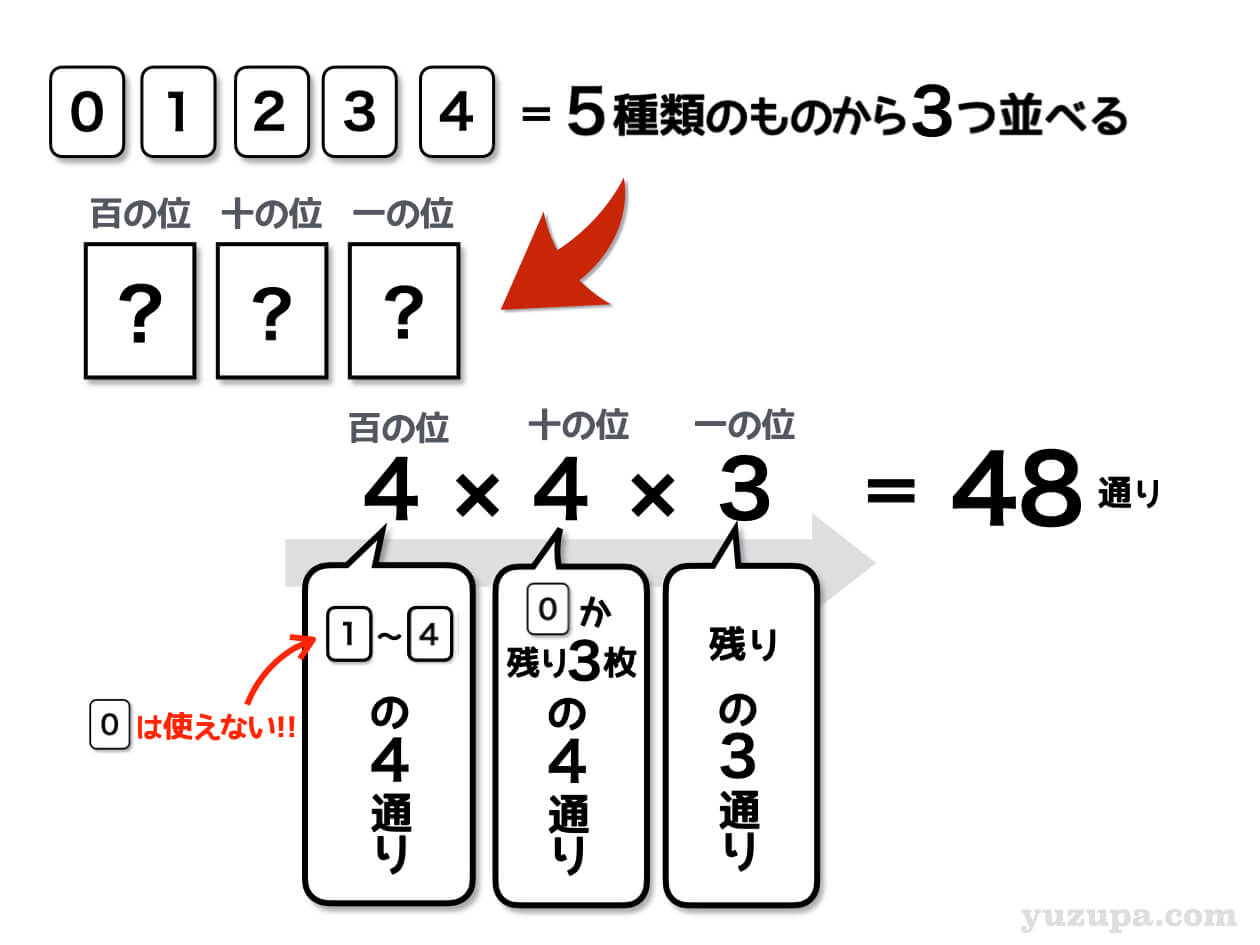
さきほどと同様に百の位から考えていきましょう。

百の位には０の数字カードが使えませんので、５種類のカードのうち０以外の４種類のカードが入る可能性があります。

十の位は、百の位に入った数字以外の３種類のカードが入る可能性がありますが、今度は、百の位では使えなかった０のカードも使えますので、４種類のカードが入る可能性があります。

最後の一の位は残りの３種類のカードが入る可能性があり、掛け合わせていくと４８通りの整数を作ることができます。

 

基本③ 同じ数のカードが複数あるパターン

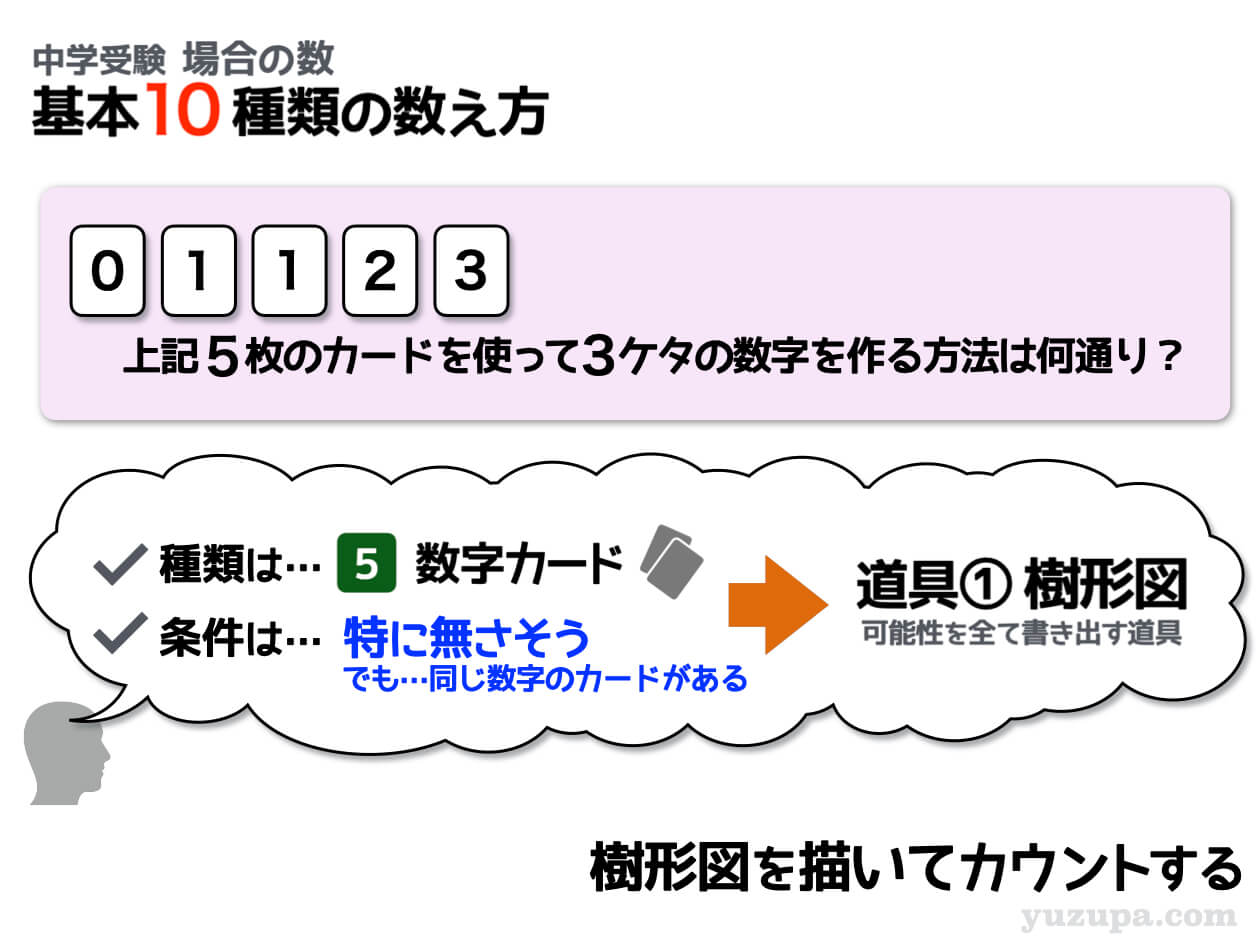
今度は配られる数字カードはバラバラではありません∑(ﾟДﾟ) カードを注意深く見てみると１のカードが２枚あります。こうなるともう並べ方の計算では太刀打ちできなさそうです(>_<)

順列の道具が使えない∑(ﾟДﾟ)
そんな時はどうするか？

オールマイティな道具である”樹形図”を使って数えることを試みましょう。樹形図は全てのパターンを書き出す道具。残念ながら超面倒臭いし、数え間違いをしないよう集中力が必要です。

しかし困った時は… 気合いを入れてこの道具を使いましょうd(^_^o)

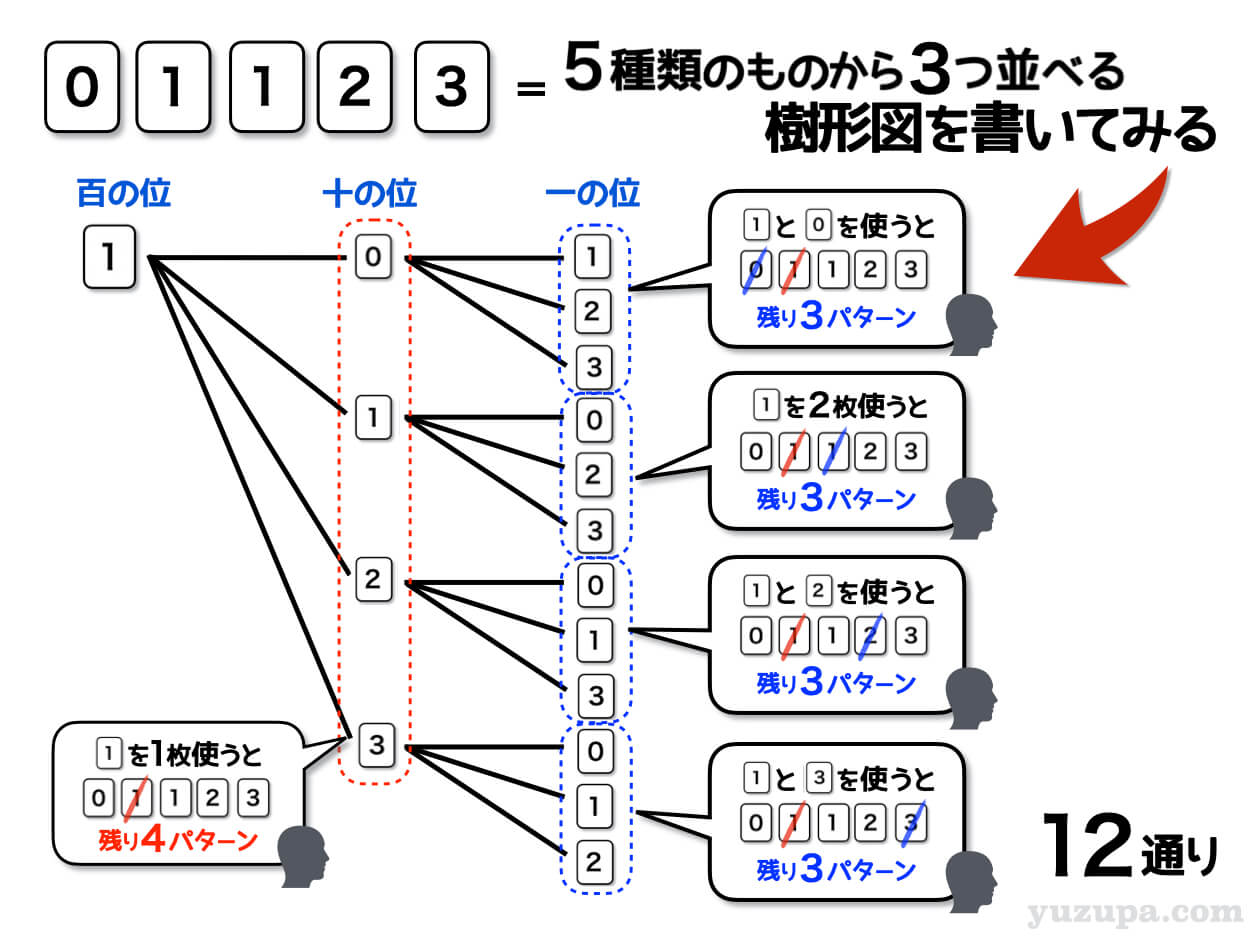
まずは…百の位に１のカードを置いてみましょう。

樹形図を描く時は “小さい方から順番に” というのが鉄則です。百の位は０のカードが使えないので、次に小さい１のカードから順番に書いていくというわけですd(^_^o)

百の位で１のカードを１枚使ったので、残ったカードは０,１,２,３の４枚 です。上記の図のように頭の中で、使ったカードには斜線を引いて消していく ことで間違いを防ぎますd(^_^o) これを頭の中でやってもOKです。

落ち着いて数えると１２通りあることが分かりました！

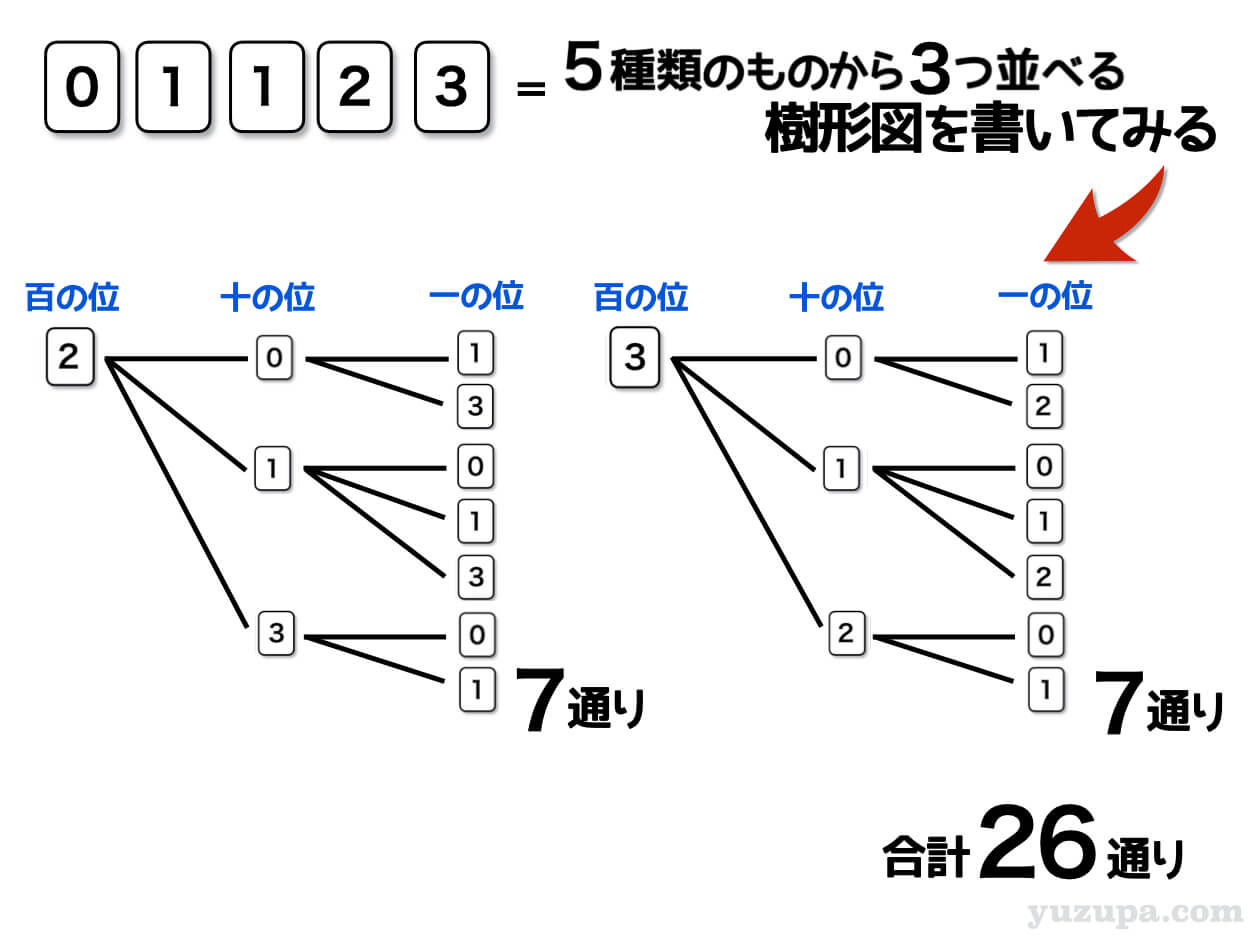
同様に百の位が２のときの樹形図。百の位が３のときの樹形図をおちついて描いていきます。描き間違いをしないようにするためのコツはたったひとつです…

使ったカードを消していくことd(^_^o)

落ち着いて樹形図を描くと、百の位が２のときは７通り、百の位が３のときも７通りであることが分かりましたね。百の位が１のときが１２通りでしたので、全部で２６通りです。

 

配られるカードによる３つの基本パターン
　(1) シンプル(バラバラのカード)パターン
　(2)０のカードが紛れているパターン
　(3) 同じ数のカードが複数枚あるパターン

しっかり把握できましたでしょうか？

 

カード問題：条件バリエーション６種

できあがる整数に条件がなければ、どんなカードが配られたとしても前項でご紹介した基本３パターンで数えることができます。

できる数字に条件があったらどうすれば良いでしょうか？

・できる整数が偶数となる
・できる整数が３の倍数となる
・できる整数が１００以上である
などの条件です…

それではひとつずつ確認していきましょうd(^_^o)

① できる数字が奇数/偶数

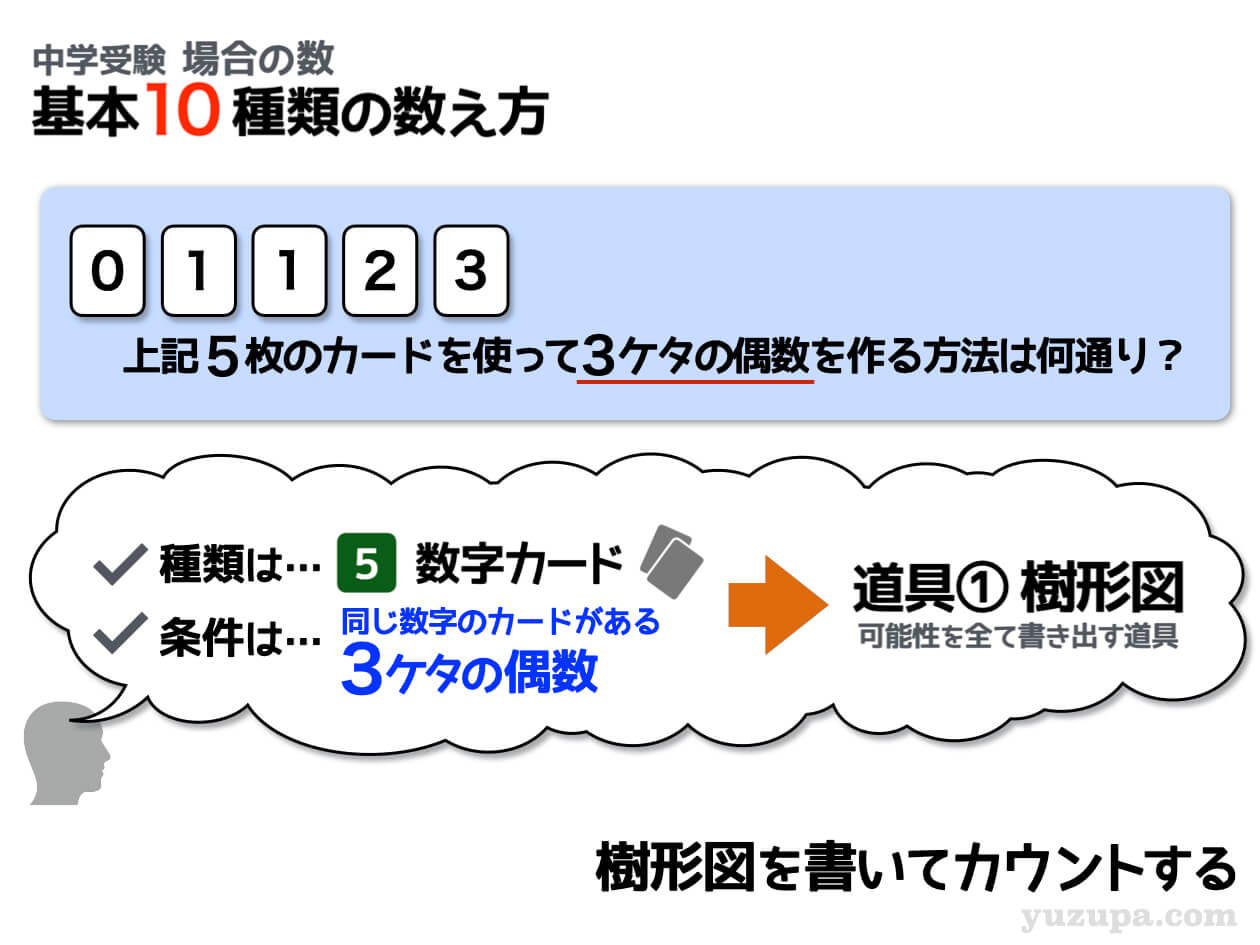
この問題の場合は、できあがる数字が３ケタの偶数という条件がついています。このようにできあがる数字に条件がついている場合は、その条件に合うものしかカウントしてはいけません。

条件外のものをカウントしたらアウトです(>_<)
間違えないために条件を“かみ砕く”必要 があります

 

偶数であるという条件を”かみ砕く”とどうなるでしょうか？

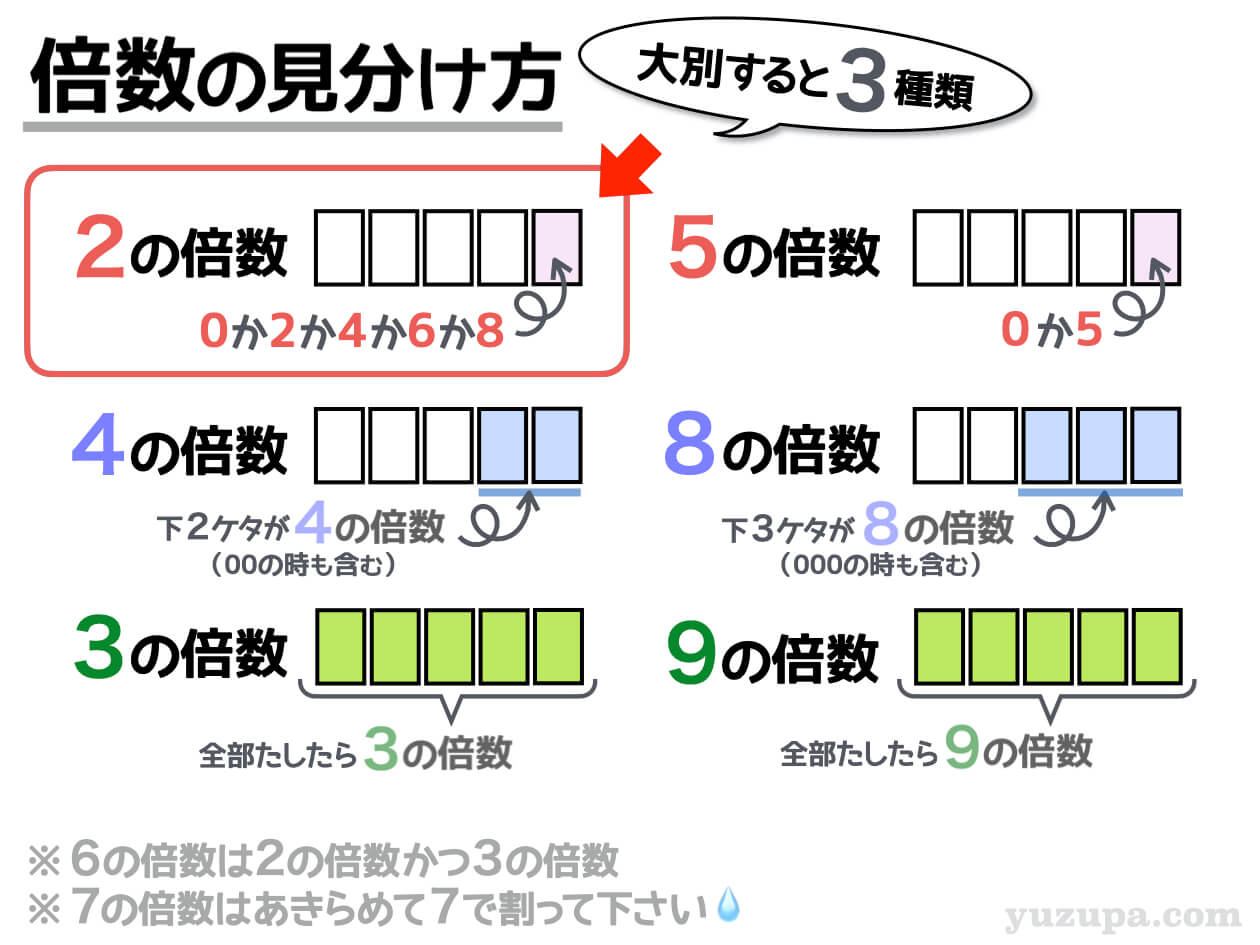
偶数を言い換えると２の倍数です。２の倍数とは２で割ることのできる整数のことを言いますが、簡単に言い換えると一の位が０か２か４か６か８の数字ということですd(^_^o)

これに合致しないモノは数えてはいけません！

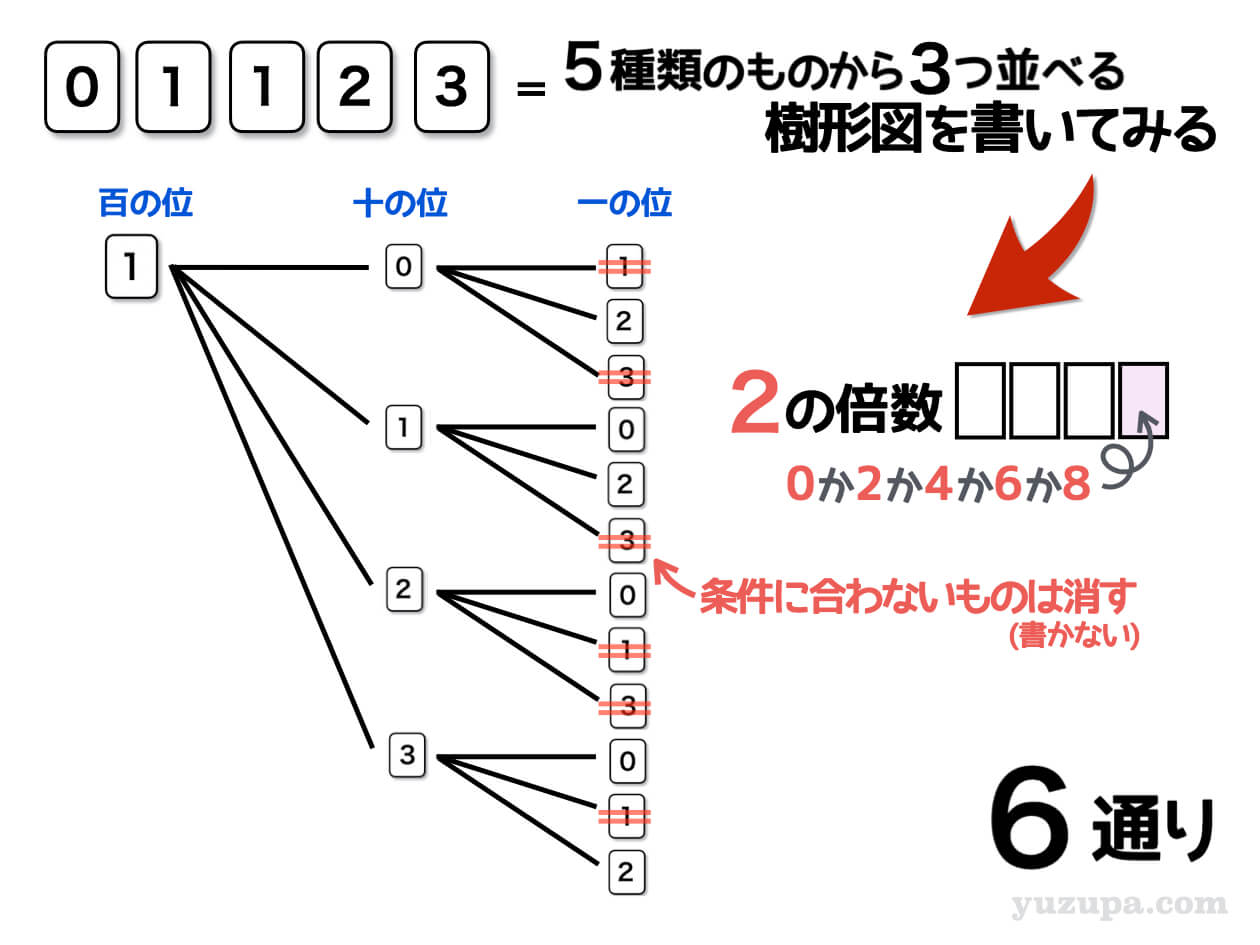
樹形図の書き方はいつでも同じですd(^_^o)

数え間違いを起こさないうように、小さいものから順番に書き連ねていきます。そして条件に合わないものだったら消していくという作業をつづけます_φ(･_･

　一の位が２か０でなかったならば不適合
　これだけに集中しながら樹形図を描きます_φ(･_･

百の位が１のカードの樹形図を描いてみると３ケタの偶数は６通りであることが分かりました。あとは百の位が２の樹形図と、百の位が３の樹形図を描けばよいですねd(^_^o) 

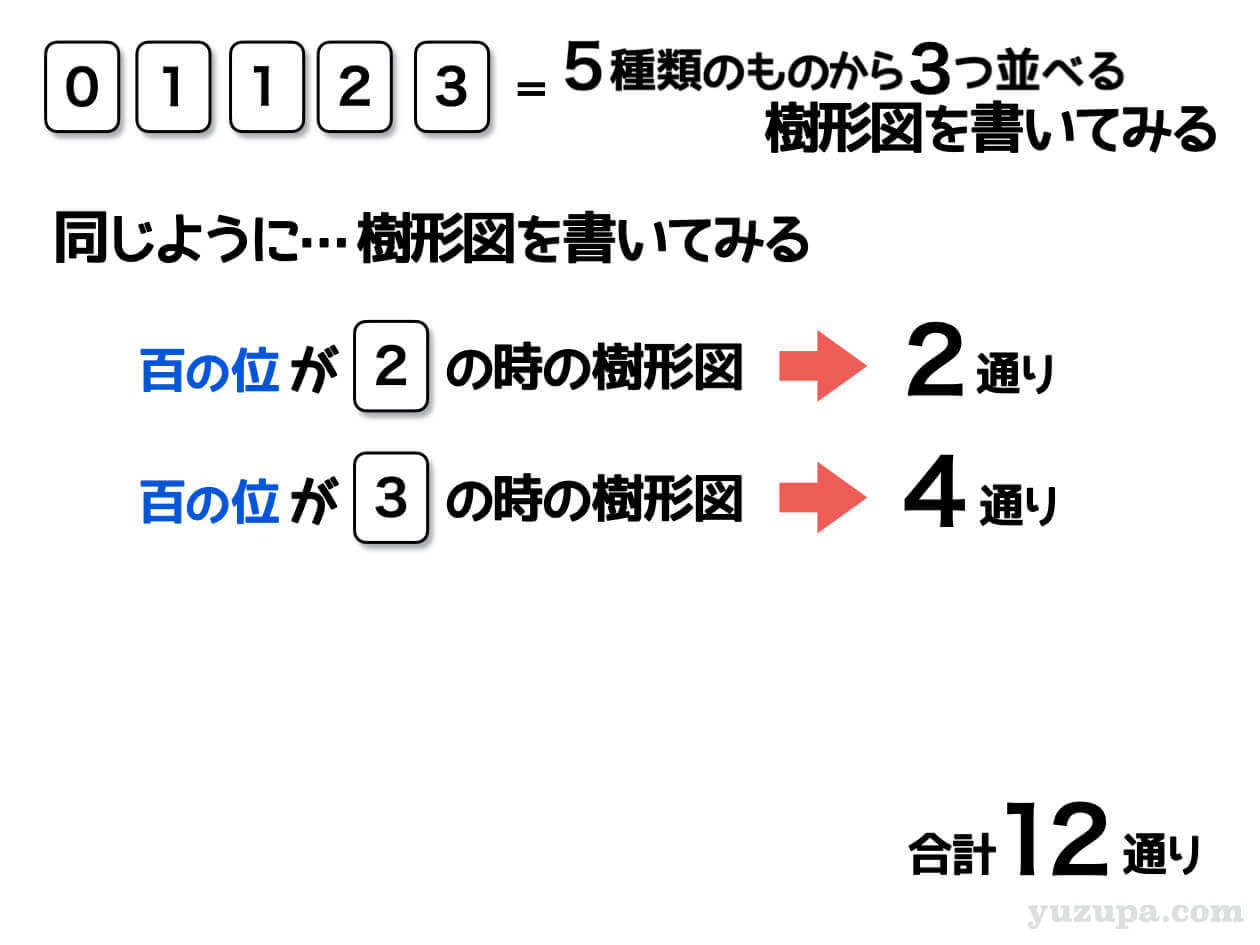
 同様に偶数(２の倍数)以外を消しながら樹形図を描いていくと、百の位が２の時は２通り、百の位が３の時は４通りであることがわかります。全てをたすと合計１２通りですねd(^_^o)

 

(別解) 先に条件で樹形図の範囲をせばめる

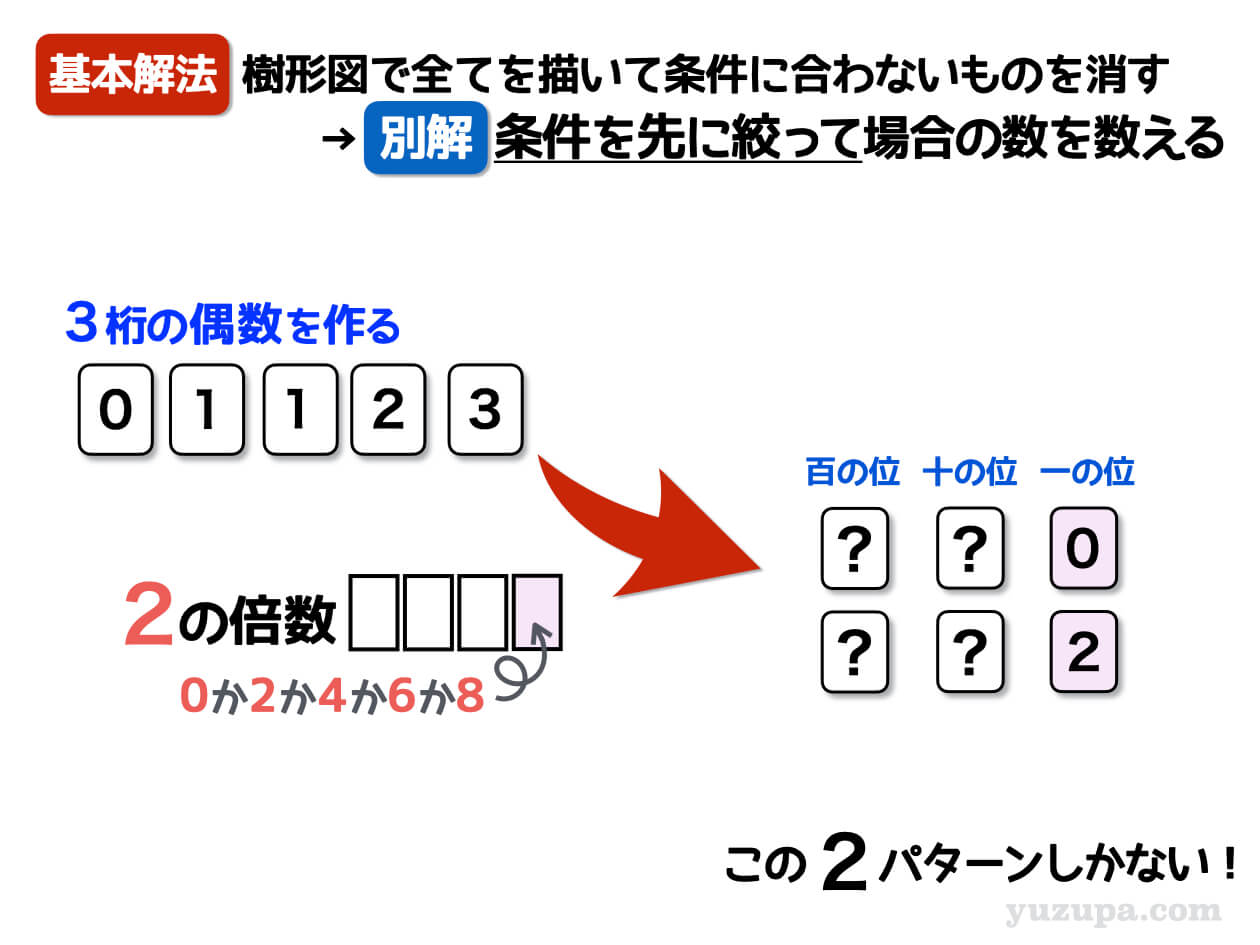
王道の解法は樹形図を落ち着いて描きながら、条件に合わないものを消していく(もしくは描かない)というものでした。別解として先に条件から書く樹形図を絞りこむ解法もありますd(^_^o)

　先に条件を考えると
　実は一の位が０か２のパターンしかない

ということが分かります。そうであれば、一の位は０と２に固定した上で、残りの百の位と十の位の樹形図を書けば、場合の数をもれなく数え上げることができそうです∑(ﾟДﾟ)

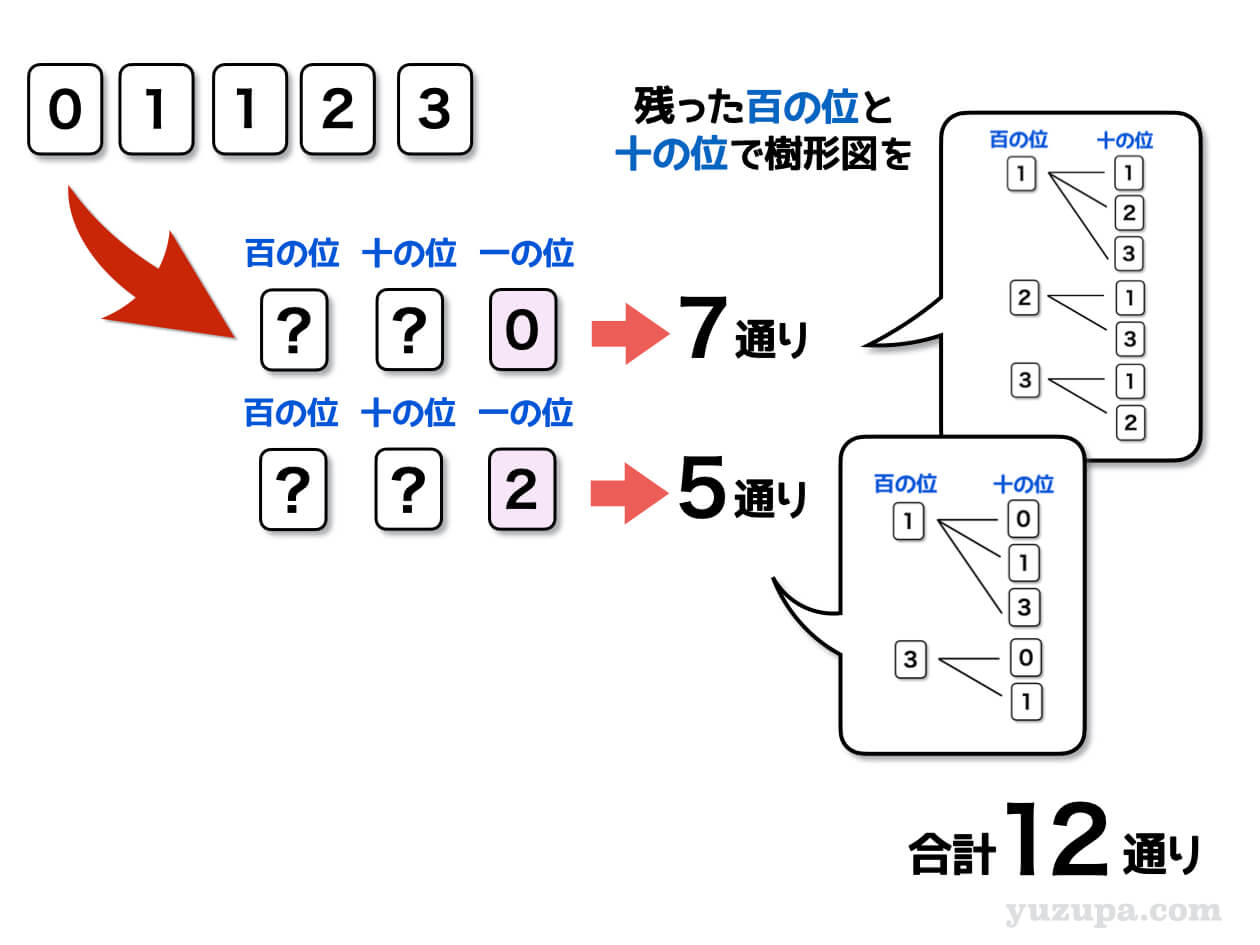
実際に樹形図を描いてみると…一の位が０のときは７通り、一の位が２のときは５通りという結果がでます。答えはもちろん同じ１２通りになりますね o(^-^)o

 

②できる数字が４の倍数

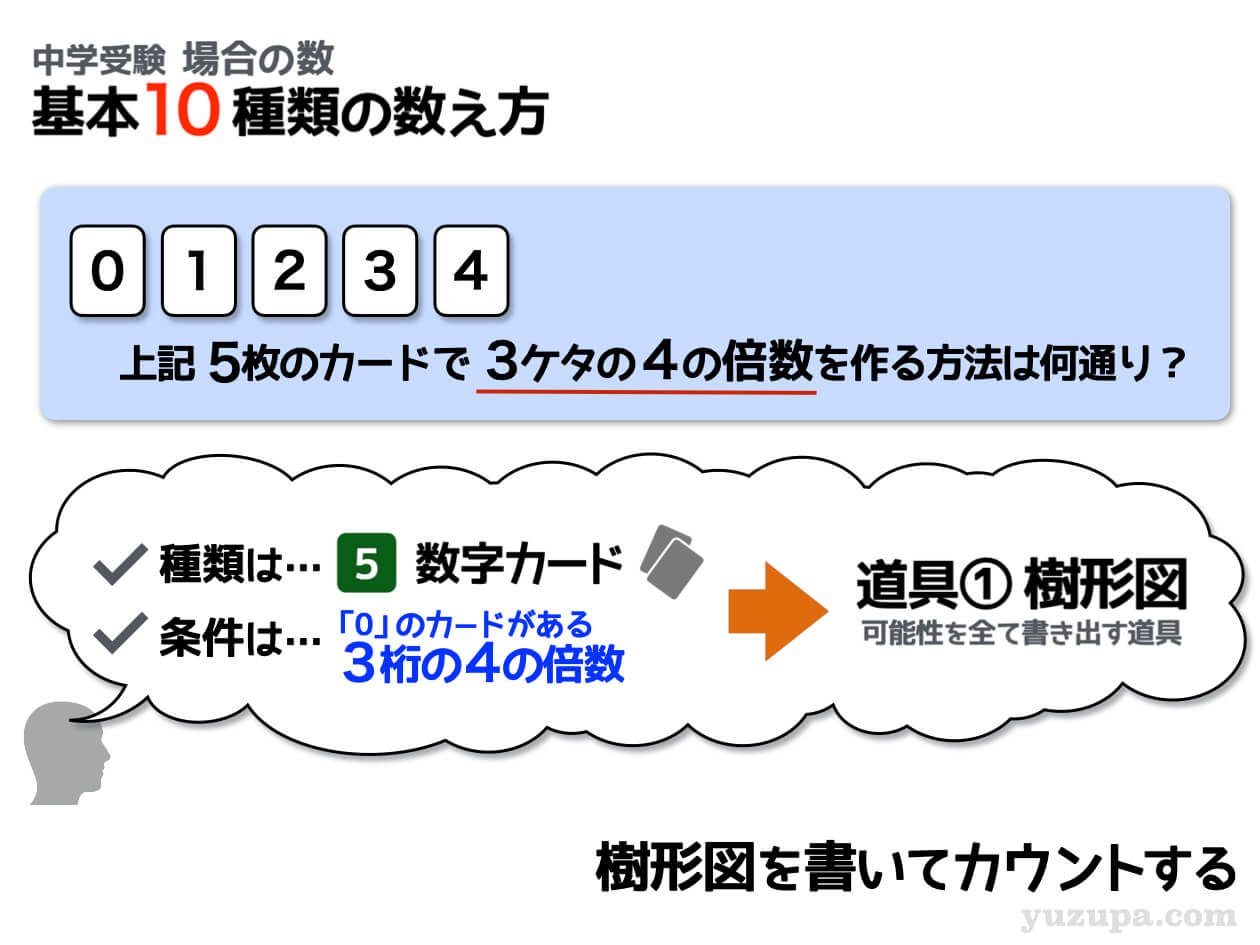
この問題の場合は、できあがる数字が３ケタの４の倍数という条件がついています。同じようにできあがる数字に条件がついている場合は、その条件に合うものしかカウントしてはいけません。

いつもどおり条件を “かみ砕く” 必要があります

４の倍数であるという条件を”かみ砕く”とどうなるでしょうか？

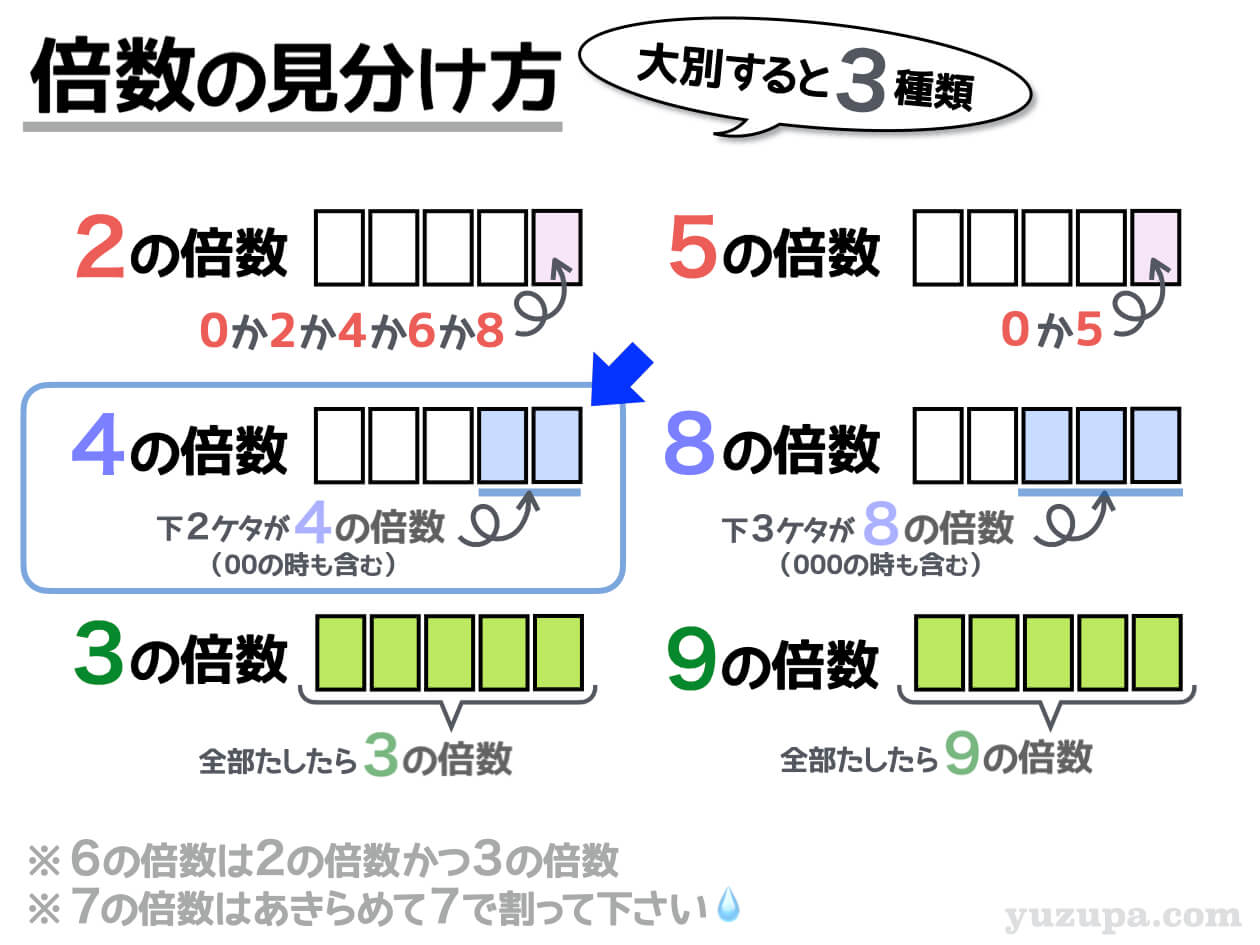
４の倍数とは４で割ることのできる整数のことを言いますが、１００が４の倍数であることから下２ケタが４の倍数であればその数は必ず４の倍数 になりますd(^_^o)

これに合致しないモノは数えてはいけません！

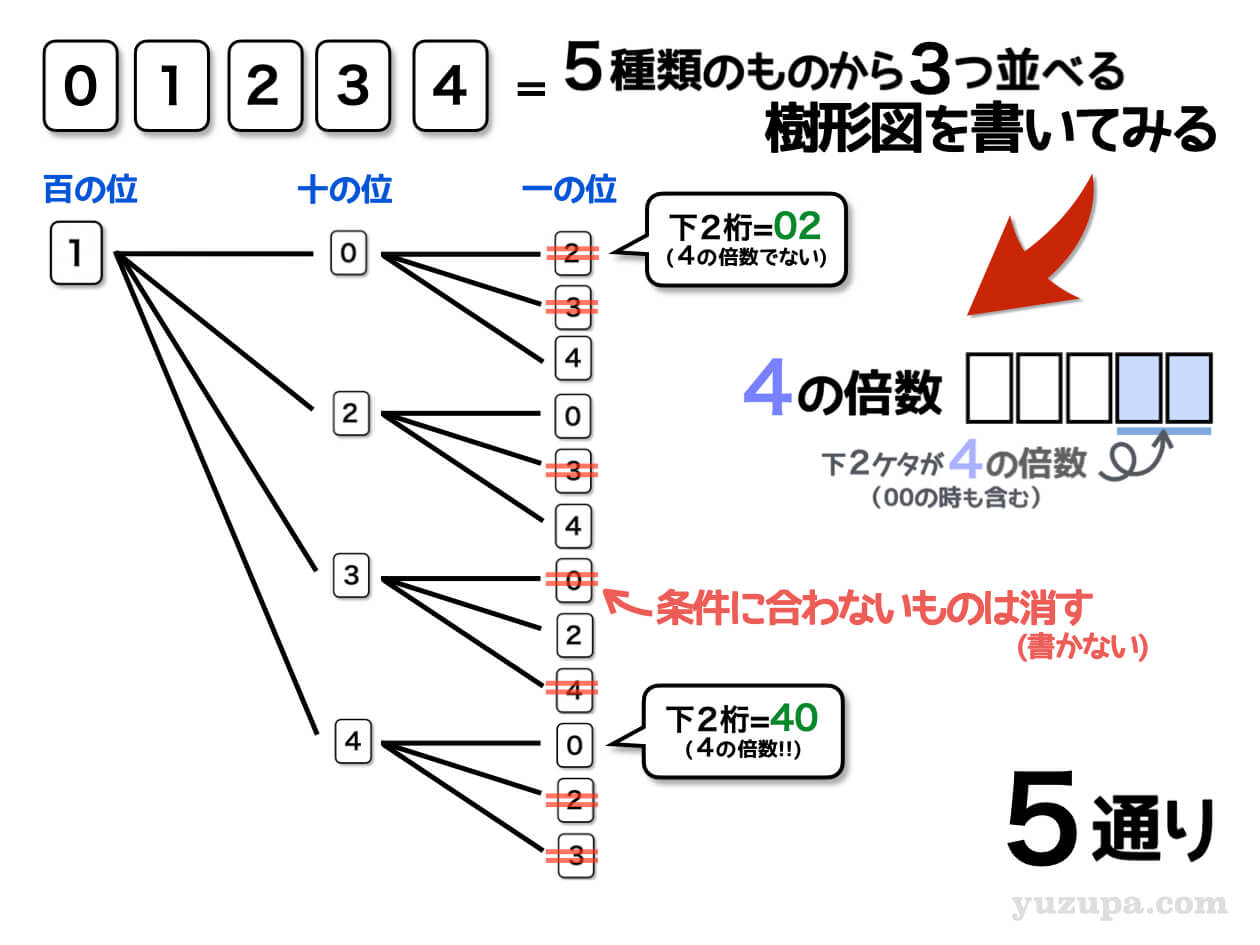
樹形図を実際に書いてみると条件に合わないモノがけっこうでてきます∑(ﾟДﾟ) しかも十の位と一の位の２つを見て条件に合うかどうかを判断しなくてはならないので注意深さが必要です。

百の位＝１、十の位＝０、一の位＝２
下２ケタは０２は４の倍数でないので数えない！

百の位＝１、十の位＝４、一の位＝０
下２ケタは４０は４の倍数なので数える！

といった感じです_φ(･_･

こうやって百の位が１のときの樹形図を注意深く描き切ると実は５通りしかないことが分かりました。この調子で百の位が２のとき、３のとき、４のときの樹形図を描いていきましょう！

そうすると、それぞれ２通り、５通り、３通りであることが分かります。みなさん落ち着いて間違えずに樹形図を描くことができましたでしょうか？ 全てのをたすと合計１５通りになります_φ(･_･

 

(別解) 先に条件で樹形図の範囲をせばめる

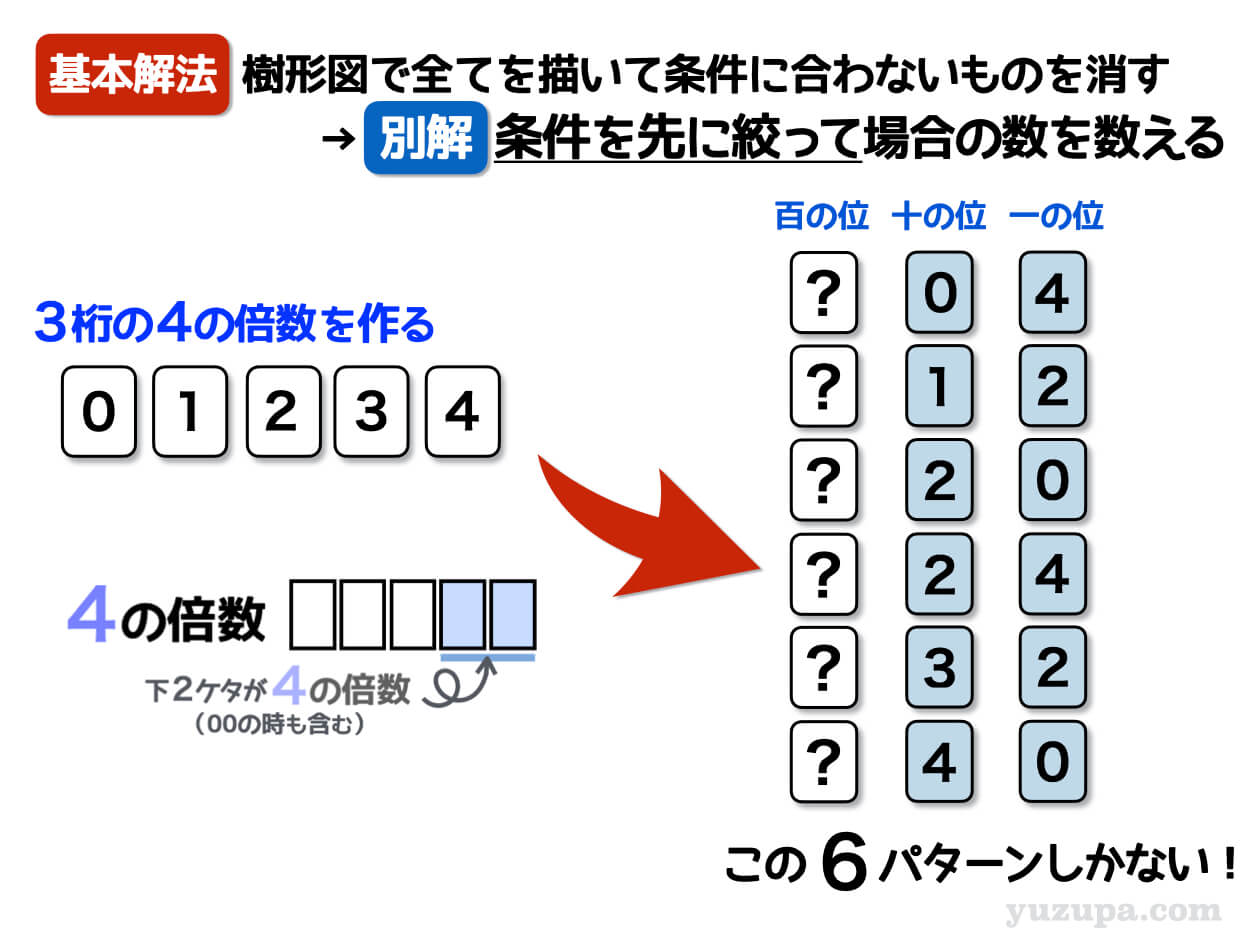
先ほどと同様に、樹形図を描きながら条件に合わないものを消すのではなく、先に条件から描く樹形図を減らせないでしょうか？この５枚のカードを２枚使って４の倍数を作ってみましょう。

そうすると６パターン作れることが分かります

もちろんこれも小さい方から順番に並べてみて４の倍数になるものをピックアップしてもとめます。

この６つのパターンで百の位に何が入るかを考えれば、全ての場合の数をもれなく数えることができそうです。それでは、実際のそれぞれのパターンで百の位を考えてみましょう。

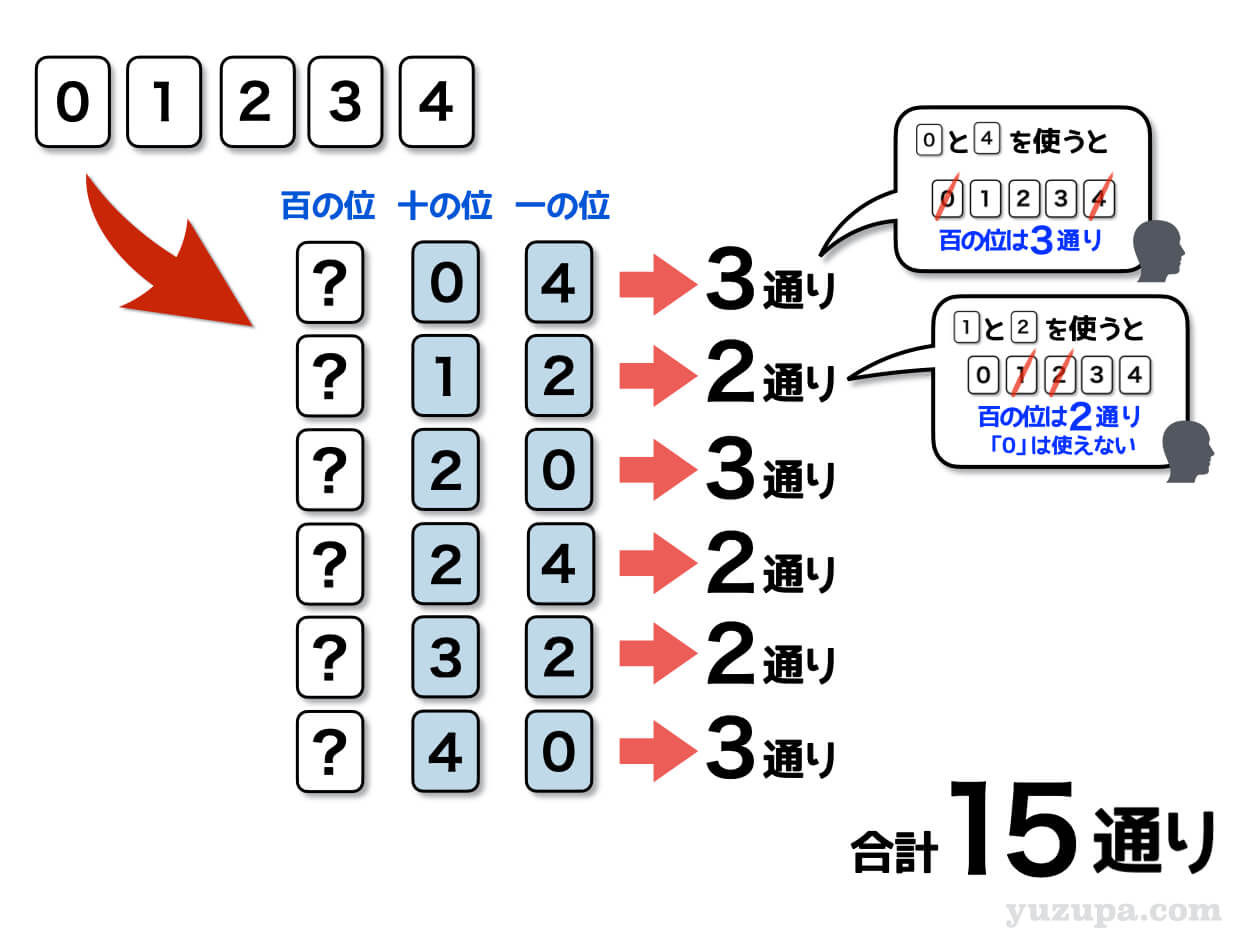
百の位に何が入るかを数えるだけなので、樹形図を描くほどでもありません。図のように使ったカードを除いてあげれば簡単に百の位に入る数字の場合の数がわかります。

十の位＝０、一の位＝４のとき
０のカードと４のカードを使ったので残りは１と２と３
だから百の位に入るパターンは３通り！

十の位＝１、一の位＝２のとき
１のカードと２のカードを使ったので残りは０と３と４
百の位には０は使えないのでパターンは２通り！

こんな感じで間違えないように数えていきます。そうすると先ほどと同じ答えである１５通りになりましたね o(^-^)o

 

③ できる数字が３の倍数

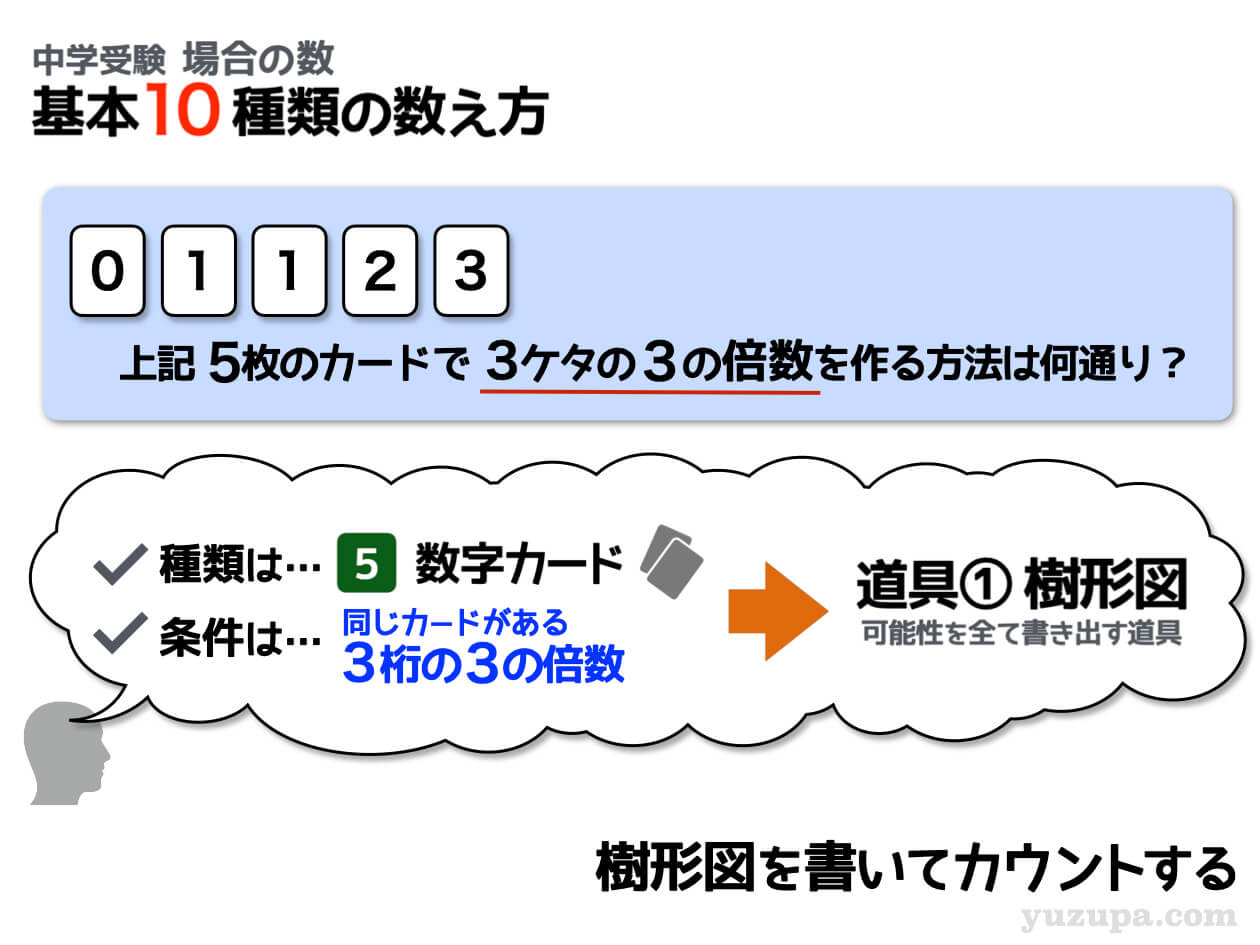
この問題の場合は、できあがる数字が３ケタの３の倍数という条件がついています。できあがる数字に条件がついています。条件に合わないものを数えないように、条件を整理しましょう。

どんな条件であっても条件を ”かみ砕く” クセをつけましょう

３の倍数であるという条件を”かみ砕く”とどうなるでしょうか？

 

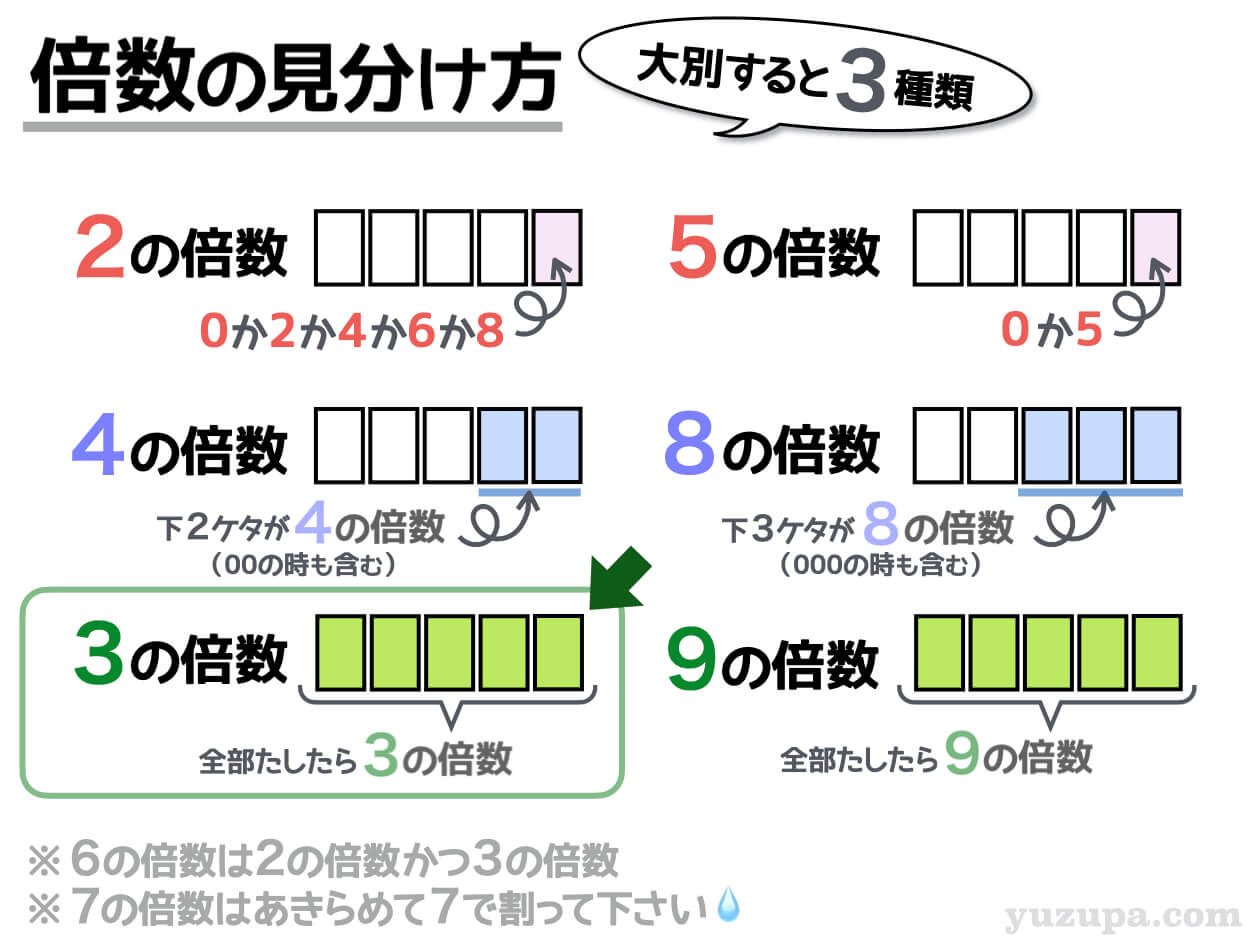
本記事は場合の数の解説なので、詳しい説明は割愛させていただきますが、３の倍数という条件をかみ砕くと すべての位の数字をたして３の倍数になればその数字全体も３の倍数である という条件を使って解いていきますd(^_^o)

全ての位をたして３の倍数にならないものは数えてはいけません！

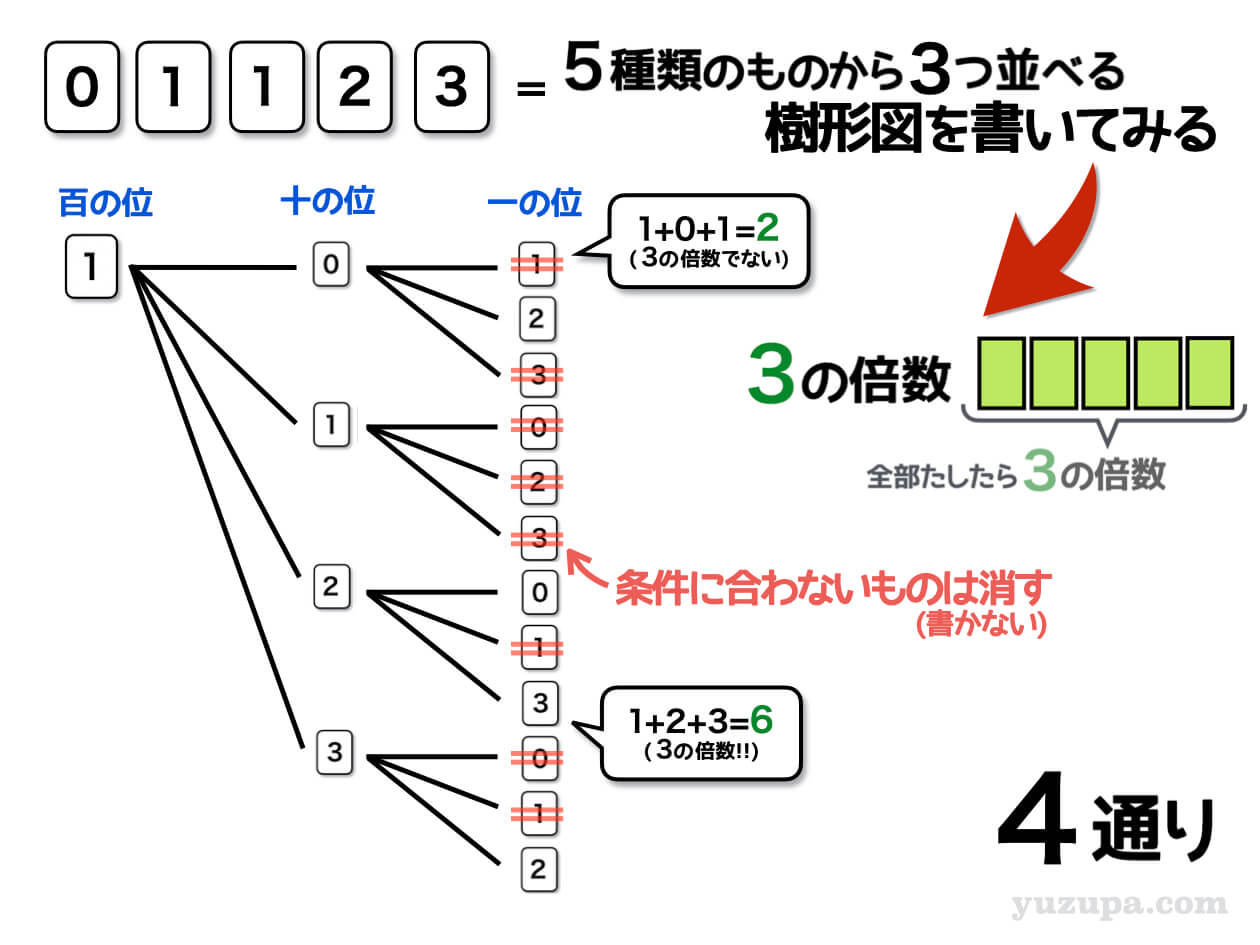
実際に樹形図を描きながら、条件に合わないものを消していきます。この条件の場合は、全てのケタの数字を見て判断しなくてはいけないので、今までの問題よりさらに注意深さが必要です。

百の位＝１、十の位＝０、一の位＝１
全てのケタの数字をたすと １＋０＋１＝２
２は３の倍数では無いから数えない！

百の位＝１、十の位＝２、一の位＝３
全てのケタの数字をたすと １＋２＋３＝６
６は３の倍数だから数える！

といった具合で注意深く樹形図を書いていきますd(^_^o) 最後まで描き終えると、条件に合うのは４通りであることが分かります。

同様に残りの百の位が２の時の樹形図と、百の位が３の時の樹形図を注意深く描いていきます。それぞれ４通り、２通りとなる結果を得られましたでしょうか？ 全てをたすと１０通りになります。

 

④ できる数字が200以上

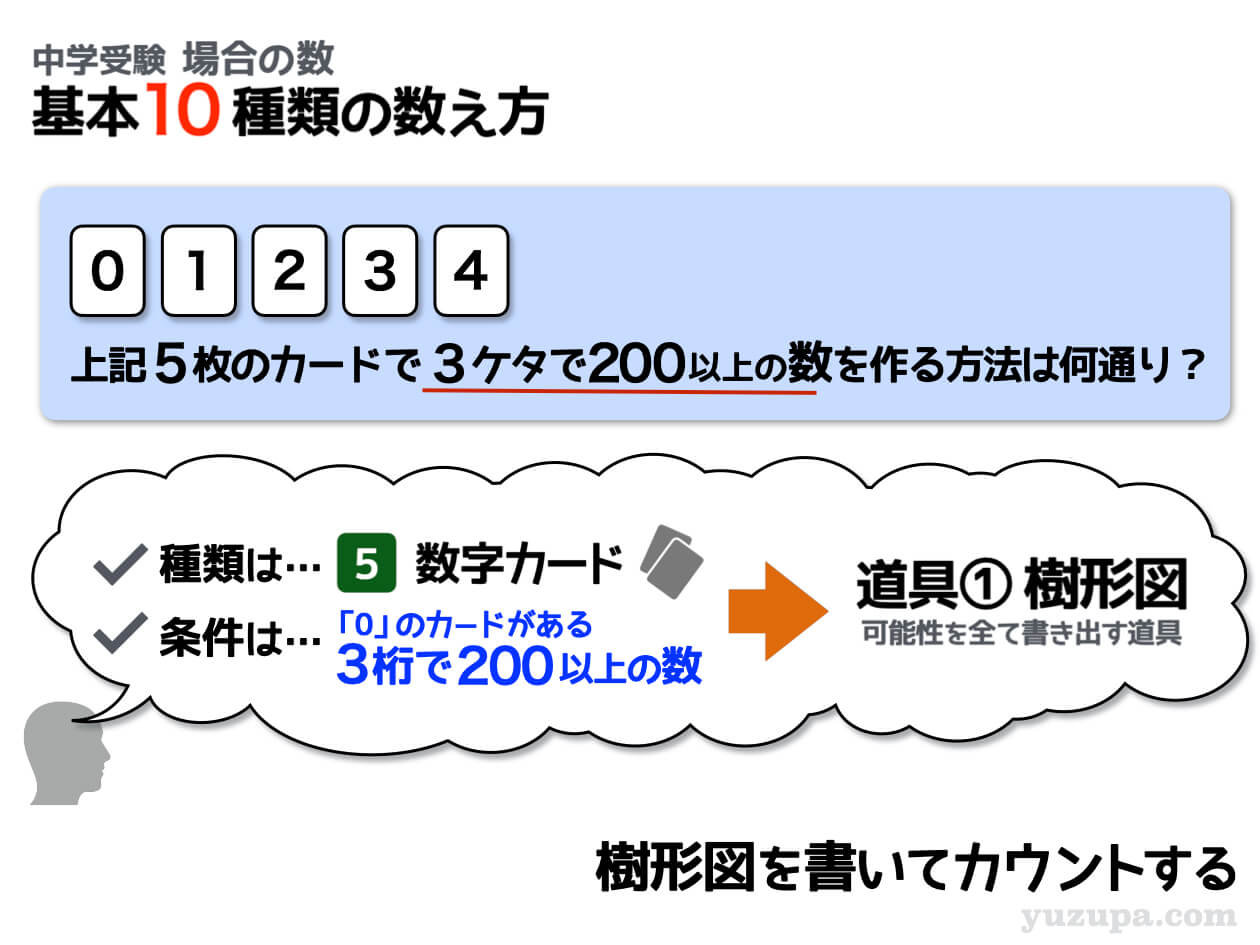
この問題の場合は、できあがる数字が３ケタで２００以上の数という条件がついています。できあがる数字に条件がついています。条件に合わないものを数えないように、条件を整理しましょう。

いつもどおり条件を ”かみ砕く” 作業に入りましょう

２００以上であるという条件をかみ砕くのは実はとてもシンプルです。百の位が２以上であれば２００以上の整数 ができあがります。この問題の場合、百の位が２か３か４になれば良いのです。

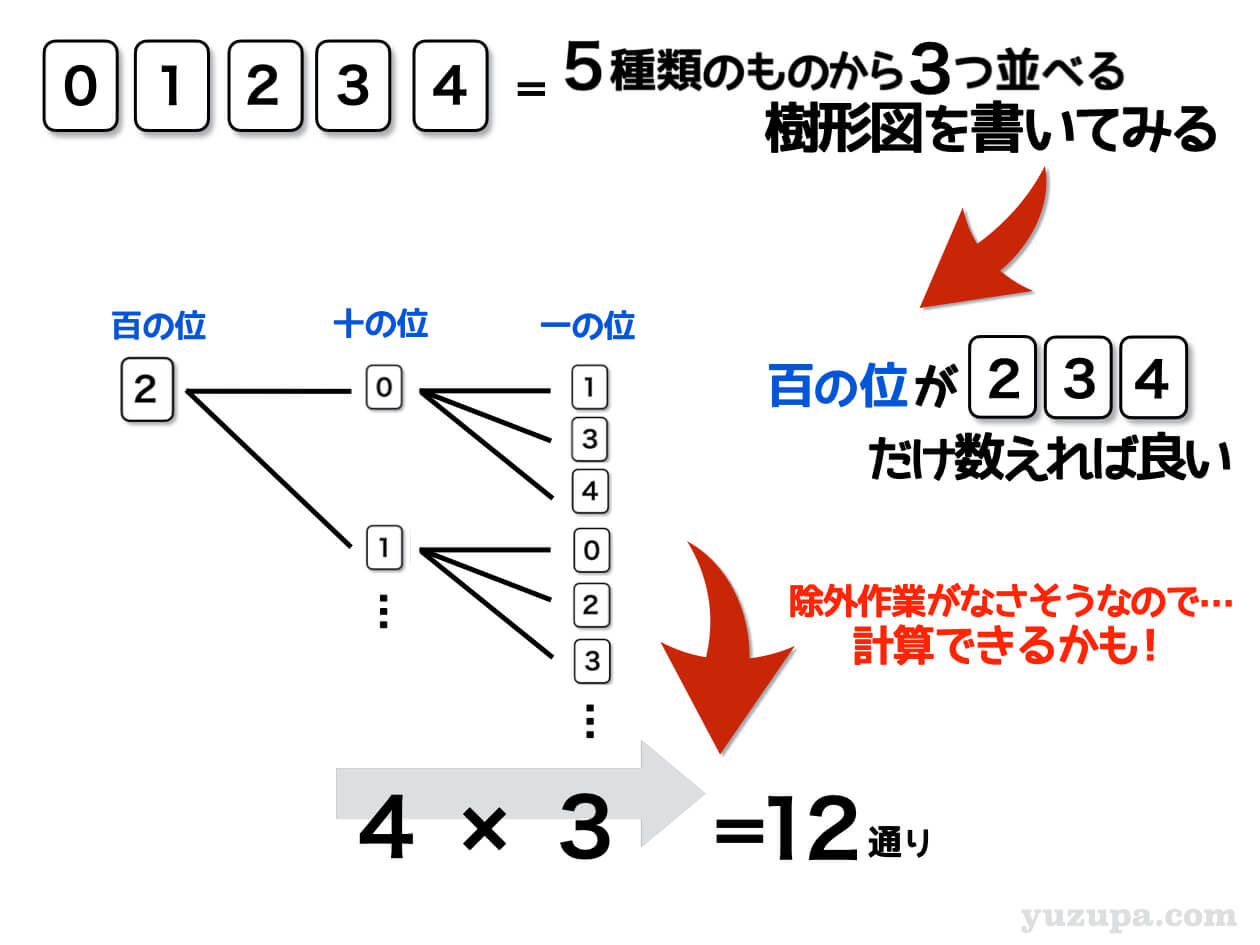
条件がはっきりしましたので樹形図にとりかかりましょう。

まずは百の位が２の樹形図からです。この問題の場合他に条件がないので条件に合わないものを消すという作業が不要そうです。また同じカードも複数ないので計算でだせそうですd(^_^o)

十の位に入るのは２を除いた０か１か３か４の４通り、一の位に入るのは十の位で使ったものを除いた残りの３通りです。それぞれをかけ合わせてあげれば１２通りであることが分かります。

残り…百の位が３の時、百の位が４の時の樹形図に参りましょう！

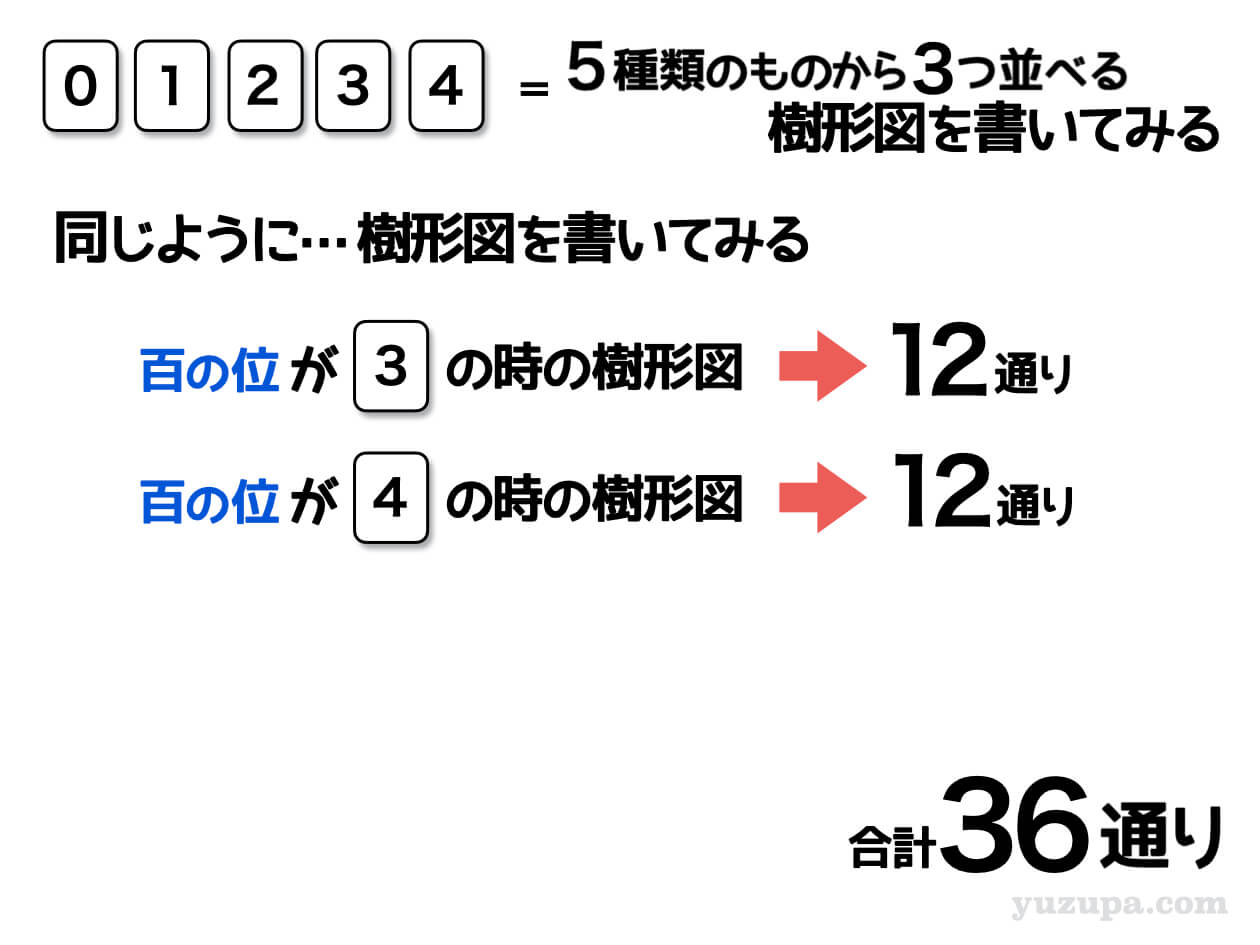百の位が３であろうが４であろうが、樹形図を描くのを省略して計算で出せるのであれば計算でパッパと出していきます。それぞれ１２通りになるので、合計では３６通りですね d(^_^o)

今回のように、樹形図を描く工程になってから以下のような場合には樹形図を省略して計算ができる可能性があるので、積極的に挑戦してみましょうd(^_^o)

 　樹形図を省略して計算できる条件
　・ 条件に合わないものを消すという作業がない
　・ 全てのカードがバラバラで同じカードがない

このような条件だった場合は樹形図を計算で求める方向へ転換することをこころみましょう！

 

⑤ できる数字が６の倍数

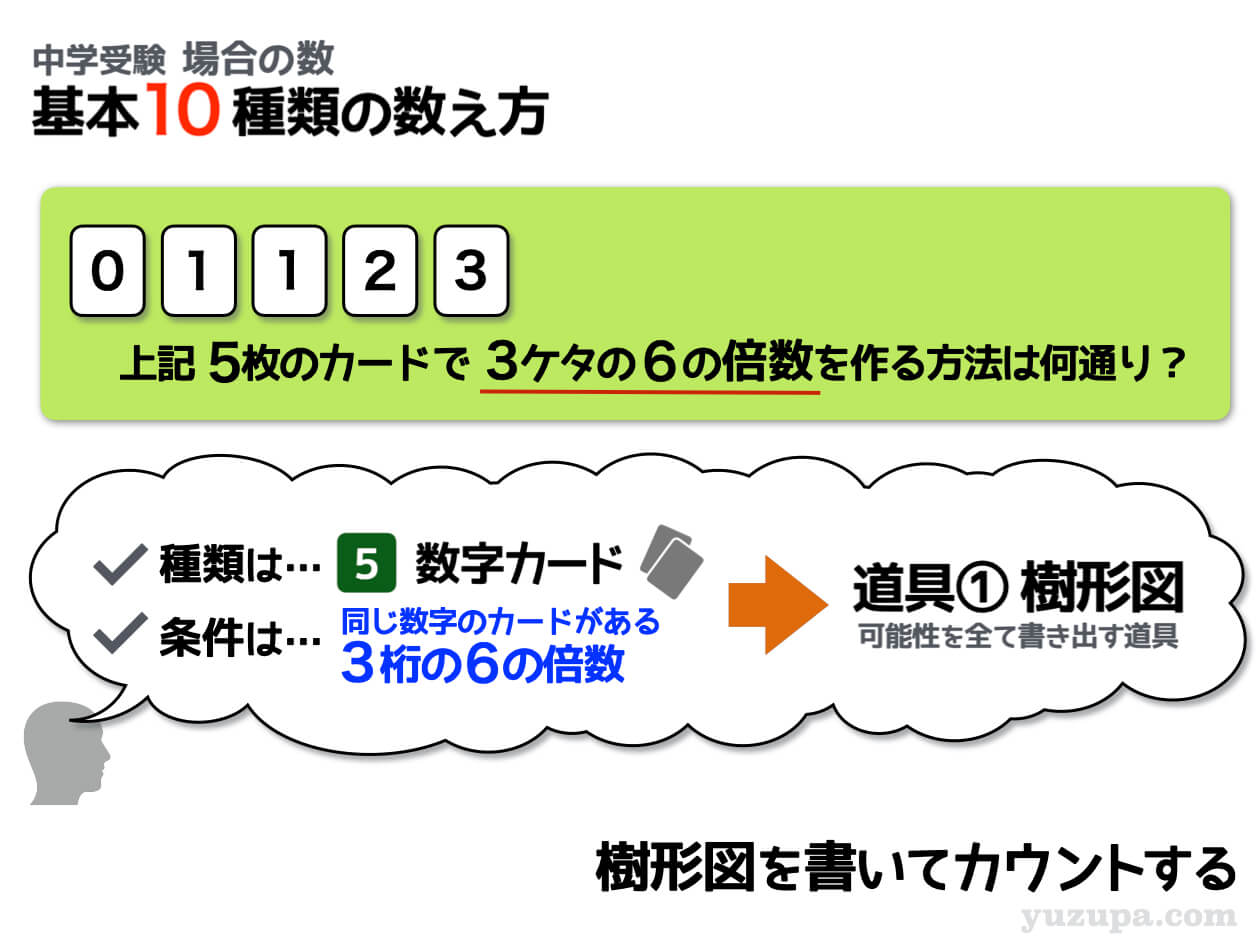
この問題は、できあがる数字が３ケタで６の倍数という条件がついています。今まで登場した偶数/奇数や３の倍数、４の倍数と同様できあがる数字に条件がついています。

これは単一に見えて複数の条件が合わさった条件です

ある数が６の倍数になるということは、２の倍数であり、３の倍数であるという２つの条件を両方の条件を満たすということ。つまり２つの条件を考える必要があります∑(ﾟДﾟ)

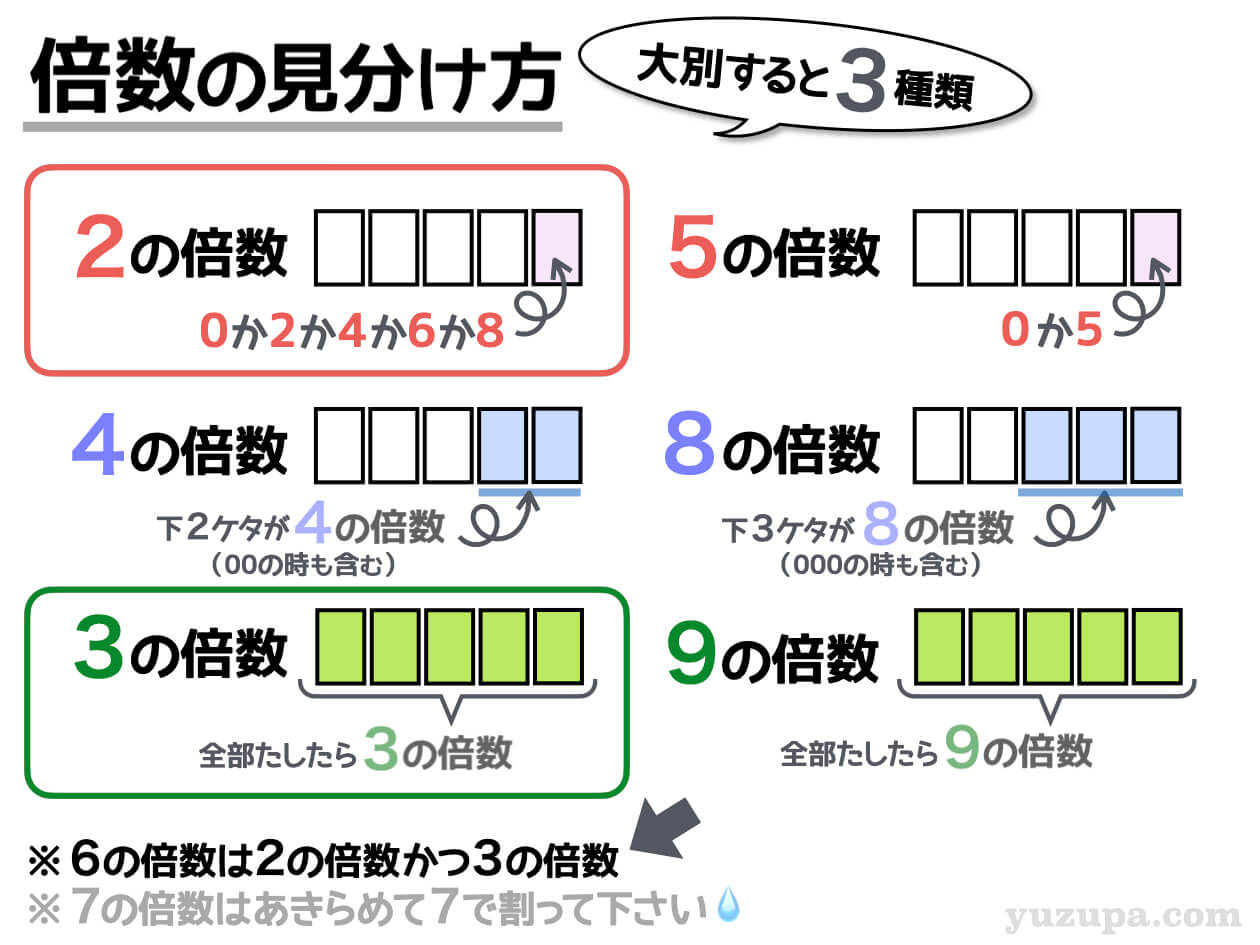
条件をおさらいしてみましょう_φ(･_･

２の倍数である条件はかみ砕くと一の位が偶数。つまり０か２か４か８であるという条件になりました。

３の倍数である条件はかみ砕くと全てのケタの数字を足したら３の倍数であるという条件になりました。

 

条件が２つ以上ある場合には注意が必要です_φ(･_･

脳は複数のことを同時に処理するとミスが多発するからです。

 

そこで複数の処理を同時にしなくても良いような工夫が必要です。代表的な２つのアプローチをご紹介します！

アプローチ① 条件をひとつずつ処理する
シンプルに１つ目の条件だけで描く樹形図をしぼりこみ、樹形図を描く際に２つ目の条件に従って数えるというもの

アプローチ② 条件を結合して１つの条件にする
２つある条件を１つの条件にしてしまうというもの。条件どうしで重複する部分を抽出するというイメージです。

 

この問題の場合はアプローチ①を試みてみます_φ(･_･

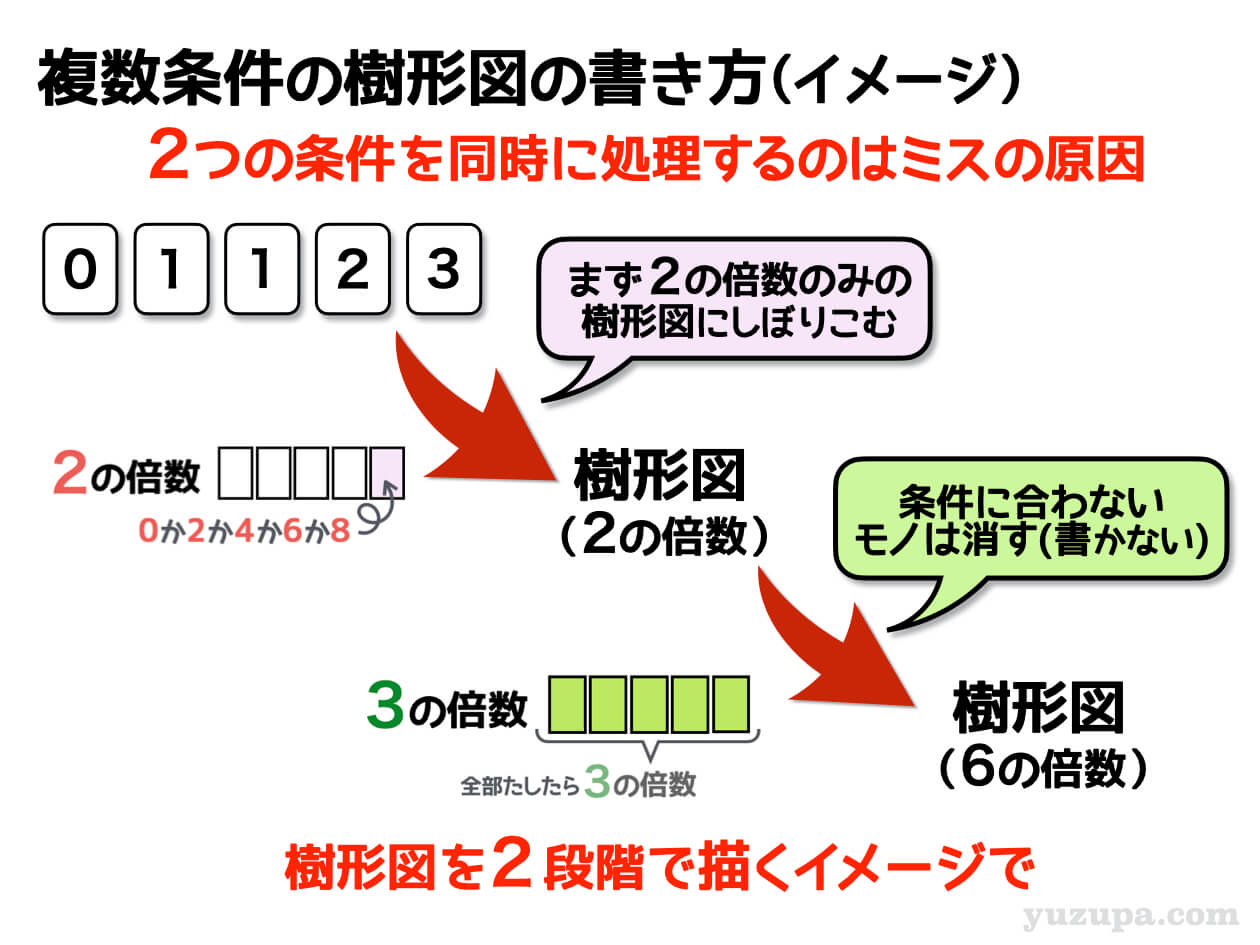
まず一段階目として分かりやすい条件である２の倍数という条件を適用して描く樹形図をしぼっていきます。この問題の場合は、一の位が０の樹形図と、一の位の２の樹形図を書けばよいでしょう。

これで１つ目の条件は網羅したことになります∑(ﾟДﾟ)

あとは２つ目の条件である４の倍数に合致しないものを数えないように樹形図を描くだけですd(^_^o)

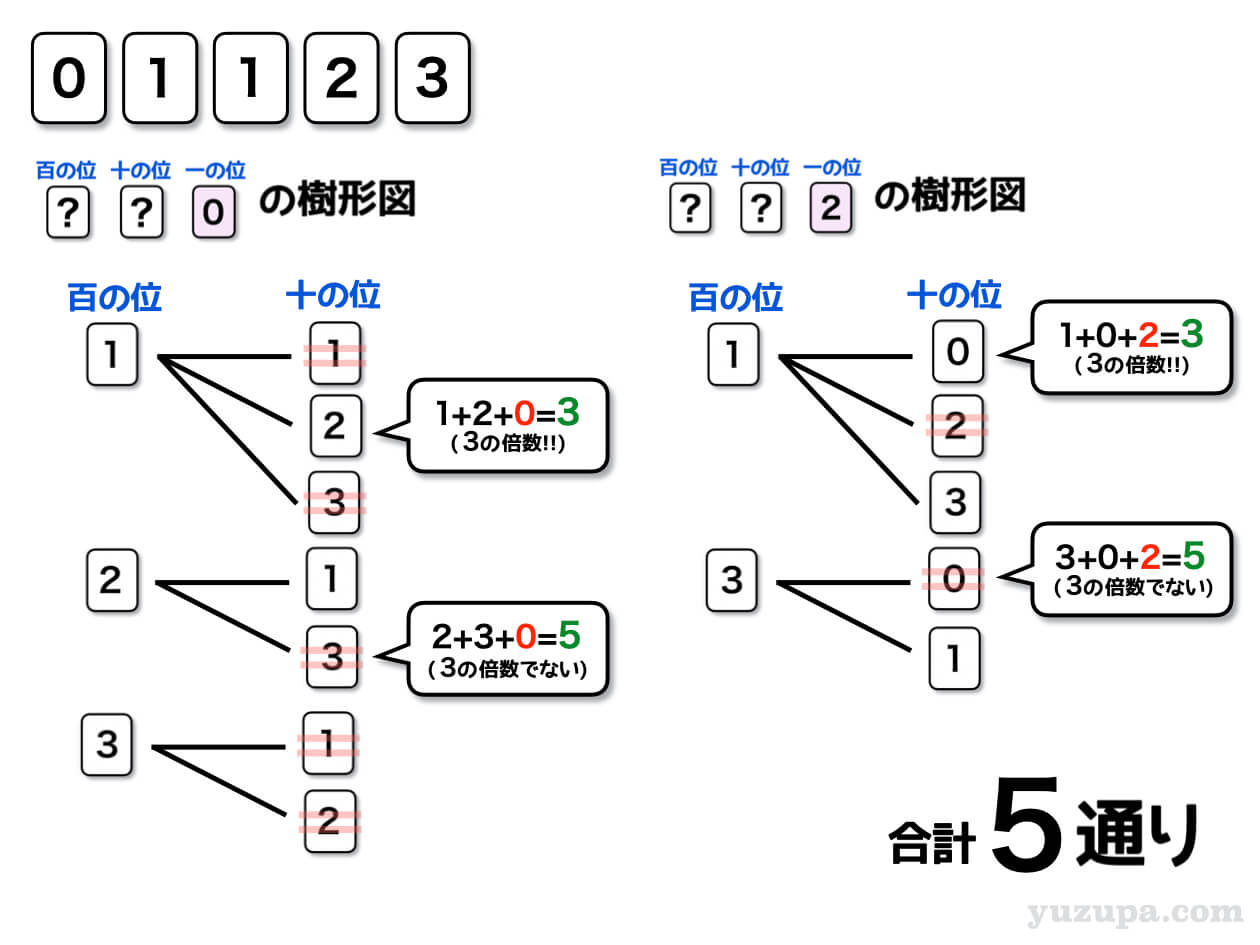
すでに２の倍数にならないパターンは排除されているので、４の倍数に当たるか当たらないかに気をつけて樹形図を書けばOKです。そうすると…全部で５通りになりましたね_φ(･_･

この問題は複数の条件を１つずつ処理しました。次の問題は複数の条件をひとつにまとめるという解法をとる問題ですd(^_^o)

 

⑥ できる数が２００以上３００以下

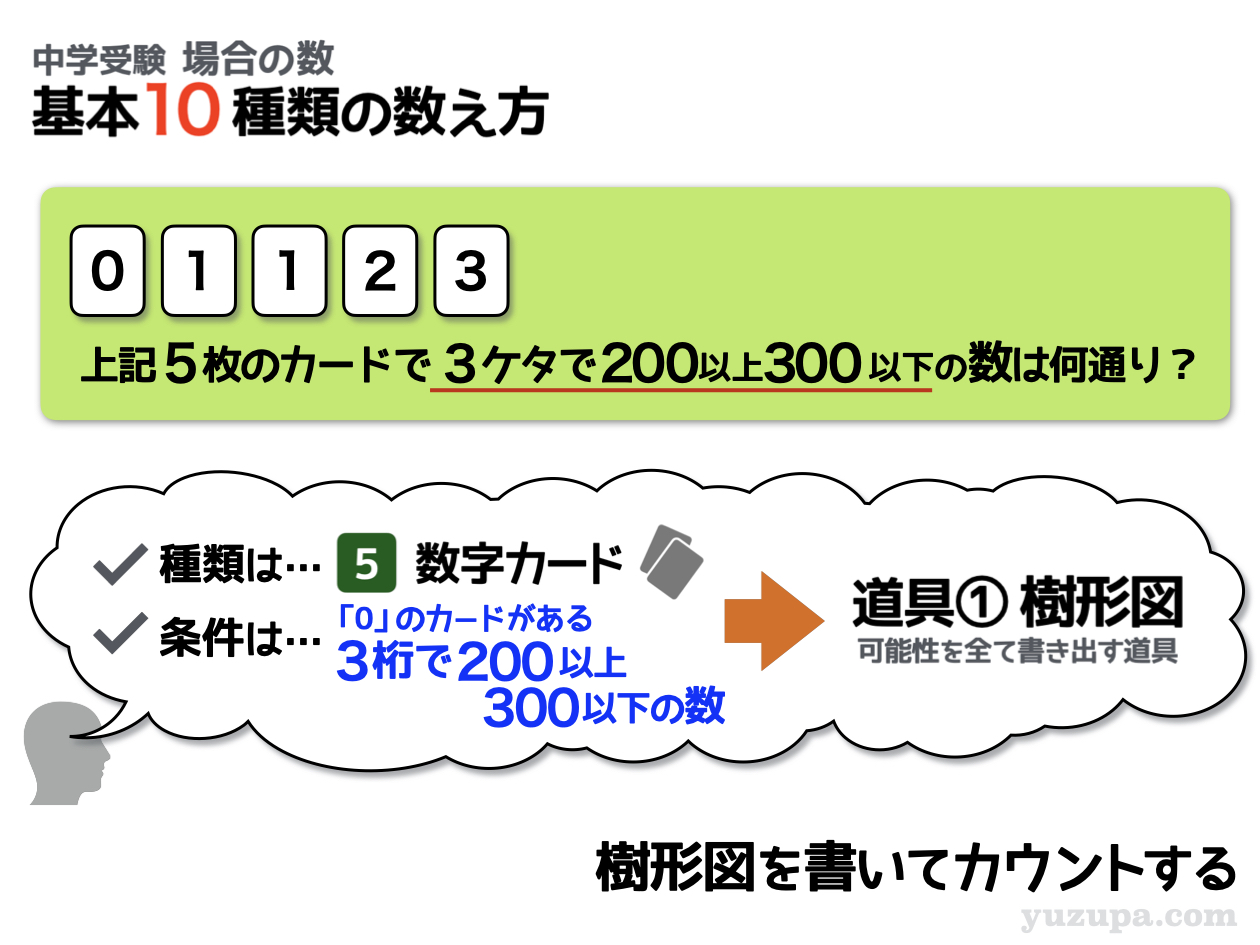
この問題は、できあがる数字が３ケタで２００以上３００以下の数という条件がついています。これも複数の条件が合わさったものと考える と良いでしょうd(^_^o)

具体的には…１つ目の条件が２００以上であるという条件、２つ目の条件は３００以下であるという条件です。

今回はさきほどと違い、２つの条件をひとつにまとめて１つの条件にしてしまうというアプローチをとります。といっても、とてもシンプルな考えで条件をまとめることができます。

では…条件を整理してみましょうd(^_^o)

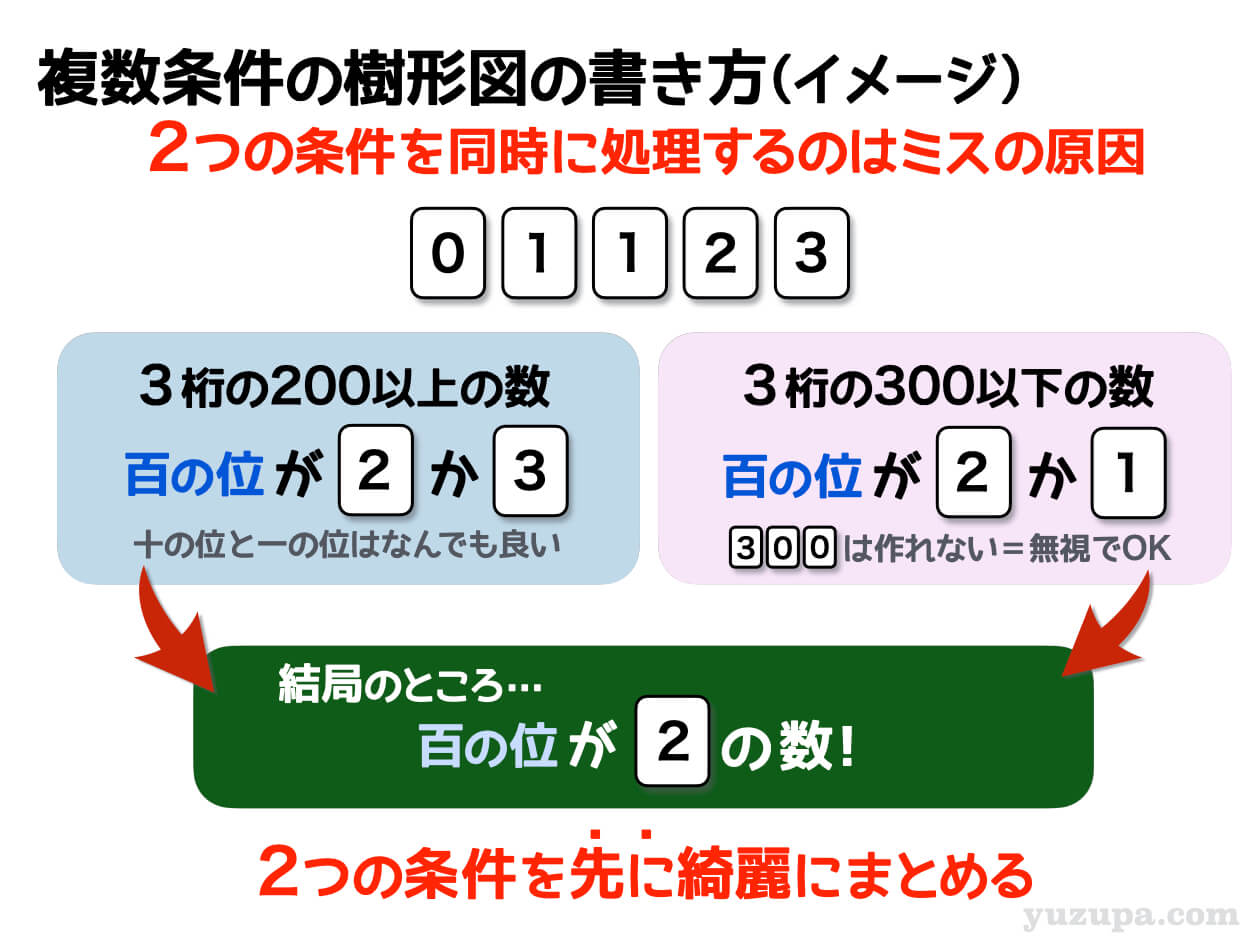
１つ目の条件は ”２００以上” という条件
かみ砕くと…百の位が２か３になるという条件

２つ目の条件は ”３００以下” という条件
かみ砕くと…百の位が２か１になるという条件

２つ目の条件の補足ですが、３００ピッタリも３００以下に含まれます。しかし配られたカードをみると３００ピッタリは作れません。なので百の位が３というのは排除してしまって良いでしょう。

この２つの条件を合わせる…
つまり共通部分を抽出するとどうなるでしょうか？

結局のところ…
百の位が２になるという条件になります∑(ﾟДﾟ)

ここまでくれば簡単です。百の位が２となるような３ケタの数字の場合の数を数えるための樹形図を描くだけです。

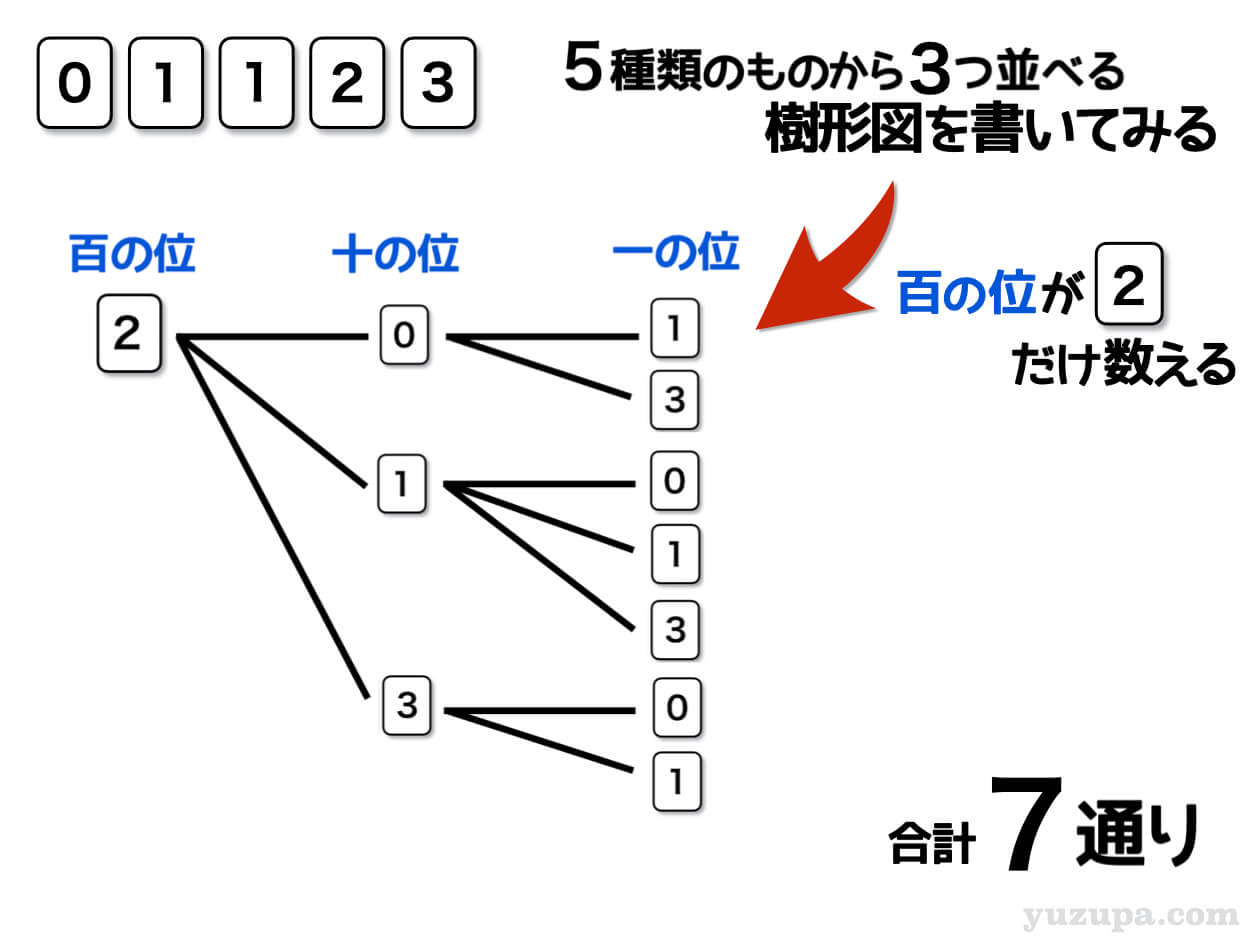
樹形図はとてもシンプルなので説明は割愛しますが、すべての場合の数を数え上げると合計で７通りになりますd(^_^o)

 

まとめ

今回は無数にあるように思われる、場合の数の問題の中からカードを使って整数を作る問題にフォーカスして解説をしてまいりました。しっかりと問題の条件を見極めることがポイントです。

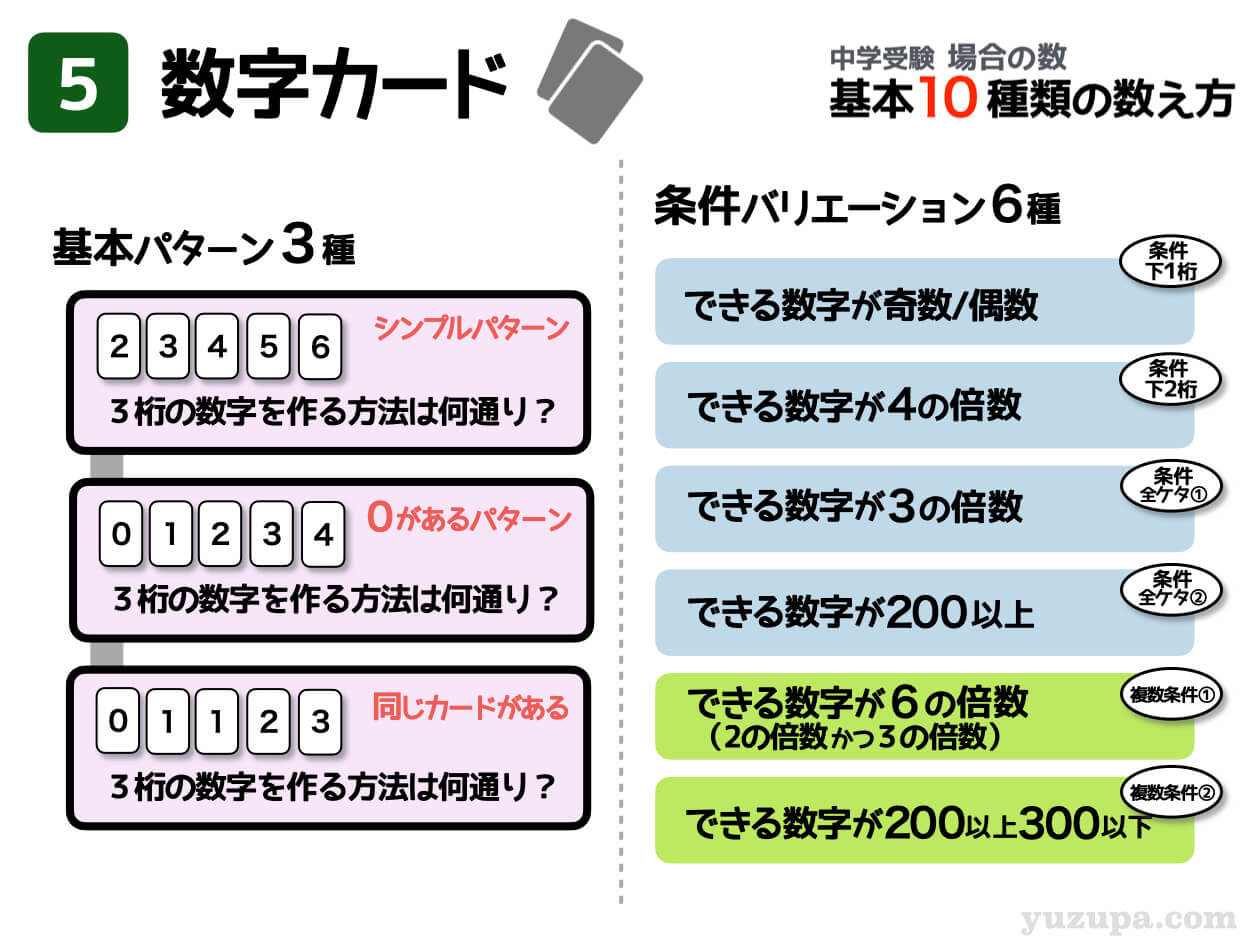
場合の数の問題は、基本的な解法をとる基本パターンと条件バリエーションのかけ算で考えましょう。

　(1) 基本パターン３種
　(2) 条件バリエーション６種

もちろん本記事でご紹介する以外の独特な条件が出されることもありますが、本記事でご紹介した６種の条件は、網羅性を考慮してピックアップしております。

正しく理解し、応用を効かせる力をつけましょう d(^_^o)

場合の数に関する以下の記事もご参照ください。

リンク：場合の数が苦手…３つの道具を使い10種の数え方をマスターせよ
リンク：場合の数の基本パターンを全網羅！ 整列と分配問題編