中学受験:円周率暗記プリント…体積問題で間違いを連発する2つの理由
円柱や円すいの体積問題でのミス連発にはシンプルな理由があった!
 こんにちは。かるび勉強部屋 ゆずぱ です。
こんにちは。かるび勉強部屋 ゆずぱ です。
私の息子が算数において、面積や体積の基本問題で最初につまずいたのが、円柱や円すいの体積を求める問題でした。5年生に入って間もなくのゴールデンウィークのあたりでした。とにかく計算ミスを連発し、式も微妙に間違ってる(・_・; なぜ…こんなにも間違ってしまうのか?
よく息子を観察してみると…とてもシンプルな理由が2つ分かってきました。
理由1:体積を ”公式” で捉えている
理由2:円周率でミスを連発している
我が息子が陥っていた、体積問題をやたら間違える状況。その原因と我が家で実施した対策をご紹介します d(^_^o) 円周率計算の暗記プリントがご入用の方… 本記事の最後にダウンロードリンクがあります!
目次
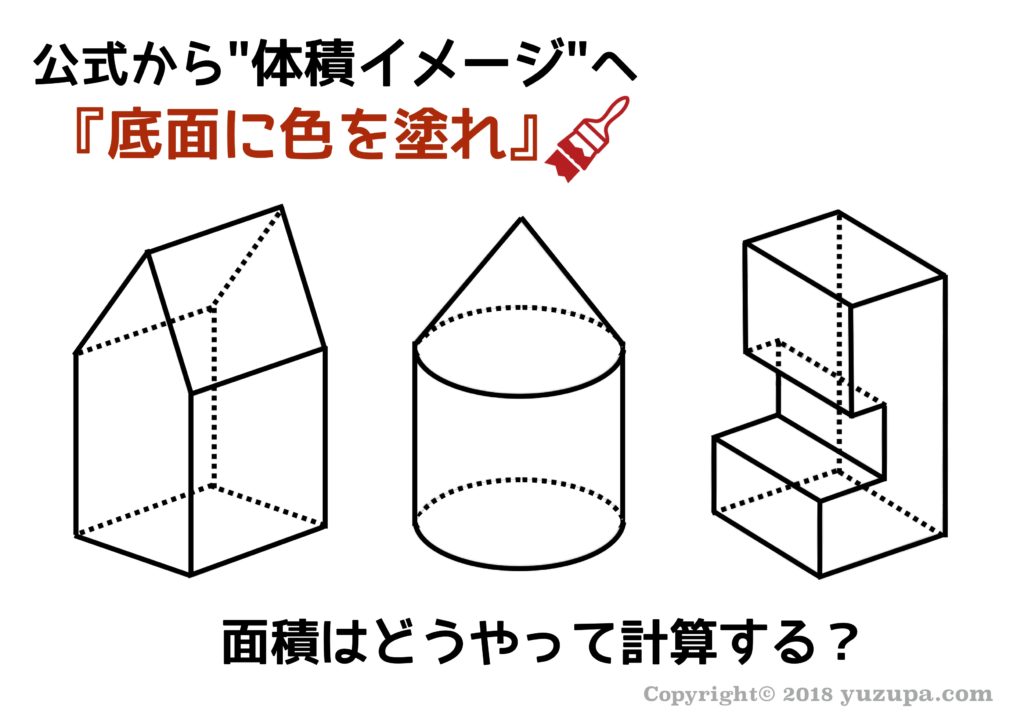
合言葉 ”底面に色を塗れ”!
面積は”公式”で捉えるな
例えば、円すいの体積の公式を式にしてみましょう。式だと文字列として覚えることになります (@_@) そんな時の鉄則はイメージに変換すること ですが、体積の公式をどうやってイメージ化すれば良いでしょうか?
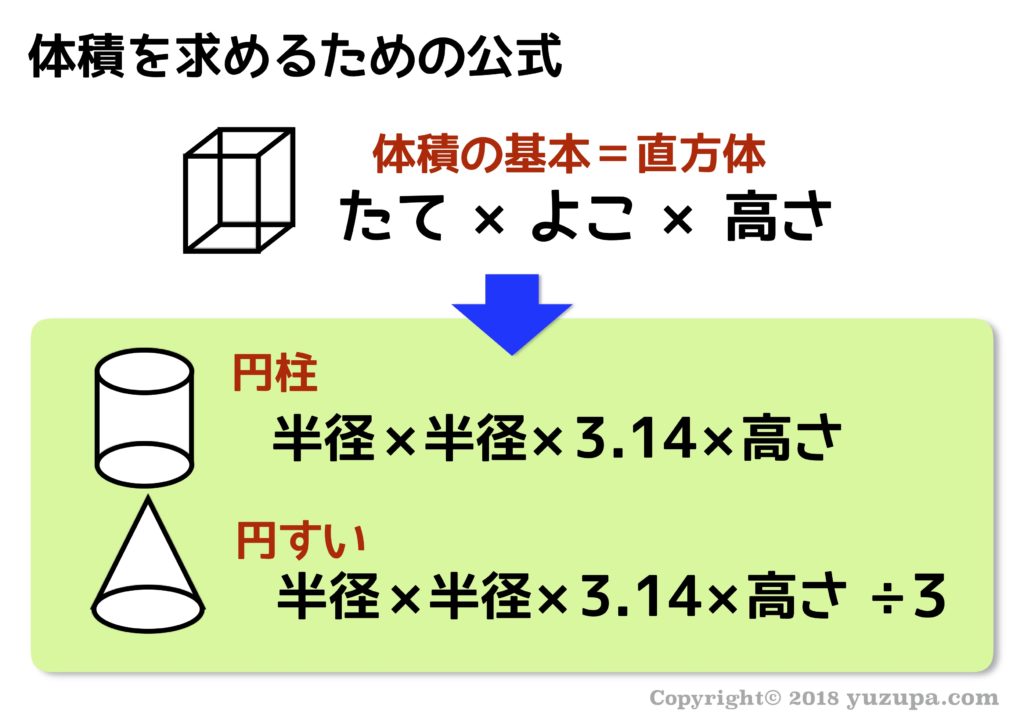
“底面に色”でイメージとして理解
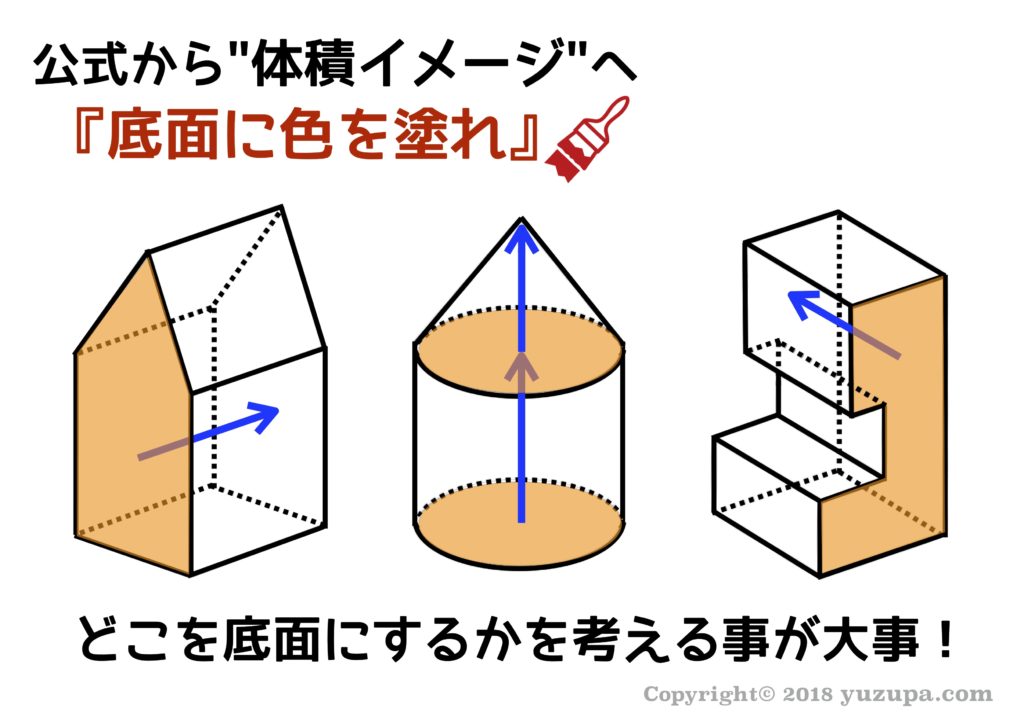
とてもシンプルですが、立体図形の底面に色を塗るという作業を行うだけで、”体積”と言うものをイメージとして捉えることができますd(^_^o) そして底面から高さを表すために矢印を引っ張ると高さをイメージとしてとらえる事ができます。
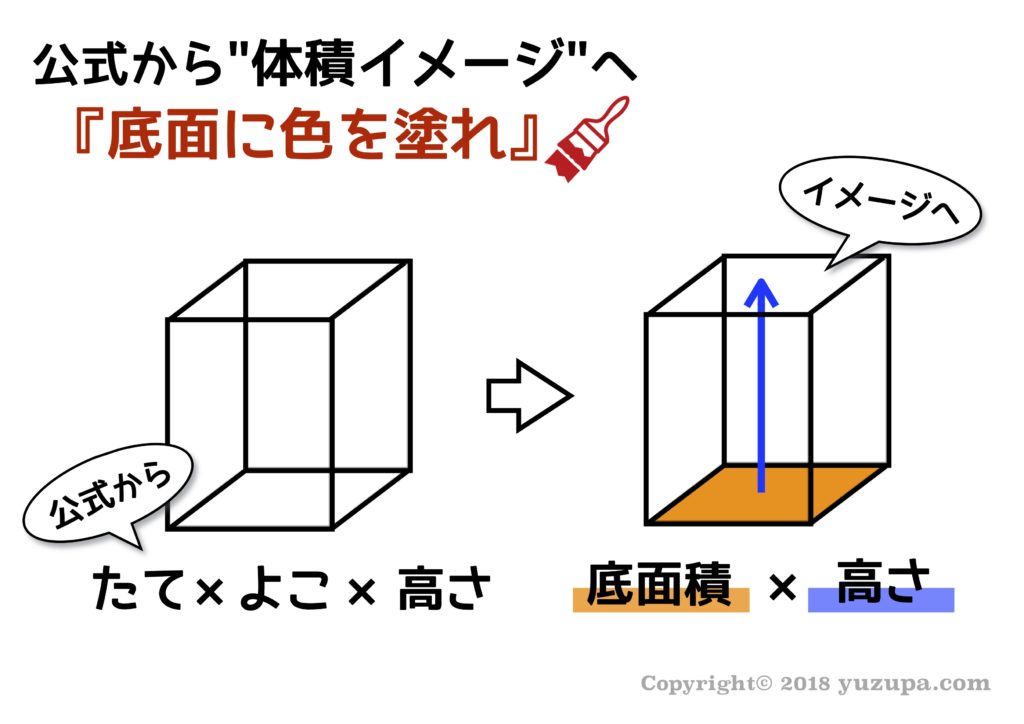
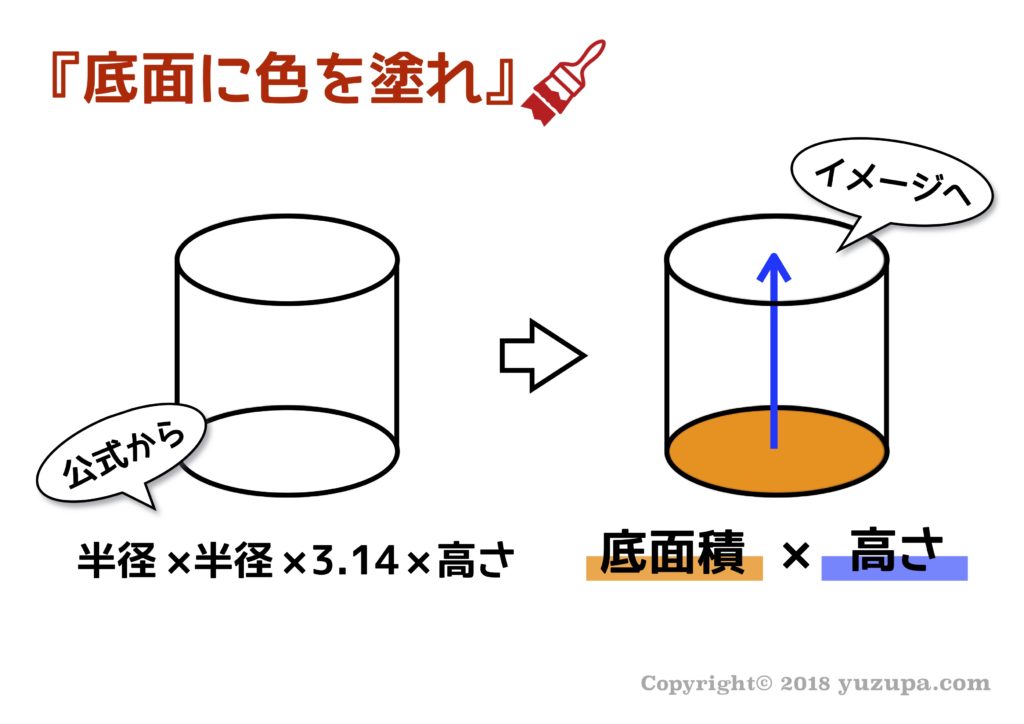
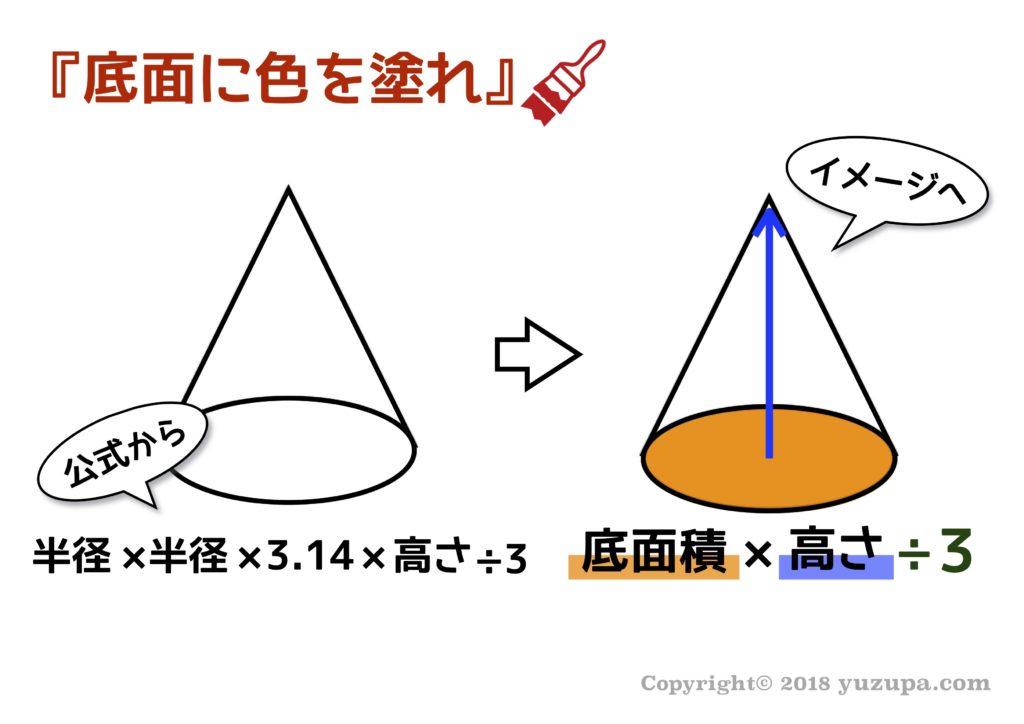
複合的な立体も理解が深まる
複合的な立体図形も底面に色を塗るという行為だけで、理解しやすくなる事があります。複合的な図形を見た瞬間に難しく考えすぎて、頭の中をグルグル回してしまう事もありますよね(・_・; 体積を極めてシンプル捉えると”底面×高さ”というイメージを元に図形を見てみましょう。
小数点の計算は最後に!
計算ミスは ”小数の計算” で起こる
ミスが最も起こりやすい計算はどんなものがあるでしょうか? ミスを誘発する計算の代表格の1つが 小数の掛け算 ですよねd(^_^o) 筆算を書いているうちに間違えてしまう。そうであれば出来るだけ小数の計算をしないようにしましょう。でも…どうやって減らす?
小数の計算を減らす “因数分解”
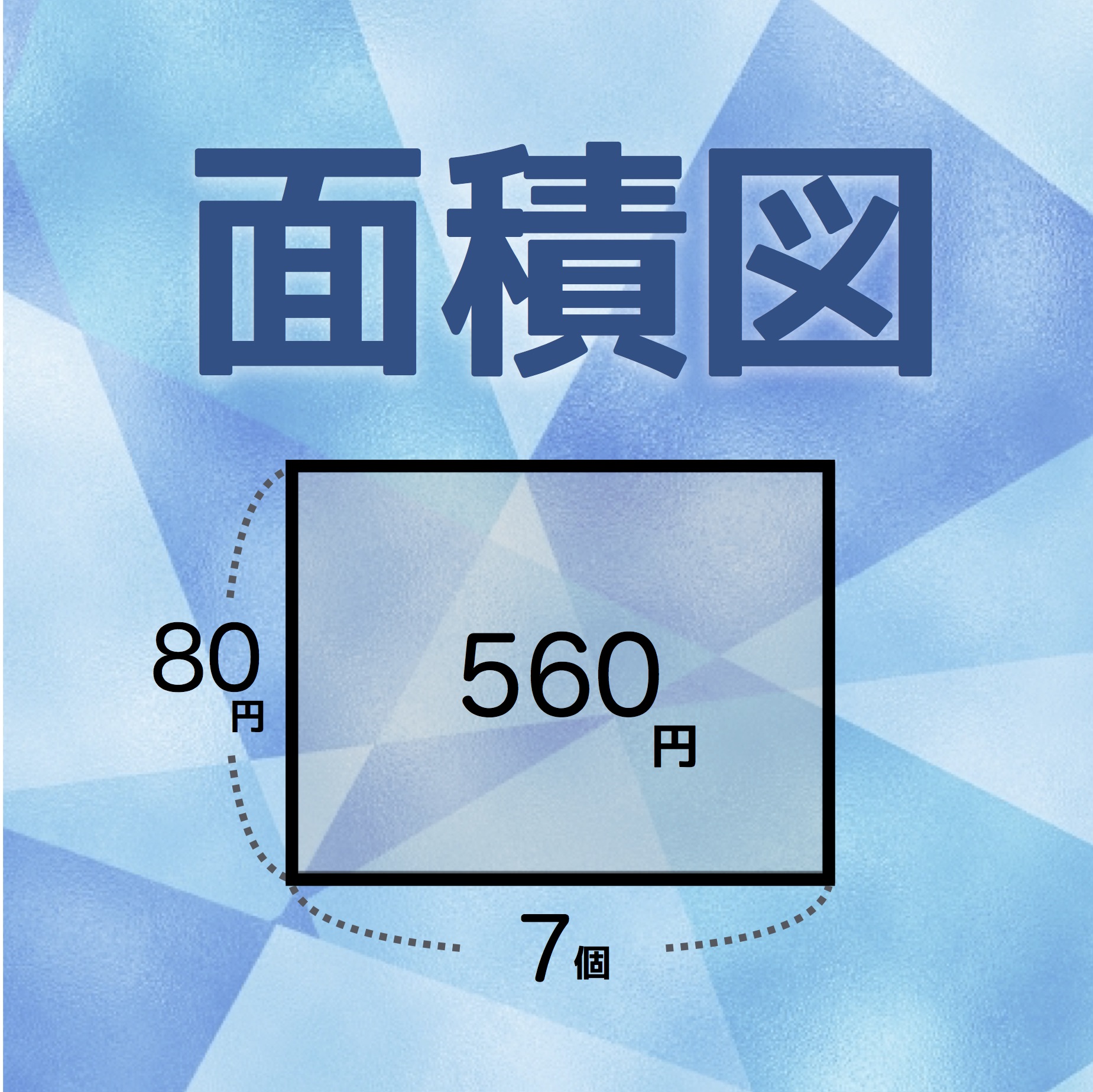
まずは出来るだけ因数分解を狙うというアプローチです。えっ…小学生に因数分解?と思われるかもしれませんが、使うのは因数分解でも最もシンプルで分かりやすい “共通因数でくくる” のみです!小学生でも比較的簡単に使いこなす事ができます。

特に円周率の計算で効果大!
さて、そんなに都合よく因数分解できる式なんか出てこないと感じるかもしれませんが ”柱体とすい体”の単元では、山ほど出てきますd(^_^o) そうです…円柱や円すいの体積や表面積を求める問題には円周率(3.14)が、これでもかというくらい出てくるんです。
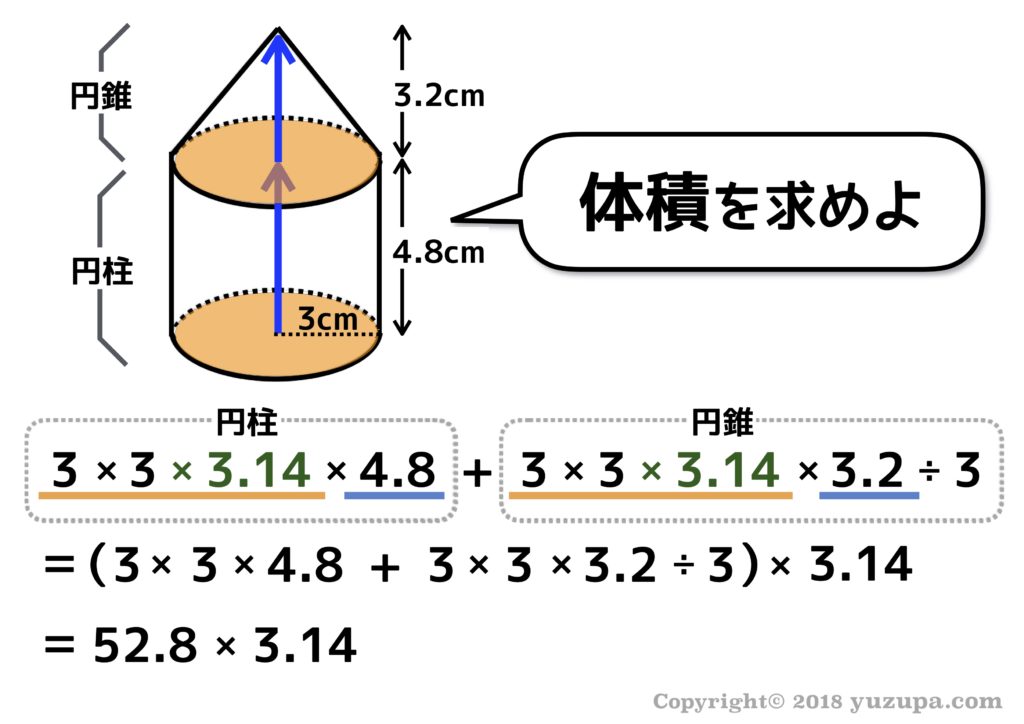
ですので、円周率(3.14)を含む計算が出てきたら、決して計算を急いではいけません!どんなに長くなっても、式を全て書き連ねてから因数分解ができないかを確認してから計算に取りかかるようにお子様と意識しましょう!
筆算を書く回数が減り、結果として時間短縮、そしてミスの軽減。大きな大きなメリットがありますd(^_^o)
円周率の計算は暗記?!
そもそも計算しないという選択肢
ミスを誘発する 小数の掛け算を減らす究極の方法があります。それは計算をせずに暗記するという方法です! 中学受験を経験していない私には目からウロコだったのですが…、円周率の掛け算を丸暗記してしまうということです。
中学受験対策の学習塾に通い始めてから、知ったのですが中学受験の世界では、円周率の掛け算を暗記してしまうという手法は常識のようです(@_@)
1ヶ月の特訓で暗記が可能
実際には 3.14×1、3.14×2、3.14×3…という具合に、3.14×30まで全て暗記です! いやぁ…無理だと思われるかもしれませんが、私の息子の場合、約1ヶ月の特訓で完璧にマスターしてしまいました…(^_^;) 子供の吸収力は本当にすごいですね。
やり方は簡単です。毎日テストをするだけ。時間を測りながら、テストをするだけです。マスターするまでに個人差は当然ありますが、塾のお友達も含めて、概ね1ヶ月間続ければ、成果が出るようです。テストに使うプリントを準備しましたので、ぜひご活用下さい!

時間の目安について… 私の息子の場合、約1分以内でこのプリントを解く事ができます。受験で使える力を目指すには最低1分から1分半でプリントを全て埋められるようにしましょう!
大幅なミス削減とスピードアップ!
因数分解に加え、”円周率の暗記”が出来れば、円柱や円すいの体積関連の計算ミスは、ほぼ無くなります。 それどころか…子供はとんでもない速さで計算をこなします! 私の仕事が休みの日は、息子といっしょに問題を解いたりするのですが、圧倒的に息子の計算の方が正確で速いです(・_・;
補足:すい体は…なぜ3分の1?
本記事では、体積は公式で捉えずに底面に色を塗ってそこに高さという厚みを持たせるイメージでの捉え方をご紹介しました。ところが円すいや三角すいなどは最後に3分の1を掛けますよね?
なぜ3分の1なのでしょうか? 厳密に計算をしようとすると積分の知識が必要になってきます。積分は高校数学で習う単元。小学生に積分を使って説明するのには、ちょっと無理がありますよね(^_^;)
すい体の体積は、底面積に高さを掛けた体積の3分の1になるという事実は、これまたイメージで説明する事が可能です。すんなり3分の1を受け入れるお子様であれば良いですが、疑問を持たれたお子様には以下のように説明しましょう。
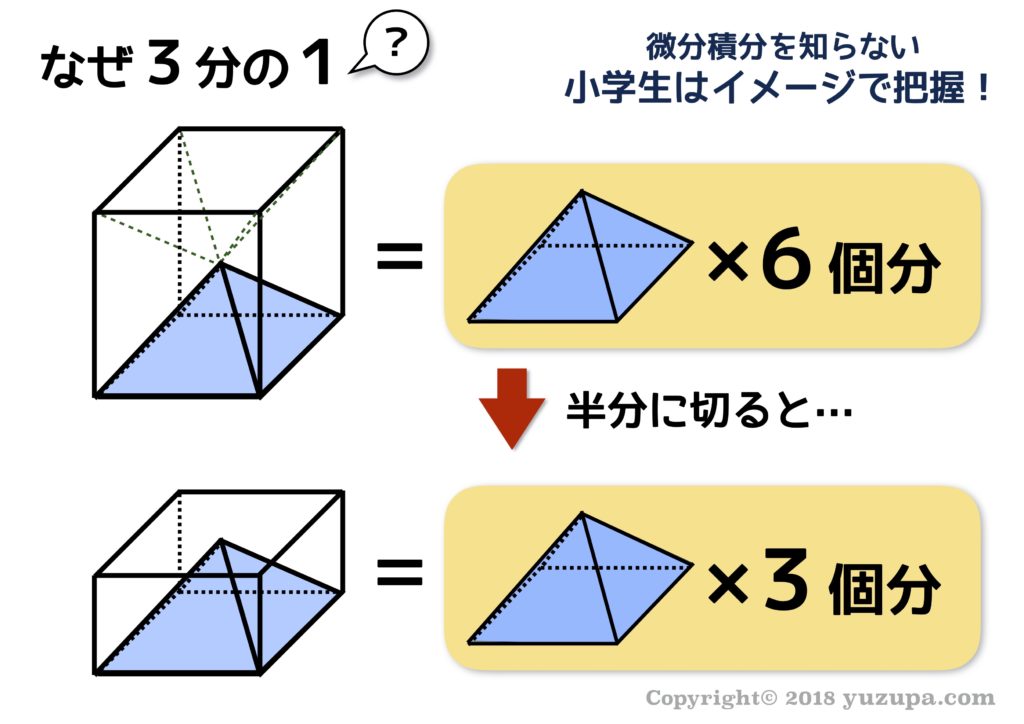
図に示したとおり、底面積に高さを掛けた直方体は四角すいが3個分であるというイメージで理解できるはずです。これは四角すいだけでなく全てのすい体で共通しているとイメージで捉えるのです。
まとめ
面積や体積の単元で、我が息子が最初につまづいた単元…それは、柱体とすい体でした。間違いを連発する理由は、息子の問題をとく様子をみれば一目瞭然でした。2つの理由を丁寧に排除できれば、ミスはほぼ無くなります!
理由1:体積を ”公式” で捉えている
対策1:体積はイメージで…底面に色!
理由2:円周率でミスを連発している
対策2:因数分解と円周率計算の暗記!
円周率の暗記をするためのプリントのダウンロードは以下からd(^_^o)











夏休み・・・受験生の夏休みが始まりました!
円周率の計算暗記!当方も驚愕でした!
暗記で3.14×9までは覚えていましたが、まさかの30までですか!!!!!!
この夏特訓に取り入れたいと思います。
ちなみに、九九の暗記で19×19までチャレンジしたいと思っていますが、
やはりプリントが有効でしょうか。
是非ご意見伺いたいです。
あべ様
当ブログへのご訪問、コメントの投稿ありがとうございます!
また、受験生にとっては勝負となる夏が始まってしまいましたね。
ご健闘をお祈りします!
さて、19×19の九九ですが、
プリントで反復をするのが有効かと思いますが、インターネット検索サイトで
「インド式 九九」で検索すると、
テクニック面での情報がワンサカあることを見つけました。
かなり合理的な方法が多いようなので
ぜひ検索してみることをオススメします。
私もインド式の九九について、もう少し勉強してみたいと思います。
今後とも当サイトに訪れていただけたら幸いです!
インド式九九拝見しました。
色々な手法がありそうですね。
早速プリントを作成したいと思います。
別件ながら、
かるびさんのサイト中の数字や画像説明の文字が大変印象に残りやすく。
フォントなど教えていただけたらありがたいです。
あべ様
コメントをいただきありがとうございます。
さて、当サイトで使わせていただいているフォントですが、
「フォントな」様の
「やさしさゴシック」というフォントを使用させていただいております。
以下のリンクからどうぞ!
フォントな
http://www.fontna.com
やさしさゴシック
http://www.fontna.com/blog/736/