中学受験：場合の数が苦手…３つの道具を使い10種の数え方をマスターせよ

場合の数とは ”全ての可能性を過不足なく数え上げること”

こんにちは。かるび勉強部屋 ゆずぱ です。

場合の数が苦手な小学生がとても多いです∑(ﾟДﾟ) 私の子供も例に漏れず、場合の数がとても嫌いでした(-_-;) でも… なぜ小学生は場合の数が苦手なのでしょうか？ 理由はおおむね２つです。
場合の数が苦手な二大理由
 ① 数えている途中でカウントミス
 ② そもそも数え方が分からない

前者の理由はとてもシンプルです。場合の数は、考えられる全ての可能性を数えること。同じものを重複して数えてしまったり、数えなくてはいけないものを数え忘れてしまったり…。

“３つの道具” の使いこなしでミスを最小限に！

後者は ”数え方”の考え方が分かっていないパターン。シンプルな問題はできるのに…。では３の倍数だと何通り？とか…では男女交互になると何通り？と条件が追加されると分からなくなる(-_-;)

“基本10種の数え方” を知ると解けるように！

それでは詳細にまいりましょう！

 

そもそも”場合の数”ってナニモノ？

道具を使い”全ての可能性を数える”こと

イキナリですが ”場合の数問題の全体像” をご覧ください。

場合の数の問題というのは、ズバリ”全ての可能性を数え上げなさい” という問題のこと。正しく問題を解くには以下の３つのステップを着実にこなすことが最も近道です。 

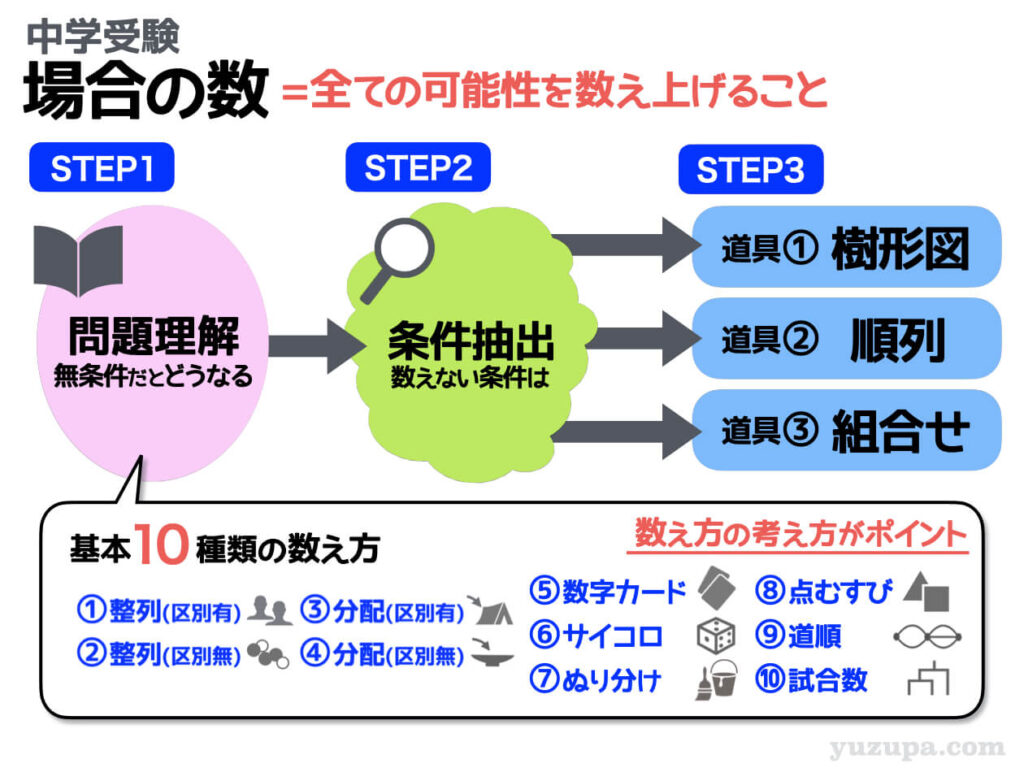
STEP1では、問題文から 何を数えたらよいのかをシッカリ把握 します。その際に役に立つのが”基本的な１０種類の数え方”です。まずは無条件の基本的なパターンを考えましょう。

STEP2では、問題文から どんな条件があるか読み取ります。偶数”だけ”数えなくてはいけなかったり、男子が両端にくる並び方”だけ”数えなくてはいけなかったり、入試の問題には必ず条件がついてきます(^_^;)

STEP3で いよいよ数え上げ をします。数えるには必ず道具を使います。樹形図はオールマイティですが、通り数の多い問題には使えません。樹形図をサボる道具として”順列”と”組合せ”があります。

この３つのSTEPで場合の数の問題を解いていくことになりますが、着実に正答を導き出すためのポイントは３つあります。３つのポイントを紹介します_φ(･_･

ポイント① ”過不足なく” 数え上げる

ポイントの１つ目は “過不足なく” 数えること。あたりまえですが、同じものを２回数えてしまったり、数えるべきものを数えなかったりしたらアウトです∑(ﾟДﾟ)

ポイント② 条件に合わないものは数えない

条件に合わないものは数えてはいけません。入試では必ずこの条件がついてきます(-_-;) 条件に合わないものは ”最初から数えない”か”数えるときに除外する”かを着実にこなすのがポイントです。

ポイント③ 道具３種類を使い分ける

場合の数ですが、可能性のあるものを全て数えれば良いので、気合を入れて樹形図を書けば全ての問題が解けてしまいます(^_^;) でも数が膨大すぎて樹形図で全てを攻略するのは不可能です。

そこで樹形図を書くのか？順列を使って計算するのか？組合せを使って計算するのか？はたまた複数の道具をいくつか組み合わせて答えを導き出すのか？入試を攻略するにはこれが最も重要です。

つまり… 問題を見てどの道具を使うのか的確に判断することが最大のポイント と言えます。

 

それでは、第二項で”３つの道具”について解説し、第三項で”基本１０種類の数え方” について詳しく説明しますd(^_^o)

 

場合の数で使える３つの道具

それでは場合の数で使える３つの道具について詳しくみていきましょうd(^_^o)

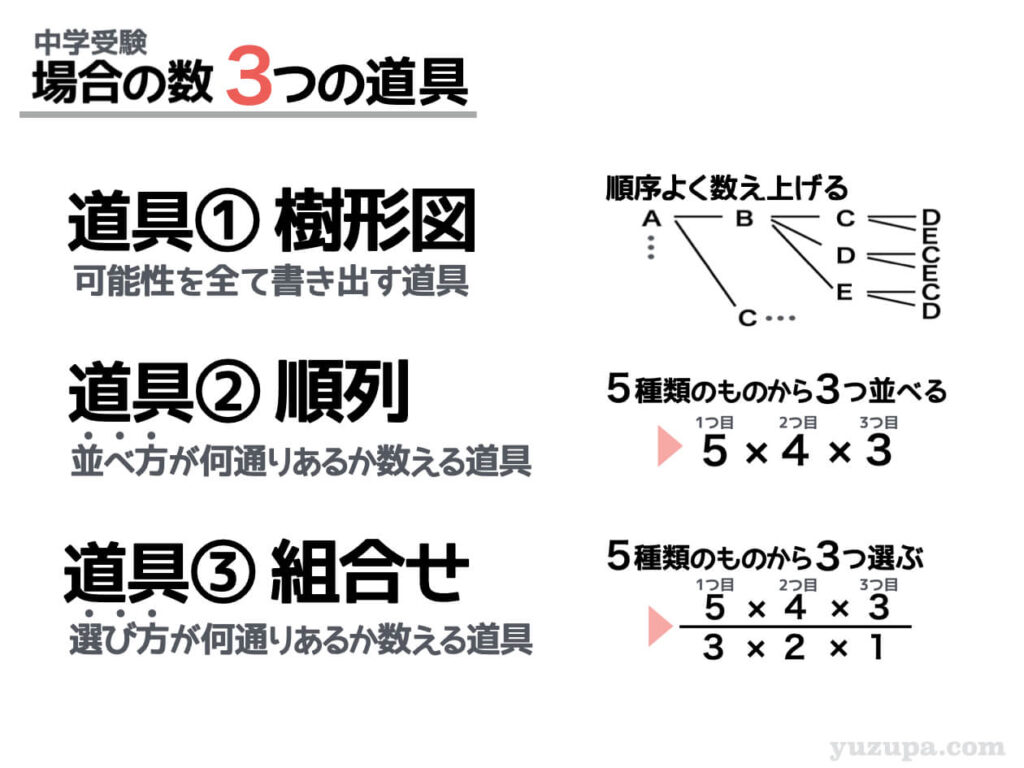
道具① 樹形図

場合の数を数える王道の道具が樹形図です。なんでも数えることができます。樹形図で求められるのは”過不足なく”数え上げること。そのために樹形図を書くときに”意識すべきこと”が３つあります。 

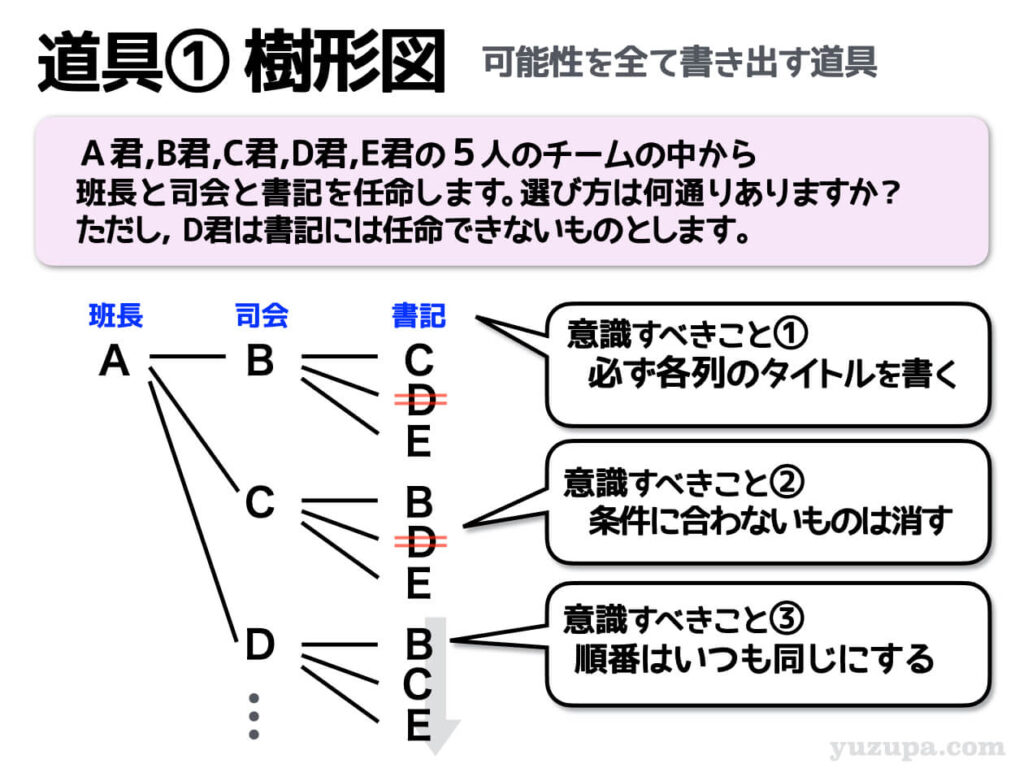
意識すべきこと① 各列のタイトルを書く

まず必ずやって欲しいのがコレです。樹形図の縦の列が何を意味するのか？そのタイトルを書くということです。

コレを書いておかないと、条件に合わないパターンを消したりするところでミスをしてしまいがちに…(-_-;)

意識すべきこと② 条件に合わないものは消す

樹形図を書くことに夢中になるとコレを忘れがちになってしまいますが、場合の数の問題では最も大切なことです。

シンプルにパターンを数える問題も出ますが ”条件” がついている問題がほとんど。正確に除外しなくてはいけません。

意識すべきこと③ 順番はいつも同じにする

カウント漏れを防ぐために樹形図は必ず順番は同じにすること。A,B,C,D,Eの順番…、1,2,3,4,5…の順番です。

あたりまえですが、順番どおりでないと頭が混乱して正しくカウントできませんよね(^_^;)

 

樹形図を書くコツは
このたった３つの意識です

 

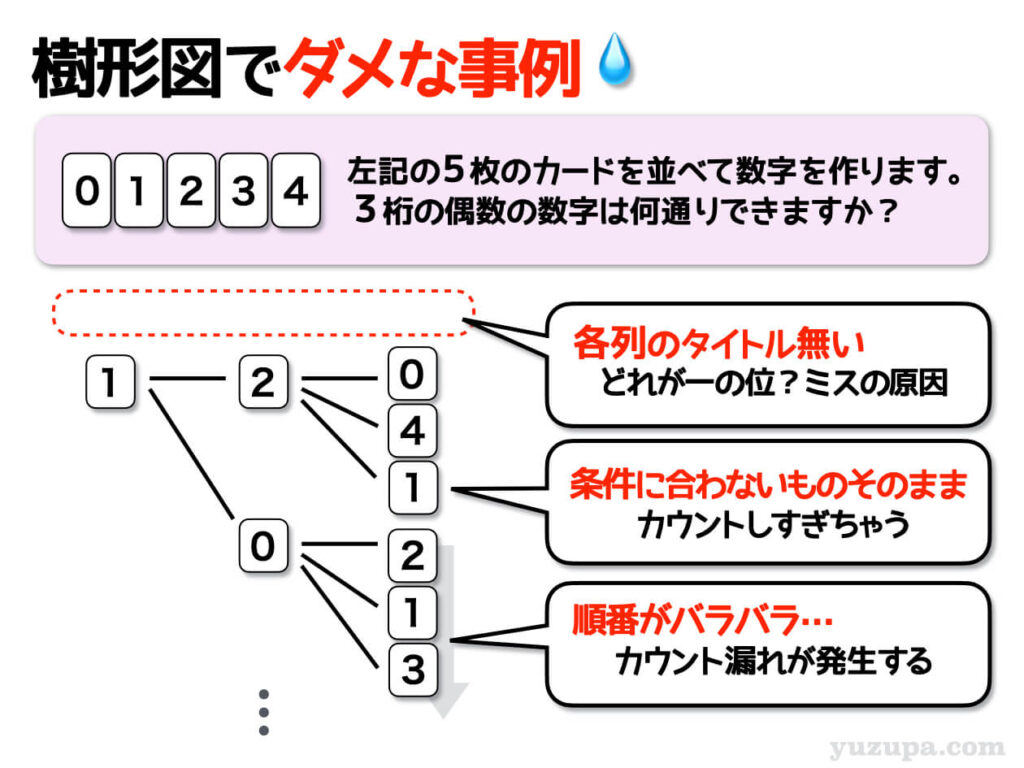
試しにダメな樹形図を見てみましょう(^_^;) これだとカウントミスがたくさん発生してしまいますね…。

 

道具② 順列

道具の２つ目は順列です。場合の数が膨大になってしまう場合に巨大な樹形図を書かなくても計算で出すことができます。

樹形図を描くのをサボって
計算で求める方法です

具体的にみてみましょう…。

 

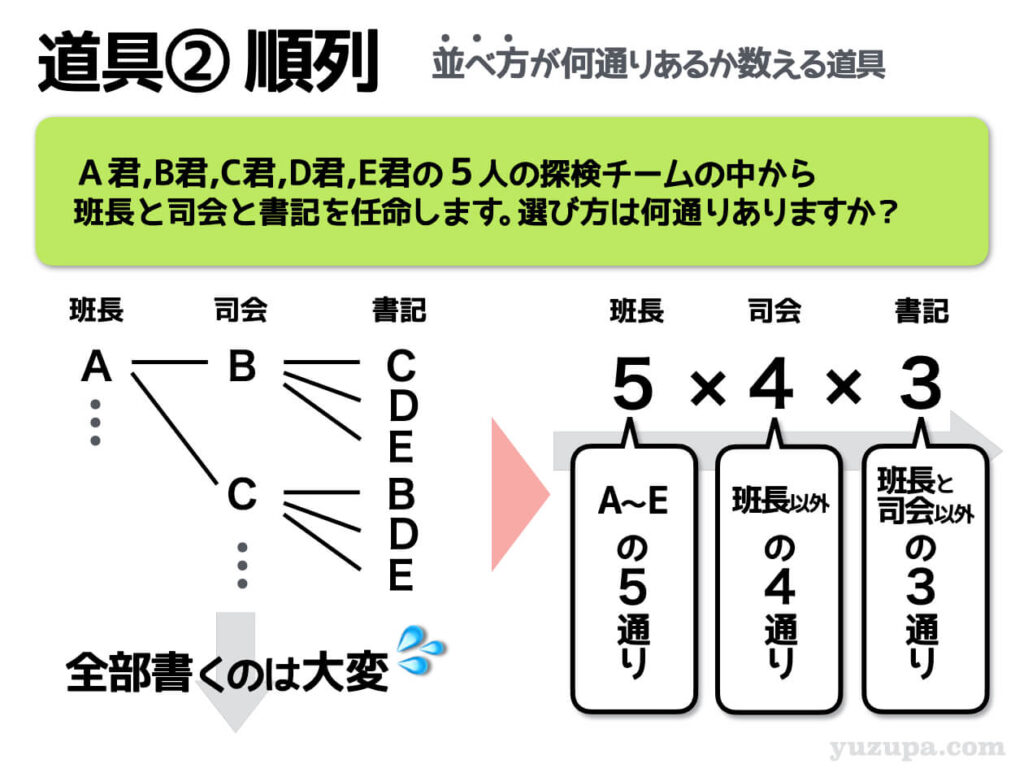
上記のように班長の列に何通りの可能性があるか、班長の横につながる司会が何通りの可能性があるか、司会の横につながる書記はなん通りの可能性があるか…

それぞれの数をかけると
樹形図の枝が何本になるか計算できちゃいます

複雑な条件が無いシンプルな樹形図であればこの順列の計算を使ってもとめることで、大幅に樹形図を書くという作業時間の短縮になります。順列が使えるか必ず吟味しましょうd(^_^o)

 

他にも順列の計算のパターンを見てみましょう。

 360通りもの枝をもつ樹形図を描くのは大変ですが、順列の計算を使うとシンプルに計算できますね。

 

道具③ 組合せ

最後は組合せです。組合せは順列に似ているのですが、条件がちょっと異なります。具体例を先に見てみましょう。 

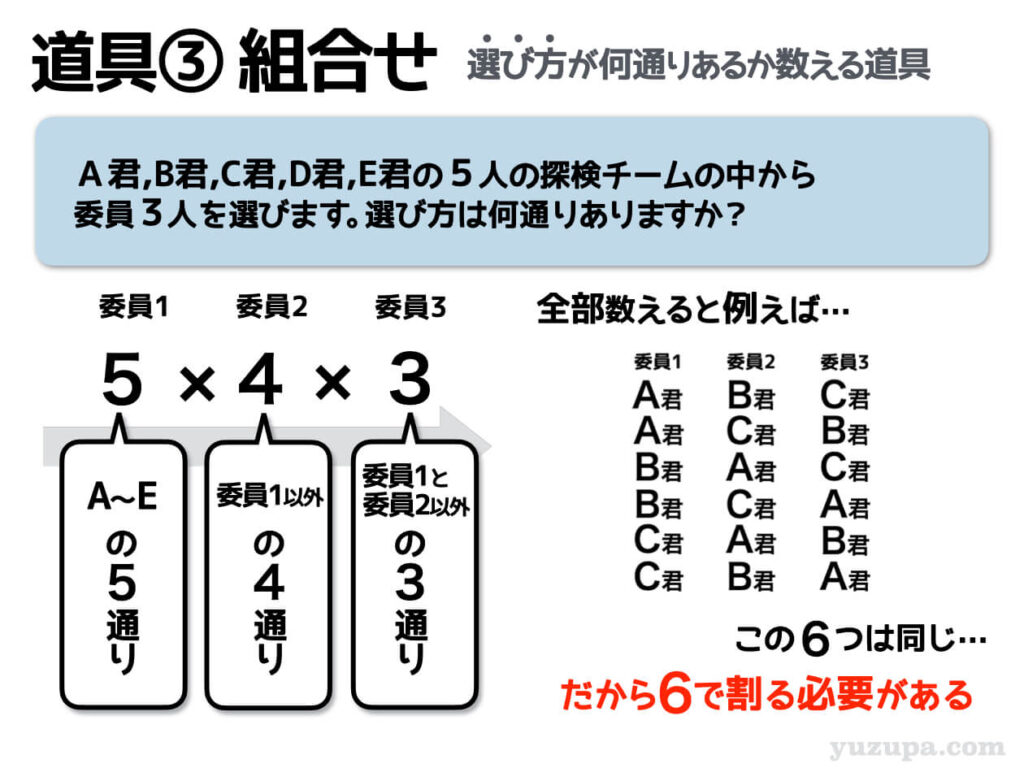
さきほどまでの問題では、班長１人、司会１人、書記１人の３人を選ぶという問題でしたが、この問題は委員３人を選ぶというもの。これだと今までの計算ではダメな点がでてきます。

同じものがカウントされているんです∑(ﾟДﾟ)

たとえば…

　委員１＝A君、委員２＝B君、委員３＝C君
　委員１＝A君、委員２＝C君、委員３＝B君

この２つ… 同じ組合せ ですよね？

同じ組合せをカウントしてしまったのであれば、同じ組合せが発生する数で割ってあげる必要 があります。３つを選ぶ問題であれば６で割る必要があります。

同様に考えてみるとこうなります _φ(･_･

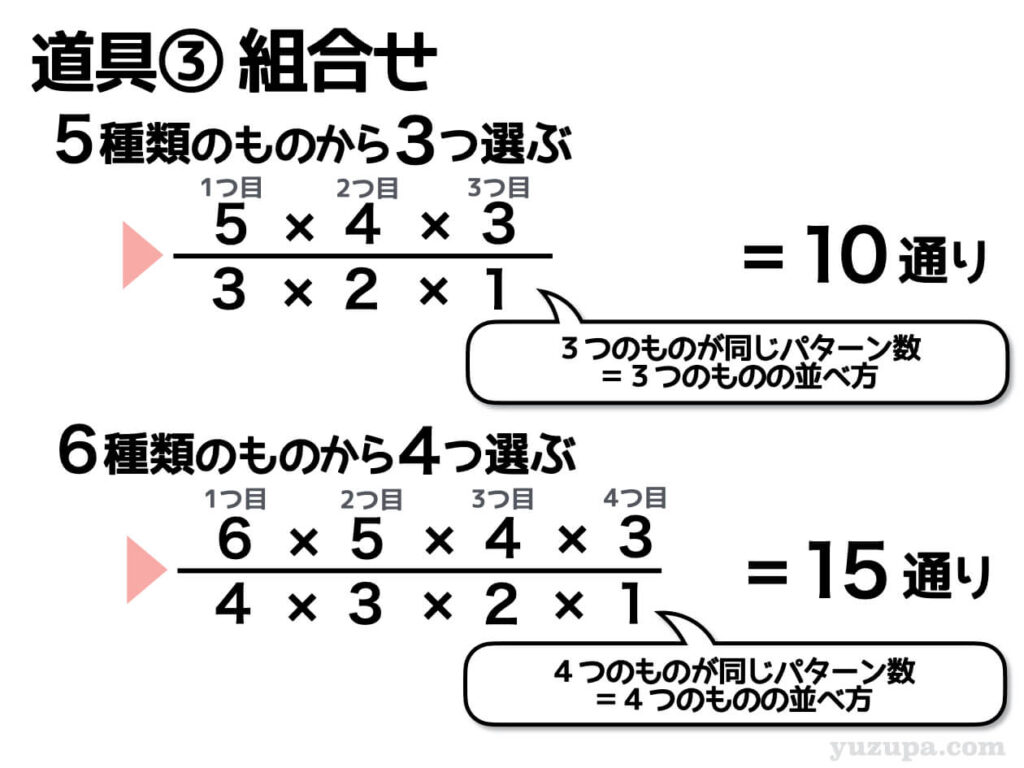
組合せは順列と似ていますが、同じ組合せをカウントしてしまっている部分を後から割ってあげるということ。

３つのものが同じになるパターンの数は３x２x１＝６パターンです。同様に４つのものが同じ組合せになるパターンは４x３x２x１＝24パターンです。それぞれ割ってあげましょうd(^_^o)

 

場合の数の問題は… 問題を読み解くと結局はこの３つの道具を使って計算するところに帰着 しますd(^_^o) まずはこの３つの道具を使いこなせるようになることが超重要です。

　道具① 樹形図 ＝ 可能性を全て書き出す道具
　道具② 順列 ＝ 並べ方を計算する道具
　道具③ 組合せ ＝ 選び方を計算する道具

さて便利な道具が使いこなせても、その道具を使うところに至るまでの”数え方”を知らなくてはいけません。次の章では、基本的な１０種類の場合の数の数え方をご紹介しますd(^_^o)

 

場合の数の基本10種類の数え方

場合の数は”全ての可能性を数えること”だと冒頭でお伝えしましたが、その 数え方は残念ながらシンプルではなく…ちょっとした工夫をこらした考え方をする必要 があります (-_-;)

まずは基本的な考え方１０種類をマスターしましょう。この１０種類がマスターできれば、はじめて見る問題にもしっかりと対応できるようになりますd(^_^o) まずはこの１０種類です！

※ 本記事では全体像の説明で…具体的な解法については 近日中に公開予定 ですd(^_^o)

 

① 整列(区別有り)

まずは ”整列” です。整列とは順番に並べること。何かを並べる方法は何通りあるか数える問題です。人間を並べる場合、AさんもBさんもCさんも同じ人間でも違う人として扱いますd(^_^o) 

条件の無い問題では、Aさん,Bさん,Cさん,Dさん,Eさんを一列に並べるというシンプルなもの。分かりますか？もちろん樹形図を使っても数えられますが ”道具② 順列”が使えますd(^_^o)

また、右側にあるような条件がつけられることがありますが、ほとんどの問題は ”道具② 順列” を使うと手早くで数えることができます。また補集合を使うと簡単になる問題もあります_φ(･_･

 

② 整列(区別無し)

つぎも ”整列” ですが…。今度は並べる対象が人ではなく、どれも同じように見えるモノです。例えば碁石。碁石はどの碁石も区別ができませんよね。この場合、場合の数は変わってきますd(^_^o) 

区別のないものを整列する場合にはちょっと考え方を変えます。５つの席から黒を置く場所３ヶ所を選ぶという考え方をします。もちろん５つの席から白を置く場所２ヶ所を選んでもOKです。

ズバリ ”道具③ 組合せ”を使うと樹形図を書かずに数えることができます。そして条件がついた場合も同様に ”道具③ 組合せ” を使いこなすとうまく解ける場合が多いですd(^_^o)

 

③ 分配(区別有り)

次は ”分配” です。分配とは何かをいくつかに分ける方法が何通りあるか数える問題です。Aさんは部屋①か部屋②のどちらかの可能性があります。同様にBさんもCさんも…同様ですね。 

Ａさんが部屋①か部屋②の２通り、Bさんも、Cさんも… と考えると部屋①と部屋②を５人分並べるいう方法が何通りあるか数えれば出せそうです。つまり ”道具② 順列” が良さそうですd(^_^o)

上記の数え方だと…例えば誰もいない部屋があるパターンも数えているので、条件によっては合わない場合を除いてあげなければいけません。また部屋に名前がついていない場合もダブルカウントを考慮してあげる必要がありますねd(^_^o)

 

④ 分配(区別無し) 

前項と同様に何かを分配する問題。今度は同じに見えてしまうモノの分配。リンゴやミカンなどもそうですね。この問題は条件が複雑なため場合により道具を使い分ける必要が ∑(ﾟДﾟ) 

お皿の区別がつく場合は、”仕切り法” という手法を使うと便利に解けたりします。例えばリンゴ３個を横一列に並べて、どこか１ヶ所に仕切りを置く方法は何通りあるか数えるという考え方です。

一方、お皿の区別がない場合には、”道具① 樹形図” で数え上げるのが最良の数え方だったりします(^_^;) このパターンの問題は、分ける先のお皿に区別があるかないかも重要なポイントです_φ(･_･

 

⑤ 数字カード 

次は定番中の定番。数字カードの問題です。数字カードを使って何桁かの数字を作り、その方法が何通りあるか数えなさいという問題。今回は基本的なパターンが３つあります d(^_^o) 

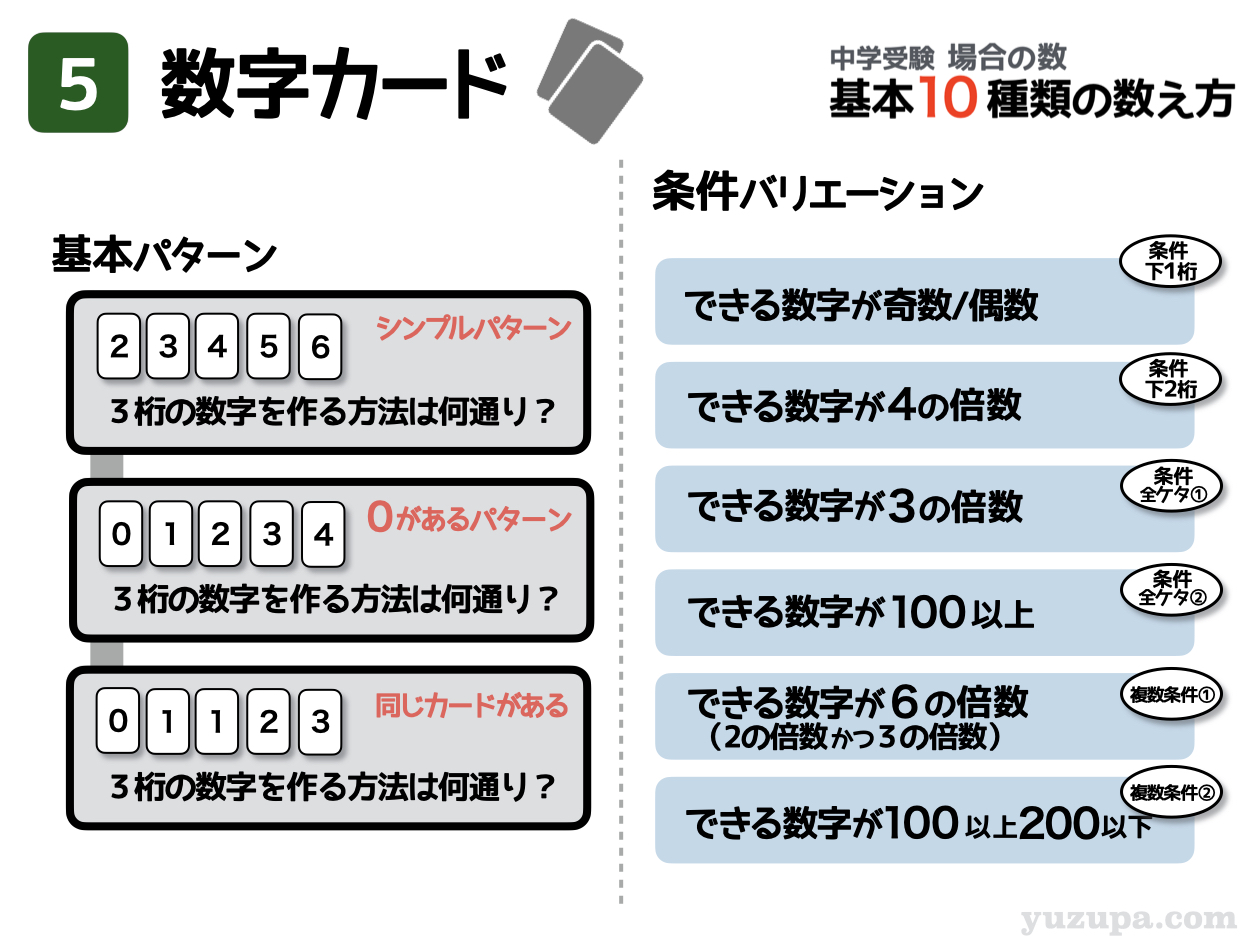
基本的に ”道具② 順列” を使って解くのが最も早く正確な手法です。複雑な条件がある場合には”道具① 樹形図”を使うこともあります。そして中学入試では必ず面倒臭い ”条件” がつきます(-_-;)

例えば…”０(ゼロ)”のカードがある場合、それは最上位の位には使えませんね。他にも…できる数字が偶数という条件があれば、一の位には奇数のカードは使えません。工夫が必要です (>_<)

 

⑥ サイコロ 

次は定番の ”サイコロ” です。サイコロをいくつか振って、その目の出かたが何通りあるかというもの。これはよく見る最もメジャーなテーマのひとつですね d(^_^o) 

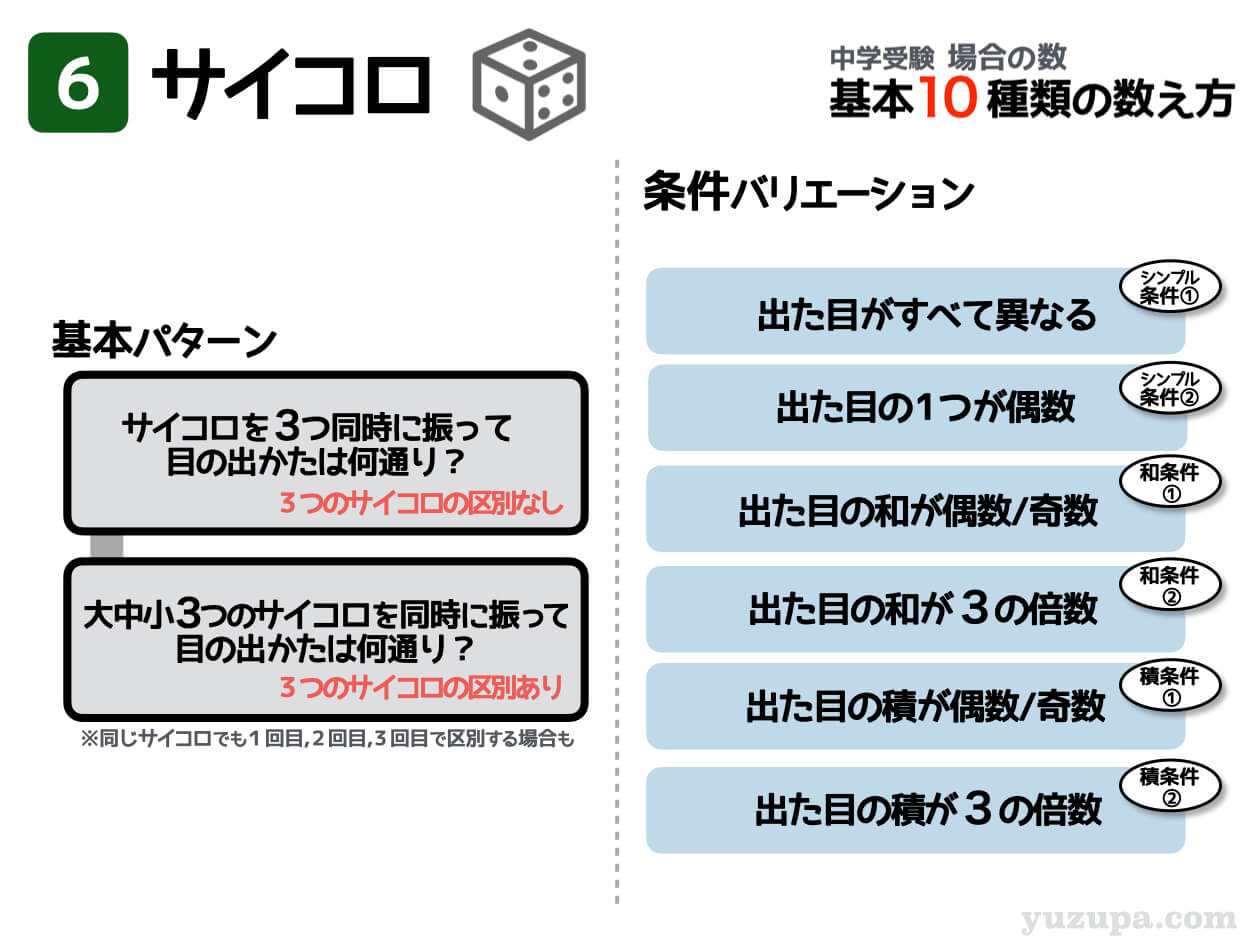
サイコロの問題は条件によって”道具① 樹形図”を使うことも ”道具② 順列”を使うことも、”道具③ 組合せ” を使うこともあり、意外にも注意な必要な問題パターンです (>_<)

もうひとつ気を付けなければならないのはサイコロに区別があるかないかです。大中小とサイコロの大きさが、違ったり１回目、２回目、３回目と１回ごとに確認する場合は区別ありと判断します。

 

⑦ ぬり分け 

８つ目は ”ぬり分け” です。問題用紙にいくつかの領域がある図形が描かれており、何色かの絵の具でその図形をぬる方法は何通りあるか数えるという類の問題ですd(^_^o) 

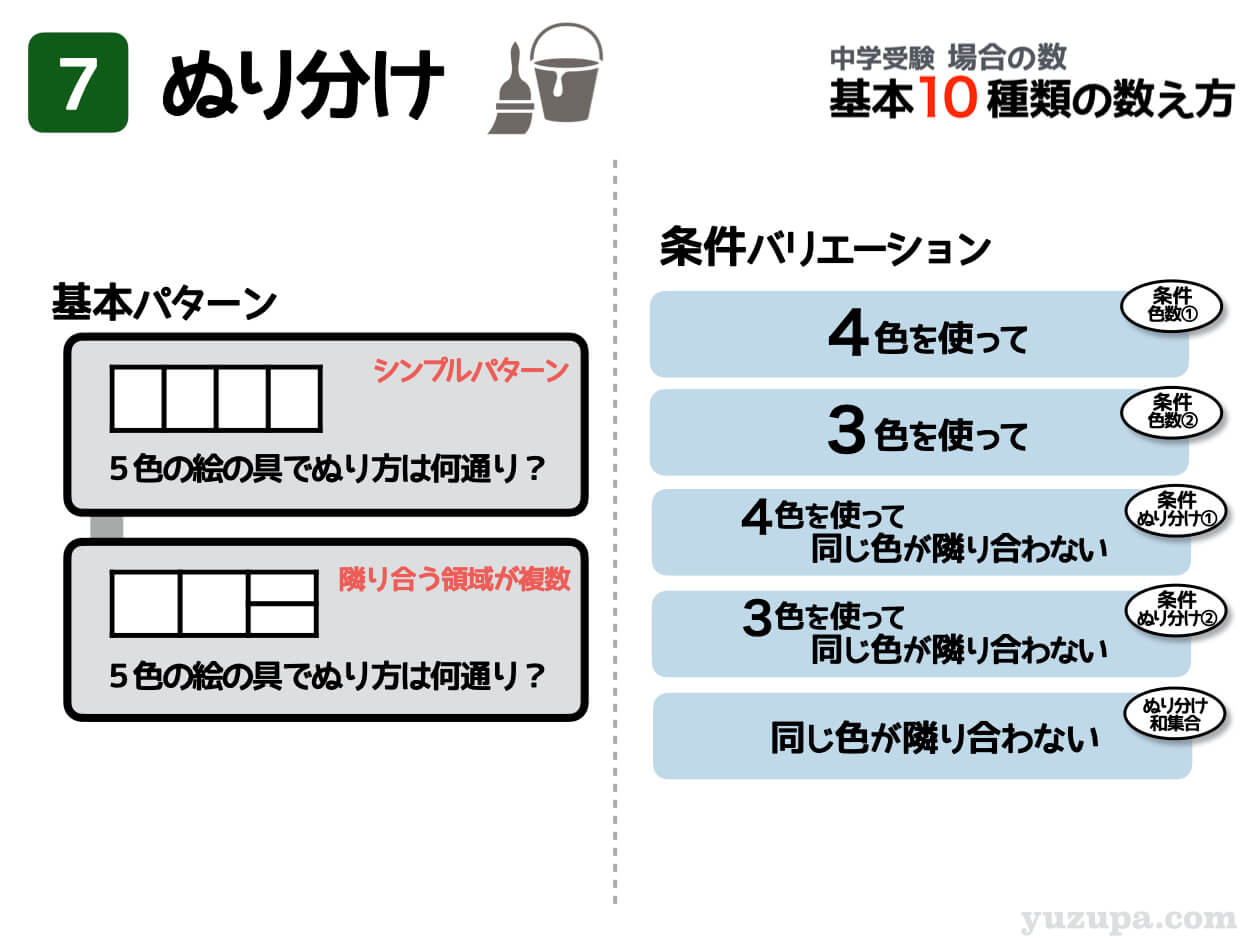
とても難しく感じる問題ですが… 実は考え方を知ってしまえば、意外とシンプルです。基本的なアプローチは、各領域に名前をつけて ”道具② 順列” 使ってぬり方を数え上げる方法です。

この問題では、同じ色が隣り合ってはいけないという条件がつけ加えられることがとても多いです (^_^;) というかほとんどがその問題です。同じ色が隣り合うぬり方を排除するのがコツです。

 

⑧ 点を結ぶ図形 

次は若干マイナーな出題形式ですが着実におさえる必要がある”点むすび” です。いくつかの点が描かれていて、その中からいくつかの点を選び図形が作れる方法は何通りあるかというもの。 

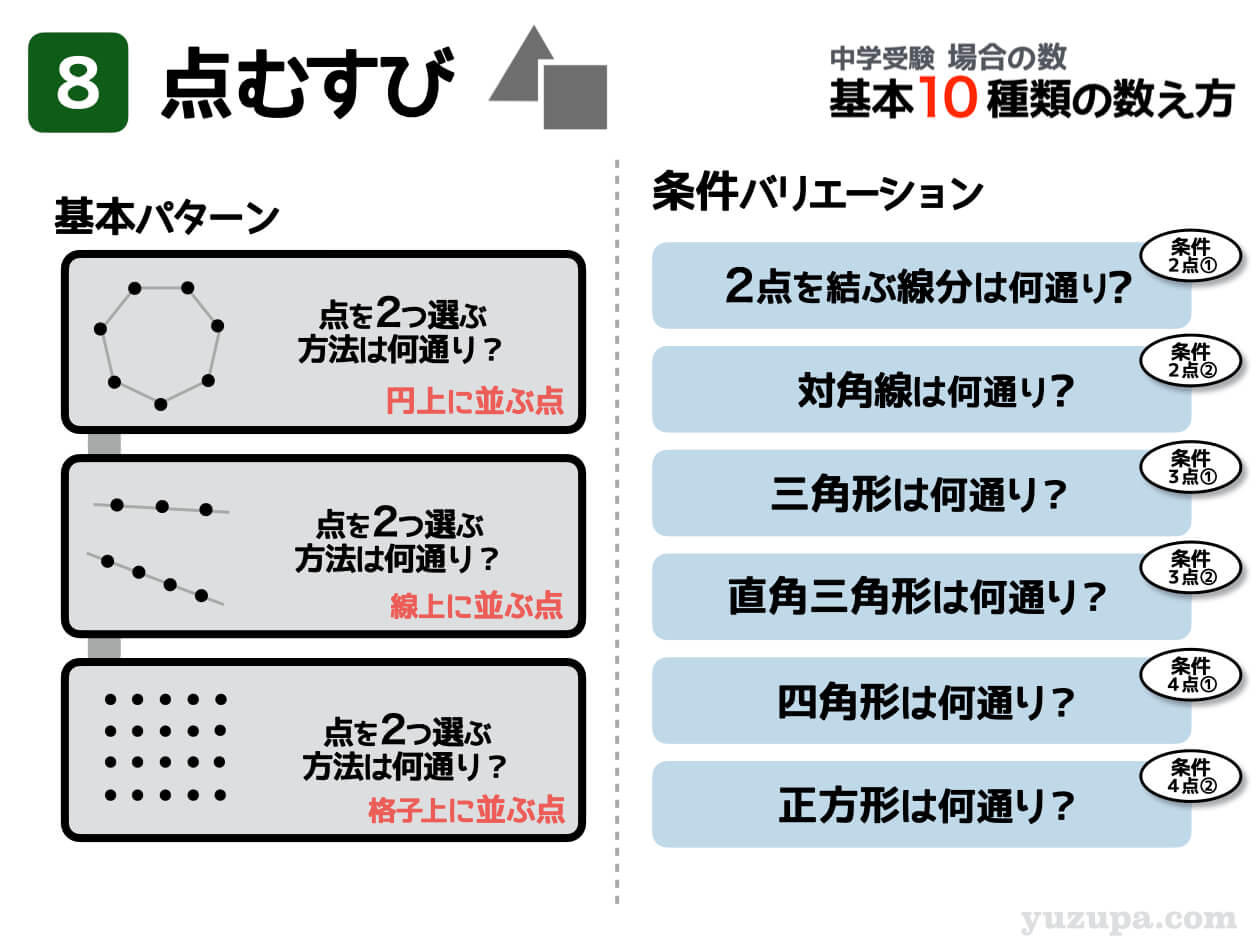
この手の問題は基本的には点の選び方を数えるので “道具③ 組合せ”を使うことを最初に考えます。例えば８つの点を使って三角形を作る方法は、８つの点の中から３つを選ぶ方法と同じです。

しかしこの問題で気を付けるべきことは、図形にならないパターンを数えてはいけないということ。例えば３つの点を選んだとしてもそれが一直線にならんでいたら三角形になりませんね (･_･;

 

⑨ 道順 

次は “道順” です。通り道が明確になっている地図が描かれており、ある地点からある地点までの道順は何通りあるか数えるというもの。これも中学受験では定番のパターンですねd(^_^o) 

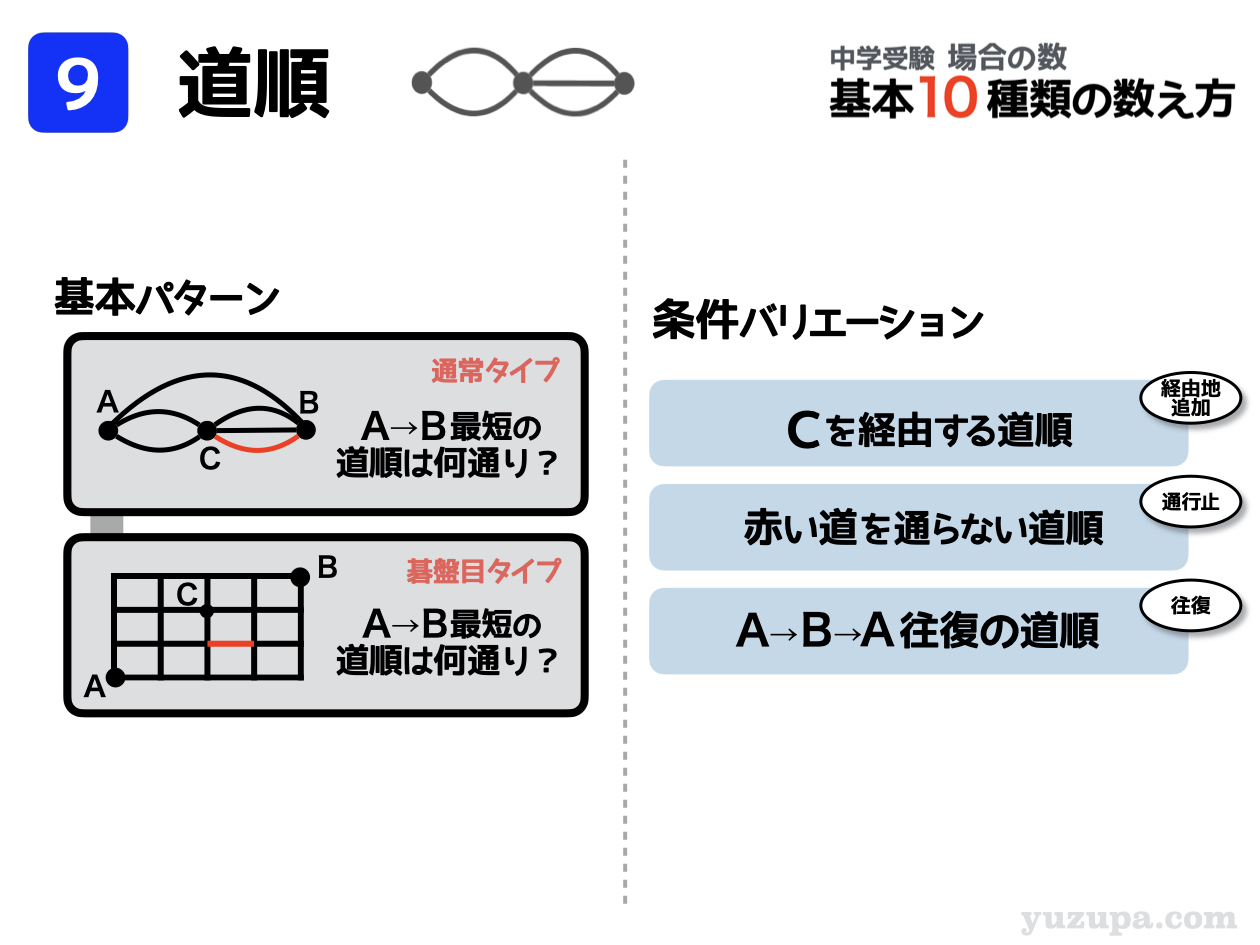
基本は、使える道を並べていくと考え ”道具② 順列” を使って解くことができます。そして地図の形は、地点どうしを道路で結んだ ”通常タイプ” と 格子状の道である”碁盤目タイプ”の２種。

条件もパターン化しています。出発地と目的地の間にどこか経由する地点があったり、どこかに通行止めの道があったり、片道ではなく往復の場合の数を求める問題が定番ですねd(^_^o)

 

⑩ 試合数 

いよいよ最後です。最後は ”試合数” です。何チームかで優勝を競う試合をする時に、その試合数は何通りあるかを問うという問題となります。この問題も定番中の定番です_φ(･_･ 

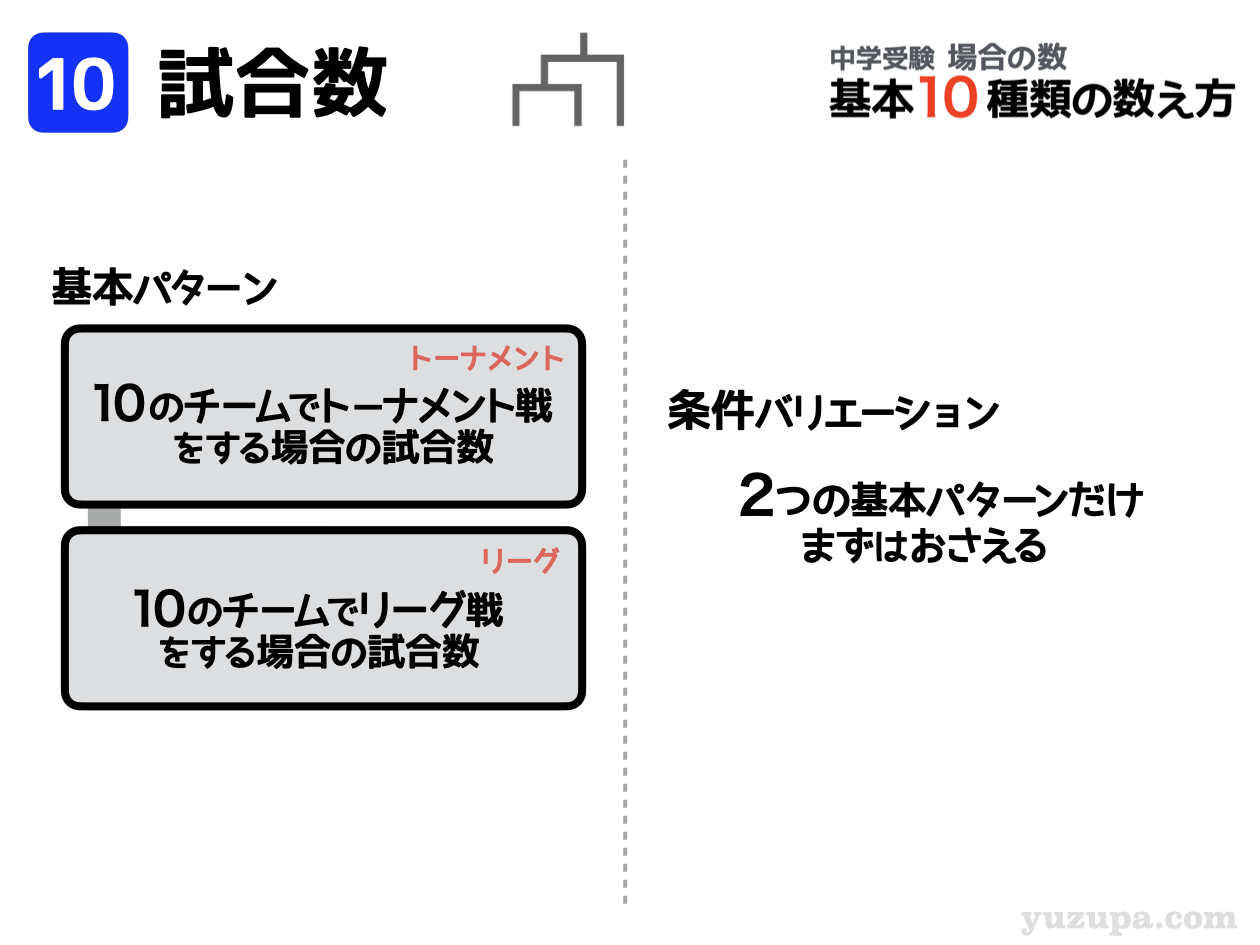
この問題は考え方はちょっと特殊なのですが、まずは基本的な２つの解法をおさえておけばよいでしょう。それは “トーナメント戦” と “リーグ戦” です。条件が加わる問題はほぼ出ませんd(^_^o)

トーナメント戦は変則的なトーナメントも考え出すと３つの道具では攻略できません。そこで “試合数＝敗退チーム”という大原則を使って解きます。またリーグ戦は、全チームから試合をする２チームを選ぶ選び方が試合数そのものになりますね d(^_^o)

 

まとめ

今回は小学生の中でも苦手とする”場合の数”について、全体像編として、場合の数を出すのに ”使える３つの道具” と “基本的な１０種の数え方” をまとめてみました _φ(･_･

場合の数が苦手と感じる２つの理由
・数えている途中でカウントミスをする
・そもそも数え方が分からない

基本的な10種の数え方 をマスターし、数える３つの道具 を使って着実なカウントをすれば、もう怖くはありません d(^_^o)

そして無限のパターンがあるのではと思える数え方も、条件の組合せであると考えると体系的に理解することができます。 

※また近日中に基本的な１０種類の数え方の具体的な問題例と解放例も公開すべく準備を進めております！