中学受験:図形の面積問題は “7つ道具” で攻略
図形問題が苦手?面積を求める時に “使える道具” を知る事から始めよう!

こんにちは。かるび勉強部屋 ゆずぱ です。
算数の偏差値がなかなか上がらない子供は “図形問題が苦手!” ということがよくあるようです(>_<) 計算も文章題もそこそこ出来るのに図形問題がとにかくできない…(-_-;)
なぜ…図形問題が苦手なのでしょうか?
図形問題は… たくさんの道具を使って試行錯誤して答えを導き出しますよね。1つ1つの道具は理解していても、自分が持っている道具の全体像を知らなかったらどうでしょうか?
図形が苦手な子は…
使える道具の全体像を知らない
と考えられます。そこで “7つ道具” シリーズの第三弾… 図形の面積を求める問題に使える道具をまとめてみましたd(^_^o)
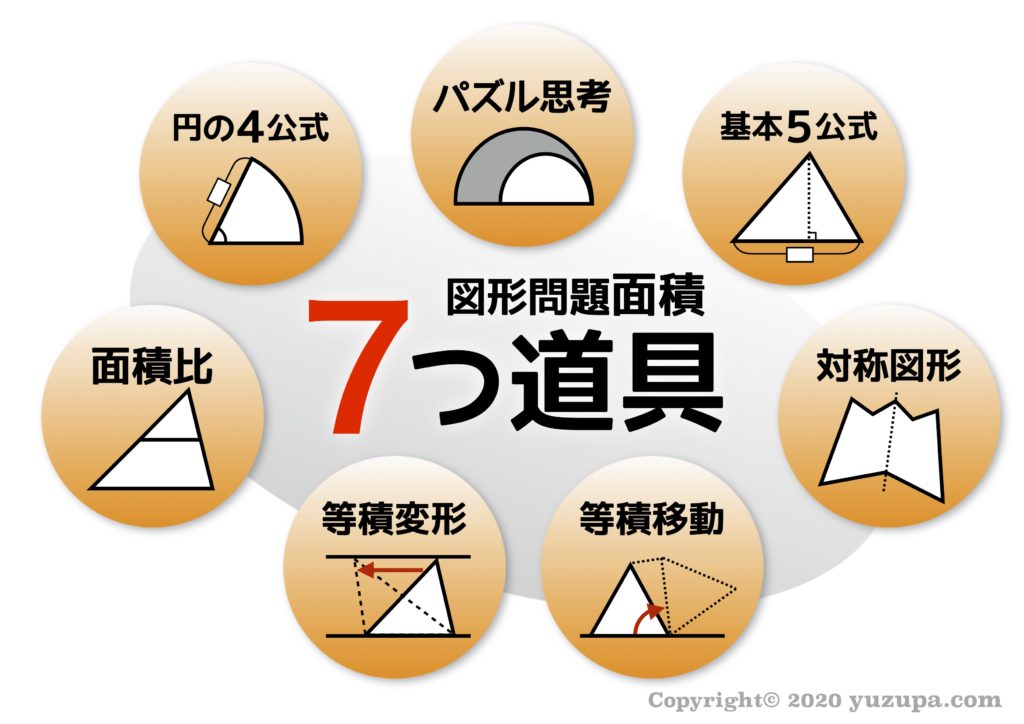
目次
道具① 面積の基本5公式
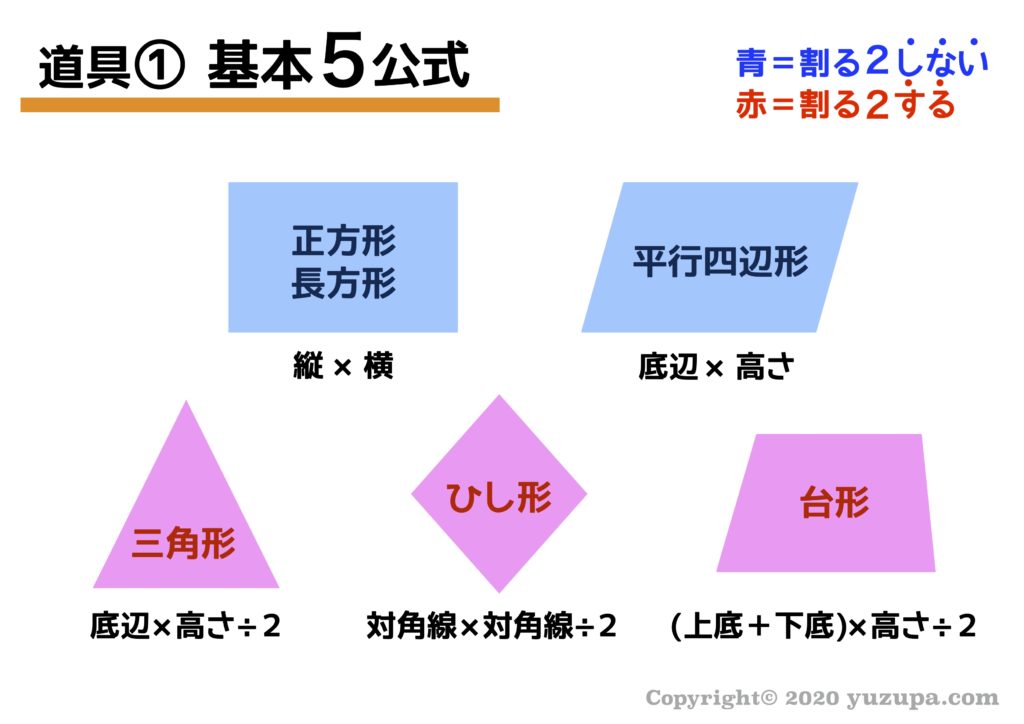
道具のひとつ目は、やっぱり公式でしょうd(^_^o) 多くの公式がありますが “基本5公式” と名付けて整理しています。面積を学習したての小学生が混乱するのが “割る2”をするのかしないのかという点…
公式ができあがる過程を知っていれば分かる!というのが一般的なセオリーですが、それは公式を忘れてしまった場合に思い出すシーンですね。時間が勝負の試験では瞬発力が必要 です(-_-;)
以下のようにイメージで体得してしまうのが良いですd(^_^o)
道具② 円の基本4公式
次は円の基本4公式です。ちょっと面積と関係のない円周の長さも含まれてしまっていますが、円の関連でおさえる公式はこの4つとなります。扇形(おうぎがた)については混乱する子供が多い ようですが…
以下のように “元になる円” を意識するとシンプル ですねd(^_^o)

円に関する問題が苦手な子供…大きく2つの理由があるようです。1つ目は3.14の計算ミス。円周率3.14を使う小数の計算でミスをしてしまうパターン。2つ目は扇形の公式をよく理解していない パターンです。
公式を理解するための考え方を…ちょっと補足します。
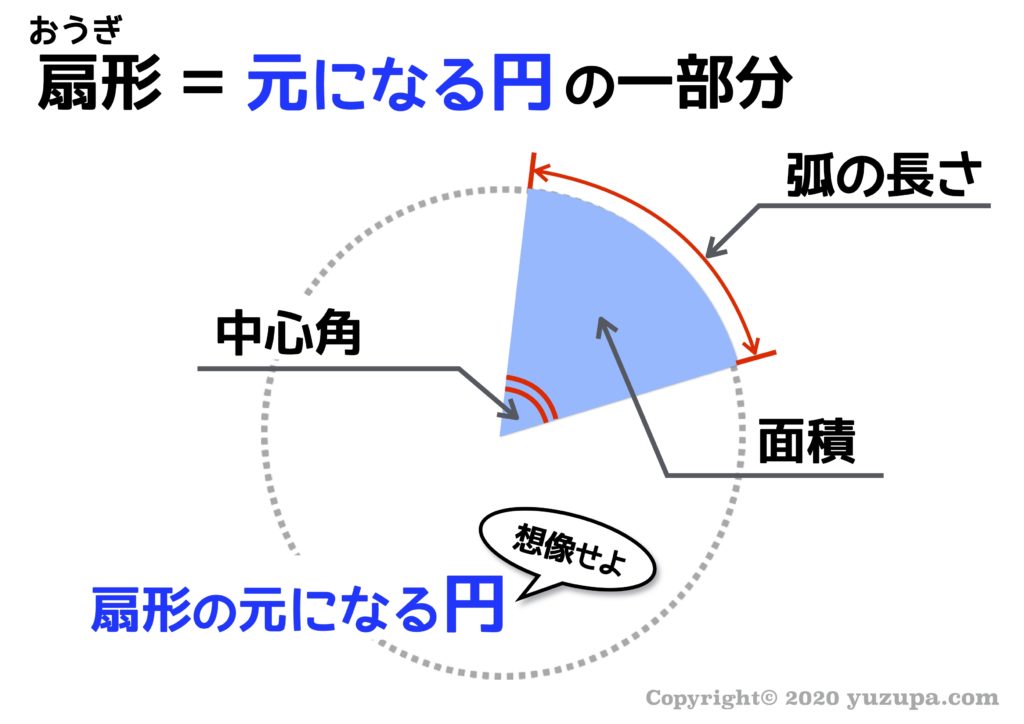
扇形が苦手なお子様へ
扇形は円の一部。これだけですd(^_^o) 扇形が苦手な子供はこのシンプルな点をイメージできていないようなんです。扇形を見たらすぐ”元になる円”を想像する よう訓練をすれば大丈夫ですd(^_^o)
道具③ パズル思考
3つめの道具は “パズル思考” です。この視点を持っていないと、中学受験の入試問題には太刀打ちすることができません。最も重要な道具でありますが、使いこなすにはイチバン練習が必要な道具 です(・_・;
パズル思考の基本は 面積の足し算と引き算 です。
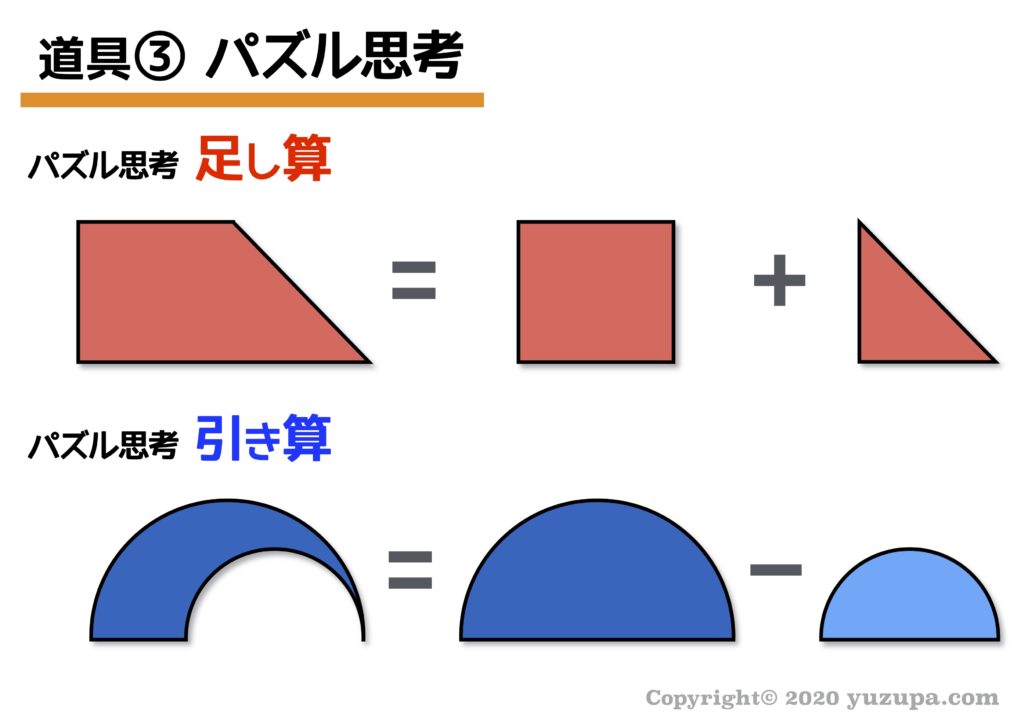
とてもシンプルなんだけど…どうしてもひらめかない。魔法のような手段はありません。こればかりは練習して数をこなすしか無いのです。ただ1つだけポイントがあります。
面積を求める図形をみたらまず…
足し算できる?引き算できる?と考えるクセを持つこと!
具体例をいくつか紹介しましょう。
パズル思考例 その1
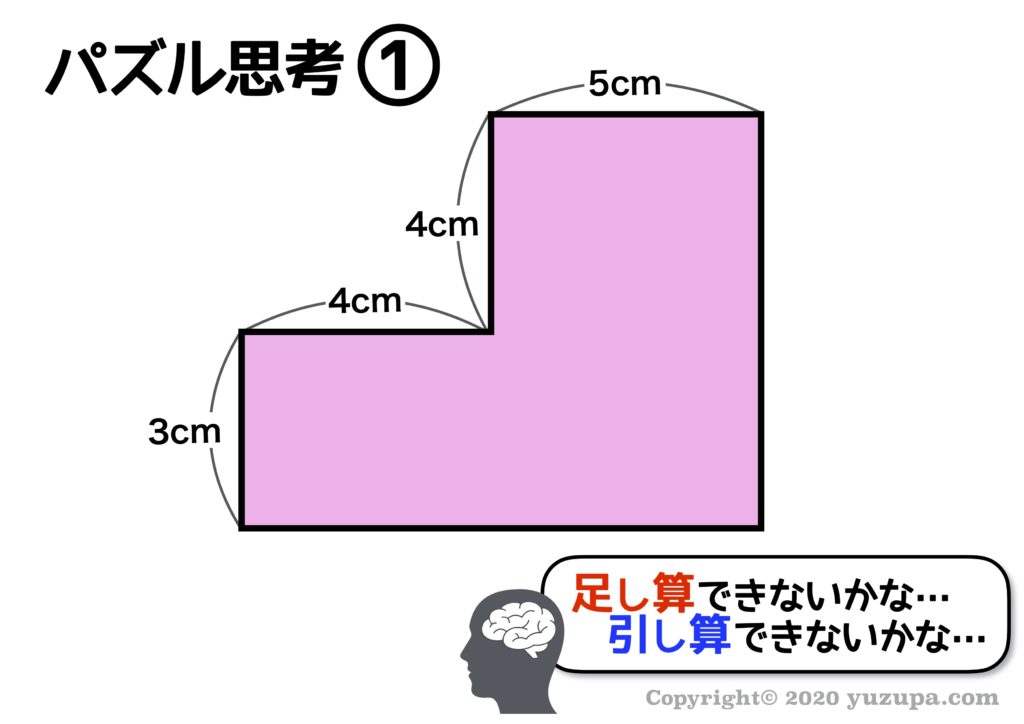
面積を求めたいのであれば… パズル思考で面積の足し算ができないか?引き算ができないか?と意識的に思考 をします。さて、結果はどうなるでしょうか?
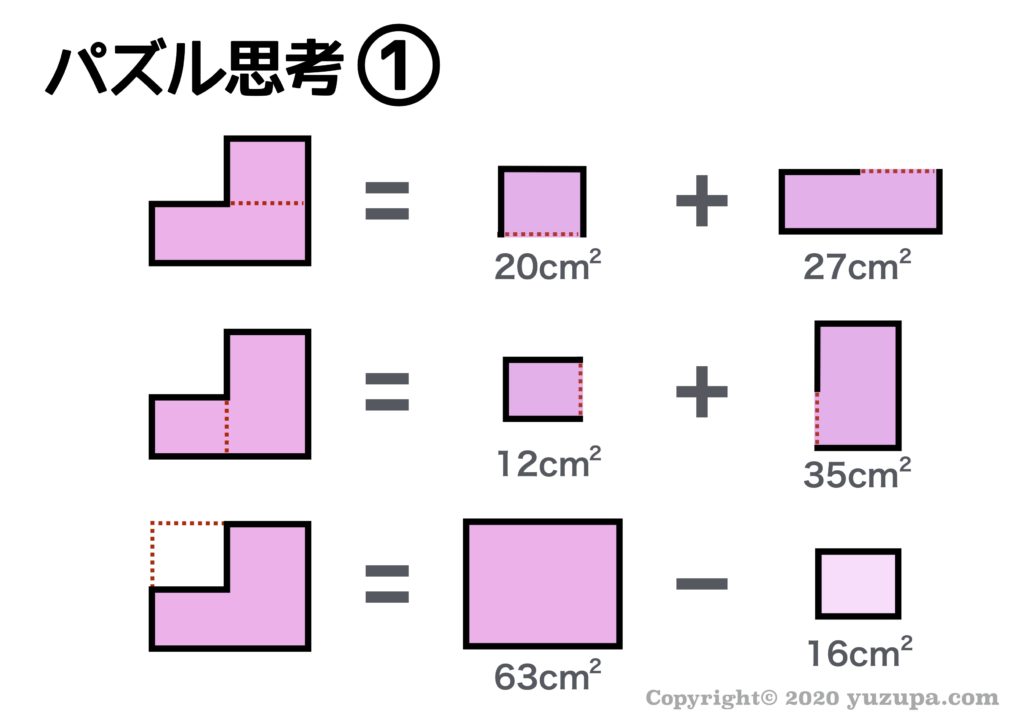
結果はいくつかパターンがあります。面積の足し算は 図形をどう分割するかによって無数にパターン があります。また 視点を変えると引き算でも求めることができることがわかりますね_φ(・_・
もちろん…どのパズル思考をしても答えは一緒 になりますd(^_^o)
パズル思考例その2
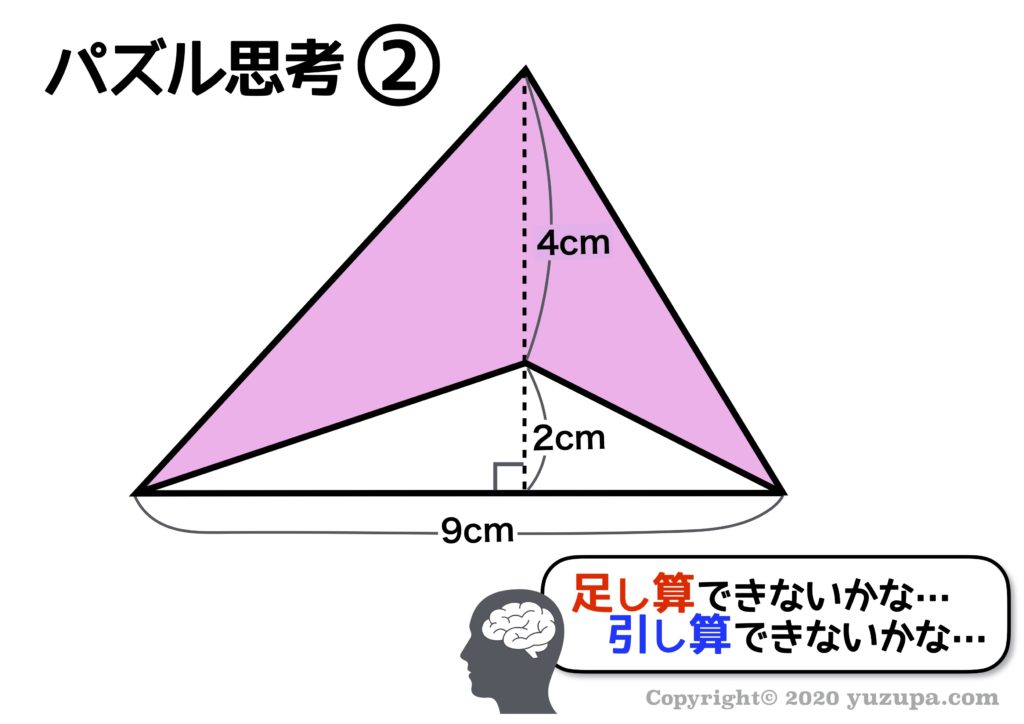
さて、今度はちょっと複雑な図形です。しかし 考えることは一緒ですd(^_^o) 足し算ができないか?引き算ができないか?という思考ですね。いかがでしょうか?
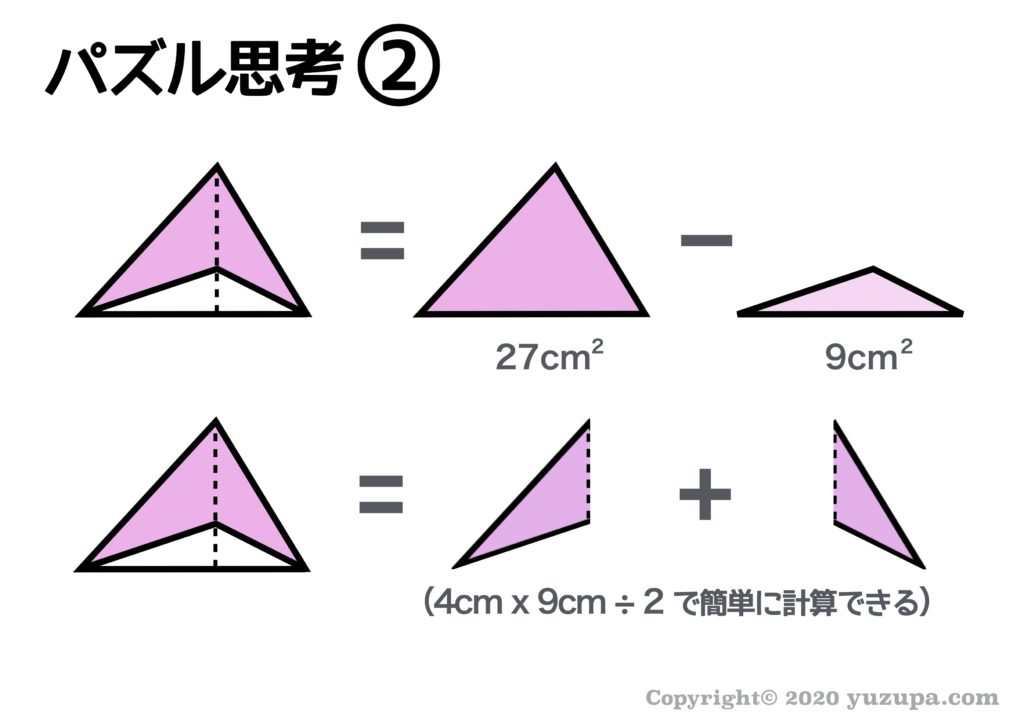
この図形は三角形の高さが分かっているのですぐに思いつくのは、上の引き算のパズル思考かと思いますが、下のように足し算というパズル思考もできます。固定観念を持たずにパズル思考することが重要 ですねd(^_^o)
パズル思考例その3
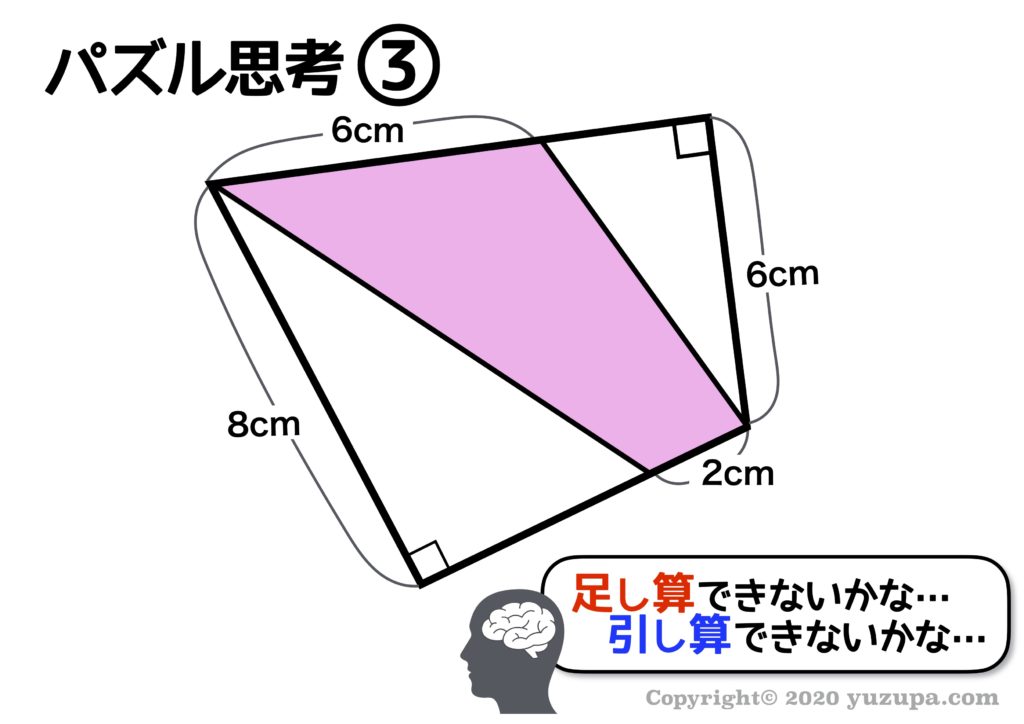
具体的な事例の3つ目です。ちょっと 複雑なように見えても…やることは一緒 です!足し算ができないか?引き算ができないか? パズル思考ですね。
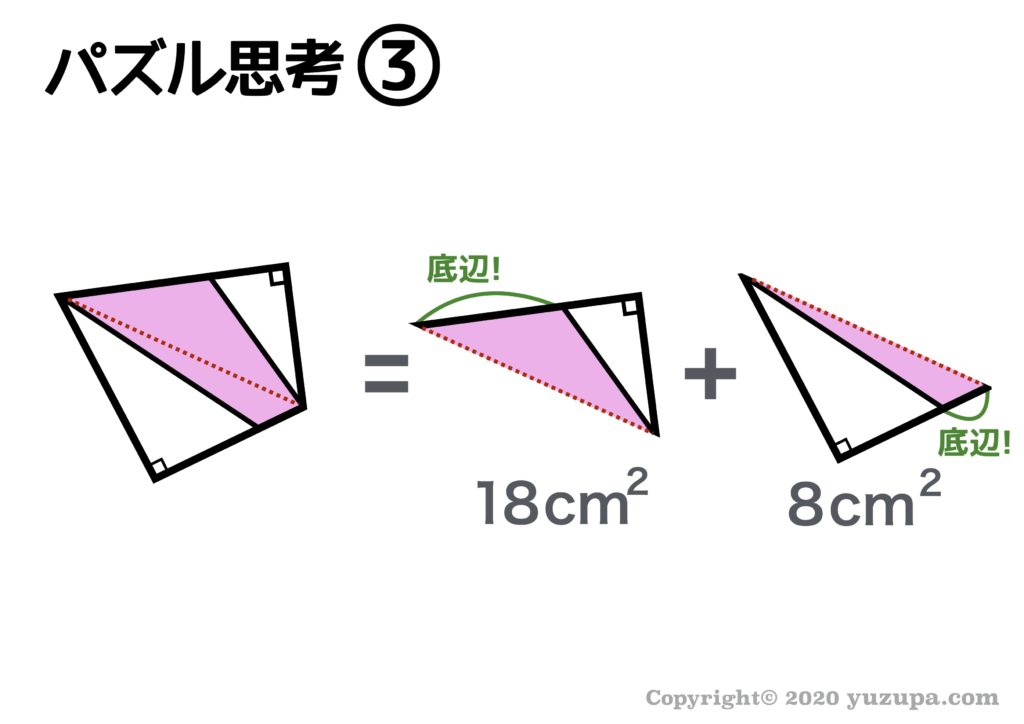
上記のように図形の角と角を結ぶような分割をすると、うまくパズル思考ができることもあります。対角線で分割するというパターンもあります。パズル思考は 練習して数をこなしていきましょうd(^_^o)
道具④ 2種類の等積移動
4つ目の道具は等積移動です。等積移動という難しい名前がついていますが シンプルに図形を移動するということ。大きく分けて2つの移動方法があります…回転移動と並行移動です 。
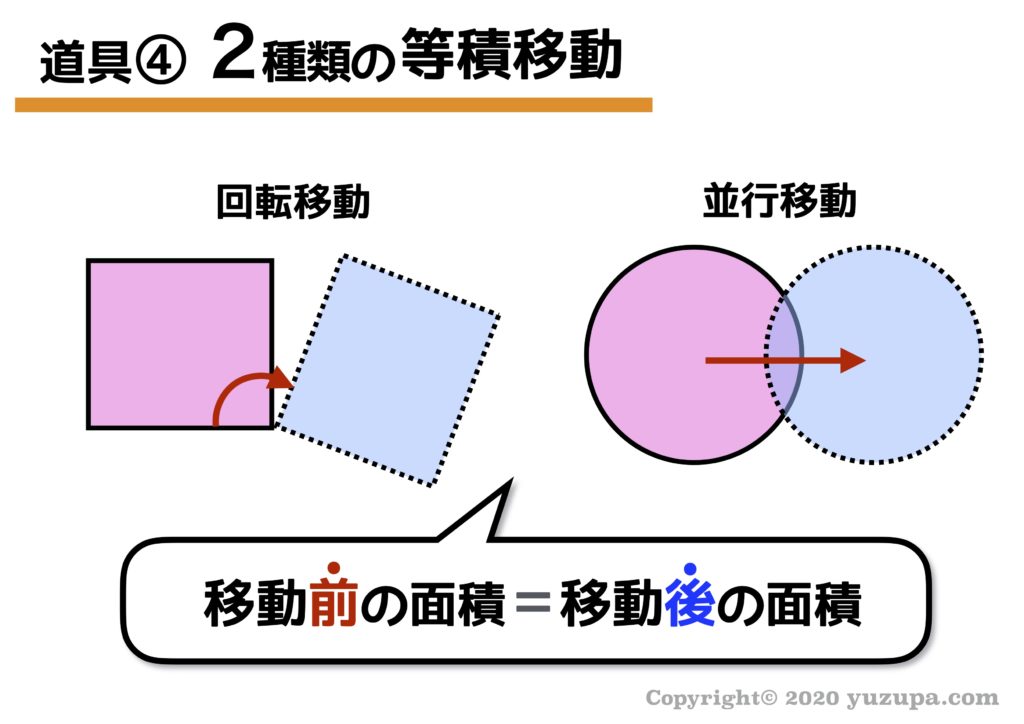
当たり前ですが、移動前と移動後の面積は一緒です よねd(^_^o) 当たり前すぎることなんですが、面積問題を解いていると意外と忘れてしまいがちな視点なんです。 それでは2つの移動を詳しく見てみましょう。
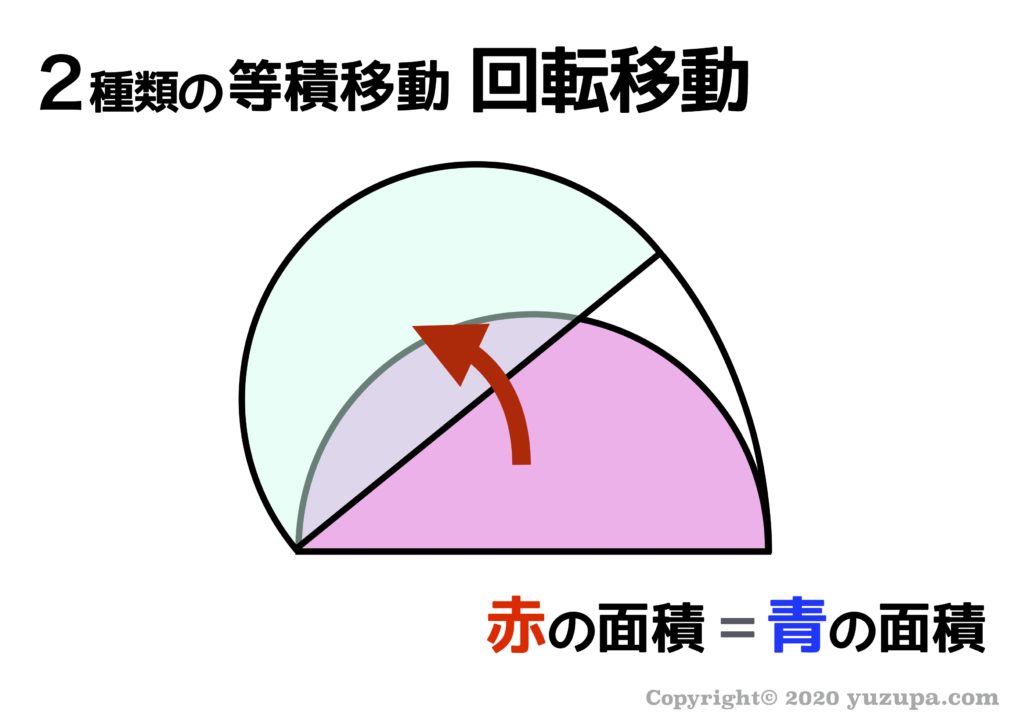
まずは回転移動です。回転移動とは 図形の1点に画鋲(がびょう)を差してグルっと回転させるイメージです。上記の例であれば赤い半円の面積と、青い半円の面積は同じになりますね。
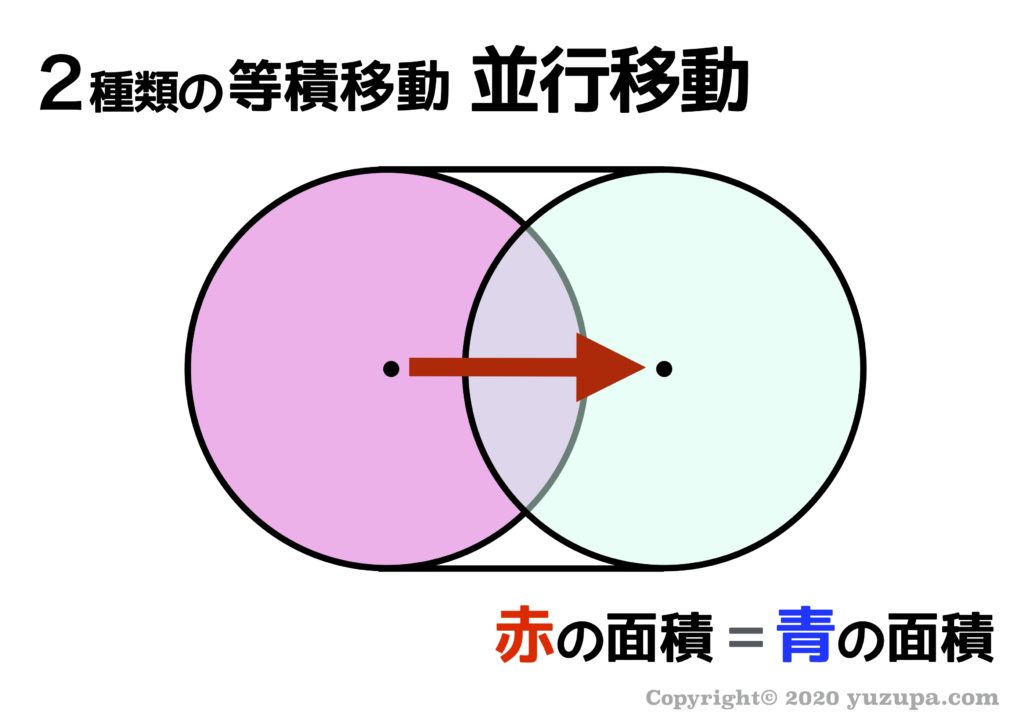
つぎは、並行移動です。並行移動とは、図形をスーッと横にずらすイメージ ですね。上記の例であれば赤い円と青い円は移動前と移動後の図形ですので、面積は同じになりますd(^_^o)
この4つ目の道具を使った具体的な問題例を何問か紹介します。
道具④を使う問題例 その1
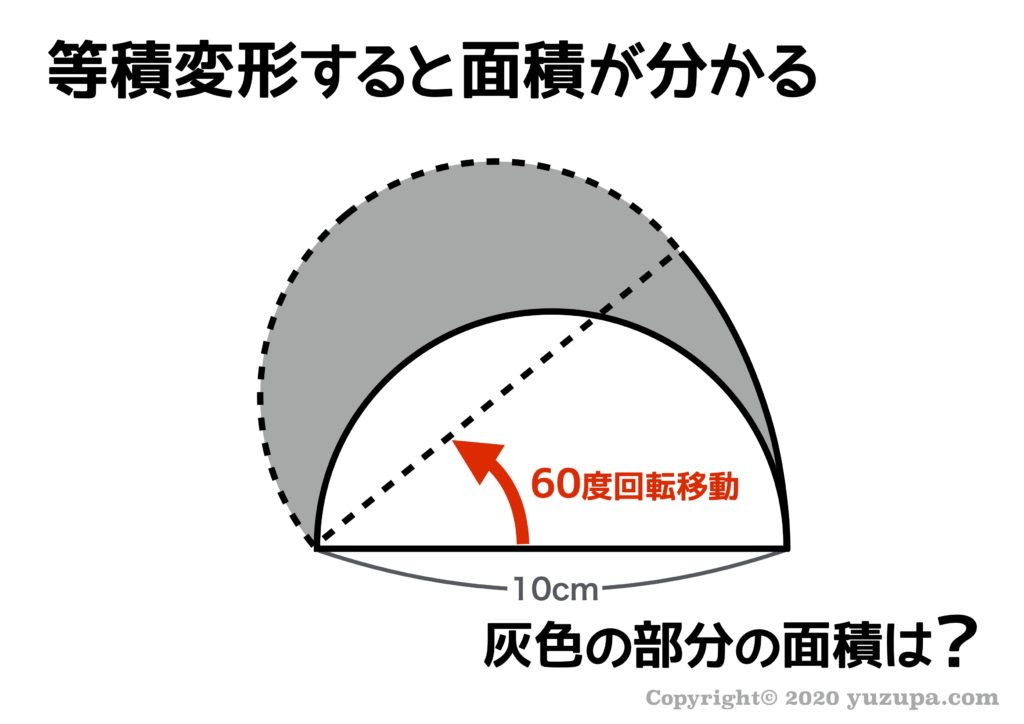
さて、灰色の部分の面積はどう求めたら良いでしょうか? 必須なのは道具③のパズル思考ですが、半円を回転移動しているので道具④を使えそう です。もちろん移動前後の面積は同じになります。
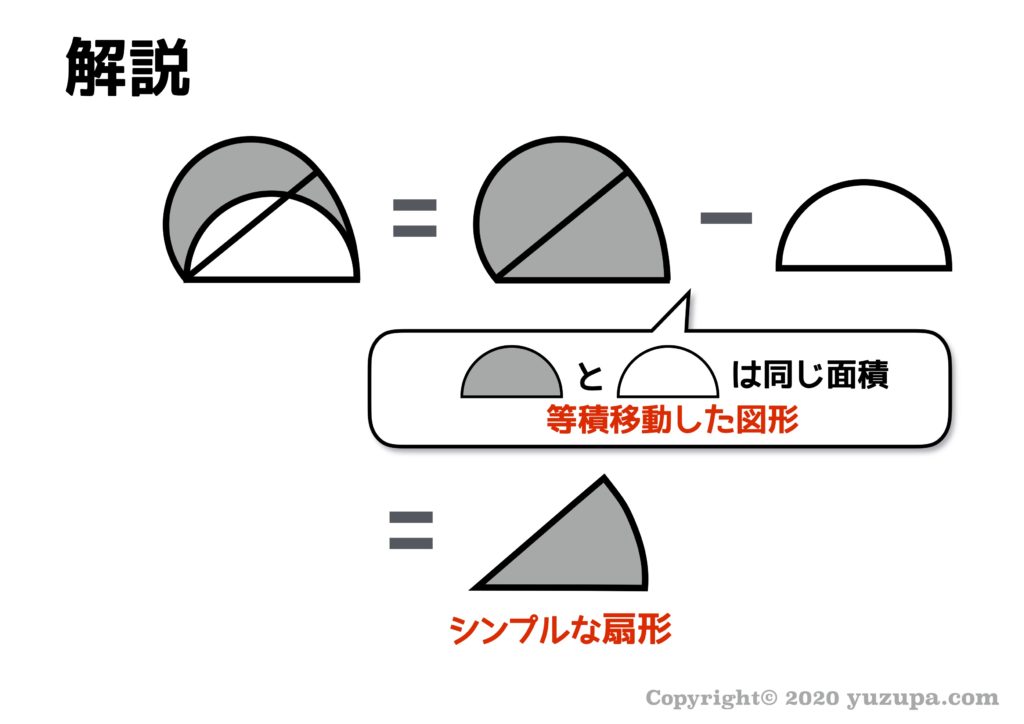
パズル思考をして、上記のような引き算の形はできましたでしょうかd(^_^o) ここで道具④の出番です。この引き算に出てくる “灰色の半円” と “白い半円” は等積移動の前後なので面積は同じ ですね。
そうするとシンプルな扇形だけが残ります。半径10cmで中心角が60°の扇形です。道具②を使って着実に計算しましょう。元になる円である 半径10cmの円 は想像できましたか?
元になる円の面積は314㎠ですので、その中心角60度分が答えですねd(^_^o)
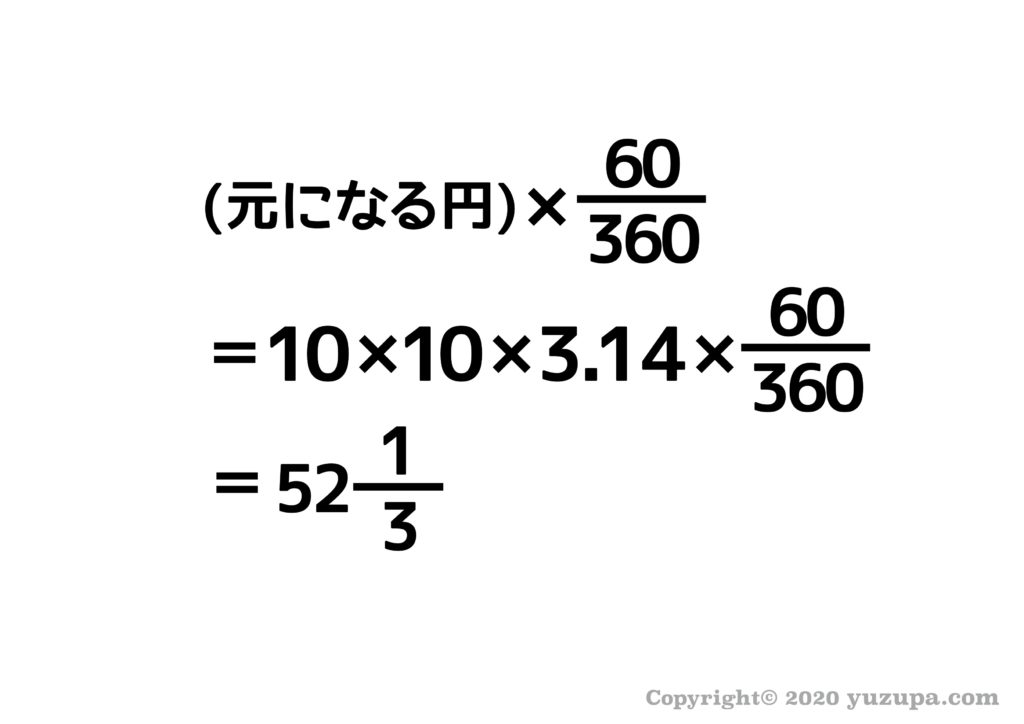
道具④を使う問題例 その2
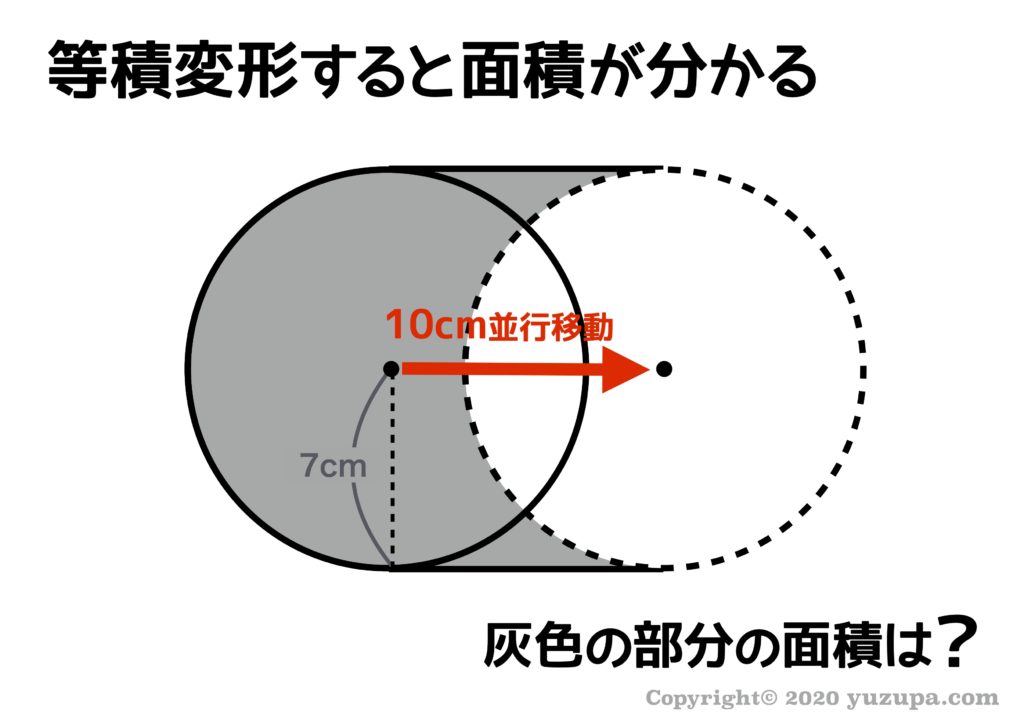
次の問題も図形の等積移動が伴う問題です。まずはパズル思考で考えてみましょう。そして 図形が並行移動しているので必ず道具④は使う ことを意識しましょうd(^_^o)
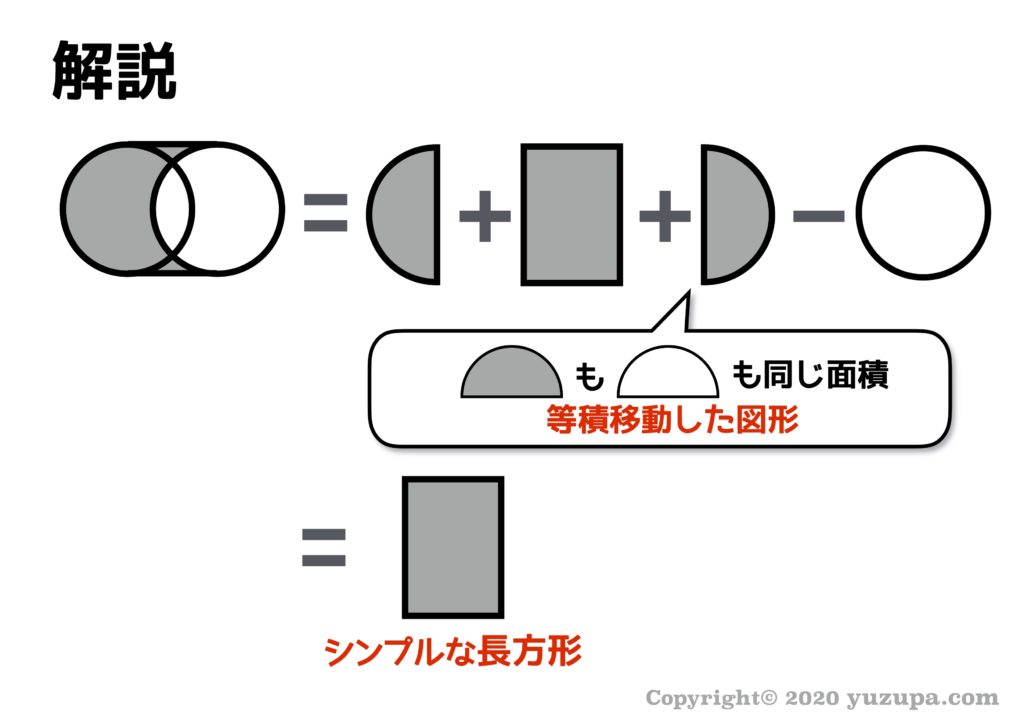
パズル思考はできましたでしょうか?パズル思考ができた後は 道具④ です。さきほどの例題と同様、“灰色の円” と “白い円” は同じ面積 ですので、本当に シンプルな長方形の計算 で解くことができますね。
縦14cm 横10cmの長方形ですので、答えは 140㎠ になります。
道具⑤ 2種類の面積比
5つ目の道具は面積比です。面積比とひとことで言っても実は 全く性質の違う2つの面積比があるので注意が必要 です。面積の公式による面積比と図形の相似による面積比ですd(^_^o)
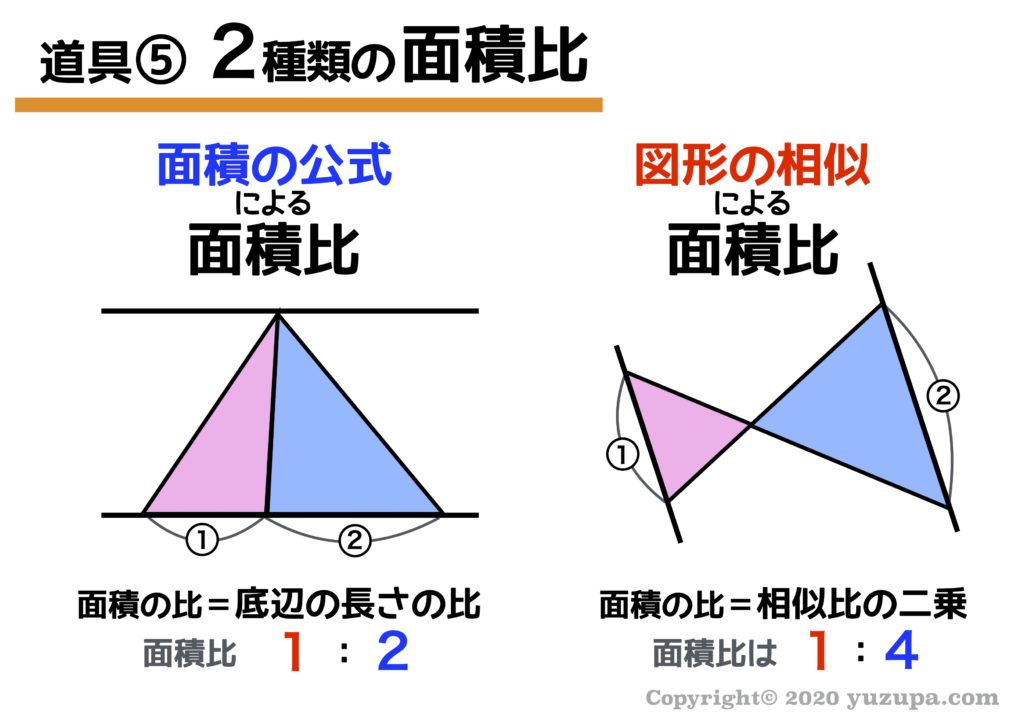
上記の図を見るとお分かるように、辺の長さの比が同じ1:2なのに面積比は1:2だったり1:4だったりします∑(゚Д゚) 意外と理解していない小学生が多いのでしっかりおさえましょう!
面積の公式による面積比
まずは、シンプルな方の 面積の公式による面積比 です。2つのパターンを紹介しますd(^_^o)
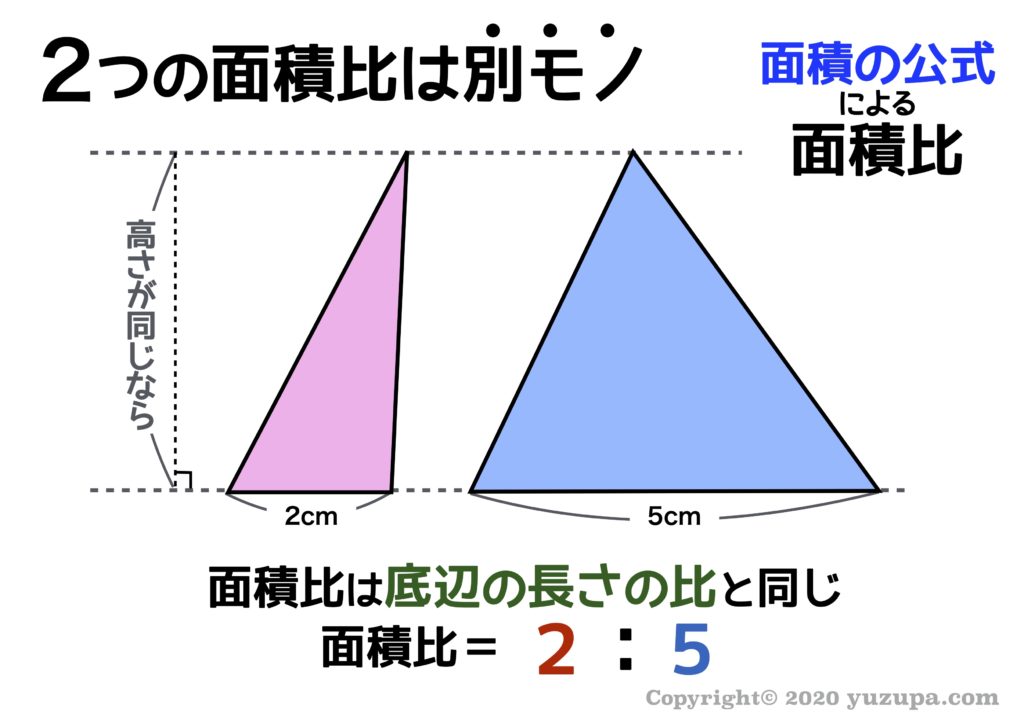
1つめは、高さが同じ三角形ならば…面積比は底辺の長さの比と同じ になるということです。上の図の場合は底辺が2cmと5cmですから、面積比も2:5になりますねd(^_^o)
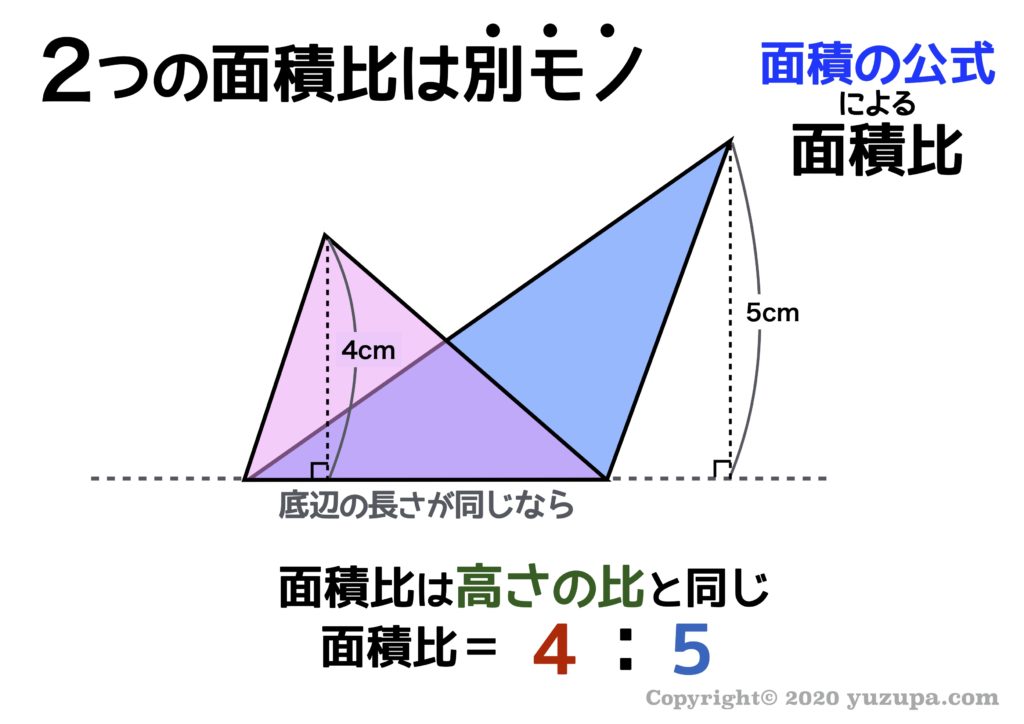
2つめは、底辺の長さが同じ三角形ならば…面積比は高さの比と同じ になるということ。上の図の場合は、高さが4cmと5cmですので、面積比も4:5になりますねd(^_^o)
図形の相似による面積比
次はちょっと複雑な 図形の相似による面積比 です。こちらも2つのパターンを紹介しますd(^_^o)
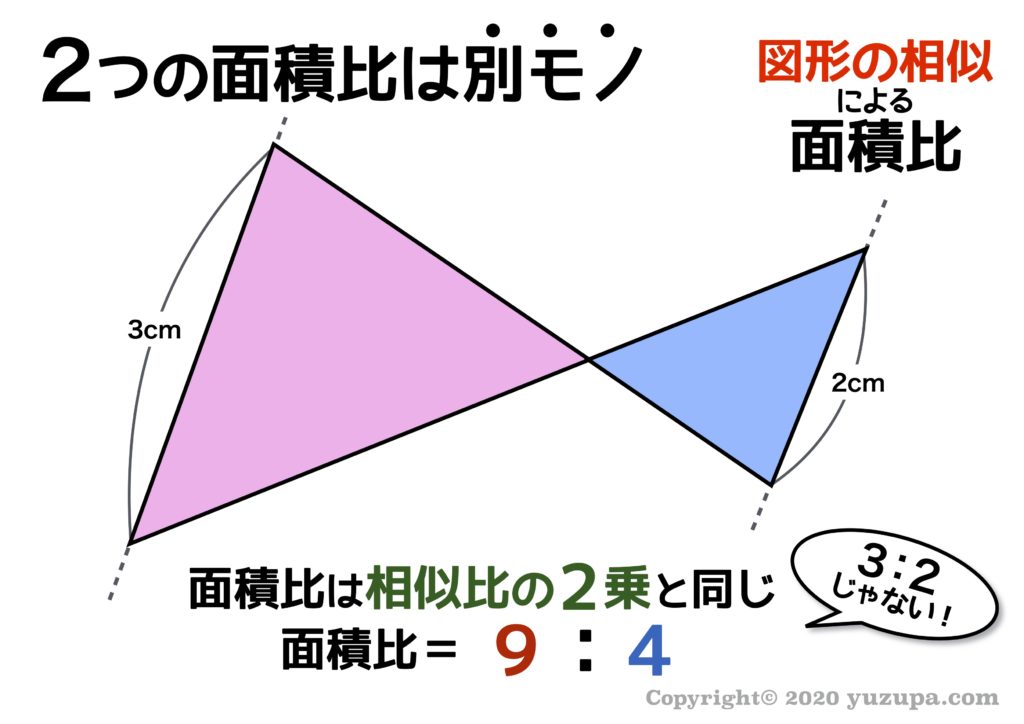
相似な図形の王道パターン “リボン形” です。図のように辺の長さの比は3cmと2cmですが面積比は3:2ではありません! 面積比はそれぞれ2乗した 9:4になります。
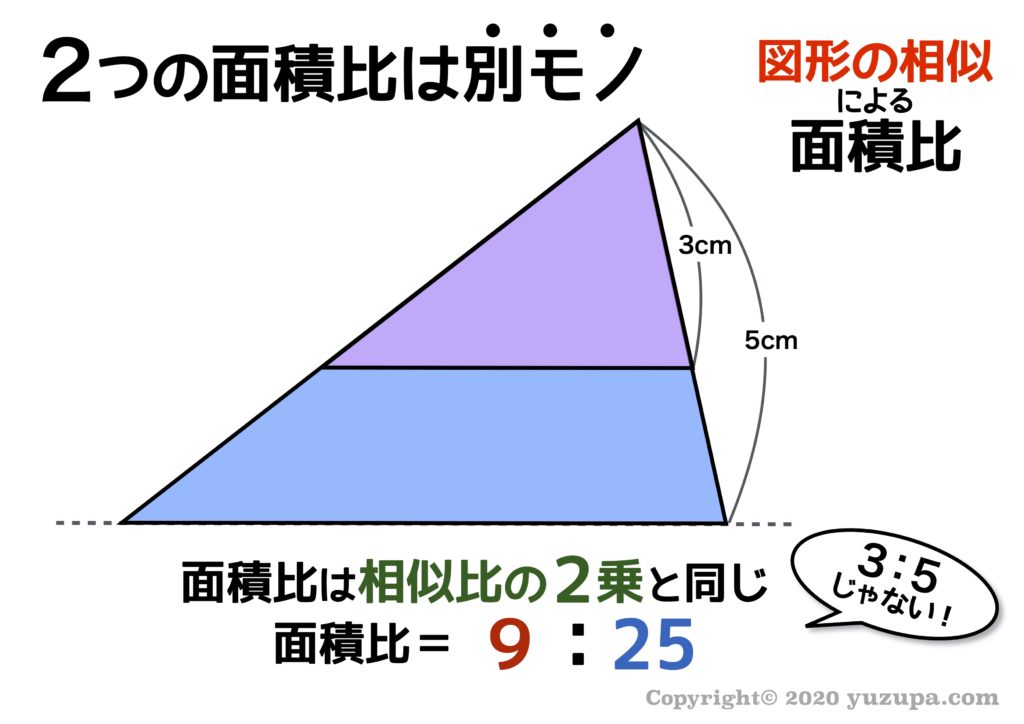
もう一つの相似な図形の王道パターン ”ピラミッド形” です。図のように辺の長さの比は3cmと5cmですが面積比は3:5ではありません! 面積比はそれぞれ2乗した 9:25になります。
それでは道具⑤ 面積比 を使う例題を紹介しますd(^_^o)
道具⑤を使う問題例 その1
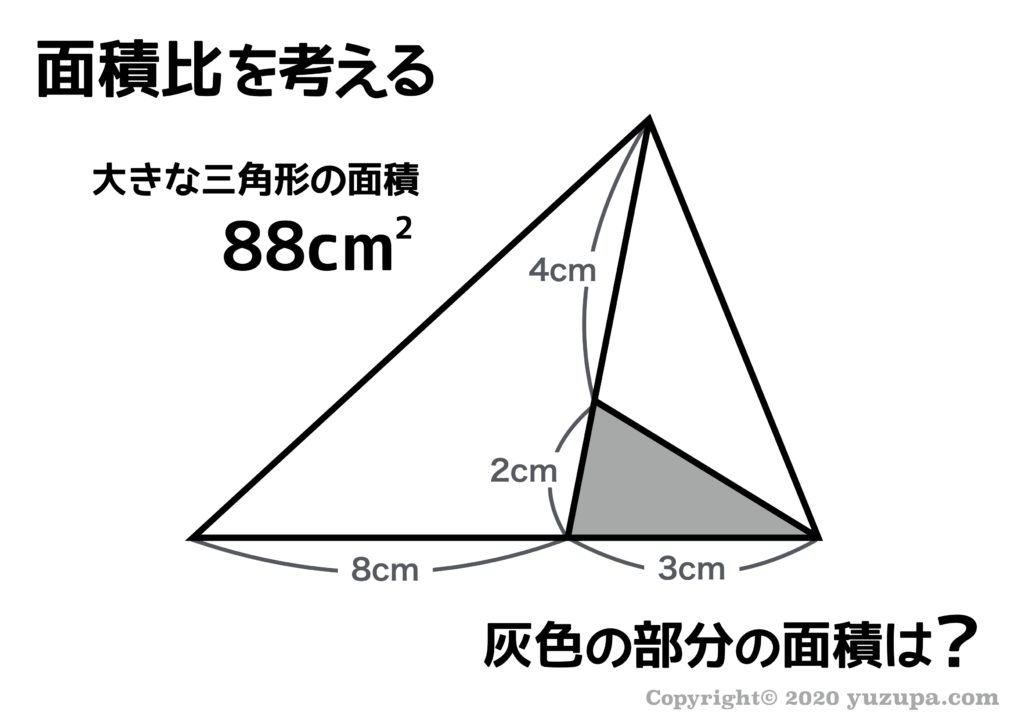
このように大きな三角形の中にいくつも線が引いてある図形を見たら道具⑤が使えるかも とヒラメキができるようになると良いですねd(^_^o) さてどうやって道具⑤を使うのでしょうか?
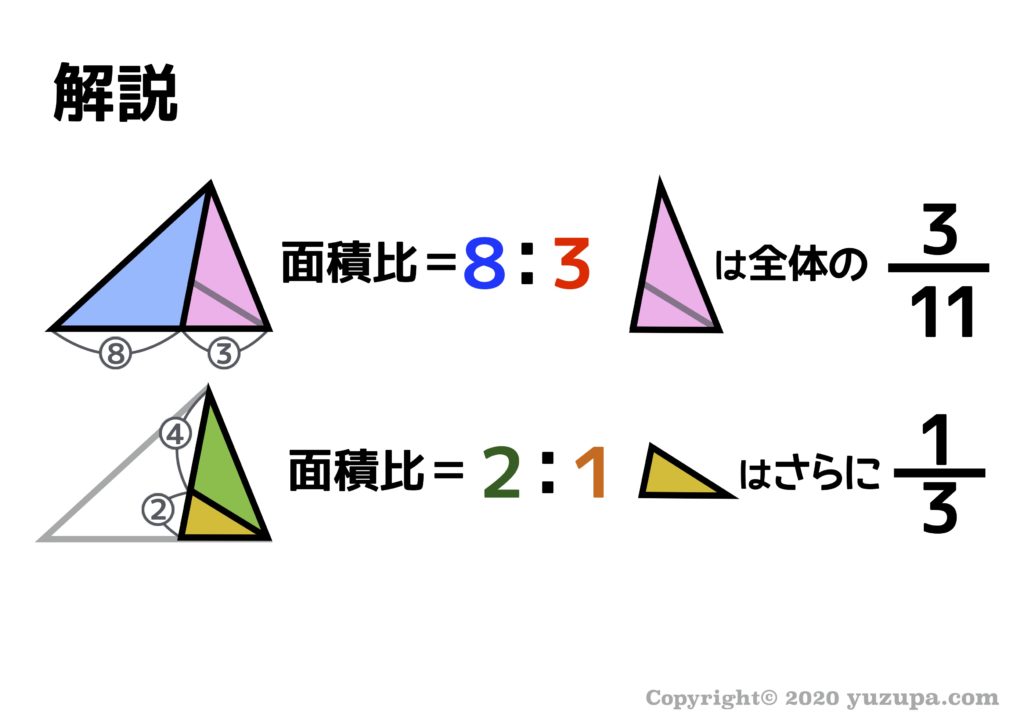
図のように、三角形の公式による面積比を2回使うと面積を求めることができます。結果として黄色い三角形は全体の11分の1になることが分かります。全体の面積が88㎠ですので、黄色い三角形の面積は 8㎠ になります。
道具⑤を使う問題例 その2
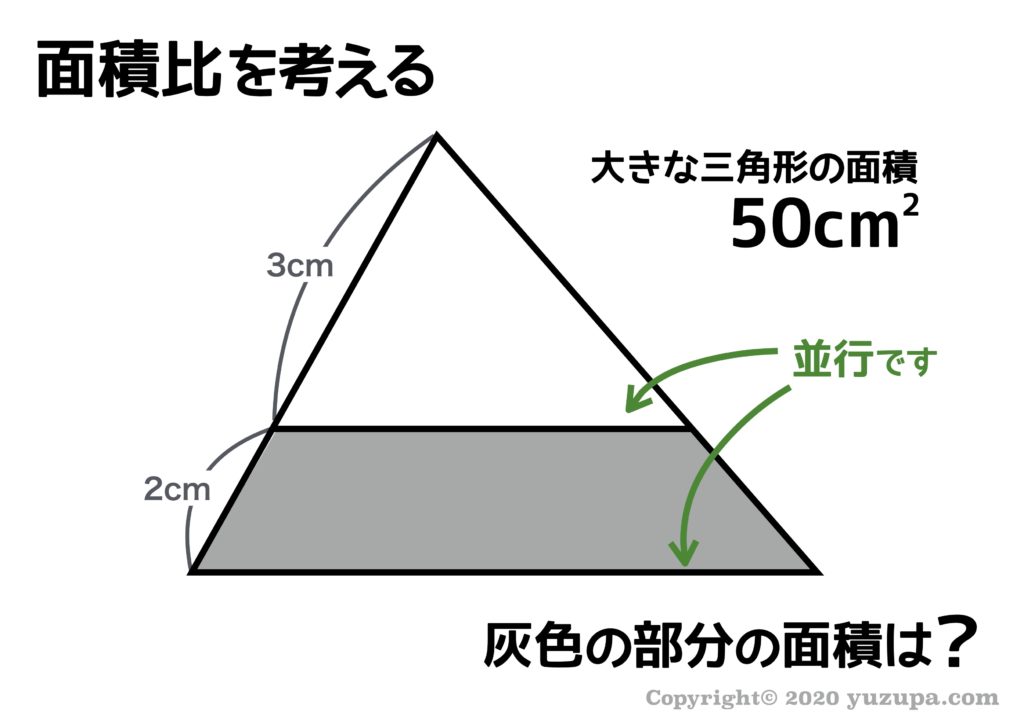
こちらの図形は、見るからに相似系ですねd(^_^o) 王道パターン “ピラミッド形” ですね。それでは、灰色の部分の面積はどのように求めたらよいでしょうか?
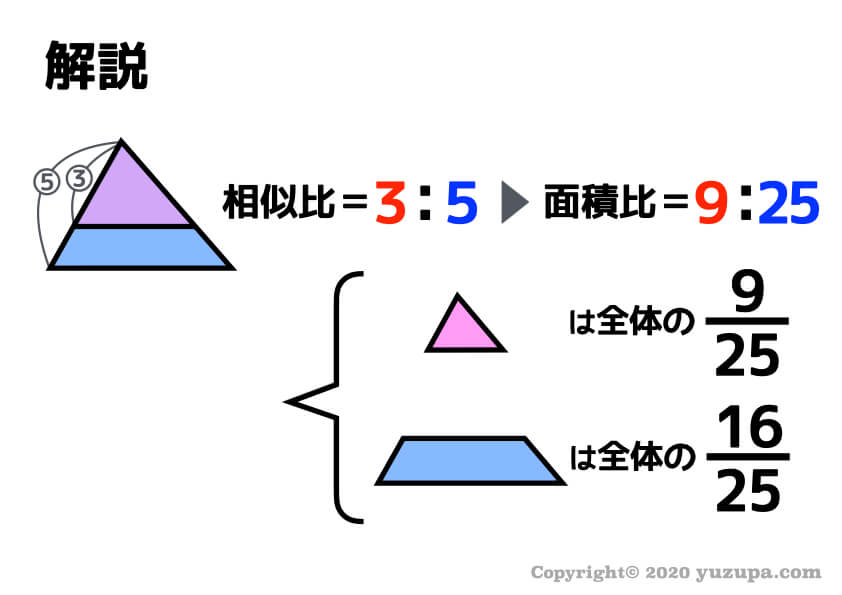
この図形の相似比はわかりますか?ピラミッド上部の辺の長さは3cm、ピラミッド全体の辺の長さは5cmなので、相似比は3:5になりますね。面積比はそれぞれ2乗して9:25 です。
面積比がわかれば計算するだけですね!

道具⑥ 三角形の等積変形
6つ目の道具は等積変形です。等積変形とは何でしょうか?その名のとおり… 等しい体積のまま形を変えることです。中学受験では三角形の等積変形をおさえておけば大丈夫です!
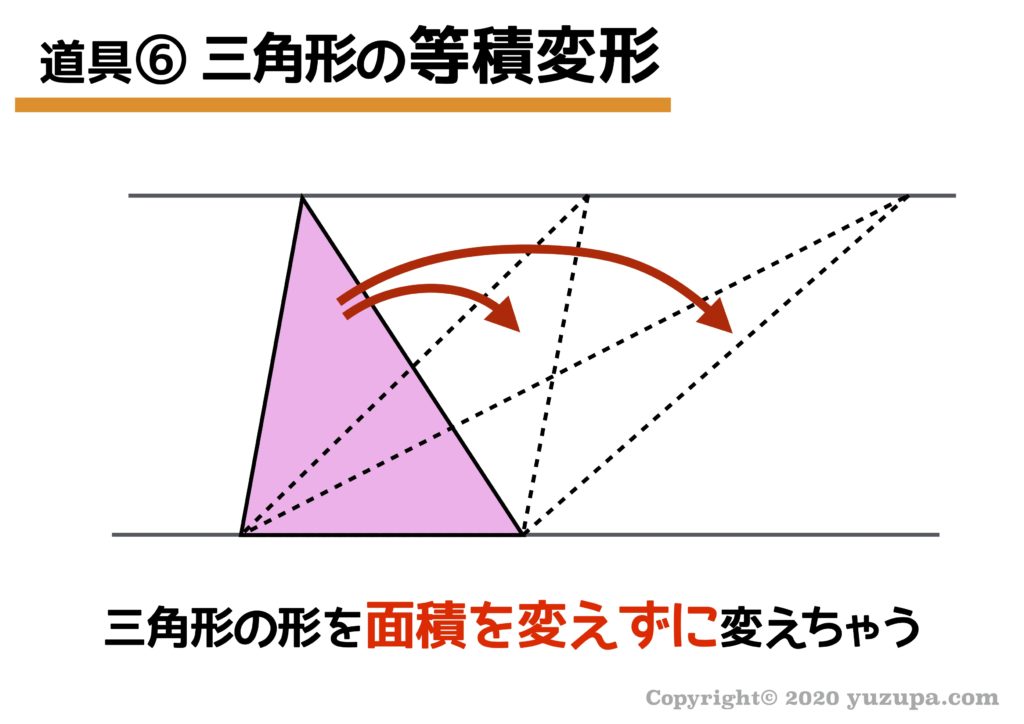
底辺を固定したまま、高さを変えないようにズラせば面積を変えずに三角形の形を変えることができますd(^_^o) それでは習うより慣れろということで例題を2題、紹介しますd(^_^o)
道具⑥を使う問題例 その1
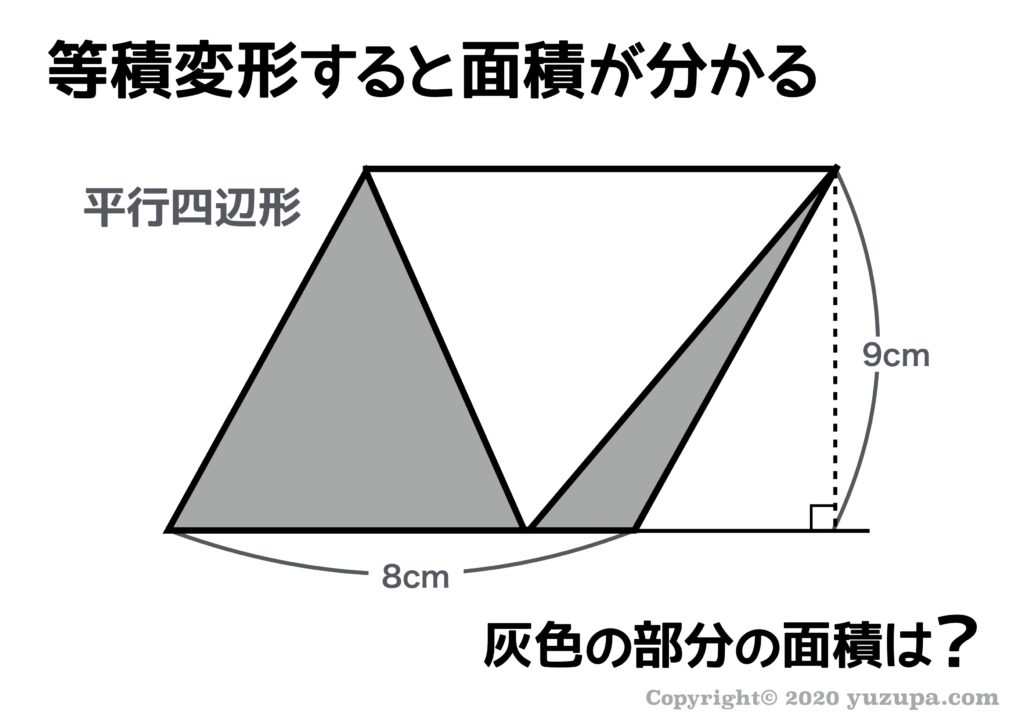
平行四辺形の中に三角形が2つありますね。高さも分かるし余裕で求められそうな感じ ですが、底辺が分からないですね。どうやったら灰色の部分の面積を求めることができるでしょうか?
答えは
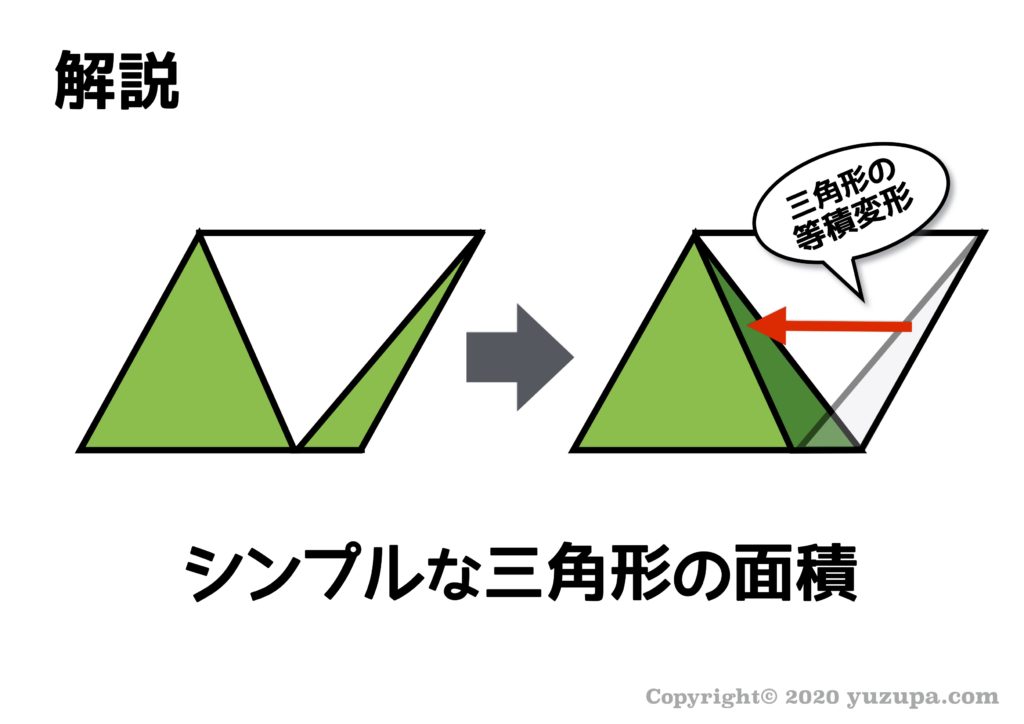
片方の三角形を道具⑥を使って等積変形してみましょう。等積変形は上記のように好きな位置まで移動できるというのがポイントです。結果としてシンプルな三角形の面積の問題になりますねd(^_^o)
答えは 36㎠ になります_φ(・_・
道具⑥を使う問題例 その2
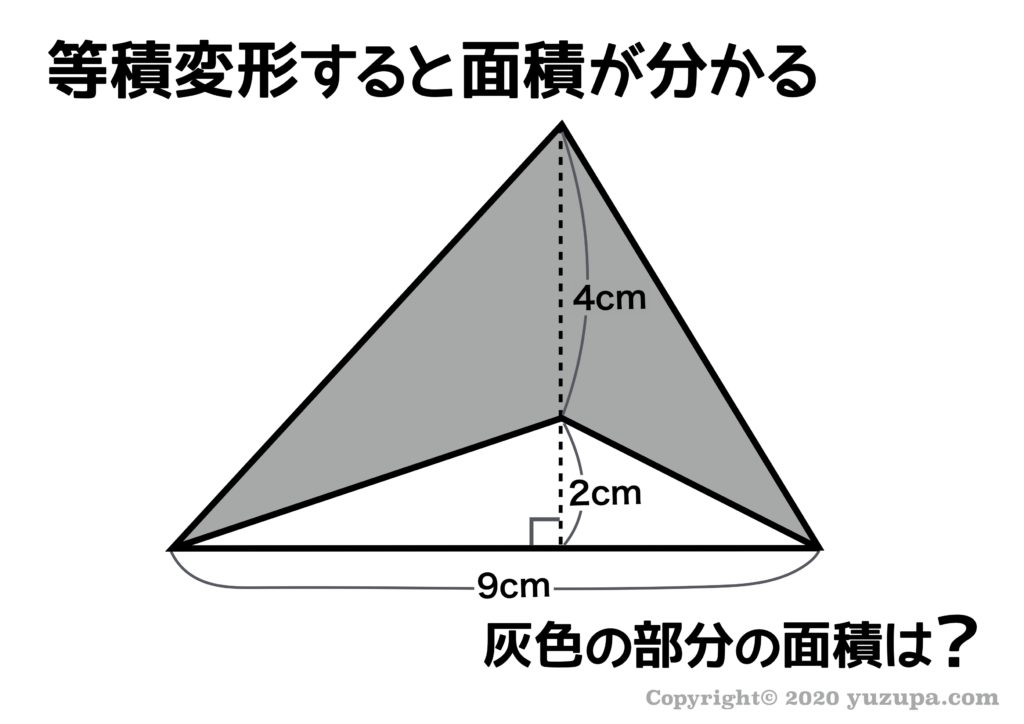
次の問題ですが、道具③の “パズル思考” のところで紹介した図形ですね。引き算の形は簡単に出すことができるかと思いますが、実は足し算の形でも答えを出すことができますd(^_^o)
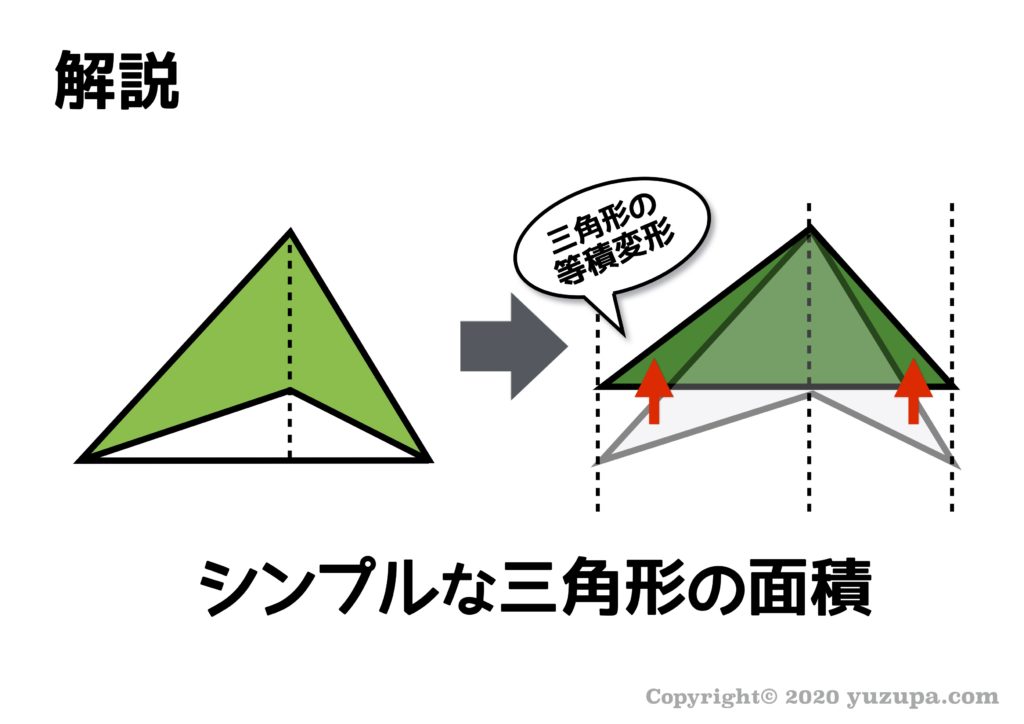
点線の両どなりにある2つの三角形の頂点を並行移動してみましょうd(^_^o) 繰り返しですが好きなところまで移動できるのがポイントです。ちょうど一直線になるところまで移動すると…シンプルな1つの三角形になります!
答えはもちろん 18㎠ ですd(^_^o)
道具⑦ 線対称と点対称
いよいよ最後の道具です。線対称と点対称の性質を利用したものです。その性質とは…対照な図形の対応する面積は等しいという性質です。まずは以下の図をごらんください。
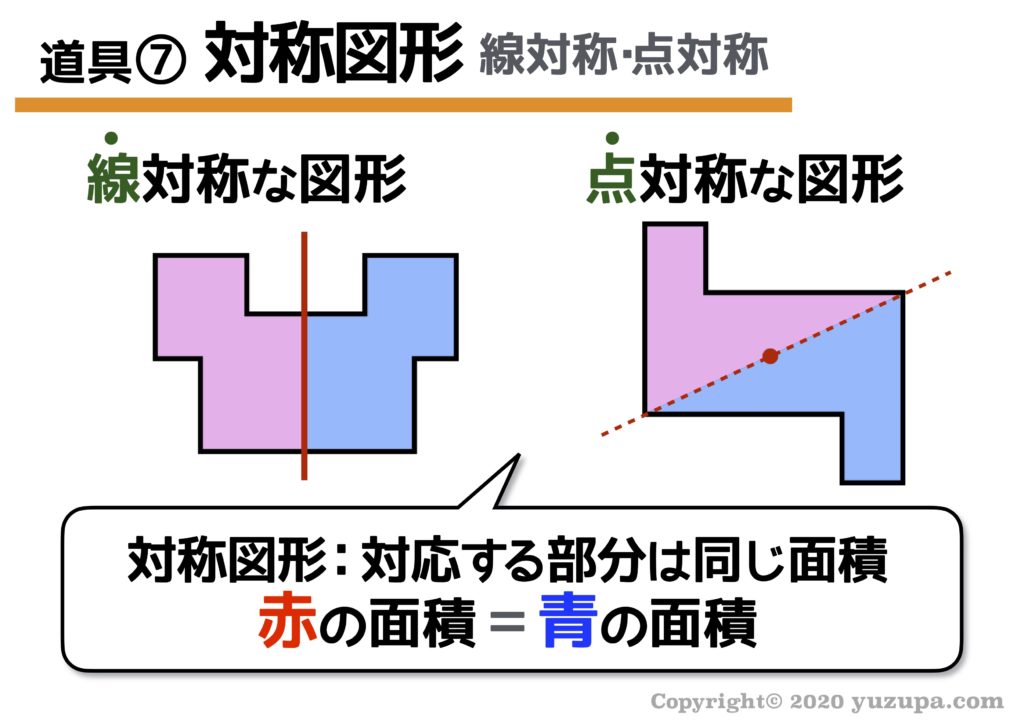
線対称であっても、点対称であっても 対称な図形の対応する部分の面積は同じ になります。上の図でいうと赤い部分の面積と青い部分の面積は同じですねd(^_^o)
さっそく具体的な問題例を見てみましょう。
道具⑦を使う問題例 その1
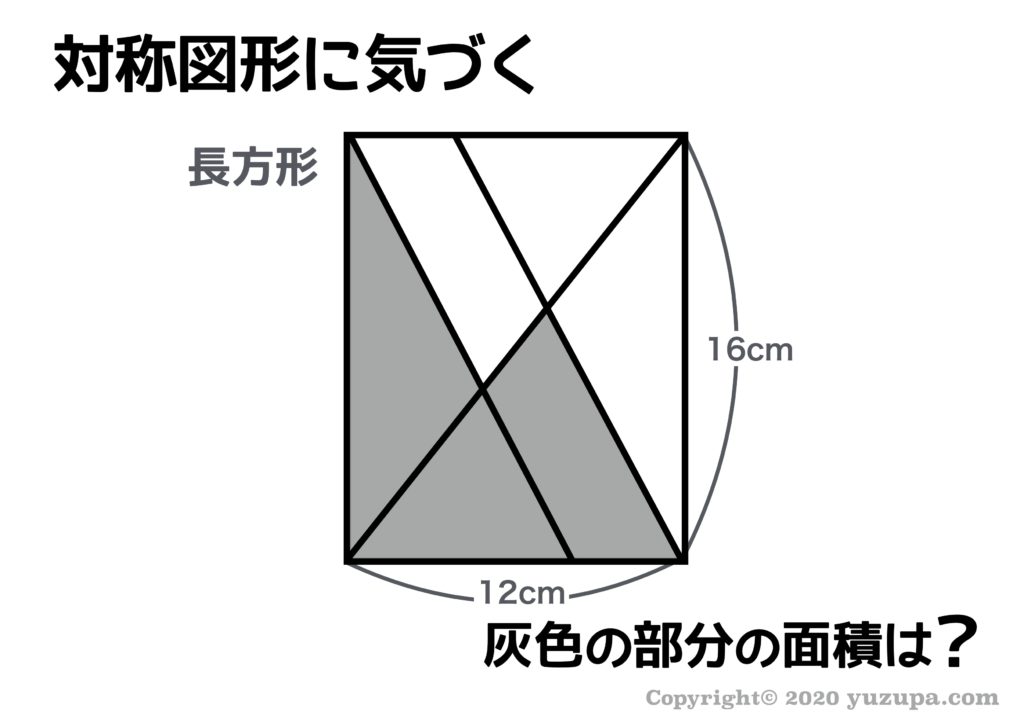
さて、灰色の部分の面積はいくつでしょうか?ちょっと複雑な図形っぽく見えますが、この図形が対照な図形であることに気づくことができれば簡単に面積を求めることができるんですd(^_^o)
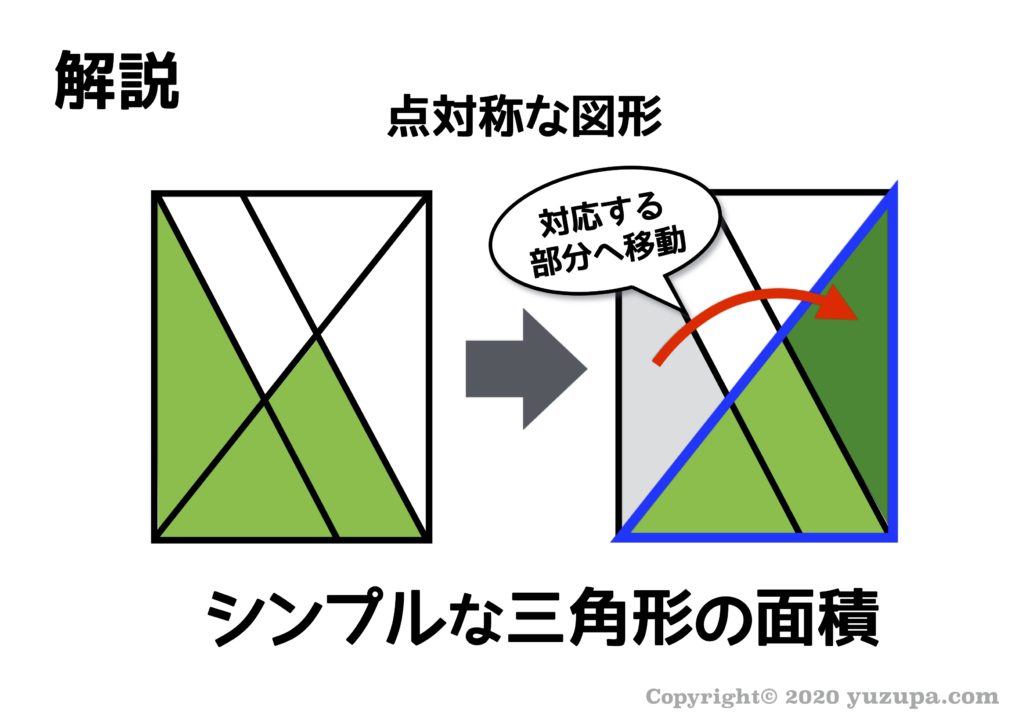
対照な図形であることに気づけましたでしょうか?対称な図形であれば対応するところに移動しても面積は変わらない ことを利用するのです。これが道具⑦の最大のポイントですd(^_^o)
移動してみればシンプルな三角形になりますね。答えは 96㎠ ですね。
道具⑦を使う問題例 その2
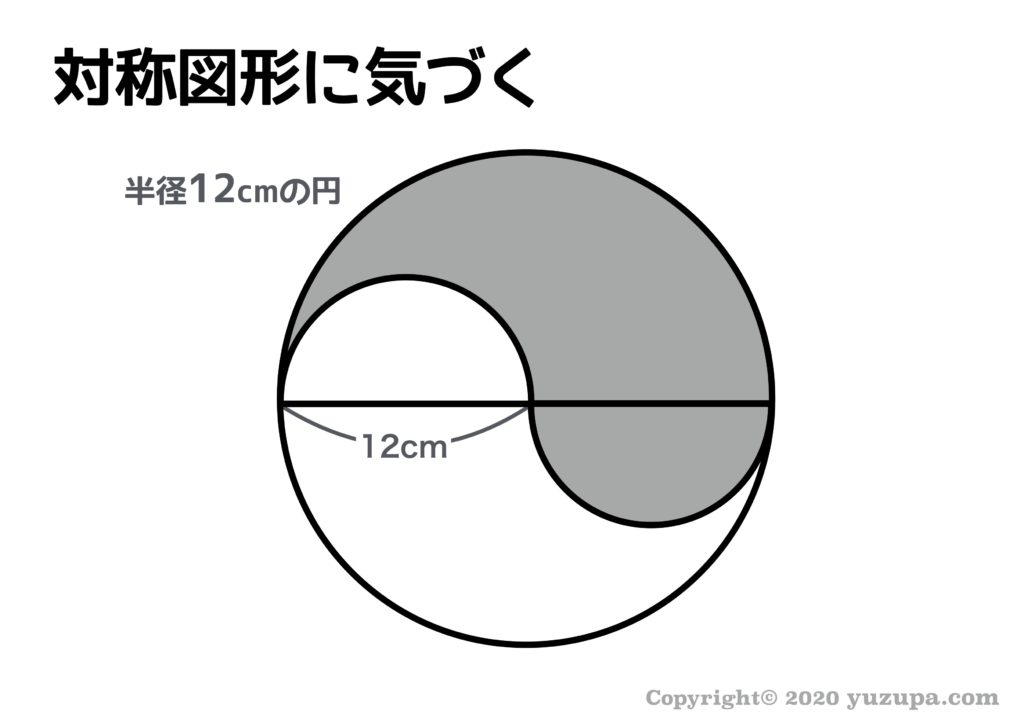
さてこの問題も見るからに対称な図形ですね。どのように図形を移動すれば簡単に面積を求められるでしょうか? こちらの問題もシンプルな問題になりますね。
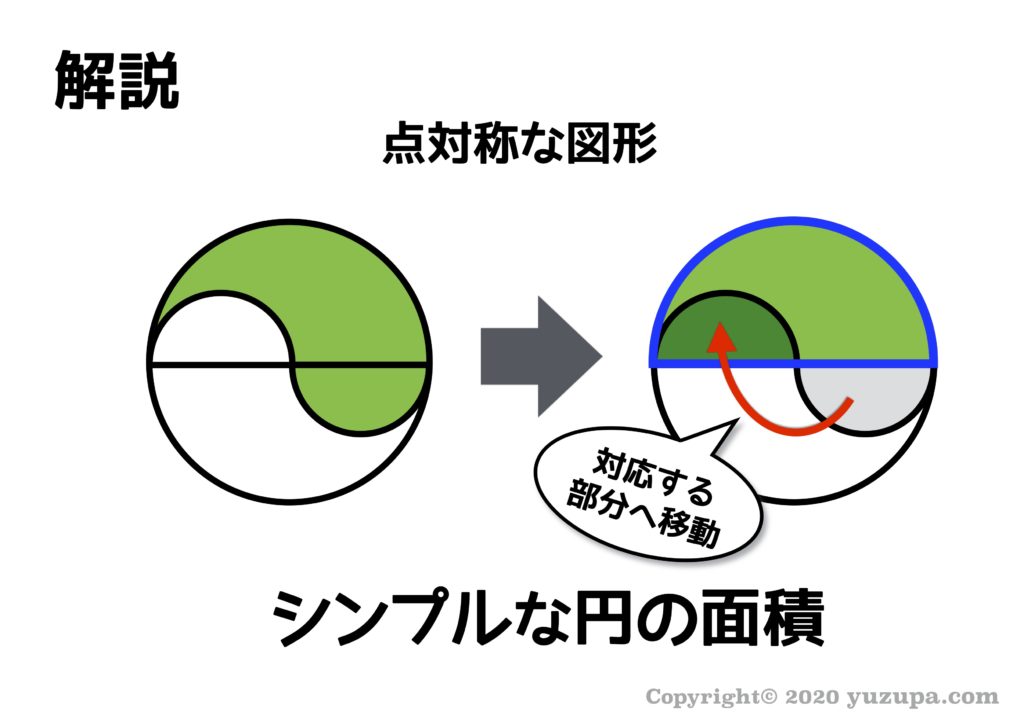
この図形も点対称な図形ですので 対応する半円を移動しても面積は変わりません ね。移動すればシンプルな円の面積の問題になります。半径12cmの円の半円ですから、答えは 226.08㎠ になります!
番外 “補助線の引き方” は存在するのか?
よく “補助線はこう引けば良い!”と力説するサイトがありますが… 我が家ではあまり意識しません。補助線を引いてからヒラメクのではなく… 使える道具を使うために補助線を引く というスタンスです。
例えば…円が出てくる問題では “円の中心から円周に向かって補助線を引け!” というノウハウ。でも、これは円の基本4公式を使いたいと思って引くもの …。あくまで補助線は試行錯誤の過程です。
補助線が先って… 本末転倒ですよね(・_・;
道具を使えないかなぁと思考した末に補助線を引けるようになるのがベスト です!
まとめ
図形問題が苦手な小学生。面積を求める問題や角度を求める問題に苦戦していますが、その理由は何でしょうか?計算ミスや練習不足というものもありますが、多くは 使える道具の全体像を知らない ことに起因します。
今回は面積を求める問題で使える道具7つを体系的にまとめてみましたd(^_^o) 四谷大塚の問題集を確認しましたが、ほぼこの7つの道具を使いこなすことで解くことができます 。
また図形問題の “角度” を求める7つ道具は以下のリンクからどうぞ!
参考リンク:図形の角度問題は”7つ道具”で攻略













とても興味深い記事でした!図形の面積問題に対する「7つ道具」のアプローチは新鮮で、実際の問題にどのように役立つか試してみたくなりました。特に具体例が参考になりました。これからの勉強に活かせそうです!ありがとうございます!
H89 SLOTSさん
かるび勉強部屋 ゆずぱ です。
コメントをいただき、ありがとうございますo(^-^)o
少しでもお役に立てるようであれば嬉しく思います。
この記事はとても役に立ちました!「7つ道具」を使った図形の面積問題の解法が分かりやすく、今後の学習に生かせそうです。具体例ももっとあれば嬉しいですね。引き続き素晴らしいコンテンツを楽しみにしています!
jayaslotさん
かるび勉強部屋 ゆずぱ です。
具体例について、ご要望ありがとうございます。
順次、コンテンツを拡充してまいりますので、
よろしくお願いいたします!
この記事、とても参考になりました!特に「7つの道具」の具体的な使い方が明確で、図形の面積問題がぐっと身近に感じられました。これからの勉強に活かしていきたいです。ありがとうございます!
rejekibetさん
かるび勉強部屋ゆずぱ です。
コメントありがとうございます!
少しもでもお役に立てたようであればよかったですo(^-^)o
この記事、とても参考になりました!図形の面積問題をこの「7つ道具」で攻略できるイメージが湧きました。特に具体例があって分かりやすかったです。これからの勉強に活かしたいと思います。ありがとうございます!
L7 Lotteryさん
かるび勉強部屋 ゆずぱ です。
コメントをいただきありがとうございます!
少しでもお役に立てるようであれば
良かったですo(^-^)o
このブログ記事で紹介された“7つ道具”は非常に役立ちそうですね!図形の面積問題はいつも悩ましいですが、これを活用して自信を持って解けそうです。特に具体例があって分かりやすかったです。ありがとうございます!
Test Essay Blogさん
かるび勉強部屋 ゆずぱ です。
ありがたいコメントをいただき、ありがとうございます!
少しでもお役に立てたようであれば、
嬉しく思いますo(^-^)o
この記事、とても役立ちました!特に「7つ道具」の解説が分かりやすく、図形の面積問題に対する不安が少なくなりました。今後の勉強に活かしていきます!ありがとうございます!
Test Essayさん
かるび勉強部屋 ゆずぱ です。
ありがたいコメントをいただき感謝いたします!
7つ道具については、他のシリーズもありますので
ぜひ、参照いただけたら幸いでございますo(^-^)o
↓7つ道具シリーズ
https://yuzupa.com/tag/seven-tools-tag/
このブログ記事、図形の面積問題を解くための「7つ道具」がとても役立ちそうですね!具体的な例や実践的なアドバイスがたくさんあって、わかりやすかったです。受験に向けてしっかり活用していきます!ありがとうございました!
cupcut apkさん
かるび勉強部屋 ゆずぱ です。
コメントをいただきありがとうございます!
お役に立てたようで良かったですo(^-^)o
ご健闘をお祈りします!
このブログ記事、とても参考になりました!図形の面積問題についての「7つ道具」は特に役立ちそうです。実際に試してみて、解法がスムーズにできるようになりたいです。ありがとうございます!
90 GAMESさん
かるび勉強部屋 ゆずぱ です。
ありがたいコメントをいただきありがとうございます!
頑張ってください!!
面白い記事ですね!図形の面積問題を“7つ道具”で解く方法がとても明確で、参考になりました。特に具体例があったのが良かったです。これからの勉強に活かしたいと思います!
6Club Supportさん
かるび勉強部屋 ゆずぱ です。
コメントをいただきありがとうございますo(^-^)o
少しでもお役に立てたのであれば、
嬉しく思います!受験生でしょうか?頑張ってください!
受験が近く、娘が図形の問題が苦手で、焦っていました。
ですが、かるび勉強部屋 ゆずぱさんのおかげで、克服することができました。ありがとうございました✨
合格したい‼️さま
かるび勉強部屋 ゆずぱ です。
お役に立てたようであればよかったです。
ご息女の合格、陰ながら応援させて
いただきます♂️
とても分かりやすく参考になりました。
ただ、道具⑤を使う問題例 その2の解説で台形は全体の14/25となっており、式では16/25となっていました。
匿名さま
かるび勉強部屋 ゆずぱ です。
コメントをいただきありがとうございます。
誤記のご指摘、たいへん感謝いたします。
すぐに修正したいと思います。
今後ともよろしくお願いいたします!
かるび勉強部屋
ゆずぱ
とても分かりやすいのでもっと問題を出してください!
絶対合格したい中学受験さま
コメントありがとうございます!
引き続き、良いコンテンツを公開できるよう
がんばってまいりますd(^_^o)