中学受験：差集め算とは？ 基本問題はできるのに応用問題ができない理由

差集め算の基本問題はできるのに応用になると突然できなくなる… 機械的にやり方を覚えていませんか？

※ 2022年9月27日 読者の皆様より有益なコメントをたくさんいただきましたのでさらに分かりやすくなるよう改善！

小５の娘が “差集め算” で苦戦している… ゆずぱ です(-_-;)

差集め算と言う単元…  塾の先生によってだいぶ教え方が違う ようです。私の息子の先生は “差集め表” による解法。娘の先生は “方程式もどき” の解法。またサイトによっては “線分図” を使っていたりします∑(ﾟДﾟ)

そして応用問題になると突然できなくなる子供… 

機械的に”やり方”を覚えているからかもしれません 

問題文に出てきた数字を “やり方” どおりに計算し割り算をする。それで解けてしまう問題もあるでしょう。でも…コレだと変化球がくると対処できません (-_-;) だから応用問題で急にできなくなるようなんです。

そして…
やり方だけ覚えてなんとなくできちゃっている状態
超キケンです∑(ﾟДﾟ)

対処法はひとつ！  “差集め算”の本質 を理解することです d(^_^o)

“差集め算” とはナニモノか？

“差集め算” とは？

差集め算とは… “１個１個の差” を全て集めると “全体の差” になる という真理を使う問題。これだけ読んでもちょっと分かりづらいかと思いますので 80円切手と50円切手の具体例をみてみましょうd(^_^o)

80円切手と50円切手が5枚ずつあります。全体の金額の差は150円ですね。これは１枚１枚の差である30円が５個集まってこの金額になっています。もうすこし分かりやすくしてみましょう。線分図の登場ですd(^_^o)

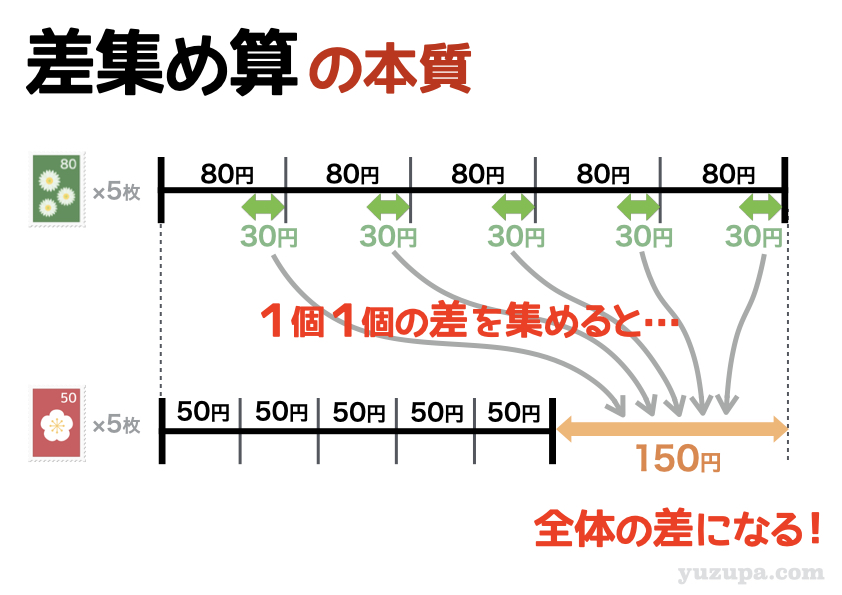
80円切手と50円切手の差は30円ですね。それらを ぜーんぶ集めてくると150円になるというイメージ をつかめますでしょうか？ “差集め算” という名前もこの ”差を集めてくるイメージ” から付けられたものと思われますd(^_^o)

そして 差集め算の本質は
それらをイコールでむすぶこと

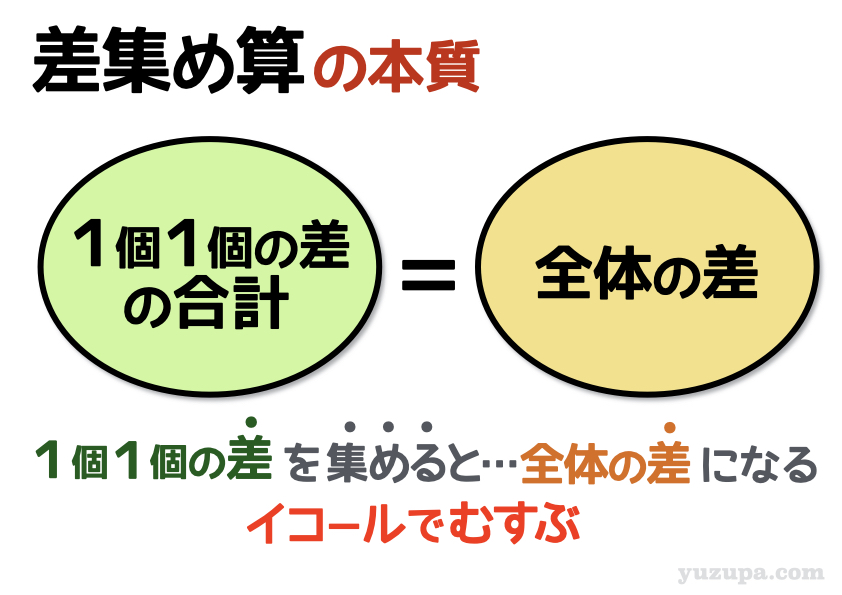
機械的にやり方を覚えていては応用がききませんが… “１個１個の差” を全て集めてきて “全体の差” とイコールで結ぶ 。この思考だけでどんな応用問題にも対処することができますd(^_^o)

具体的な例題で確かめてみましょう！

 

基本例題で確かめてみる

基本例題です。算数の世界でよくみる 一般的な “物の単価” × “物の数量” を扱う問題 なんですが、シンプルな計算では解くことができません。どうやって考えたらよいでしょうか？

問題文を正しく理解するために ” 線分図 ” を使って整理するのが良いです。なぜ “線分図” を使うのでしょうか？ 理由はシンプルです。線分図がイチバン “全体の差” をイメージしやすい からです_φ(･_･

１個２００円のドーナツを□個かう場合の線分図と、１個１８０円のリンゴを□個かう場合の線分図。２本の線分図を並べて描いてみましょう。この２本の線分図の長さの差が “全体の差” ですねd(^_^o)

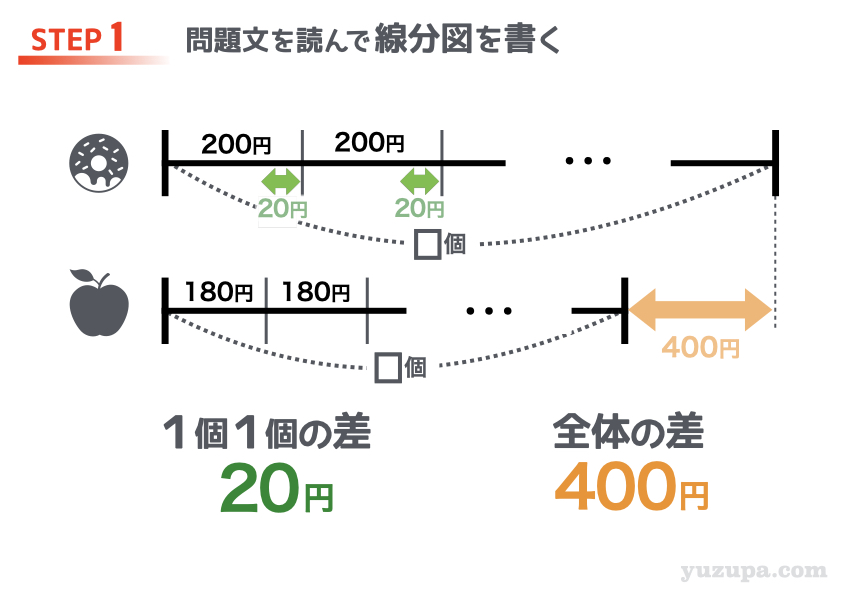
このように “線分図” で整理すると… “１個１個の差” を集めた結果が “全体の差” になる事が視覚的に分かります よね？ でもこれは序の口。このあと紹介する例題でさらに “線分図” の本領を発揮しますd(^_^o)

そして…いよいよ”差集め算”の本質 です
“１個１個の差” をぜーんぶ集めてきて “全体の差” とイコールで結んでしまいましょう！

ここまで来れば、あとは計算するだけです。□は20個になりますね。答えは 20個 ですd(^_^o)

 

なぜ “線分図” を使うのか？

塾の先生によってはこの問題を “差集め表” を使ったり、”方程式もどき” を使ったりします。でも…この２つの解法にはちょっとうちの娘には受け入れがたいデメリットがありました(-_-;)

“差集め表” は “全体の差” がよく分からなくなる という大きな課題がありました( あくまでもウチの娘の場合です(-_-;) )。“方程式もどき” は負の数の計算が出てくる という課題があります。

引き算の結果がマイナスになることを正しく理解している。つまり… 負の数の基本的な概念をマスターしているようであれば “方程式もどき” でも全く問題なく、むしろそちらの方が良いかと思いますd(^_^o)

 

 

“差集め算”をマスターするための７例題

“差集め算” の基本は理解いただいたかと思いますが、基本問題だけで攻略できるほど中学受験は甘くありませんよね(-_-;) スンナリとはいかない変化球がまぎれているのが中学入試です…。

差集め算の 基本を中心とした７つの例題 をご紹介しますd(^_^o)

 

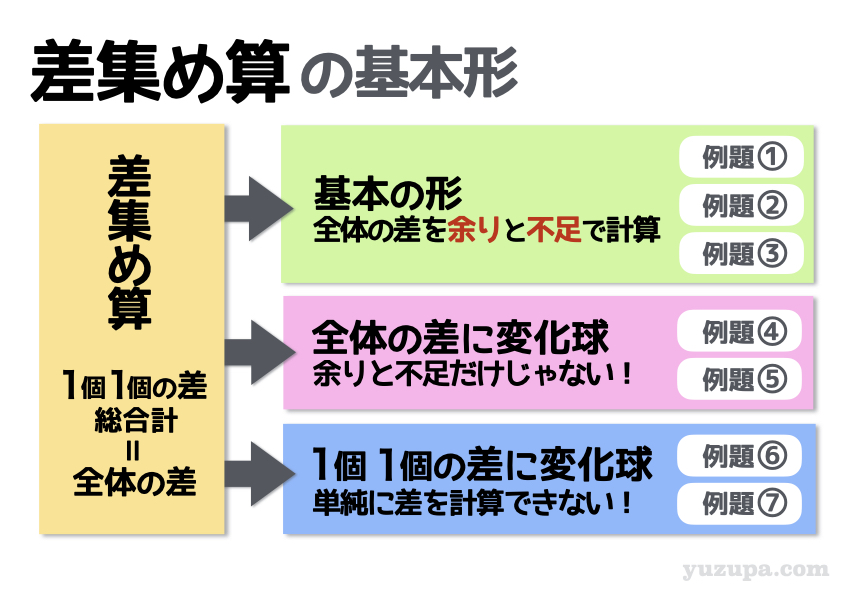
例題① 基本の形(余りが出る)

さっそく例題の１つ目です。この問題はいわゆる “過不足算” とも呼ばれる問題です。１人あたりに配る枚数が５枚だったり７枚だったりするので “１個１個の差” はすぐに分かるかと思いますが “全体の差” は分かりますか？

さっそく “線分図” を描いてみましょう。

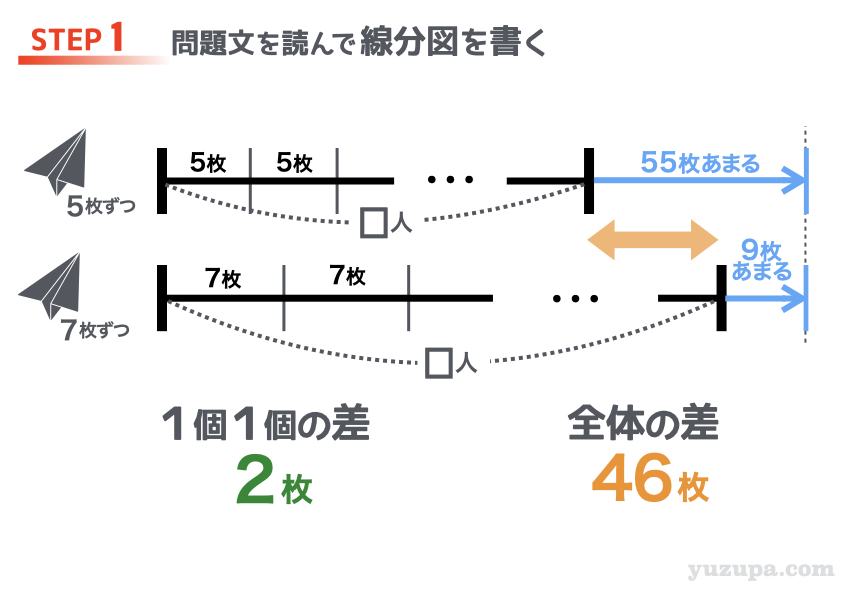
□人に５枚ずつ配った場合には… 折り紙は55枚あまるということですので、実際の折り紙の数は当然ですが、この線分図よりも55枚分だけ長くなりますd(^_^o)

□人に７枚ずつ配った場合には…折り紙は9枚あまるということですので、実際の折り紙の数は、同じく線分図よりも9枚分だけ長いということになりますねd(^_^o)

そうすると…２本の線分図の “全体の差” がイメージで分かりますねd(^_^o)

“全体の差”は 55枚ー9枚＝46枚 です。

そして 差集め算の本質ですd(^_^o)
“１個１個の差” をぜーんぶ集めて “全体の差” とイコールでむすびましょう！

ここまでくれば 残るは計算のみです。 □は２３人になりますね！

ただし注意が必要です。問題で求められているのは折り紙の枚数 ですから、5枚×23人+55枚を計算する必要があります。もちろん7枚×23人+9枚でも計算できますd(^_^o)

答えは 170枚 です

 

例題② 基本の形(ある時は不足,ある時は余る)

例題①と同様、いわゆる “過不足算” と呼ばれる問題ですが、今度は配ったものが “あまる” ばかりでなく “不足” する 条件も含まれています。これも線分図を描いて全体の差をイメージでつかみましょう_φ(･_･

さっそく “線分図” を描いてみます。

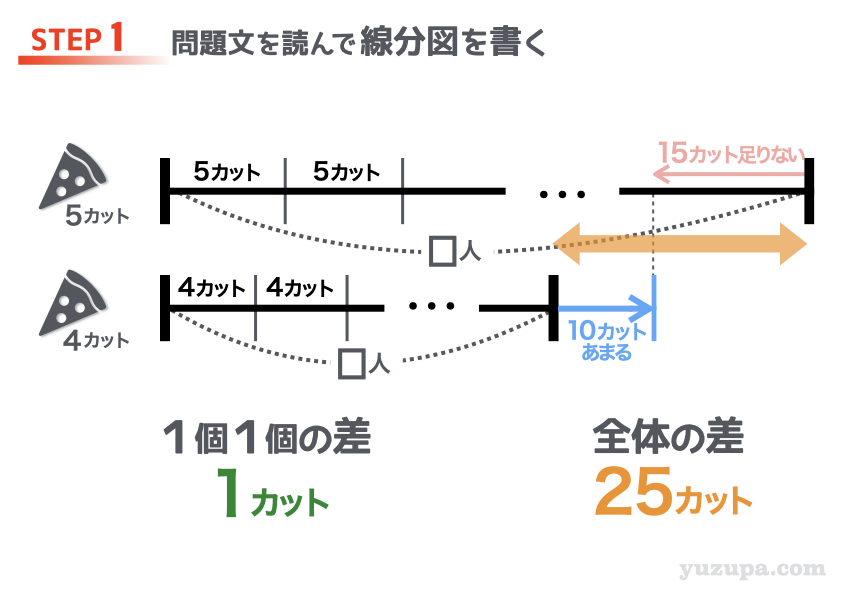
□人に５カットずつ配った場合には、15カット足りないということですので、実際のピザの枚数 は線分図よりも15カット分だけ短く なります。

いっぽう、□人に４カットずつ配った場合には、10カット余るということですので、実際のピザの枚数 は線分図よりも10カット分だけ長くなりますねd(^_^o)

そして２本の線分図の “全体の差(オレンジの矢印)” がイメージで分かりますねd(^_^o)

“全体の差” は 15枚＋10枚＝25枚です。

そして “１個１個の差” をぜーんぶ集めて “全体の差” とイコールでむすびましょう！

式を立てれば計算のみです。この問題の場合は、計算は超簡単ですね。□は25人です。問題文ではピザの枚数を問われています ので 計算で出しましょうd(^_^o)

４カット×２５人＋１０カット＝１１０カット

答えは 110カット ですd(^_^o)

 

例題③ 基本の形(不足が出る)

基本形の３つ目も “過不足算” と呼ばれるものですね。最後のパターンは 配ったものが不足しまくるパターンの問題 ですね。これも線分図を書けば “全体の差” が分からなくなることはありませんd(^_^o)

では “線分図” を描いてみましょう。

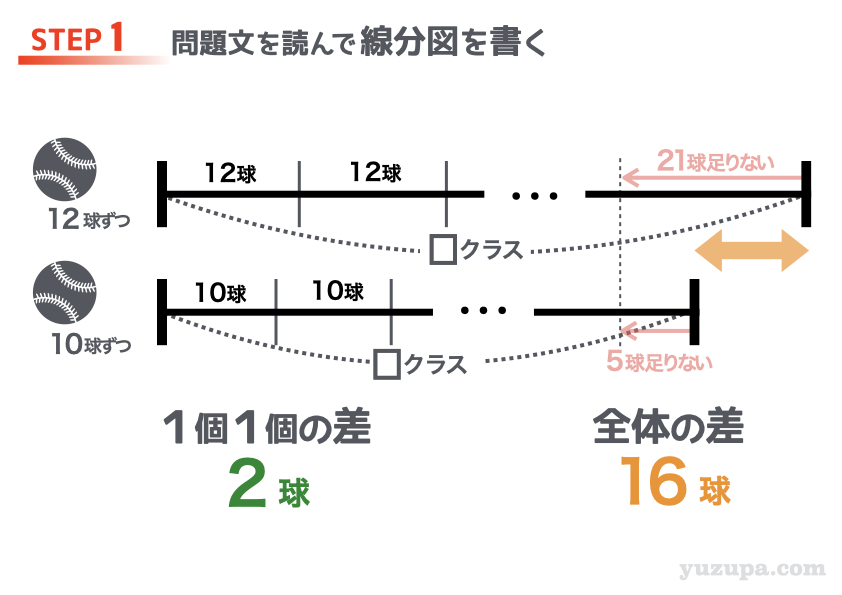
１クラスに１２球ずつボールを配った場合、２１球たりないということなので、実際のボールの数は線分図よりも２１球分だけ短く なりますねd(^_^o)

また、１クラスに１０球ずつボールを配った場合も、５球たりないということなので、実際のボールの数は線分図よりも５球分だけ短く なります_φ(･_･

２本の線分図の “全体の差” がイメージで分かります。２１球ー５球＝１６球ですd(^_^o)

線分図が描けたら “１個１個の差” をぜーんぶ集めて “全体の差” とイコールでむすびましょう！

最後は計算しましょう。□は８クラスになりますね！問題文で求められているのはクラス数ですので、答えはそのまま ８クラス となります。

 

例題④ 全体の差に変化球(1)

今までの問題は “全体の差” を 余り や 不足 を使って求めてきました。ここで変化球です (-_-;) 具体的な数字が書かれておらず、ちょっと遠回りな感じで書かれています。“全体の差” がいくつか分かりますか？

線分図を描いてみます。

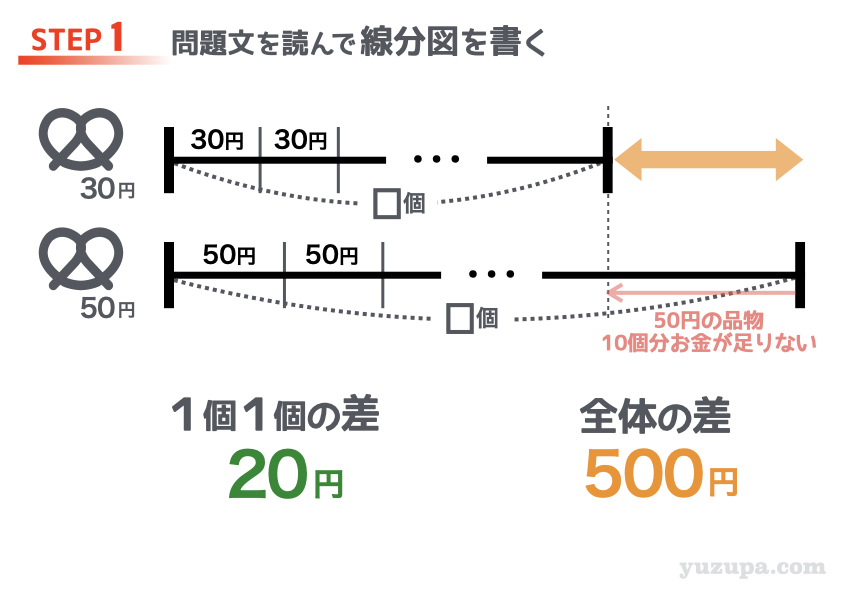
１個３０円のお菓子を□個、かえるだけのお金を持っていき、１個５０円のお菓子を同じく□個かおうとしたところ１０個分のお金が足りなかったと考えます d(^_^o) 

すなわち、２本の線分図の “全体の差” は ５０円のお菓子１０個分となります。

５０円×１０個＝５００円 です。

いつものように、”１個１個の差” を全て集めてきて “全体の差” とイコールでむすびます！

計算をしてみると、□は２５個であることが分かります。問題文で求められているのは 最初に買おうとしたお菓子の数 ですので、答えはそのまま ２５個 になりますd(^_^o)

 

 

例題⑤ 全体の差に変化球(2)

全体の差がスンナリとは分からないという例題をもうひとつご紹介します。例題④よりもさらに複雑になっていますが、線分図を描くところに集中するのがコツ ですねd(^_^o)

線分図を描いてみましょう。

4600円のカメラを□個 かうことができる所持金で、2100円の腕時計を同じ数だけ買った場合、さらに８個買う事ができる上に700円余るということ… ２本の線分図の “全体の差” もイメージできるでしょう。

１６８００円＋７００円＝１７５００円 ですd(^_^o)

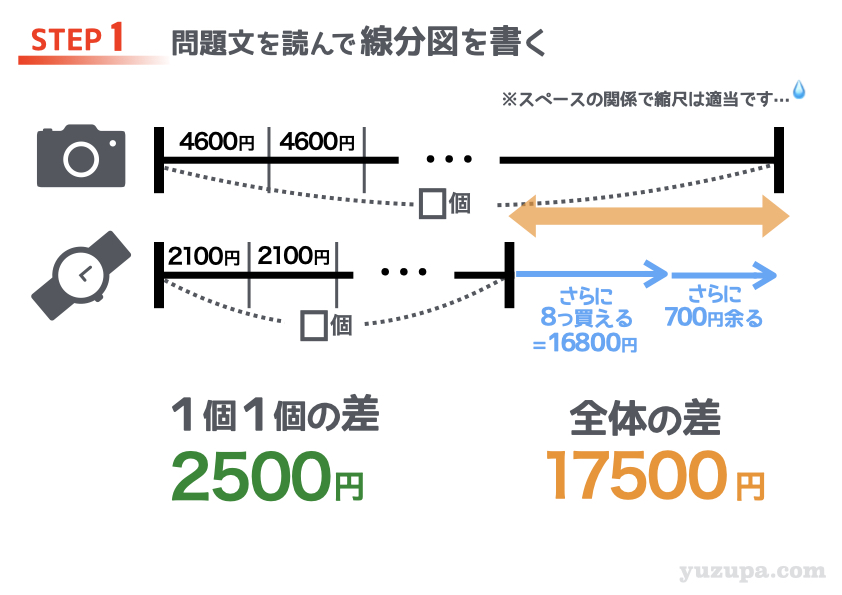
もう定番ですが “１個１個の差” をぜーんぶ集めて “全体の差” とイコールでむすびます！

計算をしてみると□は７個になりますね。問題では太郎くん所持金を求められていますので、カメラを７個買えるお金…４６００円×７個＝32200円 が答えですd(^_^o)

 

例題⑥ 1個1個の差に変化球(1)

ラスト２問です。こちらの問題は “１個１個の差” にちょっと変化球がまぎれこんでいる問題 です。”１個１個の差” をぜーんぶ集める時に注意が必要ですd(^_^o)

さっそく線分図をかいてみましょう！

１つのテントに５人ずつ入った場合の線分図はシンプルに描けますね。１つのテントに６人ずつ入ると最後の１つのテントは２人 になったということから以下のような線分図が描けます。

最後のテントだけ差が違うので…
“１個１個の差”が途中で変わってしまうように感じます∑(ﾟДﾟ)

ポイントは”１個１個の差”が途中で変わったと感じても気にしないことですd(^_^o)

落ち着いて考えると “最後のテントが２人”というのは…“(テントを全部埋めるには)４人足りなかった”と言い換えることができますね。

見方を変えただけで基本問題になりました！

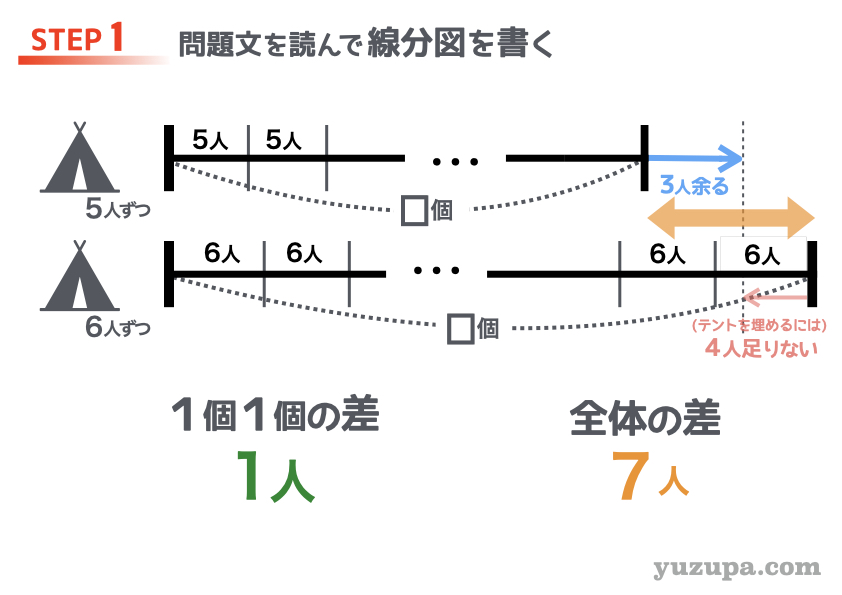
ここまできたらいつもどおり”１個１個の差”を全て集めて”全体の差”とイコールで結びましょうd(^_^o)

計算をすると□は７個になりますね。この問題ではクラスの人数が何人かを聞かれています。 ５人×７テント＋３人＝３８人となり、答えは３８人となりますd(^_^o) もちろん ６人×７テントー４人でも計算できます。

 

例題⑦ 1個1個の差に変化球(2)

いよいよ最後の例題です。今までの問題は “１個１個の差” は実際の数から分かるようになっていましたが、この問題は差だけが分かっている問題 です。いっけん難しそうですが本質が分かっていれば楽勝です d(^_^o)

いつもどおり線分図を描いてみましょう。

高級いちごを１４個買うお金で、普通のいちごは２０個買えるということは… 普通のいちごは高級いちごと同じ数の１４個を買ったとしても、さらに６個買えるということですねd(^_^o)

“１個１個の差” はそれぞれの値段がわからなくても 問題文に１５円と書かれています∑(ﾟДﾟ) そして “全体の差” は普通のいちごの値段 △円×６個 になります。

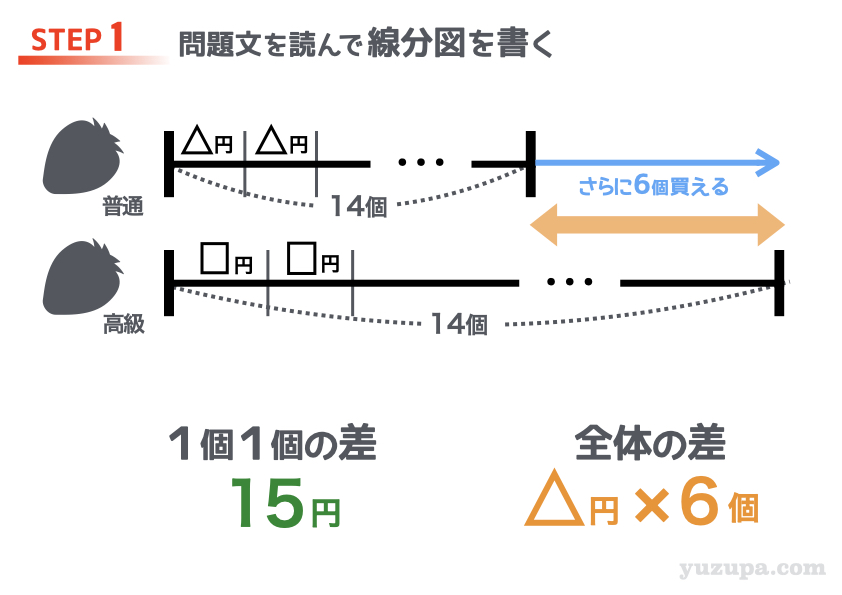
いよいよ最後です…　”１個１個の差” を全て集めてきて “全体の差” とイコールでむすびましょう！

計算をすると△は３５円となります。普通のいちごの値段は１つ３５円、高級いちごの値段は１つ５０円 ですね。問題文で求められているのは高級いちごの値段ですので 答えは５０円 となります。

 

まとめ

今回は娘が苦戦した “差集め算” について解説しましたd(^_^o)

応用問題になると途端にできなくなってしまうのは…なぜなのだろうか？ 理由はシンプルで “本質” ではなく”やり方”で覚えてしまっているから。本質は “１個１個の差” を全て集めると “全体の差” になること。

つまり…問題を解くキーワードは
“１個１個の差” を全て集めてきて
“全体の差” とイコールで結ぶ！
ですd(^_^o)

中学受験の世界では “特殊算” と呼ばれる、独特の世界観があります。当ブログ調べでは２３種もの特殊算が市民権を得ているようです。特殊算については以下の記事をご参照くださいd(^_^o)

参考：特殊算は何種類ある？算数の文章題の見分け方