中学受験：集合算とは？ ベン図を使ったシンプルなパズル問題だ！

ベン図が描ければ解けます…そしてベン図は２つのステップで描け！

こんにちは。かるび勉強部屋 ゆずぱ です。

集合算がナニモノなのか分からない… どうやって問題を解けば良いのか… ベン図を使えって言われるけど書き方がよく分からない… パズルが思うようにできない…　

ベン図は２つのステップを意識すると
意外とアッサリ描けます

子供がベン図を描けない様子を観察すると、まず数字を埋めるところ でつまづき、次にベン図どうしが 重なったところの扱い につまづいている模様です…(-_-;)

さっそく 具体的な２つのステップにまいりましょう！

 

集合算とは…人や物や数の集団を扱う問題

集合算は 特徴のある集団 を扱う

ベン図の扱い方を説明する前に…　どんな時にベン図を使えば良いのか？ そのあたりからおさえておきましょう_φ(･_･

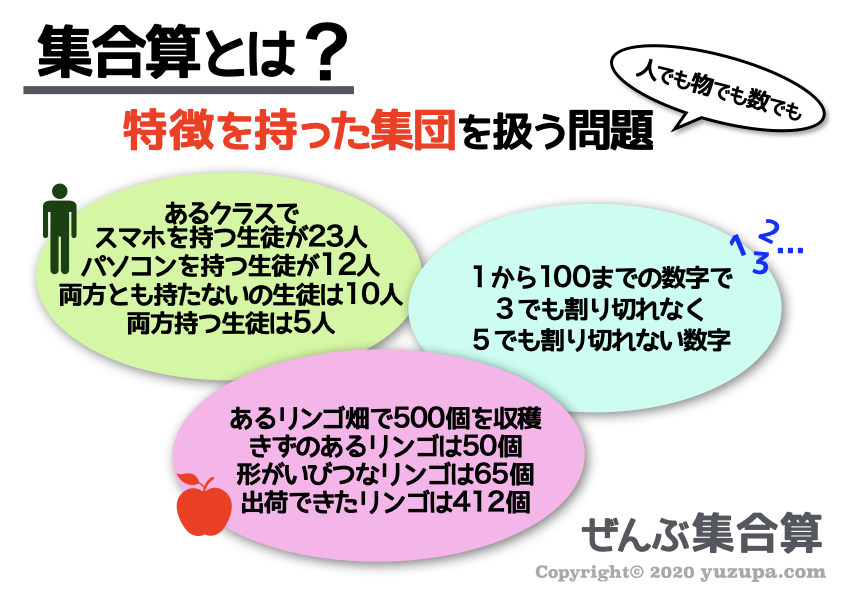
集合算はナニモノかを一言で表現すると… 特徴を持った集団 を扱う問題 です。人でも物でも数もですd(^_^o)

メジャーなのがクラスの生徒を 特徴ごとにグループ化してその人数が示される 問題です。もちろんクラスだけではありません。

リンゴの特徴で分けた集団を扱ったり、３で割れる数 とか ５で割れる数 みたいな数字の集団 でも集合算の解き方が有効です。

 

ベン図を描く２つのステップ

集合算を解く時には 意識すると良いこと がありますd(^_^o)

それは… ベン図を描くときに ２つのステップを意識する こと。たったコレだけで驚くほど描きやすくなります ∑(ﾟДﾟ)

 

１つ目は…まずベン図の基本となる ”４つの領域”と”３つの数字”を意識 して問題文を読み、数値を埋めていくという点。

２つ目は… 問題文からは直接的には読み取れない部分を埋めていく時に ３つの計算テクニックを使う という点。

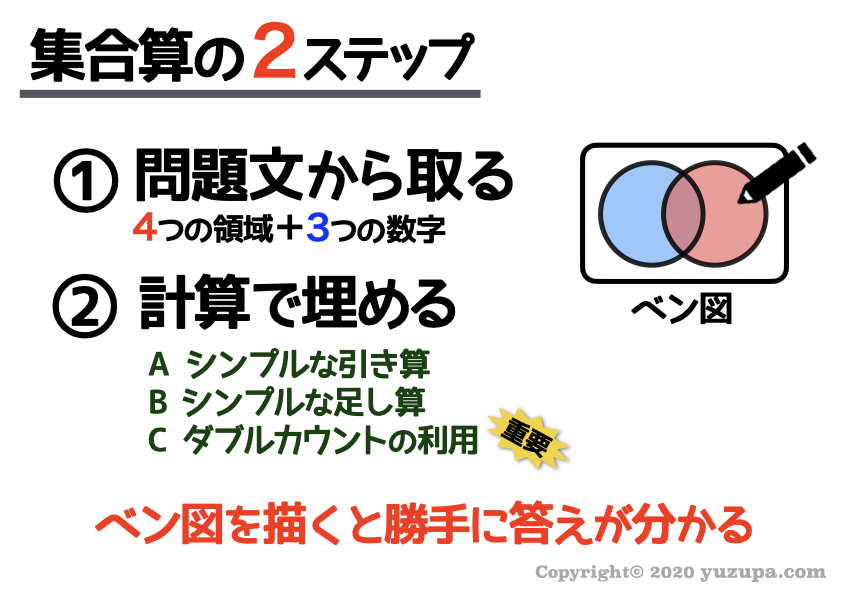
特に 集合算の独特の考え方となる ”ダブルカウントを利用” した計算テクニックは超重要です d(^_^o)

それでは、以下の例文をもとに１つずつ詳細をみてみましょう。

 

絶対に意識すべき”４つの領域”と”３つの数字”

お子様はヤミクモにベン図を描こうとしていませんか？

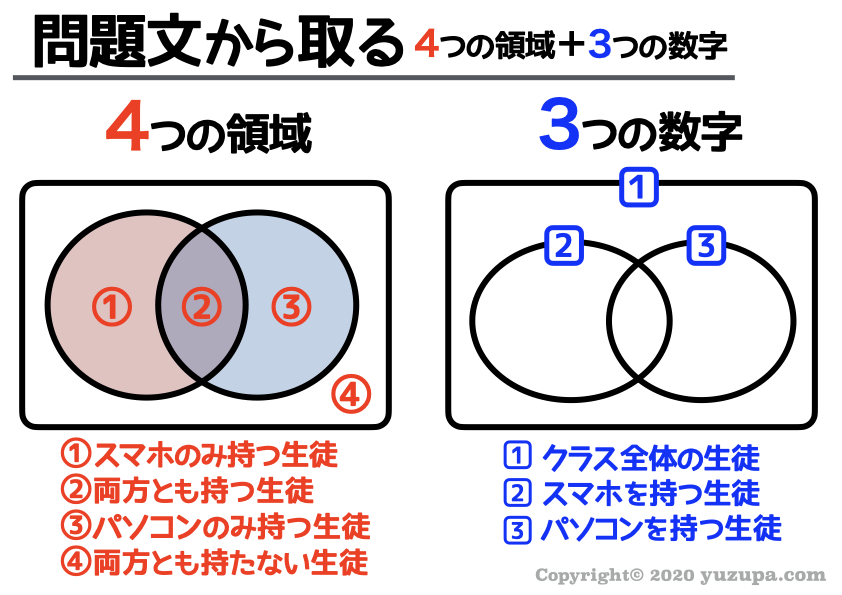
ヤミクモにベン図の数字を埋めようとするるのではなく、上記の４つの領域と３つの数字を埋めることを目標にする！

 

左側の図は ベン図を構成する４つの領域 です。この４つの領域の数量さえ分かってしまえば全てが分かります∑(ﾟДﾟ)

右側の図は 問題文によく出てくるヒントです。具体的には 全体の数量 と ひとつの特徴だけに着目した数量 です_φ(･_･

 

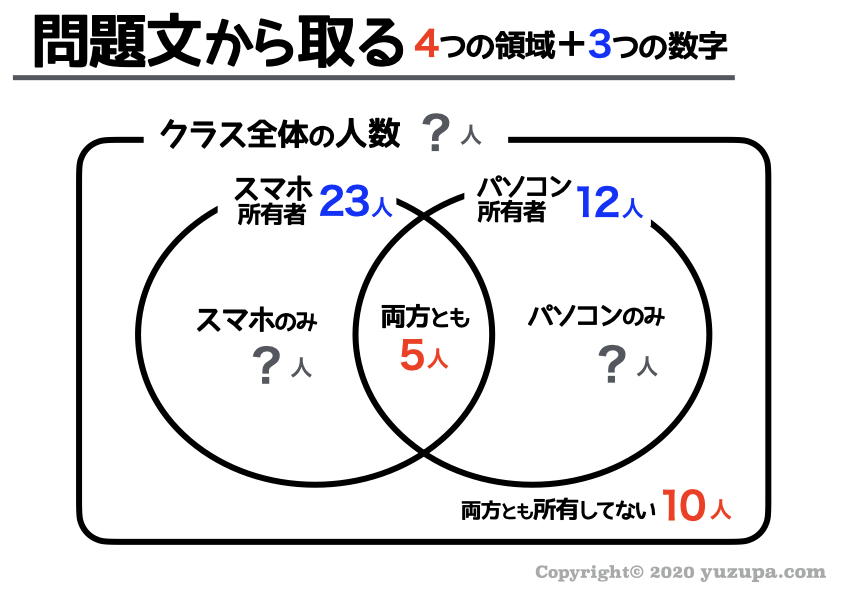
実際に問題文に書かれている４つの数字を埋めると以下のようになります。”４つの領域” と “３つの数字” のどれかという視点を！

 

未知の部分を埋める計算テクニック３つ

問題文から直接的に埋めることができる数字を全て埋め切ったら、今度は未知に部分を計算で 埋めていきますd(^_^o)

３つの方法がるので１つずつ紹介します。

 

a. シンプルな引き算

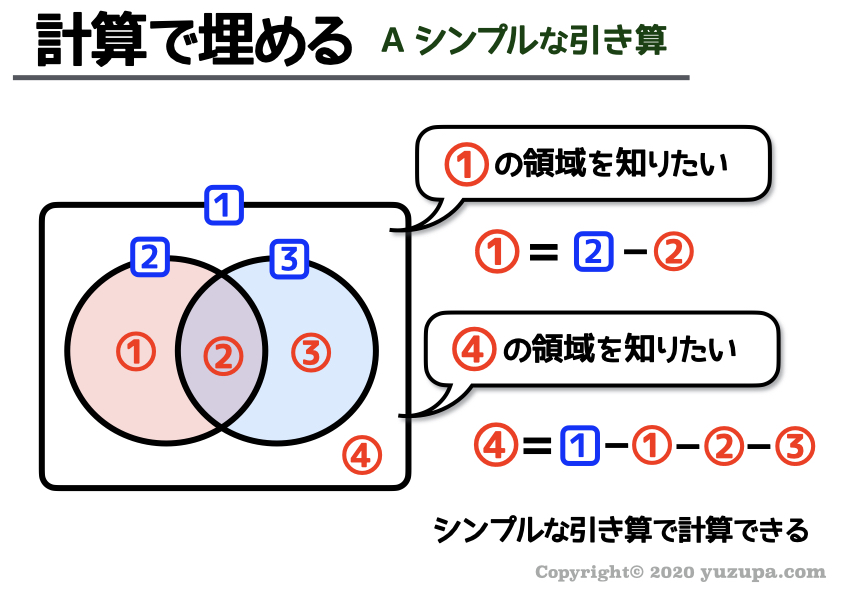
シンプルな引き算で未知の数字を埋めることができますね。面積の問題と同等の考え方です。引き算のパズルですd(^_^o)

 

b. シンプルな足し算

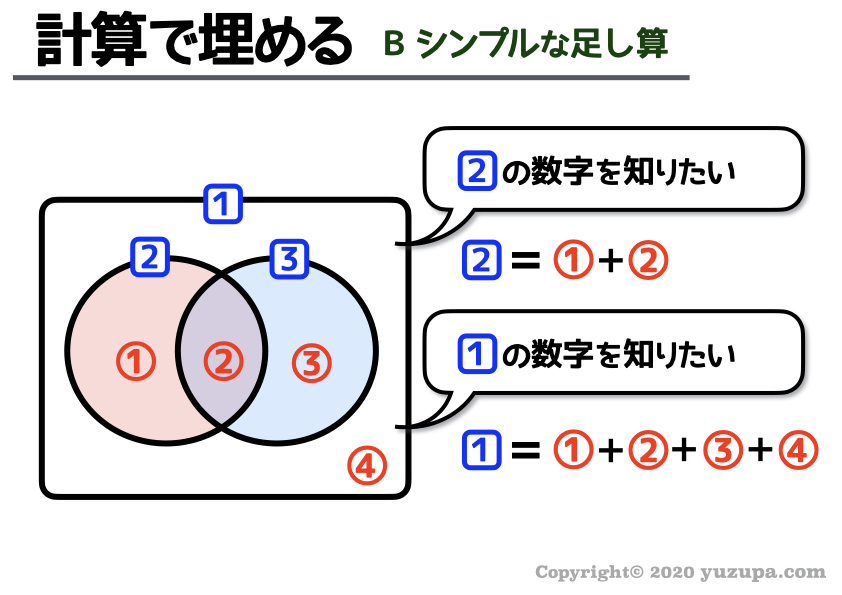
今度はシンプルな足し算です。これも面積の問題ではお馴染みですね。領域の数量をガンガン足していきましょう(^_^;)

 

c. ダブルカウントを利用

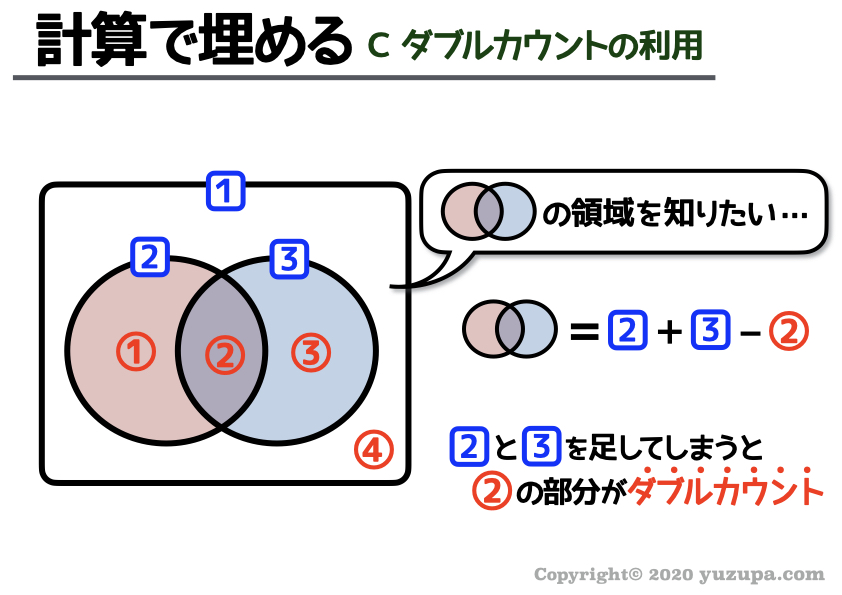
コレが集合算ならではの超重要ポイントです。図のような領域の数字を知りたい時に ２回足してしまったところを後から引いてあげる というテクニックですd(^_^o)

集合算でパズルがうまくいかないなぁと思ったら… このダブルカウントを試してみる と高確率でゴールにたどり着けます∑(ﾟДﾟ)

 

上記３つの計算テクニックを使って、冒頭の問題文のベン図を埋めてみると以下のようになります。

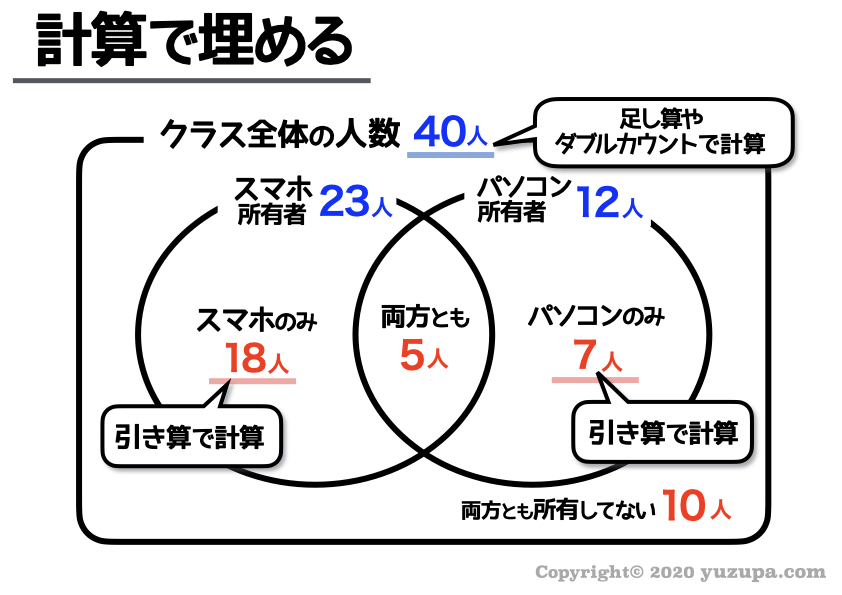
ベン図を書ききると勝手に答えがでます∑(ﾟДﾟ)

これが集合算の特徴。ベン図を２つのステップでひたすら描く作業 をしているうちに答えが自然と導き出されます。

このクラスの人数は４０人  というのが答えですね。

 

 

実際の集合算をベン図で解いてみる(1)

集合算の問題の解き方がわかったところで、もういっちょ行ってみましょう。今度は人ではなくリンゴの集団 ですd(^_^o)

 

① 問題文から取る

さっそくベン図を描きはじめましょう。意識する点はもちろん ”４つの領域” と “３つの数字” ですね d(^_^o)

問題文に出てくる数字を全て埋めることができましたか？

 

② 計算で埋める

今度は直接問題文には書かれていないところを計算で埋めていきます。ところが…パズルがむずかしいですね(-_-;)

パズルが難しかったらどうする んでしたでしょうか？

迷ったら ”ダブルカウントの利用” を試してみましょう！これは集合算の鉄則です。さて…どうなるでしょうか？

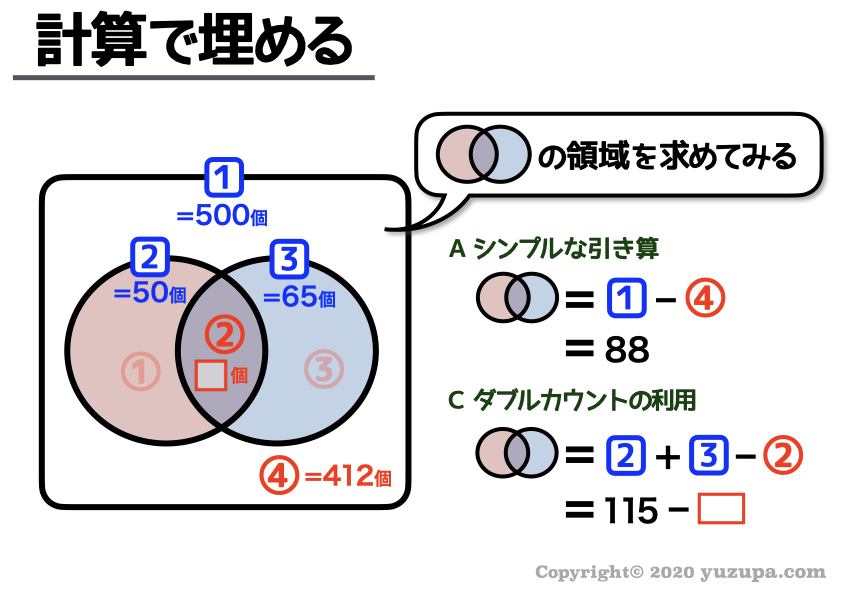
この ”ダブルカウントの利用”の部分に着目すると、答えが見えてきます。引き算で計算すると88になります。ダブルカウントの利用で計算すると115-□という式になります。

そうすれば □が27であることが計算できます ねd(^_^o)

 

求める答えが27なので、これ以上 ベン図を埋める必要はありませんが、念のため…。完成したベン図は以下です。

 

実際の集合算をベン図で解いてみる(2)

せっかくなのでもう１問といてみましょう。今度は人でも物でもなく 苦手な子供も多い数の集団 ですd(^_^o)

問題を解く前に２つの必要知識

この問題ちょっと厄介じゃありませんか？

なんとなく数字の集団が扱われているのですが、具体的にその数量がひとつも問題文に書かれていない んです(･_･;

 

集合算の本質に入る前に…

この問題を解くのに 必要な２つの知識 をご紹介します。

１つ目は ”割り切れる数” のとらえ方です。といっても超シンプルですd(^_^o)  ○で割り切れる数＝○の倍数と考えればOK です。

２つ目は “倍数の個数の数え方” です。1から100までの数字の中に色々な 倍数がいくつ含まれているかは割り算で わかりますd(^_^o)

必要な２つの知識をオサライしたところで、さっそく問題を読みながらベン図を書いてみましょう！

 

① 問題文から取る

この問題のポイントは ”３で割り切れる数” を “３の倍数” ととらえなおしてベン図を描くことにありますd(^_^o)

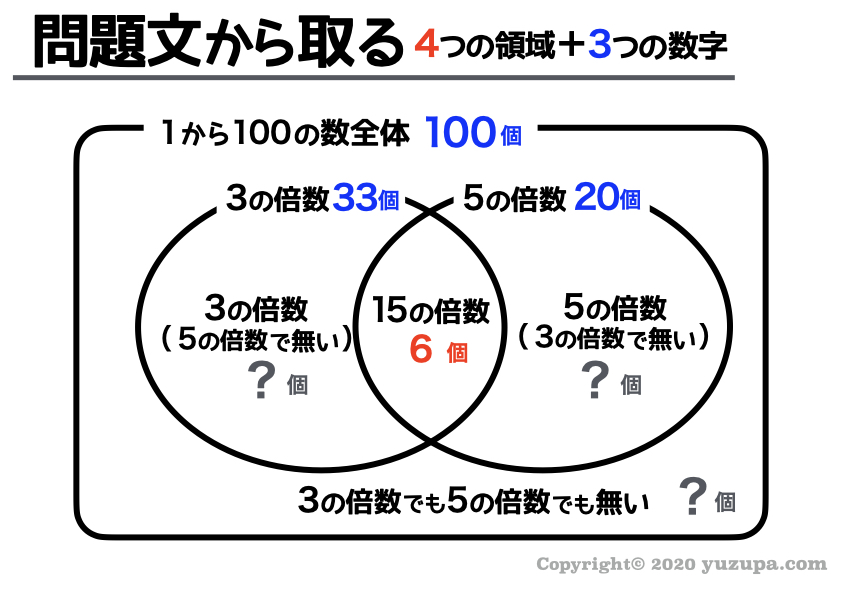
ちなみに…３の倍数でありながら５の倍数である数字(つまりベン図が重なったところ)は15の倍数 ですね_φ(･_･

 

② 計算で埋める

今度は直接問題文には書かれていないところを計算で埋めていきます。今度は シンプルな足し算や引き算でガンガン埋まります ね！

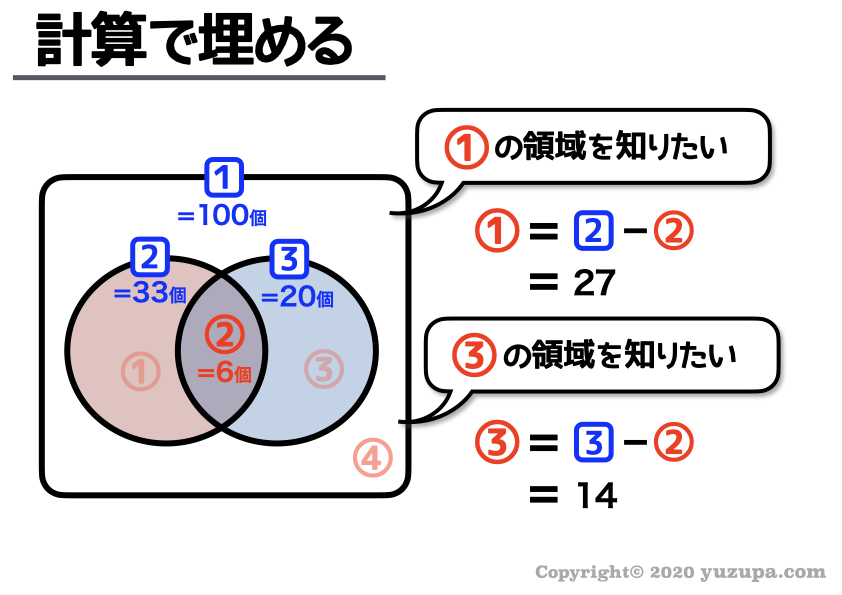
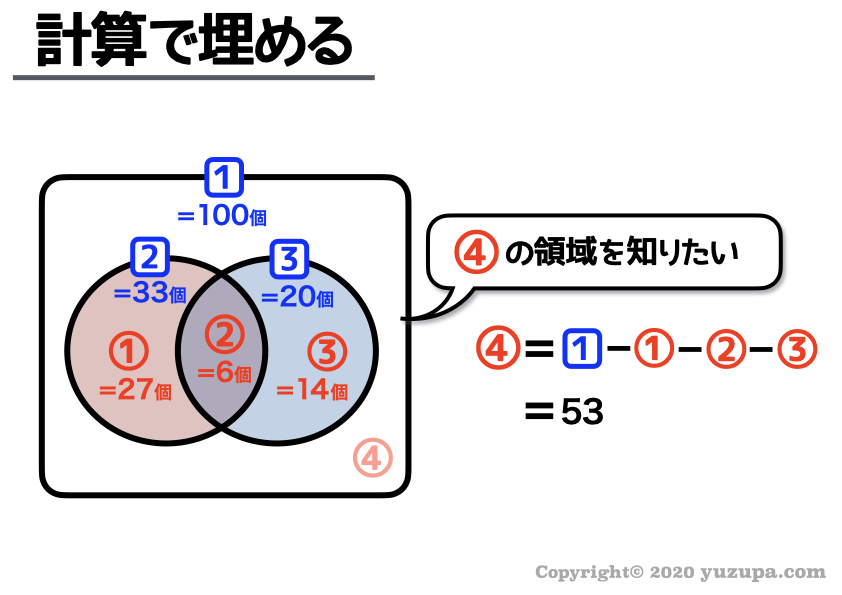
そして完成したベン図が以下のようになりますd(^_^o)

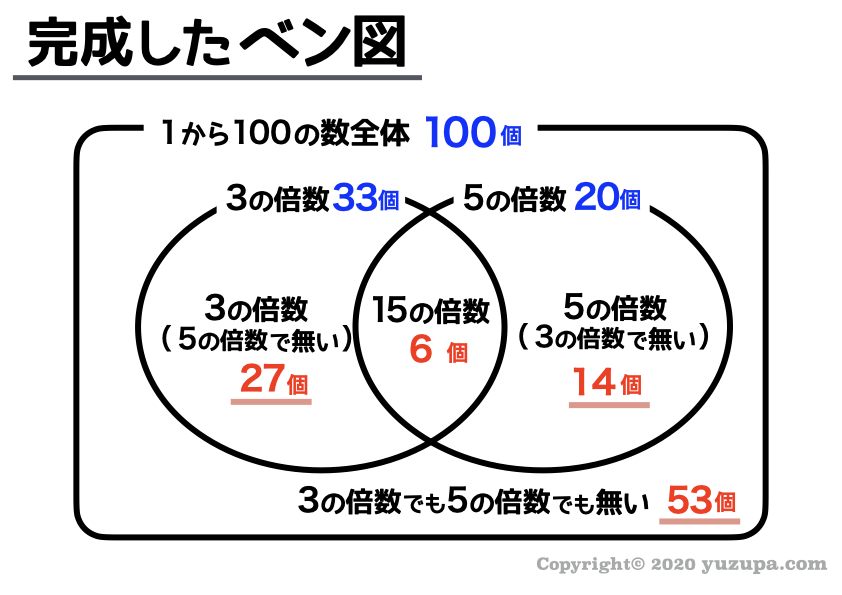
今回求められているのは、３でも５でも割り切れない数 ですので、答えは５３個 になります。

 

以下はご参考 ( 別の解法 ) です。

実は ダブルカウントの利用 を使うと… コツコツとベン図を埋めなくてもサクっと答えがでちゃいます∑(ﾟДﾟ)

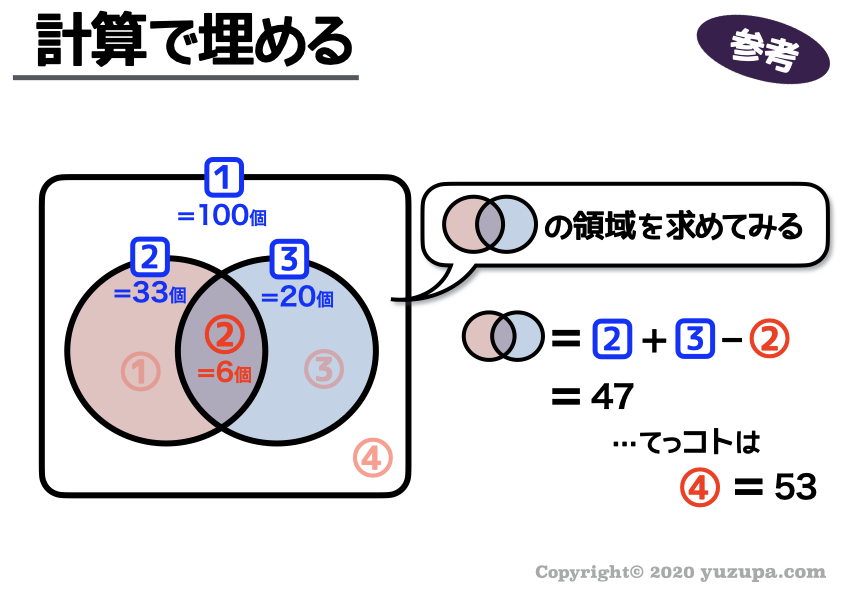
集合算においては このダブルカウントの利用 が超重要 ですので、できるかぎり使うようにしましょう。

 

 

応用問題…条件が増えても慌てるな！

条件が３つでも慌てずにベン図を描く

最後に応用的な集合算をご紹介します。

集合算の中には、条件が３つ以上のもの があります ∑(ﾟДﾟ) 問題文もやたら長く…慌ててしまいそうです(-_-;)

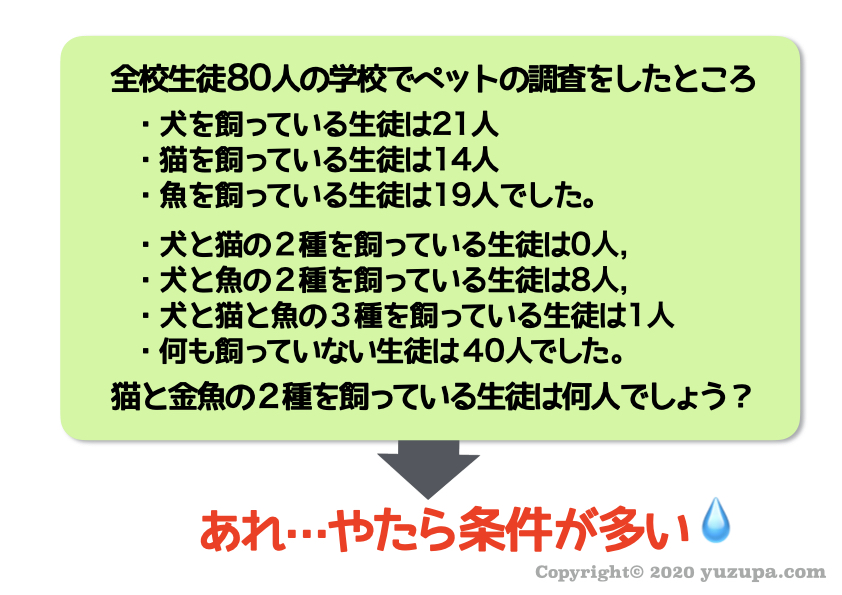
そんな場合でも慌てずにベン図を描きましょう。

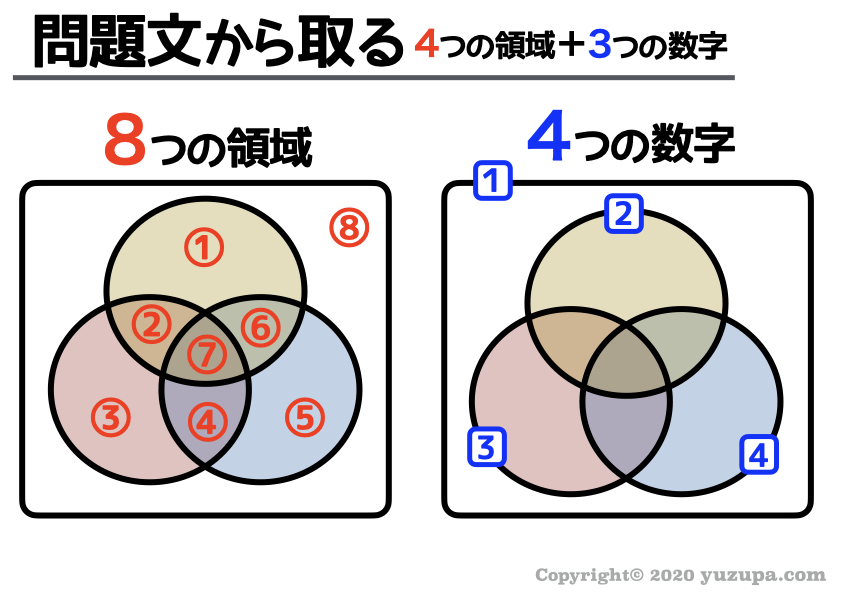
ただし 条件が３つの場合には領域が８つ に増えますので、以下の図を参考に問題文から吸い出しましょう。

 

トリプルカウントを利用せよ

そして…計算方法もレベルアップする必要があります。

トリプルカウントの利用 です∑(ﾟДﾟ)

難しいようですが ダブルカウントの利用 を理解していれば、難しいことはありませんd(^_^o)

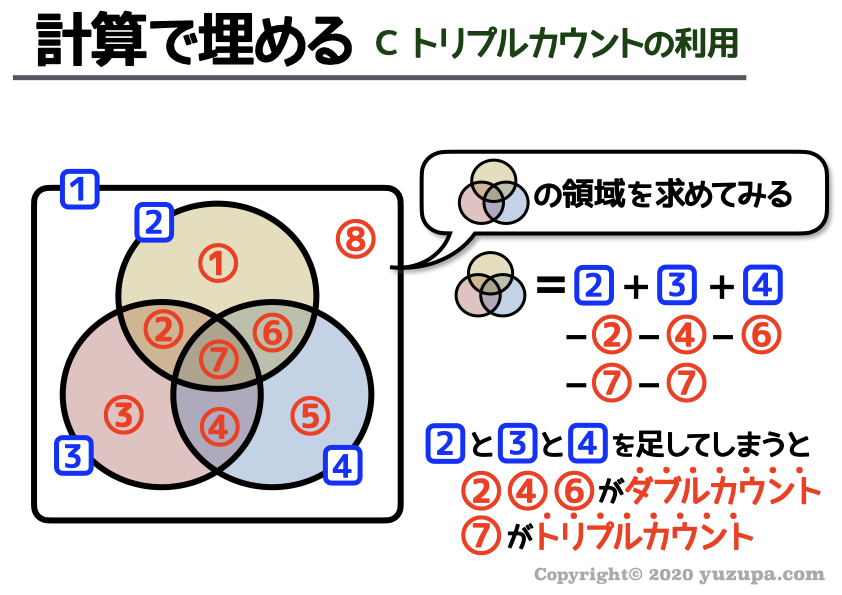
注意すべきところは ダブルカウントしてしまったところは、単純に引いてあげれば良いのですが トリプルカウントしてしまったところに関しては２回 引いてあげる必要 があります_φ(･_･

 

まとめ

今回は集合算について解き方のコツをご紹介しました。

基本的にはベン図さえ描けてしまえば解けるのですが、そのベン図の描き方が分からない…(-_-;)

ポイントは２つのステップで描くこと！