中学受験：植木算の公式は忘れろ！ “スキマ”と”植木”の対(つい)を作れ！

植木算は区画整理をした上で “スキマの数”と”植木の数”で対を作れ！

こんにちは。かるび勉強部屋 ゆずぱ です。
植木算という算数の解法があることをご存知でしょうか？ 例のごとく私は子供の中学受験を経験するまで知りませんでした(^_^;) 特殊算と呼ばれる算数の解法のひとつですが…

植木算の公式なるものが存在してるんですが…
応用がきかず使い物にならない∑(ﾟДﾟ)

植木算もしっかりと 順序を踏んで情報を整理していけば簡単に解く事ができます。本記事では公式では無く…植木算の解き方を詳しく解説しています。ぜひご参考くださいd(^_^o)

参考リンク：特殊算は何種類ある？算数の文章題の見分け方

 

そもそも植木算とは？

植木算とは何か？

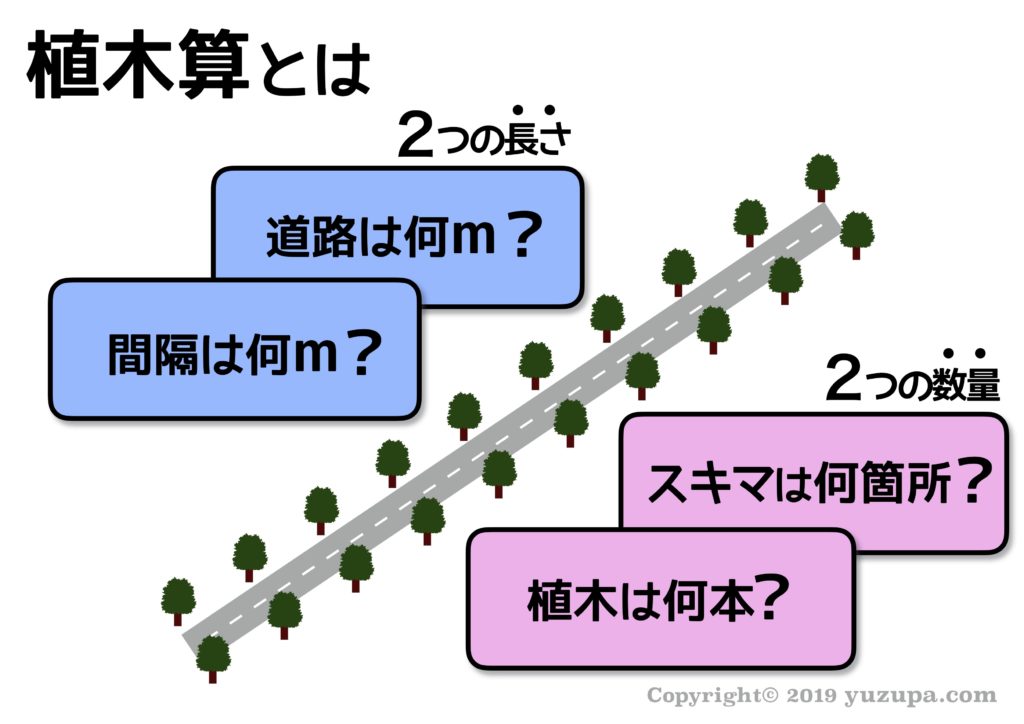
植木算の正体は… 道路の両脇に並木を整備するようなシーンで、必要な木の本数を求めたり、木と木のスキマの距離を求めたり、道路全体の長さを求めたりする問題 ですd(^_^o)

そして…道路だと直線上に木を植えますが、円形状の湖の周りに木を植える場合もあったり、畑のような平面に木を植える場合もあります。でも全て共通している事があります。

それは ２つの長さと２つの数量…全部で４つの要素 で考えるという事ですd(^_^o)

植木算…まずは”区画整理”

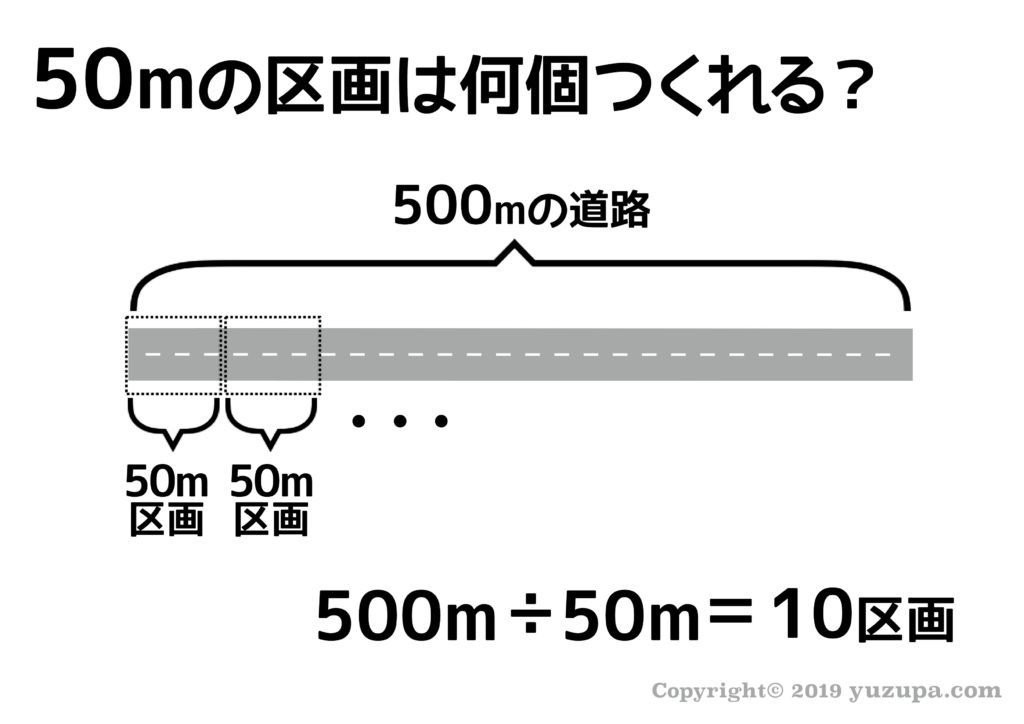
植木算で最初に考えること…それはいわゆる “区画整理” です。５００mの道路から５０mの区画は何区画とる事ができるでしょうか？ 計算で割り出すことができますねd(^_^o) ５００÷５０で１０区画です_φ(･_･ 

平面でも一緒です。縦２４０m 横４８０mの土地から、縦１２m 横１２m の区画はいくつとることができるでしょうか？ 計算は省きますが、縦は２０区画とれ、 横は４０区画とれますのでで８００区画取ることができます_φ(･_･
※ ちなみに１２m×１２mの土地はおおよそ４５坪です(^_^;)

“スキマの数”と”植木の数”に気をつけろ！

これこそが 植木算の本質ではないでしょうか？ 植木算の公式とやらを作った人も… きっとコレが言いたかったのでしょう。”スキマの数”と”植木の数” は同じ数でしょうか？同じ場合もあれば違う場合もあるんですd(^_^o)

ポイントはシンプル…
“スキマ”と”植木”を対(つい)にすること！

 

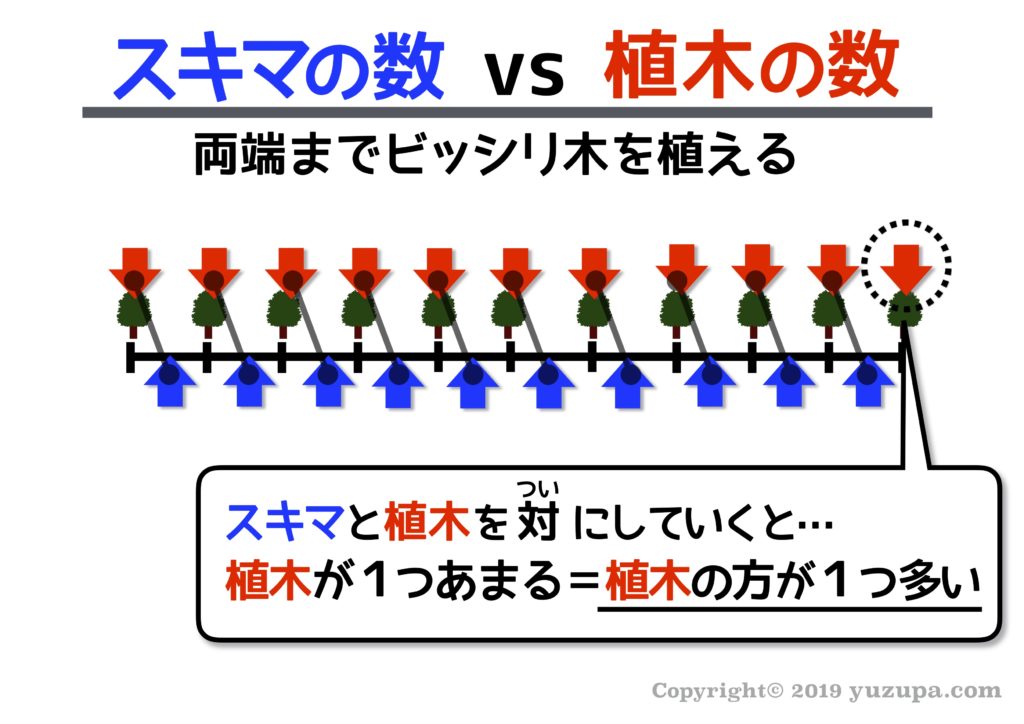
上図のような植え方の場合… “スキマ”と”植木”を対(つい)にしてみると植木が１つあまってしまいます ねd(^_^o) つまり”スキマ”よりも”植木”の方が１つ多いという事がわかりますd(^_^o)

上図の場合はどうでしょうか？今度は”スキマ”がひとつあまりました。この植え方の場合は”スキマ”の方が”植木”よりもひとつ多いということがわかりますねd(^_^o)

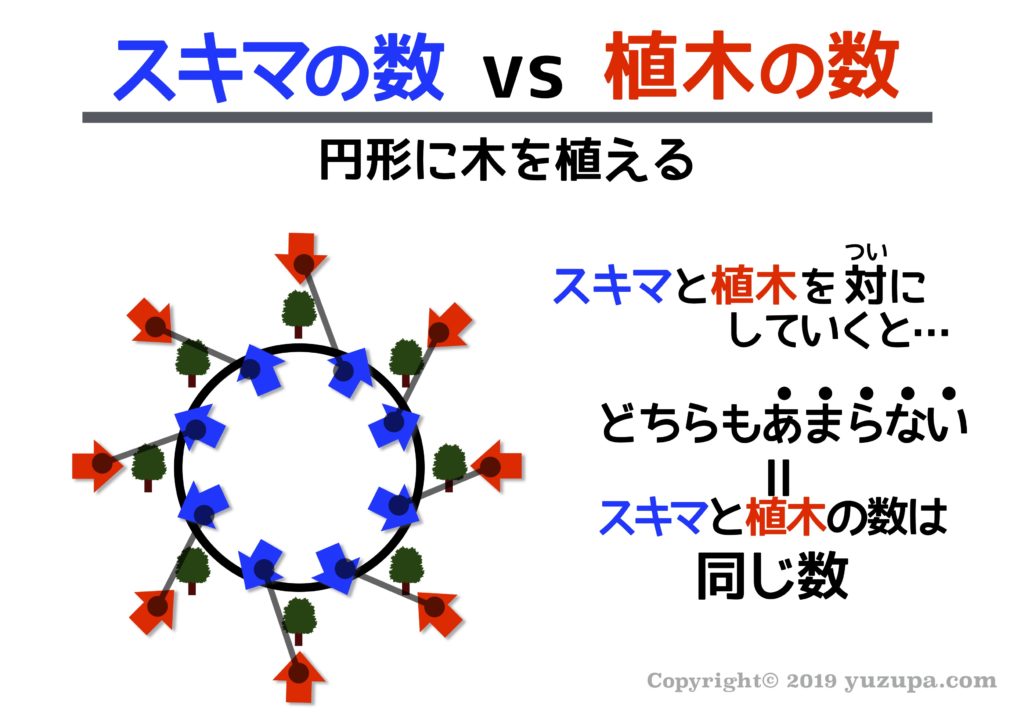
では木を円形に植える場合はどうでしょうか？ 同様に”スキマ”と”植木”を対(つい)にしてみると…今度はどちらもあまることなくピッタリ一致しました。つまり”スキマ”と”植木”は同じ数ですd(^_^o)

以上はほんの一部でパターンはいくらでもありますd(^_^o)

ですので 公式なんか忘れてしまい…
“スキマ”と”植木”を対(つい)にしてみる事を覚える！

 

植木算の解き方

植木算を解くための２ステップ

植木算を解く際の２つのステップをご紹介します。応用問題であってもこの２つのステップで考えを整理していけば、概ね答えにたどり着くことができます d(^_^o)

STEP1：まずは…区画整理のベースを描く

まずは問題文を読みながら全体を俯瞰して区画整理をイメージします。直線であっても平面であってもこの工程が大切ですね。その時に意識するのは２つの長さですd(^_^o)

STEP1：ふたつの長さ
　① 間隔の長さ(木と木のスキマ)
　② 全体の長さ(道路の全長)

STEP2：植木算の “４要素” を書き出す

区画整理のイメージができたら、今度は２つの数量を整理していきます。その際に気をつけるべきところは”スキマの数”と”植木の数”の対(つい)です！数量の違いに気をつけてることですねd(^_^o)

STEP2：ふたつの数量
　① “スキマ”の数
　② “植木”の数

 

植木算の例題を６題！

それでは例題で植木算の解き方を解説したいと思いますd(^_^o)

例題① 直線上に植える問題(木の本数は？)

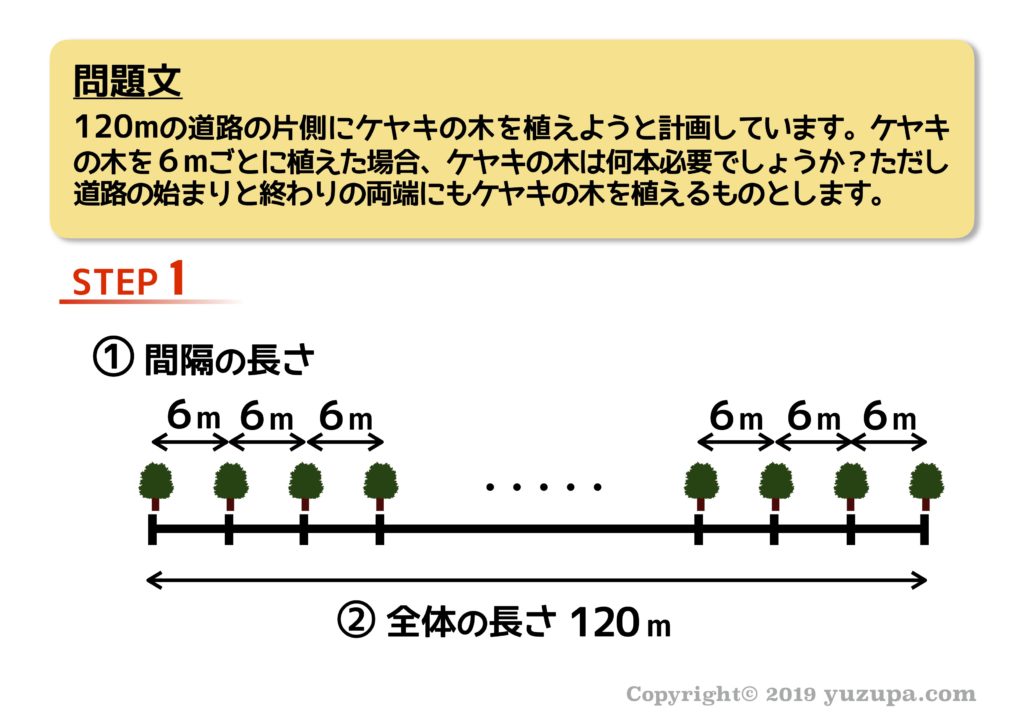
STEP1では…ふたつの長さを整理します。この問題の場合は 問題文にふたつの長さとも明記されている ので、とても簡単ですね…。かなりシンプルですd(^_^o)

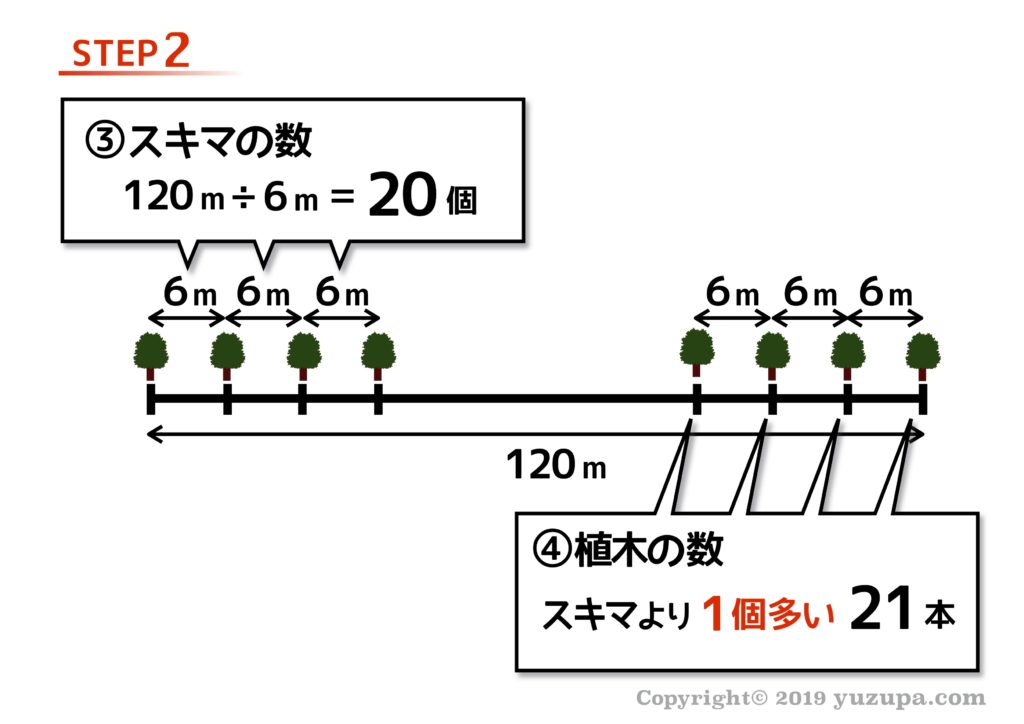
STEP2では…２つの数量です。まず”スキマ”の数はいくつでしょうか？ 道路全体の長さが120mで１区画の長さが6mなので20区画 ですねd(^_^o) 

そして”スキマ”と”植木”を対(つい)にしてみると “植木”の方がひとつ余るので “植木”の方が１個多い ので植木の数は２１本であることが分かります。この問題の答えは２１本 になります。

 

例題② 直線上に植える問題(間隔の長さは？)

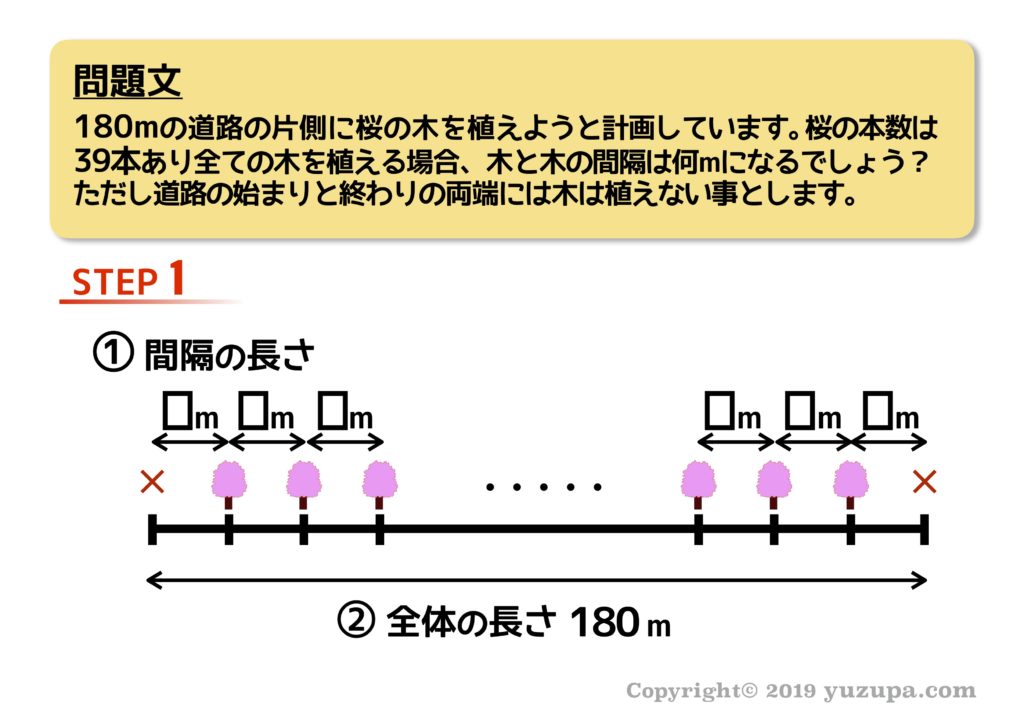
さっそく、ふたつの長さを整理します。この問題の場合、全体の長さは問題文に明記されていますが、うーん、間隔の長さは分からないので四角に しておきましょうd(^_^o)

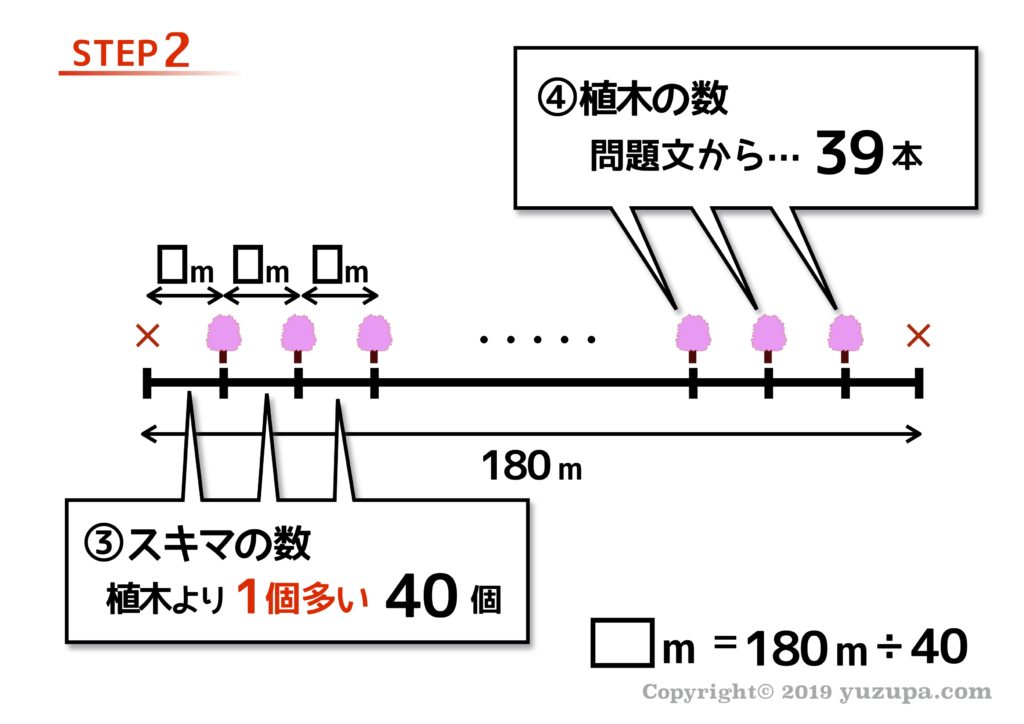
次はふたつの数量です。植木の本数は問題文に書かれていますね。”スキマ”と”植木”を対(つい)にしてみると”スキマ”の方が１つ多いので４０個であることが分かります。

スキマ１つ分の長さは、道路の全長をスキマの数で割ってあげれば計算できます。この問題の答えは４.5m　になりますねd(^_^o)

 

例題③ 直線上に植える問題(道路の長さは？)

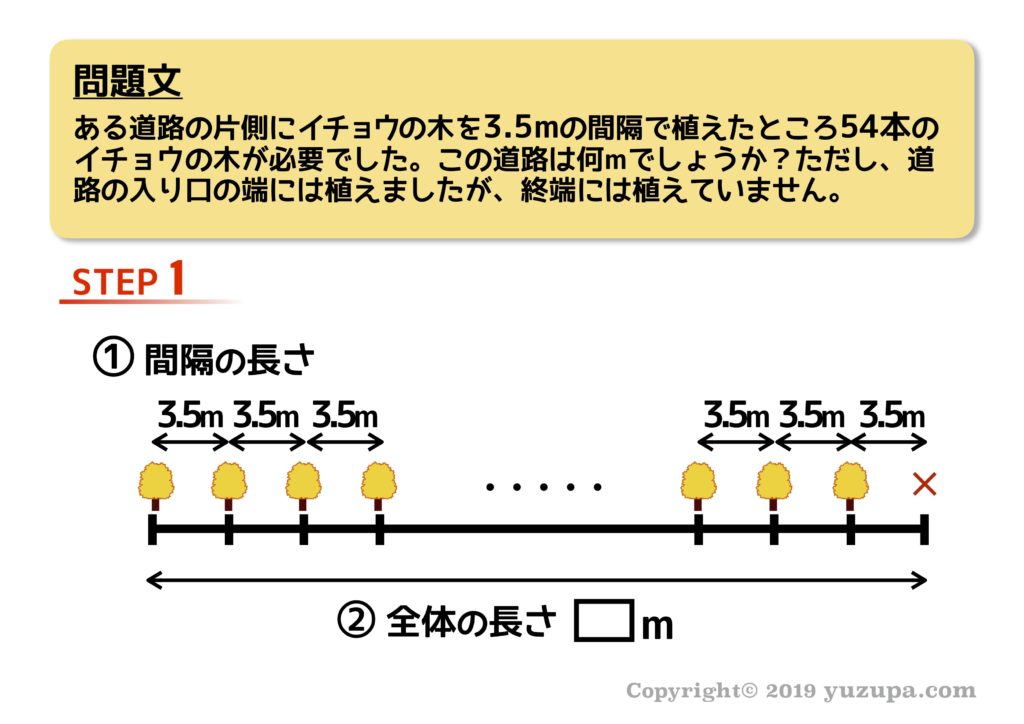
まずは２つの長さです。この問題の場合は、間隔の長さが問題文に明記されていますが、全体の長さ(道路の全長)は分からないので四角 にしておきましょう。

次はふたつの数量です。植木の数は問題文に明記されています。さて…いつもどおり”スキマ”と”植木”を対(つい)を作ってみましょう。余り無く対(つい)ができるので “スキマ”と”植木”は同じ数です。

3.5mのスキマが54個あるので、道路全体の長さは189m となりますd(^_^o)

 

例題④ 円形に植木を植える問題

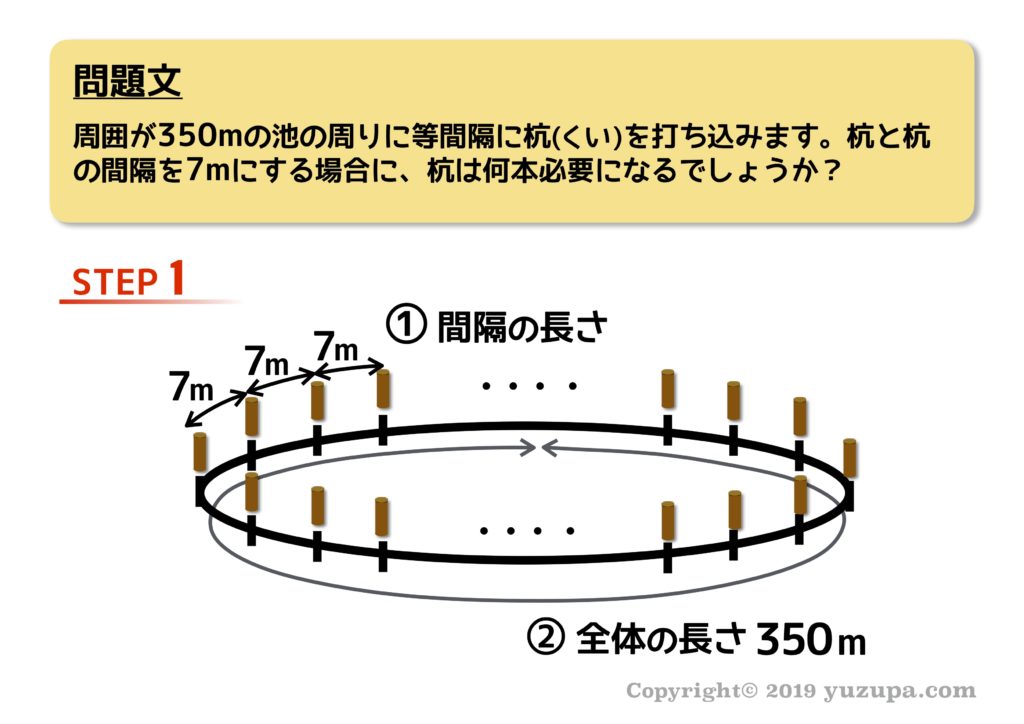
さて今度は 円形ですが情報の整理の仕方は同じ です。ふたつの長さですが… 間隔の長さ も 全体の長さ も問題文に明記されていますねd(^_^o)

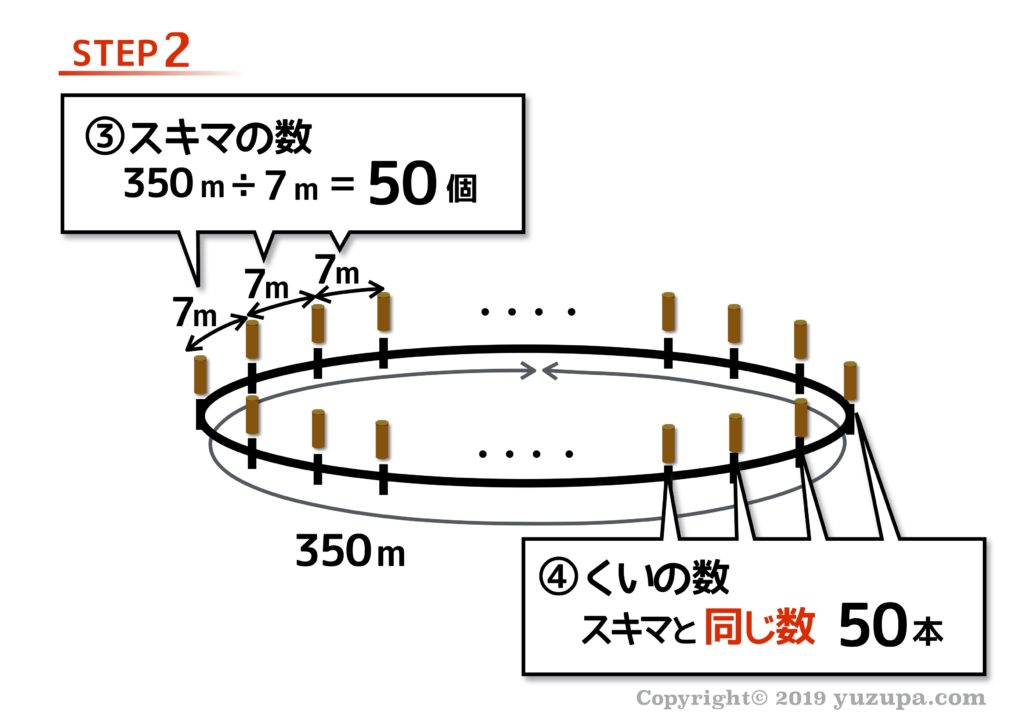
STEP2では ふたつの数量です。スキマの数は計算で求めることができますね。円周の長さが３５０mで１区画の長さが7mなので５０個です。

“スキマ”と”植木(くい)”の対(つい)を作ってみると同数です。くいの数は５０本 となりますd(^_^o)

例題⑤ ２列に植木を植える問題

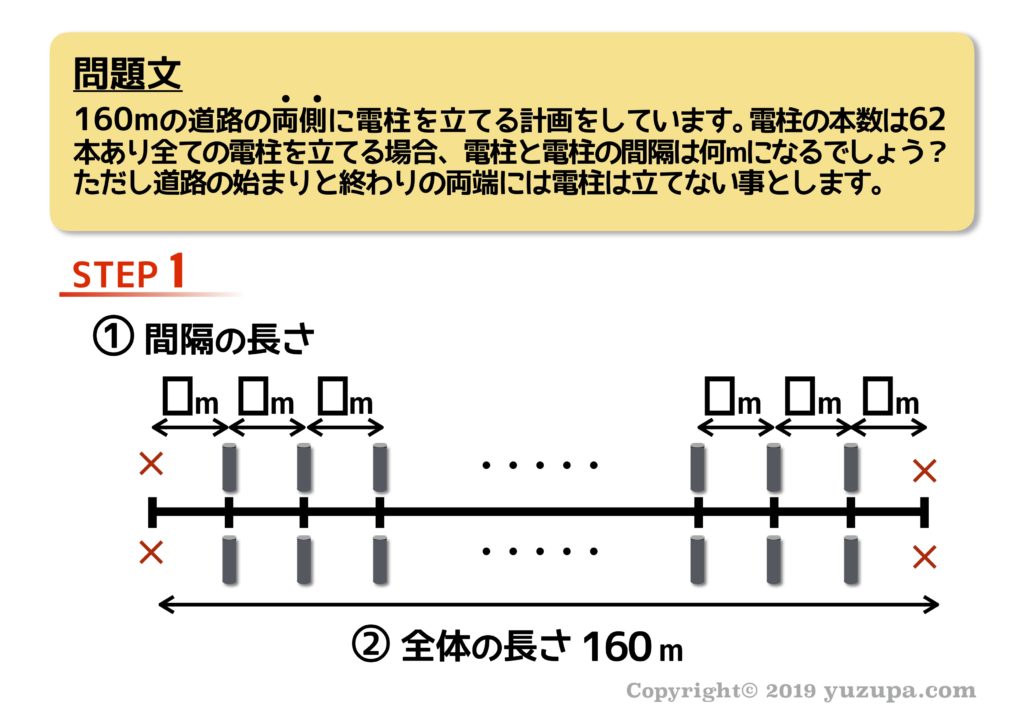
今度は道路の両側… つまり２列に植木します。２列であっても情報の整理手順は一緒 です。間隔の長さは分からないので四角、全体の長さは問題文に明記されています。

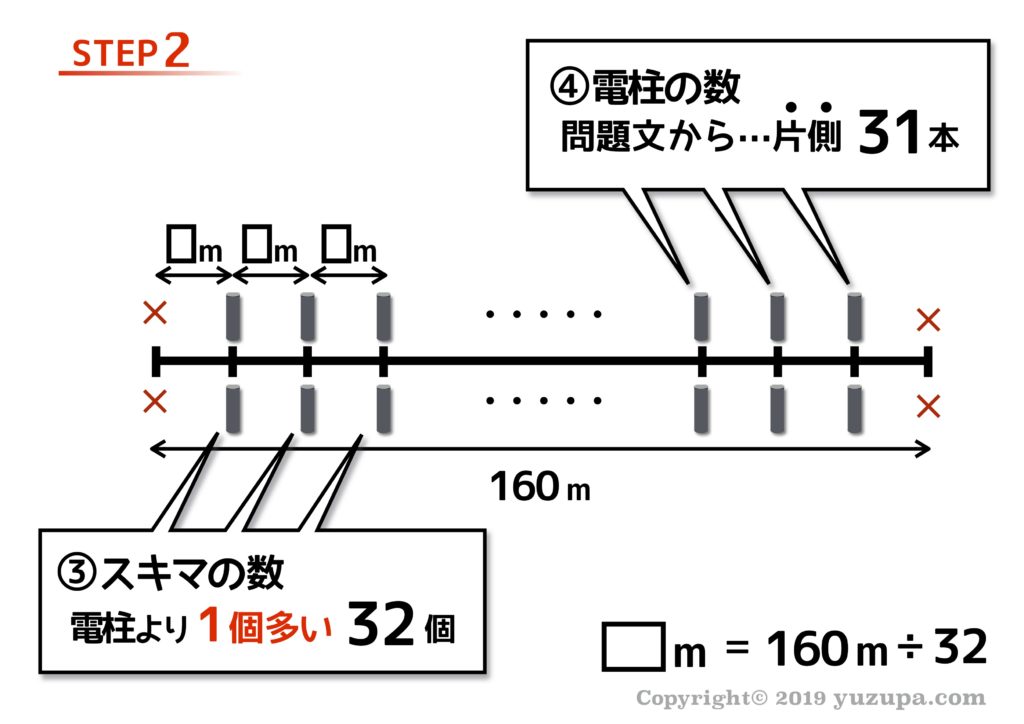
２つの数量はどうでしょう？ 植木(今回は電柱ですね…)の数は問題文に明記されていますが…片側の本数は半分の３２本です。今度はスキマの数を求めてみましょう。いつもどおり対(つい)を作ります。

“スキマ”の方がひとつ多いので…スキマは３２個ですね。全長１６０mに３２区画あることになりますので、１区画の長さは５m になりますねd(^_^o)

例題⑥ 平面に植木を植える問題

平面であっても…情報整理の手順は同じです。ふたつの長さを 縦と横それぞれで整理してみます。縦も横も問題文に明記されていますねd(^_^o)

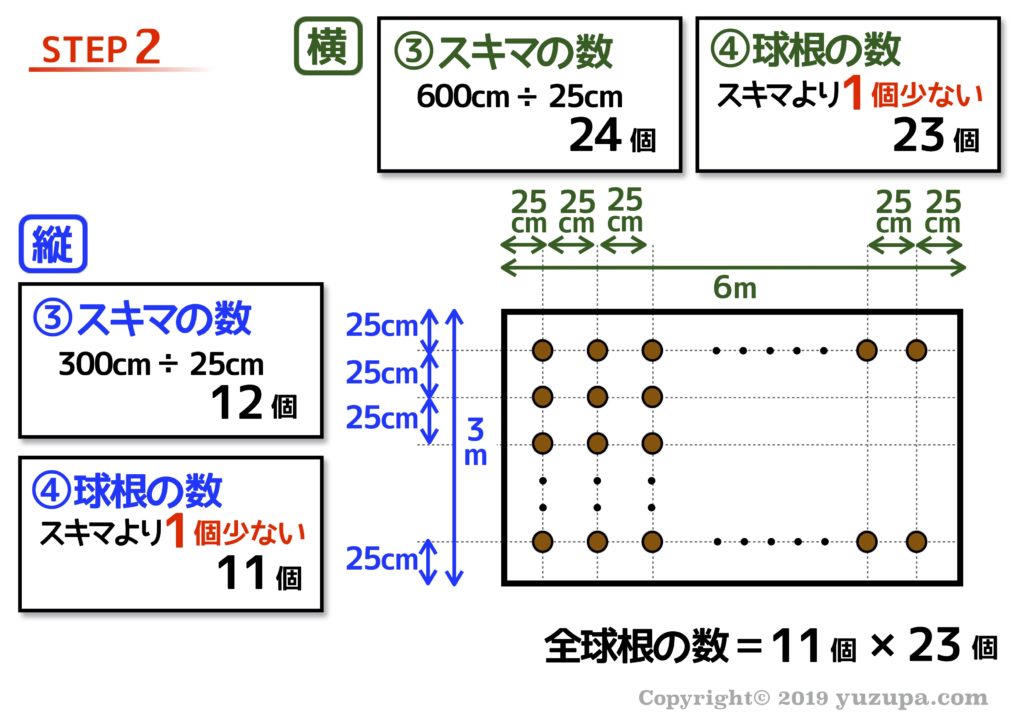
今度はふたつの数量です。スキマの数は縦も横も全体の長さを１区画の長さで割れば出てきますね。そして“スキマ”と”植木(今回は球根)”の対(つい)を作ってみると縦も横も”球根”の方が１つ少ないですね。

縦の球根の数と横の球根の数が分かれば、全球根の数も掛け算で分かります。植えることのできる球根の数は２５３個になりますねd(^_^o)

 

まとめ

今回は植木算の本質をご紹介しました。“植木算の公式”とやらは忘れてしまった方が良い…理由は応用がきかないからです∑(ﾟДﾟ) 植木算のポイントは情報の整理の仕方にあります。

情報の整理の仕方
２つの長さ：① 間隔の長さ ② 全体の長さ
２つの数量：③ スキマの数 ④ 植木の数

公式は忘れてしまえ！
“スキマ”と”植木”を対(つい)にしてみる！

いちど慣れてしまえば… どんな応用でもこの情報整理の手法で対応できるかと思いますd(^_^o)