中学受験：数列の規則性を確実に見つける…小学生のための７つ道具

自分の使える道具を知り、正しい試行錯誤のやり方をすれば100%見つけられます
※2021年5月5日 “数列の７つ道具” を全体的に改良しましたd(^_^o)

こんにちは。かるび勉強部屋 ゆずぱ です。

数列を見ても規則性に全く気づくことが出来ない… ヒラメキの力をどうやって鍛えたら良いか分からない…(-_-;)

ヒラメキに必要なのは”試行錯誤”
自分の使える道具を知ることが超重要

規則性を見つけるのが得意な子は、自分が使える道具を記憶から無意識に引き出し、ダメなら次…ダメなら次…と試しているうちに規則性に気づく んです ∑(ﾟДﾟ)

 

だったら… 自分の使える道具を整理すればよい！
そして…  その道具をひとつずつ試せばよい d(^_^o)

 

とてもシンプルです。この正しい試行錯誤のやり方を知るだけで、ヒラメキが降りてくる確率が格段に上昇 します∑(ﾟДﾟ)

それでは詳しく見てみましょう！

 

数列の規則性を見つけるには道具が必要

試行錯誤をするには使える道具の把握が必要

数列を見て規則性に気づきたい！どうすれば良いでしょうか？

ヒラメキの力を鍛えるのは難しいことでしょうか？そもそもヒラメキに強い子はどんな思考回路なのでしょうか？

① まずは自分の使える道具を知ること
② そしてそれを１つ１つ試すこと

知識を頭にいれただけでは、いきなりパッと見て気づくようにはなりませんよね… (-_-;)

道具を１つ１つ使う様子は、本記事の末尾に例題でイメージをのせましたのでご参照くださいd(^_^o)

 

数列の規則性を見つける７つ道具

それではさっそく試行錯誤に使う道具をご紹介します。私のブログではシリーズ化してきましたが ”７つ道具” と名付けて紹介します(^_^;)

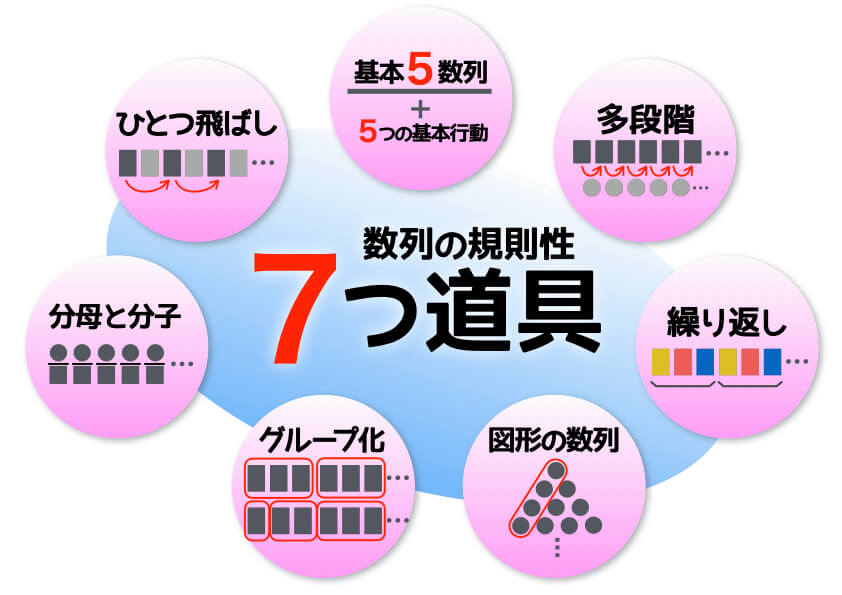
全ての道具は、数列をみた時に ”試してみる行動” を示したもの… ダメなら次…ダメなら次…という使い方ですd(^_^o)

 

数列の規則性 “７つ道具” を詳しく

道具① メジャーな５つの数列

まずは１つ目の道具ですが、メジャーな５つの数列です。そしてそれぞれに取るべき行動が準備されています。

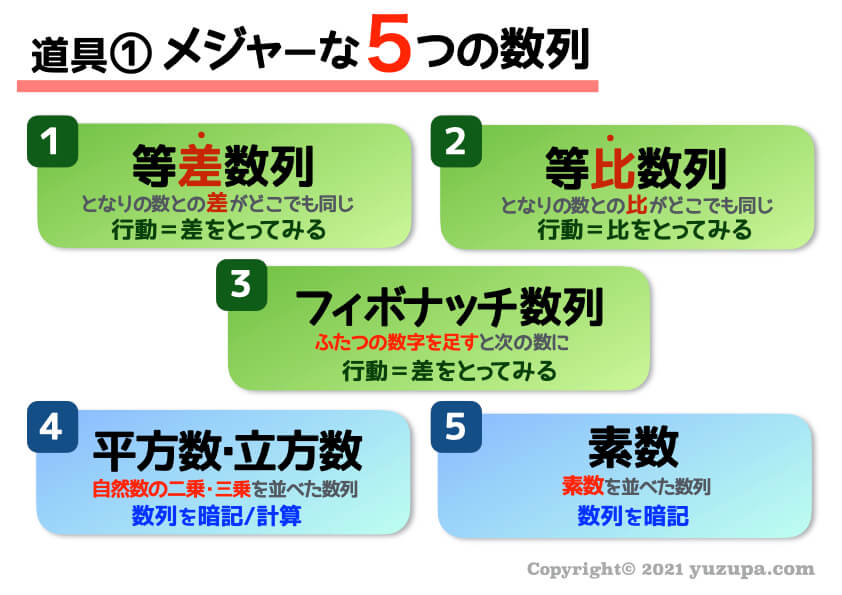
① 等差数列 ② 等比数列 ③フィボナッチ数列 の３つは となりあった数字の”差”や”比”をとることで気づくことができます。

④ 平方数の数列 ⑤ 素数の数列 の２つは、数列そのものの暗記で気づくことができますd(^_^o)

ひとつずつ見ていきましょう。

 

① 等差数列

超有名な等差数列です。隣り合う数字の差をとればすぐにわかりますねd(^_^o)

 

② 等比数列

こちらもメジャーな等比数列です。となりどおしの数字の比をとればすぐに見つけることができます_φ(･_･

 

③ フィボナッチ数列

 

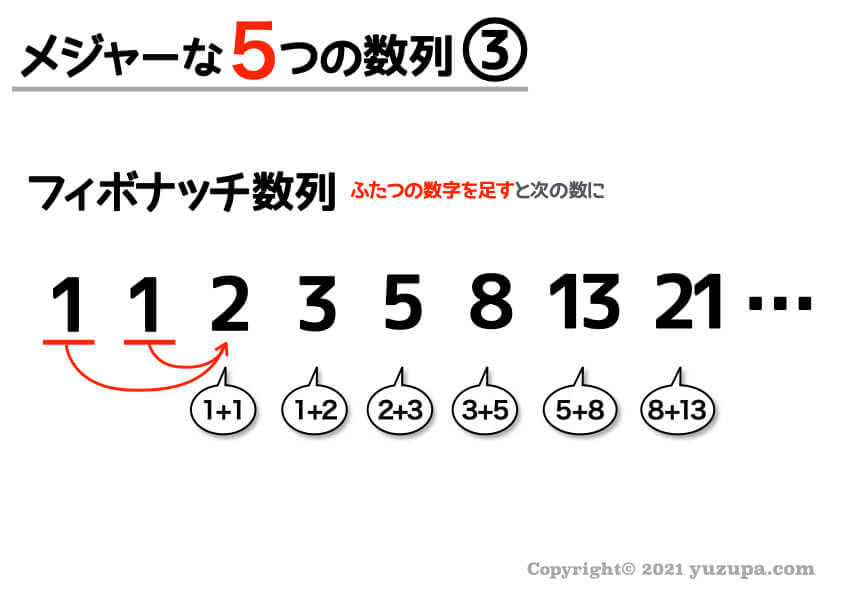
次はフィボナッチ数列です。１番目と２番目の数字を足すと３番目の数字になるというルールで並べられた数列です。

フィボナッチ数列は差をとるとフィボナッチ数列がでてきます∑(ﾟДﾟ) 差をとれば気づくことができます。

 

④ 平方数・立方数

次は平方数です。シンプルな数列ですが差や比をとっても気づくことはできません(-_-;) 数列をそのまま暗記しましょう。

そして立方数です。こちらもシンプルな数列なんですが…気づくのが難しい(>_<) これも暗記ですね。

 

⑤ 素数の数列

最後は素数です。これ急に出てくると意外に気付きません。うちの子供も気づきませんでした(^_^;)

 

以上が ５つの基本数列 です。

中学入試では ほぼ全ての問題がこの５つの数列に帰着 しますので、最終的にこの５つの数列に気づくことが目的です！

 

道具② ひとつ飛ばし

ここから先は 隠れた５つの基本数列を見つけるための道具たちです。最初は ”ひとつ飛ばし” ですd(^_^o)

いっけん何の規則性もない数列ですが…

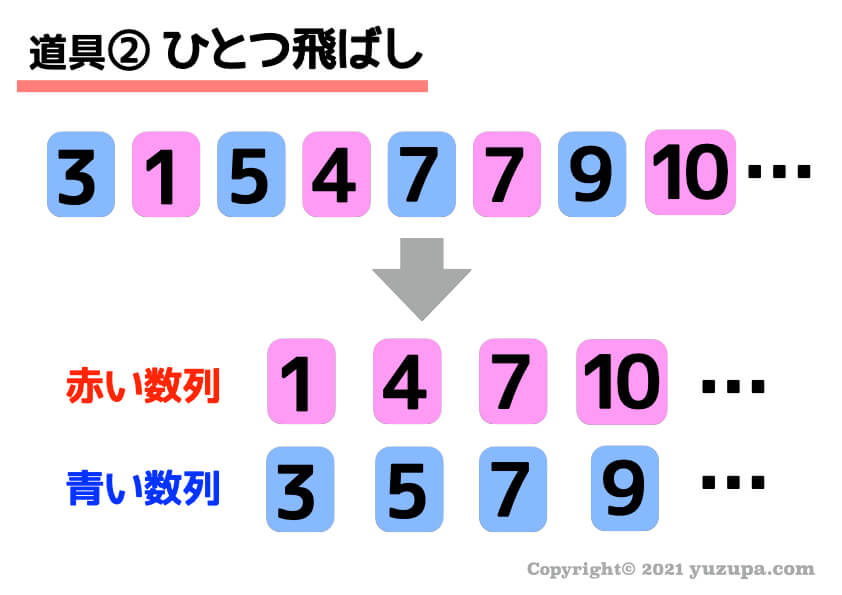
ひとつ飛ばし…つまり偶数番目の数字と 奇数番目の数字を分離 してみると２つの数列が現れます。

そして…５つの基本数列を見つけることができました∑(ﾟДﾟ) 両方ともシンプルな等差数列 ですねd(^_^o)

 

道具③ 多段階

３つ目の道具は ”多段階” です。

５つの基本数列を見つけるために差や比をとってみてもダメ です。そんな時… その差や比が規則性のある数列になっていませんか？

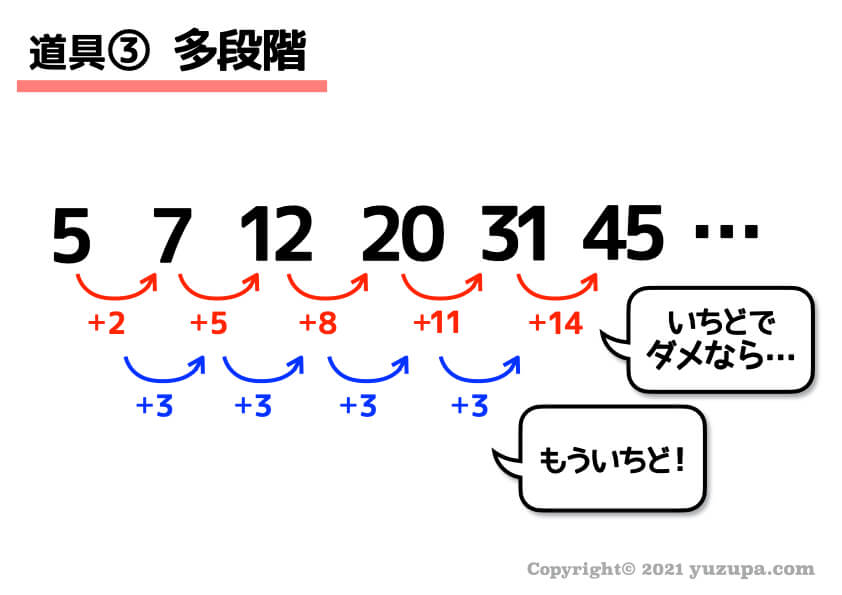
そうすると５つの基本数列が見えてくる場合があります。

この例の場合は 差をとってダメだったので もういっかい差をとったら等差数列が現れました ねd(^_^o)

多段階にはバリエーションが無数にあります

例えば、最初の 数列の差をとったら素数の数列が現れるなんてことも∑(ﾟДﾟ) まさに試行錯誤が解決のキーになる真骨頂といえます d(^_^o)

 

道具④ 分母と分子

次は ”分母と分子” です。

分数がやたら並んでいる数列の場合は、分母と分子がそれぞれ別のルールで数列になっている可能性がありますd(^_^o)

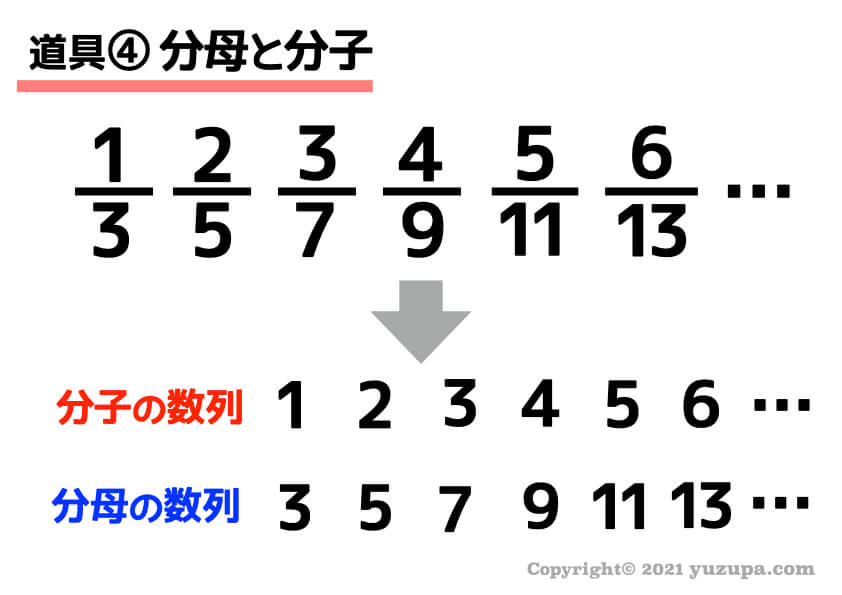
この場合、分子は自然数の数列、分母もシンプルな等差数列 になっていますね∑(ﾟДﾟ)

 

道具⑤ 繰り返し

５つ目の道具は ”繰り返し” です。

５つの基本数列が見つからない場合は、適当な数列が繰り返されていることがあります(･_･;

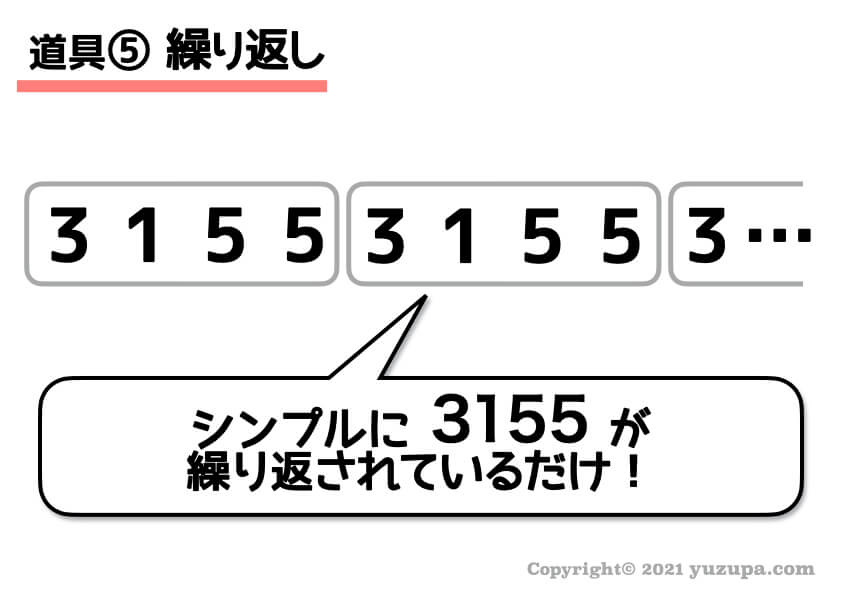
この数列の場合 ”3 1 5 5” という４つの数字でできた数列がひたすら繰り返されています…。

これ…意外と気づかないので ７つ道具の１つとしてリストアップされていれば試行錯誤の候補に なりますd(^_^o)

 

道具⑥ グループ化

最後の道具は ”グループ化” です。

この数列の場合、２、３、４と順調に等差数列が並んでいる とおもいきや次の “３”で裏切られる(>_<)

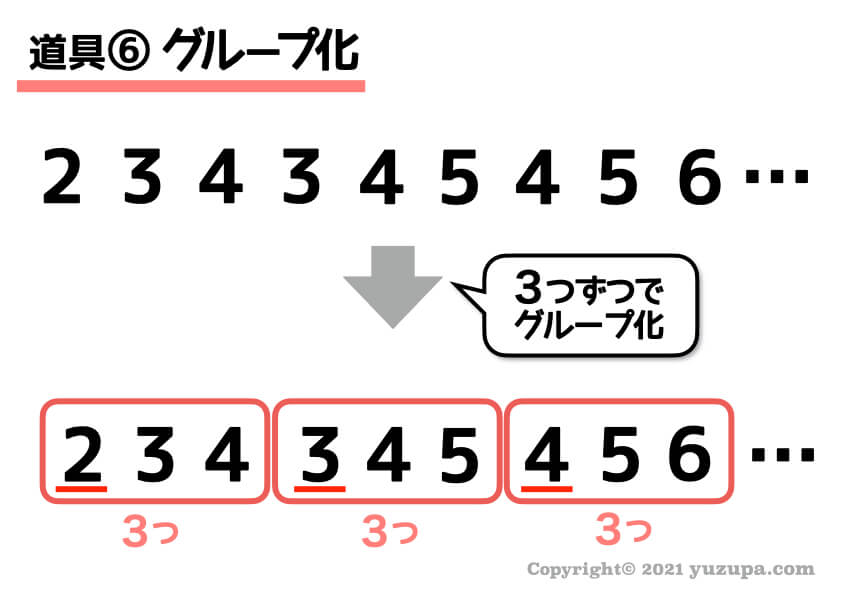
だったら…裏切られた単位でグループ化してみる という道具です。この場合は ３つずつグループ化するとそれぞれのグループが等差数列になっていることが発見できました。

 

 

もうひつのグループ化の例です…１、２、３…みたいな 等差数列のコマ切れのようなものがたくさん 含まれていますね(-_-;)

でも先ほどのグループ化と違って３つずつ…みたいに切ってもきれいな数列にはなりません。そんな時は階段状です_φ(･_･

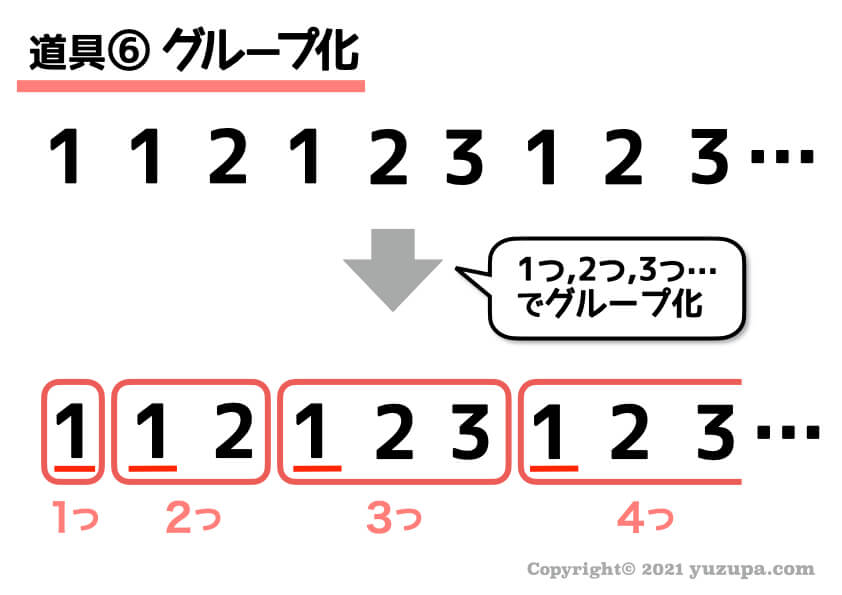
きれいな等差数列でグループ化することができました。

 

以上が 数列の規則性に気づくための試行錯誤に使える７つの道具 でした。この ７つの道具を複数組み合わせることで無限の数列に気づくことができる ようになりますd(^_^o)

それでは、最後に実際に試行錯誤する様子をお示しします。

 

道具⑦ 図形の数列

最後の道具は ”図形の数列” です。

横一列にズラーっと並んだ数字ではなく、三角形や四角形の形に数字が並んでいるクセモノです。

この図形の数列にはコツがあります
３つの要素を落ち着いて整理すれば良い

具体的に…３つの例を見てみましょうd(^_^o)

１つ目の例は正方形にそって数字が並んでいる数列です。

上記のように１段目、２段目、3段目となっていることを意識して整理しましょう。

次は ② 端っこがどんな数列になっているか？ ③ 各段の数字の個数がいくつあるか を整理します。

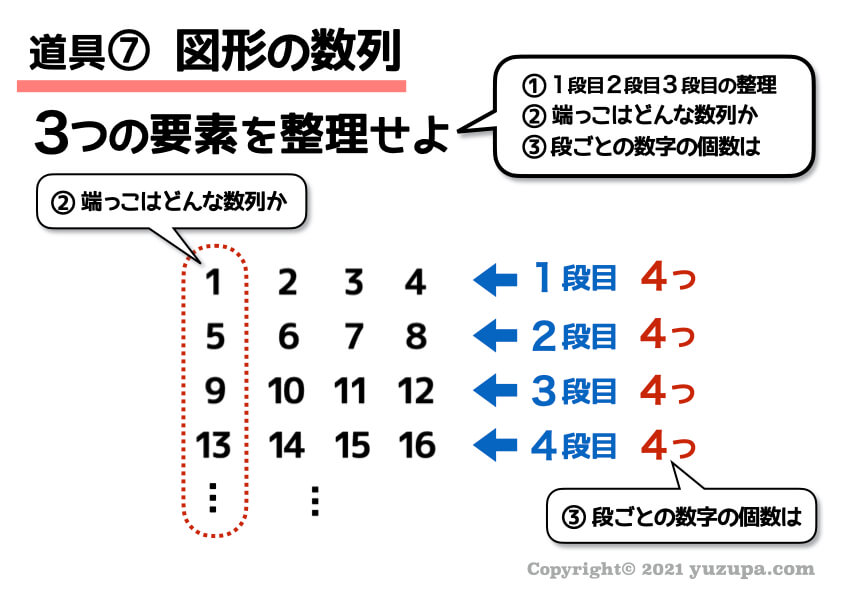
この場合、端っこの数列は 1 , 5 , 9 , 13… と当さ数列になっていますねd(^_^o)

そして各段にある数字の個数ですがずっと４つですね。

こんな感じで３つの要素を整理すると 何段目の何個目にどんな数字が来るか計算 できますね！

 

２つ目の例です。

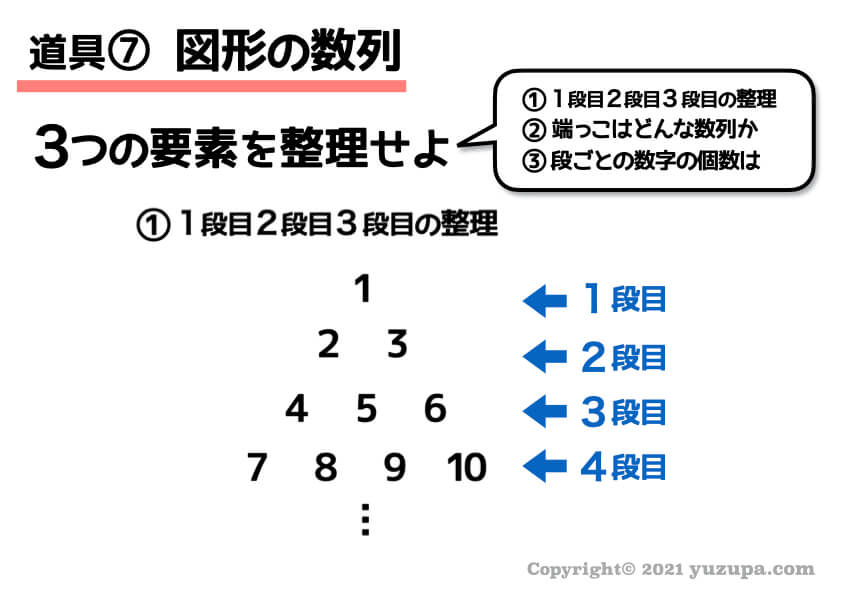
同じように要素を整理してみまようd(^_^o)

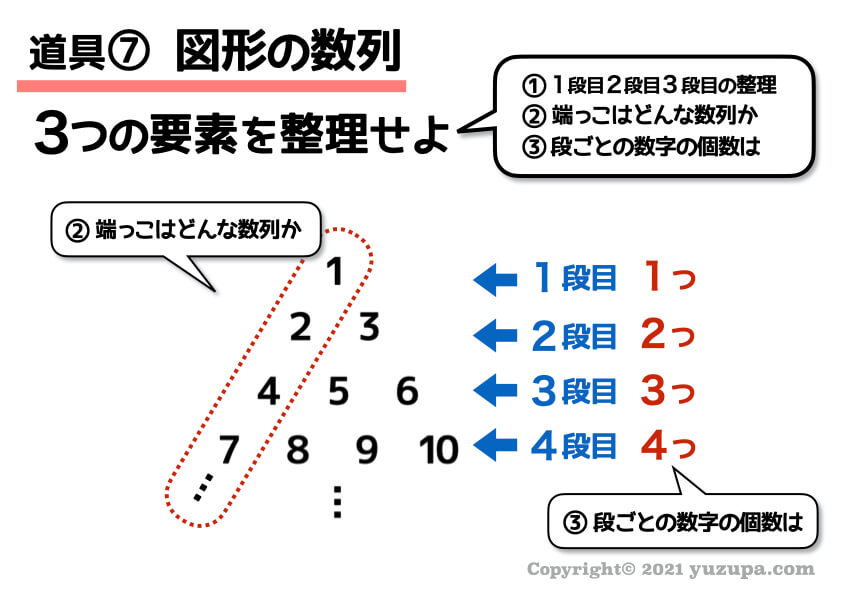
端っこの数列は 1 , 2 , 4 , 7 …という数列。差をとってみるとその法則性が分かりますd(^_^o)

そして数字の個数も規則的ですね！

３つ目の例です。

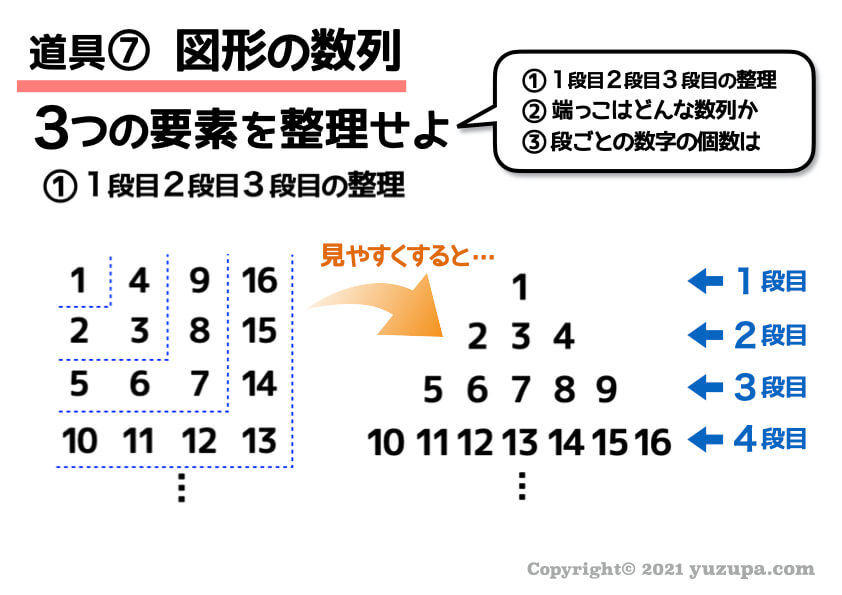
ちょっと分かりにくいので、右の図のような形で１段目,２段目,３段目を整理します。

一気に分かりやすくなるでしょうo(^-^)o

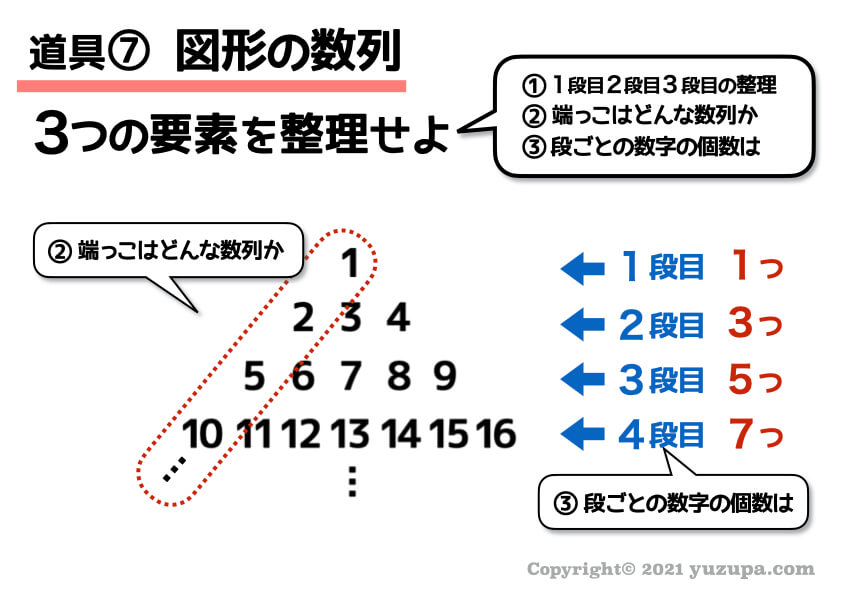
端っこの数列はちょっと難しいですが各項の差を取ると規則性が見えてきます。

段ごとの数字の個数も規則的ですねd(^_^o)

道具⑦だけはちょっと特殊なものですが、数列の一種ということで頭に入れておくと数列を試行錯誤する時に有効です_φ(･_･ 

 

具体的に７つ道具を使ってみる

では具体的に７つ道具を使ってみるための例題を５つ準備しましたd(^_^o) 子供の頭の中も合わせて解説します。

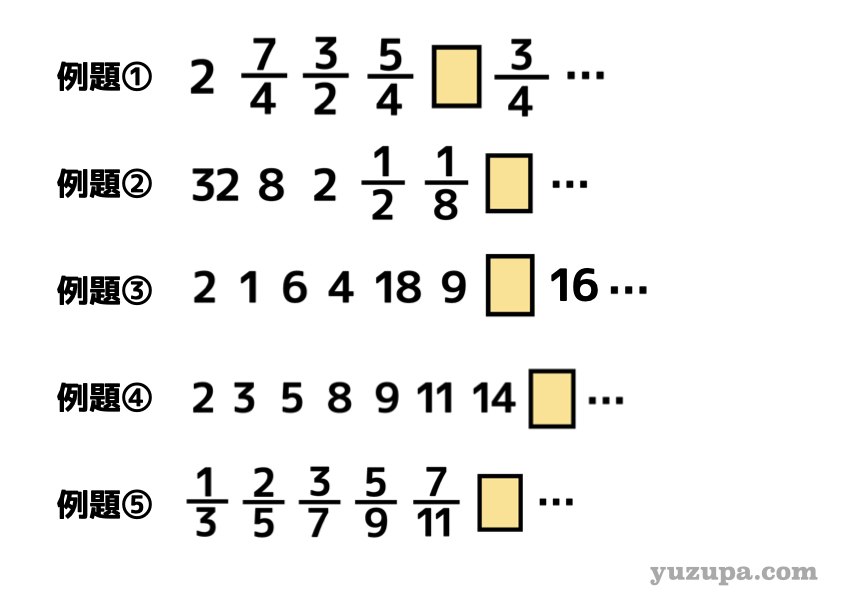
５つの例題…パッと見ただけでは規則性は分からない かと思います。さっそく“正しい試行錯誤”のやり方 を交えて見ていきましょうd(^_^o)

 

例題①

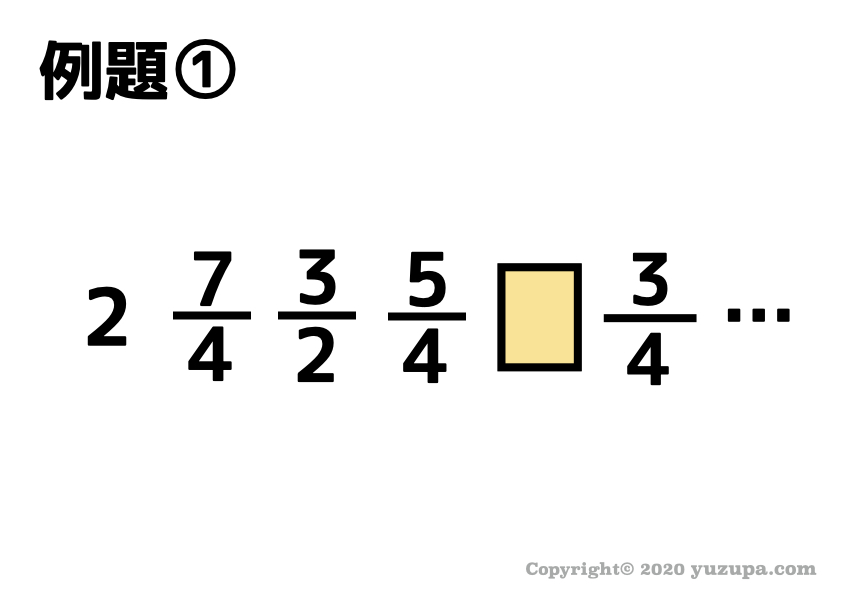
まずは 道具①から試してみるのが王道 です。となりどおしの数字の差や比をとってみたり、平方数や素数がないか探してみたり…

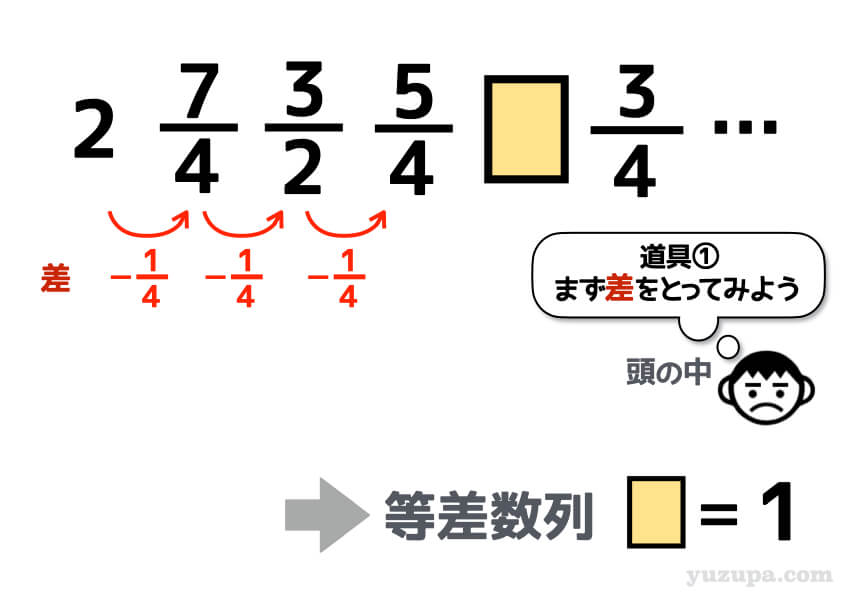
パッとみた感じでは分かりませんでしたが、差をとってみてはじめて等差数列であることに気づいたのでは ないでしょうか？

 

例題②

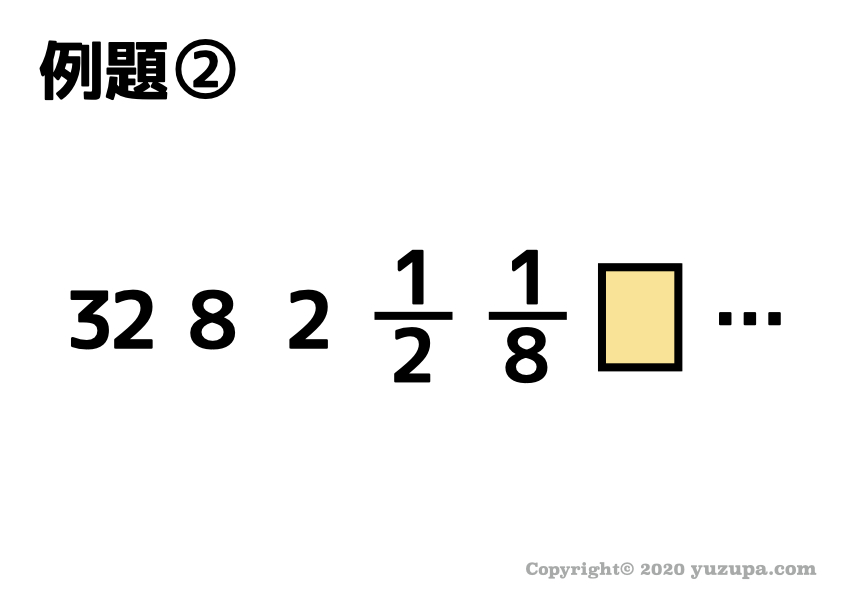
いつもどおり王道の道具①から試してみましょう。となりどおしの数字の差や比をとってみたり、平方数や素数をさがしたり…

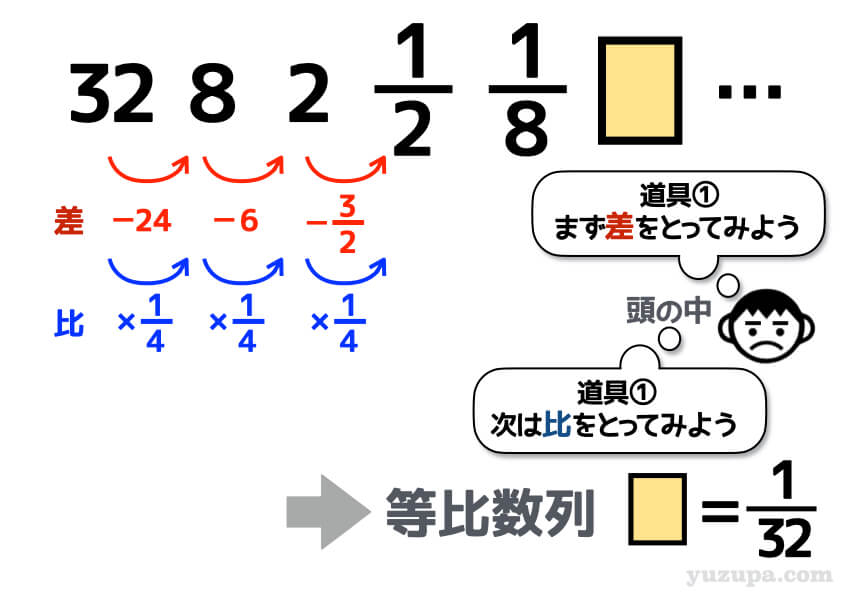
差をとってみてもダメ でした。比をとってみると… おっ！？ 比が同じになっている等比数列であることがわかりますd(^_^o)

例題①と同様、パッと見た感じでは気づかなかったのではないでしょうか？ 試行錯誤…大切ですd(^_^o)

 

例題③

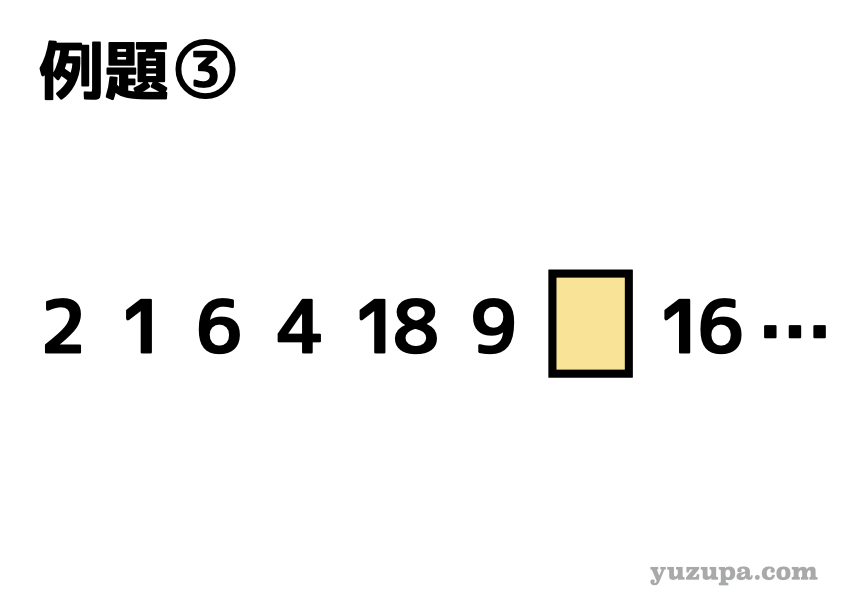
さあこの問題はどうでしょうか？ はい…いつもどおり道具① です。基本は差や比をとるところからはじめましょうd(^_^o)

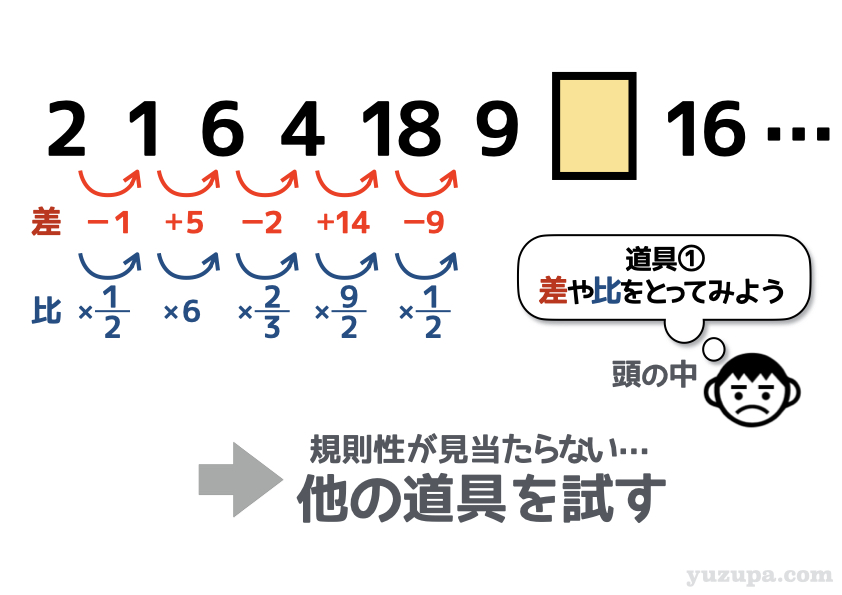
あれ… 差をとっても比をとっても５つの基本数列が見えてきません。さてどうしましょう。他の道具を試してみましょう。

手始めに道具②から 試してみましょう。

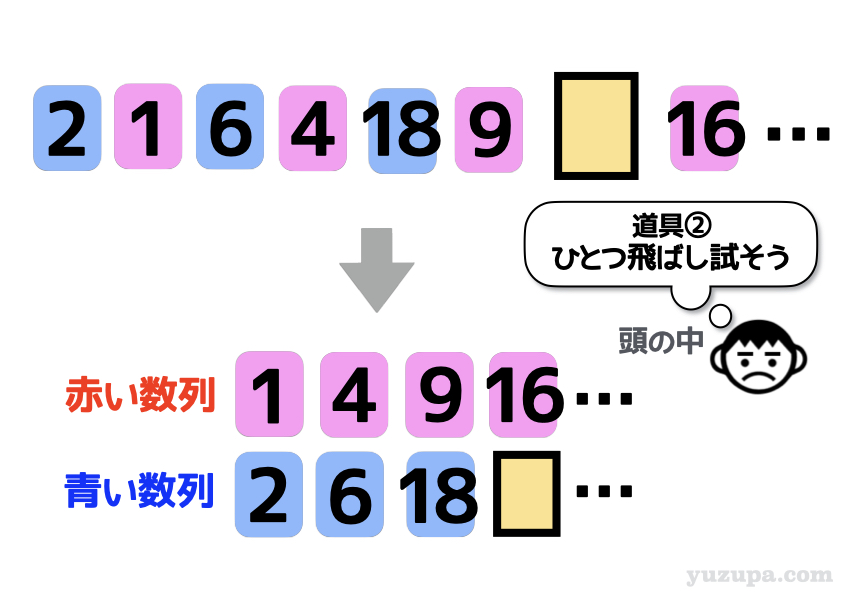
そうすると、２つの数列が見えてきました。２つの数列を改めて確認すると５つの基本数列が見えてきましたか？

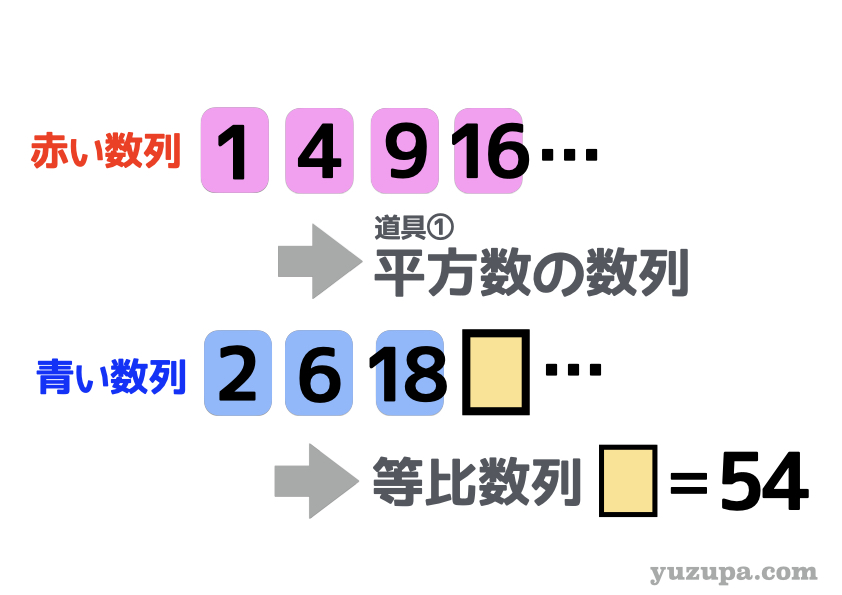
見つかりました！赤い数列は “平方数の数列”、青い数列はシンプルな ”等比数列” ですね d(^_^o)

ここでひとつ注意！

今回は 道具②の”ひとつ飛ばし” を試してみてイキナリ規則性を見つけることができましたが… これは説明の都合 です(^_^;)

道具③がダメで、道具④もダメで…と繰り返した末、道具②で規則性を見つける というのが試行錯誤の正しいやり方です。

そして人間には ”第六感” という ”無意識に合理的な判断をする” 脳の機能 があり、いずれ試行錯誤の正答率があがっていきますd(^_^o)

 

例題④

例題の４つ目も 例のごとく道具①から 試してみましょう。となりどおしの数字の差をとってみます。ダメですね。

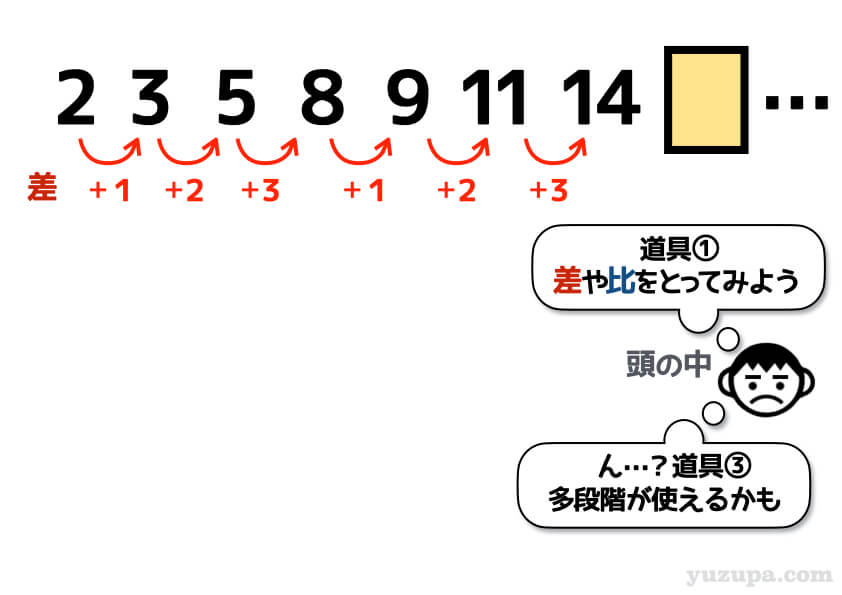
ここで、差の数列が何となく規則性がありそう… ちょっと道具③の多段階を試してみましょうd(^_^o)

 

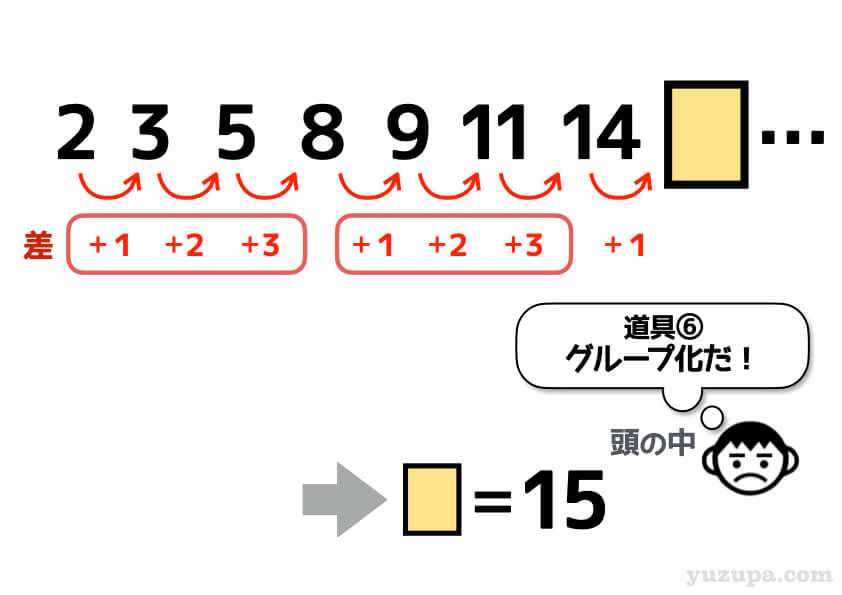
数列の中に １、２、３と部分的な等差数列がありますので、道具⑥のグループ化 ですね！ 試行錯誤の結果ですd(^_^o)

 

例題⑤

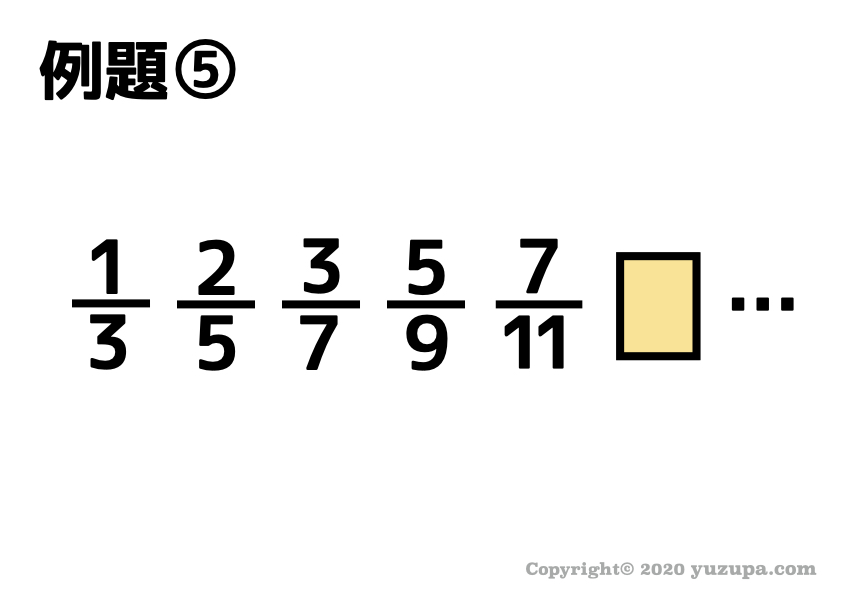
最後の例題です。問題の数をこなしてくると…差や比がパッとみただけでダメなことが分かるようになってきます。

試す道具も “これは分数が続いているから 道具④ 分母と分子かも…” といった感じでわかるようになってきますd(^_^o)

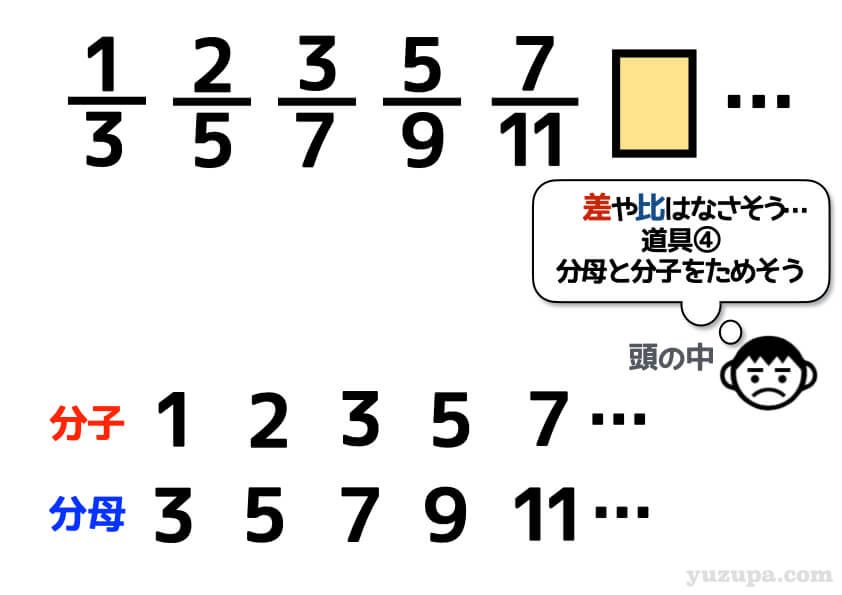
そして、分子の数列と分母の数列に分けた瞬間に５つの基本数列を思い浮かべることができるようになります。

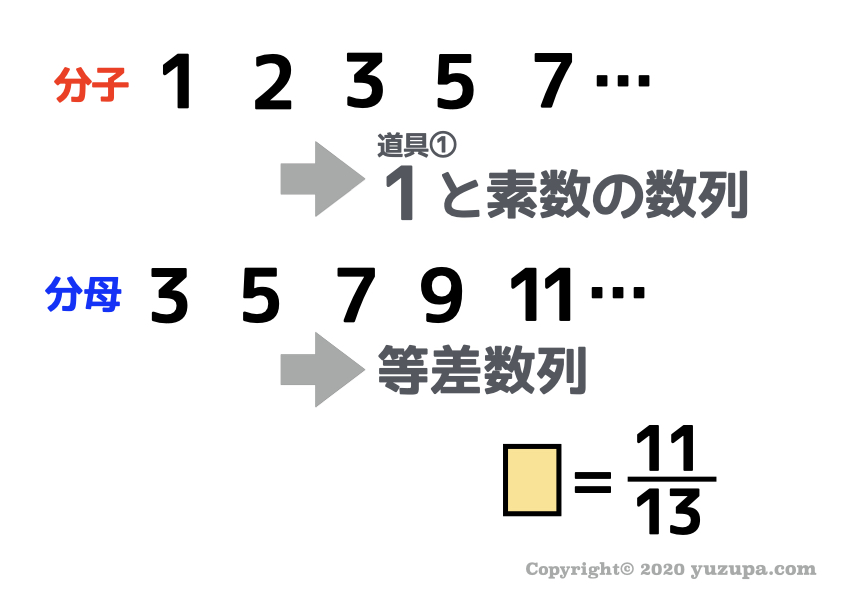
分子の素数の数列は意外と気づかない数列 です。が…７つ道具をしっかりおさえていれば気づくことができますね d(^_^o)　厳密には１は素数ではないので１＋素数の数列ですねd(^_^o)

 

以上、５つの例題を ”試行錯誤する過程” を中心に解説しました。

 

まとめ

数列が嫌いな子供は多いようです。その理由は 数列を見ても何もヒラメキがないからです。それもそのはず…

正しい試行錯誤をしていないから
ヒラメキがおりてこない

正しい試行錯誤には２つのステップがあります。この２つのステップで正しい試行錯誤を繰り返せば、数列の規則性もほぼ見つけることができるようになりますd(^_^o)

① 自分が使える道具を知る(７つ道具)
② 道具をひとつずつ試す ”試行錯誤”をする

今回は例題を５つご紹介しましたが “規則性はこうでした” という種明かしだけではなく、試行錯誤する過程を中心に解説してみました。いかがでしたでしょうか？

 

 

 

エッセンス動画