中学受験：場合の数の基本パターンを全網羅！ 試合数問題編

試合数の問題…２つの基本パターンだけ攻略せよ

こんにちは。かるび勉強部屋 ゆずぱ です。

場合の数が苦手な子供が多い・・・(-_-;) 問題の解法が無数にあり体系化されていないためモヤモヤするようです。そんな場合の数の問題の中でも、たった２つのパターンをおさえれば攻略できるのが試合数の問題です。

 

試合数の場合の数…２つの基本パターン
トーナメント戦とリーグ戦

試合数の問題の全体の中の位置付けを場合の数の全体像から確認しましょう。場合の数の問題は、代表的なものとして10種類の問題があります。試合数の問題はその10種類のうちの1種類となりますo(^-^)o

おさらい：場合の数の３つの道具

道具を使い”全ての可能性を数える”こと

”場合の数問題” の全体像をご覧ください。
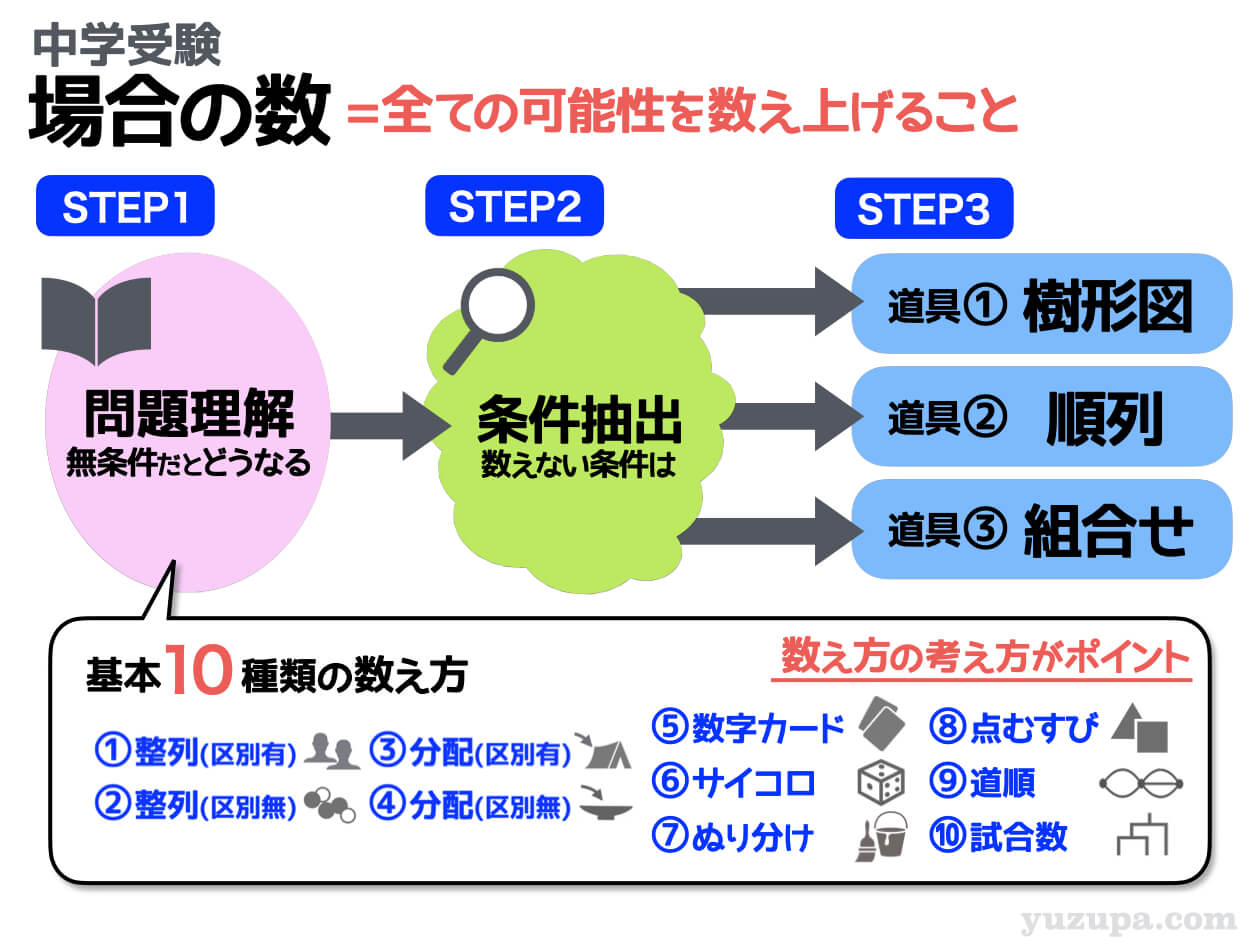場合の数の問題というのは、ズバリ”全ての可能性を数え上げなさい”という問題 のこと。正しく問題を解くには以下の３つのステップを着実にこなすことが最も近道です。

 

STEP1では、問題文を読んで”いったい何を数えたらよいのか”をしっかり把握します。その際に役に立つのが”基本的な１０種類の数え方”です。まずは基本パターンを考えましょう。

STEP2では、条件を理解します。偶数”だけ”数えなくてはいけなかったり、男子が両端にくる並び方”だけ”数えなくてはいけなかったり、入試の問題には必ず条件がついてきます(^_^;)

STEP3でいよいよ数えます。数えるには必ず道具を使います。樹形図はオールマイティですが、通り数の多い問題には使えません。樹形図をサボる道具として”順列”と”組合せ”があります。

 

 

３種類の道具を使って数える

３つの道具とは”樹形図”と”順列”と”組合せ”のことです。

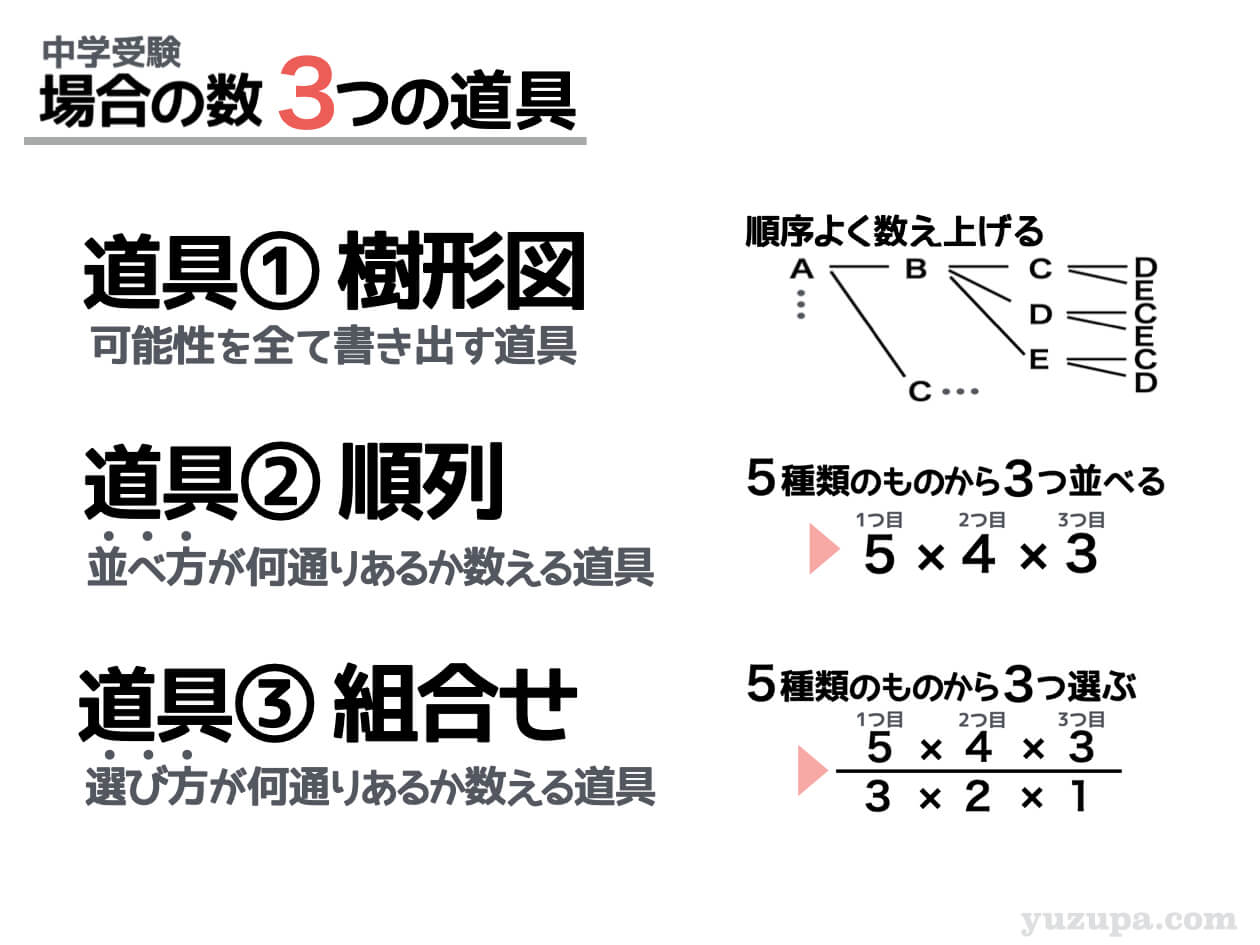
樹形図はオールマイティな道具です。どうやって数えたら良いか迷ったらまずは樹形図で数え始めてみてもよいでしょう。書いていているうちに数え方のヒラメキがあることもあります。

順列は並べ方が何通りあるか数える道具です。シンプルに何かを並べる場合の数を求める問題の他に、並べること以外の題材を並べる行為に置き換えて数えることもよくあります。

組合せは選び方が何通りあるか数える道具です。例えば１０種類のケーキがあり、３つだけ食べて良いと言われたら何を選びますか？ この道具を使えば選び方が何種類あるか分かります。

 

場合の数の全体像を確認したい場合は、ぜひ以下の記事をご参照してみてください。スッキリしますd(^_^o)

参考：場合の数…３つの道具を使い10種の数え方をマスターせよ

 

試合数を数える場合の数 全体像

試合数問題の全体像

試合数の問題というのは・・・ 優勝者を決めるのに何試合する必要があるか数えてください という問題です。とうぜん優勝者を決めるためのルールがあり、そのルールの場合、何試合必要か？という問いになります。

ところがそのルールというのが…
たった２種類しかありません∑(ﾟДﾟ)

 

その２種類というのが「トーナメント戦」と「リーグ戦(総当たり戦)」という２つのルールです。この２つのルールで優勝者を決める時の試合数の数え方をおさえましょう。複合問題も解けるようになりますd(^_^o)

 

基本的な２パターンの問題

(1) トーナメント戦
トーナメント戦はけっこう有名なルールなので、いわずもがなかもしれませんが。１回負けてしまうと敗退となり、最後まで勝ち続けた人が優勝となるルールです。試合数は、工夫して簡単に数えることができます。

(2) リーグ(総当たり)戦
リーグ戦は別名を総当たり戦といいます。総当たり・・・その名のとおり、参加チームは、他の全てのチームと１試合ずつ試合をして、その勝率で優勝者を決めるというものです。こちらは場合の数の定番ツールを使うのが良いです。

 

それでは２つのパターンの具体例を見ていきましょう！

 

試合数問題…２つの基本パターン

基本① トーナメント戦のパターン

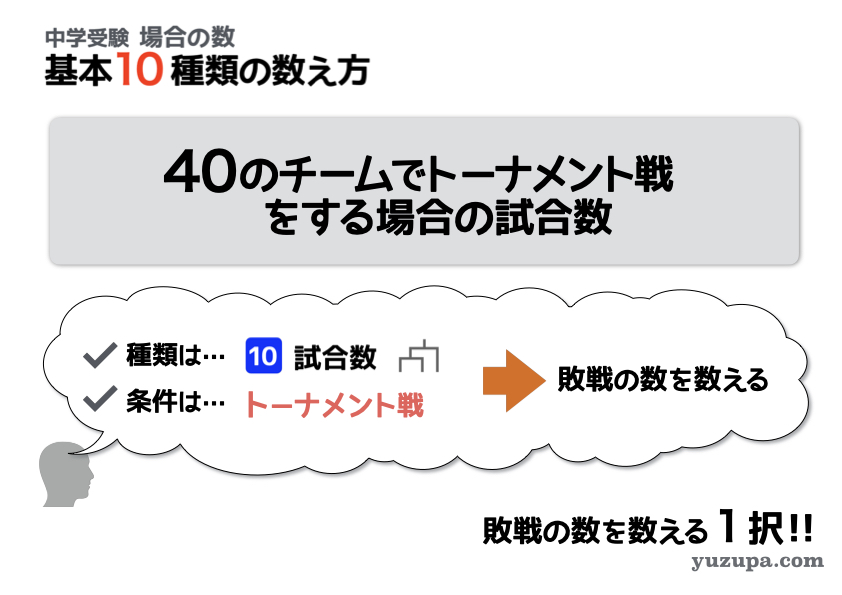
ひとつ目のパターンはトーナメント戦。

問題を見た瞬間に、場合の数の10番目の種類である試合数の問題であることがわかります。そしてルールはトーナメント戦です。

この場合のアプローチは一択です

敗戦の数を数えるというアプローチです。これはトーナメント戦のルールを正しく理解していれば、導きだせる求め方となりますd(^_^o)

 

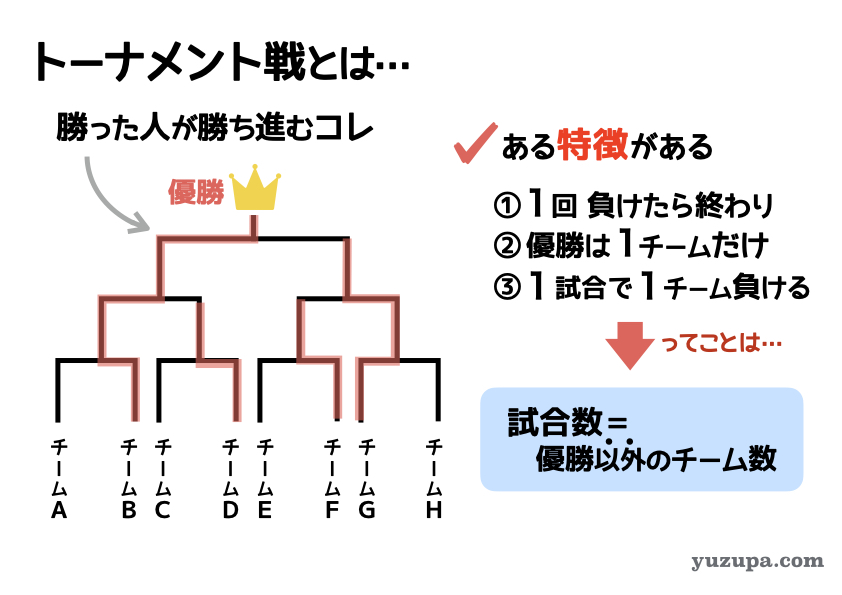
トーナメント戦とは、上記の図のように・・・

・あらかじめ決められた対戦相手と勝負をし
・負けたら終わり、最後まで勝ち続けた人が優勝

というお馴染みのルールです_φ(･_･このトーナメント戦にはいくつかの特徴があります。１回負けたら終わり。優勝は１チームだけ。１試合やると必ず１チームが負ける。ということ。

…てことは優勝チーム以外は全チーム１回ずつ負けている
試合数を知りたければ、敗戦の数を数えればよい

ということがわかりますねd(^_^o)

ここまで来たら簡単です！

この問題の場合、参加チームは40チーム。優勝以外のチーム数は39チームです。この39チームが１回ずつ負けていますので、試合数は39試合となります。とても簡単ですねo(^-^)o

答えは 39試合 となります

 

基本② リーグ(総当たり)戦のパターン

ひとつ目のパターンはリーグ(総当たり)戦。

こちらも問題を見た瞬間に、場合の数の10番目の種類である試合数の問題であることがわかります。そしてルールはリーグ戦です。

この場合は道具③の組み合わせを使うことを試みます

なぜ道具③の組み合わせを使うのか・・・？こちらは実際の問題を見ながら確認していきましょうd(^_^o)

 

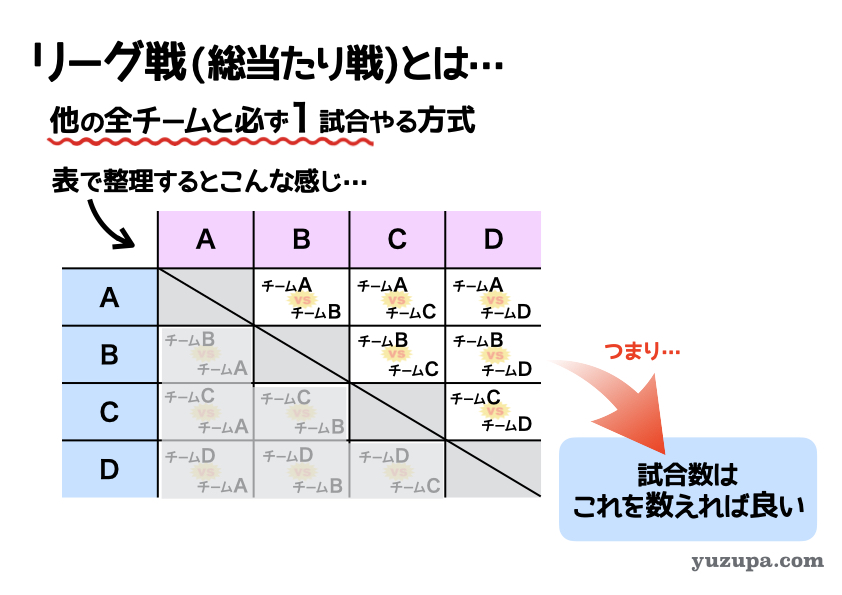
リーグ戦とは、別名を総当たり戦と言われています。総当たりという名前のとおり、参加チームは、他の全チームと１試合ずつ試合をすることになります。優勝者はその勝率できまります

 リーグ戦を表で整理すると上図のようになります

 この表は参加チーム数が４チームの場合を例に書いていますが・・・AチームはBチーム、Cチーム、Dチームの４チームと試合をすることになります。

この表にまとめられた試合数を数えれば良いのですが、どうやって数えたら良いでしょうか？

 

 

考え方は超シンプルです。

参加チームは他の全チームと必ず１試合やるということなので、全チームの中から対戦する２チームを選ぶ選び方は何通りあるか数えれば良い_φ(･_･

これはまさに組み合わせの考え方です

今回は20チームの中から対戦する２チームを選ぶので20×19で計算することができます。同じパターン分を割るのを忘れずに！

答えは 190通り となります

 

複合的な問題

原則はいままでご紹介した２つの基本パターンだけおさえておけば良いのですが、複合的な問題も出題されたりします。ただ・・・恐れる必要はありません。基本パターンをおさえておけば、簡単に解けちゃいます！

いくつか事例をご紹介したいと思いますo(^-^)o

(1) トーナメント × トーナメント

原則はトーナメントで優勝者を決めるのですが、トーナメントで負けてしまった人たちだけ集まって、もう１つのトーナメントを行い、最後に両トーナメントの優勝者同士があらそって、１人だけ優勝者を決めるという方式。

(2) リーグ ×　トーナメント

リーグ戦をやって上位者で決勝トーナメントをやるみたいな方式です。具体的には、リーグ戦をやって上位10人だけを集めてその10人で優勝者を決める決勝トーナメントをやるみたいな方式です。

いずれにしても、問題文に書かれているルールを理解し、２つの基本パターンの解法の組み合わせで解くことができますd(^_^o)

 

まとめ

今回のテーマは場合の数のうち、試合数の数え方についてです。場合の数は可能性のある通り数を数えるというシンプルな問題なのですが、無数にパターンがあり、かつ、手動で数えることができない問題もあり、苦手な子供が多い。

 

そんな中でも試合数の場合の数はシンプルでした
トーナメント戦 と リーグ戦 の２つの基本パターンです

 

これらの数え方は、場合の数の分野の中でも、知っていれば確実に解けるといえるほどシンプル簡単です。しかもたった２パターンですので・・・出題されたら多くの生徒が正答します。確実に解けるようにしましょうo(^-^)o