中学受験：場合の数の基本パターンを全網羅！ 整列と分配問題編

場合の数は ”全ての可能性を過不足なく数える” 

こんにちは。かるび勉強部屋 ゆずぱ です。

場合の数が超苦手 (-_-;) そう訴える小学生はとても多いです。ただ可能性のあるパターンを数えるだけなのに… なぜそんなに苦手と感じる小学生が多いのでしょうか？

それは数え方があまりにも多すぎるので
全体像が見えずにモヤモヤするから…

確かに色んなパターンがあります ∑(ﾟДﾟ) しかし、実際の入試問題を分析してみると、無数にあるように見える場合の数の問題も、その出題パターンは１０種類であることが分かります。

参考：場合の数が苦手…３つの道具を使い10種の数え方をマスターせよ

この１０種類の出題パターンのうち、子供が混乱しやすい整列問題と分配問題の２つについて具体的な問題をベースに確認してまいります。それでは詳細に参りましょうd(^_^o)

 

おさらい：場合の数は”３つの道具”で数える

場合の数は３つのステップで解法を考える

まずは ”場合の数問題” の全体像 をご覧ください。

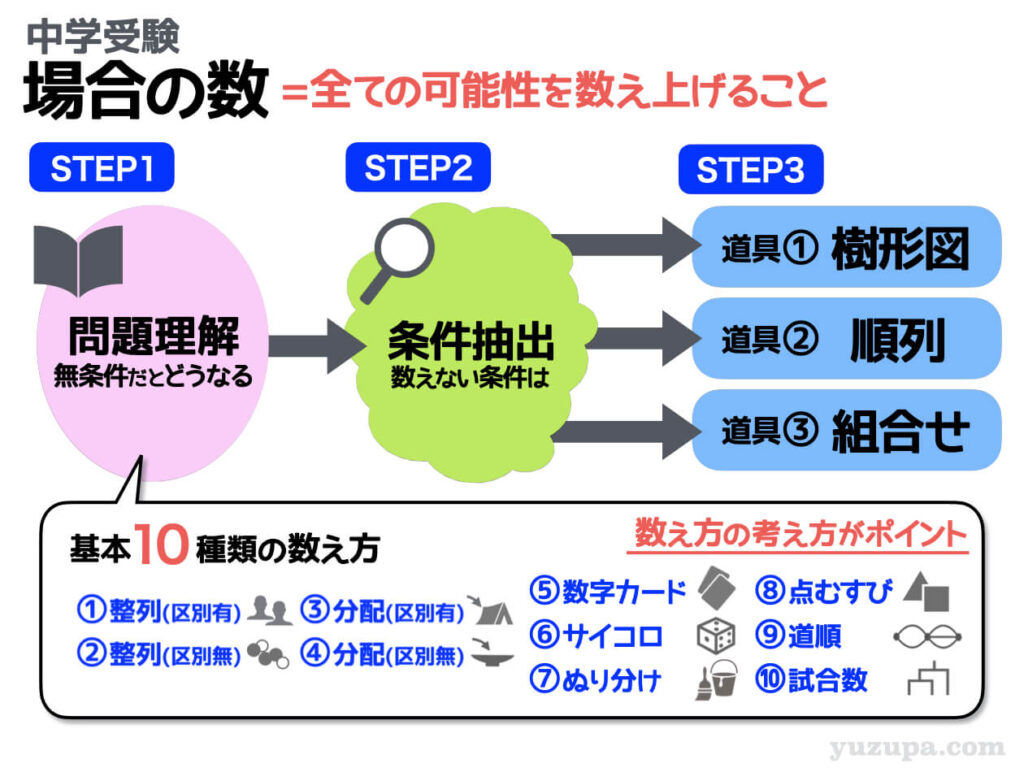
場合の数の問題というのは… ズバリ”全ての可能性を数え上げなさい”という問題 のこと。正しく問題を解くには以下の３つのステップを着実にこなすことが最も近道です。

 

STEP1では、問題文を読んで”いったい何を数えたらよいのか”をしっかり把握します。その際に役に立つのが”基本的な１０種類の数え方”です。まずはどの基本パターンに該当するかを考えましょう。

STEP2では、条件を理解します。偶数”だけ”数えなくてはいけなかったり、男子が両端にくる並び方”だけ”数えなくてはいけなかったり、入試の問題には必ず条件がついてきます(^_^;)

STEP3でいよいよ数えます。数えるには必ず道具を使います。樹形図はオールマイティですが、通り数の多い問題には使えません。樹形図をサボる道具として”順列”と”組合せ”があります。

 

３種類の道具を使って数える

３つの道具とは”樹形図”と”順列”と”組合せ”のことです。

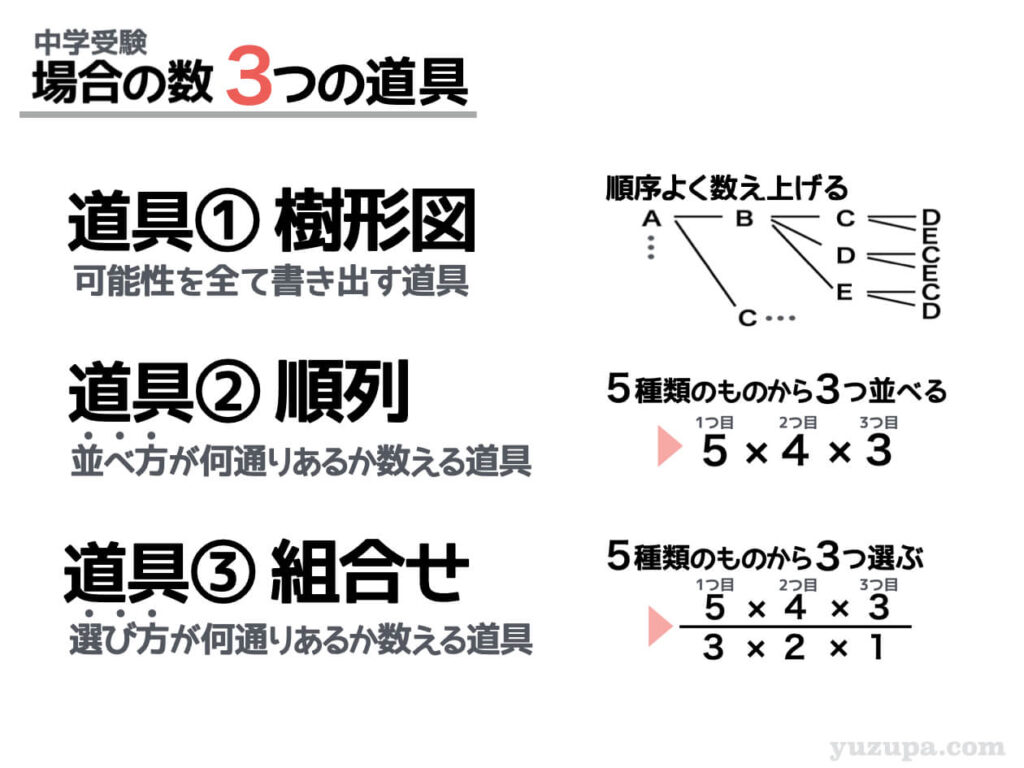
樹形図はオールマイティな道具です。どうやって数えたら良いか迷ったらまずは樹形図で数え始めてみてもよいでしょう。書いていているうちに数え方のヒラメキがあることもあります。

順列は並べ方が何通りあるか数える道具です。シンプルに何かを並べる場合の数を求める問題の他に、並べること以外の題材を並べる行為に置き換えて数えることもよくあります。

組合せは選び方が何通りあるか数える道具です。例えば１０種類のケーキがあり、３つだけ食べて良いと言われたら何を選びますか？ この道具を使えば選び方が何種類あるか分かります。

 

場合の数の全体像を確認したい場合は、ぜひ以下の記事をご参照してみてください。スッキリしますd(^_^o)

参考：場合の数が苦手…３つの道具を使い10種の数え方をマスターせよ
 

場合の数の基本問題を全網羅

グループ① 区別の有るモノの整列

まずは区別のあるモノの整列です。区別のあるモノの代表例は”ひと”です。場合の数の問題で”ひと”が出てきた場合は、原則として１人１人区別ができる別のモノとして扱います。

ただし、大人/子供と言ったり、男子/女子みたいな書かれたをしている場合は、区別のないモノとして扱います。大人は誰であっても大人。男子は誰であっても男子として扱います。

そして最初に 試みる道具は順列 となりますd(^_^o)

基本問題とそのバリエーションは以下のようになります。

それでは具体的な問題を見てまいりましょう。

 

整列(区別あり) 基本パターン

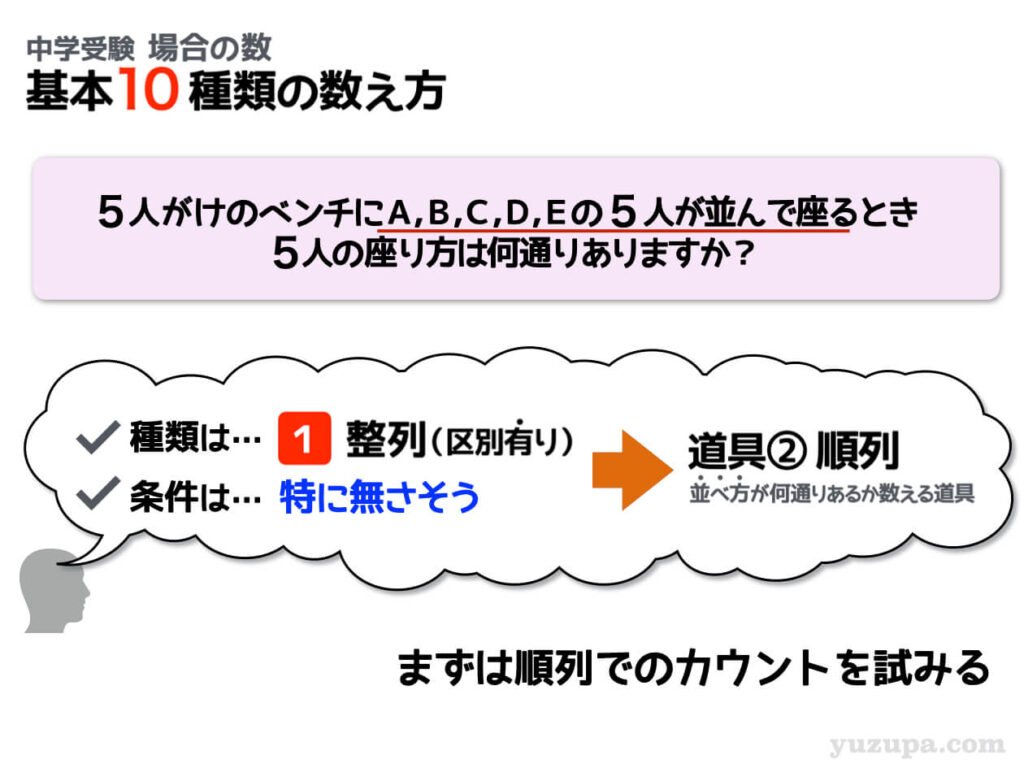
５人の”ひと”が登場する上に、AさんやBさんといった名前までついていますので当然これは”区別あり”ですね。５人が並んで座るシーンですので”並べ方”の問題です。そして出題者を悩ませる厄介な条件も無さそうですので、５人をシンプルに並べれば良さそうです。

整列の問題なので  順列の道具 を試してみましょう。

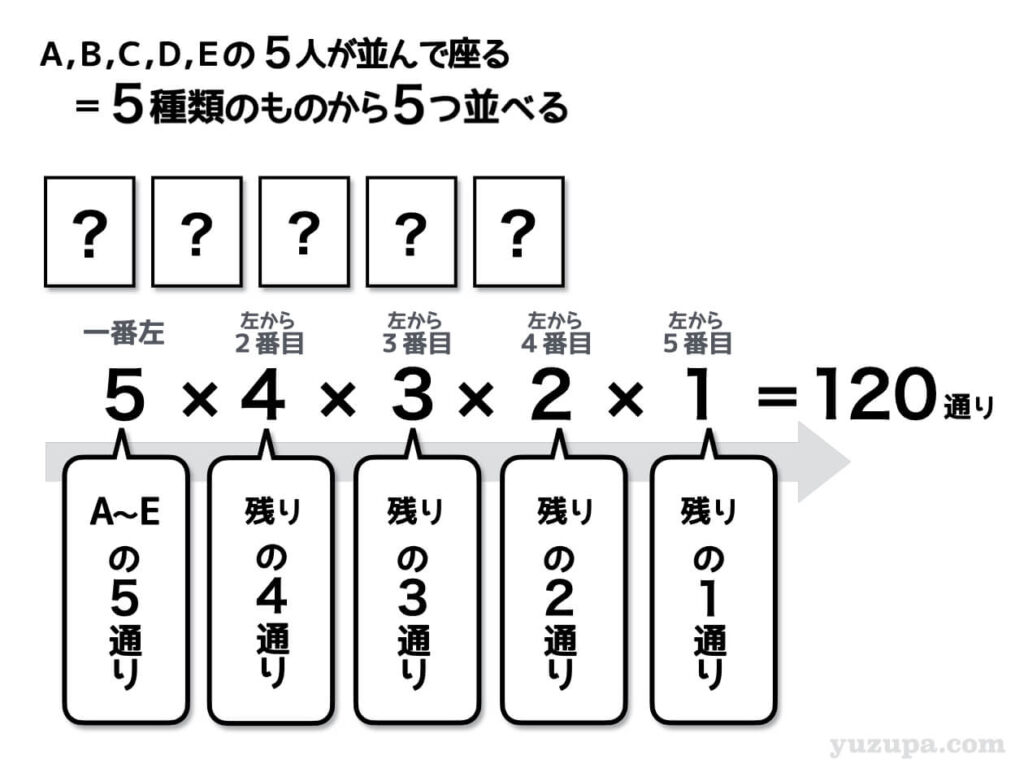
順列はあらかじめ準備された箱の中にモノを左から順番に置いていくイメージでパターン数をかけ合わせていきます。座る人は全部で５人いますので、一番左の席に座る可能性のあるのは５通りです。

左から２番目の席はどうでしょうか？

一番左の席に座った以外のひと。つまり残り４人のうち誰かです。ですので左から２番目に座る人は４通りです。同様に最後の席まで通り数を計算していきましょう。

答えは120通りになります。

 

同等の問題に、５人の中から班長と副班長と書記を決めるというような問題があります。その場合は、班長という箱、副班長という箱、書記という箱、を準備して左から順番に人を置いていくイメージで解くことができます。

 

整列(区別あり) １箇所が固定

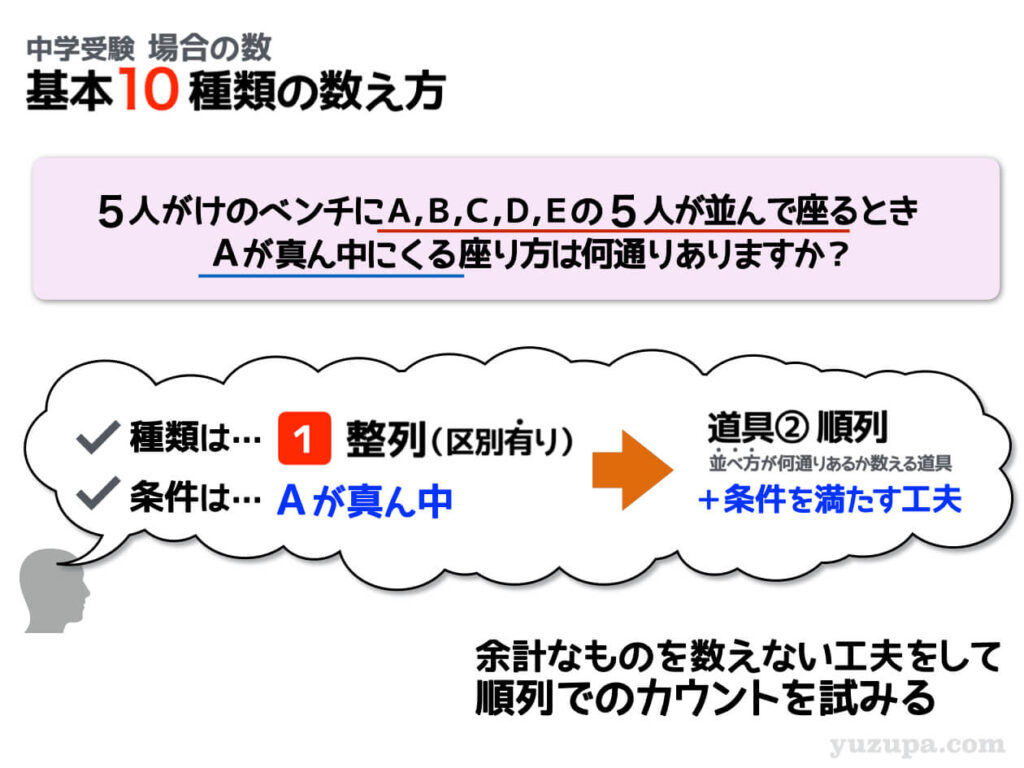
同じように５人の”ひと”を並べる問題です。AさんやBさんという名前がついている区別あるモノの整列問題ですね。ところが 今度は厄介な条件 がついています。Aさんが真ん中であるという条件です。

モノを並べる問題ですので、やはり 順列の道具 を使うことを試みてみましょう。

ただし、今回の問題は “Aさんが真ん中である” という条件があるので、数えてはいけないパターンを数えないようにする工夫が必要です。

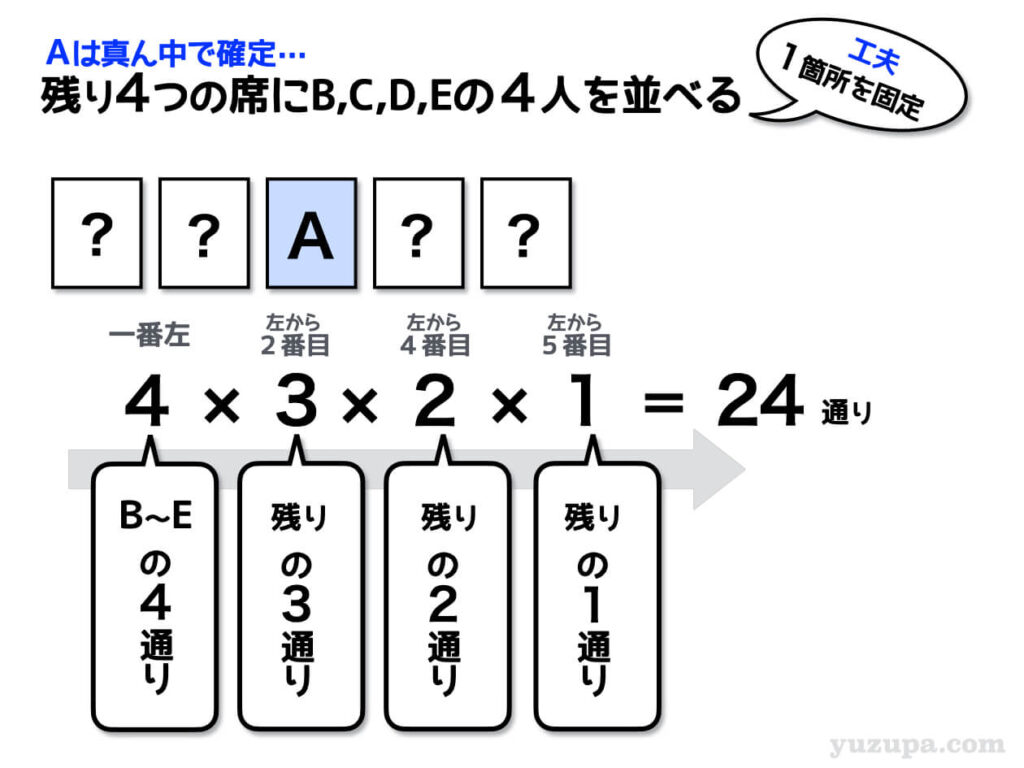
順列ですので基本どおり箱を準備しますが、真ん中の箱はAさんであらかじめ予約します。Aさんは最初に真ん中の箱に固定してしまいましょう。これがこの問題を解くポイントです。

あとは残りの４つの席に、左から順番に配置していくパターンを数えていきましょう。一番左の席につく可能性があるのはAさん以外の４人ですので４通りです。左から２番目の席は、Aさんと一番左の席に座ったひとを除いた残り３人が座る可能性があるので３通りです。

このようにかけ合わせると答えは２４通りとなります。

 

整列(区別あり) ２箇所が固定

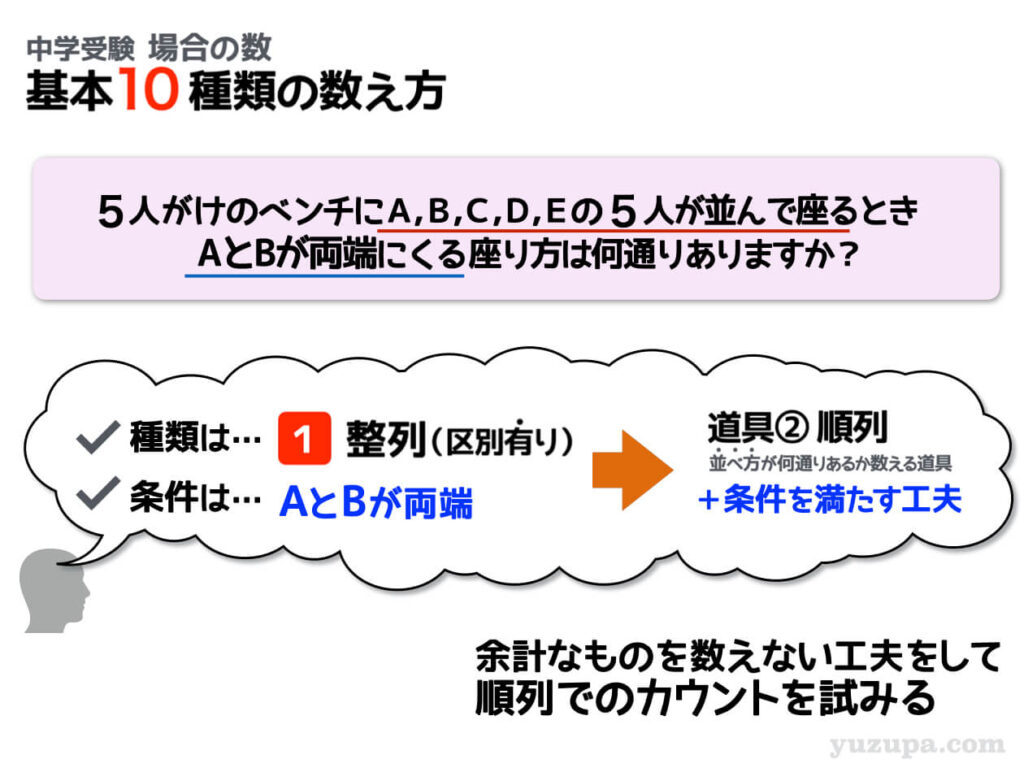
同様の問題が続きます。問題の種類は同じように区別のあるモノの整列となりますが。またまた厄介な条件がついています。AさんとBさんが両端にくるという条件がついています。

整列の問題ですので やはり順列を使って解く ことを試みます。

さて…条件と合致しないものを数えないようにしなくてはいけませんが、どのように工夫をしたら良いでしょうか？

 

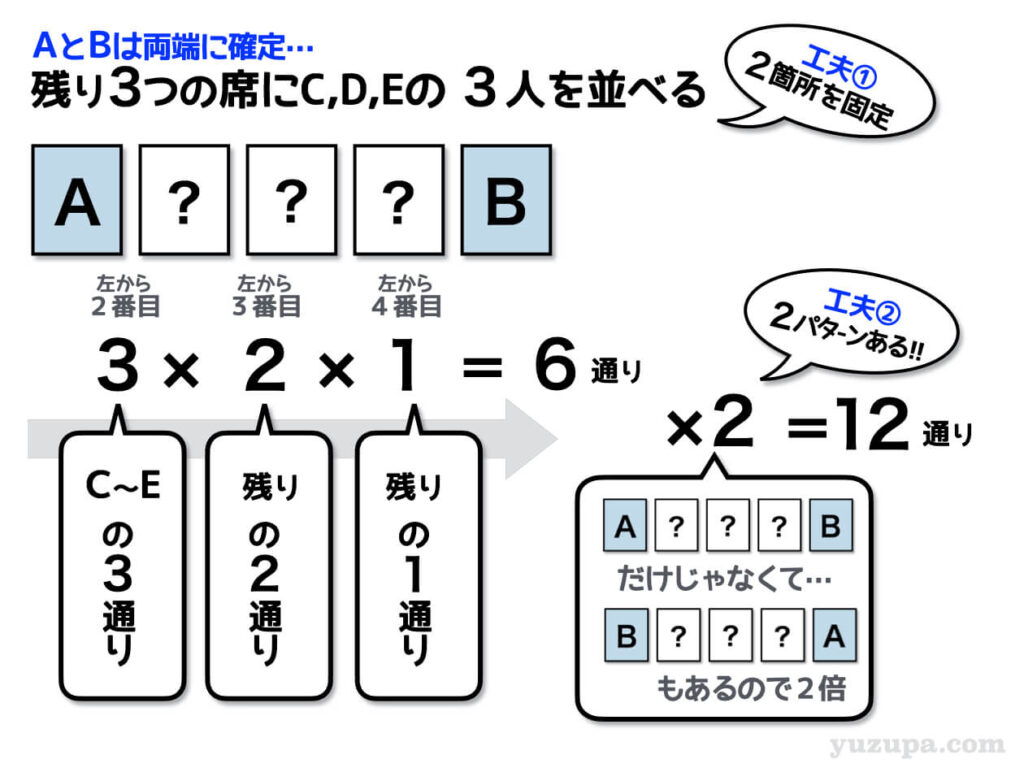
両端にAさんとBさんがくるというのだから、素直にAさんとBさんを両端にあらかじめセットしてしまいましょう。両端が予約されているので残る席は３つです。この３つの席に残りの３人を並べていきましょう。その結果、残りの３つの席に残りの３人が座る並べ方は６通りあることが分かります。

AさんとBさんが両端にくるのはこれだけではありません。

左端にAさん/右端にBさんのパターンを数えてみましたが、当然ですが 左端にBさん/右端にAさんのパターンも同様に６通りある ことを忘れてはいけません。６通り＋６通り＝１２通りとしても良いですが、２をかけていまってもよいでしょう(^_^;)

 

整列(区別あり) カタマリ①

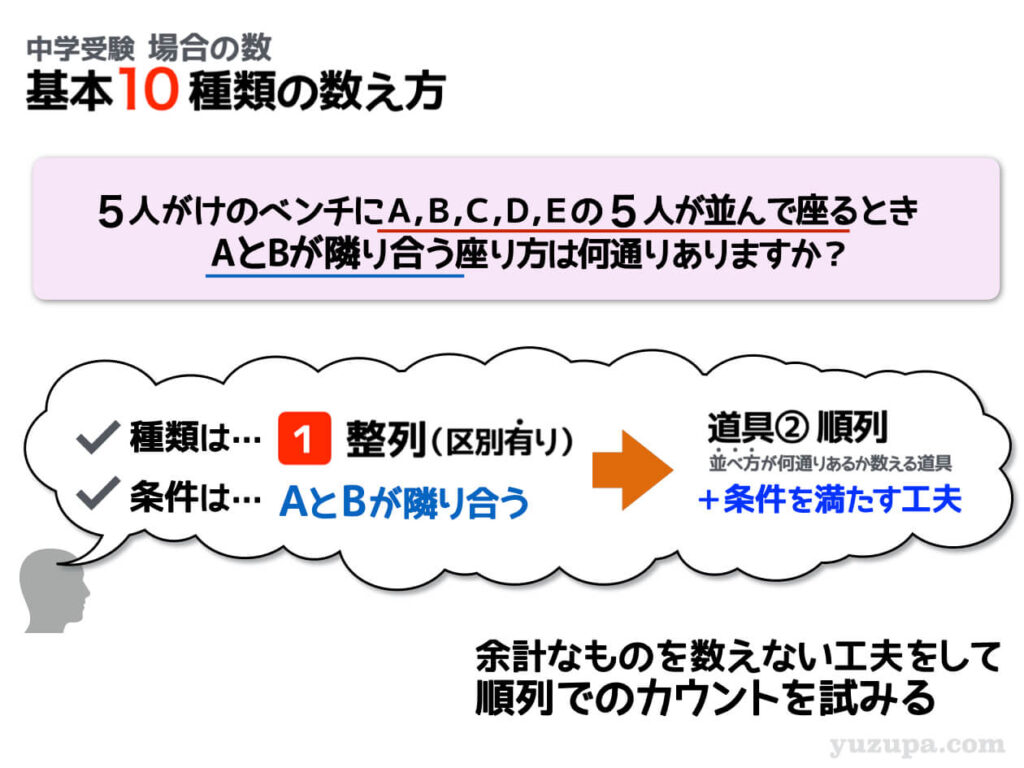
今度も区別のあるモノの整列問題であることはすぐに分かるかと思いますが、今回ついている条件は、AさんとBさんが隣り合うという条件です。先ほどまで使ってきた工夫は使えなさそうですのであらたな工夫が必要です。

問題は整列ですので 順列の道具 を使うのが王道でしょう。

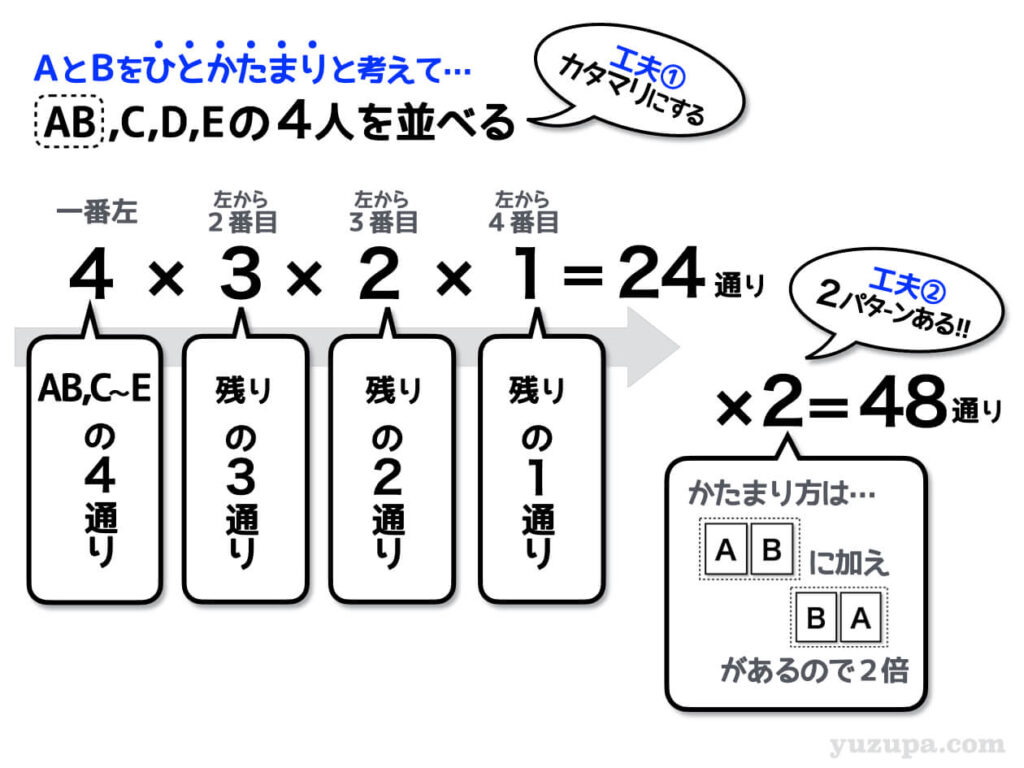
今回の問題ではAさんとBさんが隣り合っている並び方を数えなければいけません。そうであれば…AさんとBさんを1つのカタマリとして考えてしまいましょう。

AさんとBさんを1つのカタマリと考えてしまうと、５つのモノの並び方ではなく４つのモノの並び方を数えることになります。箱を４つ用意して４人の並び方を数えると２４通りありそうです。

そしてカタマリ方は左からABだけではなく BAという反対の並びも 考えられます。なのでABの並びが２４通り、BAの並びが２４通りで４８通りになります。

 

整列(区別あり) カタマリ②

問題のベースはいままでと同じ区別あるモノを並べる問題ですが… 次はさらに 複雑に思えてしまう条件 です∑(ﾟДﾟ) AさんとBさんの間にCさんだけがくるという条件ですね。

でも複雑そうに見えて実は簡単です。AとBの間にCだけがくる並び方というのは、AとCとBがカタマリとであると考えて良いでしょう。そうであればアプローチは簡単です。

カタマリを考えて順列を使って数える！

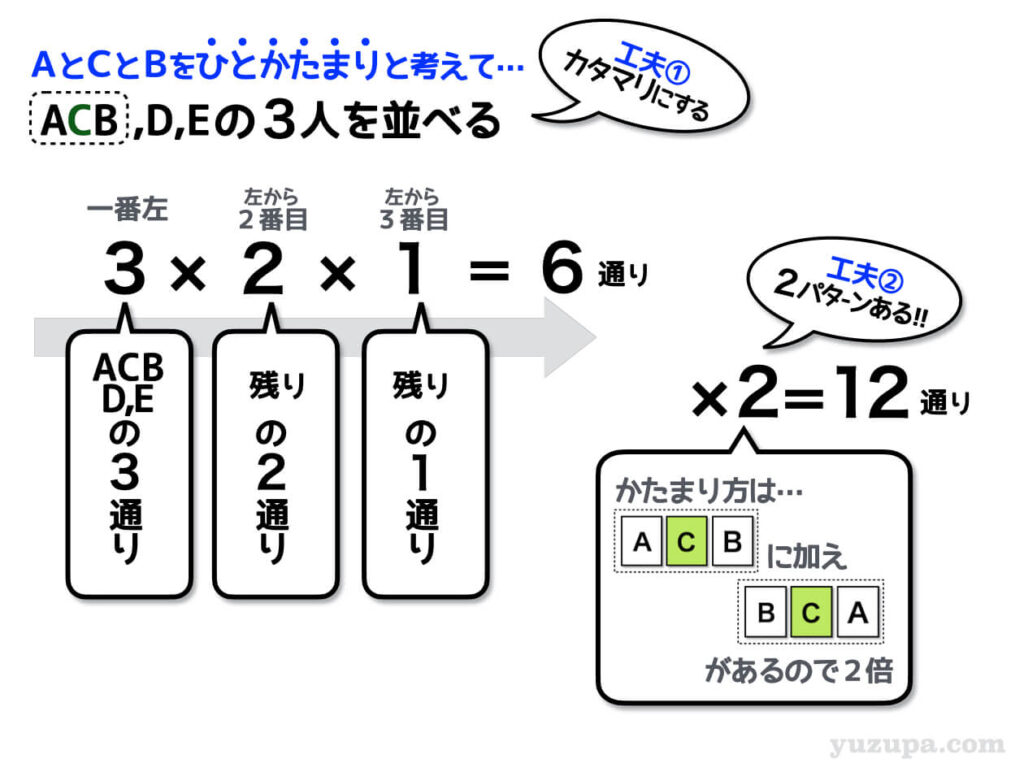AとCとBがカタマリと考えると、３つのモノの並び替えを考えればよさそうです。いつもどおり３つの箱を用意して３つのモノの場合の数を数えていきましょう。

そしてカタマリにパターンがないかの確認ですd(^_^o)

AさんとBさんの間にCさんがくるパターンは、Aさん-Cさん-Bさんのパターンもありますが、もうひとつBさん-Cさん-Aさんのパターンがあります。それぞれに６通りずつあるので、答えは１２通りですねd(^_^o)

 

整列(区別あり) 補集合①

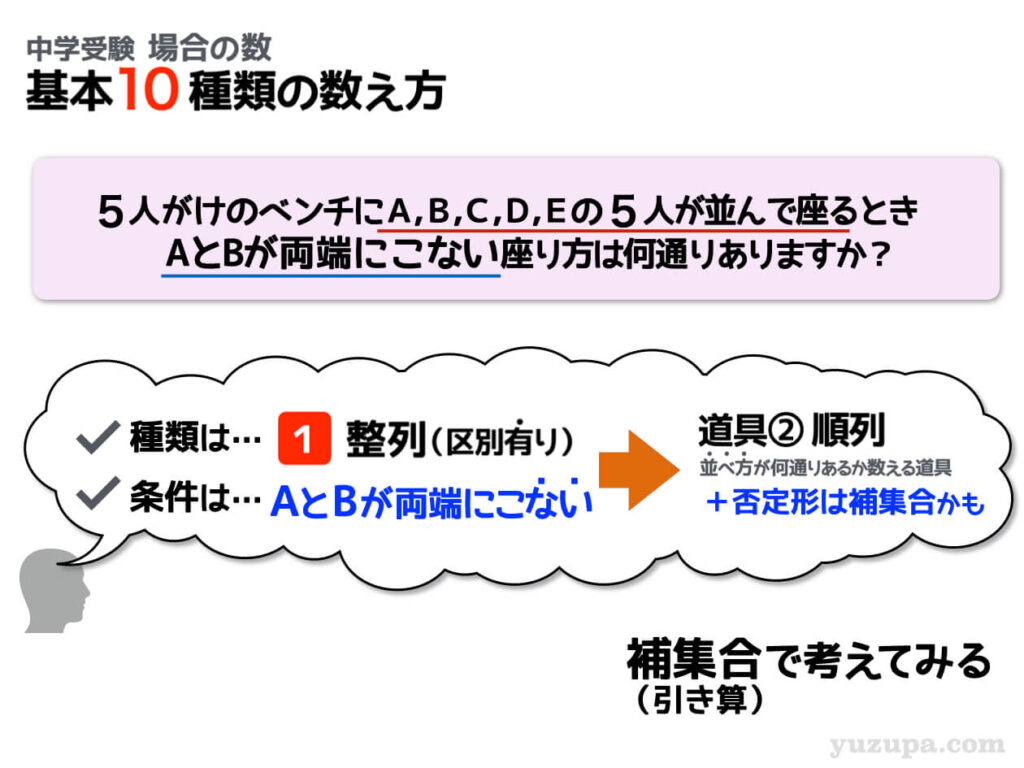
問題は区別のあるモノの整列問題です。条件はまだまだありますd(^_^o) 今度はAさんとBさんが両端にこないという条件です。整列の問題なので使う道具は順列がよさそうですが、ひとつ工夫をすると答えにたどり着くことができます。

このように否定形の条件がついた場合は補集合が使える可能性があります。

AさんとBさんが両端にこないパターンを数えるには、全体からAさんとBさんが両端にくるパターンを引いてあげれば良いという考え方ですd(^_^o) この考え方を補集合と言いますが、実際に補集合で考えてみましょう。

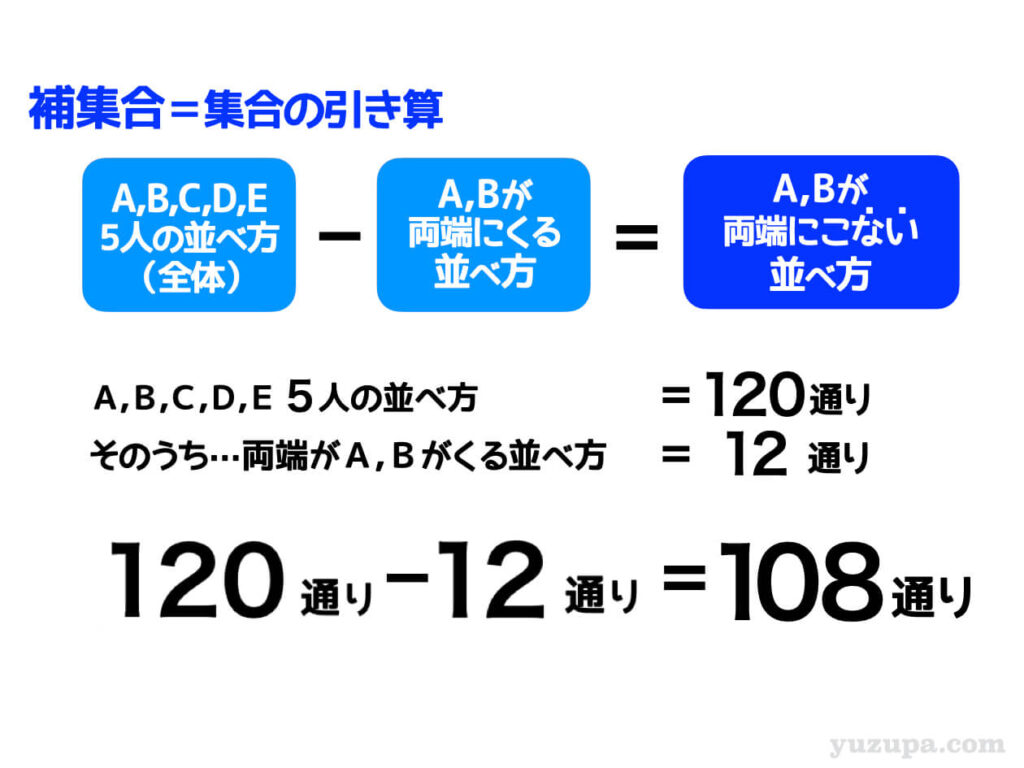
５人が横一列のベンチにならぶ場合の数は１２０通りでした。そして、その中でAさんとBさんが両端にくる並び方は１２通りでした。AさんとBさんが両端にこない並び方は、この２つの数字の引き算で出すことができますね。

これが補集合の考え方ですd(^_^o)

 

整列(区別あり) 補集合②

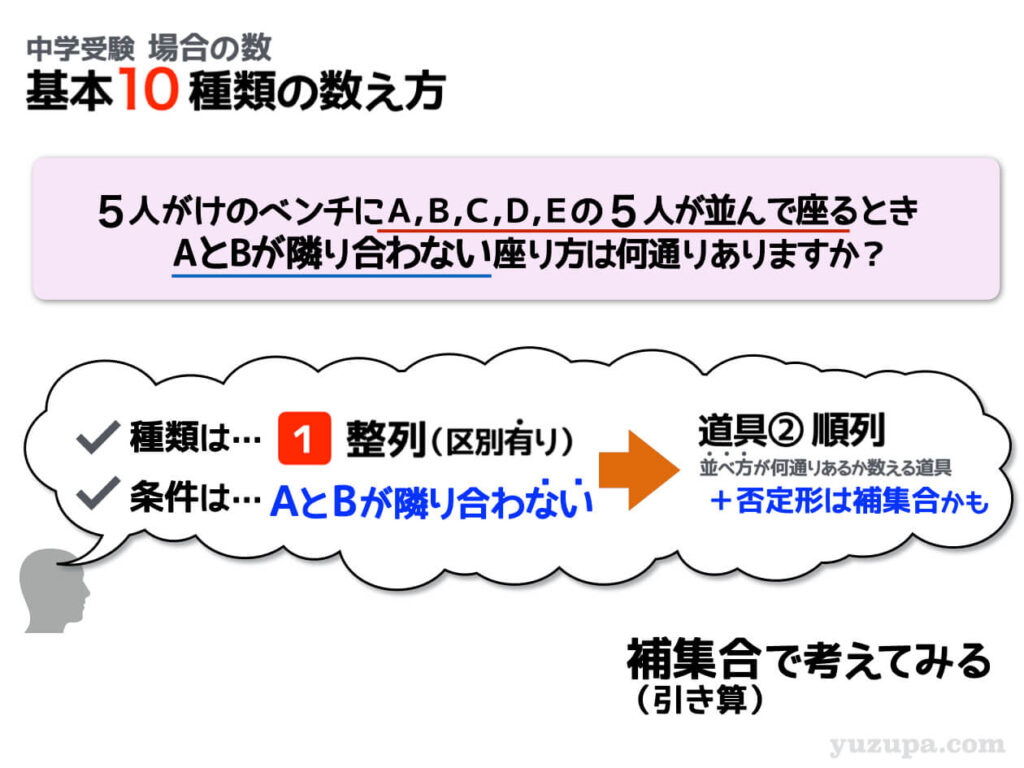
続いても区別あるモノの整列問題です。今度の問題はさきほどと同様、AさんとBさんが隣り合わないという否定形の条件がついています。もう分かりますね？ 補集合を使って場合の数を求めてみましょう。

AさんとBさんが隣り合う場合の数が４８通りでしたので、全体から引いてあげれば、その逆の場合の数を求めることができます。否定形が出てきたときには補集合を考えましょう。

 

 

グループ② 区別の無いモノの整列

次は区別の無いモノの整列です。人と違いモノは基本的には区別がありません。りんごが１０個あったとしましょう。よーく観察するとひとつひとつ異なる個体で区別がつきます。

ところが中学受験の入試問題では同じモノとして扱いますd(^_^o)

りんごはどのりんごも同じ。当然ですが… ひとりひとり違うひとを並べる時よりも、場合の数は小さくなります。そして区別のないモノの整列は 道具として組合せ を最初に試しす_φ(･_･

百聞は一見にしかず、具体的な問題例をみて参りましょう！

 

整列(区別なし) 基本パターン

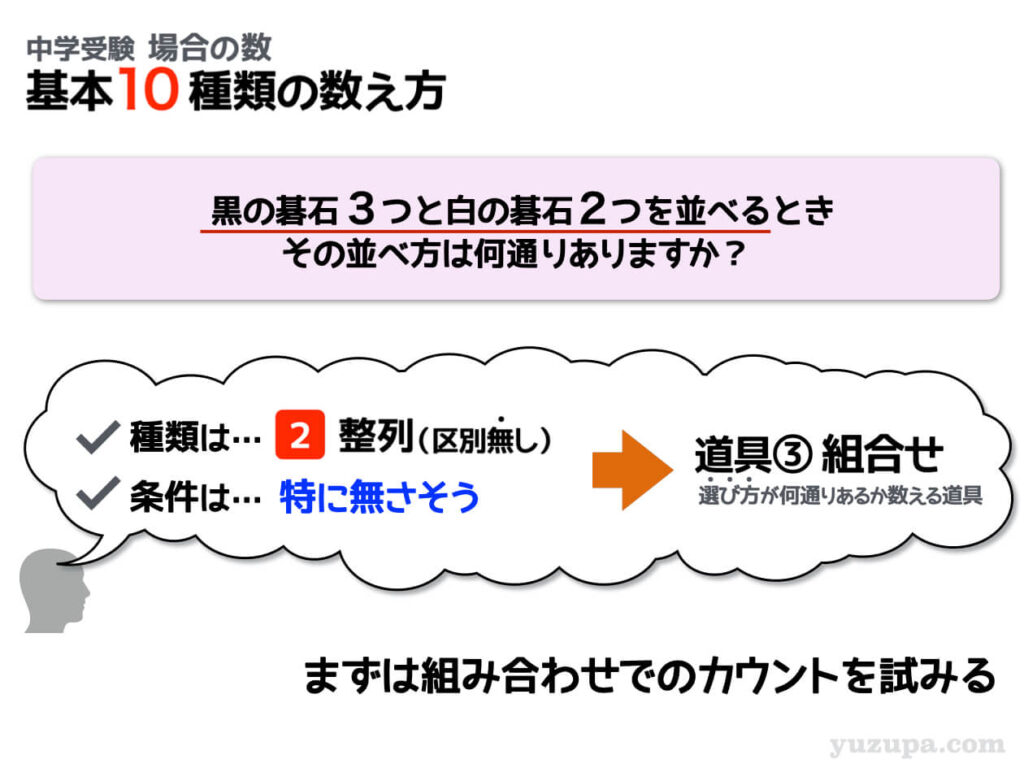
並べるモノは碁石です。２つ並べた碁石を見て普通の人は見分けがつきませんよね。碁石は区別がつかないモノの代表格です。問題は並べ方を聞いているので順列を使いたくなりますが…

区別がないモノを並べる場合は組合せを使います

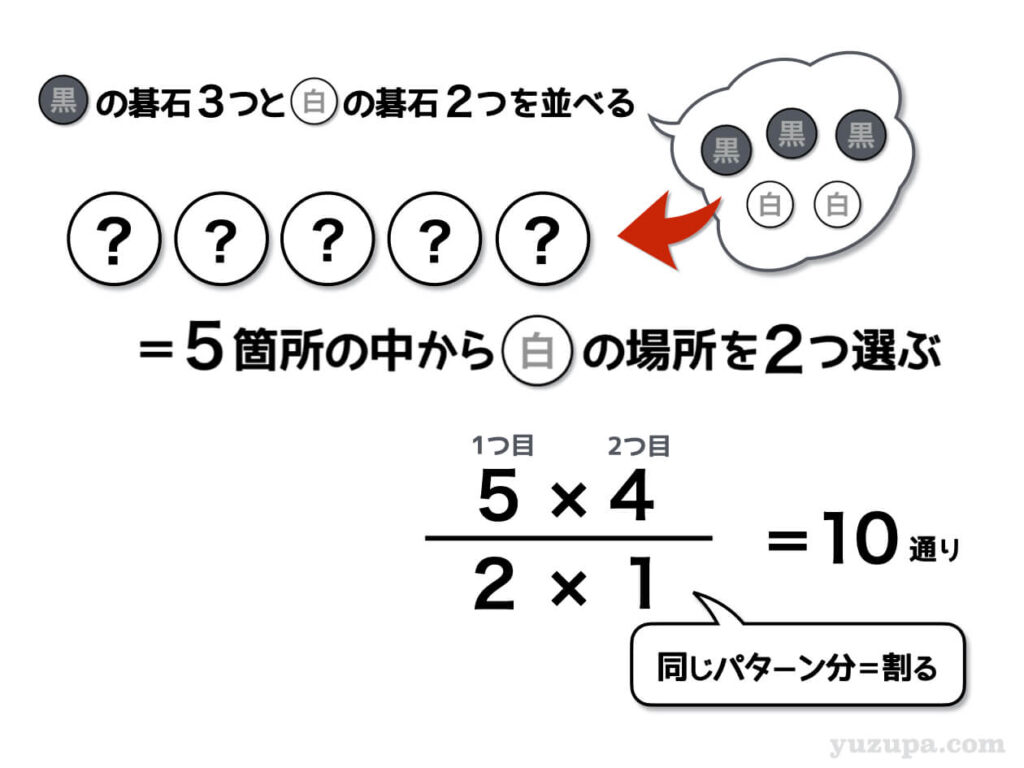
合計５つある碁石の箱を横一列に並べるところまでは順列と考え方は一緒です。そして、碁石は区別がつかないので、この５つの箱の中から白の碁石が置かれる場所を２箇所選ぶという考え方をするとスンナリ数えることができます。

1つ目の白が置かれる場合の数は５通りで、２箇所目の白が置かれる場所は残りの４通りです。同じパターンを重複で数えないようにちゃんと２で割ることを忘れないようにしましょう。

もちろん５箇所の箱の中か黒を置く３箇所を選ぶ場合の数を数えても全く同じ答えになります∑(ﾟДﾟ)

 

整列(区別なし) １箇所が固定

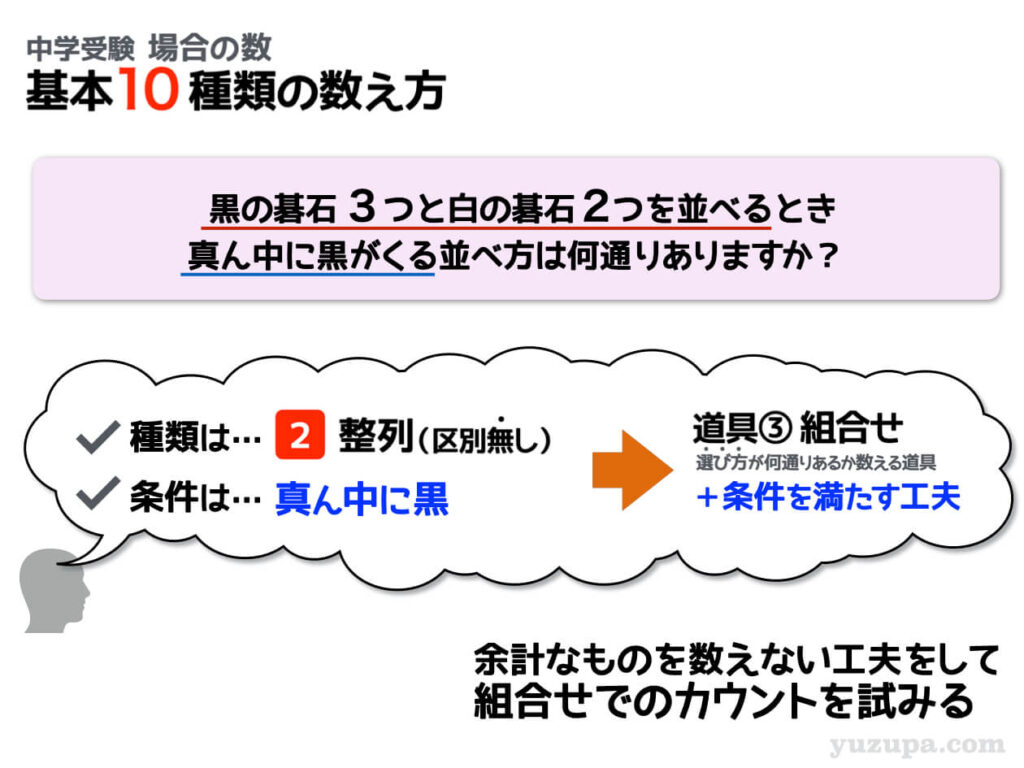
同じように区別のない碁石を並べる問題ですが、真ん中に黒い石がくるという条件 が追加されました。これは人を並べるときと一緒の工夫が使えます。条件にあった並べ方を数えるために 黒い碁石ひとつを固定 するという工夫です。

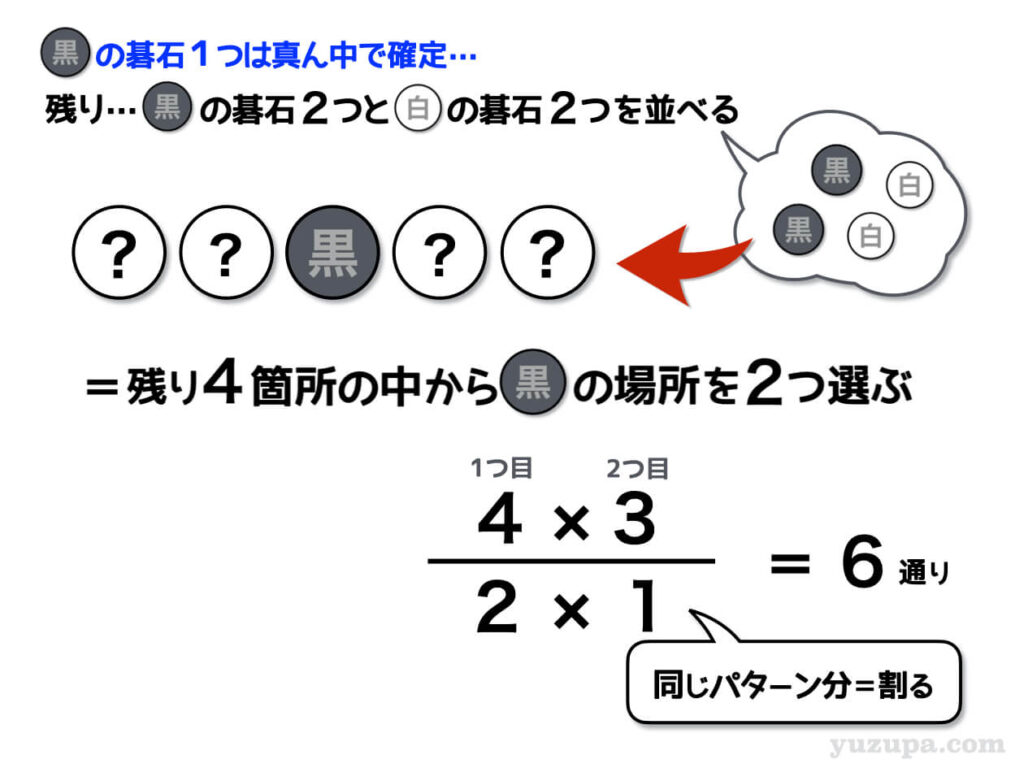
黒の碁石のうち１つをあらかじめ真ん中の席に置いておきます。残りの席は４つです。この４つの席に、残った黒の碁石２つと、白の碁石２つを並べれば良いと考えるのです。

ここまで来れば簡単ですね o(^-^)o

４つの席の中から黒い碁石を置く席を２つ選ぶ場合の数を求めれば良いのです。１箇所目は４通り、２箇所目は３通りです。そしていつもどおり、重複の分を割ってあげれば答えがでます。

 

整列(区別なし) ２箇所が固定

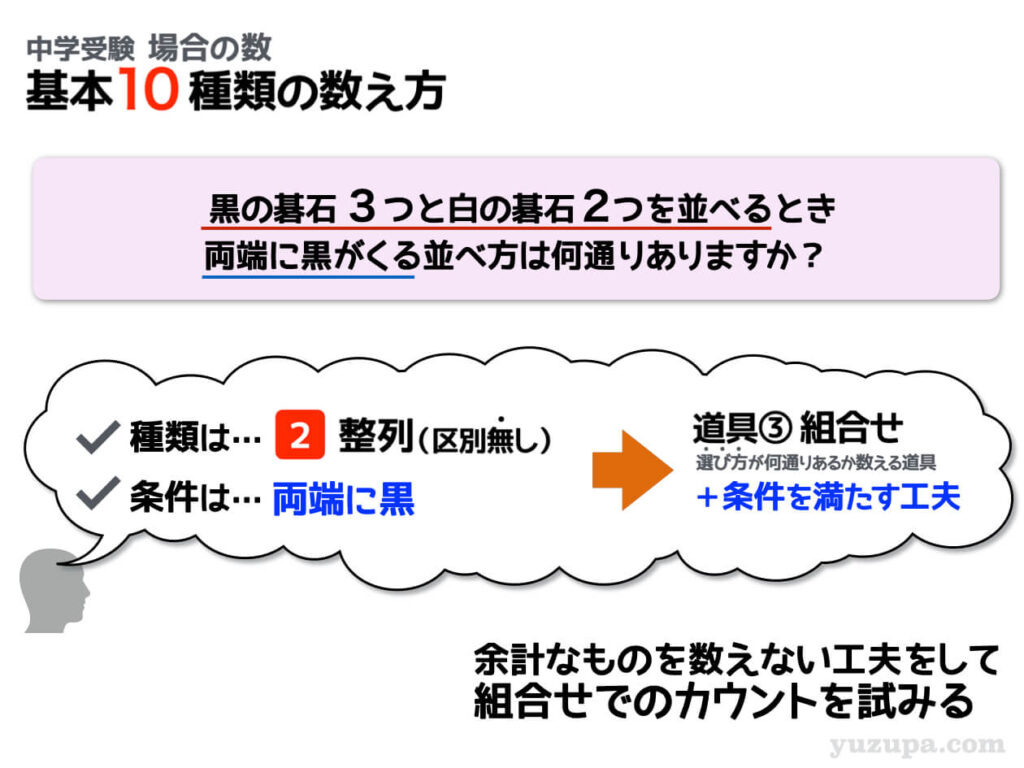
同様の区別のない碁石を並べる問題です。今度の条件は…両端に黒がくるパターン。あらかじめ予約をする席が２つに増えたということです。固定席がひとつからふたつに変わっただけですね。

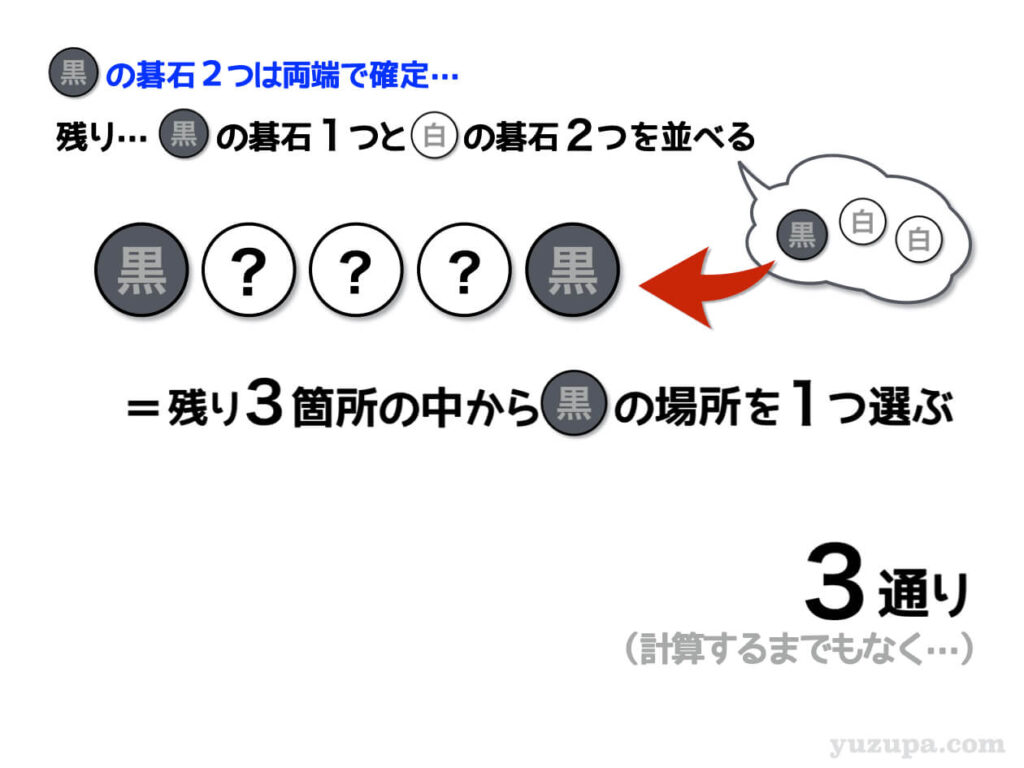
両端の席に黒の碁石を置くので、残った座席は真ん中の３席です。そして残った碁石は、黒が１つと白が２つです。この３つの座席の中から黒１つを置く場所を選ぶ場合の数を求めましょう。

もちろん答えは３通りです
計算するまでもありませんね…

ちなみに、残った３席の中から、白を置く２席を選ぶ場合の数を計算したとしても、答えは同じ３通りになります。

どちらでも正解にたどりつくことができますが 計算が楽になる少ない方で求める ようにしましょうd(^_^o)

 

整列(区別なし) カタマリ①

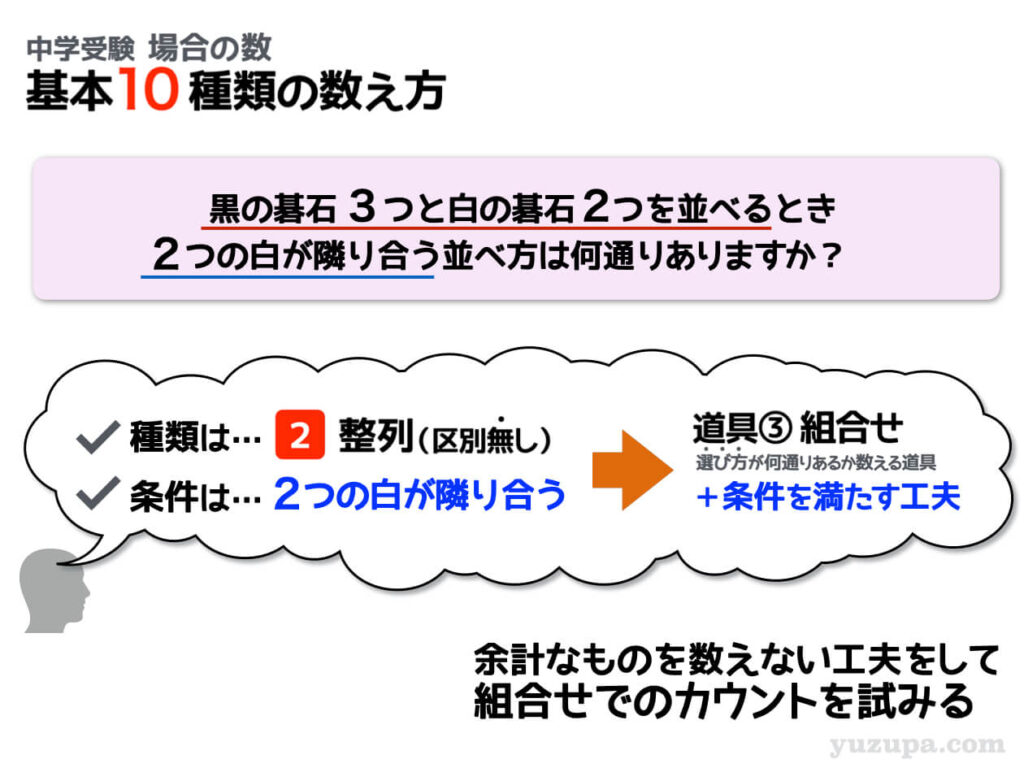
同じく区別の無い碁石を並べる問題ですが、今度の条件は 白い碁石が隣り合う という条件つきです。隣り合う…もう分かりますね？ 隣り合う２つの白い碁石をカタマリとして考えましょうd(^_^o)

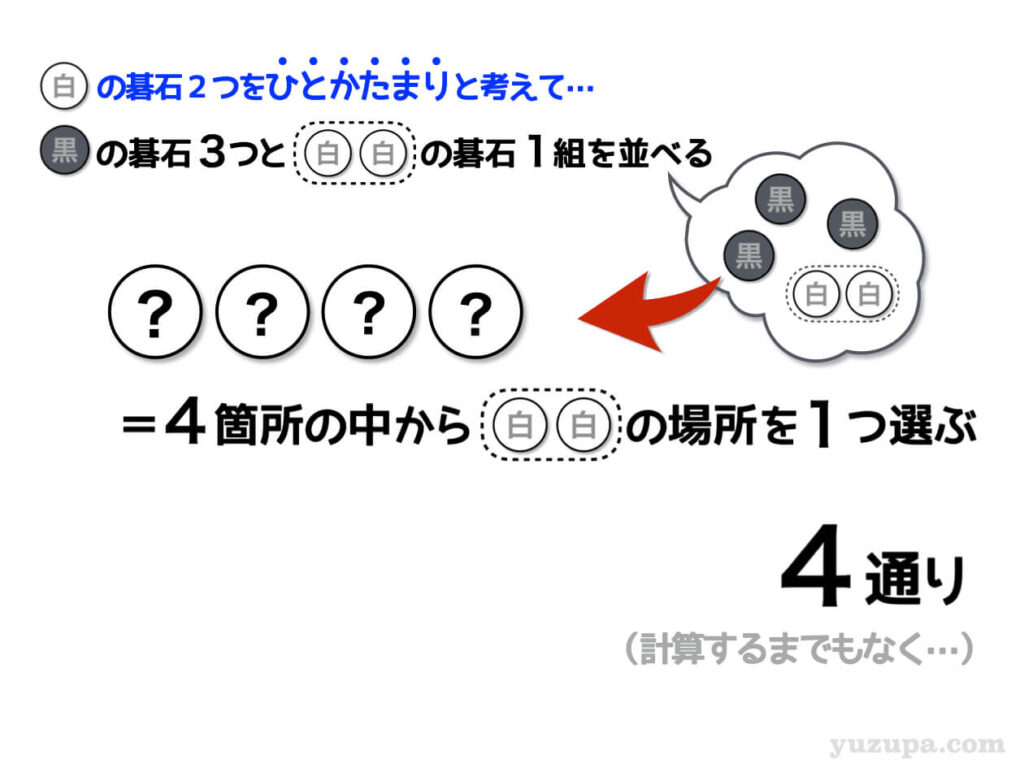
白い碁石２つをセットにしてカタマリと考えます。黒い碁石３つと白い碁石２つのカタマリが１つ…これら４つを並べる場合の数を数えればよいのです。

具体的には４つの箱の中から白２つのカタマリをどこに置くかを選びます。計算するまでもなく４通りですね_φ(･_･

毎度のことで恐縮ですが、４つの箱の中から黒の碁石３つを置く場所を選ぶと考えても、答えは同じ４通りになりますd(^_^o)

 

整列(区別なし) カタマリ②

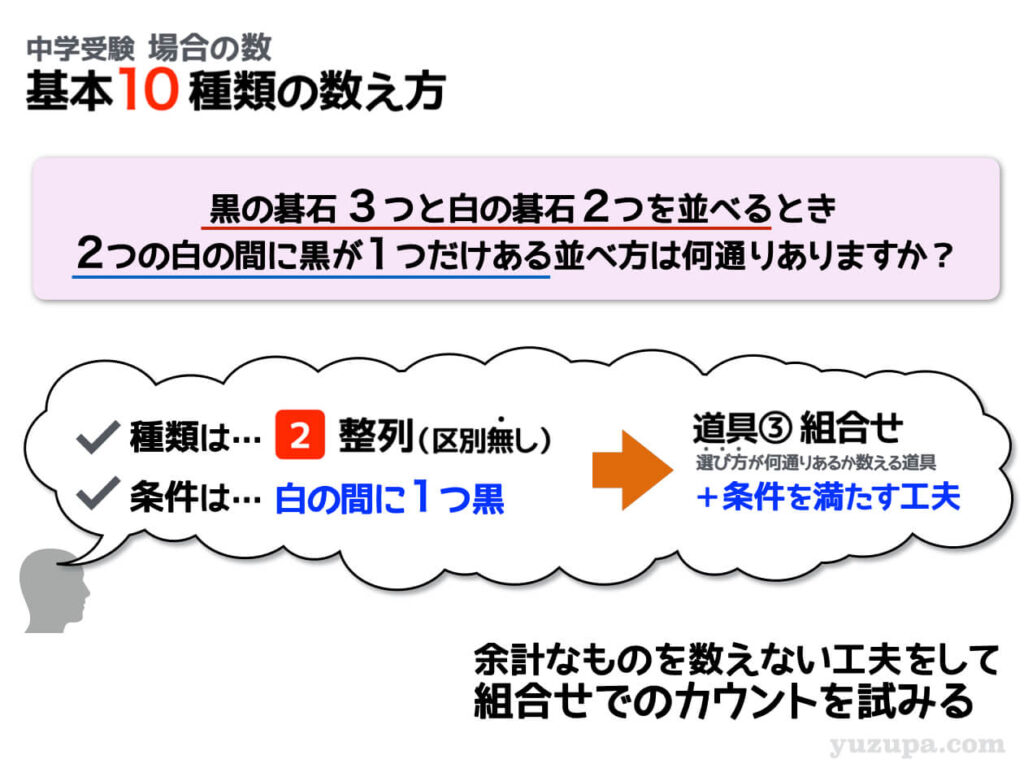
区別のない碁石を並べる問題ですが、今度の条件は２つの白い碁石の間に黒い碁石が１つだけくるというもの。カタマリっぽく見えなくても… 白-黒-白 という３つの碁石がカタマリになると考えますo(^-^)o

カタマリが見えたら答えはすぐそこです！

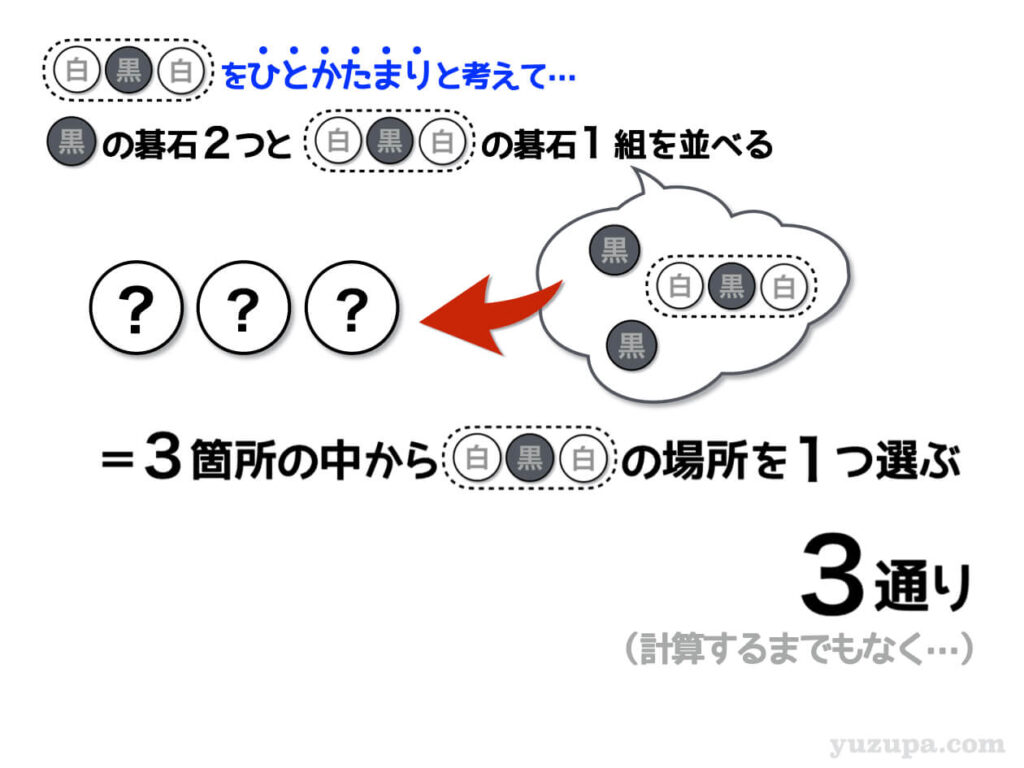
白-黒-白をひとつのカタマリと見ると、黒い碁石２つとカタマリ１つという４つのモノを並べることになります。いつも通り４つの箱から白-黒-白のカタマリを置く場所の選び方を考えます。

計算するまでもなく３通りですねd(^_^o)

しつこいようですが…(^_^;) ３席の中から黒い碁石を置く２席を選ぶという計算をしても、答えは同じ３通りになります。

 

整列(区別なし)　補集合①

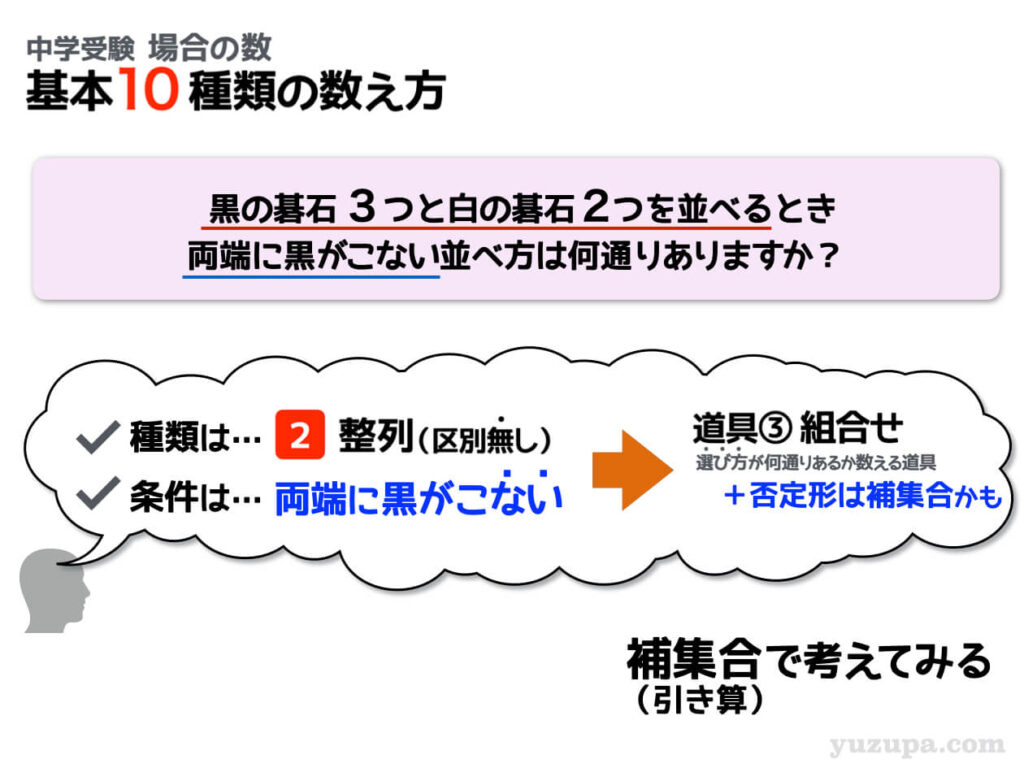
同じく区別のない碁石を並べる問題です。そして条件は両端に黒がこない。きました…”否定形の条件”です。否定形の条件は、補集合を考えると答えが簡単にでることがあります。今回の条件もバッチリ答えに辿り着けそうですd(^_^o)

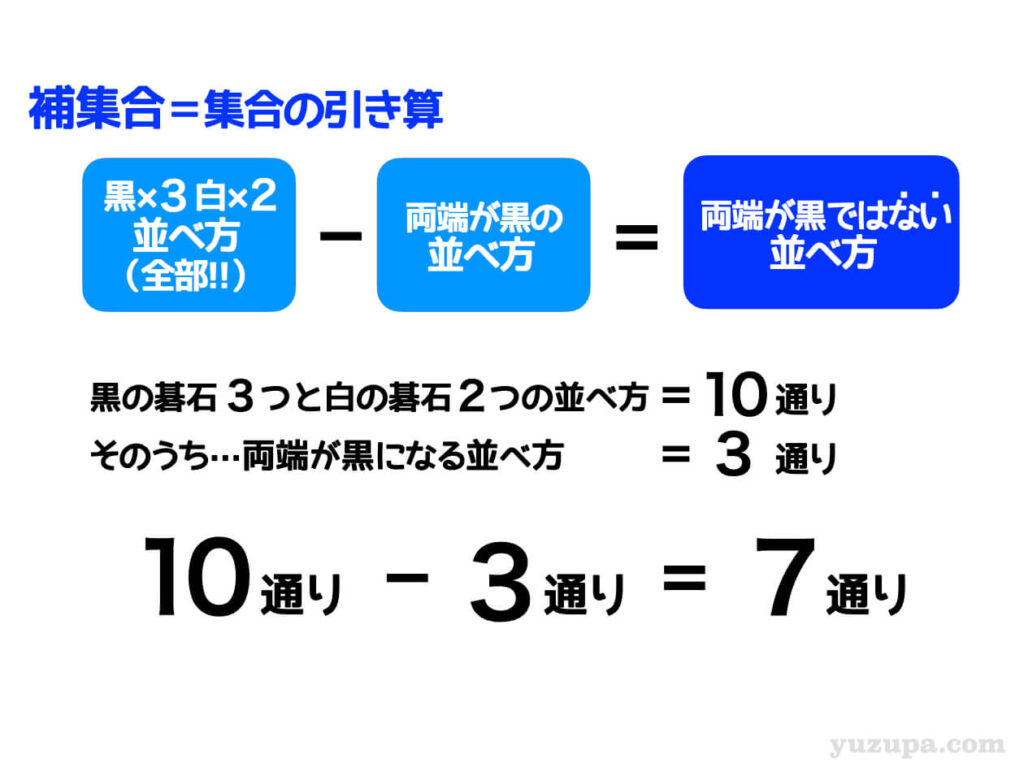
全ての並べ方の場合の数１０通りから、黒が両端にくる並べ方３通りを引いてあげれば答えが出てきそうです。もう答えは出てしまいました(^_^;) 答えは７通りとなります。

否定形の条件が出てきた時には、補集合での解法を疑いましょう！

 

整列(区別なし)　補集合②

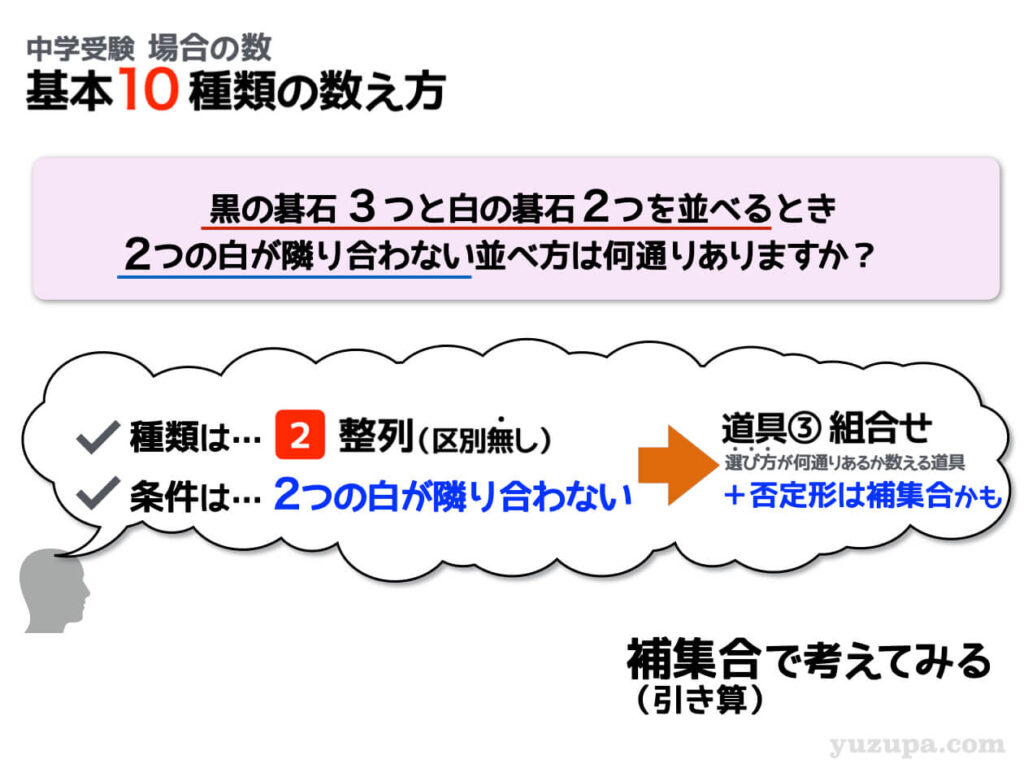
区別のない碁石を並べる問題ですが…またまた否定形の条件です。２つの白い碁石が隣合わないという条件です。そのまま考えてしまっては迷宮に迷い込んでしまいそうですが、カタマリと補集合を知って入れば余裕ですね d(^_^o)

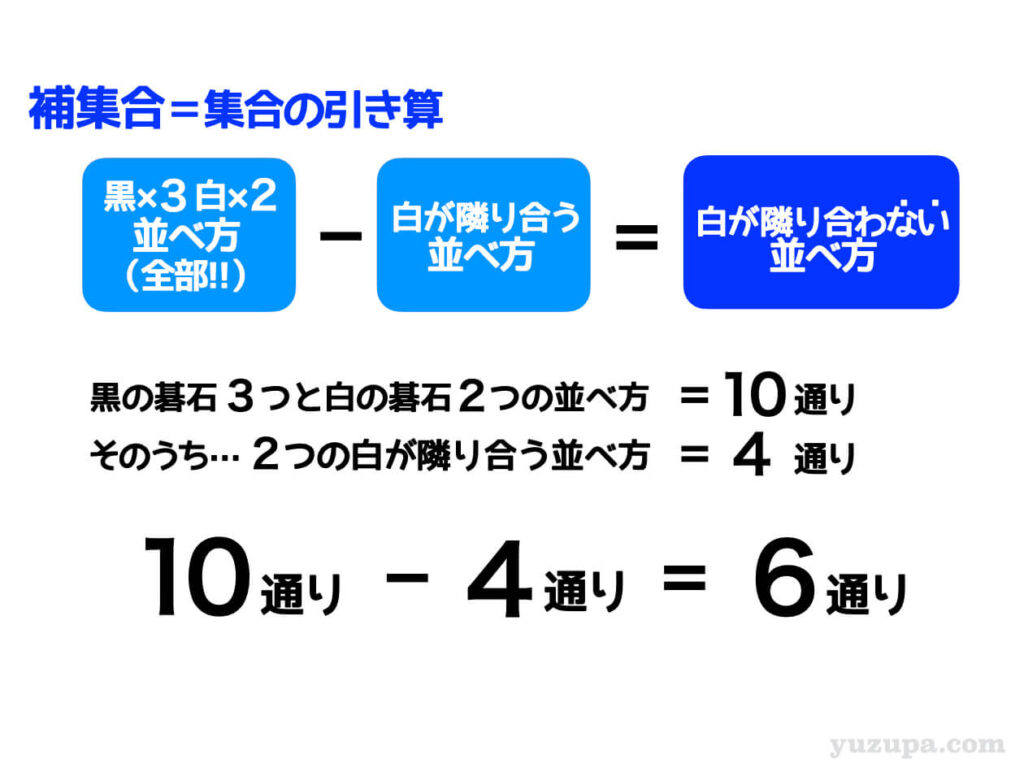
２つの白い碁石が隣り合う並べかたはカタマリと考えて求めることができました。求めるべきはその補集合です。全体から２つの白が隣り合う場合の数を引けば、２つの白が隣り合わない場合の数がでますd(^_^o)

 

グループ③ 区別のあるモノの分配

場合の数の問題で”整列”の次に頻出するテーマは”分配”です。何かを複数に配り分ける場合のパターン数はいくつか？という問題です。そして、配られるものは区別のあるモノ、ないモノ含めて多岐に渡ります。

飴玉のようなモノを分配することもあれば、
人を分配することもあります∑(ﾟДﾟ)

人はひとりひとり名前がついており、見分けがつくので区別あるモノとして扱われます。それらをいくつかの仕事に分配したり、いくつかの部屋に分配したりしますd(^_^o) そして区別のあるモノの分配は 樹形図から入ることをオススメ していますd(^_^o)

区別があるモノの分配では、樹形図で基本的なパターン数を数えあげた後に、条件に合わないモノを引いたり割ったりして省く という王道の流れがあります。この流れを意識して問題を解いてみましょう。

 

 

 

分配(区別あり) 基本パターン

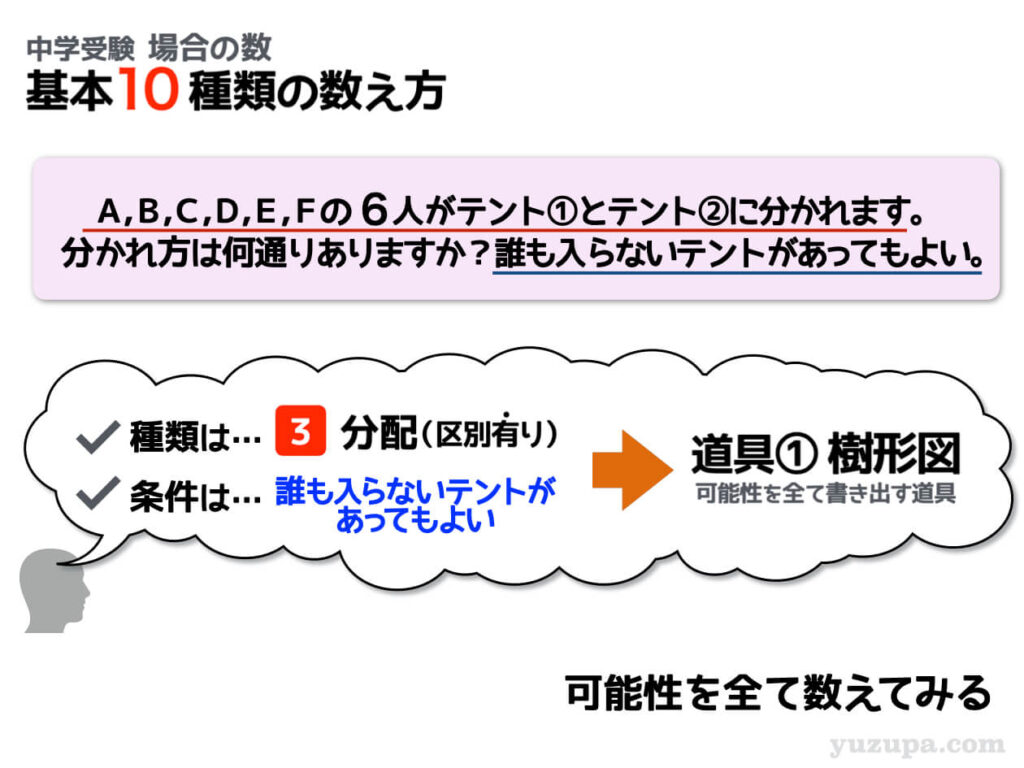
さっそく基本パターンの問題を見てみましょう。区別できるモノの代表格は”ひと”です。６人の”ひと”を名前のついた２つのテントに分配するという問題ですd(^_^o) 典型的な 区別のあるモノの分配 問題となります。

分配の問題は 並べ方を数える”順列”や、選び方を数える”組合せ”がスンナリ使えないので、オールマイティな樹形図から試します。
さて… さっそく樹形図を書いてみましょう！

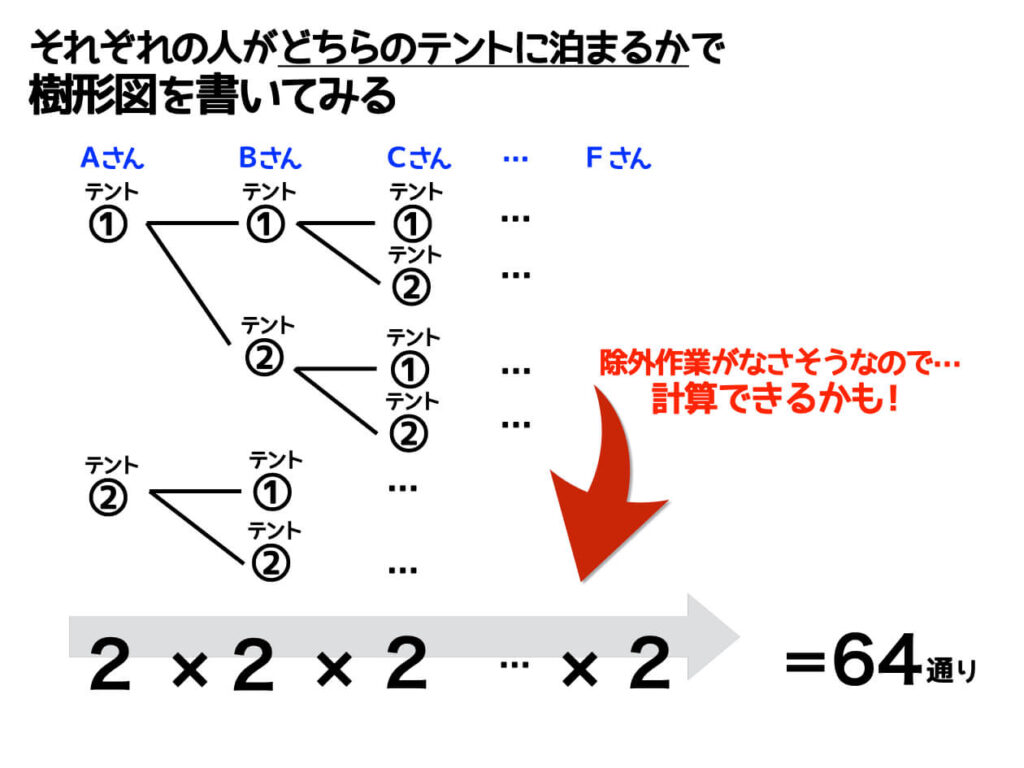
Aさんはテント①とテント②のどちらに分配されるか？ 同じくBさんはテント①とテント②のどちらに分配されるか？ それぞれの人がどちらのテントに分配されるかに着目するとよさそうです。

では具体的に樹形図を書いてみましょう

Aさんはテント①に泊まる場合と、テント②に泊まる場合の２通りがあって… Bさんもテント①に泊まる場合と、テント②に泊まる場合の２通りがあって… Cさんもテント①に泊まる場合と、テント②に泊まる場合の２通りがあって…

あれ…これみんな同じパターンだな…
そう気づければ、樹形図をコツコツ描くという作業をサボって計算で途中から計算にシフトしますd(^_^o)

※ 実は同じモノを何度使っても良い並べ方は 重複順列 というちゃんとした名前がついています∑(ﾟДﾟ)
公式的なものもあるのですが…樹形図を想像すればすぐに計算できてしまうので樹形図での考え方を紹介しています。

 

分配(区別あり) 分配先に区別あり①

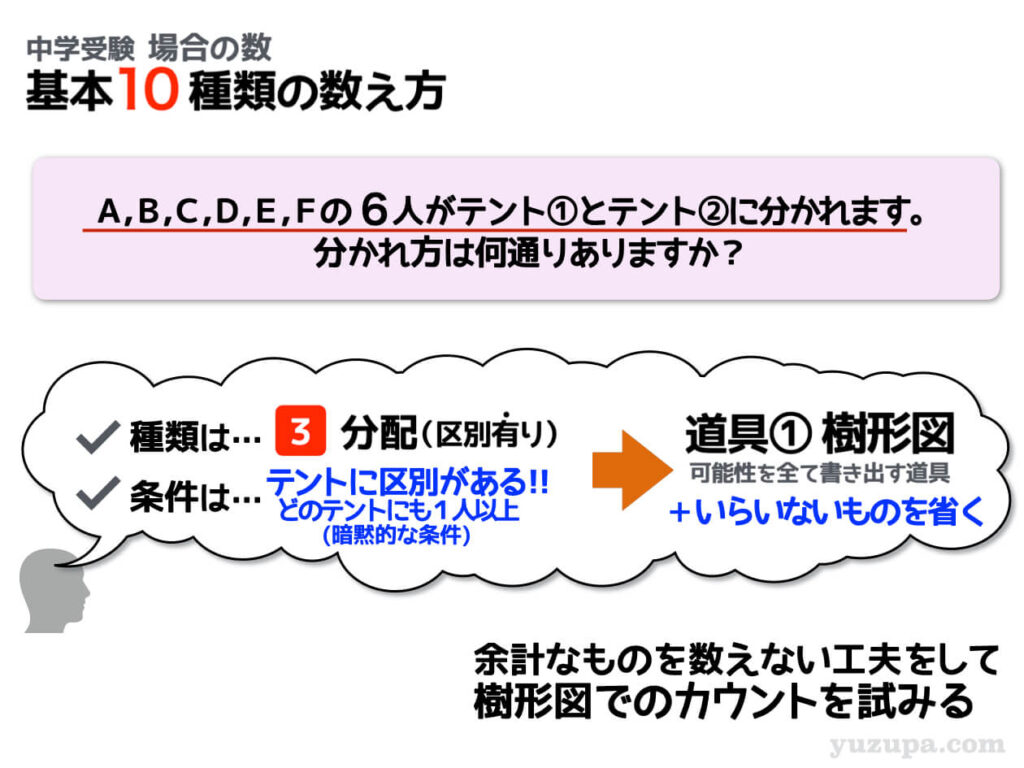
今度も区別あるモノを分配する問題です。今度の問題は、あれ…条件がないように見えます∑(ﾟДﾟ)

さきほどの問題は ０人のテントがあってもOKという注釈がありましたが、今回はありません。しかし問題文に”分ける”と書いてあるので、０人のテントがない方が自然です。

特に断りがない限り、０人の分配は許されないと考えましょうd(^_^o)

 

そしてこの問題は、樹形図で基本的なパターン数を数えあげた後に、条件に合わないモノを引いたり割ったりして省く という王道の流れで解いていきます。まずは…０人のテントができてしまうパターンを引いていきましょう！

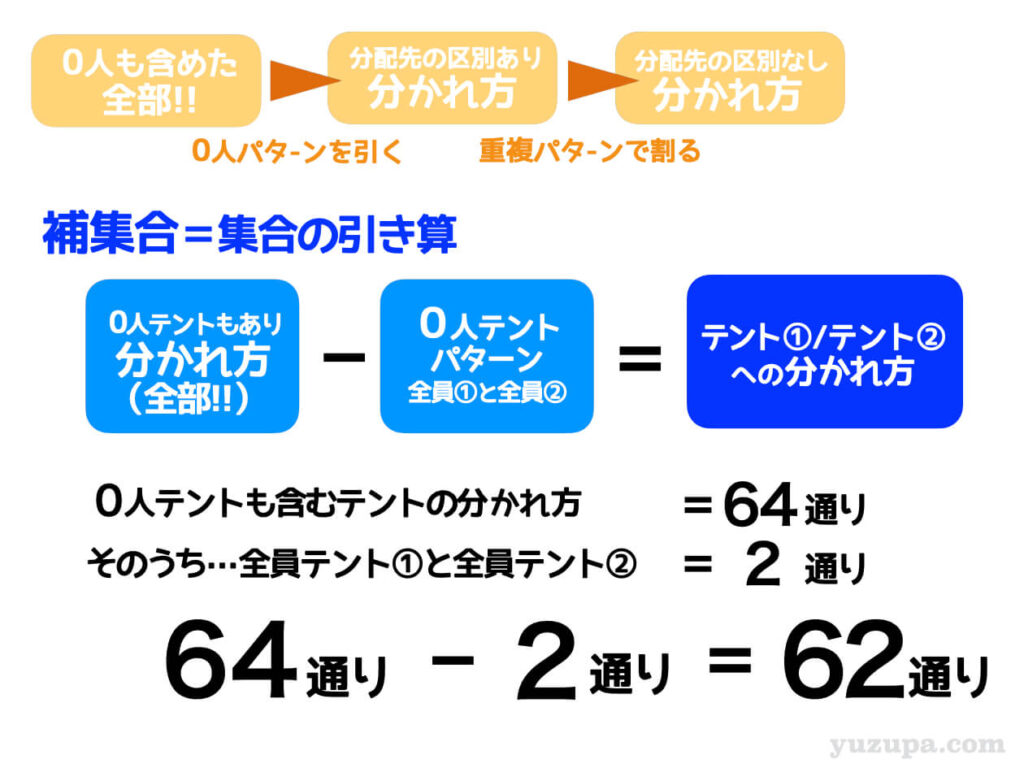
０人への分配も含む全ての場合の数。これはさきほど求めた６４通りですね。そこから、０人のテントができてしまうパターンを引けば 答えがでそうです。でも０人への分配の場合の数はどうやって求めればよいでしょうか？

０人テントが発生する分配は…
　全員テント①に入るパターン
　全員テント②に入るパターン
この２通りしかない

ですので２通り分を引いてあげれば、０人テントを許さない分配パターン数が出てきますd(^_^o)

 

分配(区別あり) 分配先に区別なし①

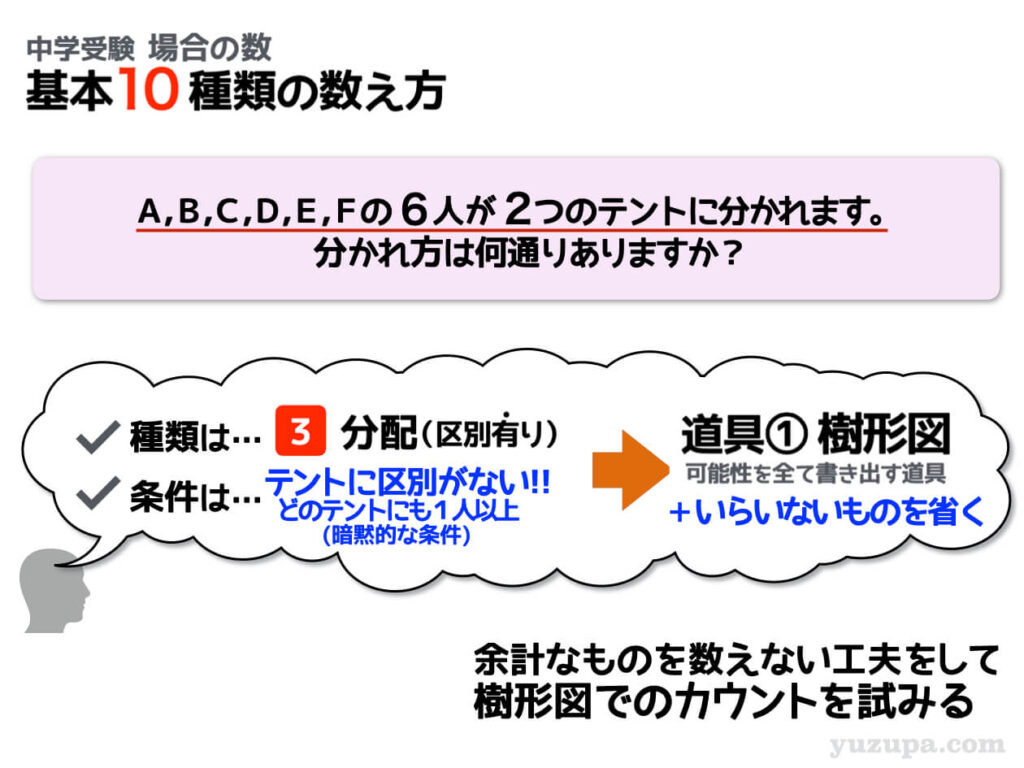
今度の問題も区別あるモノの分配ですが… 今度はテント①とテント②ではなく２つのテントという記述になっています。これは分配先であるテントに区別がないということを意味します ∑(ﾟДﾟ)

 

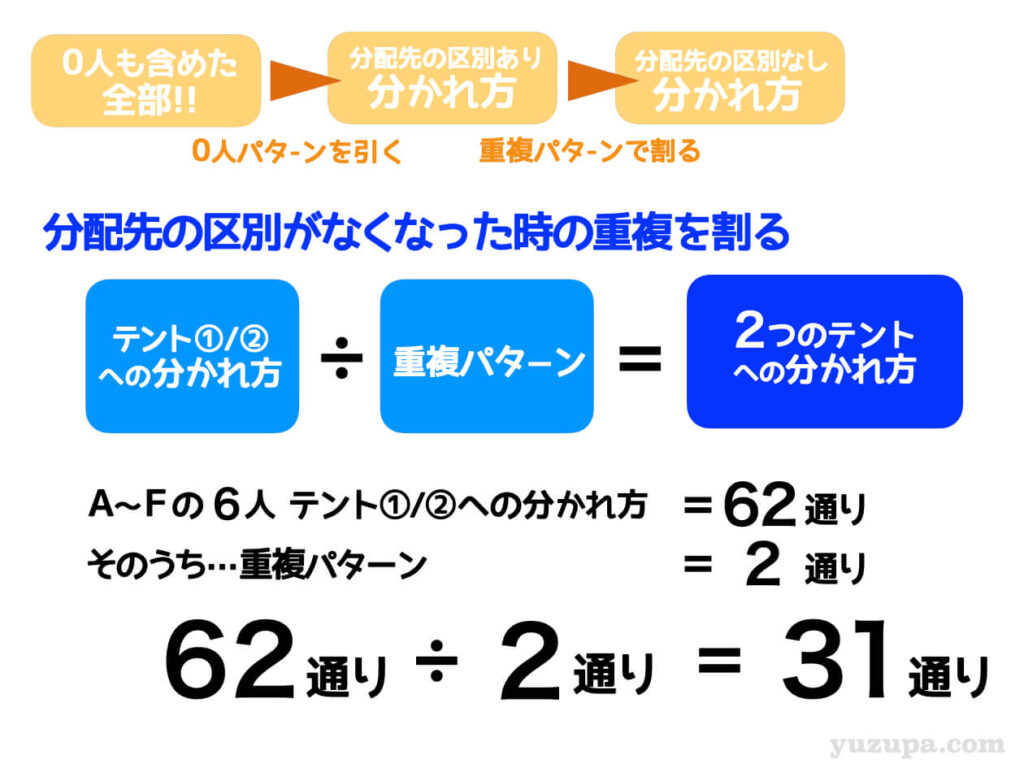
テントに区別がないということは、２人-４人で泊まる場合と４人-２人で泊まる場合は同じということ。

今までの考え方だと、重複してカウントしているパターンがたくさんありそうです。それらを排除するのがポイントです。

４人-２人と２人-４人は同じ…１人-５人と５人-１人は同じ…逆になったパターンは全て同じパターンと考えます。

全体の場合の数を２で割ってあげれば答えが出ます d(^_^o)

 

分配(区別あり) 分配先に区別あり②-1

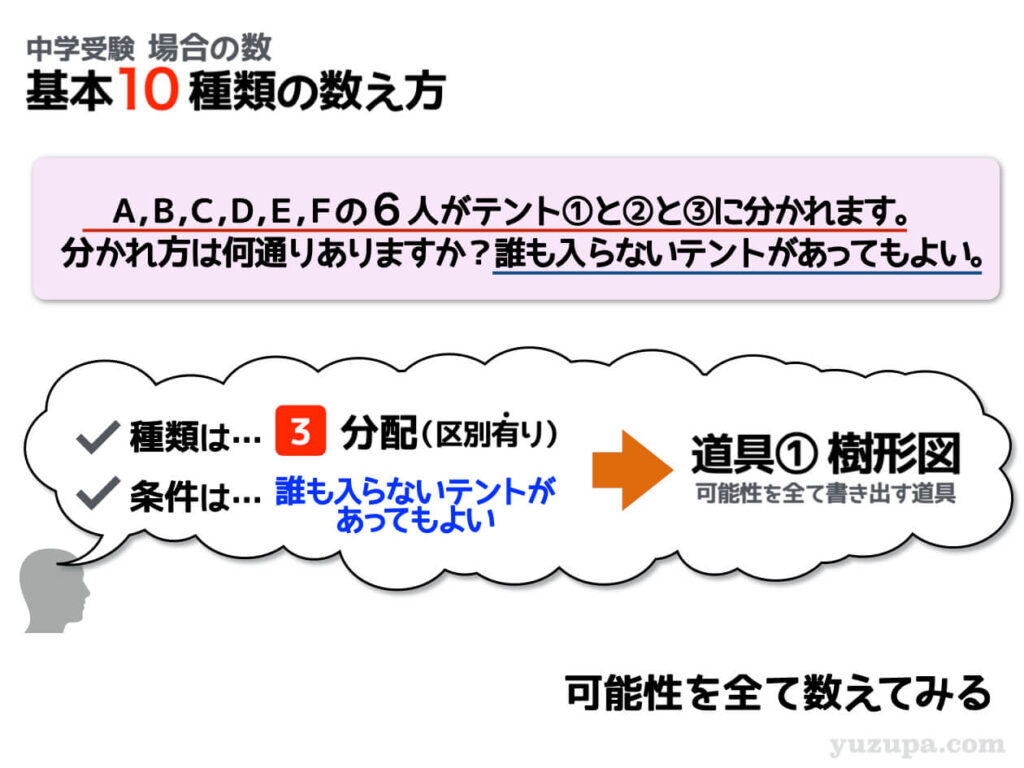
今まで２つのテントに分配する方法を考えてきましたが…テントの数が増えました(-_-;) 今度はテントの数は３つです。テントの数が２つだろうが３つだろうが関係なく樹形図です！

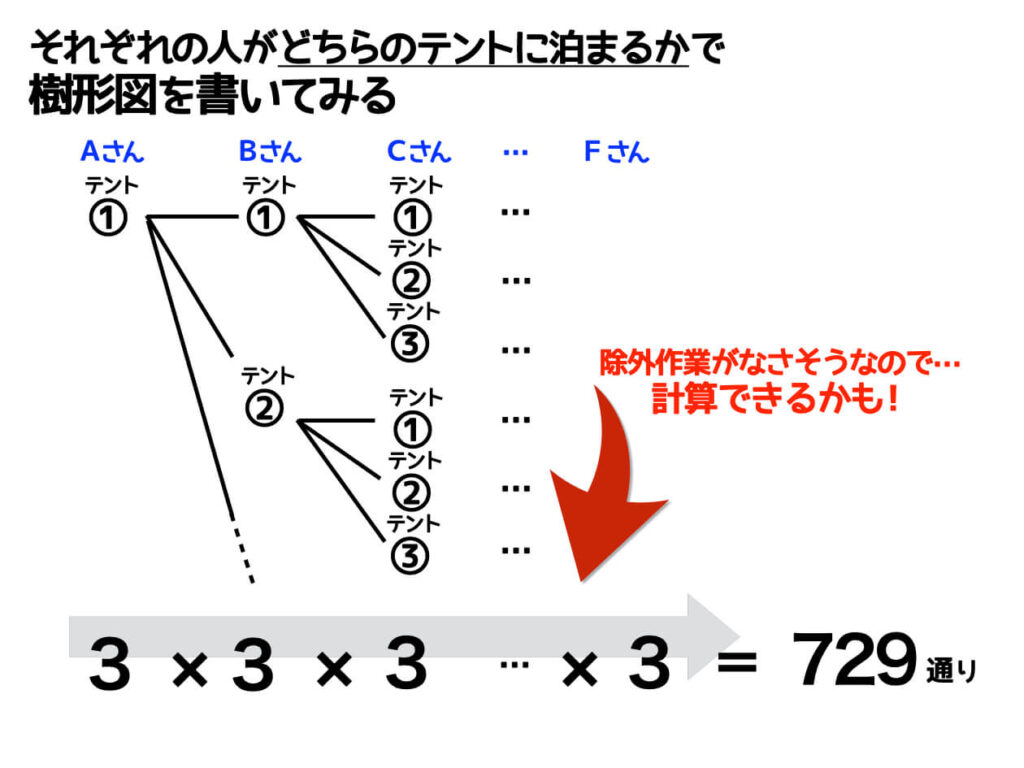
実際に樹形図を書いていくと…

同じようにコレは計算で求められるということが分かります。Aさんはテント①に泊まるか、②に泊まるか、③に泊まるかの３通り。BさんもCさんもDさんもみんないっしょです。

全員が３通りの泊まり先の可能性があるので計算で求めるのが賢明ですね。答えは729通りになります_φ(･_･

 

分配(区別あり) 分配先に区別あり②-2

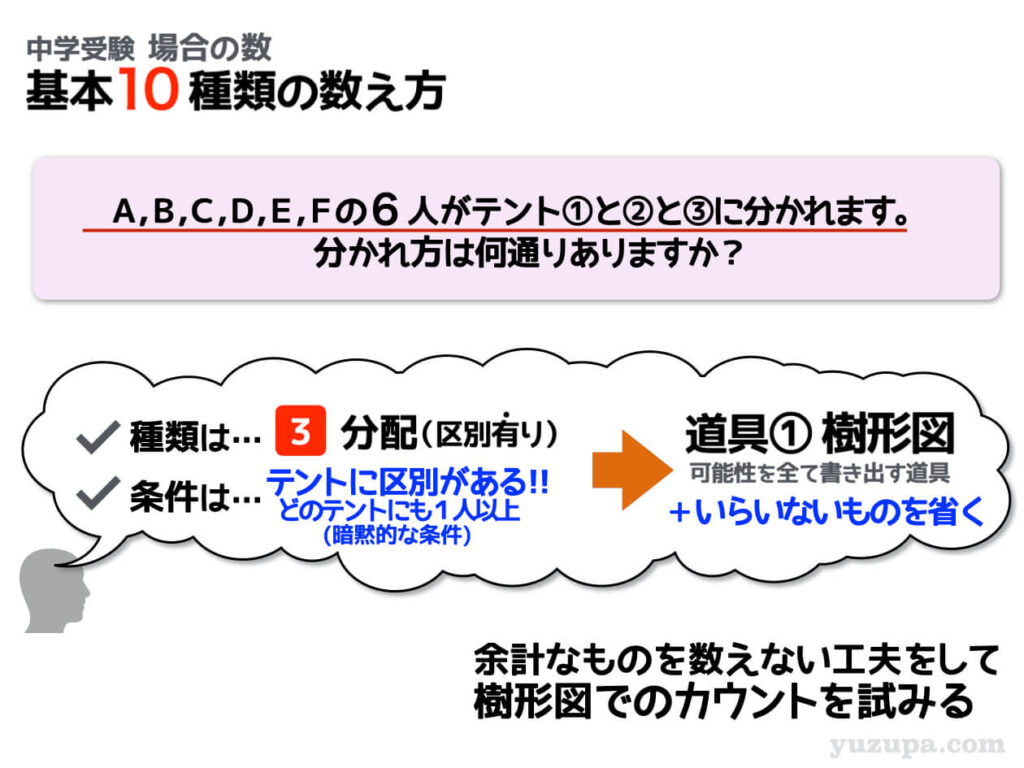
今度は特に注釈がないので０人のテントが許されません∑(ﾟДﾟ)

テントが２つであった時は、０人テントは超シンプルでした。全員テント①の場合と全員テント②の場合の２パターンでした。

でも ３つテントがある場合…０人テントのパターンは超複雑 です。

どうやって、０人テントの場合の数を数えればよいでしょうか？この問題は中学入試では、実際に出題されていますが難しい問題に分類されます。必要に応じて学習しましょうd(^_^o)

結論から先にお伝えすると０人テントは１８９通りになります。なので… 全体の７２９通りから０人テント分を引いた５４０通りが答えとなります。０人テントが１８９通りというのはどうやって求めるのでしょうか？

以下の補足をご覧ください d(^_^o)

 

０人テントになるパターンは２つあります。

(1)どこか１つのテントが０人

これはシンプルです。

全員がテント①、全員がテント②、全員がテント③
という３つのパターンしかありません。

(2) どこか２つのテントが０人

これが厄介です(-_-;)

例えばテント①だけが０人の場合です。
それはテント②とテント③に６人が分配されるパターンです。
これは２つテントの問題で求めましね。６２通りです。

さらにテント②が０人の場合、テント③が０人の場合があるので、
実際には６２通り×３ということになります(>_<)

 

これらをたすと１８９通りになります_φ(･_･

 

分配(区別あり) 分配先に区別なし②

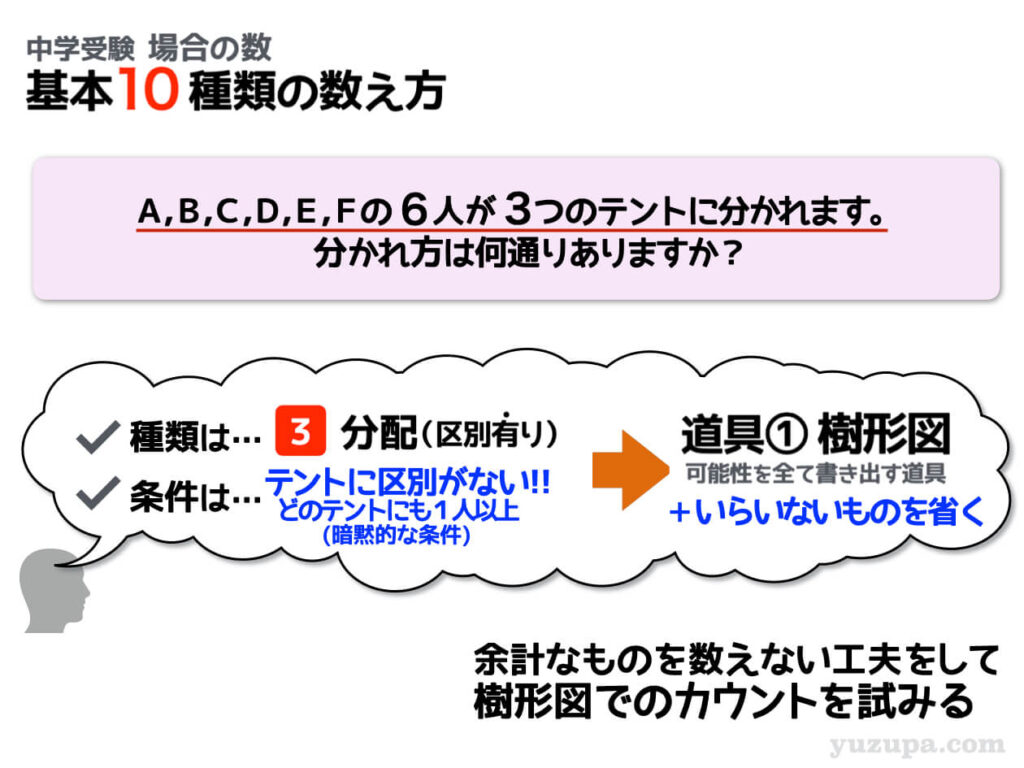
今度は３つのテントでテントに区別がありません。つまり…

　① １人-２人-３人
　② １人-３人-２人
　③ ２人-１人-３人
　④ ２人-３人-１人
　⑤ ３人-１人-２人
　⑥ ３人-２人-１人

これら６つのパターンはすべて同じとして扱います。そうであれば重複したパターンで割ってあげれあば良いのです。３つの分配先の場合は、上記のとおり、６通りの同じパターンがありますので６で割ってあげます。

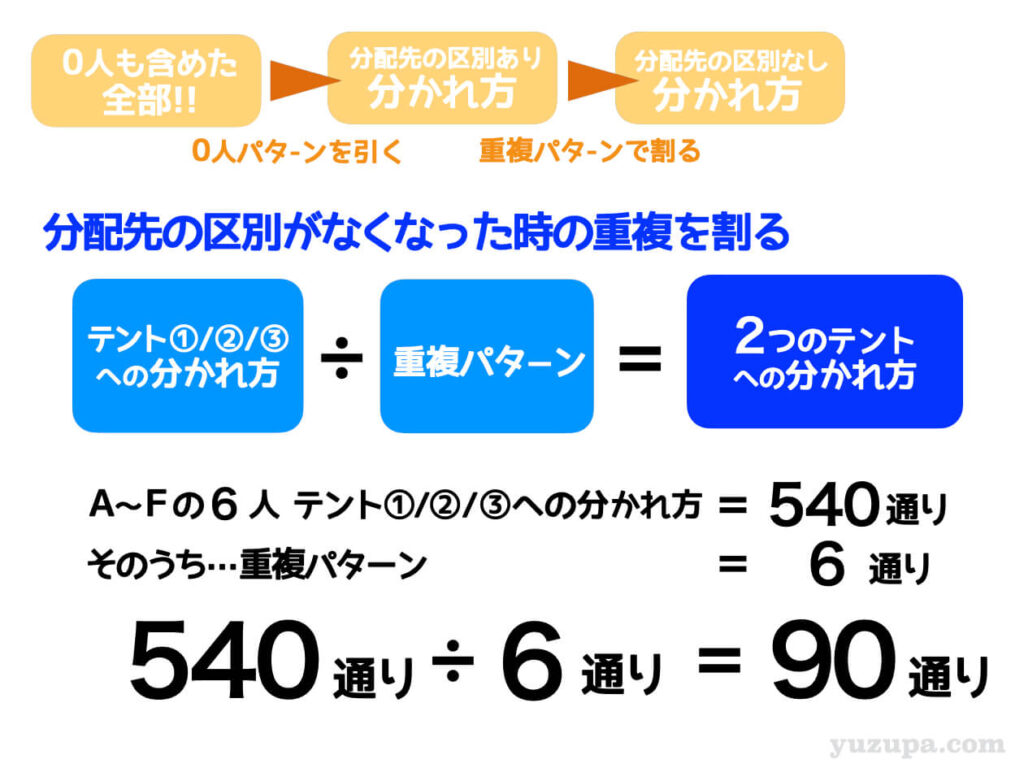
答えは９０通りになりますね_φ(･_･

 

分配(区別あり) 定員数の指定

最後は定員数が指定されているパターンです。

定員数が指定されているということは、部屋の名前がついていて、さらに人数まで指定されているということ。条件としては最も厳しい条件といえるでしょうd(^_^o)

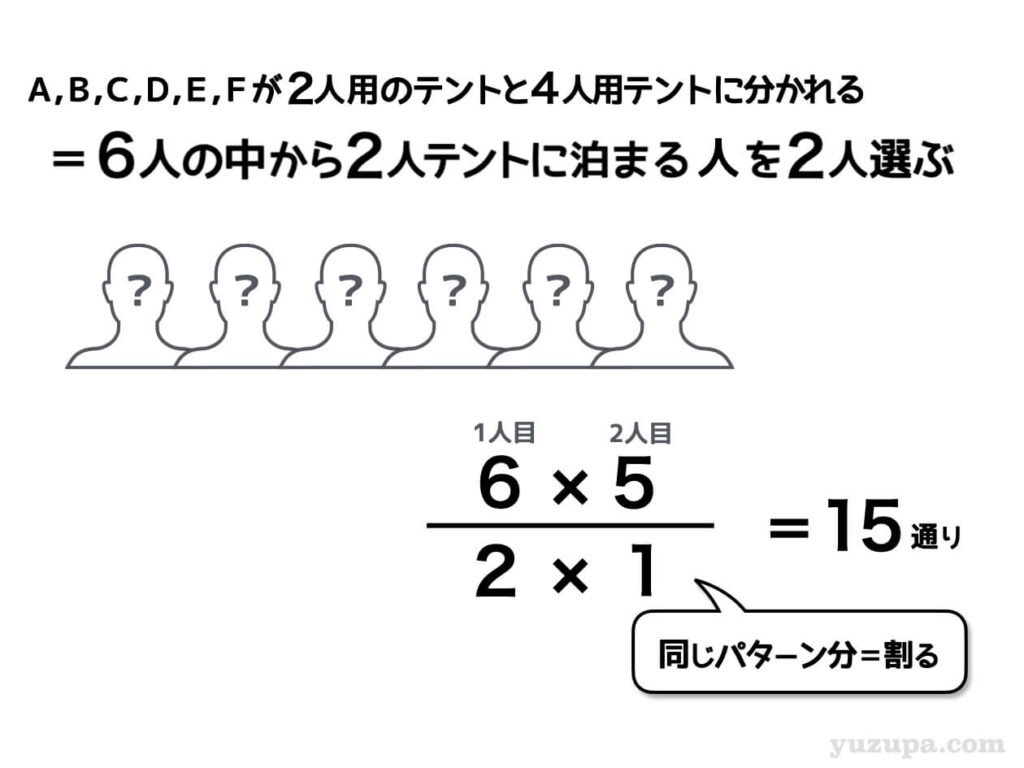
厳しすぎる条件は、かえって数えるのが簡単だったりしますd(^_^o)
６人の中から２人テントに泊まる２人を選ぶ だけ！

６つの中から２つ選ぶの場合の数なので、計算は簡単です。１人目は６通り、２人目は５通りを掛け合わせ、ダブった部分を割ると答えの１５通りがでてきますo(^-^)o

 

グループ④ 区別の無いモノの分配

整列と分配の最後は、区別の無いモノの分配です。

８個のりんごを２つのお皿にわけたり、３つのお皿に分けたりする場合の数がいくつあるかを問われる問題です。区別が無いので、場合の数は小さい数になる傾向にあります。

そして基本的には
樹形図でアプローチすることになります

 

分配(区別なし) 基本パターン

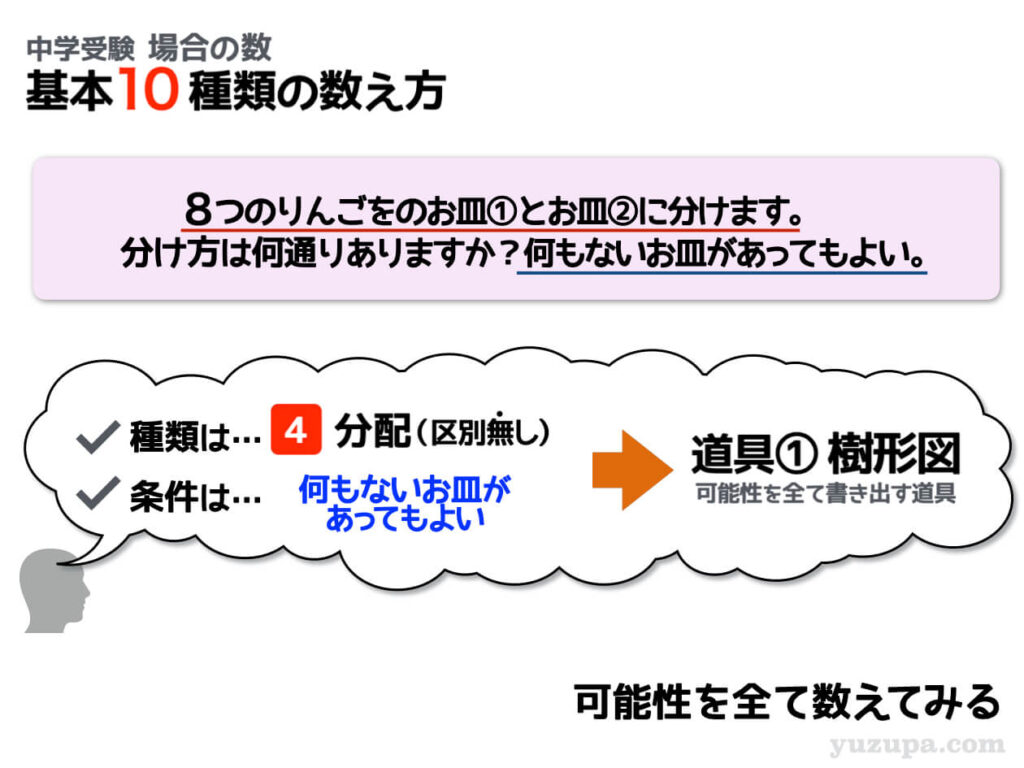
区別の無い８つのりんごを２つのお皿に分ける問題です。区別の無いものの分配は原則は樹形図で書き出していきます。さっそく書き出しを始めてみましょう。

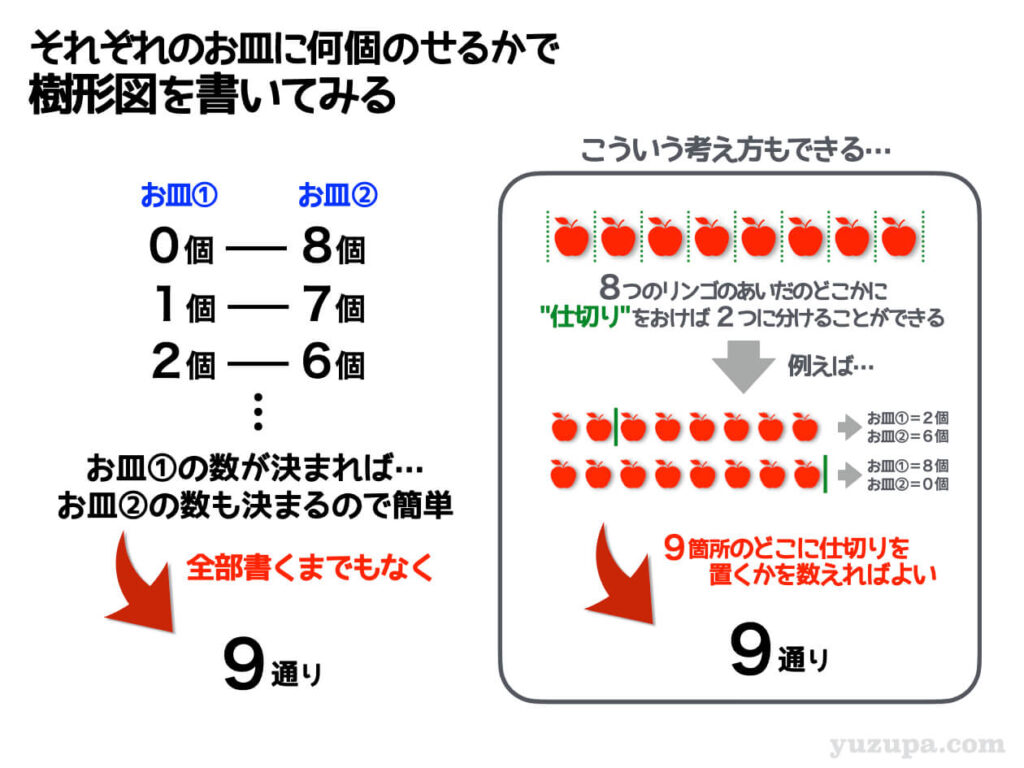
お皿①が０個ならお皿②は８個…お皿①が２個ならお皿②は６個… もう数えるまでもありません。お皿①が０個〜８個までの９通りあることが樹形図を全て書かなくてもわかりますd(^_^o)

この問題ですが…もうひとつ考え方があります

８つのりんごの間に仕切りを置くという考え方です。お皿にひとつもりんごが無いのをOKとするならば、仕切りが置ける場所は９つです。その９つから１つ選べばよいので、同じく９通です。

 

分配(区別なし) 分配先の区別あり①

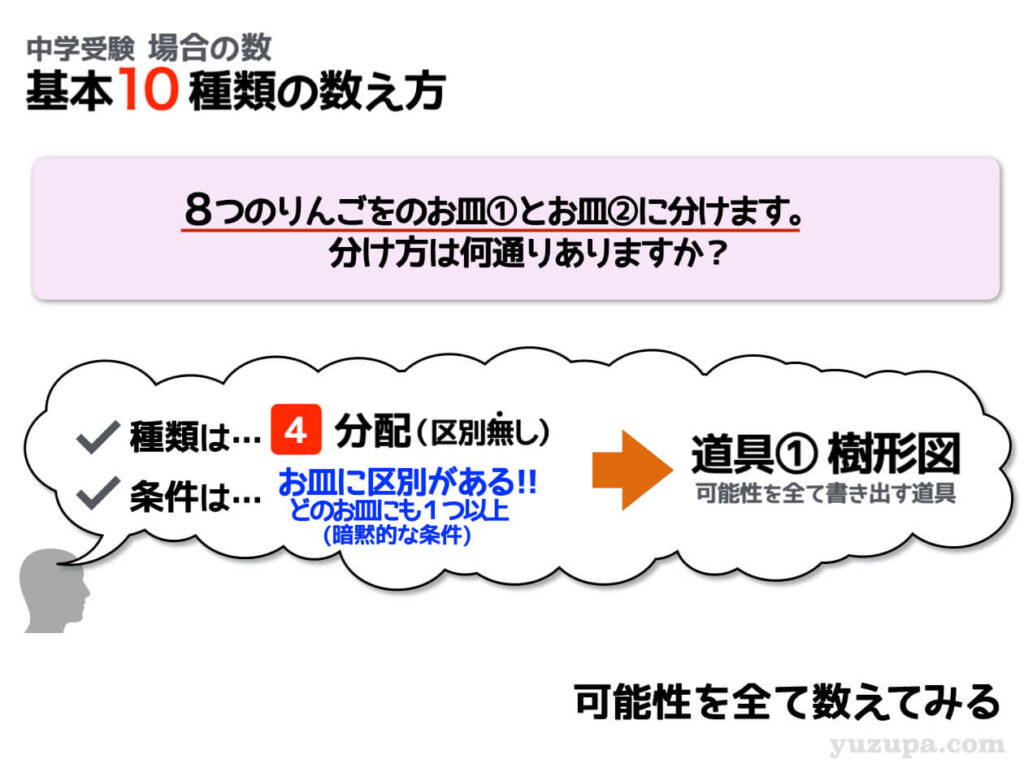
区別の無い８つのりんごを２つのお皿に分ける問題ですが 文脈から０個のお皿があってはいけないと解釈 します。

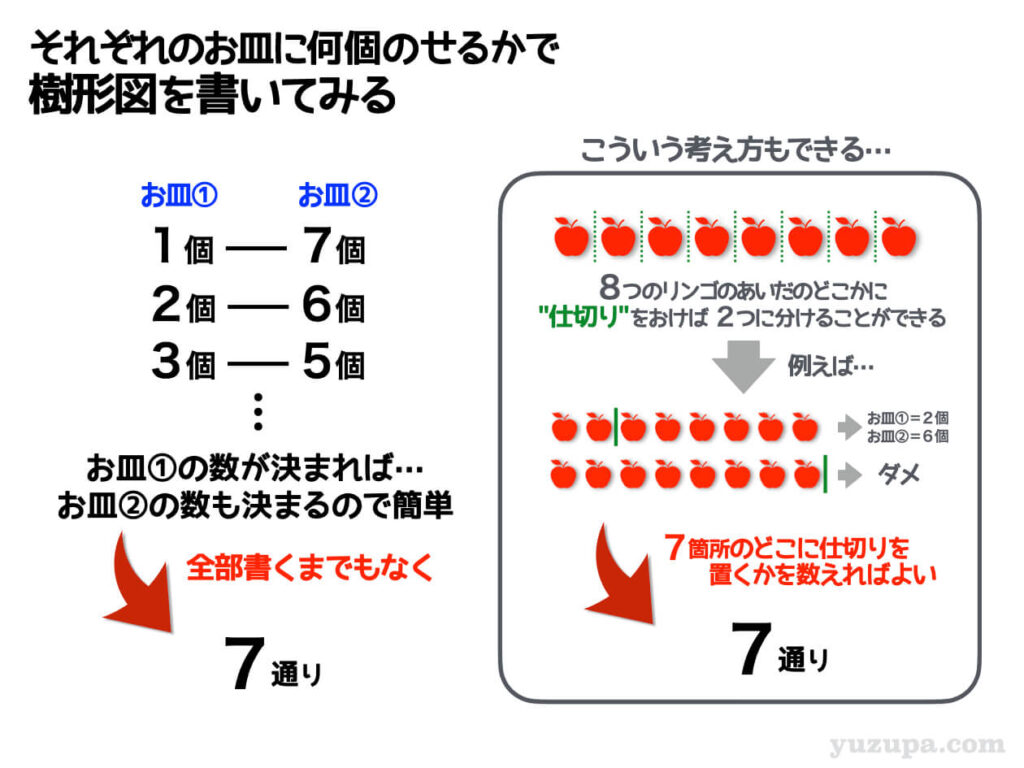
樹形図を書いてみるとシンプルです。

お皿①のお皿②も “０個” は許されないので、それを意識しながら樹形図を書いていけば、計算するまでもなく７通りであることが、分かるでしょう。

前述ど同様に仕切りを置く場所を選ぶという別解もありますd(^_^o)

今度は０個のお皿が許されないので 仕切りは左端と右端には置くことができません。仕切りを置くことができる場所は、７箇所となります。この７箇所かr１箇所選べば良いわけです。

また、最初に求めた全てのパターン９通りから、お皿①が０個になるパターンとお皿②が０個になるパターンの２通りを引いても全く同じ答えがでますね。補集合の考えかたですd(^_^o)

 

分配(区別なし) 分配先の区別なし①

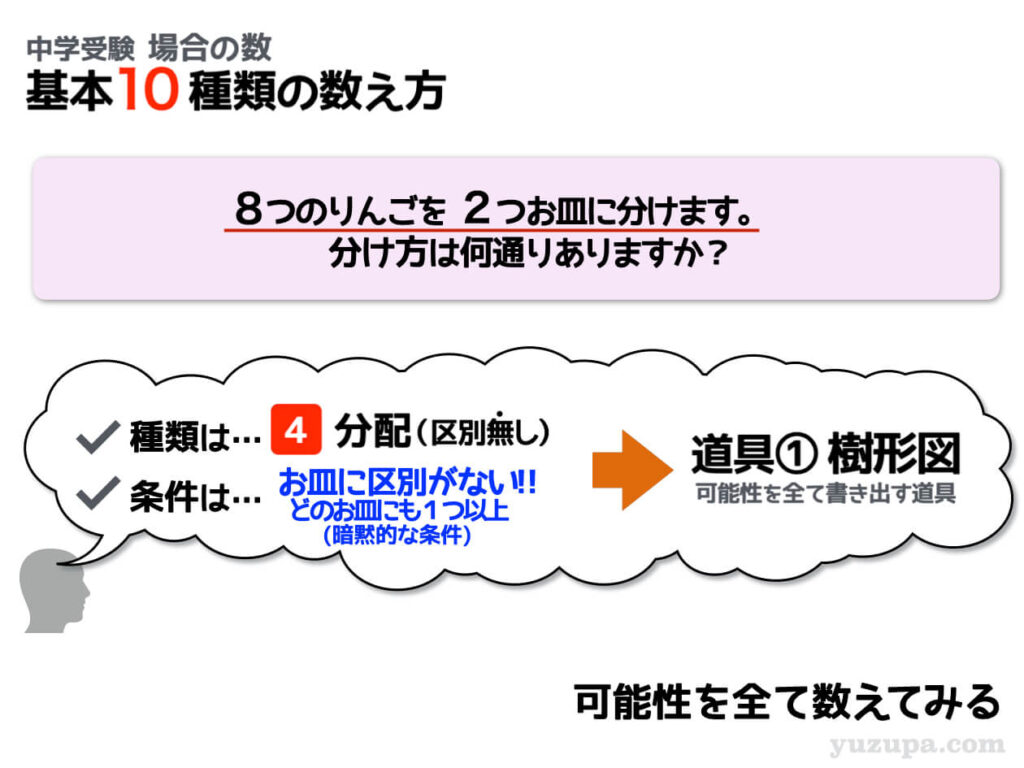
前問題と同様に区別のない８つのりんごを２つのお皿に分けますが、今度はお皿①やお皿②のようにお皿に名前がついていません。お皿の区別がついていないので、樹形図を書く時には 同じものを２回数えてしまわないように注意 しましょう。

さっそく樹形図を書いてみましょう_φ(･_･

気をつけなくてはいけないことは同じものを２回数えないようにすることです。例えば５個-３個は、３個-５個と同じですので数えてはいけません。落ち着いて樹形図を書くと４通りになります。

 

間違えて同じモノを足さないための工夫

樹形図は闇雲に書くのではなく小さい数字から順番に書いていくのが鉄則です。その時に樹形図の右に行けば行くほど数字が大きくなるというルールで書いていくことを意識するのです_φ(･_･

樹形図を順番どおり書く時に… 右の数字の方が小さくなるパターンは既に同じものを数えている可能性 があります。しっかり順序よく樹形図を書いていれば、ほぼ100% 検出できますd(^_^o)

 

分配(区別なし) 分配先の区別あり②

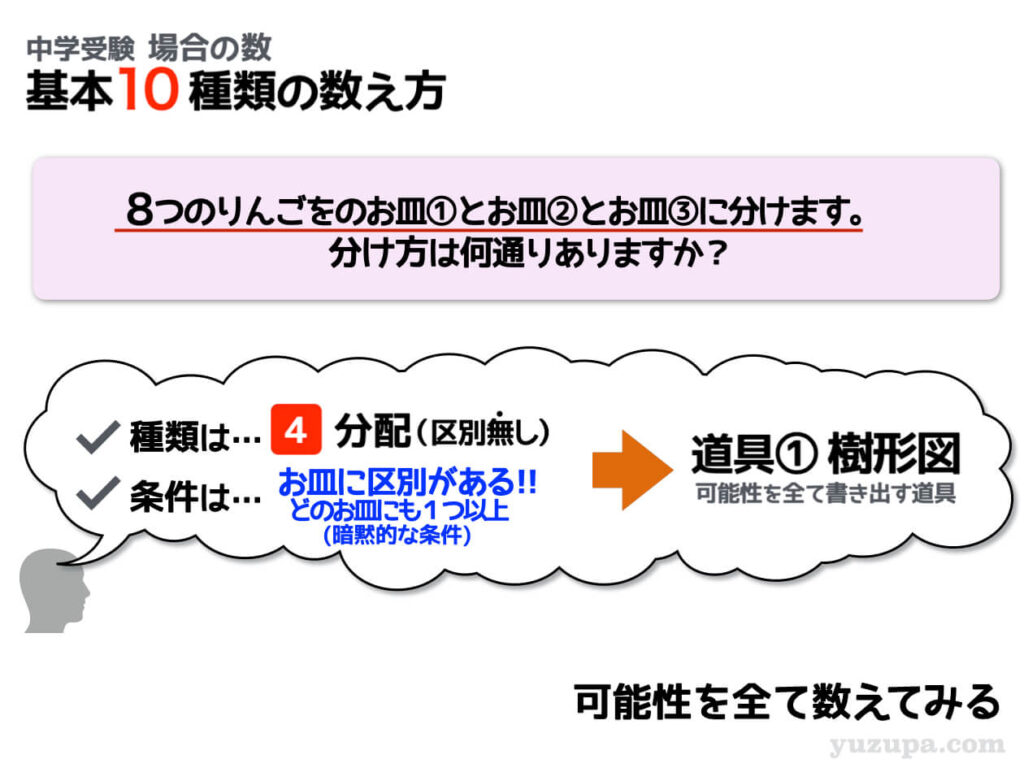
今度はお皿の数が３つに増えました∑(ﾟДﾟ)

分配対象が増えれば増えるほど樹形図が複雑になるので丁寧さと根気強さが試されますd(^_^o) 問題の条件は、区別のないりんご８つを名前のついたお皿に分配するパターンです。

樹形図を落ち着いて書いていきます_φ(･_･

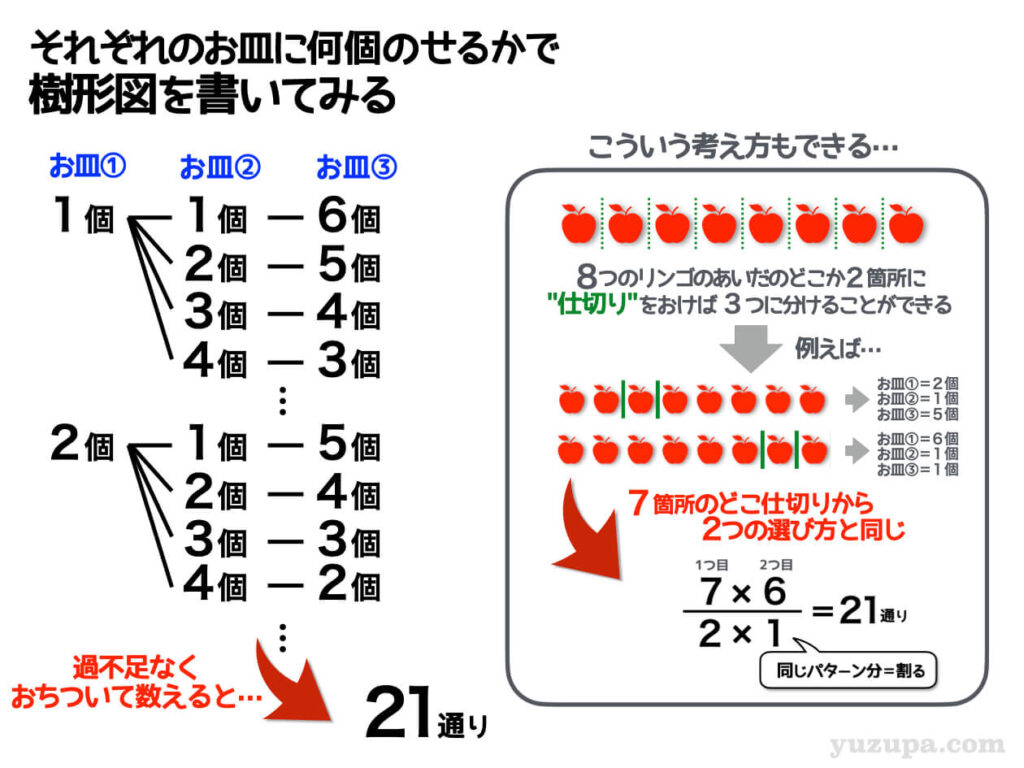
丁寧に根気強く…樹形図を描き終えると２１通りという答えがでてきます。２１通りぐらいであれば、なんとかギリギリ樹形図が書ける分量かと思います。お皿に名前がついているので…もちろん仕切りをおく別解もあります。

りんごの間に”仕切り”を２つ置けば、３つのお皿に分けることができそうです。実際に７つの箇所から仕切りを２箇所選ぶ組合せの計算をしてみると…樹形図の結果と同じ２１通りですd(^_^o)

分配(区別なし) 分配先の区別なし②

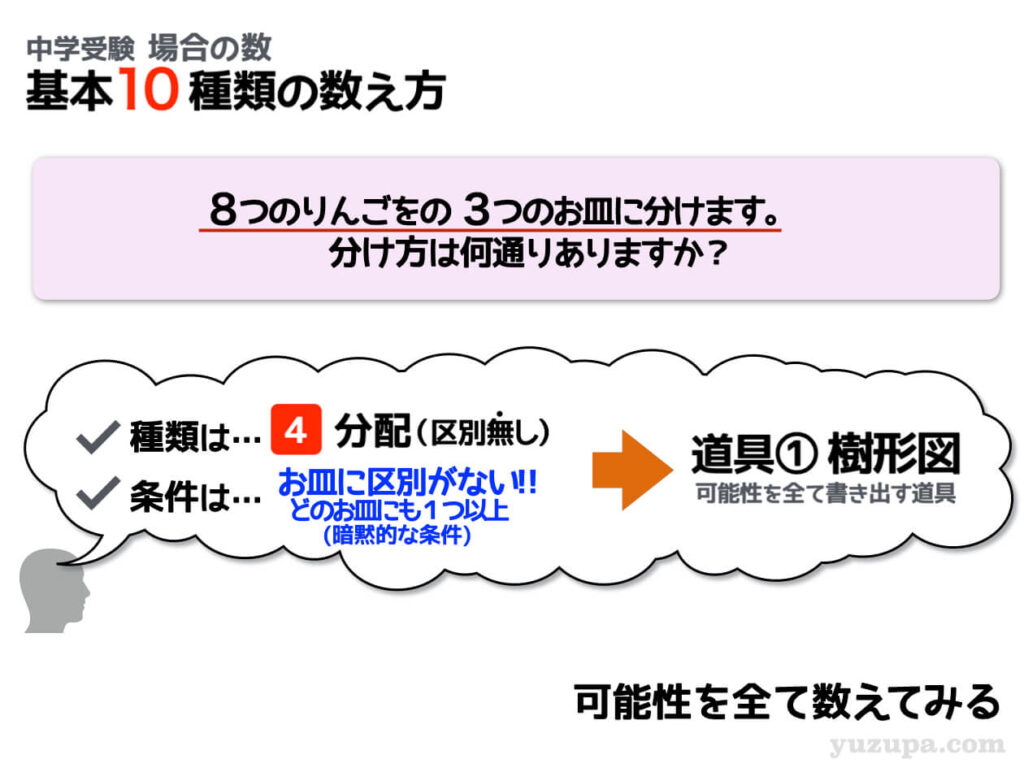
最後は区別のないお皿３つですd(^_^o)

分配先に区別がない場合に気をつけなければいけないことは何でしょうか？ 同じものを数えないようにすることです。樹形図を順序よく書いていきましょう！

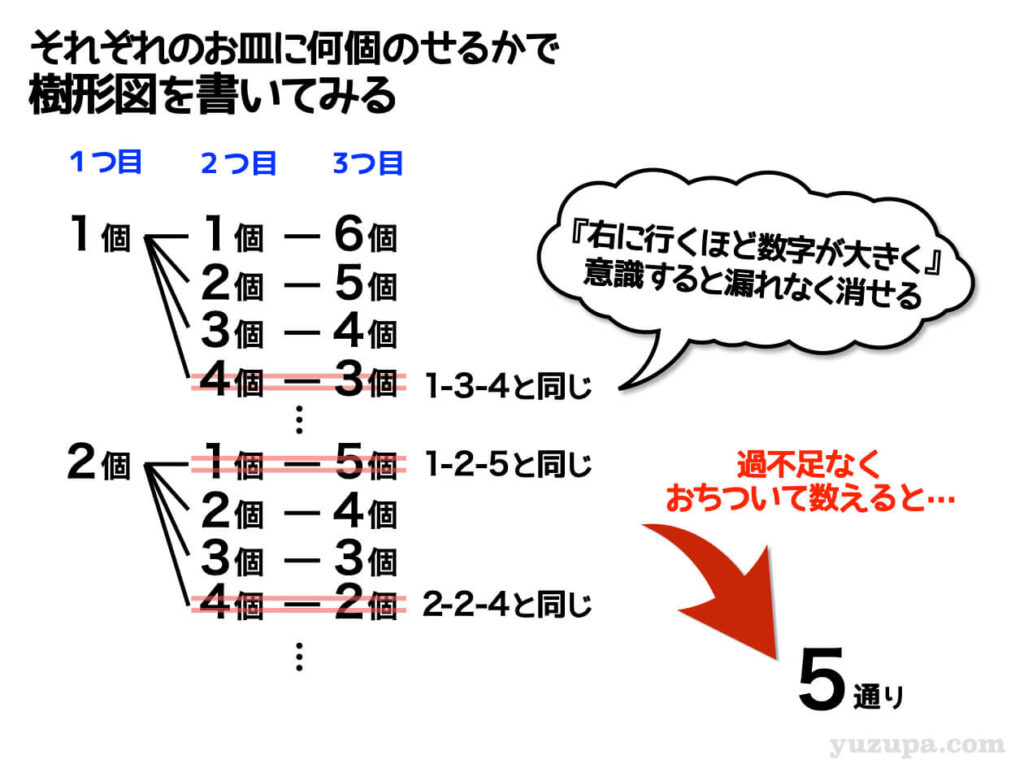
樹形図を過不足なく数えると答えは５通りになります_φ(･_･

間違えて同じパターンを２回数えてしまわないための工夫も同じです。右に行けば行くほど数字が大きくなるルールです。樹形図を書いていて、右の数字が小さいパターンは…きっと既に数えられているものですので、よく確認した上で消してしまいますd(^_^o)

 

まとめ

今回は小学生の中でも苦手とする”場合の数”について、具体的な問題をベースにその解き方を解説いたしました。本記事では整列問題と分配問題について３０問あまりを解いてみました_φ(･_･

STEP1では、問題文を読んで”いったい何を数えたらよいのか”をしっかり把握します。その際に役に立つのが”基本的な１０種類の数え方”です。まずは基本パターンを考えましょう。

STEP2では、条件を理解します。偶数”だけ”数えなくてはいけなかったり、男子が両端にくる並び方”だけ”数えなくてはいけなかったり、入試の問題には必ず条件がついてきます(^_^;)

STEP3でいよいよ数えます。数えるには必ず道具を使います。樹形図はオールマイティですが、通り数の多い問題には使えません。樹形図をサボる道具として”順列”と”組合せ”があります。

場合の数の全体像を確認したい方は…以下の記事をご参照くださいo(^-^)o

参考：場合の数が苦手…３つの道具を使い10種の数え方をマスターせよ
参考：場合の数の基本パターンを全網羅！ カード問題編
参考：場合の数の基本パターンを全網羅！ 整列と分配問題編