中学受験:和差算とは? 線分図の “3つの本質” で簡単に解ける
和差算ってナニ?中学受験の独特世界…ほとんどの問題が解けてしまう”3つの本質”を意識せよ
 こんにちは。かるび勉強部屋 ゆずぱ です。
こんにちは。かるび勉強部屋 ゆずぱ です。
和差算ってナニモノ?線分図ってナニモノ?中学受験の世界を知らない人にとっては意味不明な領域…。私も子供の受験勉強を開始したときに面食らいました ∑(゚Д゚)
和差算とは和と差が示された問題…
ただし…方程式を使わず解け(・_・;
もちろん 方程式を使えば簡単に解くことができます …が小学生に教えるには1つだけ大きなハードルがあります。それが…負の数の計算です(-_-;)
じゃあ、どうやって解くのか…?
線分図という謎ツールを使います
それでは具体的にいってみましょう!
目次
和差算とは…和と差が示された問題
線分図を書けば応用も攻略できる
まず最初に… 線分図とはナニモノでしょうか? 実際にみてみましょう。
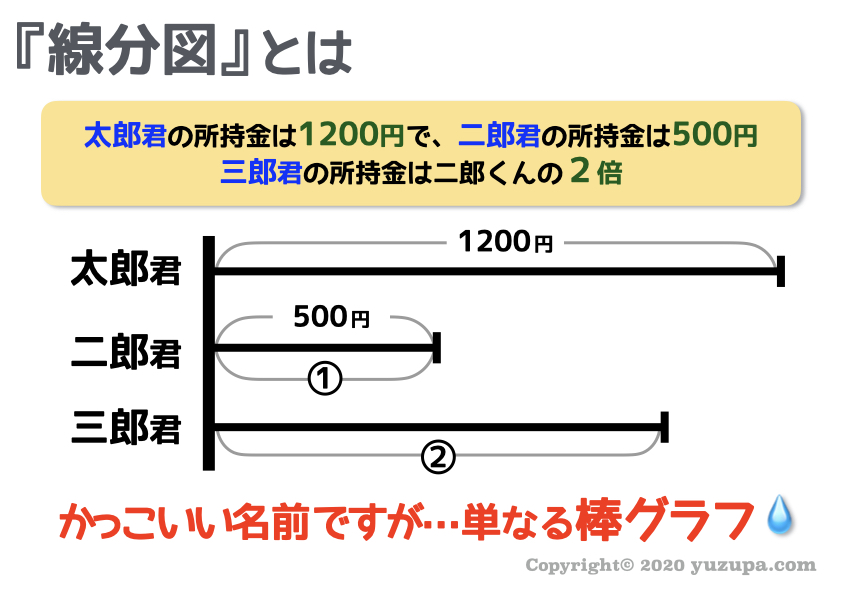
線分図というカッコいい名前が付いていますが 単なる棒グラフ と考えれば良いでしょう(^_^;)
とてもシンプルですね…。この線分図を 使いこなすには絶対に必要な”3つの本質” があります…
線分図の3つの本質とは?
さっそく線分図の3つの本質を見てみましょう!

実は線分図を使う問題は、この3つの本質をマスターするとほとんどの問題が解けてしまいます∑(゚Д゚)
具体的に説明します!
本質① 差に着目して数字を埋める
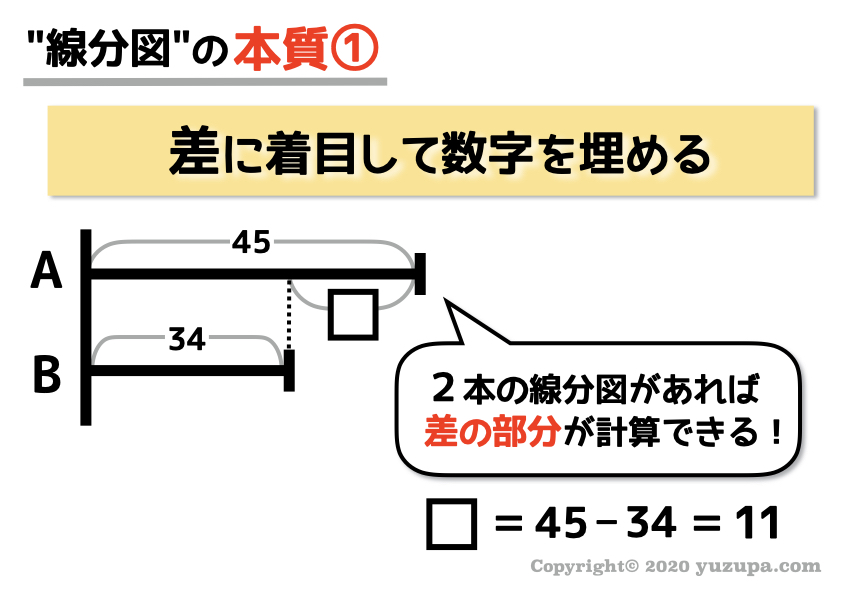
ひとつめは ”差に着目して数字を埋める” です。線分図を書けば どこかに”差” が隠れている はずです!
その”差” を見つけたら、すぐさま引き算をして線分図に数字を書き込んでいきましょうd(^_^o)
本質② 背の高さをそろえて割る
ふたつめは “背の高さをそろえて割る” です。特に和差算ではこの本質が大切 ですd(^_^o)
同じ高さの線分図が2本以上あれば 割り算をして1本あたりの背の高さが分かる というものです。

本質③ 数字と割合のペアを見つける
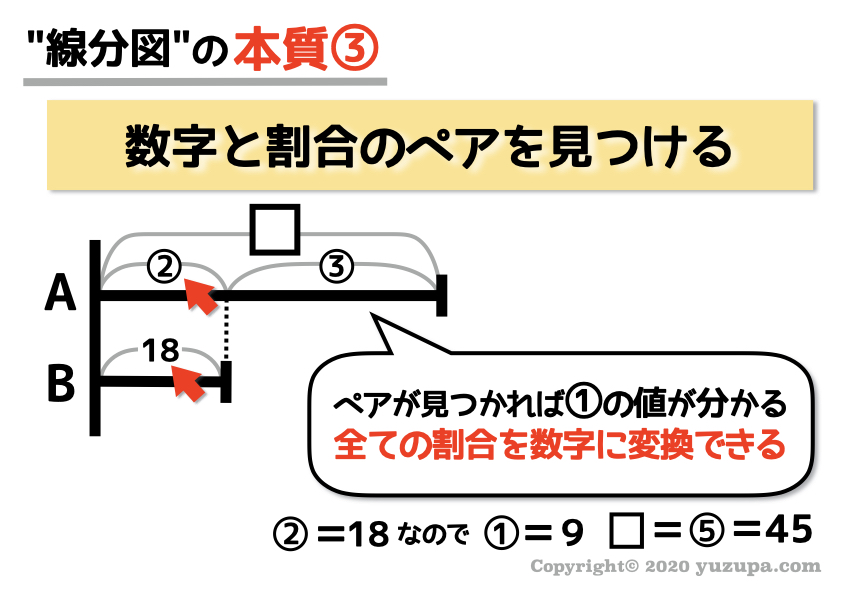
最後は “数字と割合のペアを見つける” です。この ペアが見つかれば一気に問題解決に進む ことが多いです∑(゚Д゚)
1つでもペアを見つけられれば、他の割合の部分も一気に数字が埋まってしまうことが多いためですね_φ(・_・
実際の例題で試してみる
例題① 2つの数の和差算
まずは問題をごらんください。

問題を読むと分かるように 2つの数字の和と差が問題に書かれています ね。和差算の典型的な問題です(^_^;)
さっそく線分図を描いてみましょう!
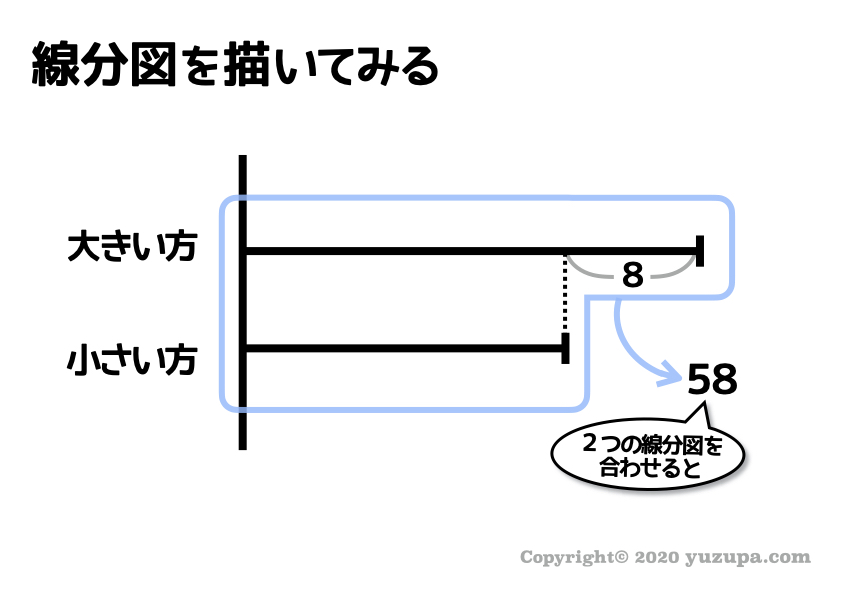
和は2本の線分図を合わせた数ですね。そして差は図に示すような部分に該当しますので数字をしっかり書き込みましょう!
線分図が描けらたらいよいよ3つの本質です。
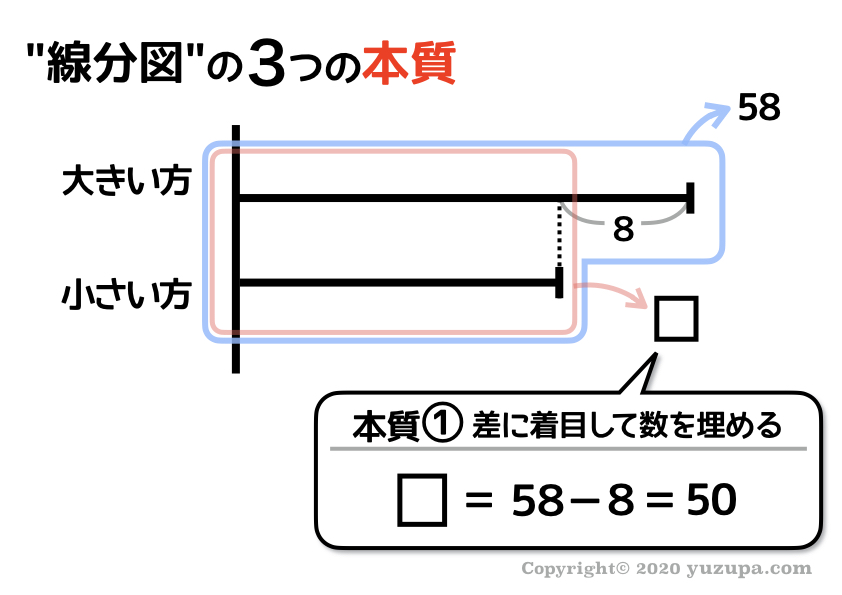
この線分図から ”差” を見つけることができましたでしょうか? 青い囲いから8を引くと赤い囲い部分になります ∑(゚Д゚)
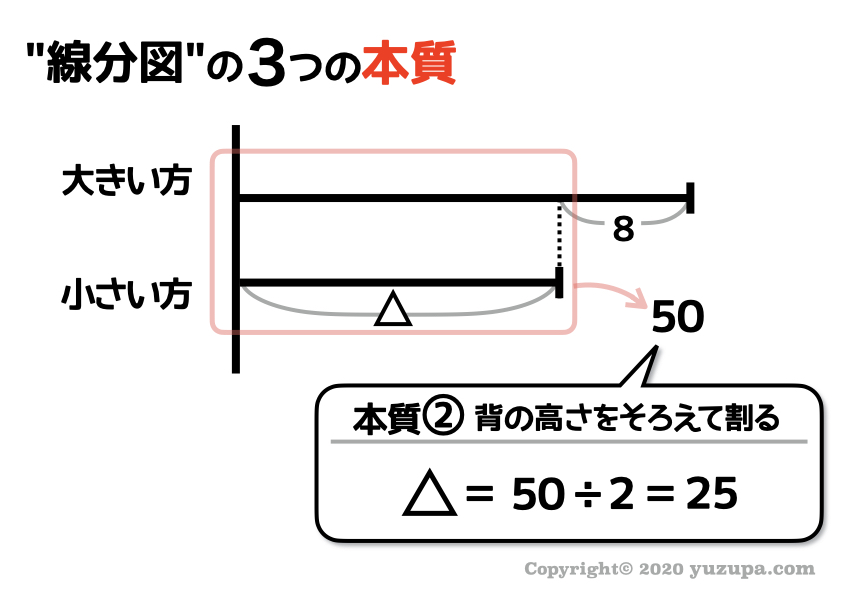
なぜワザワザ赤い囲み部分を求めるのか…それは 本質②の背の高さをそろえることを意識 しているからですd(^_^o)
背の高さがそろった2本の線分図がありますので、2で割ってあげれば1本分の背の高さを求めることができます。
よって答えは25になりますねd(^_^o)
例題② 3つの数の和差算
まず問題文をごらんください。

○○よりも大きい…△△よりも小さい…という表現を用いていますが、これは”差”のこと ですd(^_^o)
つまり…これも和差算か!? そうであれば線分図が使えそうです。さっそく線分図を描いてみましょう…。
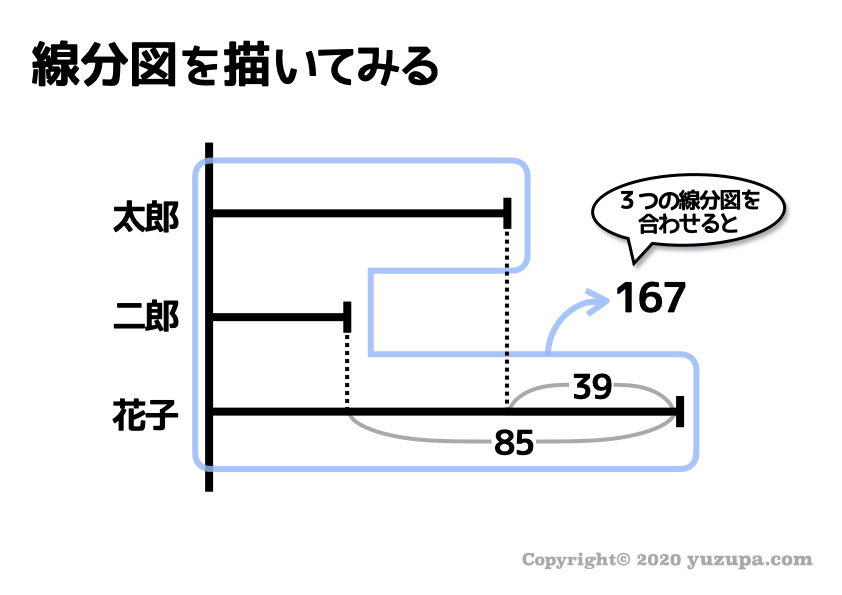
線分図が描けたら3つの本質を頭に浮かべながら、線分図をじっくり眺めましょうd(^_^o)
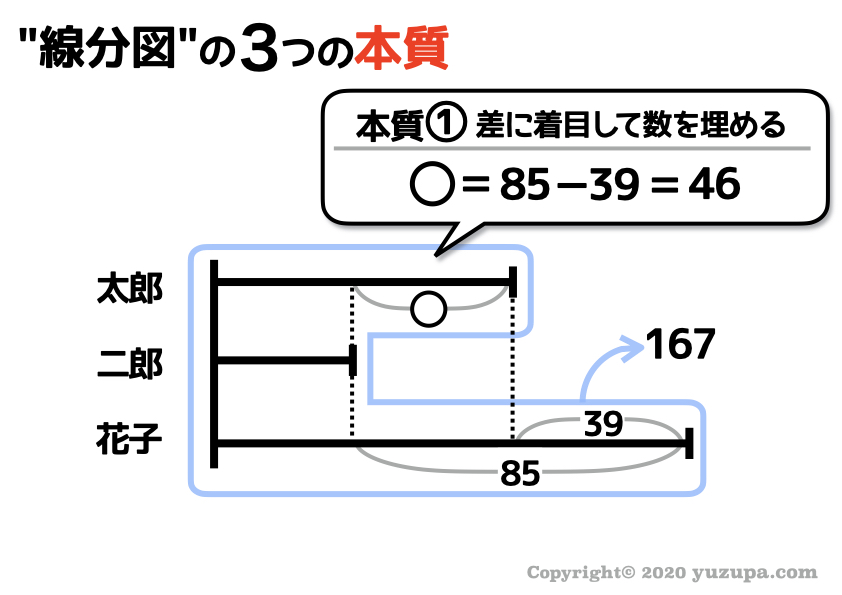
すぐに分かるのは 上記の図の部分でしょう。線分図の中に数字が2つ出てきたら ”差” になっていないかという視点 ですね。

そうすると さらに ”差” が出てきました ね。例題①と同様に3本の線分図の背の高さをそろえるように。
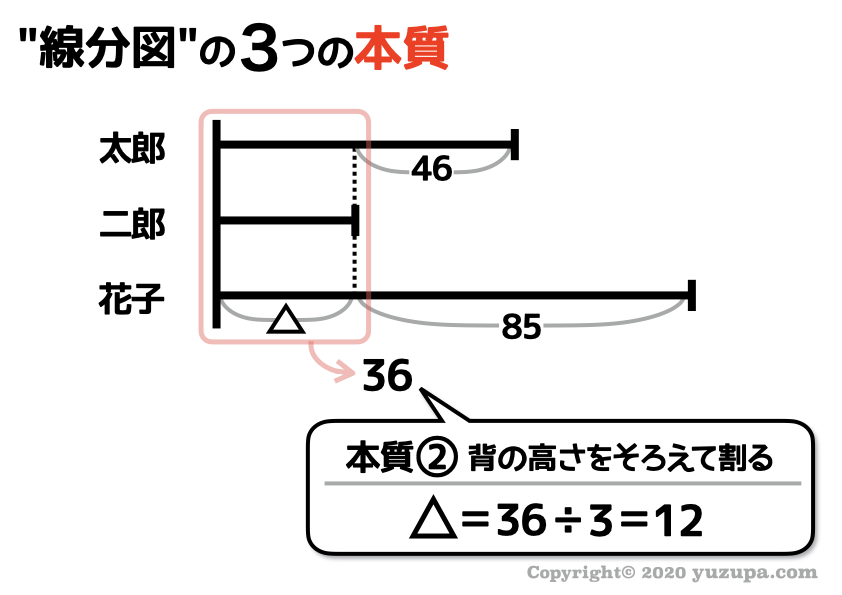
3本の線分図の背の高さがそろいました ので、3で割って1本の背の高さを求めることができます。
求められているのは花子さんの点数ですので、12+85=97となり97点が答えになりますd(^_^o)
まとめ
今回は和差算について解説をしてみました。私ゆずぱが子供の中学受験で最もカルチャーショックを受けた問題のひとつです∑(゚Д゚)
方程式ではなく線分図という謎のツールを使うのがポイントです。ただ線分図には “3つの本質” があります…。

この線分図の”3つの本質”さえマスターしてしまえば、和差算のほかにも線分図を使う問題がほとんど解けてしまいます∑(゚Д゚)
その他の特殊算については以下にまとめていますのでご参考くださいd(^_^o)











わかりやすい
匿名さん
ありがとうございます!!