中学受験：ひし形の面積の求め方…ひとつの公式にとらわれるな！

面積の公式は ”使い分け” が重要です…ひとつの公式だけでは攻略できません

こんにちは。かるび勉強部屋 ゆずぱ です。

今回は ”ひし形” の面積について解説したいと思いますが…そのキッカケは、私の子供が 超シンプルな面積を求める問題が解けなかった ことに起因します∑(ﾟДﾟ)

ひし形の面積を求める公式で最もメジャーなものは
もちろん 対角線 × 対角線 ÷ ２ ですが…

でも…これだけではダメです

ひし形の定義を知り、色々な四角形の関係を知り、公式を柔軟に使い分けることができないと…思わぬところでつまづいてしまいます。本記事で ”その柔軟性” について解説します。

それでは 詳細に参りましょうd(^_^o)

 

まず”ひし形”の基本的な部分をおさえる

ひし形とはどんな図形か

まずはじめに。”ひし形” とはどんな図形でしょうか？ その定義はとてもシンプルです _φ(･_･

４つの辺が全て同じ長さである四角形

この条件に当てはまる四角形はすべて ”ひし形” です。ってことは 正方形も ”ひし形” の一種 ですねd(^_^o) 

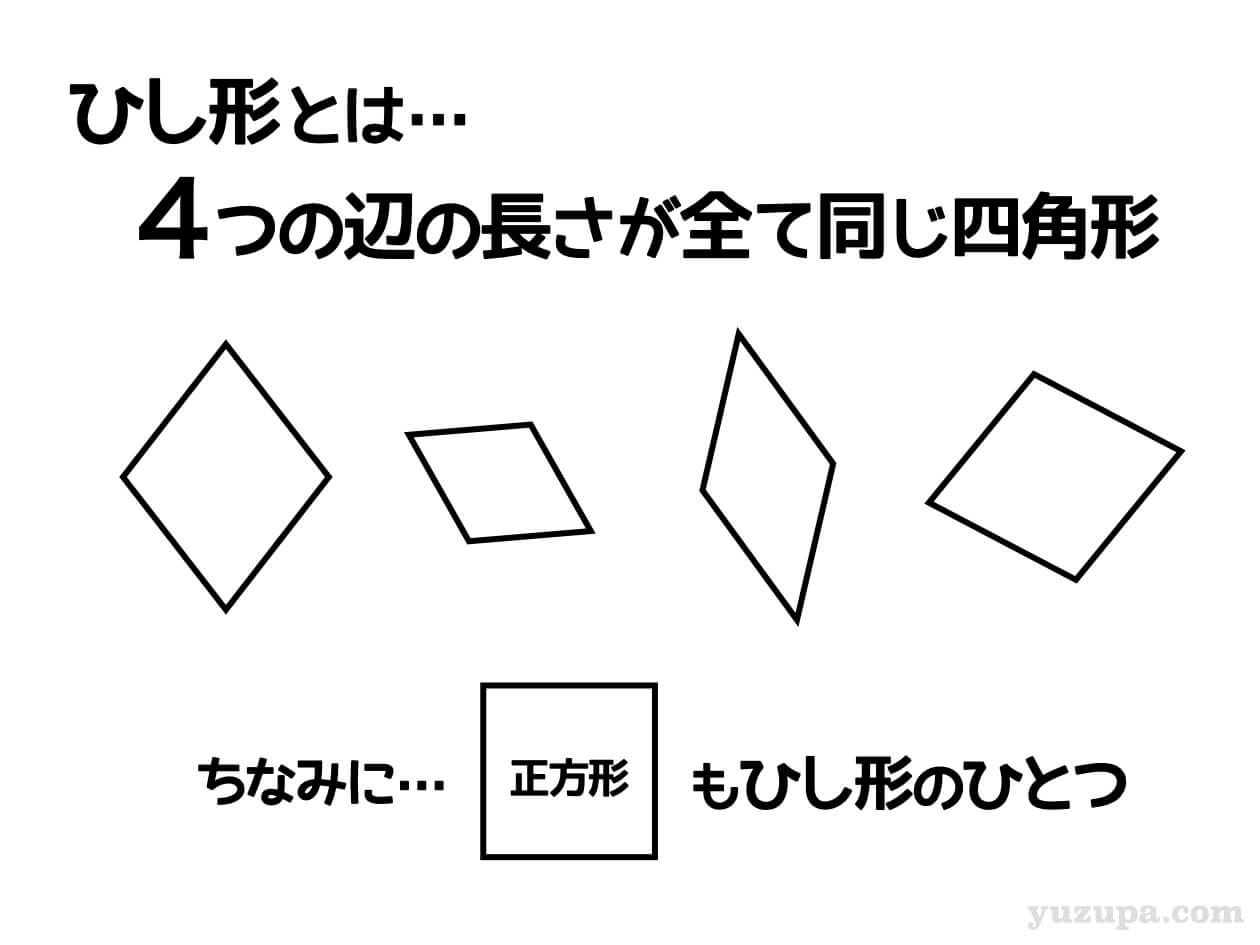
ちょっとイメージしやすいように言い換えると…正方形を押しつぶしてゆがませた形 ですね (^_^;)

 

ひし形の面積の公式

“ひし形”がナニモノかわかったところで、いよいよ面積を求める方法をおさえていきましょう d(^_^o) 

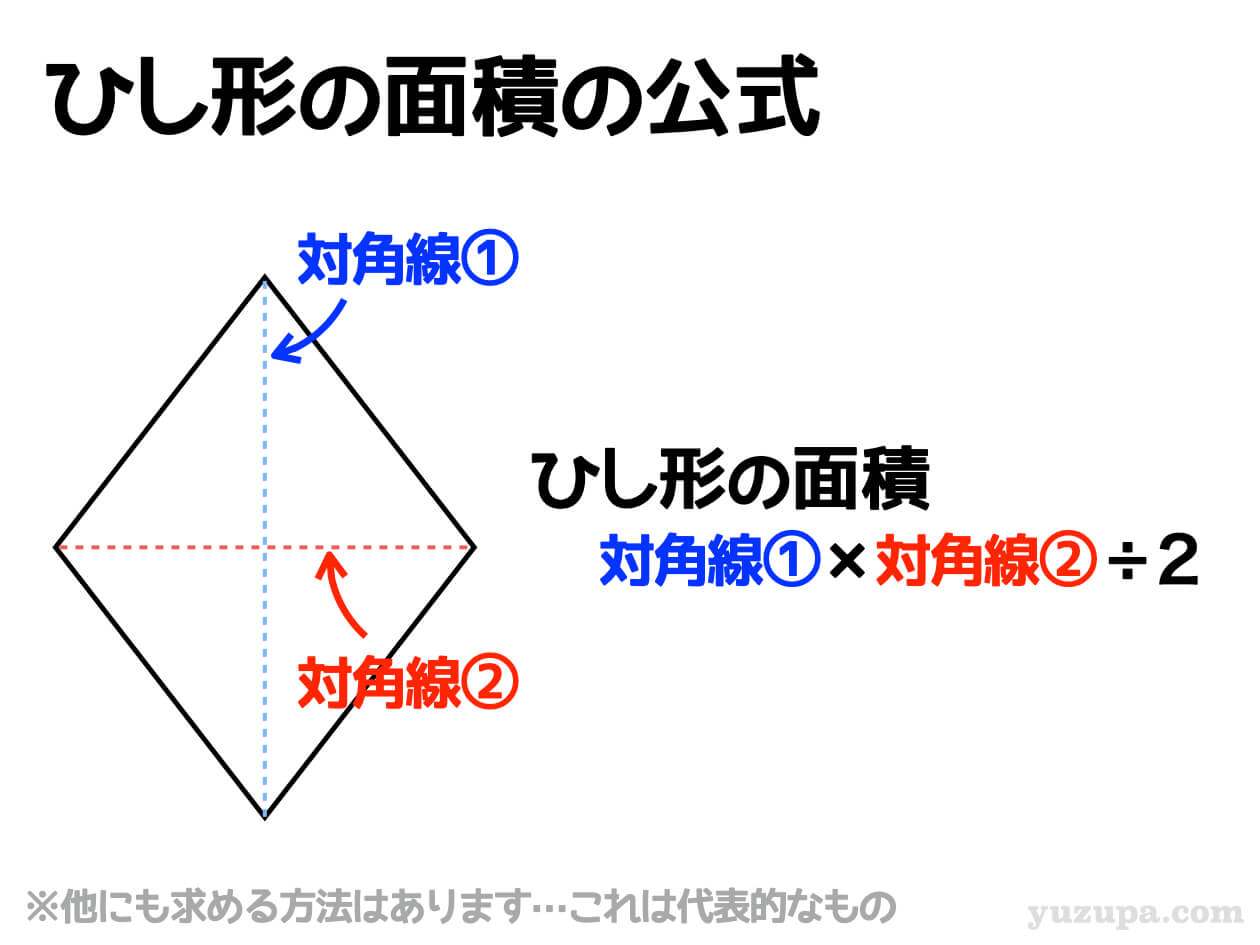
“ひし形”の面積を求める公式として 最もメジャーなのが ”対角線×対角線÷２”という公式 です_φ(･_･

※ 他にも面積を求める方法はありますが最も代表的なものです。このあたりは２項で詳しくご紹介します…

 

大切なのは、この公式でなぜ面積が求まるのか をシッカリと理解しておくことです。でも意外とシンプルですd(^_^o)

 

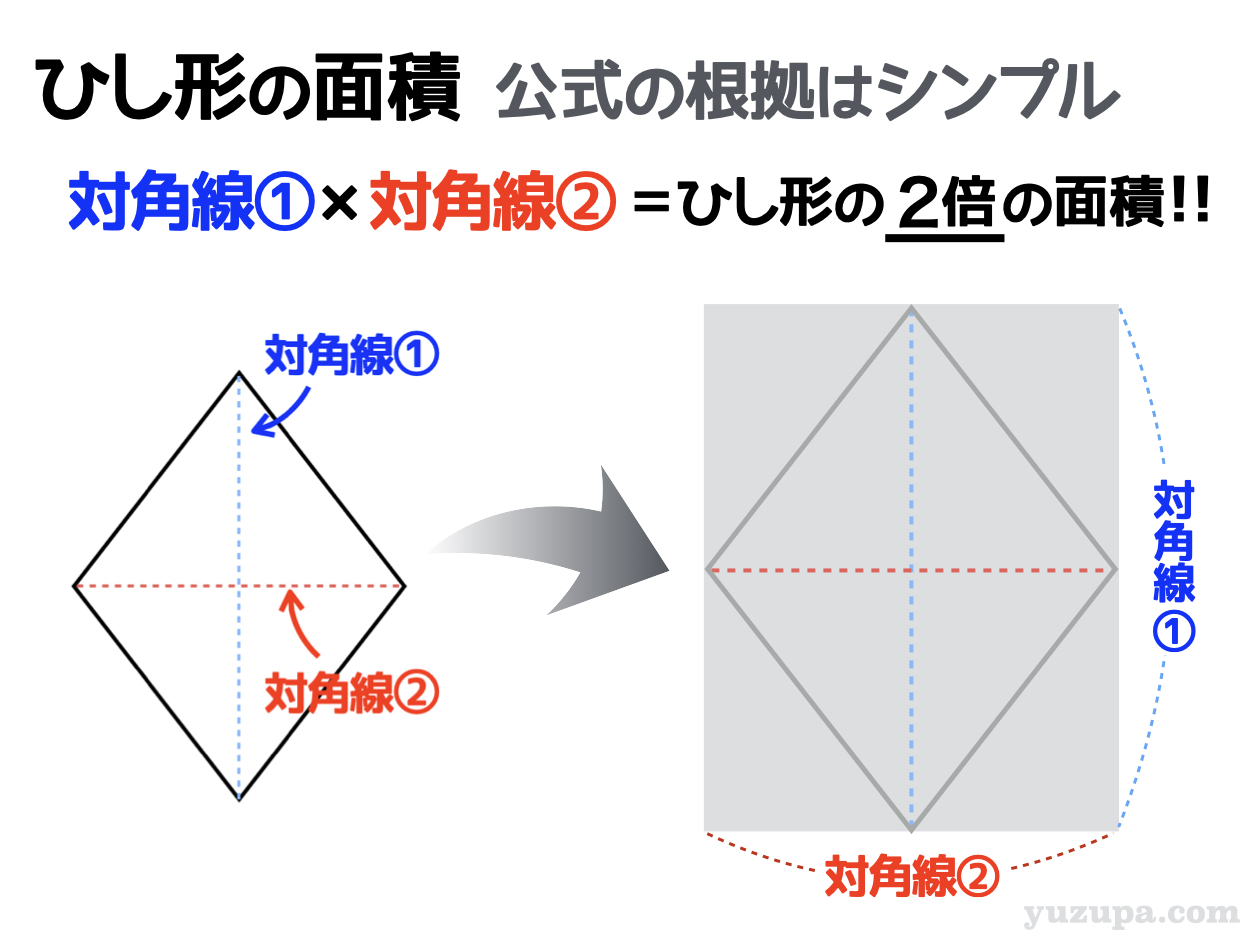
試しに… ”ひし形” の２本の対角線をかけてみましょう。そうすると出てくるのが図のような長方形ですね。

この長方形は元々の “ひし形”の面積の２倍 ある長方形です。

だったら…対角線×対角線で出てきた値を ２で割ってあげればひし形の面積になる というワケですd(^_^o)

意外とシンプルですね！

 

ひし形の２つの性質

次は ”ひし形” の性質を２つおさえましょう。細かい性質は多数ありますが、最も大事なのはこの２つですd(^_^o) 

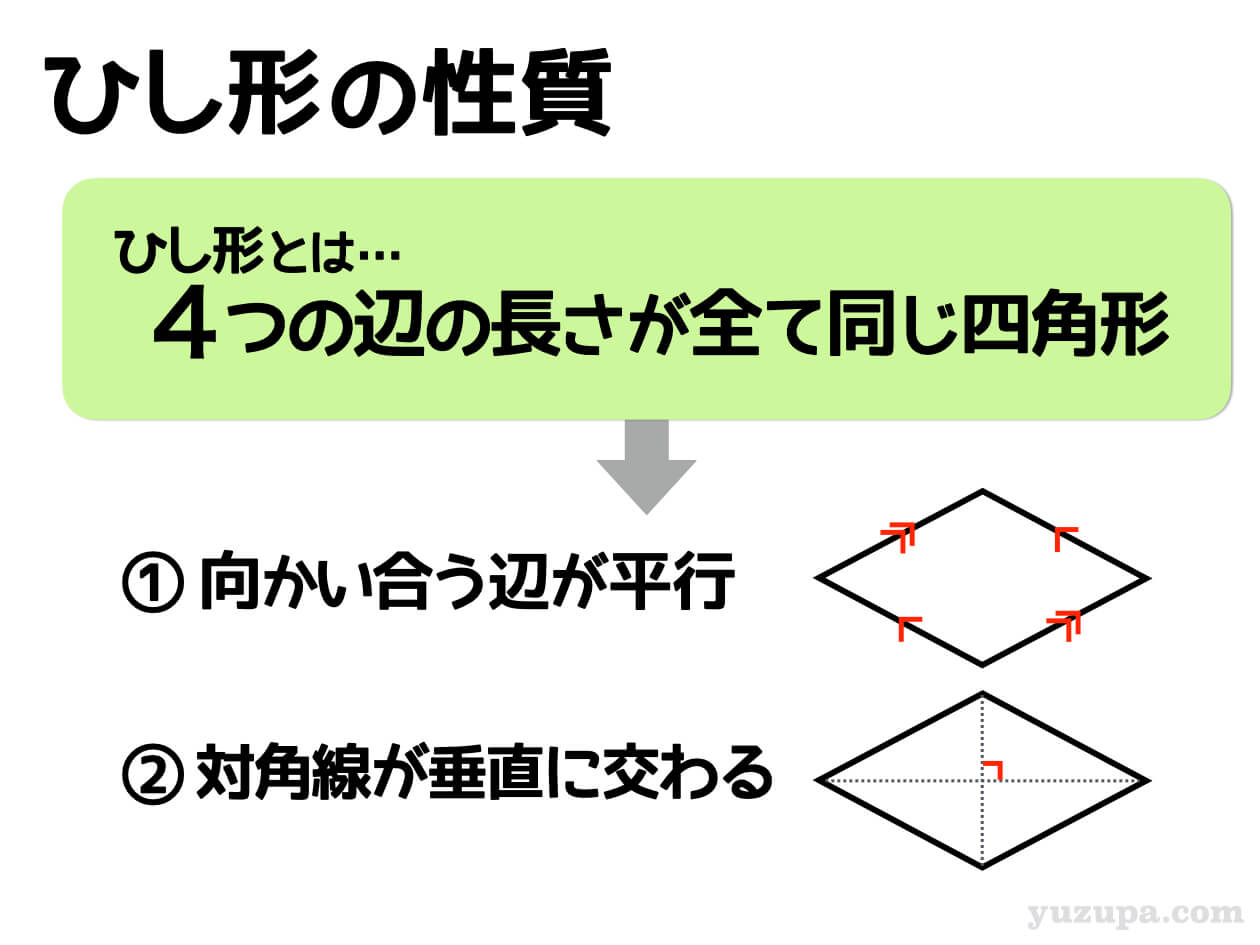
① 向かい合う辺が平行

ひとつ目の性質は ”向かい合う辺が平行” ということ。

“ひし形” は “必ず” 向かい合う辺は平行になります。どうして必ず平行になるのでしょうか？

詳しい証明は省略しますが、”ひし形”を対角線で２つの三角形に分割すると 合同な２つの二等辺三角形が現れることから簡単に証明することができちゃいます d(^_^o)

ちなみに…向かい合う辺が平行ということは ”ひし形” は平行四辺形の一種 であるということもわかりますね∑(ﾟДﾟ)

 

② ２本の対角線は垂直に交わる

ふたつ目の性質は ”２本の対角線は垂直に交わる”ということ。

こちらも同様に ”ひし形”の対角線は “必ず” 垂直に交わります。どうして必ず垂直なのでしょうか？ 

ことらは ”ひし形” を２本の対角線で４つの三角形に分割すると、隣り合う三角形が合同であることから、簡単に証明することができます。今回は証明は省略しますm(_ _)m

実は…さきほど紹介した 面積の公式が正しいという根拠はこの性質を使ったもの です (^_^;)

 

四角形の種類をおさえる

冒頭でご紹介したように “ひし形” とは４つの辺の長さが全て等しい四角形のこと… そして “ひし形” の性質として向かい合う辺は平行ということがわかりましたね…

つまりこういうことです d(^_^o) 

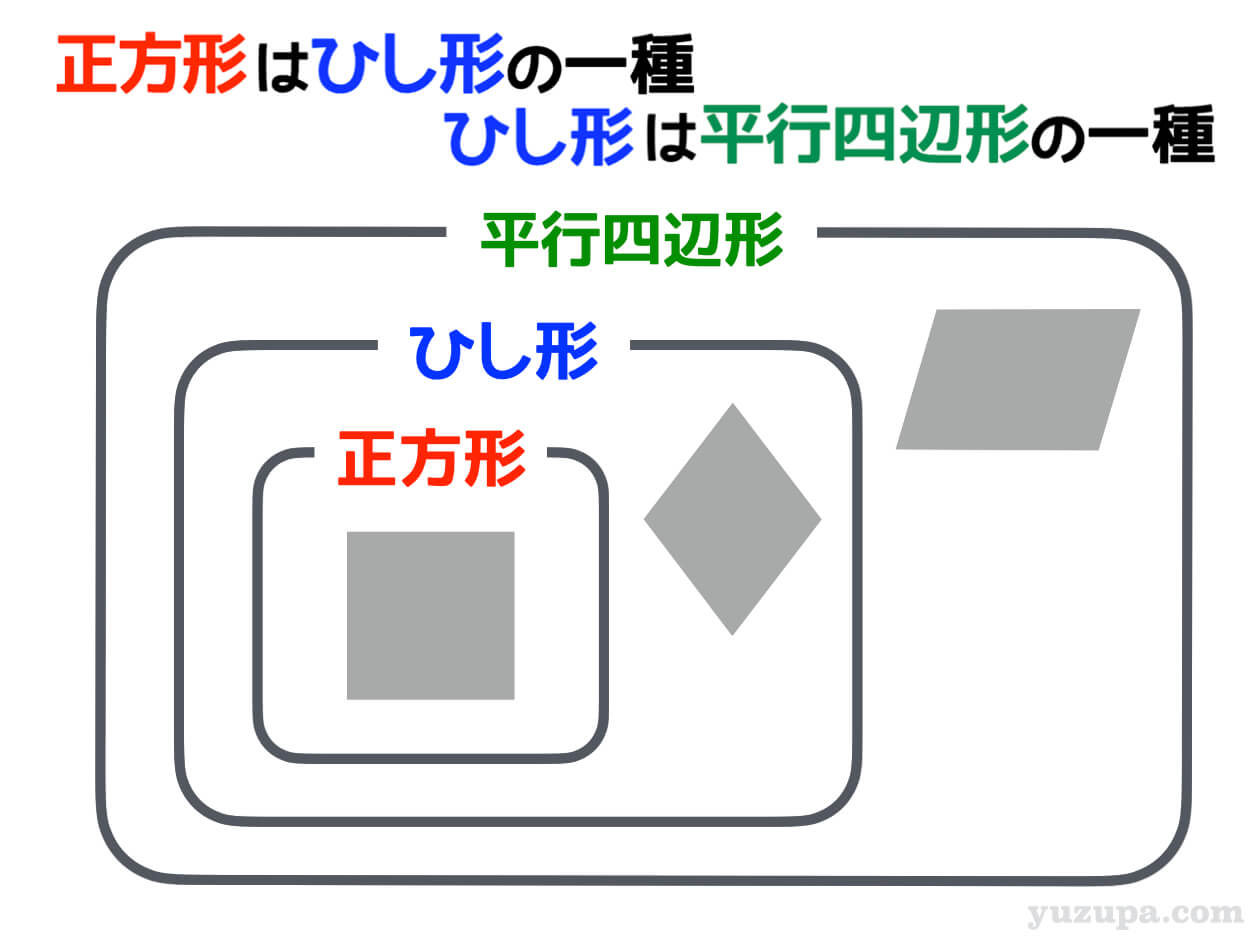
この関係性を理解しておくと…面積を求める問題などで 変な固定観念から問題が解けなくなってしまうということを防ぐことができます。

正方形をみたら ”ひし形の一種だ”と考え、ひし形をみたら ”平行四辺形の一種だ”と考えられると良いですねd(^_^o)

 

それでは…入試では最も大切なパートにまいりましょう。ひし形の面積にかんするいくつかのテクニックですd(^_^o)

 

面積の公式を柔軟に使いこなす

では実際の具体的な例で “ひし形” の面積の公式を使いながら問題を解いていきましょうd(^_^o)

① 正方形はひし型の一種

さっそく問題をご覧ください。 

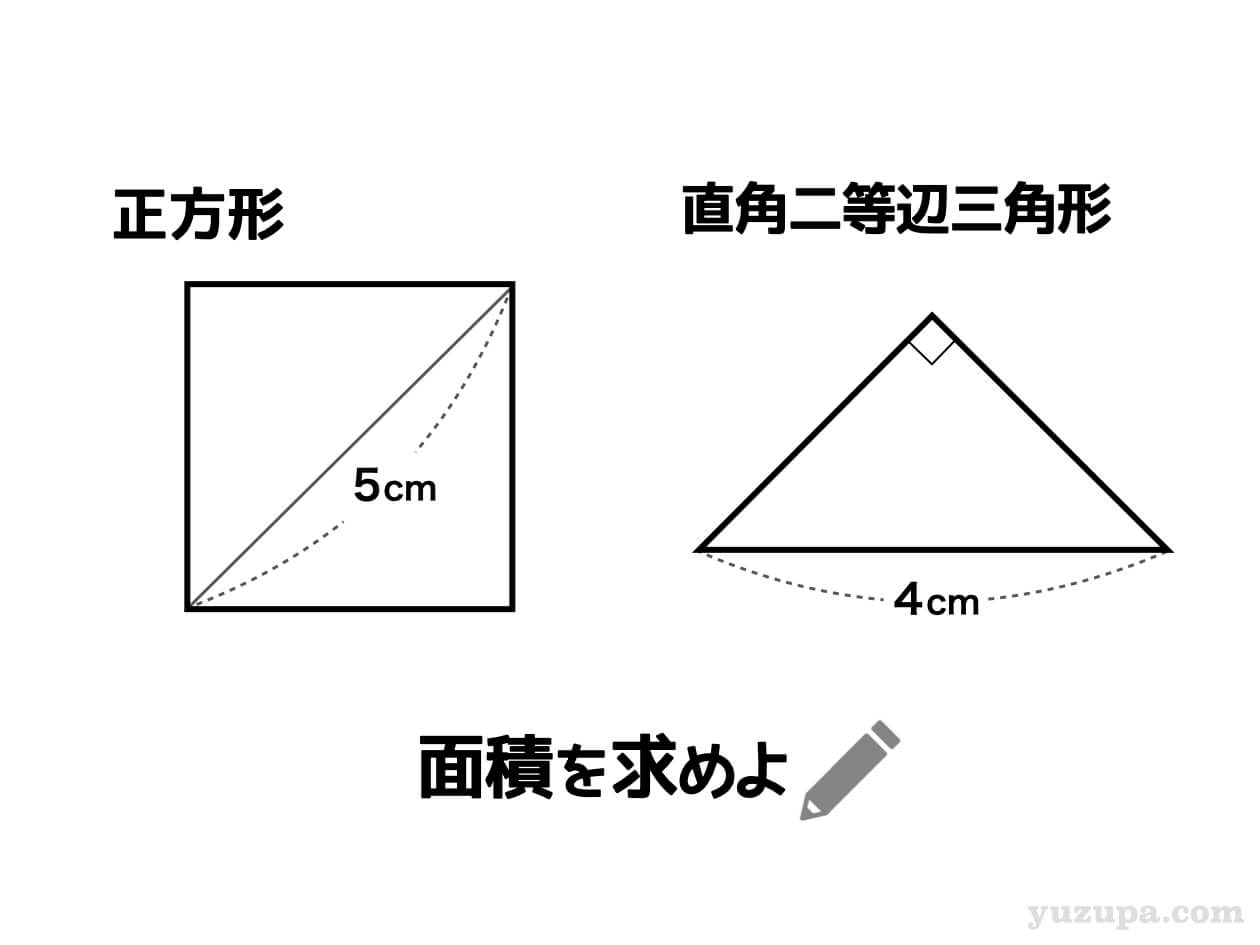
正方形と二等辺三角形の面積を求めるという超シンプルな問いです。とても簡単そうですね d(^_^o)

正方形の面積を求めるときに最初に思いつく求め方は” 縦 × 横 ”ですね。でもその公式に固執してしまうとこの問題はとけません。 

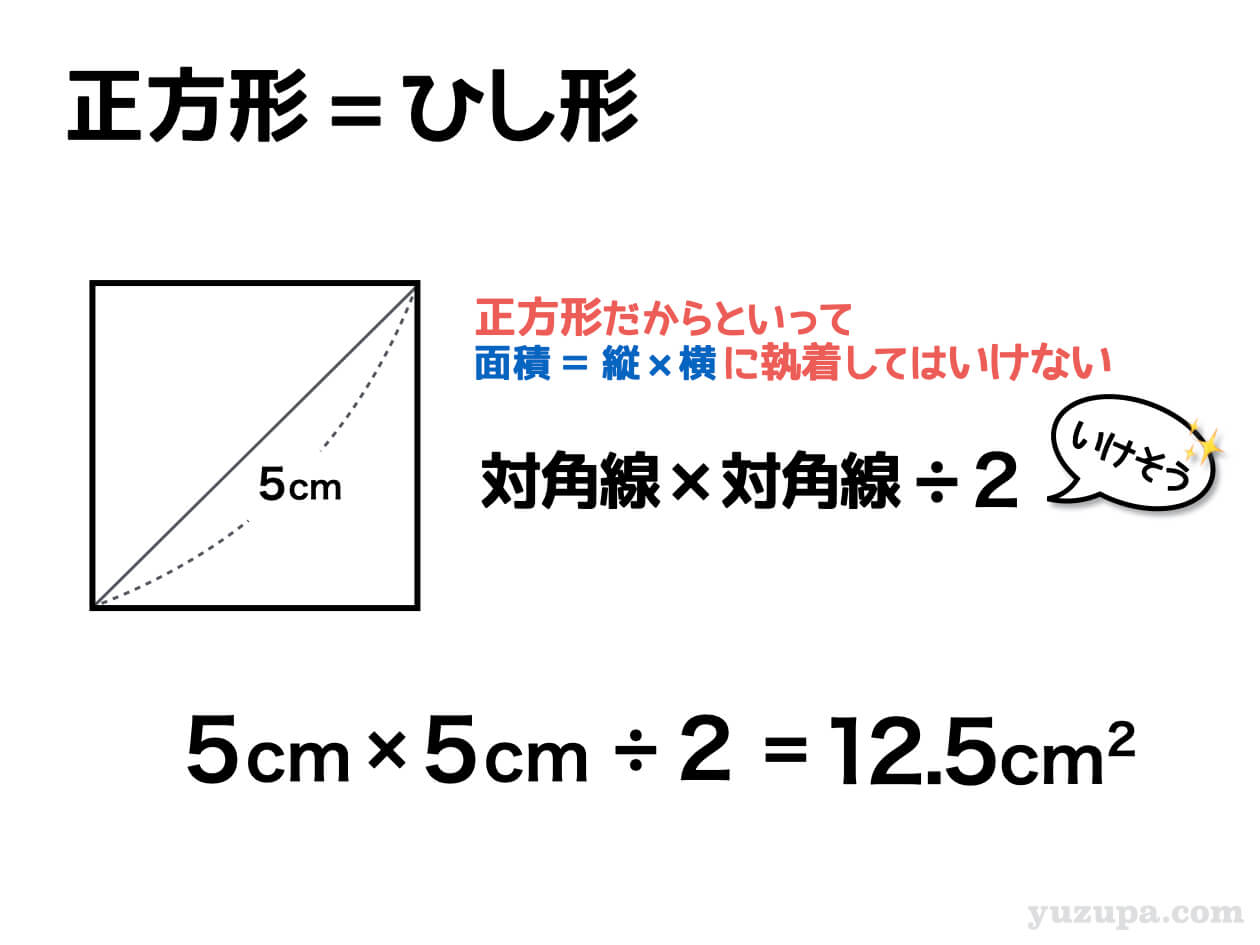
実はこの対角線の長さから正方形の面積を求める形…もうちょっと複雑な図形問題にけっこう登場します_φ(･_･

 

二等辺三角形の方も同じです。

三角形の面積を求めるときに ” 底辺 × 高さ ÷ ２ ”がとっさに思いつきますよね。同様にこれに固執してしてはいけません。

 

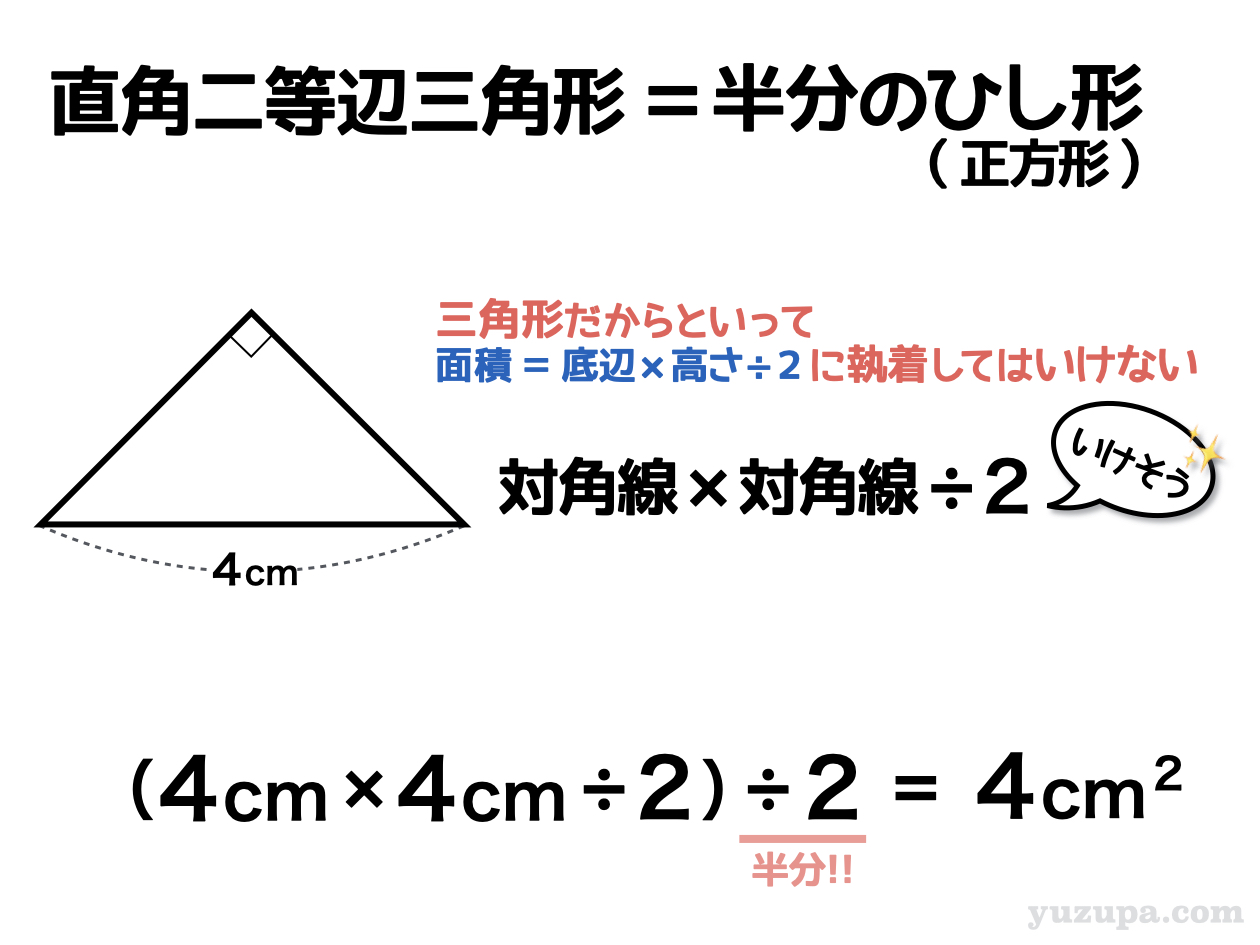
直角二等辺三角形は正方形を半分に切ったもの。つまり…”ひし形を半分に切ったもの” とも言い換えることができます。

必死になって底辺と高さを探してもなかなか解けない問題ですが、ひし形を半分に切ったものと考えると見え方が変わりますd(^_^o)

 

② ひし形は平行四辺形の一種

次の例題にまいりましょう。 

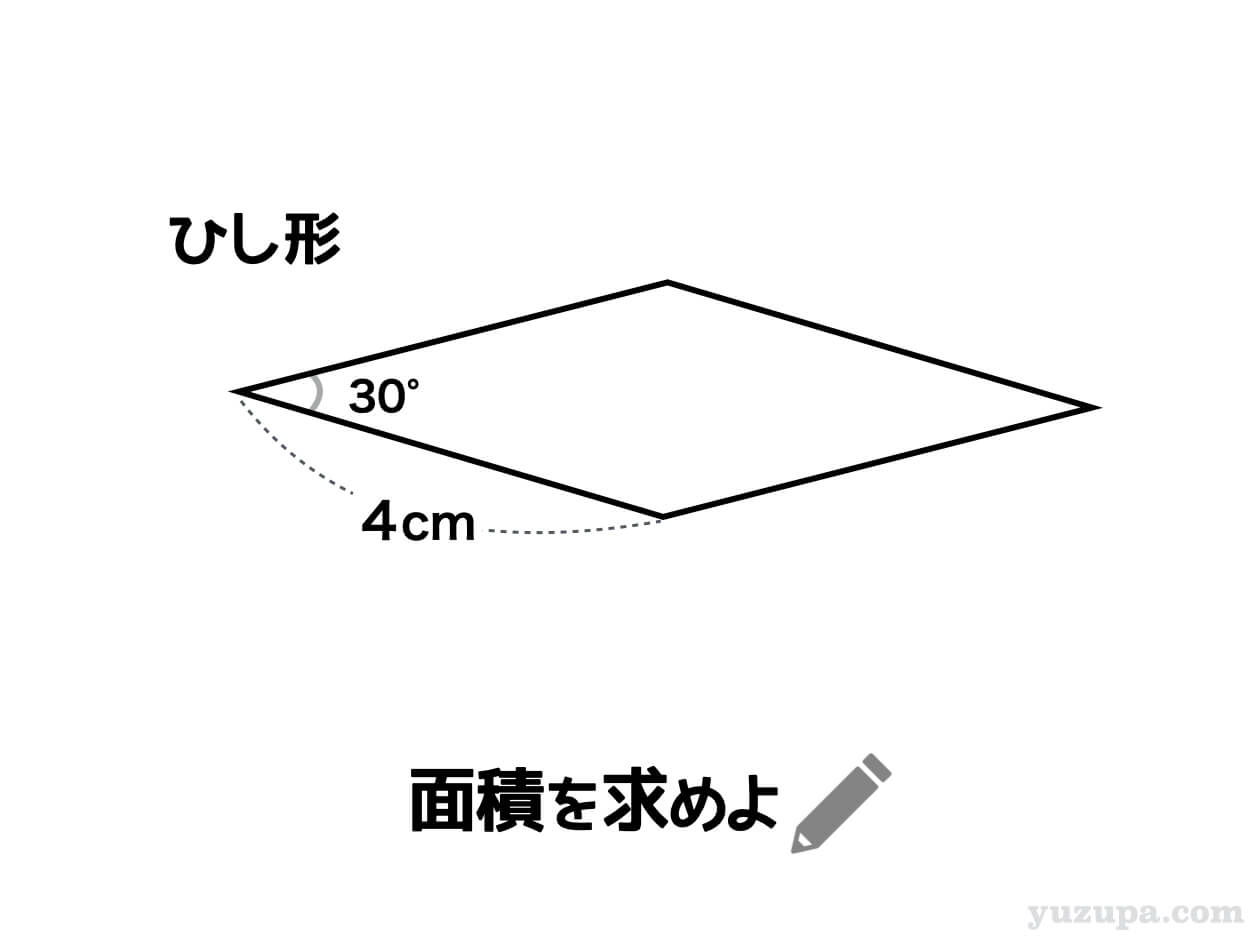
これは ”ひし形” なので、最初に思いつく公式は ”対角線×対角線÷２” かもしれません…が対角線の長さがわからない(-_-;)

“ひし形”だからといって、この公式に執着してしまうとなかなかこのひし形の面積も求めることができません。

 

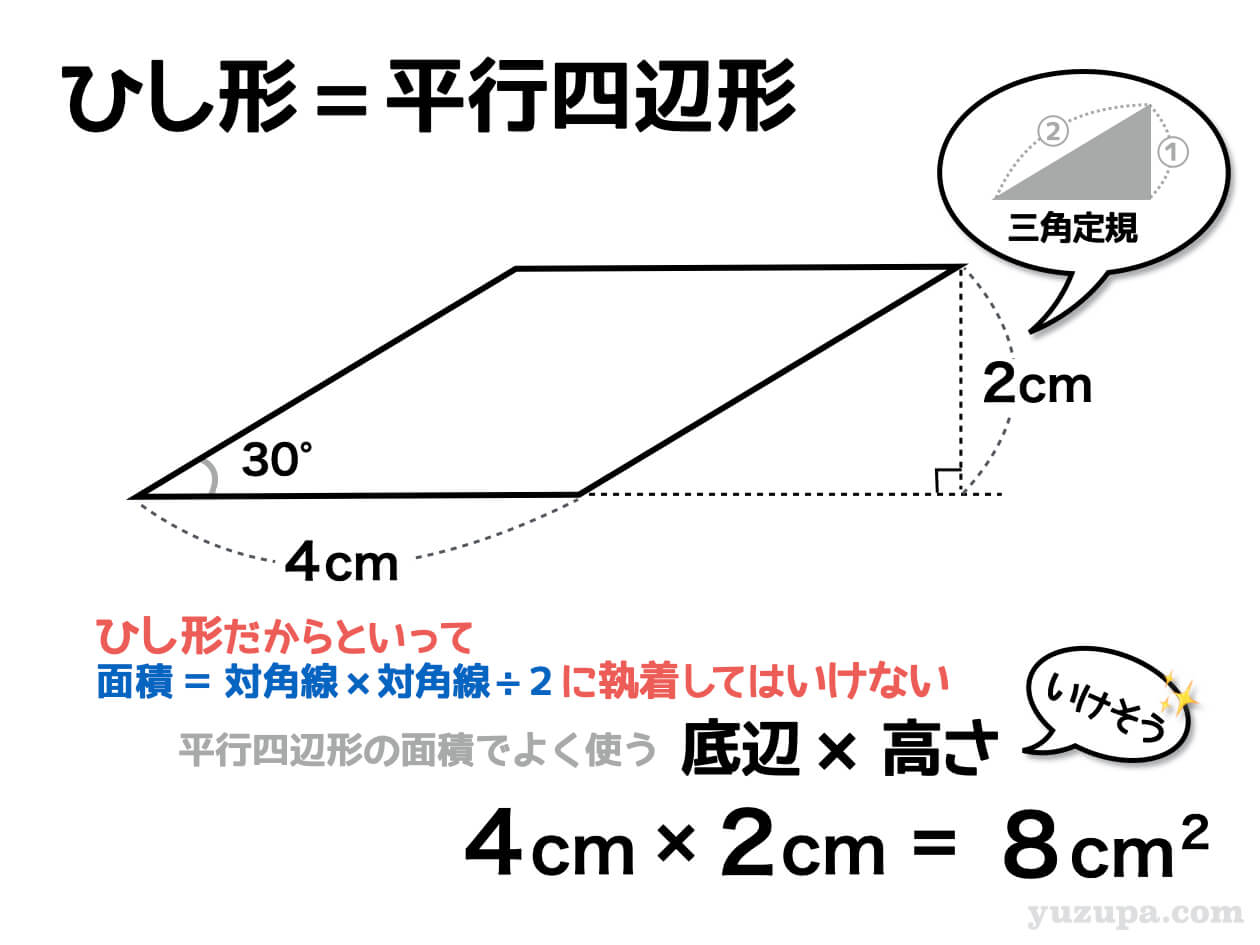
 ひし形は平行四辺形の一種。一般的に平行四辺形の面積の公式として定着している “底辺×高さ” もモチロン使えます。

この問題の場合、底辺はすぐに分かるものの、高さを求めるのにちょっと工夫は必要ですが、高ささえ分かってしまえばとてもシンプルに面積を計算することができますd(^_^o)

ひし形というキーワードから “対角線×対角線÷２” という公式に固執しすぎると解けない問題です (>_<)

※ ちなみに…三角定規の辺の比を使うと高さがわかります。

 

まとめ

今回は ”ひし形” について面積を中心に解説をしてまいりました。特に…面積の公式というのは固定観念によって、問題を解くさまたげになることがあります。

面積の公式はひとつにとらわれるな

正方形を見て” 縦 × 横 ”に固執してしまう… ひし形を見て ” 対角線×対角線÷２” に固執してしまう… けっきょく問題が解けない(-_-;) 公式はひとつにとらわれずに柔軟に使い分けることが大切ですね！