中学受験：素数とは？簡単に分かりやすく！イメージでおさえろ

素数がイマイチ分からない…定義だけでなくその利用イメージを

こんにちは。かるび勉強部屋 ゆずぱ です。

小学生が取っ付きにくい算数の単元…その 代表格は ”素数” です。そもそも定義すら理解できない。やっとのことで ”素数” の定義を理解しても…子供は次のように考えます(-_-;)

で…これって何が嬉しいの？

本記事では まず素数というものがナニモノなのかをイメージで理解できるよう説明します。そして後半はその”素数”を使うと何ができるのかを説明しますd(^_^o)

この２つのセットで素数の問題がチンプンカンプンな生徒も本質を理解することができ、結果として中学入試の問題が解けるようになってきますd(^_^o)

それでは詳細にいってみましょう！

 

素数とはナニモノ？簡単に分かりやすく！

定義だけ見てもよく分からない

まずは 教科書に書いてある定義 をごらんください…

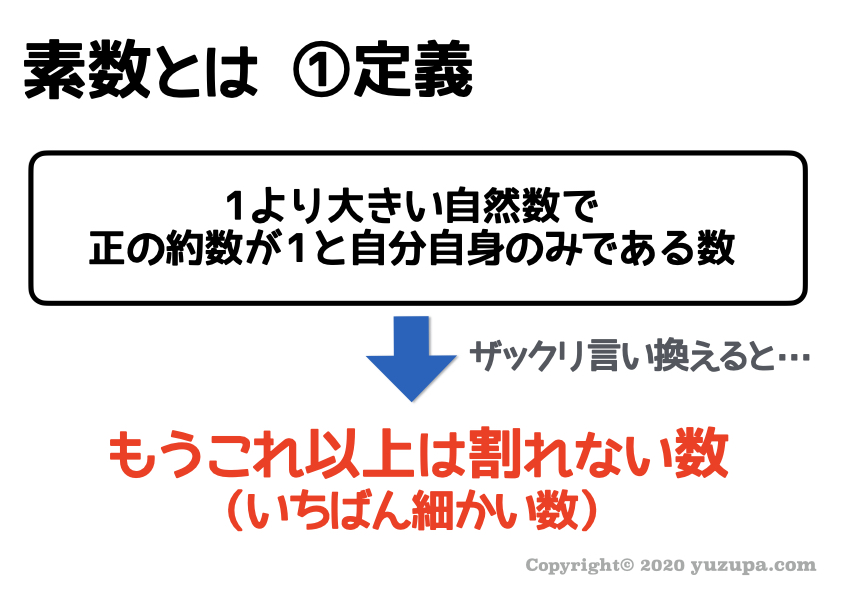
ちょっと数学的な表現で分かりにくいので噛み砕いてみます。素数は…１を除けば もう自分自身でしか割ることができない数字。

つまり…それ以上割り切れないイチバン細かい数 のこと！

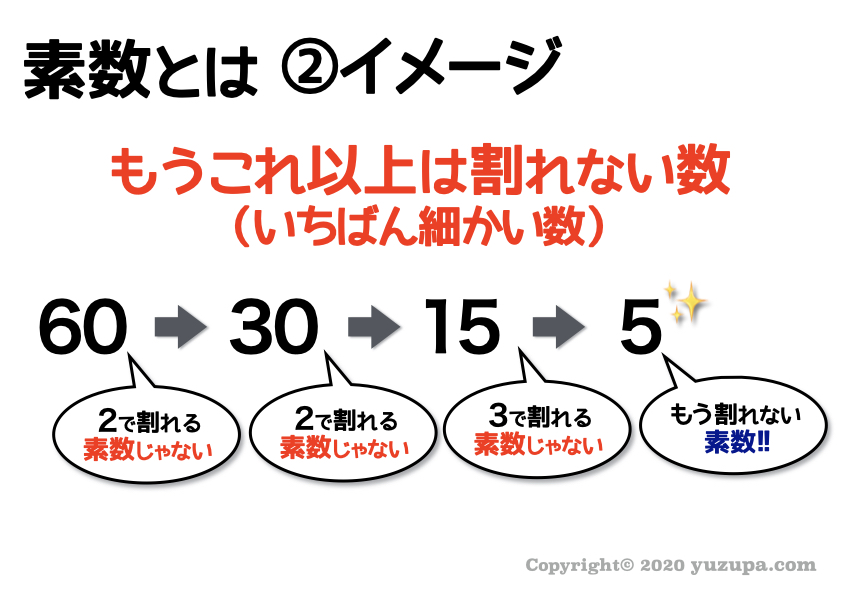
実際に６０という数字を適当な数で割り算していきます。ところが５まで来たときに もうこれ以上割れない状況 になります。

つまり５という数字はこれ以上割ることのできないイチバン細かい数、つまり…素数 となります_φ(･_･

こんなイメージを伝えると子供は素数というもののイメージを持ってくれることでしょう _φ(･_･

ほぅほぅ…イチバン細かい数ね
なんとなくは分かったけど…

ここまできてはじめて具体的な素数を示してあげます。素数は無限にあるので小さい方から１０個程度で良いでしょうd(^_^o)

 

 

目的を知るとなんとなく分かってくる

さて…定義だけ見ると全く目的が分からない定義だと子供は感じます。何のためかよく分からない数をナゼ定義するのか…？

素数の利用目的(算数の世界で最もメジャーな使い方)は、数字をこれ以上分解できないイチバン細かい数まで分解 すること！

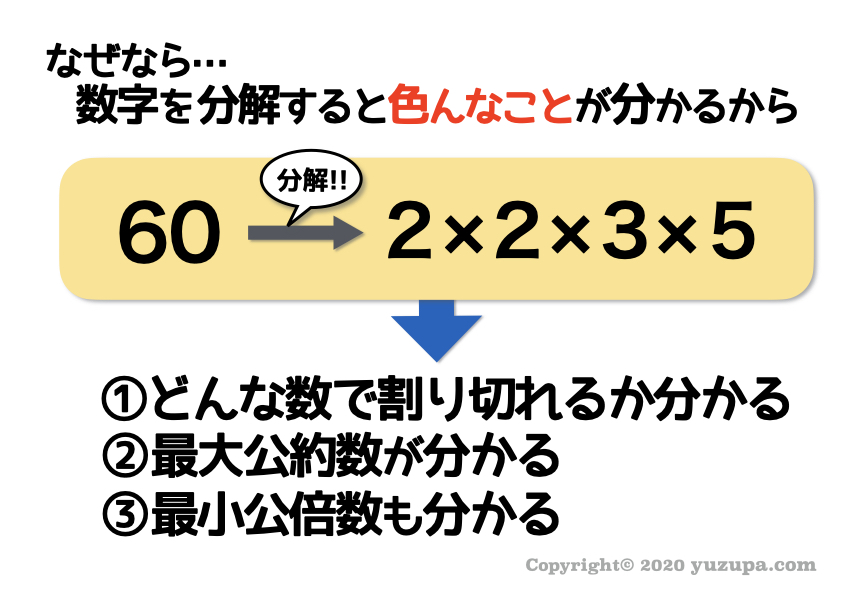
そして、数字をイチバン細かい数の掛け算の形にするとその数字のいろんなことが分かる。これが利用目的なんですd(^_^o)

それでは３つの利用目的について詳しく紹介します。

 

 

目的を正しく理解する分かる３つの利用例

利用例① どんな数で割り切れるか分かる

まず…６０という数字をこれ以上分解できないイチバン細かい数まで分解すると以下のようになりますd(^_^o)

そうすると…この６０という数字がどんな数で割り切れるかが 一目瞭然 となります∑(ﾟДﾟ)

掛け算の形に２や３や５が含まれるので、２や３や５で割り切れるのはパッと見ただけでも分かりますねd(^_^o)

 

それだけではありません…

分解された素数をよくみると ２×２や３×５といった２つ以上の掛け算も含まれている ことが分かります。

 

最後は同じ数で何回も割ってみましょう…

６０という数字を２で何回も割ってみましょう。１回割るごとに２が消えていきます が、３回目になるともう消すことができません∑(ﾟДﾟ)

つまり６０という数字を２で次々と割っていくと、２回は割り切れて、３回目は割り切れないということが分かりますd(^_^o)

 

上記のとおり素数に分解すると、どんな数であっても自由自在に色んな掛け算の形に変換することができる んですd(^_^o)

 

 

参考： 約数がいくつあるかも分かる

それでは…ちょっと応用です。どんな数で割り切れるかは素数に分解された式を見れば分かりましたね。

では 割り切れる数(つまり約数) はいくつある でしょうか？

これは場合の数の問題に変換することができますd(^_^o)

２を最大２回、３を最大１回、５を最大１回つかった掛け算の形のパターン数を”場合の数”の考えで求めれば良いでしょう。

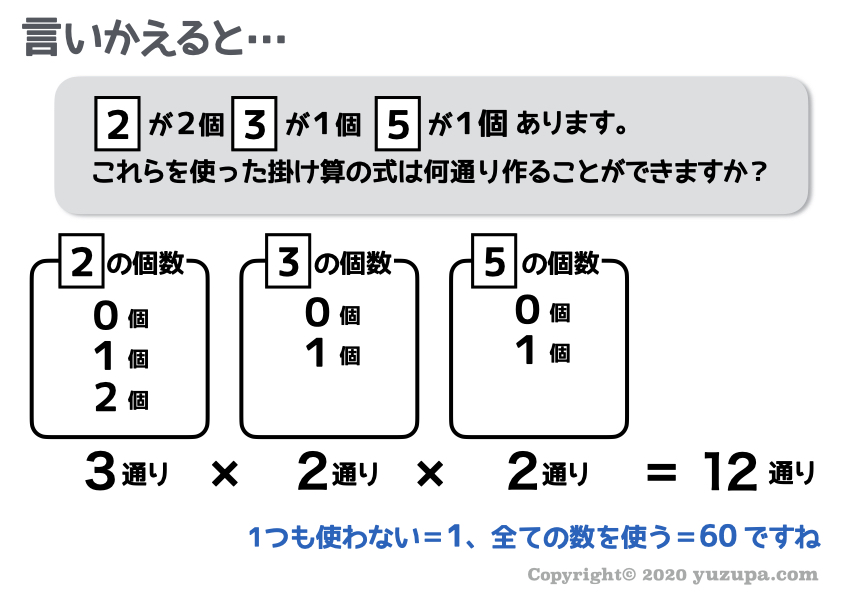
結果として６０の約数は１２個あることがわかります_φ(･_･

 

 

利用例② 最大公約数が分かる

数字が素数に分解されていると最大公約数も試行錯誤ではなく ”論理的に” 導くことができますd(^_^o)

まずは６０という数字と、４２という数字を素数に分解すると以下のようになります。公約数はどうなるでしょうか？

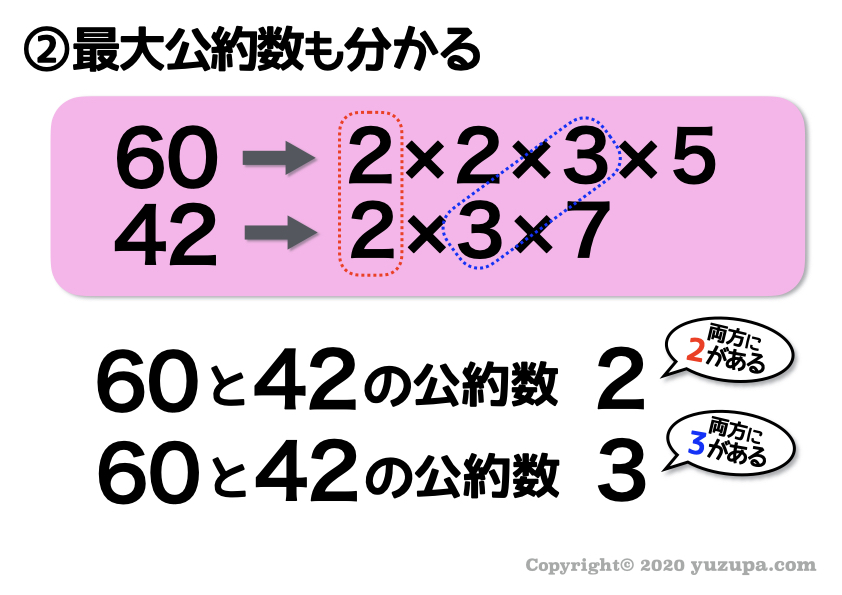
上記のように６０にも４２にも２という素数が含まれています。つまり２は６０の約数でもあり、４２の約数でもあります。

では最大公約数はどうでしょう？

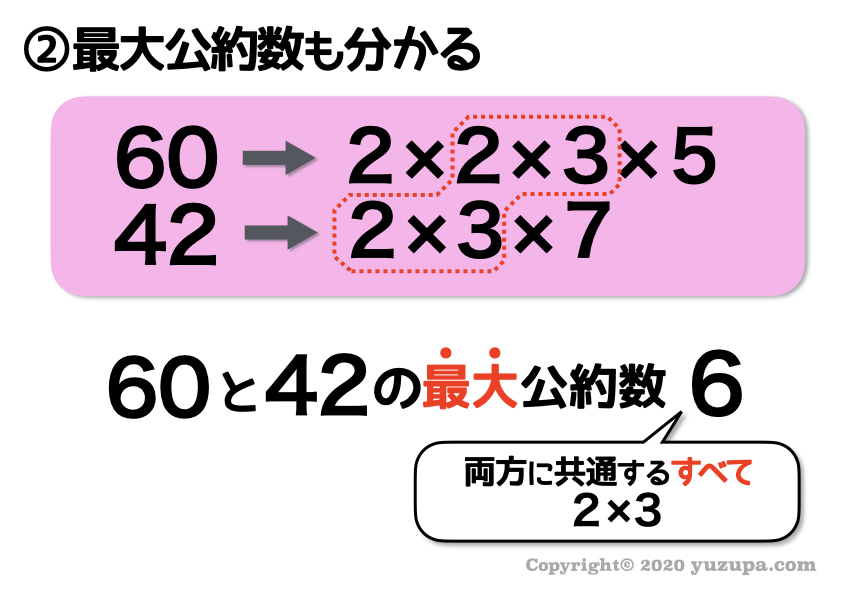
共通の素数が公約数でした。”最大”公約数であれば、共通の素数をぜんぶ持ってきてあげればよい のです d(^_^o)

 

 

利用例③ 最小公倍数が分かる

同様に最小公倍数も試行錯誤することなく”論理的に”求めることができますd(^_^o) まずは倍数はどんな数か表してみましょう。

上記のような６０と４２の倍数が同じになるものが公倍数ですが、それが…

最小になるような□と○に入る数字はなんでしょうか？

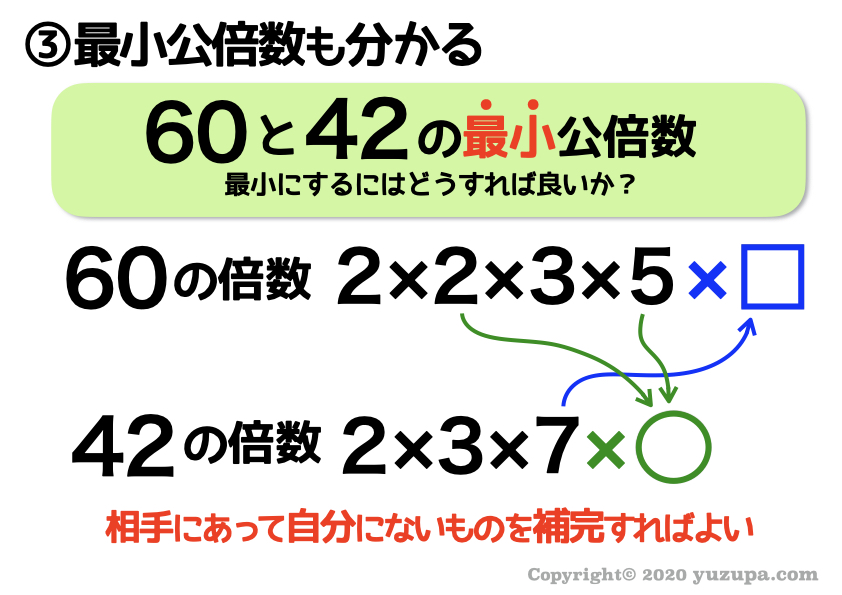
最小にするには 自分にはないけど相手にある素数を補完 すれば良いのです。余計なものを一切省いているので最小になります。

結果として６０と４２の最小公倍数は２×２×３×５×７＝４２０になることがわかりますねd(^_^o)

以上、素数の３つの利用方法をご紹介しました。

 

 

まとめ

今回は算数でとっつきにくい単元の代表格 “素数” についてその定義とイメージ、そして利用目的を紹介しました。

定義だけではどうしてもナゼそんなものをワザワザ定義するのか分からない… 数字を掛け算の形に分解した時の最小単位 であるというイメージを持つことが理解につながりますd(^_^o)