中学受験：倍数の見分け方…３種類の見分け方を使いこなせ！

倍数を一瞬で見分ける方法… やり方は３種類に大別される

こんにちは。かるび勉強部屋 ゆずぱ です。

イキナリですが… “ 81342 ” という数字はは 9の倍数 です。81342 を 9 で割ってみて、割り切れたら 9の倍数 であることがわかりますが… もっと簡単に知る方法がありますd(^_^o)

それが倍数の見分け方テクニック
コレを知っていると超便利です

本記事の末尾には印刷用のPDFもご用意しております。それでは詳細に参りましょうd(^_^o)

 

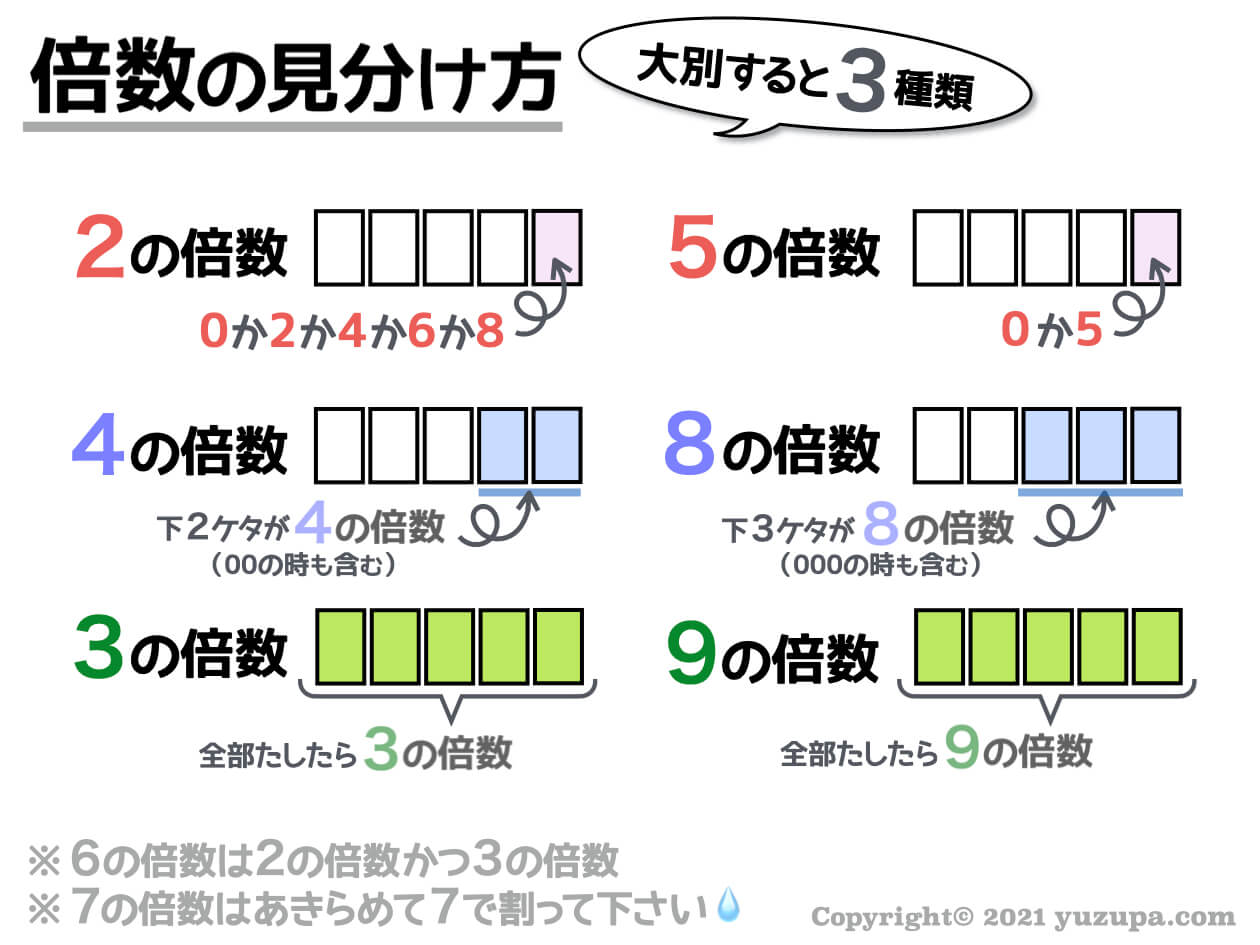
倍数の見分け方の全体像

倍数の見分け方は３種類

ひとことで 倍数の見分け方 といっても… 実は ザックリ分類すると３種類 の見分け方に分類することができます∑(ﾟДﾟ)

 

(1) 一の位の数字で判断（ 2の倍数/5の倍数）

２の倍数や５の倍数は…一の位の数字を見た瞬間に判定することができます。最も有名な見分け方ですね…d(^_^o)

(2) 一部だけ見て判断（ 4の倍数/8の倍数）

４の倍数や８の倍数は…全ての数字を見なくても下２桁や下３桁だけを見るだけで判断することができますd(^_^o)

(3) 全ての数を足して判断（ 3の倍数/9の倍数）

３の倍数や９の倍数は… 一の位の数、十の位の数、百の位の数…と数を足した結果を見て判断できますd(^_^o)

 

色々な倍数の見分け方がありますが、大きく分けてこの３つのパターンをおさえることで使いこなすことができます。

テクニックをヤミクモに覚えるよりも、こうやって特徴ごとにグループ化すると覚えやすいですねd(^_^o)

 

万能な最終手段 ”素因数分解”

そして倍数を調べる方法として万能な最終手段 ”素因数分解” も忘れてはいけません。倍数が登場する問題でシッカリ意識しなくてはいけないのは ”素因数分解” です。

例えば ”60” という数字を素因数分解してみましょう。

当然ですが…60はそこに含まれる素数の倍数です。2の倍数であり3の倍数であり5の倍数であることが分かります。

さらにはその素数の組み合わせで、4の倍数であることも、6の倍数であることも、12の倍数であることもわかりますね∑(ﾟДﾟ)

 

パッと見ただけで判定できる倍数の見分け方に加え、オールマイティな ”素因数分解” も立派な見分け法の一種です_φ(･_･

参考：素数とは？簡単に分かりやすく！イメージでおさえろ

 

倍数の見分け方…例題で詳しく

① 一の位の数字を見て判断

まずは… 一の位の数字を見ただけで一瞬で判定できる２の倍数と５の倍数です。これは有名なのでご存知ですね d(^_^o)

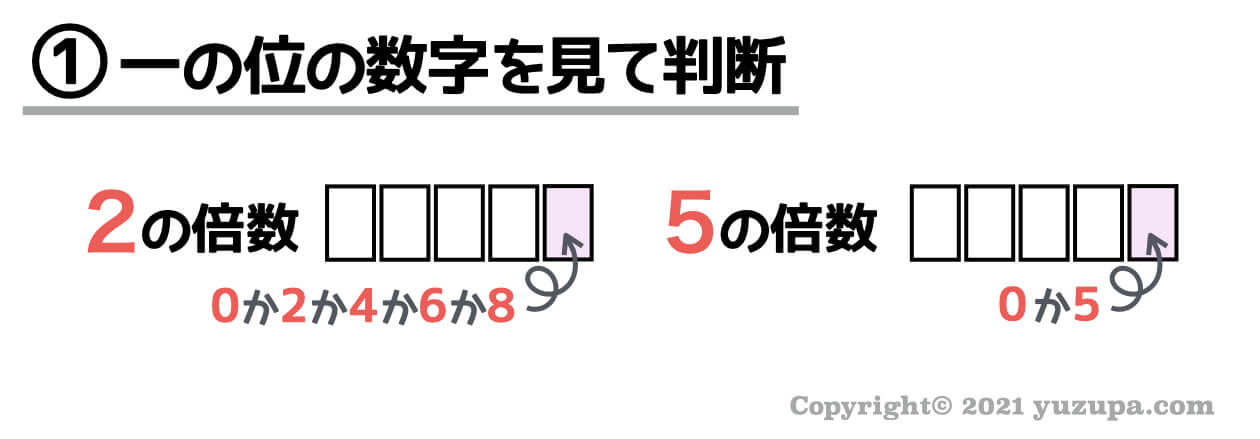
一の位の数字が0か2か4か6か8であれば、それは２の倍数です。2の倍数というのは偶数のことなので当たり前ですね d(^_^o)

一の暗いの数字が0か5であれば、それは５の倍数です。5の倍数は5ずつ増加するので一の位は必ず0か5になるのです。

それでは具体的な例を見てみましょう。

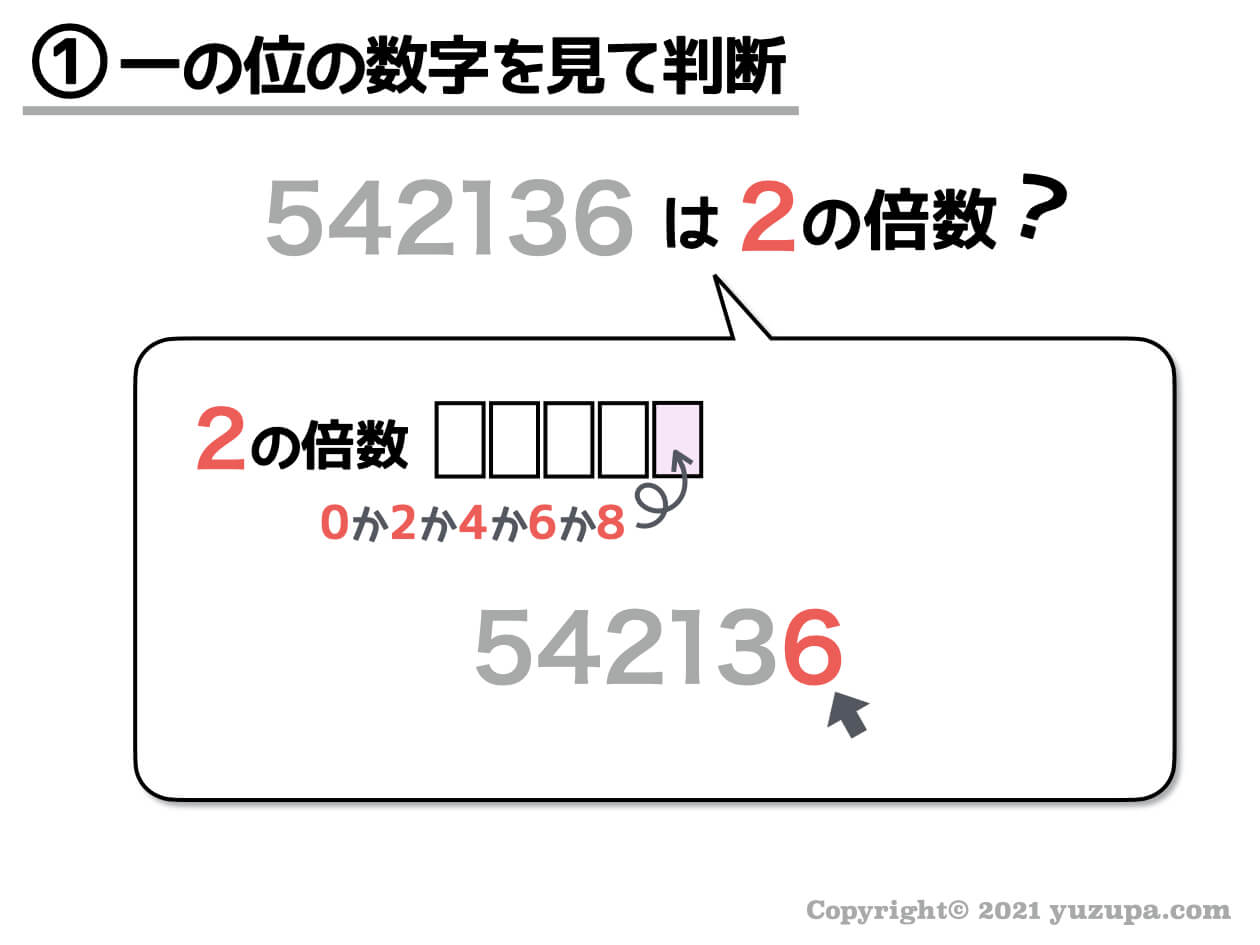
542136という数字。やたら桁数が多いですが…見た瞬間に２の倍数だと分かります。一の位が6だからですねd(^_^o)

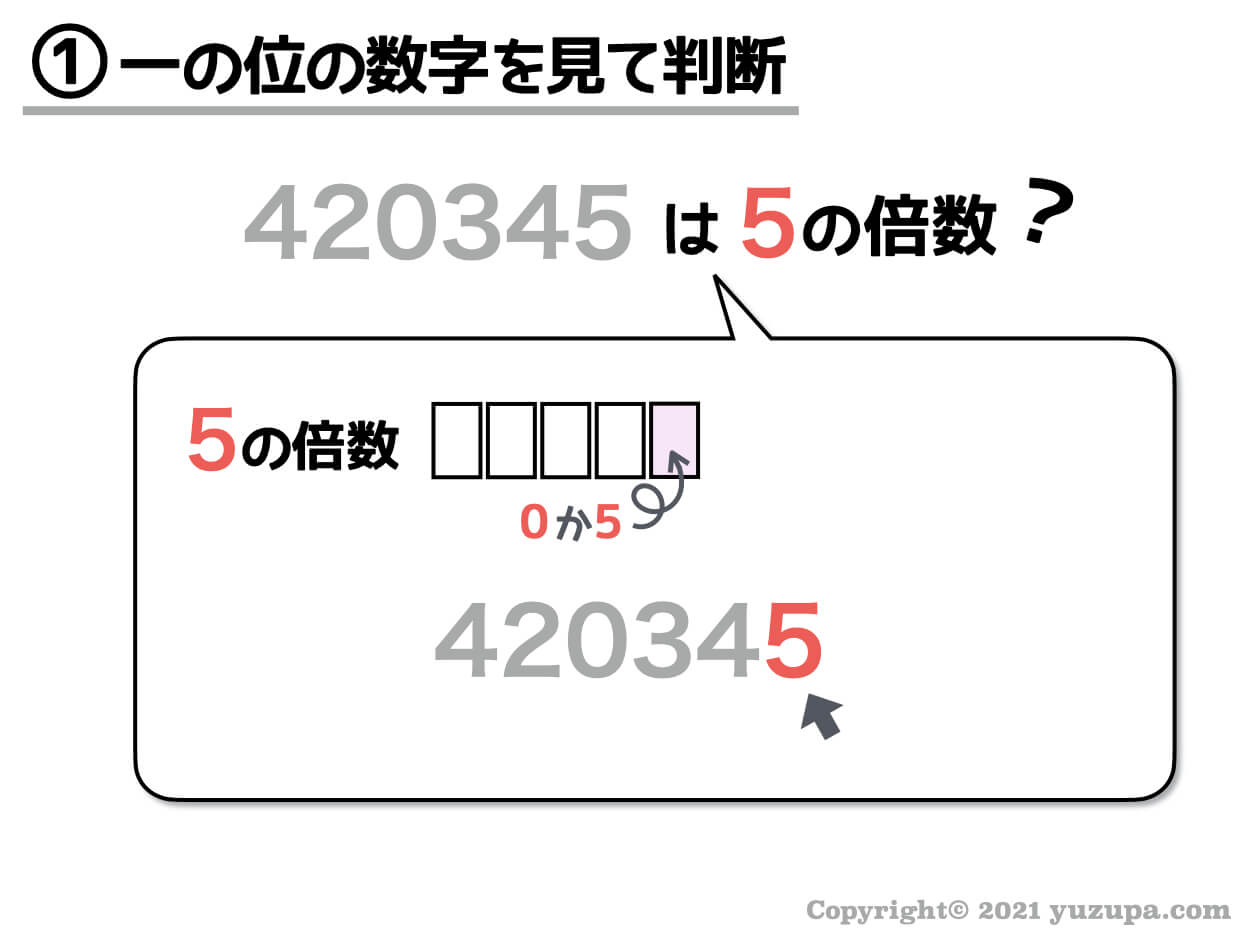
420345という数字。こちらもやたらでかい数字ですが、一瞬で５の倍数だと分かりますね。一の位が５だからです。

 

② 一部だけ見て判断

次は… 数字全体を見なくても下２桁や下３桁だけ見れば判定できる４の倍数と８の倍数です。

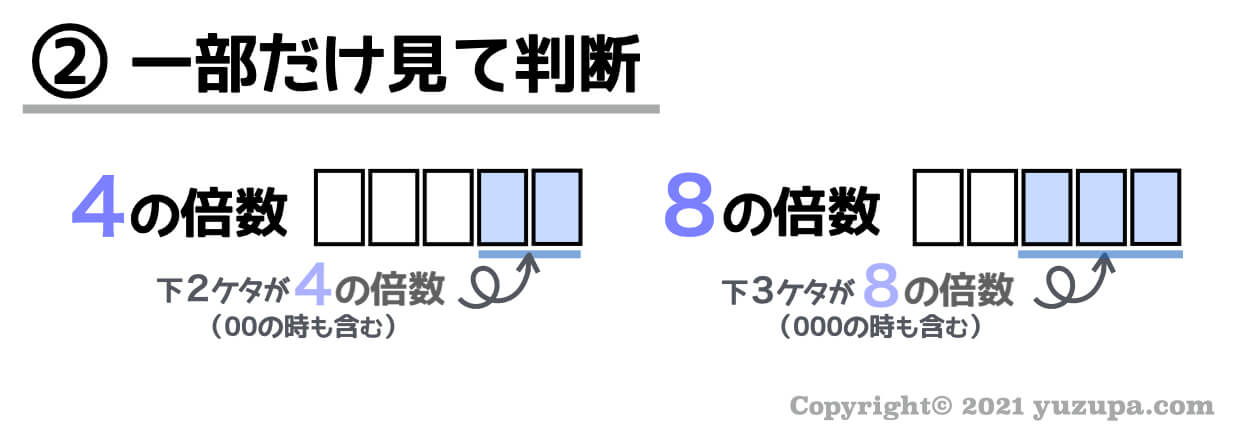
下２桁が４の倍数であれば、その数字は４の倍数です。百の位の最小単位である100が４の倍数なので、百の位より上は必ず４で割り切れるから調べるまでも無いのです。

そして下３桁が８の倍数であれば、その数字は８の倍数です。同様に千の位の最小値である1000は８の倍数だからですねd(^_^o) ４の倍数と同様の理由です _φ(･_･

こちらも例をいくつか紹介します。

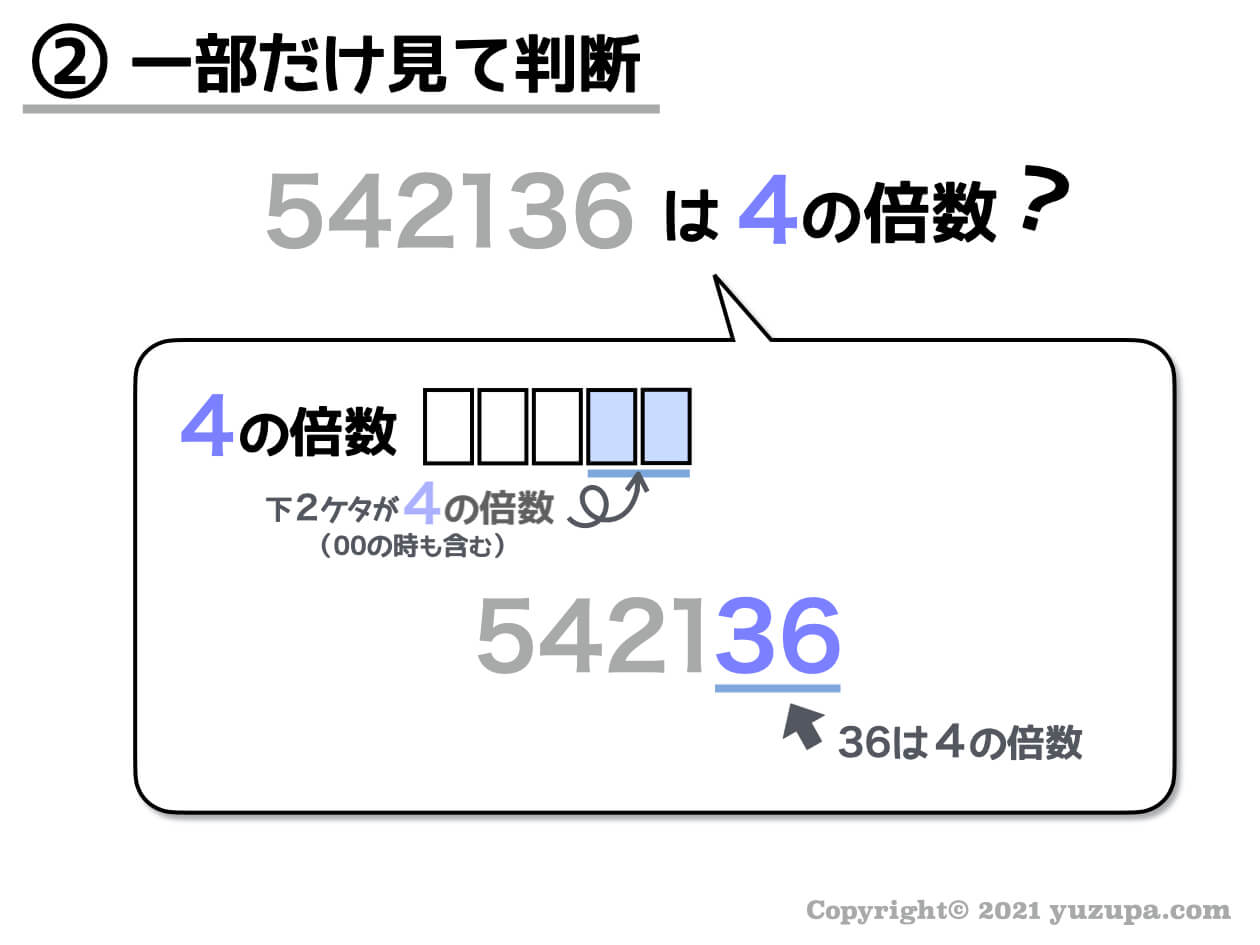
542136という数字。下２桁は36ですね。36は4の倍数なので、この数字全体も４の倍数であると判断できます。

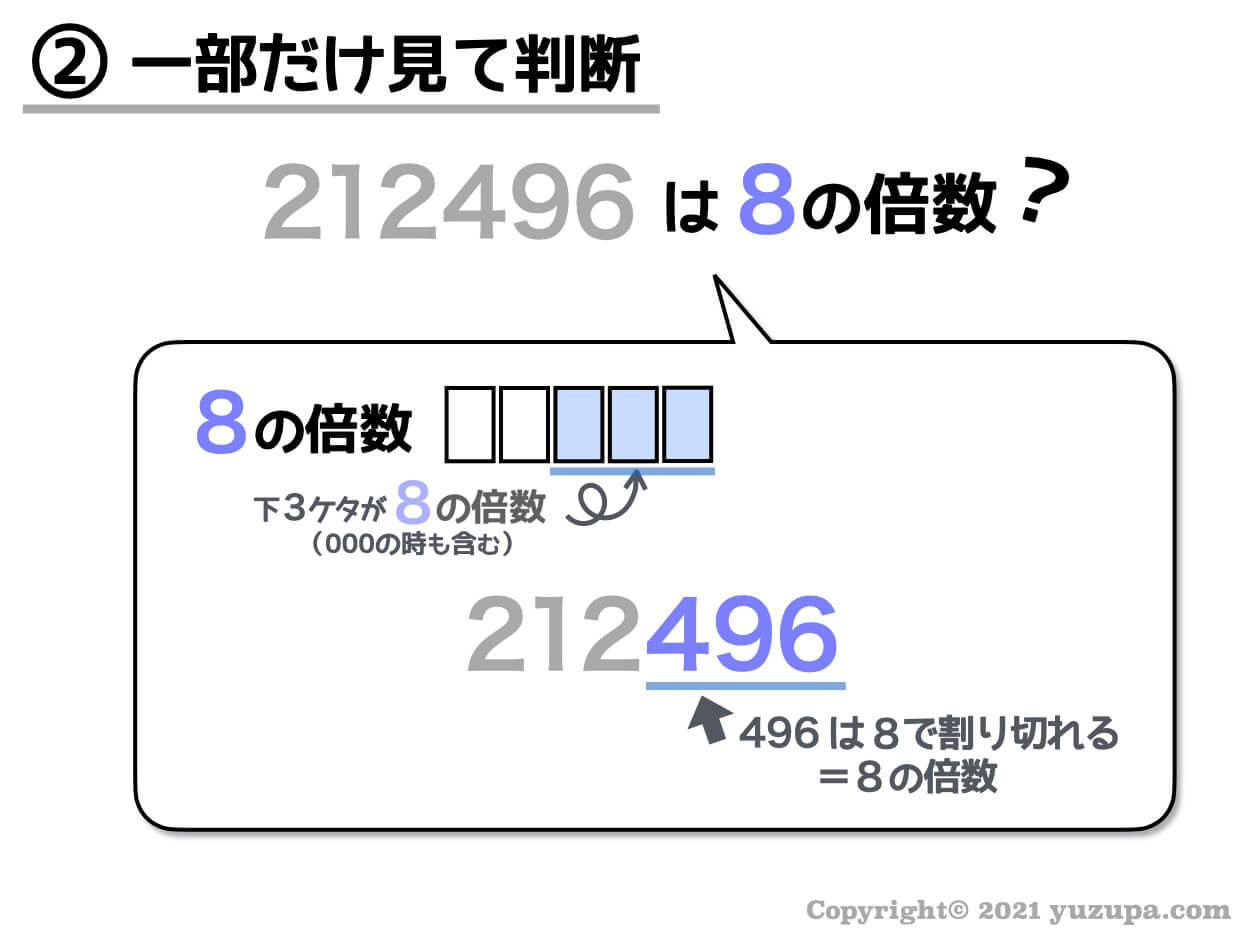
212496という数字。下３桁は496という数字。試しに8で割ってみるとちょうど割り切れます。下3桁が8の倍数になっているので、この数字全体も8の倍数であると判断できます。

 

③ 全ての数字を足して判断

最後は…全ての位の数字を足して判断できる、３の倍数と９の倍数です。ちょっと不思議な感じですが数学的に証明できます。

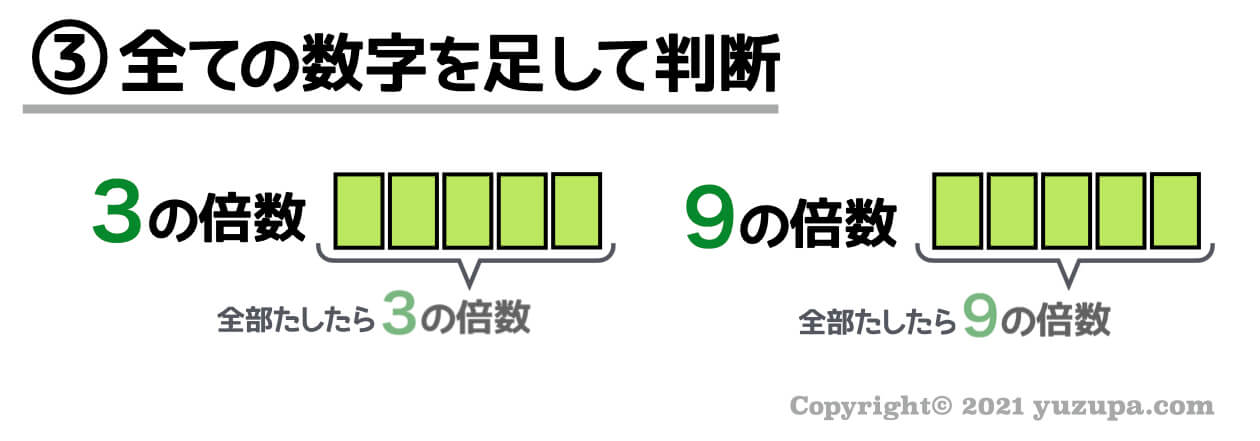
一の位の数、十の位の数、百の位の数…と全て足して出てきた数字が３の倍数であれば、その数字は３の倍数と判断できます。

同様に、全ての位の数字を足して出てきた数字が９の倍数であった場合は、その数字は９の倍数であると判断できます。

こちらも具体例を見てみましょう。

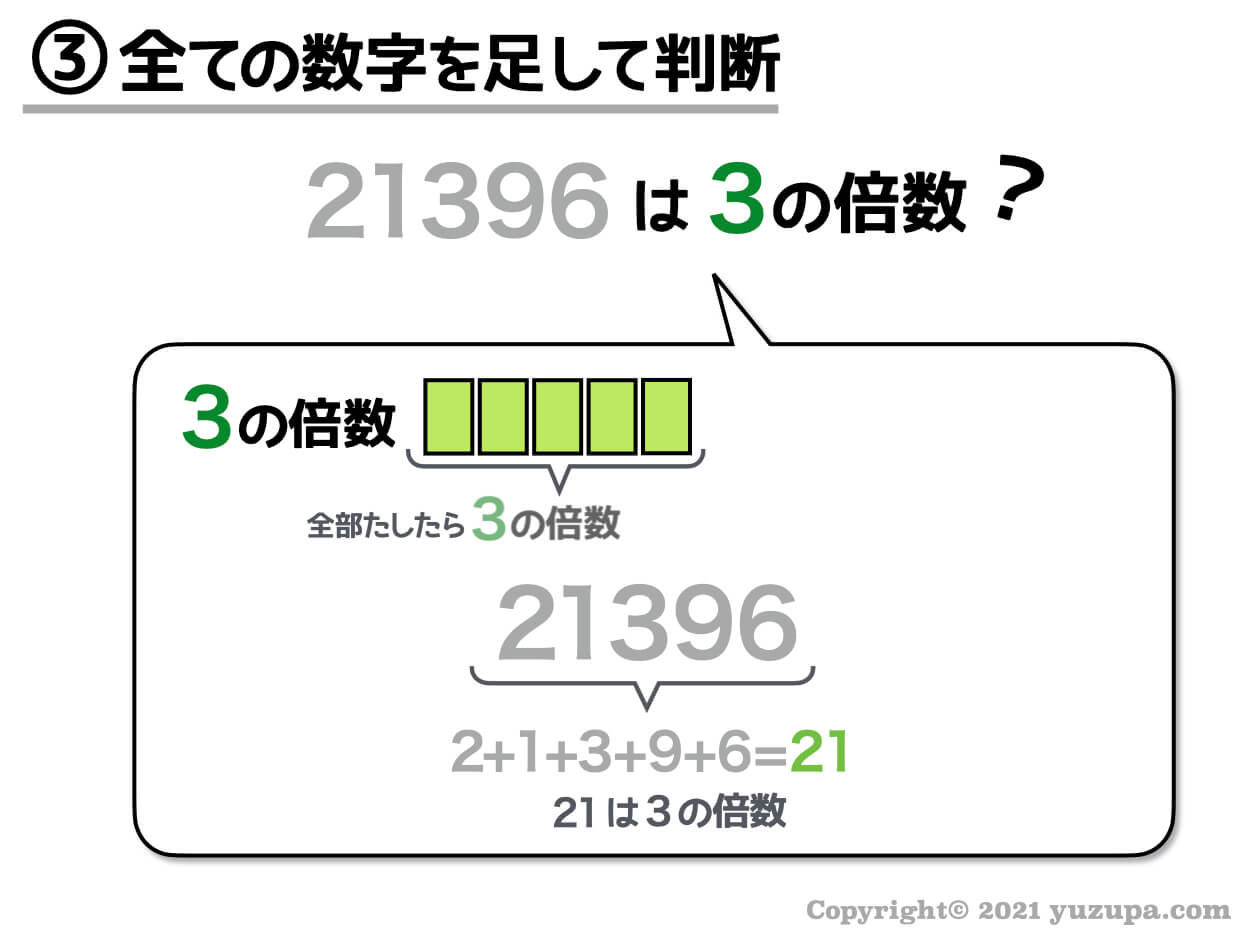
21396という数字。全ての位の数字を足してみると…21になります。21は３の倍数なので、21396という数字も３の倍数であると判定できますd(^_^o)

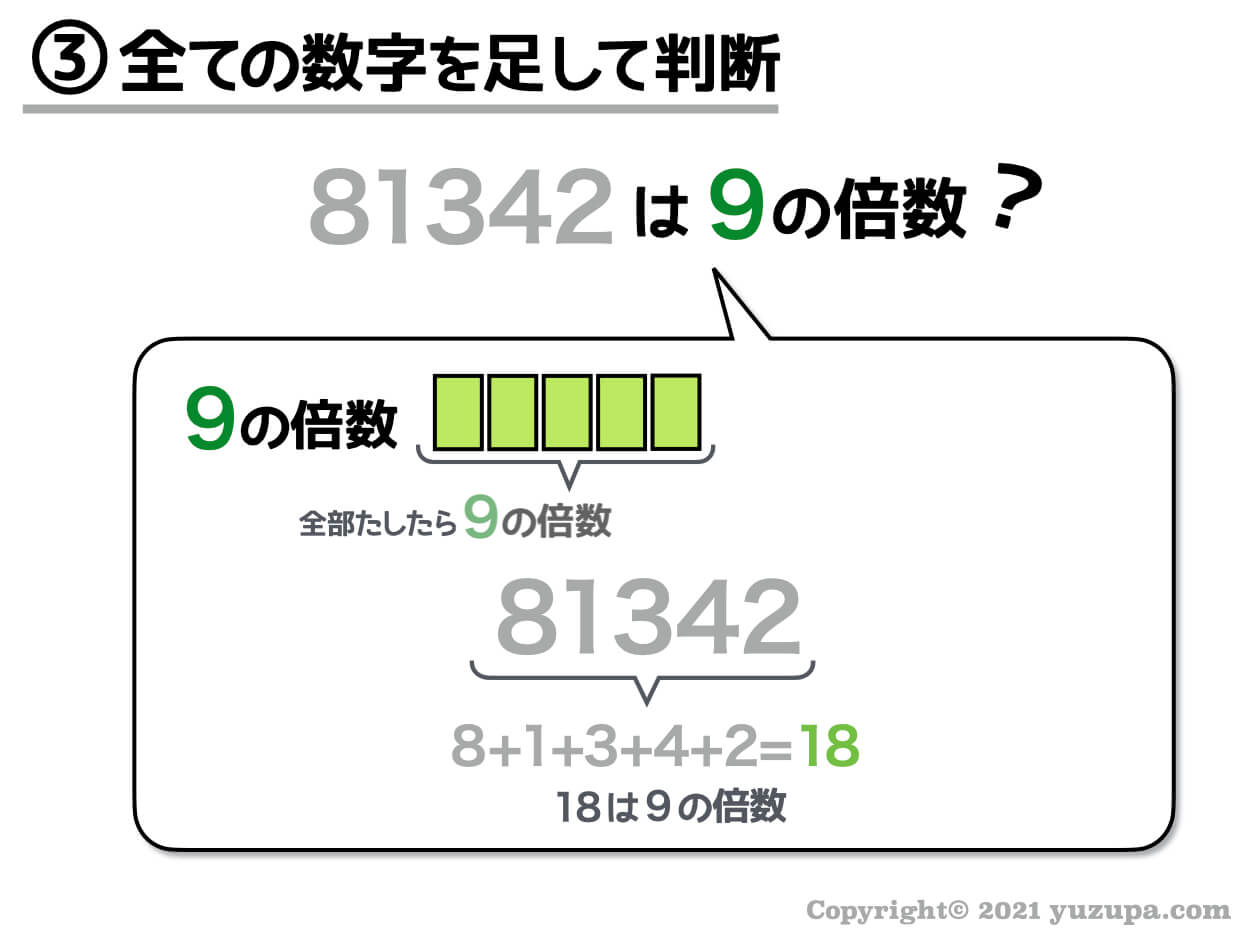
81342という数字。こちらも同様に全ての位の数字を足すと18になりますね？ 18という数字は9の倍数です。ですので81342も９の倍数であると判定できます。

 

３種類の倍数の見分け方は理解できましたでしょうか？

それでは最後に、倍数を調査する方法としては、万能の最終手段である ”素因数分解” についてご紹介しますd(^_^o)

 

万能な倍数調査法は”素因数分解”

素因数分解とは？

本題に入る前に ” 素因数分解 ”についておさらいしましょう。

素因数分解をザックリと説明するならば… 数字をこれ以上分解できない最も細かい数 (つまり素数) に分解すること！

 

例えば60であれば 上記のように分解できます。

どんな数字でも必ず最も細かい数字である素数の掛け算の形に表すことができますd(^_^o) 

 

素因数分解をすると何の倍数かわかる

数字を素因数分解して ”素数の掛け算” の形にしておけば、その数が何の倍数なのか…手にとるように分かるようになりますd(^_^o) 

こちらも具体的な例を見てみましょう！

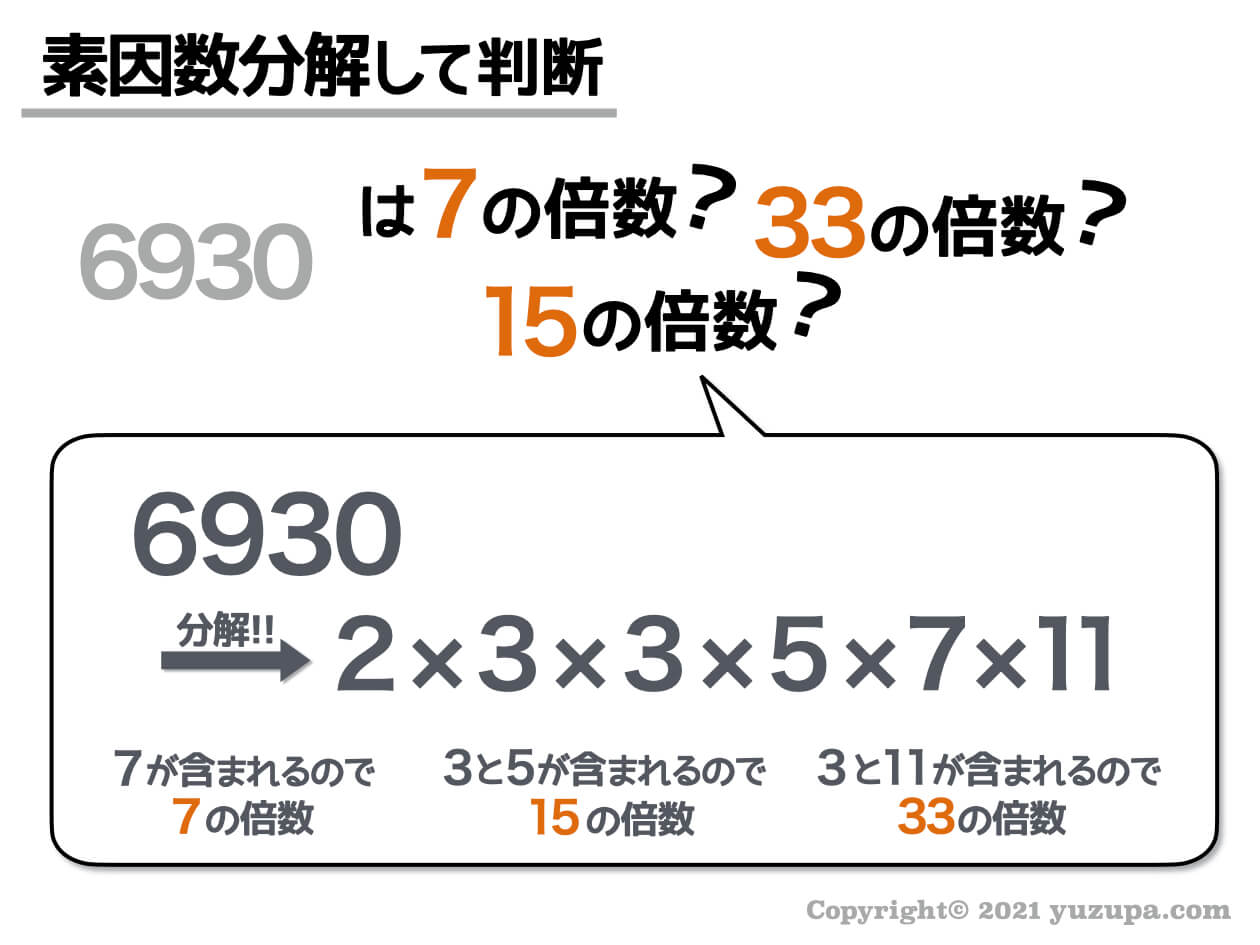
6930という数字。この数字は7の倍数でしょうか？15の倍数でしょうか？ 33の倍数でしょうか？

いちいち割り算をしていたら日が暮れてしまいますね(-_-;)

そんな時は素因数分解をして調査する方法が手っ取り早いです。素因数分解をした結果、上記のように分解できます。

6930を “素数の掛け算”の形にすると…7が含まれていますね？ですから6930は7の倍数であることが分かります。

さらに…3と5も含まれるので15の倍数であり、3と11も含まれているので33の倍数でもあります。いくらでも倍数が調査できます。

 

素因数分解はその数字が何の倍数であるのかを調べるのに有効です。詳細は以下の記事からどうぞd(^_^o)

参考：素数とは？簡単に分かりやすく！イメージでおさえろ

 

まとめ

今回は ”倍数の見分け方” についてまとめました。ポイントは見分け方といっても大別すると３種類に分けられること！ 

３つのパターンへ分類して上記のようにおさえておくと、混乱せずに使いこなすことができます d(^_^o)

そして倍数を調べるのに万能な”素因数分解”もお忘れなく！

 

印刷用のPDFは以下からダウンロードできます。必要な方は是非ご利用ください！