中学受験：場合の数の基本パターンを全網羅！ 道順問題編

地図タイプによって解き方を変えろ！条件は 経由地/通行止/往復 の3種類！

こんにちは。かるび勉強部屋 ゆずぱ です。

読者の方々からもリクエストの多い場合の数… 今回は道順問題編です_φ(･_･ それにしても… 場合の数の問題が苦手な子供が多い 模様です(>_<) その原因はどうやら以下のとおり…。

場合の数とは”全て可能性を数えること”
その数え方が多岐にわたりモヤモヤするから…

 

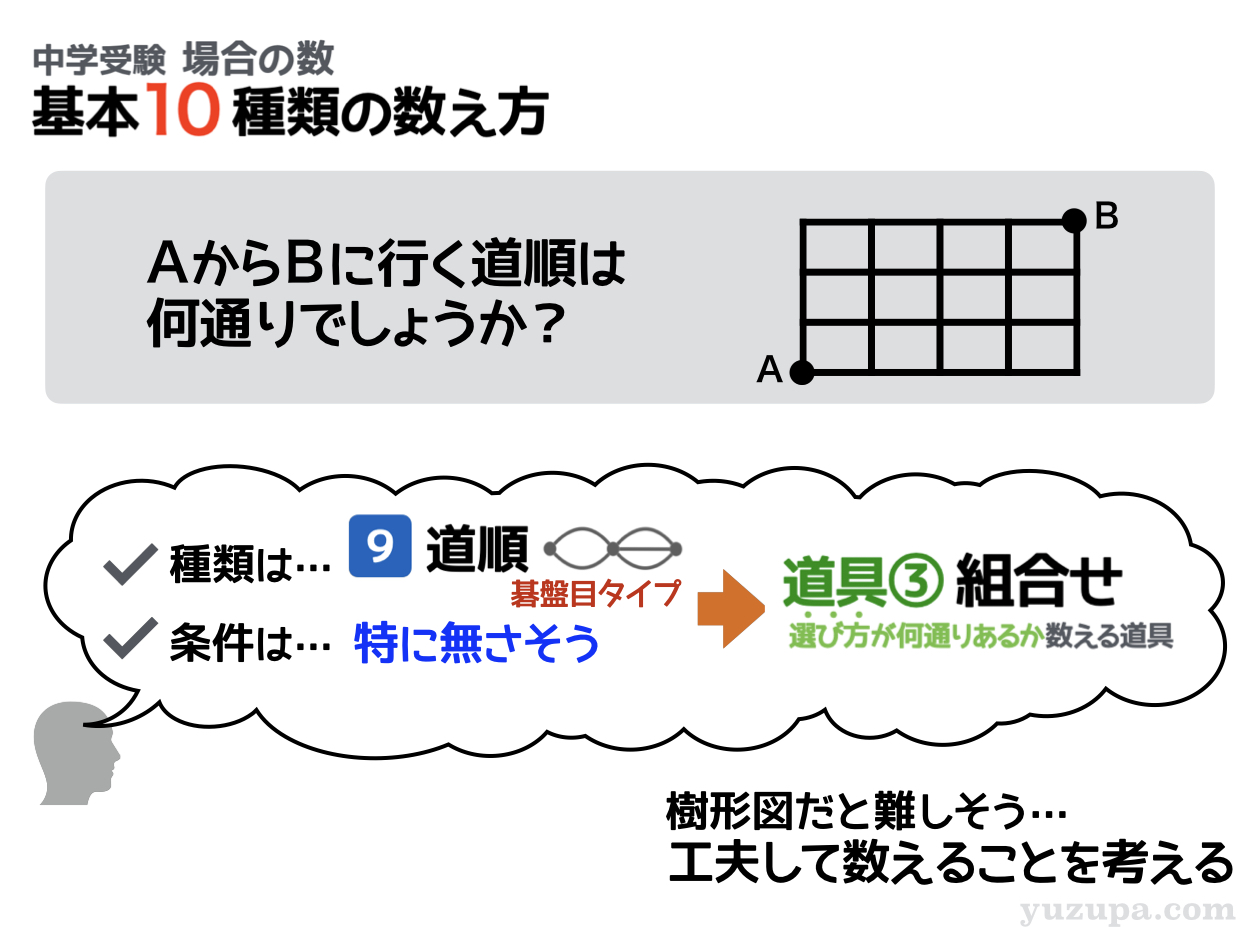
数え方の全体像が分からずモヤモヤする。そうであれば 全体像を勝手に決めちゃえば良いっ∑(ﾟДﾟ) 中学受験であれば… 基本的な10種類の数え方を全体像として 考えれば概ね攻略できます！

そして…実際に”全ての可能性を数える”ときに、頻繁に使う道具があります。代表的な３種類の道具があり、これらの道具の使い方をマスターすることも超重要 です d(^_^o)

本題の道順問題の前に… 場合の数の全体像をオサライします。具体的な問題の解説は第２項へお進みください d(^_^o)

 

おさらい…場合の数には３つの道具がある

道具を使い”全ての可能性を数える”こと

”場合の数問題” の全体像をご覧ください。

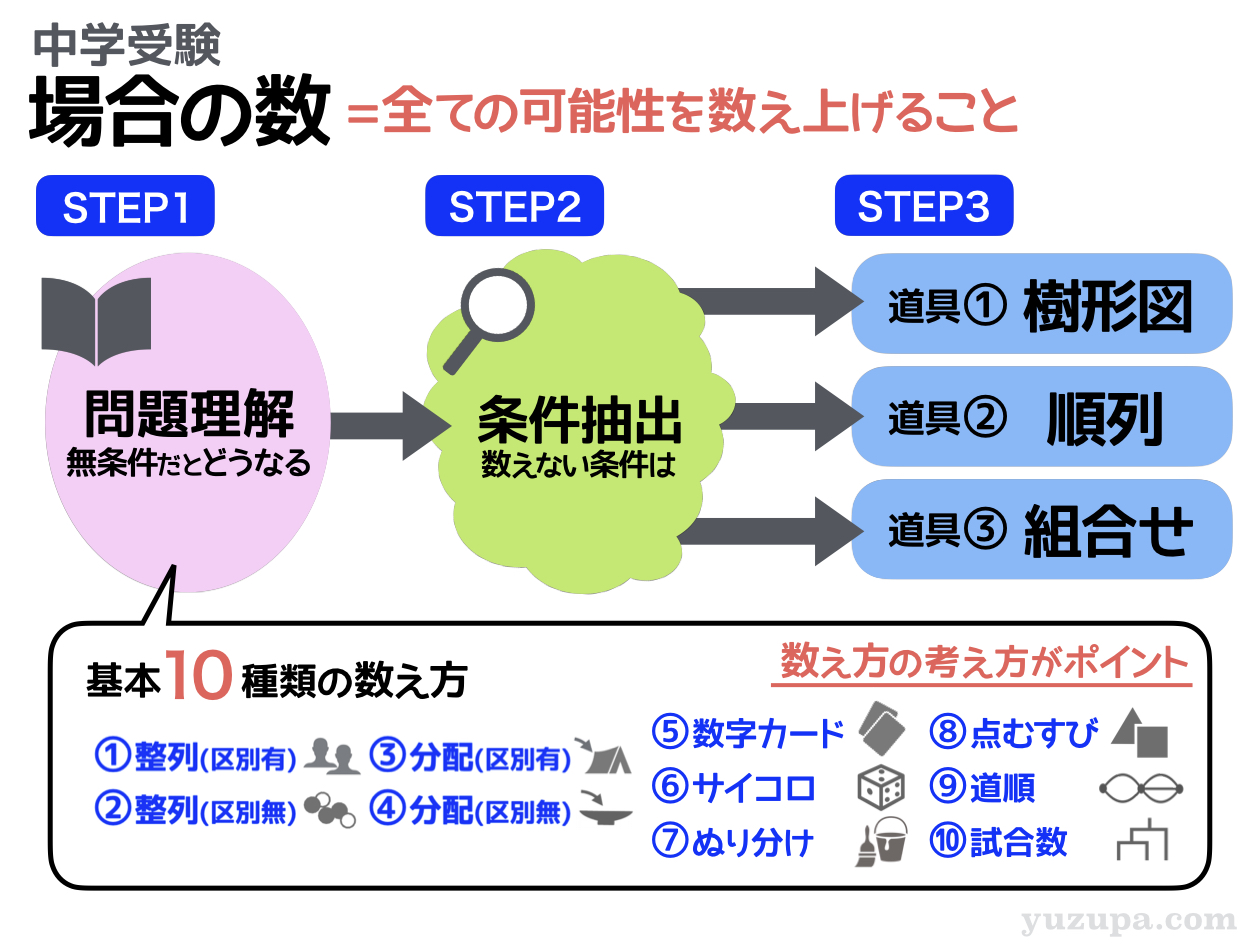
場合の数の問題というのは ズバリ”全ての可能性を数えあげる”という問題 のこと。正しく問題を解くには以下の３つのステップを着実にこなすことが最も近道です。 

STEP1では、問題文を読んで”いったい何を数えたらよいのか”をしっかり把握します。その際に役に立つのが”基本的な１０種類の数え方”です。まずは基本パターンを考えましょう。

STEP2では、条件を理解します。偶数”だけ”数えなくてはいけなかったり、男子が両端にくる並び方”だけ”数えなくてはいけなかったり、入試の問題には必ず条件がついてきます(^_^;)

STEP3でいよいよ数えます。数えるには必ず道具を使います。樹形図はオールマイティですが、通り数の多い問題には使えません。樹形図をサボる道具として”順列”と”組合せ”があります。

 

３種類の道具を使って数える

３つの道具とは”樹形図”と”順列”と”組合せ”のことです。

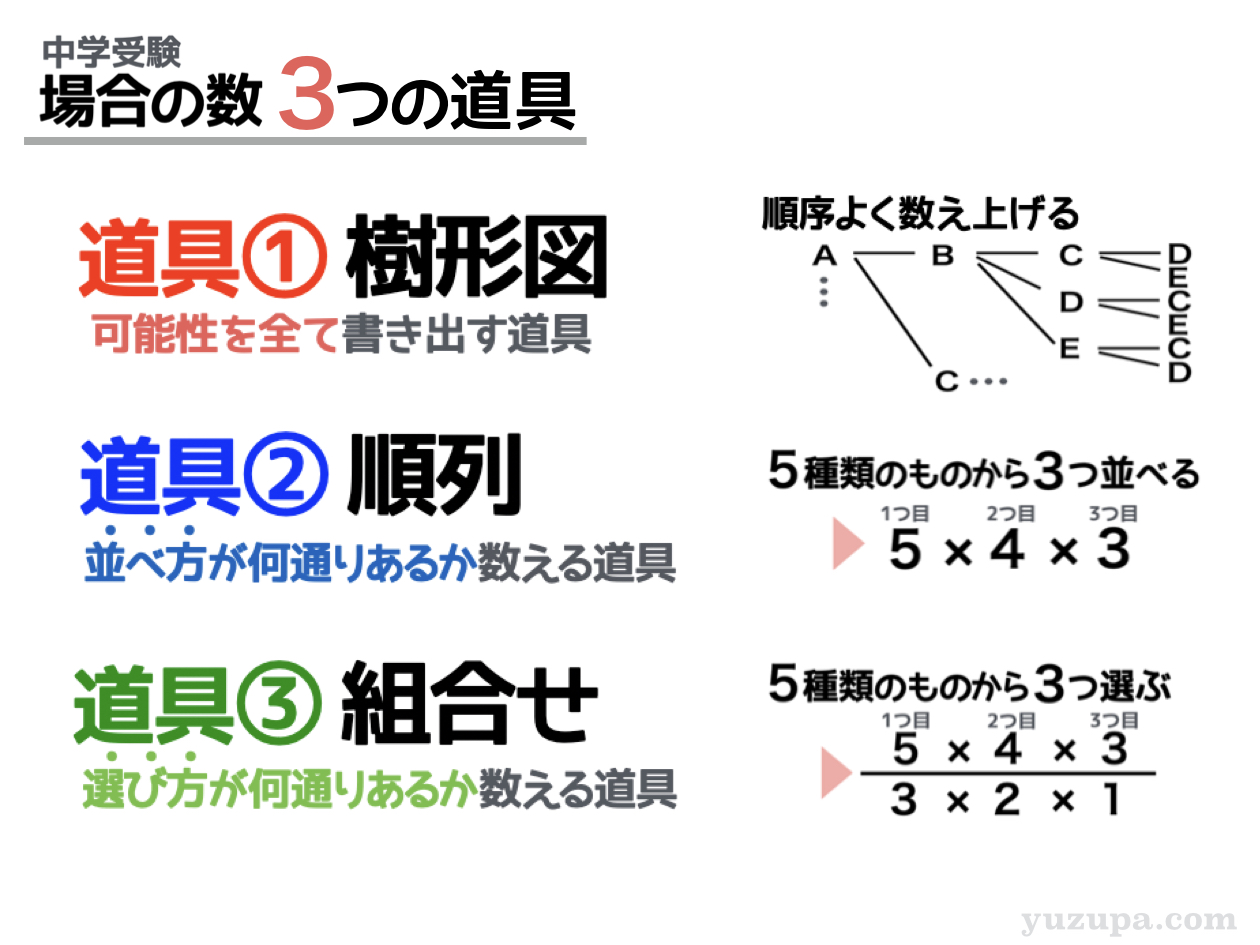
道具①樹形図は何でも数えられるオールマイティな道具です。どうやって数えたら良いか迷ったらまずは樹形図で数え始めてみてもよいでしょう。書いていているうちに数え方のヒラメキがあることもあります。

道具②順列は並べ方が何通りあるか数える道具です。シンプルに何かを並べる場合の数を求める問題の他に、並べること以外の題材を並べる行為に置き換えて数えることもよくあります。

道具③組合せは選び方が何通りあるか数える道具です。例えば１０種類のケーキがあり、３つだけ食べて良いと言われたら何を選びますか？ この道具を使えば選び方が何種類あるか分かります。

 

場合の数の全体像を確認したい場合は、ぜひ以下の記事をご参照してみてください。スッキリしますd(^_^o)
参考：場合の数が苦手…３つの道具を使い10種類の数え方をマスターせよ

 

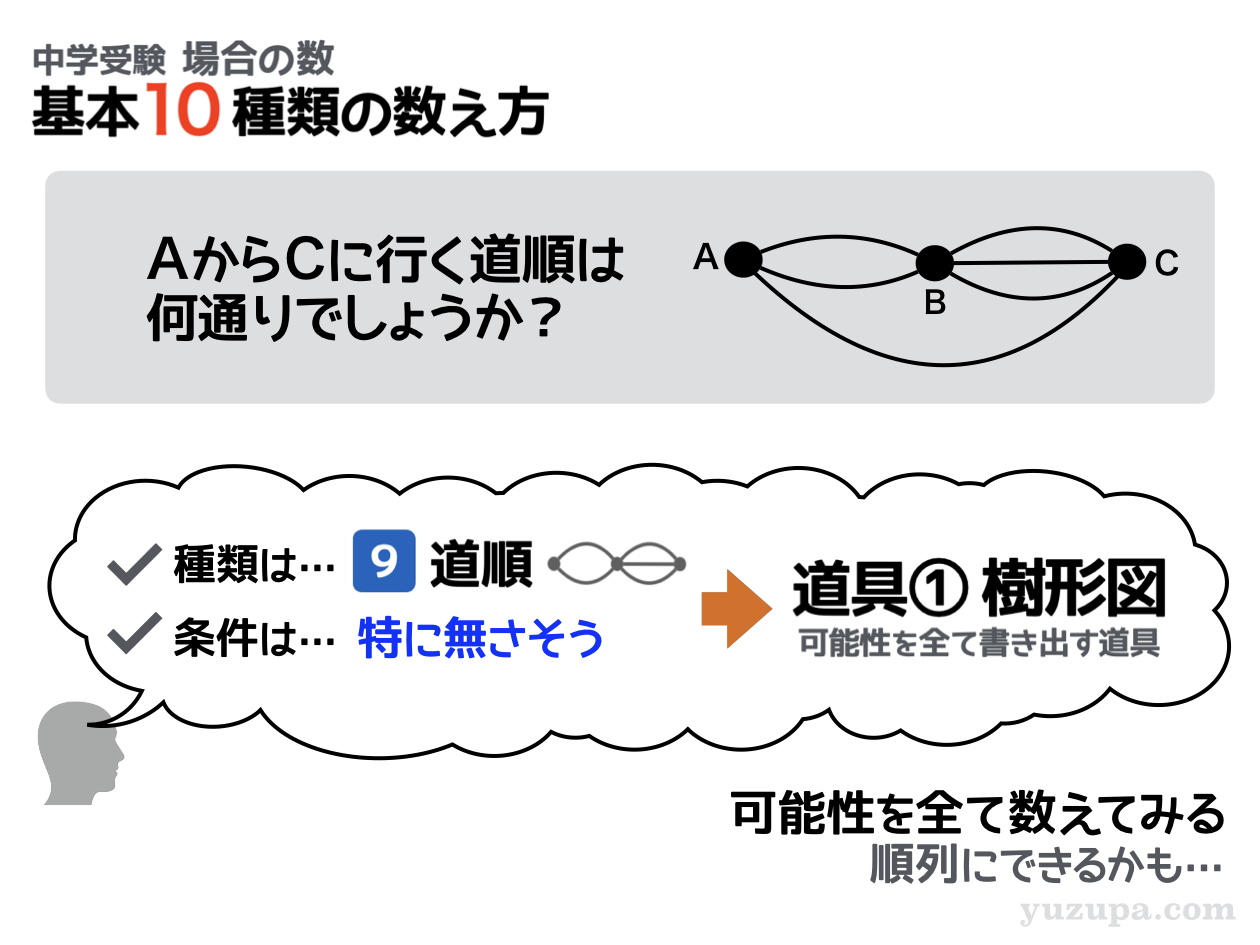
道順の場合の数の問題を全網羅

道順問題の全体像

道順の問題とは スタート地点からゴール地点まで移動するのに複数の行き方 がある問題。どの道を使ってゴールまで行くのか？その 道順を数えなさいという問題 です∑(ﾟДﾟ)

シンプルな問題もありますが
経由地があったり…通行止めがあったり…します(-_-;)

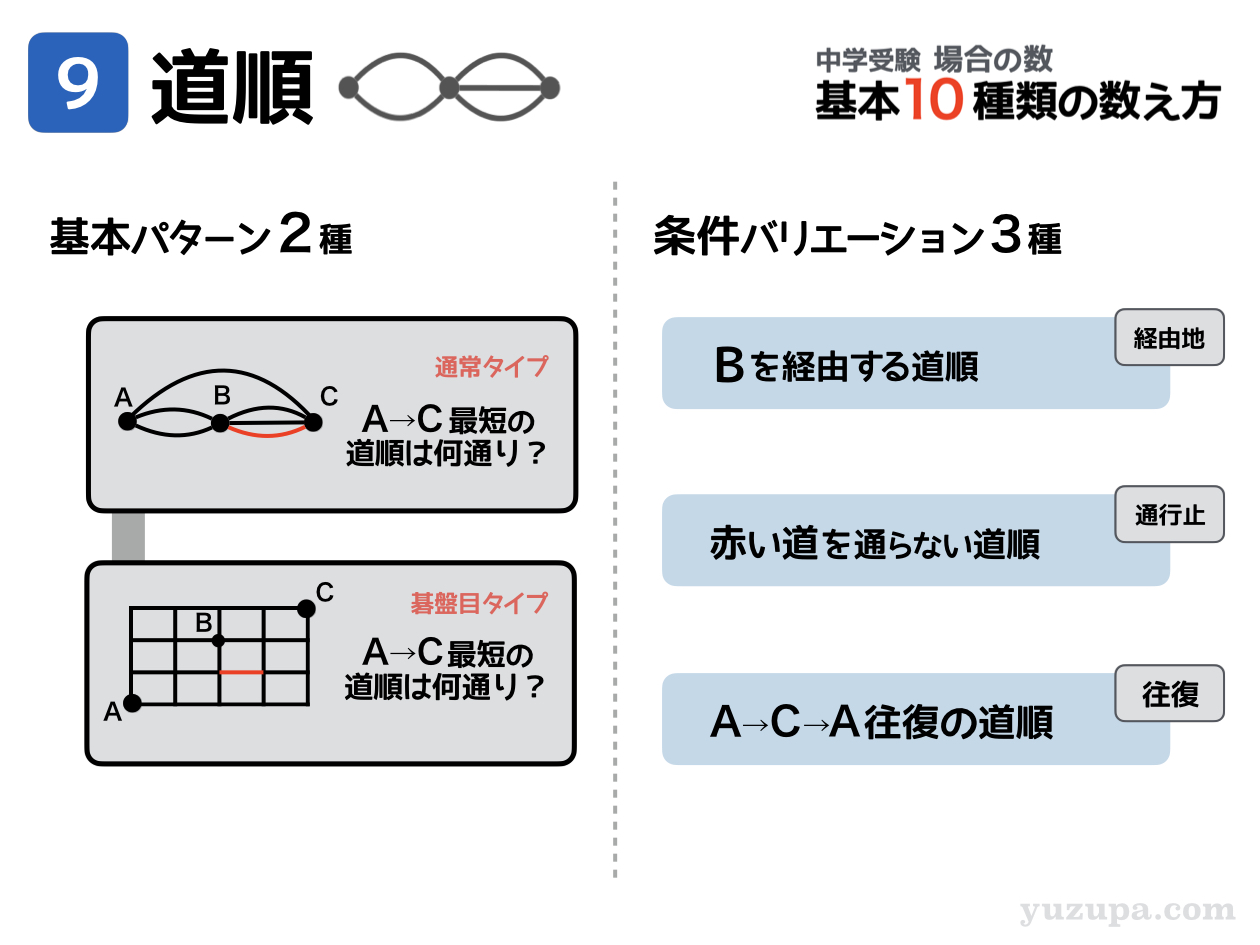 基本パターン

まずは… よく出る代表的な２つの基本パターンをおさえましょう。地図を見てそのタイプを判断します。地図を見るときは”地点”と”通路“がどんな感じでつながっているかに着目しましょう_φ(･_･

(1) 基本タイプ
“地点”と”通路”が特に規則性もなくつながっているパターンです。規則性がなく適当な感じなので、難しく感じるかもしれませんが、これが ”基本タイプ” となります_φ(･_･

(2) 碁盤目タイプ
そして地図が ”京都の街並み” のように、通路が碁盤目状になっているタイプです。碁盤目になっているので”地点”も”通路”も沢山あり数えるのも大変…工夫が必要だ∑(ﾟДﾟ)

もちろん他にも地図のタイプはあります(@_@) ですが…この代表的にな２つのタイプの地図の解き方をマスターすれば、応用的に考えることができますよ_φ(･_･

 

条件バリエーション

地図のタイプは”基本タイプ”と”碁盤目タイプ”の２つの種類をおさえましたが、そこに色々と条件がつきます。カーナビで目的地を設定するときも、条件をつけたりしますよね (^_^;)

よくでるのが３種類の条件です_φ(･_･

経由地：目的地の前にどこかに寄り道をする
通行止：経路の一部が通ることができない
往復　：目的地に行くだけでなく帰りもある

場合の数の道順問題に出会したら…どのタイプの地図をベースにした問題なのか？そしてどの条件がついているのか？その”基本パターン”と”条件バリエーション”のかけあわせを意識せよ！

それでは、具体的な問題を見ていきましょう。まずは２つの基本パターンからいきましょう d(^_^o)

 

道順問題…２つの基本パターン

基本① 地図が基本タイプ 

問題文を読んでみて、道順が何パターンあるかを数えさせる問題であることが分かりますね？ 地図はどうでしょう。Ａ～Ｃの３つの”地点”が６本の”通路”でつながれているタイプですね。

条件はどうでしょうか？“経由地”も“通行止”もなさそうです。そして“往復”の道順を求める問題でもなさそうです。シンプルにＡからＣに行く道順が何パターンあるか数えればよさそうです (-᷅_-᷄๑)

とりあえず樹形図を描きはじめてみる…

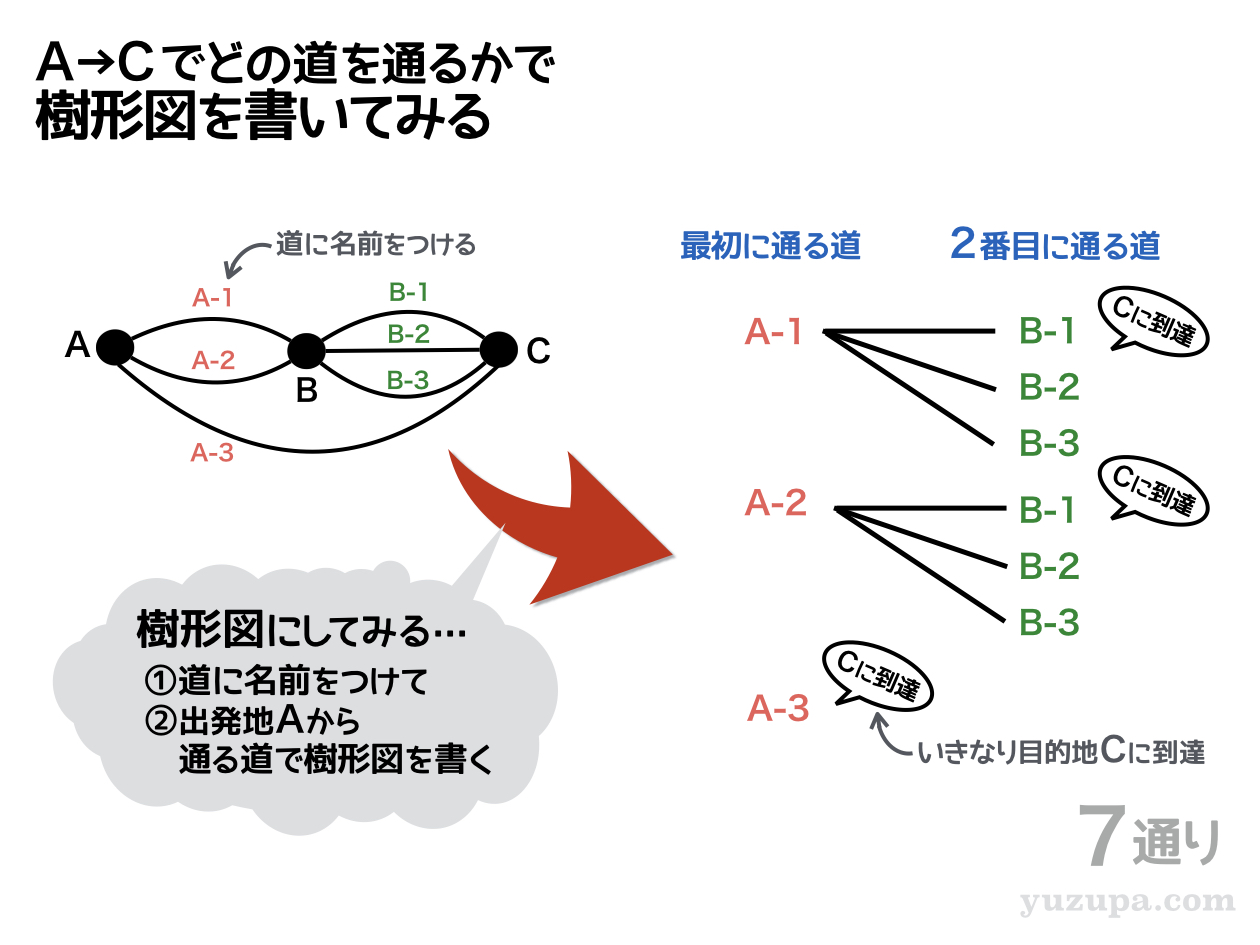
樹形図を描きやすくするために、通路にテキトウに名前をつけちゃい ましょうd(^_^o) 上の図のように、地点Ａから出ている３つの通路にはＡ-１, Ａ-２, Ａ-３… みたいに分かりやすい名前を！

そしてスタート地点である地点Ａから”最初に通る道” “２番目に通る道”…という感じで ゴール地点である地点Ｃに到達するまで樹形図を順序よく漏れなく描いてみます_φ(･_･

これくらいの通路数であれば…
意外にも一瞬で描けちゃいますd(^_^o)

たった２つの通路を通ったところでだいたい目的地である地点Ｃに到達しちゃいます。なので樹形図といってもすぐ描けちゃう。Ａ-３に至っては１つの通路でイキナリ目的地に到達します(･_･;

樹形図より 答えは７通り となります。

でもコレ樹形図を描くのを
ちょっとサボれそうな気がする…Σ(-᷅_-᷄๑)

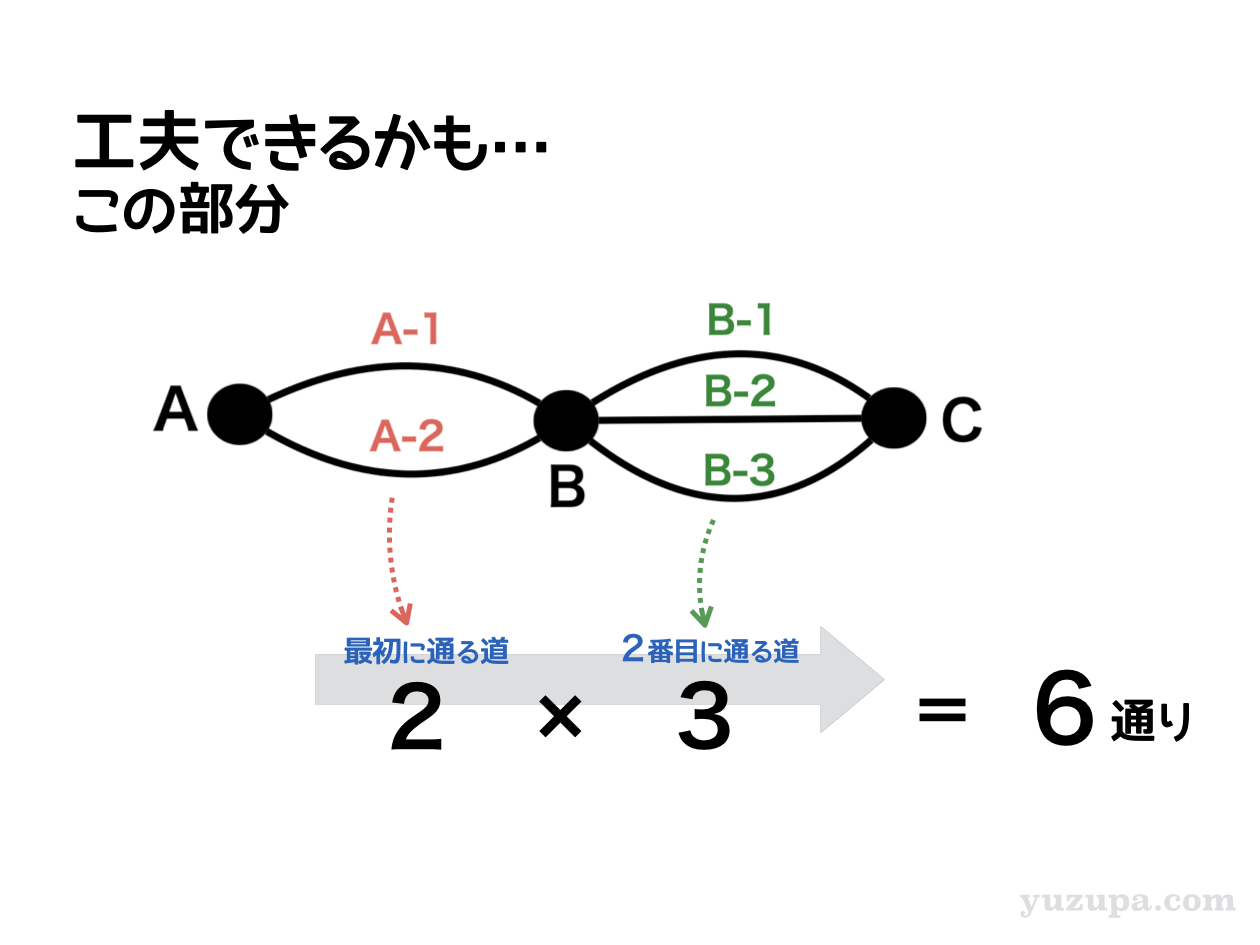
この部分だけ抜き出してみると… わざわざ樹形図を描かずとも、“最初に通る道”が２通り、”２番目に通る道”が３通りなので…かけ算の原理で  簡単に計算し６通り が出てきます。

上記の６通りに加えて、Ａ-３の通路を通る１通りがあるので 答えは７通り であることがパッと分かりますd(^_^o)

参考：場合の数が苦手…３つの道具を使い10種類の数え方をマスターせよ

 

基本② 地図が碁盤目タイプ 

さて今度は地図が ”碁盤目タイプ” の場合です。

問題文を読めば、道順のパターンを数えさせる問題であることが分かり、地図に目を向けると、”通路” が縦と横に等間隔に…京都の街並みのような碁盤目のタイプであることが分かりますねd(^_^o)

条件はどうでしょうか？“経由地”も“通行止”もなさそうです。そして“往復”の道順を求める問題でもなさそうですね。安心してＡからＢに行く道順が何パターンあるか数えれば良さそう_φ(･_･

うぅ…ここまで通路数が多いと樹形図は厳しそう
とはいえ工夫を見つけるためにも樹形図にトライします

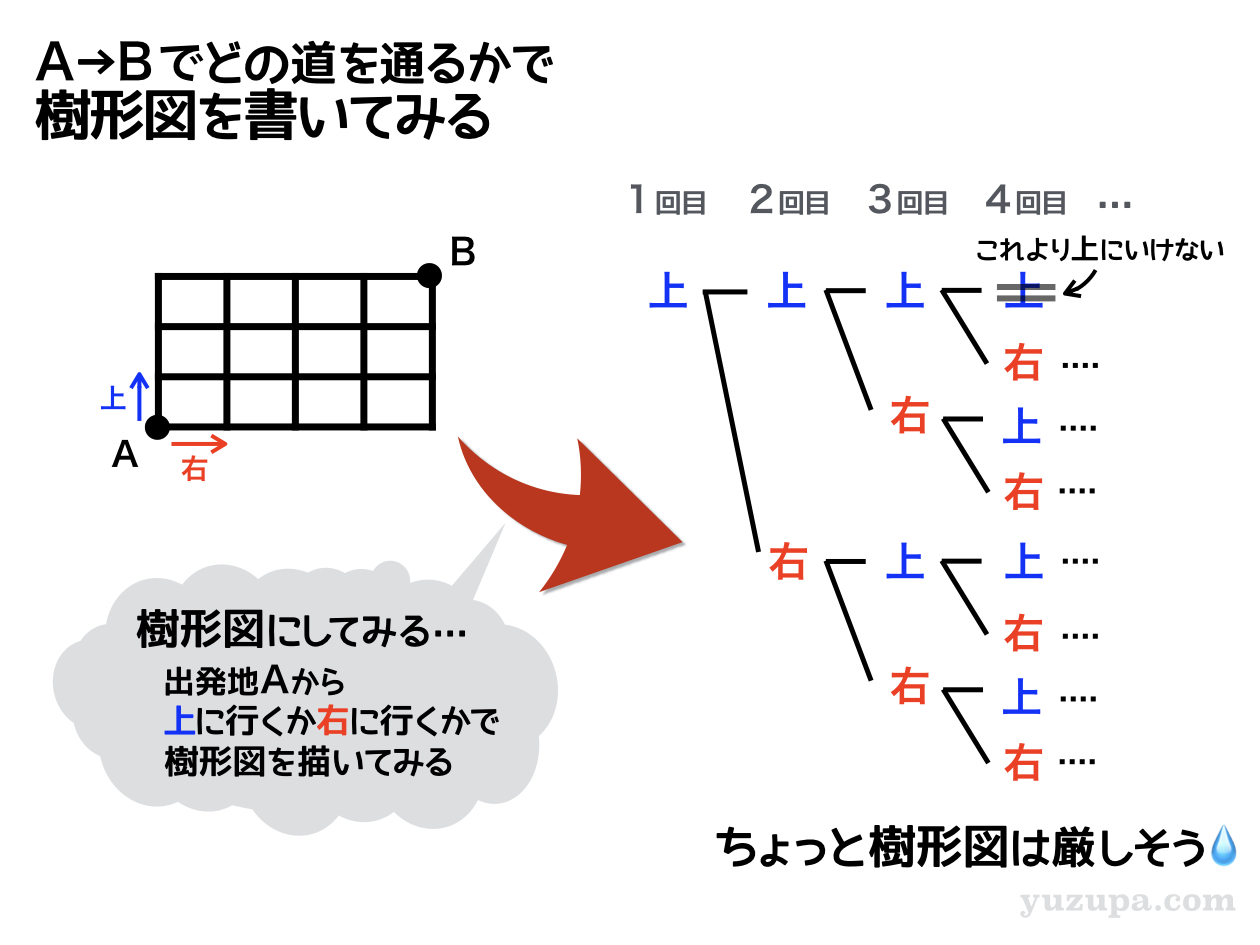
地図が基本タイプと同様に ”１回目に通る道” ”２回目に通る道”  ”3回目に通る道”…という感じで樹形図を 描いていきます。でも…これだけ通路があると通路に名前をつけるのは無理 (>_<)

なので…“上方向” か “右方向”かで樹形図を描きます！

１分～２分ほど樹形図を描いていると、膨大な数になるのでコレは無理だと感じることでしょう。仮に描けたとしてもこの規模になると途中でミスが発生して数え間違えることも…

そこで…工夫することを考えますΣ(-᷅_-᷄๑)

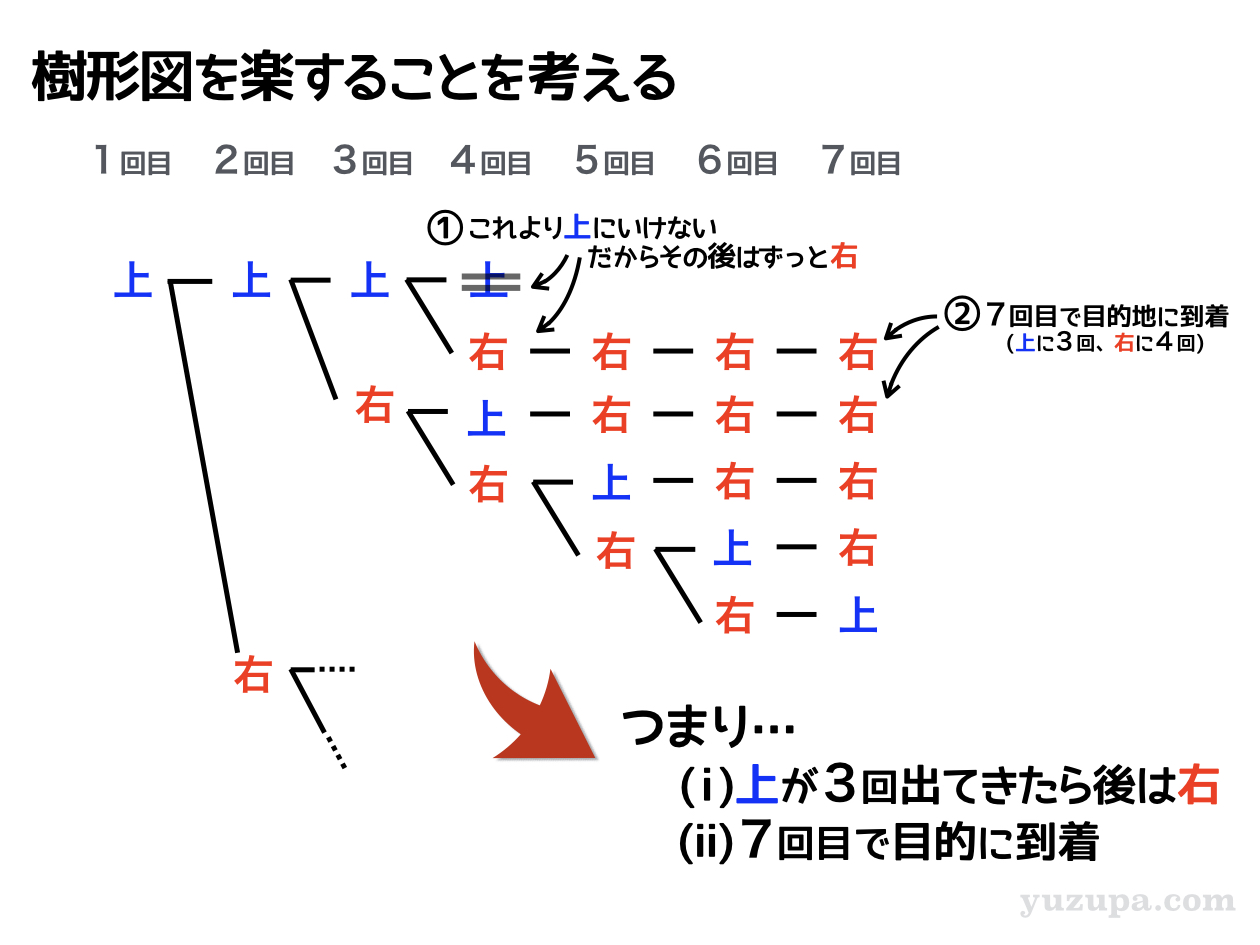まず 樹形図を描いていて”気付いたこと” をまとめます

ひとつ目は… ”上“は最大３回しか登場しない ということ！この問題では 縦３通路 × 横４通路の地図 なので、当然 ”上”には３回しか行けない。残りはぜんぶ ”右” になりますね d(^_^o)

ふたつ目は… 必ず７回目で目的地に到達する ということ！この問題では 縦３通路 × 横４通路の地図 なので、順番はどうであれ、“上” に３回、“右”に４回移動すると必ず目的地に着きます ∑(ﾟДﾟ)

 

樹形図だと見にくいので横方向に並べてみます

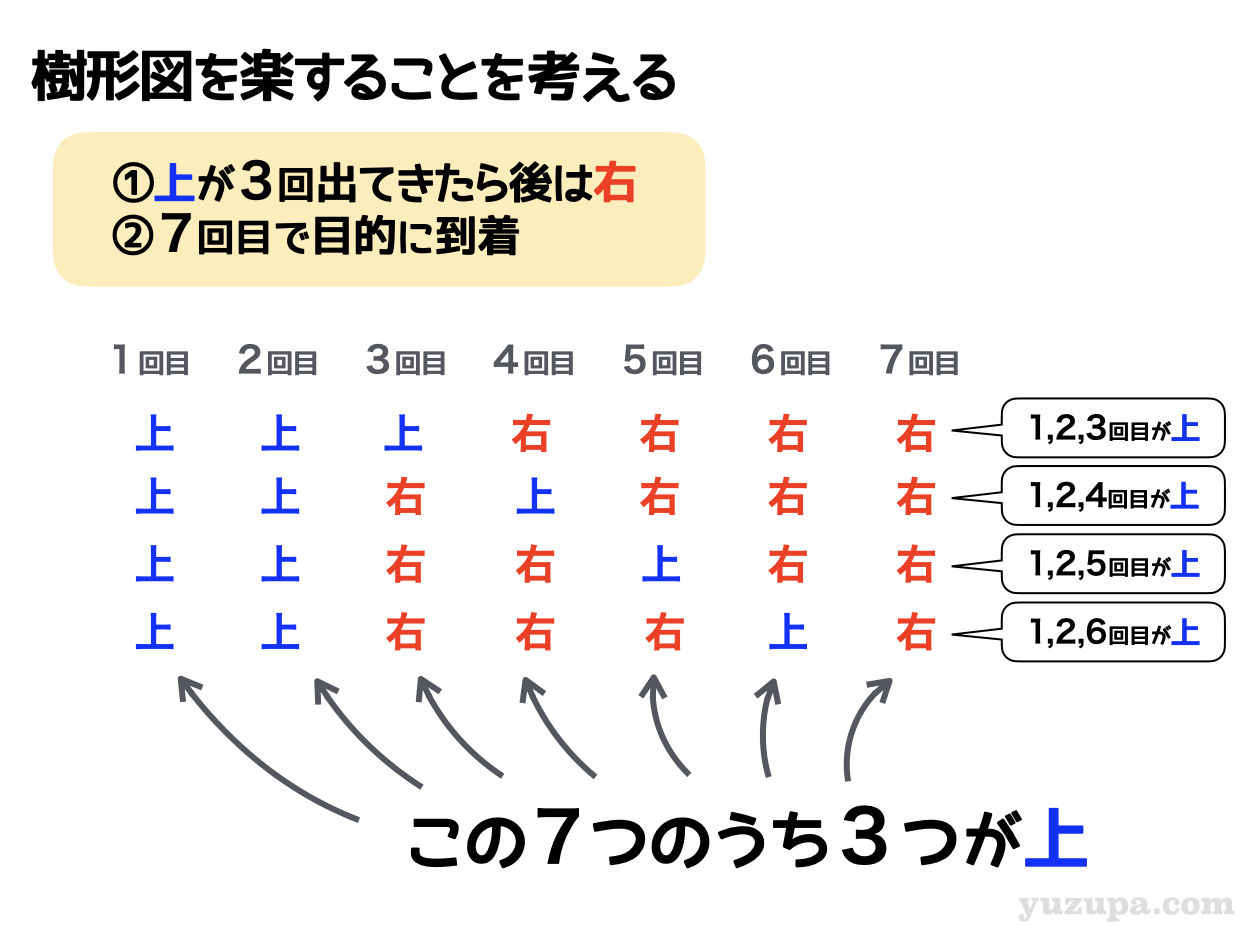
こんな感じになりました_φ(･_･

こうやってみると、どのパターンを見ても１回目～７回目の中のどこかに”上”が３回登場しているのが分かりますね_φ(･_･ 

一段目の行き方であれば…１回目と２回目と３回目が ”上”、四段目の行き方であれば…１回目と２回目と６回目が ”上” ですね。

コレって、１回目～７回目の中から”上”になる場所を３つを選ぶ選び方と同じという事になります ∑(ﾟДﾟ)

ここまでくれば…道具③組合せを使って計算するのみ！

7つの中から3つを選ぶ選び方は ”道具③ 組合せ”を使えば簡単に計算することができますね。答えは35通りとなります。

碁盤目タイプの道順問題…ポイントは２つですd(^_^o)

(1) 上には最大何回いくことができるか？
(2) 何回目で目的地に到達するか？

この２つだけ整理できれば組合せで計算できますd(^_^o)

 

条件バリエーション

基本的な道順の数え方をマスターしたところで…いよいよ条件バリエーションに入りますd(^_^o) 道順の問題でとにかくよく出てくる条件を３つだけ おさえておきましょう_φ(･_･

どんな条件があったでしょうか…オサライです。

経由地：目的地にいく前に寄り道をする
通行止：経路の一部が通ることができない
往復　：目的地に行くだけでなく帰りもある

さっそく、ひとつずつ見ていきましょうo(^-^)o

 

経由地：目的地の前に寄り道する 

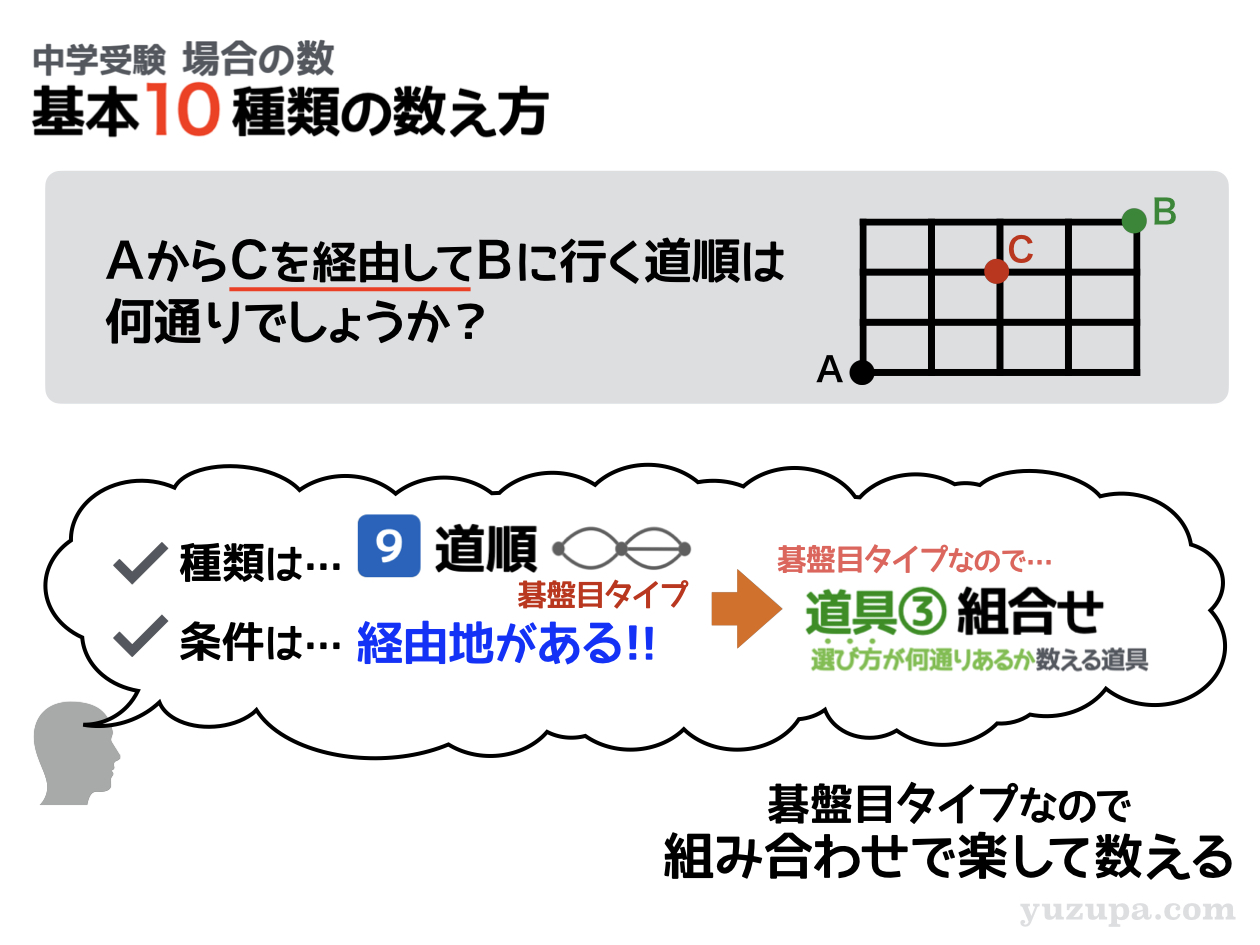
この問題を読むと…地図のタイプは”碁盤目タイプ” ですね。碁盤目タイプなので 道具①樹形図ではなく、道具③の組合せを使った方が良さそうです_φ(･_･

また “Ｃを経由して” と書かれている∑(ﾟДﾟ) これは目的地Ｂに行く前に必ず地点Ｃに寄り道するという意味。すべての経路の中からＣ地点を通る経路だけを数えろってコトですd(^_^o)

言い換えると以下のようになります

スタート地点Ａから経由地Ｃに行って…そのあと経由地Ｃから目的地Ｂにいく道順を数えろということです。それぞれの道順が何パターンあるか数えて掛けてあげれば良さそうです。

それぞれの道順を数えてみましょう_φ(･_･

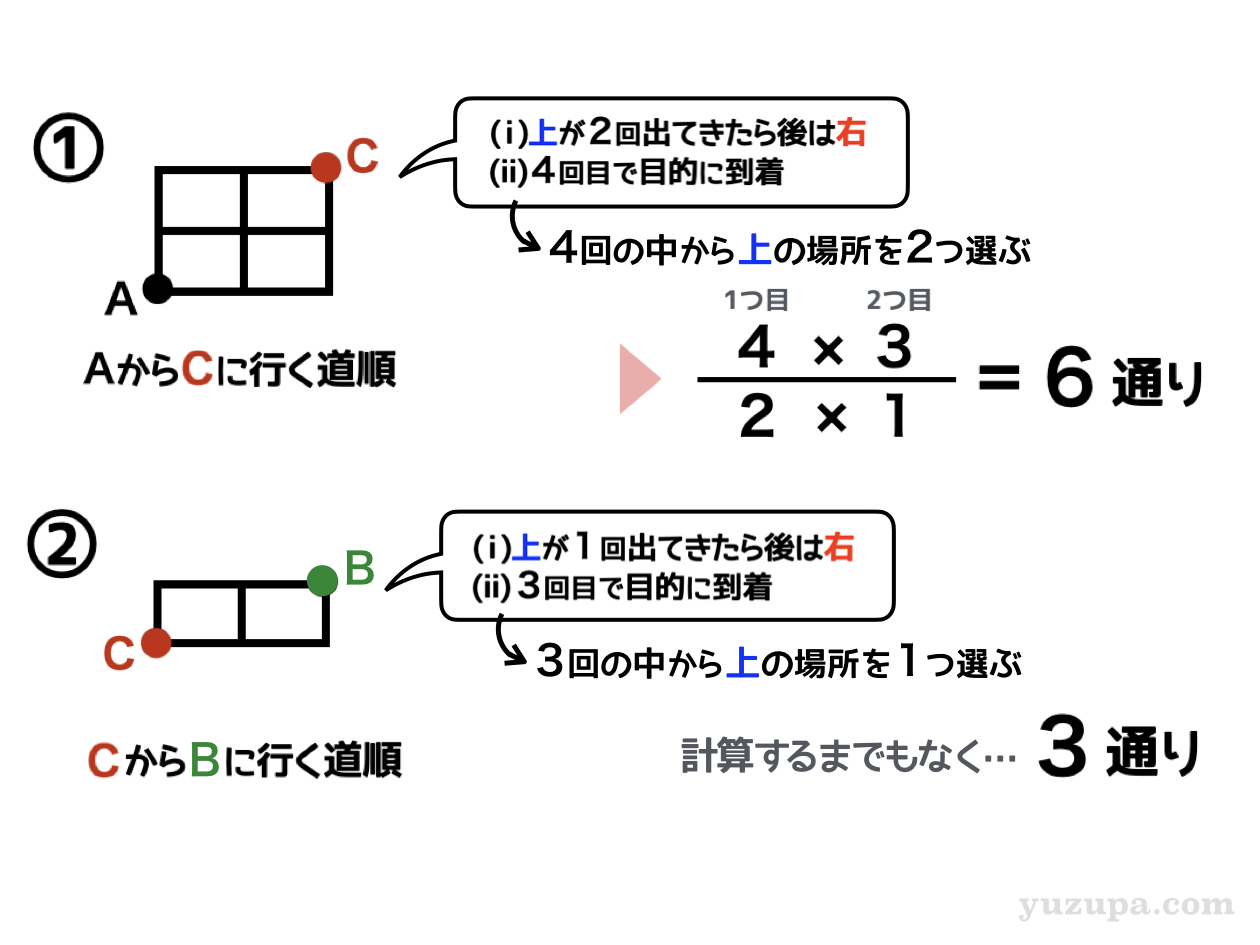
① Ａ→Ｃの道順を数える

地点Ａと地点Ｃを含む部分だけ切り出してみると…２×２の碁盤目の地図になります。コレって条件のない碁盤目タイプの基本パターンと同じやり方で数えられそうです(･_･;

碁盤目のふたつのポイントを覚えていますか？

(1) 上には最大何回いくことができるか？
(2) 何回目で目的地に到達するか？

地図は２×２の碁盤目なので、上には最大２回まで 行くことができます。そして ４回目で目的地に到達 できる地図です。計算は４回の中から上の場所を２つ選びかたなので６通りとなります。

 

② Ｃ→Ｂの道順を数える

同じように地点Ｃと地点Ｂを含む部分だけ切り出してみると…今度は１×２の碁盤目の地図 になります。上には最大１回まで 行くことができ、３回目で目的地に到達 できる地図ですね。

計算は３回の中から上の場所を1つ選ぶ場合の数。これは計算するまでもなく３通りとなりますね_φ(･_･ 

 

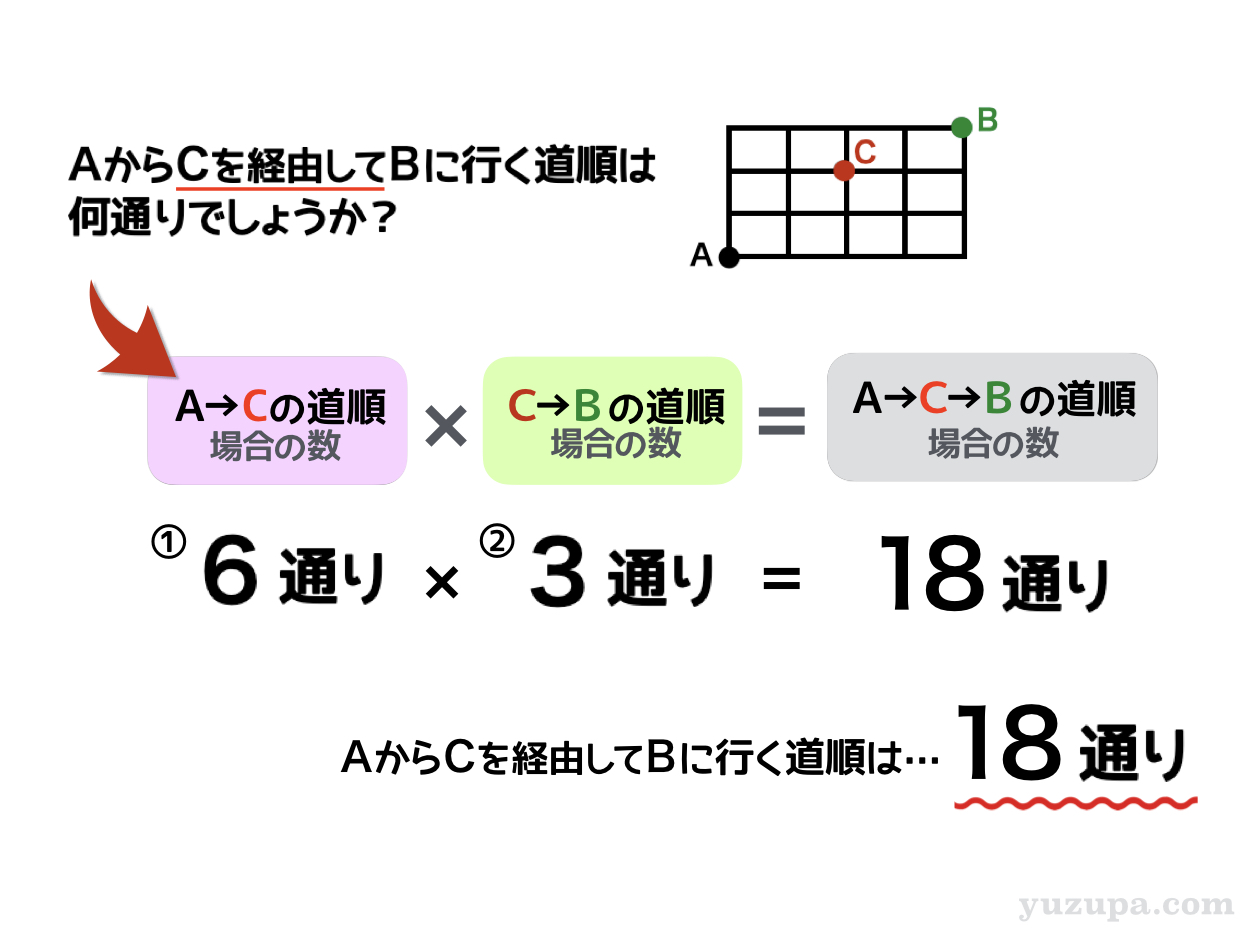
結果として…地点Ａから地点Ｃを経由して地点Ｂまでの行き方は 全部で18通り になります。

経由地がある場合の問題をオサライしましょう。

考え方はシンプル…。スタートから経由地まで、経由地からゴールまでに２つに分けて考える！ 以上です o(^-^)o

 

通行止：経路の一部が通れない 

この問題を読むと、地図のタイプは同じく”碁盤目タイプ” ですね。碁盤目タイプなので 道具③組合せ を使うことを考えます。

今度は “赤通路を通らずに” と書かれています∑(ﾟДﾟ) これは赤通路は ”通行止め” という意味。この赤通路を通る経路は数えてはいけないってコトですd(^_^o)

言い換えると以下のようになります。

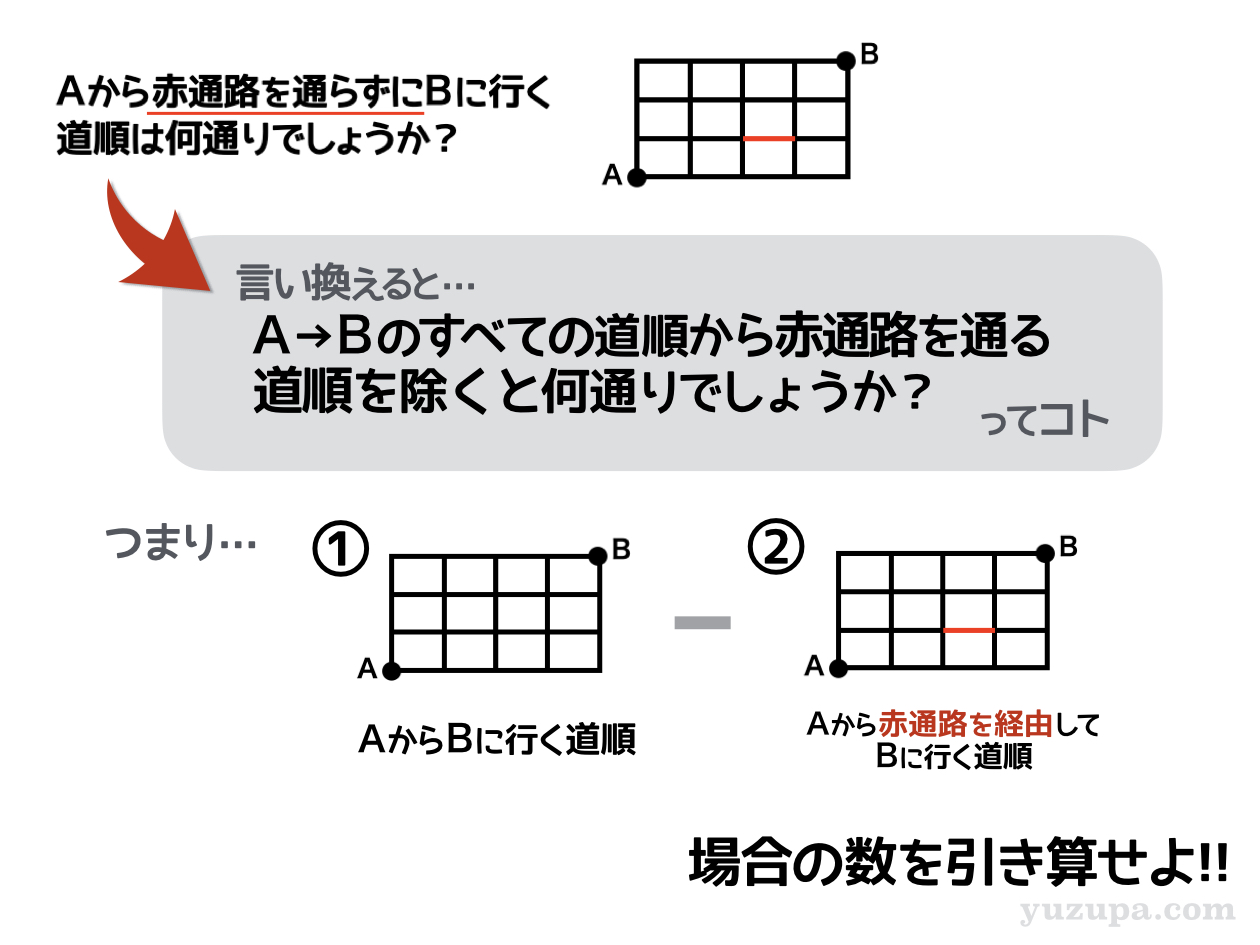
スタート地点 Ａから目的地Ｂへのすべての道順から、赤通路を通る手順を除くと何通りか数えろと言い換えることができます。本来は通れない赤通路を通る経路を数えるというのがカギ です。

それぞれの道順を数えてみましょう_φ(･_･

ちょっとその前に…
赤通路を通る道順ってどうやって数えればよいんだ(･_･;？ 

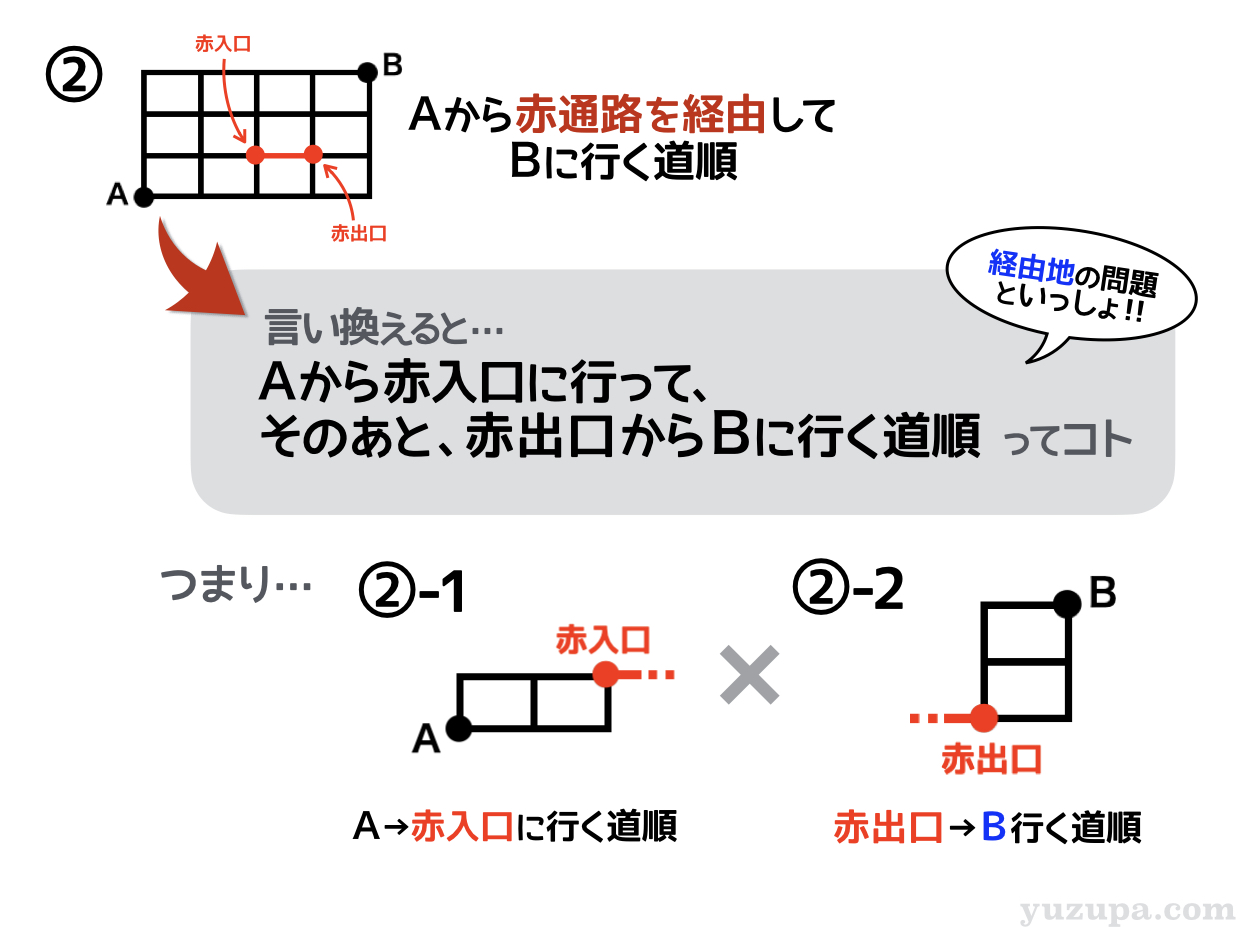
赤通路を経由する道順を数える。コレって経由地の条件と似ている∑(ﾟДﾟ) まさにその通り！

“地点”であろうと”通路”であろうと”経由地”は”経由地”！

ただ経由地が”通路”の場合は、その通路の”入口”と”出口”というものを考えます。そして…スタート地点から経由地の入り口、経由地の出口からゴール地点の２つに分けて考えましょう！

ではひとつずつ計算してみましょう！

 

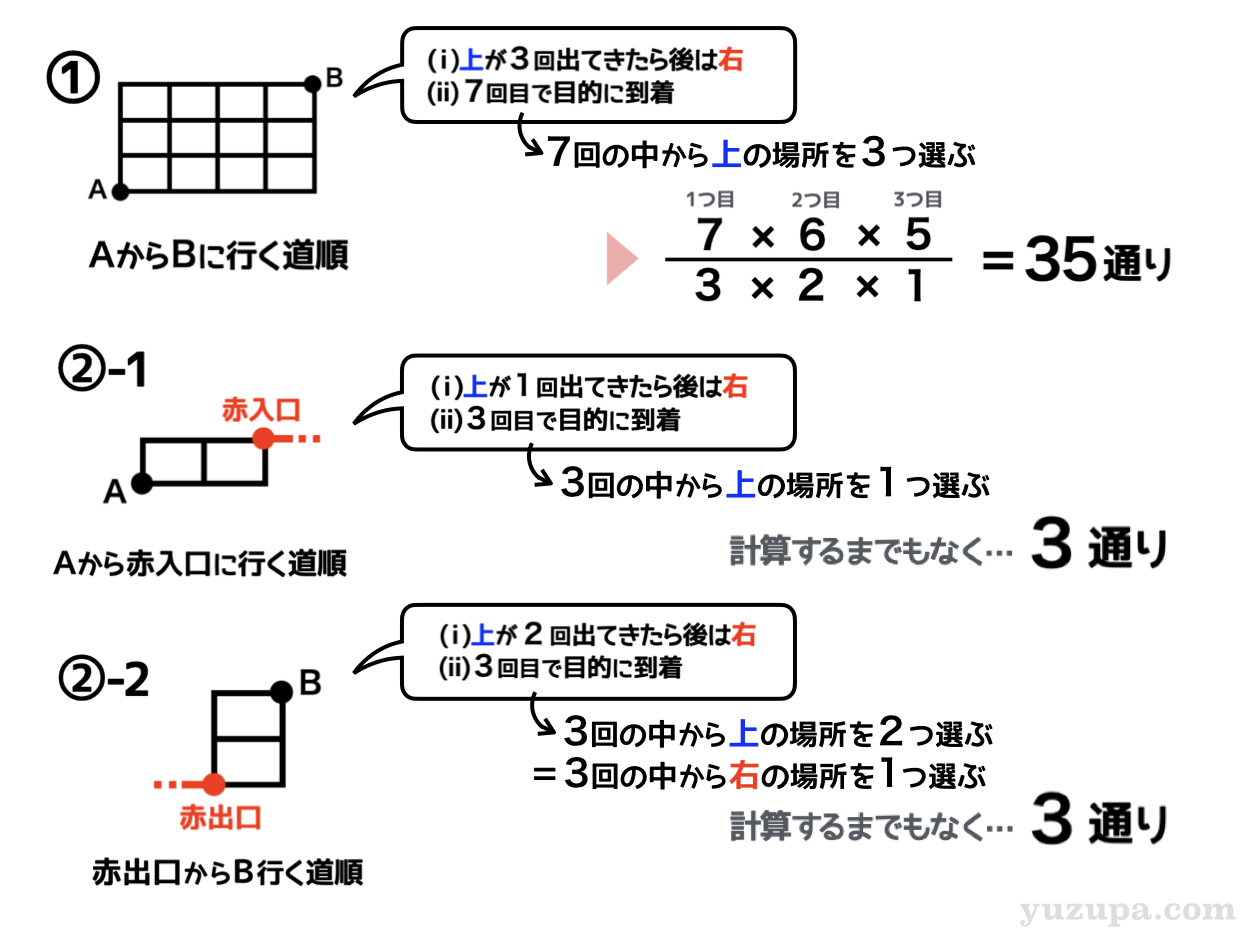
① Ａ→Ｂの道順を数える

地図は３×４の碁盤目なので上には最大３回まで行くことができます。そして７回目で目的地に到達できる地図。計算は７回の中から上の場所を３つ選び方なので３５通りとなります。

 

②-1 Ａ→赤入口の道順を数える

地図は１×２の碁盤目です。上には最大１回まで 行くことができ ３回目で目的地に到達 できる地図ですね。いつもの計算。３回の中から１つを選ぶ場合の数なので３通りです。

 

②-2 赤出口→Ｂの道順を数える

地図は２×１の碁盤目です。この地図では 上には最大２回まで 行くことができ ３回目で目的地に到達 できる地図ですね。計算は３つの中から２つを選ぶ場合の数になります_φ(･_･

３つの中から２つを選ぶってコトは３つの中から選ばない場所を１つ決めるってコトなので、３つの中から１つを選ぶ選び方と同じ場合の数になります。３通りになります。

 

最初の式にもどって計算をすると…

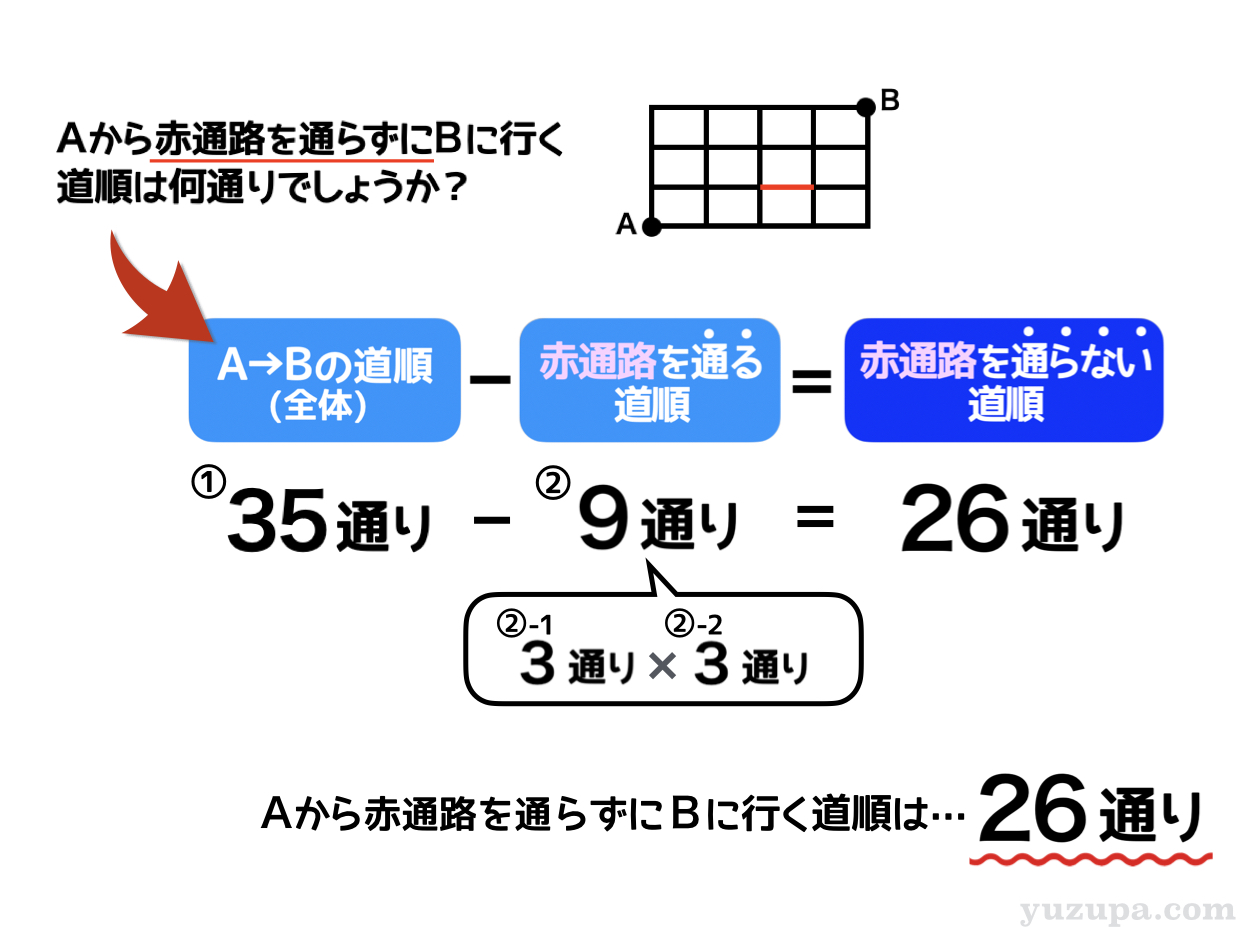
地点Ａから赤通路を通らずに地点Ｂまでの行き方は 全部で26通り になります。

 

通行止がある場合の問題をオサライします！

考え方はシンプル…。全部の道順を数えて、通行止を通る道順を引く！ 以上です o(^-^)o

 

往復：行きだけでなく帰りも含める

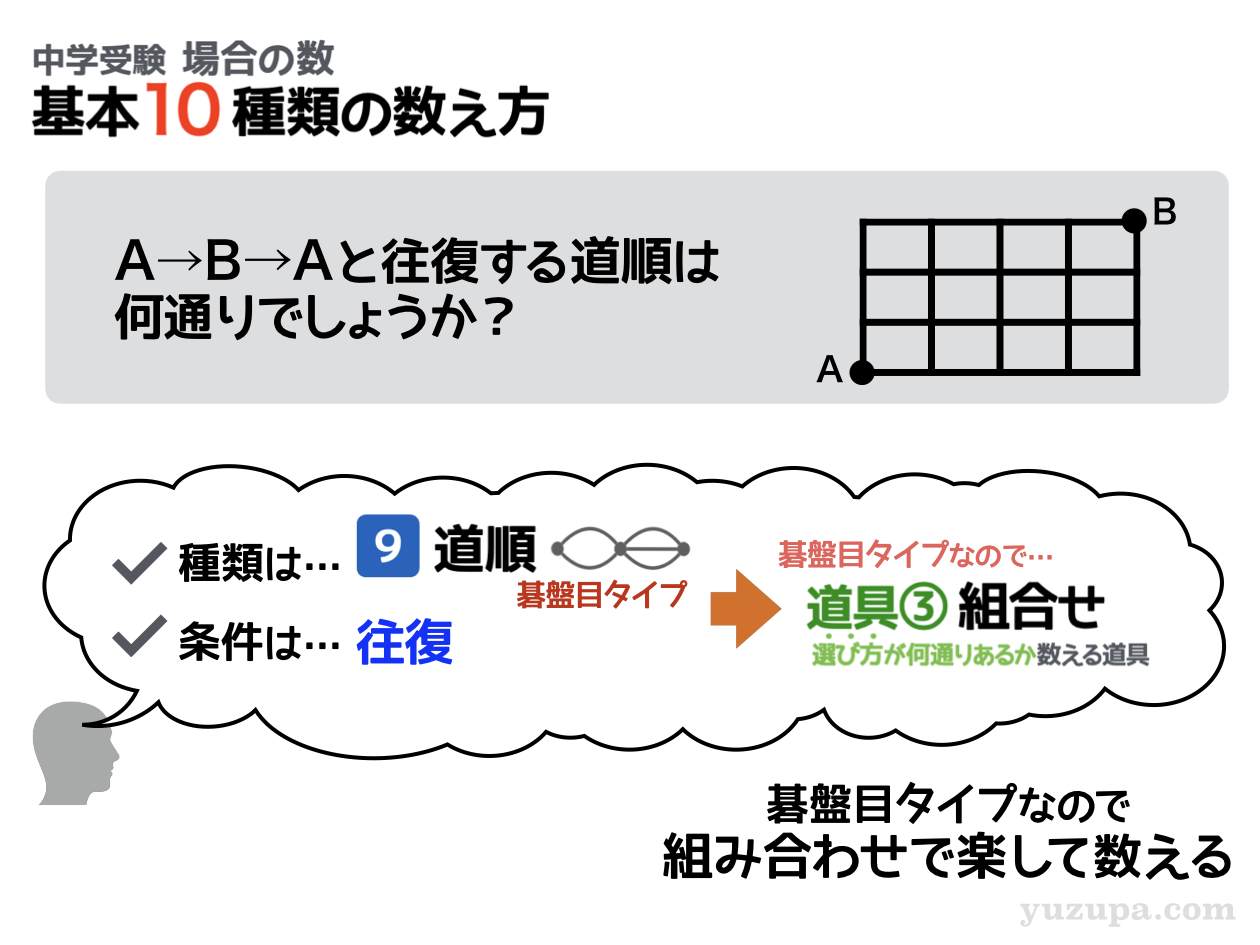
この問題を読むと、地図のタイプはがやはり”碁盤目タイプ”ですね。碁盤目タイプなので 道具③組合せ を使うことを考えます。

この問題の場合 “往復する道順” と書かれています(o_o) これは行きだけではなく、帰ることも含めて道順を数えなさいというコト。”行き”と”帰り”の両方の道順を数えましょう_φ(･_･

意外と簡単かも？
さっそく…ひとつずつ計算してみましょう！ 

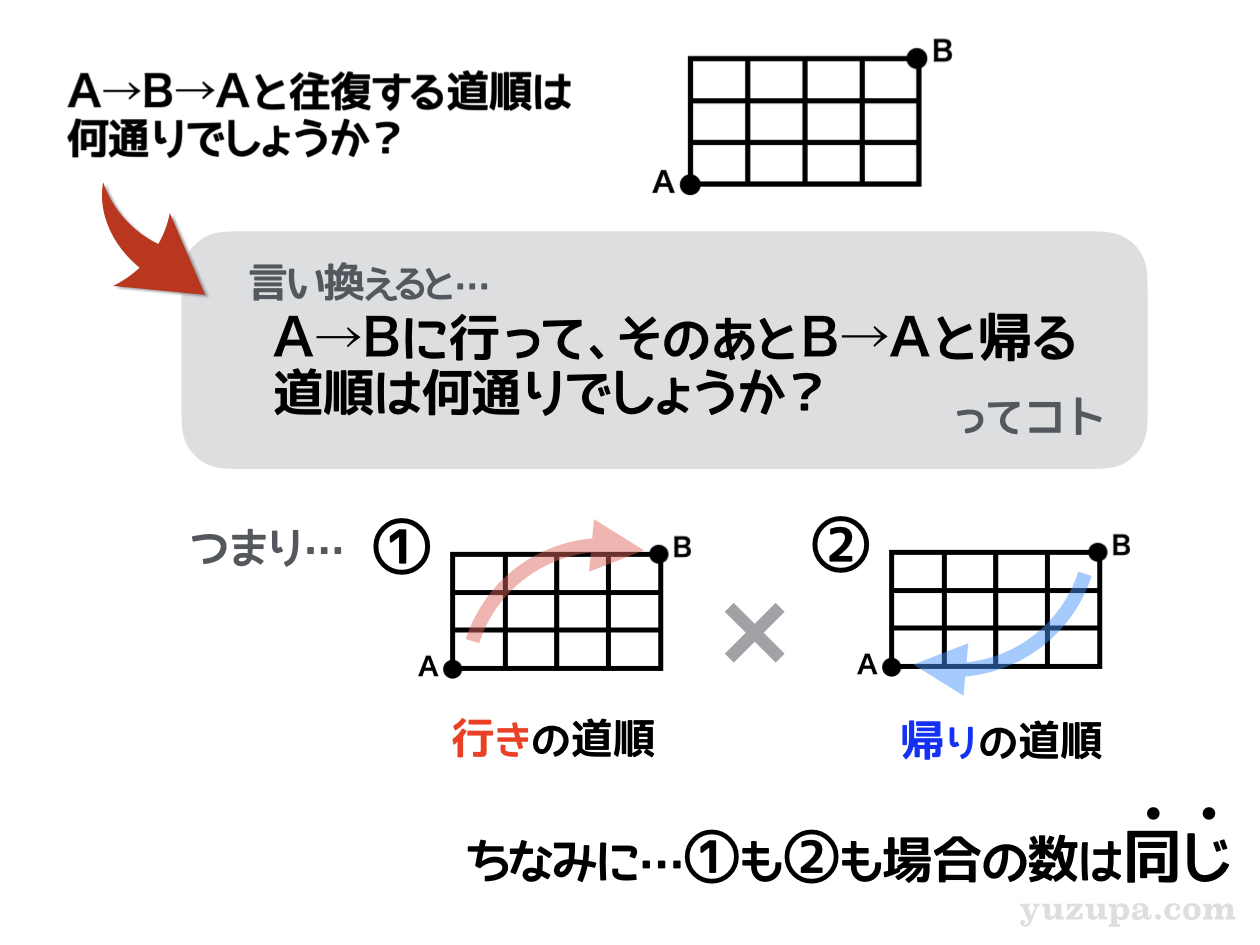
① Ａ→Ｂの道順を数える

地図は３×４の碁盤目なので上には最大３回まで行くことができます。そして７回目で目的地に到達できる地図…。７回の中から上の場所を３つ選び方なので３５通りとなります。

① Ｂ→Ａの道順を数える

行きと全く同じ地図で追加の条件もない。帰りの道順の数はというと…もちろん 行きの道順の数と同じ！３５通りとなります。

 

ちなみに…帰りだけ新たな条件が加わることもあります∑(ﾟДﾟ)

帰りだけ”経由地”があるとか、帰りだけ”通行止”があるとか、ちょっと応用編だと帰りは”行きに通った道は通らない”とか…

いずれにせよ ”行き”と”帰り”を分けて道順を数えましょう_φ(･_･

では本編にもどって、最後の計算をしてみましょう！

 

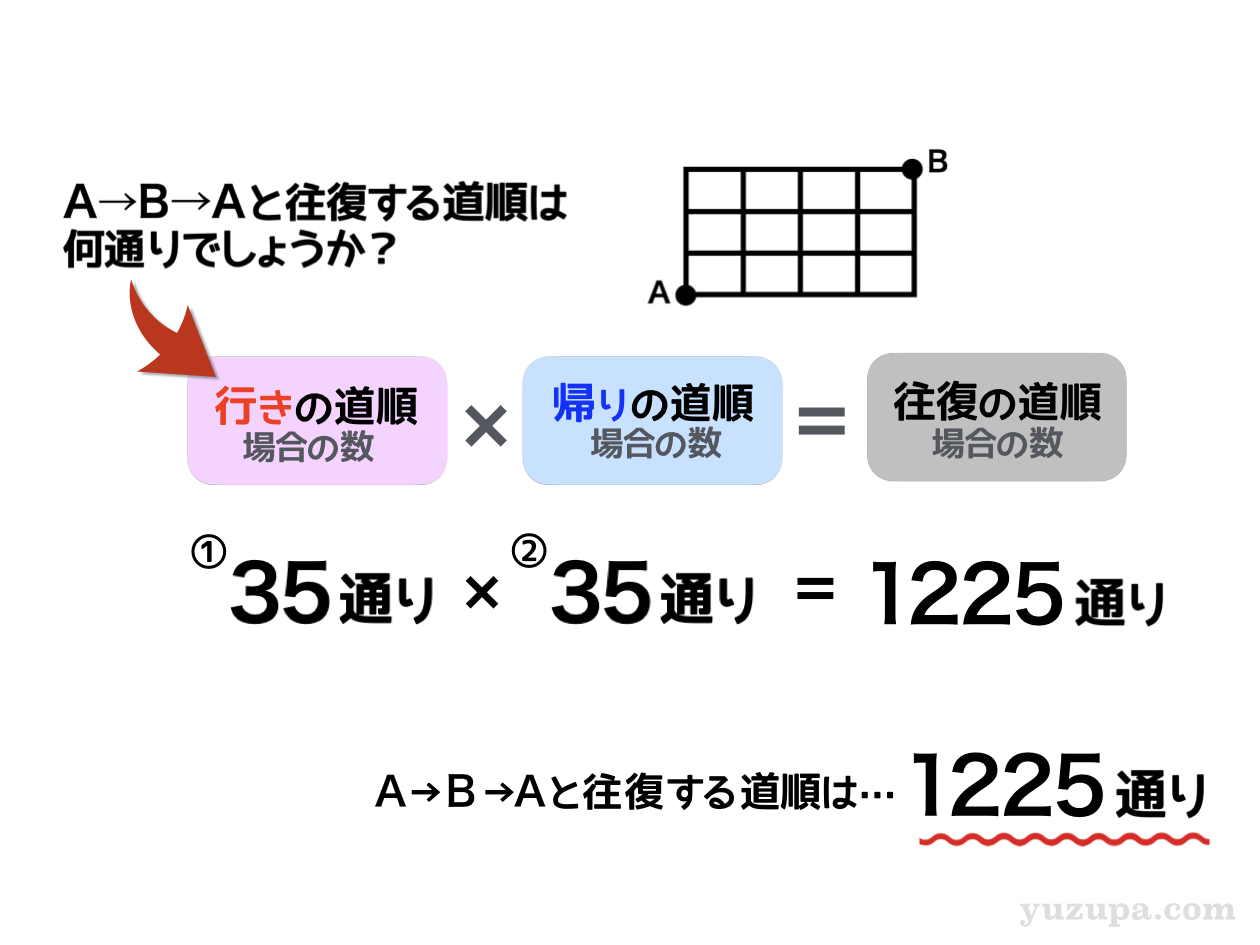
“行き”が35通り、”帰り”も35通りですので、往復する道順の数は1225通りですd(^_^o) 

 

往復の道順の問題のオサライをします。

往復でも落ち着いて。行きの道順を数えて、帰りの道順を数えて…かけ算をすればよい！  o(^-^)o

 

まとめ

今回は苦手意識をもつ生徒も多い場合の数の問題の中から道順の数を数える問題にフォーカスして解説をしてまいりましたo(^-^)o

まず、地図のタイプによって２つの基本パターンがあること。”経由地”やら”通行止”やらの条件がありました。それぞれをまとめると以下のようになります。

基本パターン

・通常タイプ    → 樹形図で数えることにトライ
・碁盤目タイプ → 組合せで数えることにトライ

条件バリエーション

・経由地：スタートから経由地、経由地からゴールの２つに分けて！
・通行止：全体から通行止を通る道順を引く！
・往復　：行きの道順と帰り道順の２つに分けて！

 

場合の数の全体を学習したい場合はこちらへ d(^_^o)
参考：場合の数が苦手…３つの道具を使い10種類の数え方をマスターせよ