中学受験：Ｎ進法とは？たった５つの基本でシンプルに理解できる

Ｎ進法は“５つの基本”と”３つの出題パターン”で攻略せよ！

※2021年1月15日 出題パターン①の４進法のケタの間違いを修正いたしました。

こんにちは。かるび勉強部屋 ゆずぱ です。

２進法で書かれた数字が暗号にしか見えない… 入試での出題パターンを知りたい… 数字以外の表現方法の読み取り方がまったく分からない… (-_-;) シンプルな理解法はないのか？

Ｎ進法は”５つの基本”で
シンプルに理解できます

Ｎ進法の本質となる ”５つの基本”さえ理解していれば意外とシンプルに攻略 することができます。また後半では 実際の入試問題を分析してまとめた ”３つの出題パターン” もご紹介します。

それでは詳細にまいりましょうd(^_^o)

 

Ｎ進法とは？５つの基本でシンプルに理解

基本① Ｎ進法とは…数字の表現方法のこと！

そもそも…Ｎ進法とはナニモノ？

ざっくりと表現するならば ”数の表し方” のこと

上記のように”Ｎ”の部分には具体的な数字が入ります。10進法、５進法、16進法… 種類はいくらでもあります∑(ﾟДﾟ)

ふーん…(-_-;) これだけでは”Ｎ”の部分に数字が入ることは分かったが、イマイチよく分からないので本質をお伝えします。

 

基本② 本質は ”いくつでケタが上がるか”

Ｎ進法の本質はズバリ
いくつでケタが上がるかですd(^_^o)

10進法なら10でケタがひとつ上がる、5進法なら5でケタがひとつ上がる、2進法なら2でケタがひとつ上がる…という感じです。

具体的にみてみましょう_φ(･_･

 

10進法のケタの上がり方

小学生が ふだん使っている数字は10進法で 9の次の数字でケタがひとつあがります ねd(^_^o) だから10進法です。

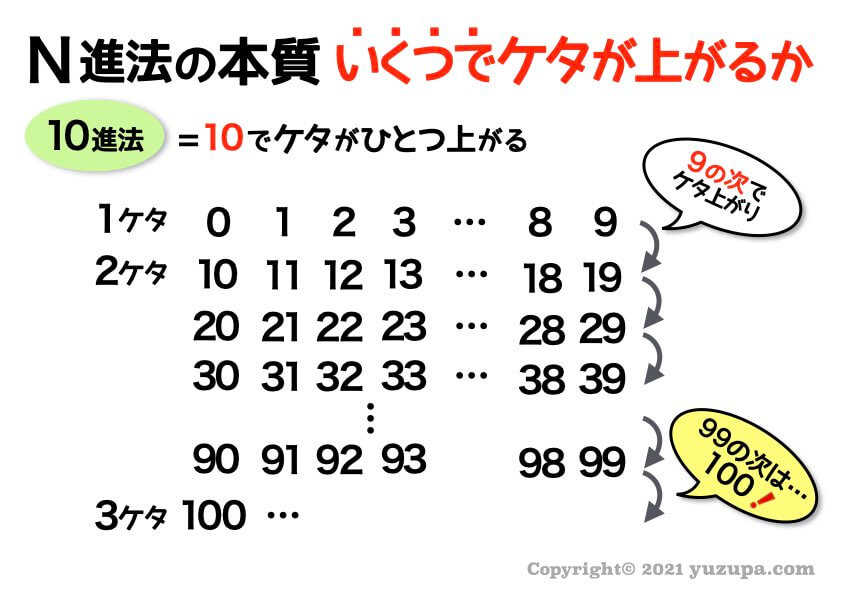
５進法のケタの上がり方

５進法なら４の次の数字で…ケタが上がります。

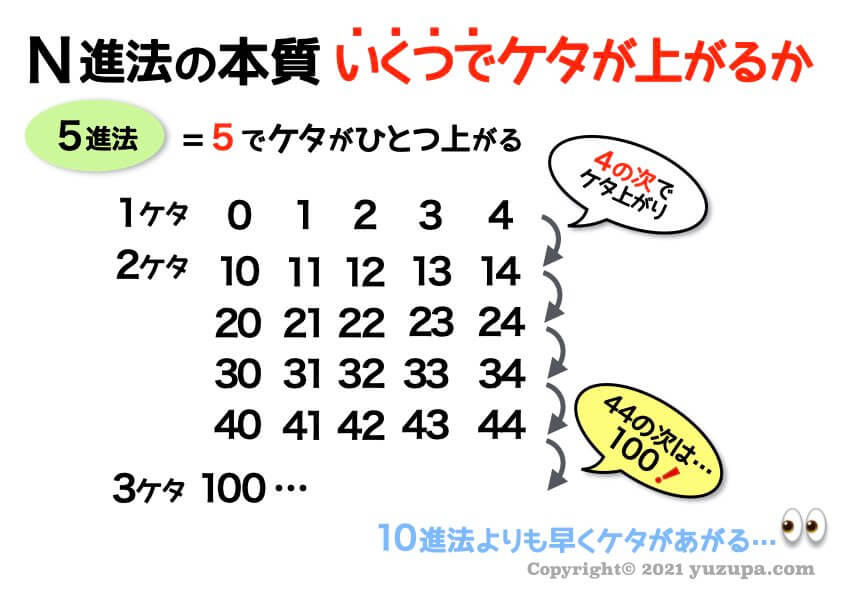
３進法のケタの上がり方

３進法なら２の次の数字で…ケタが上がります。

２進法のケタの上がり方

２進法なら１の次の数字で…ケタが上がります。

とてもシンプルですねd(^_^o) これがＮ進法の本質です。Ｎの部分がどんな数字になっても同じ考え方です。

 

最後に10進法、5進法、3進法、2進法を表に並べてみます。

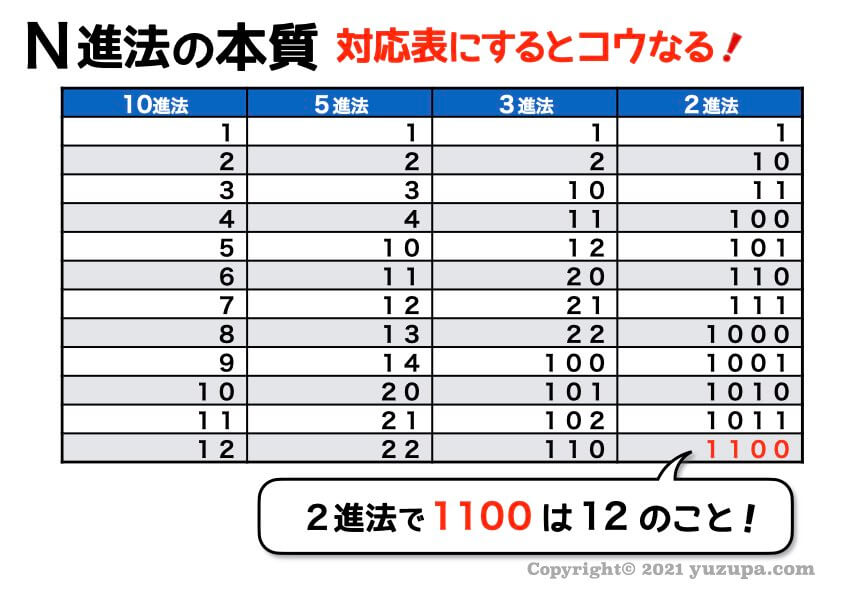
例えば ２進法で表された 1100 は10進法の 12 のこと ですd(^_^o)

 

基本③ “ケタごとのカタマリ”を理解せよ

Ｎ進法の本質が理解できたら、今度は ”ケタごとのカタマリ” を意識する練習 をしましょうd(^_^o)

まずはふだんから見慣れている10進法で見てみます。

 

10進法のケタごとのカタマリ

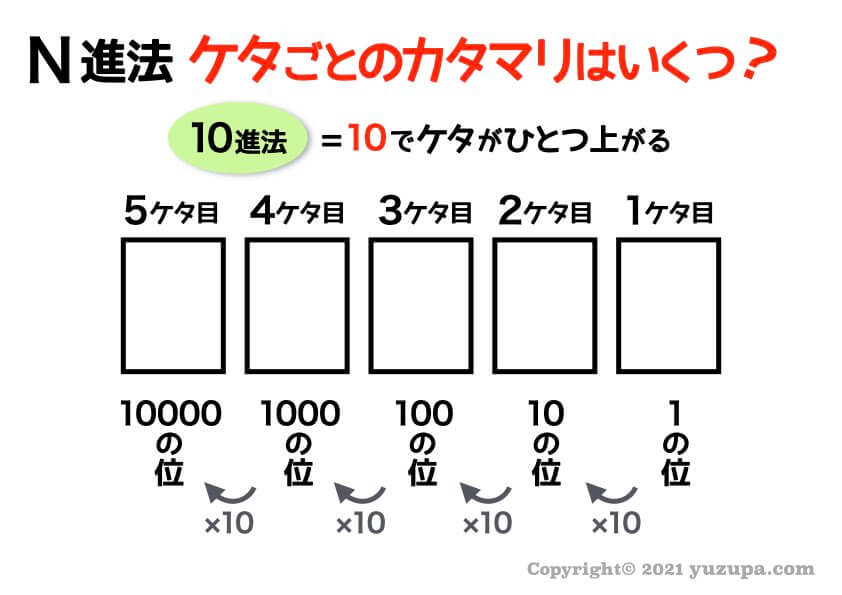
10進法の数字は１ケタ目は１の位、２ケタ目は10の位、３ケタ目は100の位…という感じですよね？

例えばこの10進法ので “4023”は 何を意味するでしょうか？

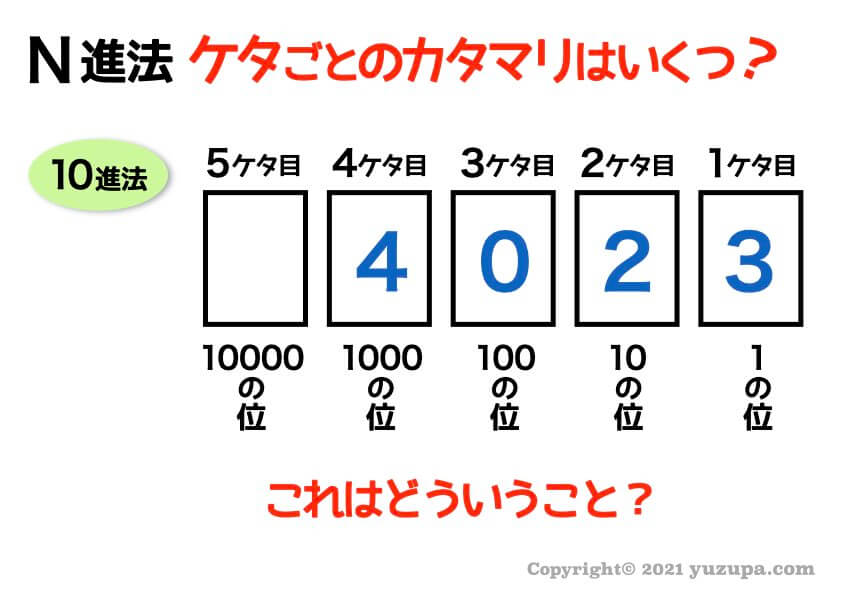
これは １のカタマリが３つ、10のカタマリが２つ、1000のカタマリが４つ あるという意味ですね。

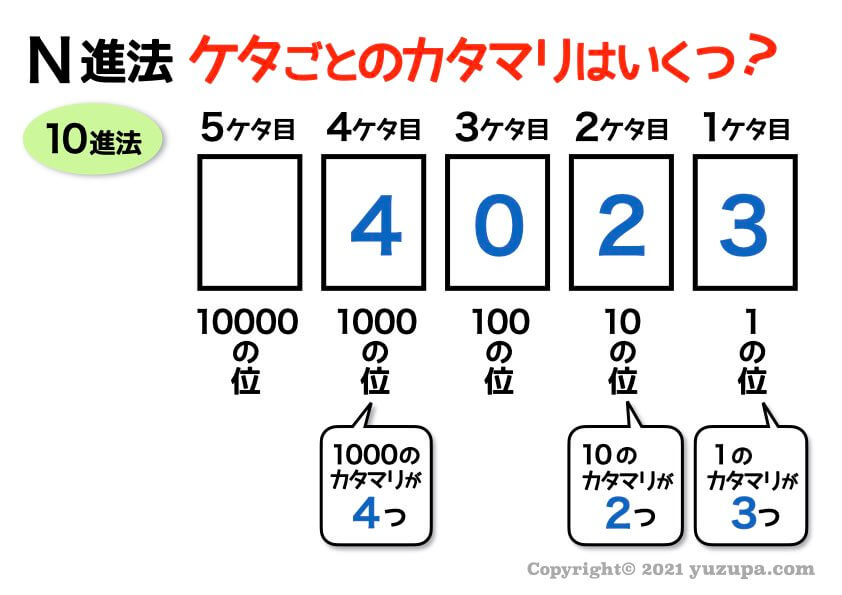
それそれの ケタは数字のカタマリである ことを意識しましょうd(^_^o)

 

５進法のケタごとのカタマリ

５進法でも同じですd(^_^o)

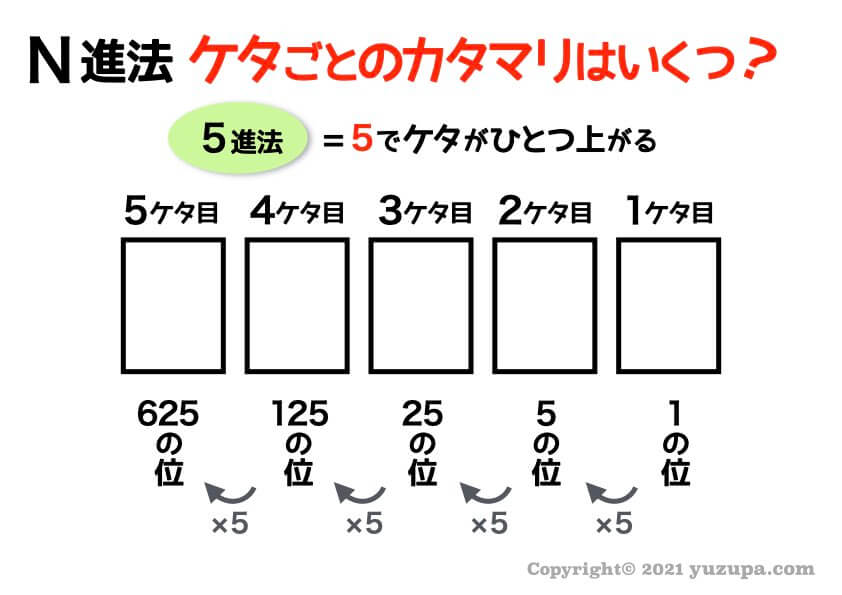
１ケタ目は１の位、２ケタ目は５の位です。５進法では５でケタがひとつ上がるので２ケタ目は ”５のカタマリ” です。

そして３ケタ目は ”５のカタマリ” が５つ集まったものなので”２５のカタマリ” ですね_φ(･_･

じゃあ５進法で ”3042” ってどういうことでしょう？

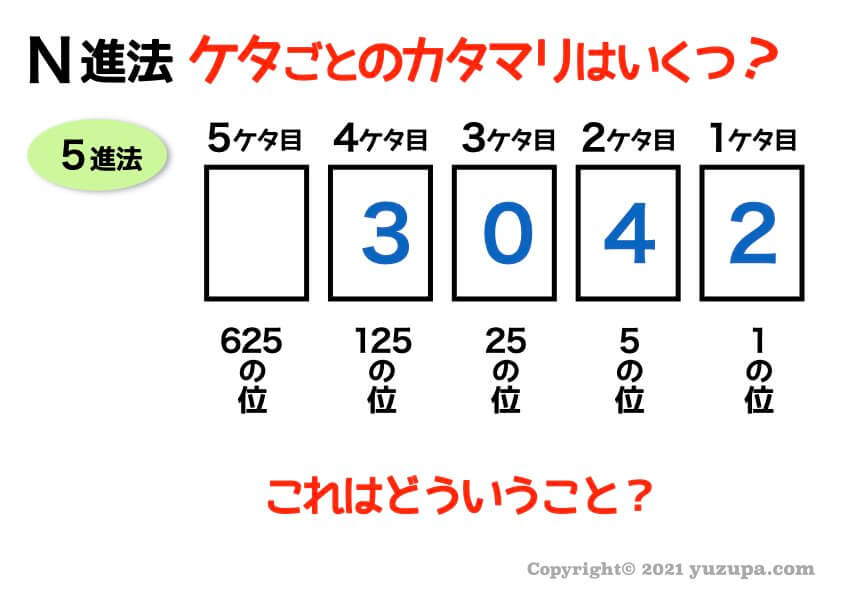
 10進法と同様に 各ケタのカタマリがいくつあるか 考えます。

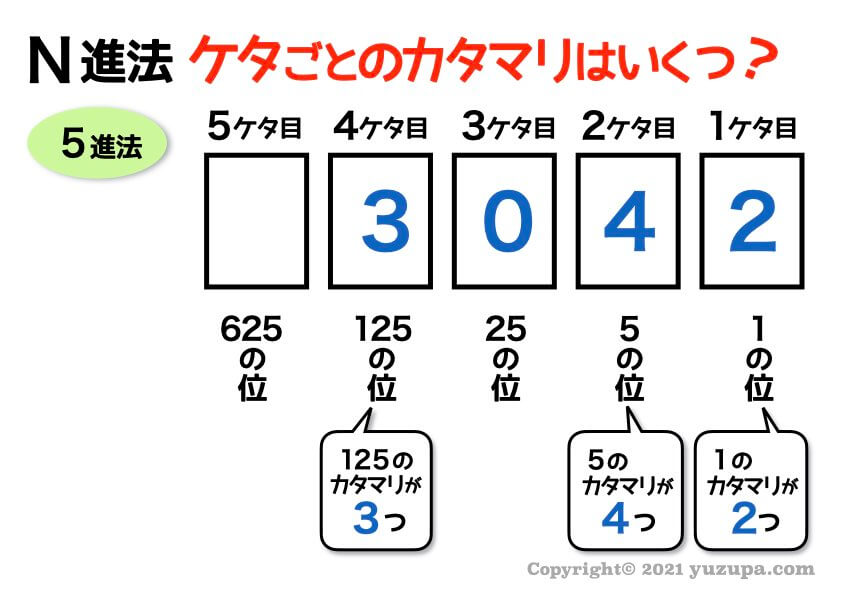
５進法の ”3042” は、１のカタマリが２つ、５のカタマリが４つ、125のカタマリが３つ、合わさった数字ということです_φ(･_･

 

２進法のケタごとのカタマリ

最後に２進法でも同じように見てみましょう。

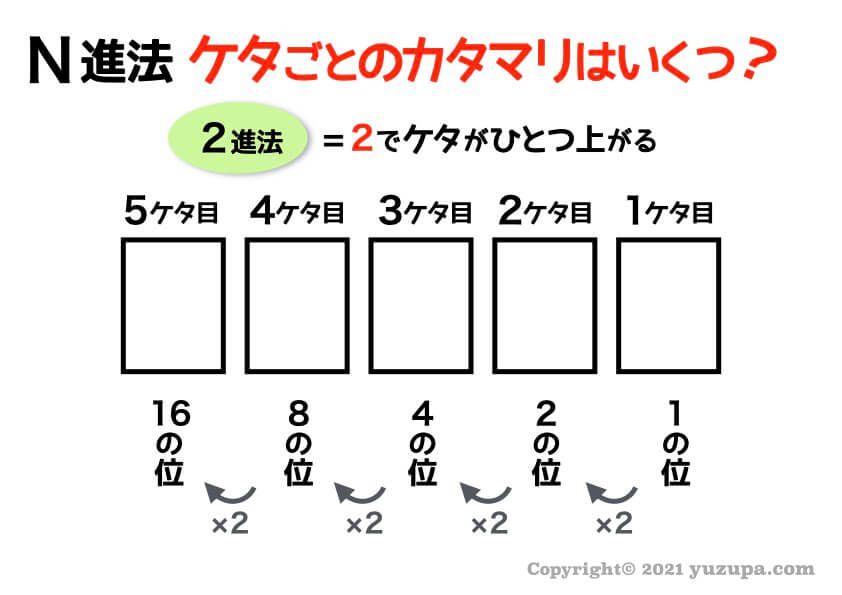
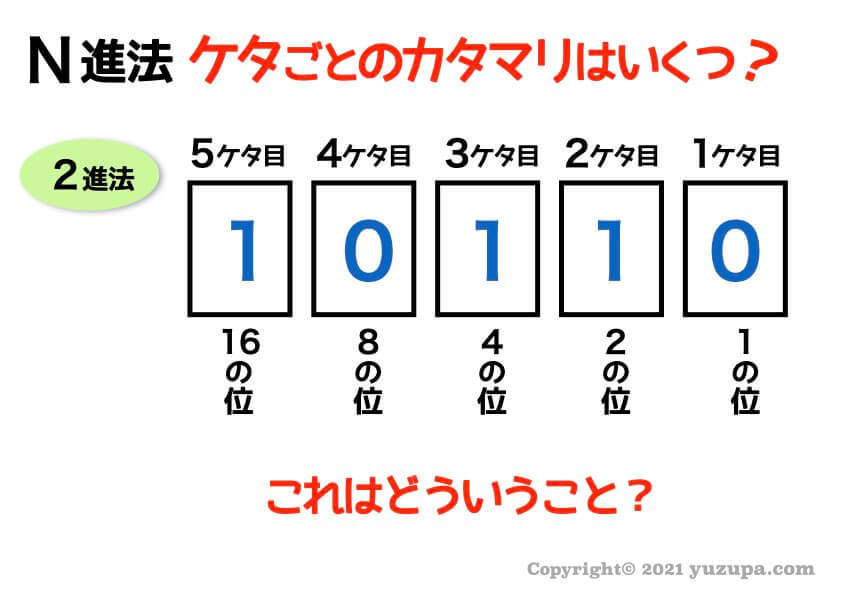
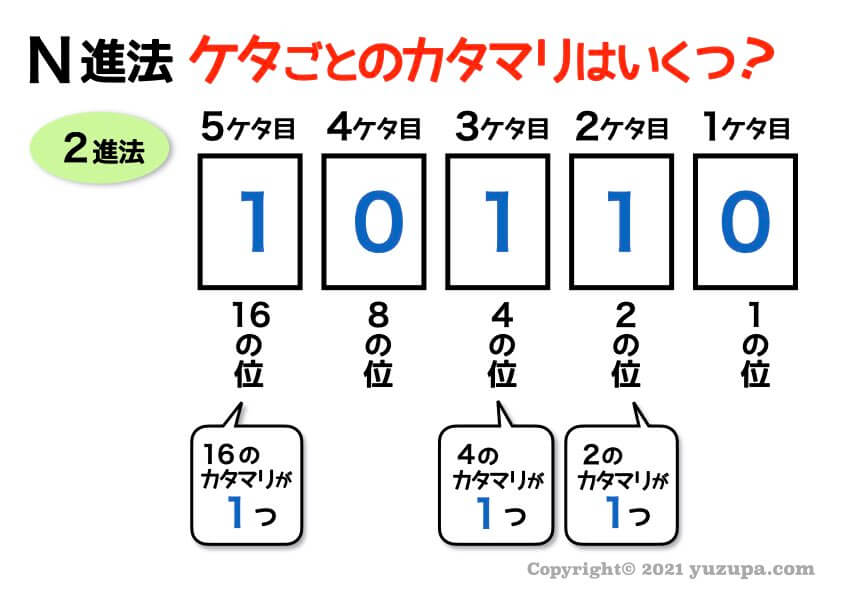
Ｎ進法のＮがどんな数字であっても考え方は全ていっしょですd(^_^o) 落ち着いて考えればできます！

 

基本④ 表現方法はたくさんある

さて… Ｎ進法を今まで数字で表してきましたが、入試では数字意外の表現方法がよく出されます∑(ﾟДﾟ)

いくつかのパターンをご紹介しますが、まずはオーソドックスな数字によるＮ進法の表現から…

数字以外の例…まずは 入試で頻出しているソロバンっぽい表現 です。各ケタに箱が用意されていてそこに玉を入れるイメージです。

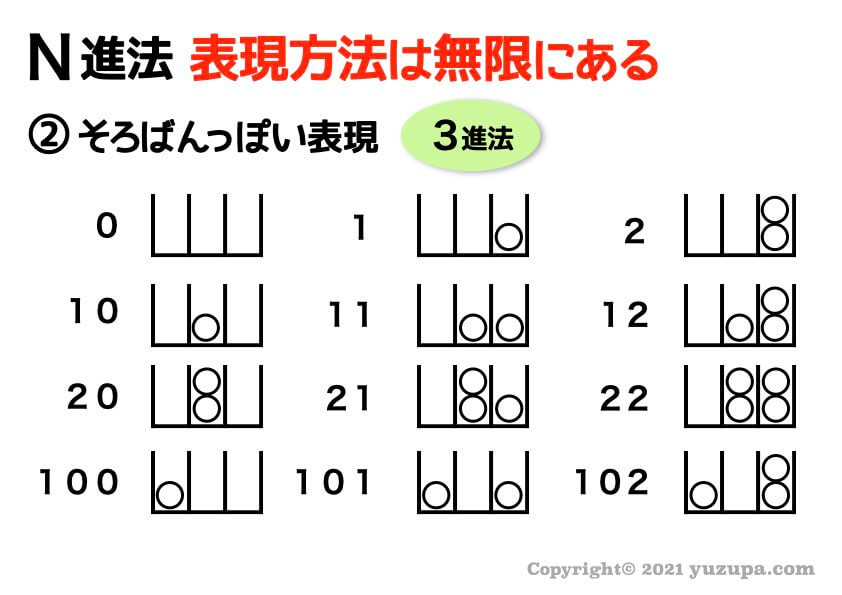
次は 図形の色塗りで表現されるパターン です。これはＮ進法を知っていないと気づけないかも…(-_-;)

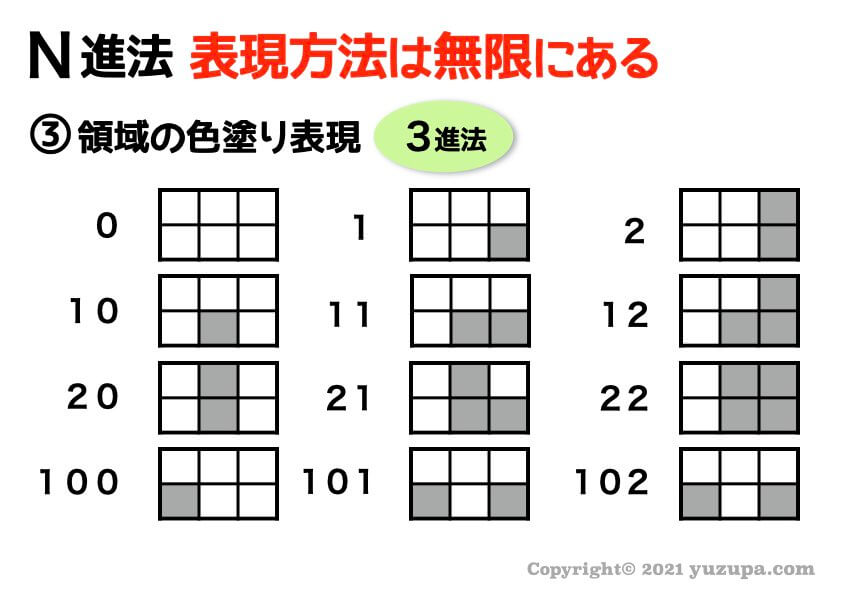
最後に 独自パターンによる表現 です。これは一例ですが記号と数字が対応していて、さらにＮ進法でケタ上がりするというもの。

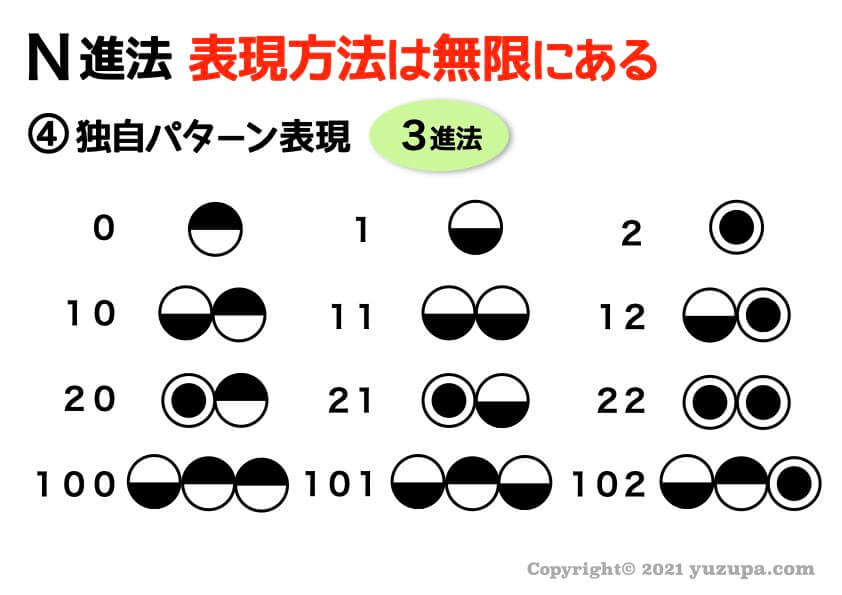
まずはこの４パターンの表現をおさえておけば、入試会場でもひらめくことができる可能性がグンと上がりますd(^_^o)

 

基本⑤ 身近なN進法を知る 

最後は入試で直接とわれることはありませんが、知識として知っておいた方がよいＮ進法の身近な事例ですd(^_^o)

① アラビア数字

ふだん使っている数字は”アラビア数字”と呼ばれている数字の表記方法です。このアラビア数字…もちろん10でケタが上がるので10進法ですね d(^_^o)

② ローマ数字

時計の文字盤などで使われる”ローマ数字”… ５を ”V” と表し、10を”X”と表します。５ごとに新しい記号が割り当てられているので５進法の一種と分類されています。

③ 時間の単位

時刻を示す単位である ”秒” や ”分” や “時間” は60進法です。1秒が60個集まると1分にケタ(単位)上がりし、1分が60個集まると1時間にケタ(単位)上がりしますd(^_^o)

④ コンピュータ

最後はコンピュータの中にある数字です。コンピュータの中の数字はすべて２進数が使われています。電気や磁気ではオンとオフの２種類しか表現できないので２進法が使われています_φ(･_･

 

中学入試での３つの出題パターン

Ｎ進法の本質がわかったところで…いよいよ実際の入試出題パターンにまいりたいと思います。

そして全ての問題は以下の王道アプローチで解いていきましょう！

それでは具体的な３つの出題パターンをご紹介しますd(^_^o)

 

パタン① この図形はいくつ？

まずはもっともよく出題されるパターンです。

Ｎ進法を表現する図や数字が問題文に書かれており、Ｎ進法に気づかせた上で”この図形の表す数字はいくつでしょう”というもの。

具体的な問題例をみてみましょう。

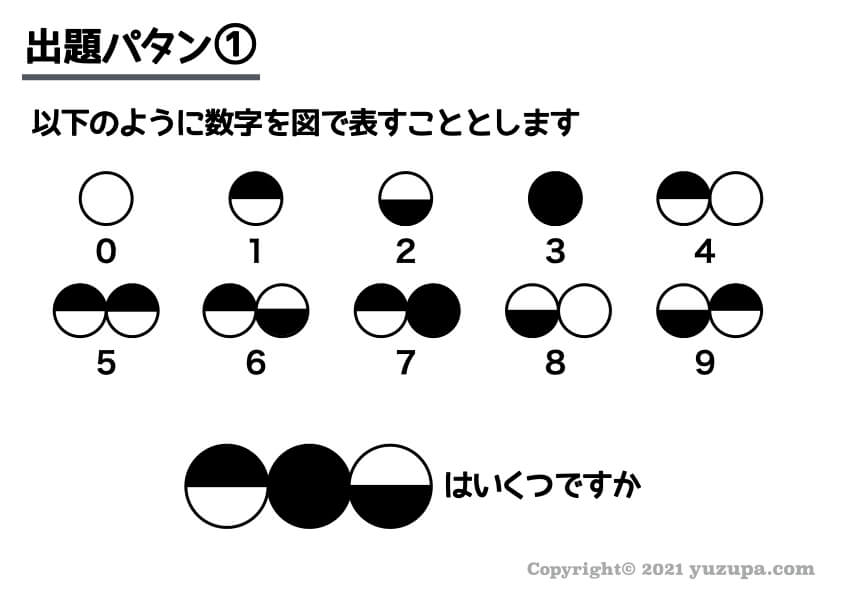
この問題を解くためには、まずこれがどんなルールで記述されているかを特定するところから入ります。

Ｎ進法っぽいことに気づいたら、いくつでケタ上がりしているかをさぐっていきましょう_φ(･_･

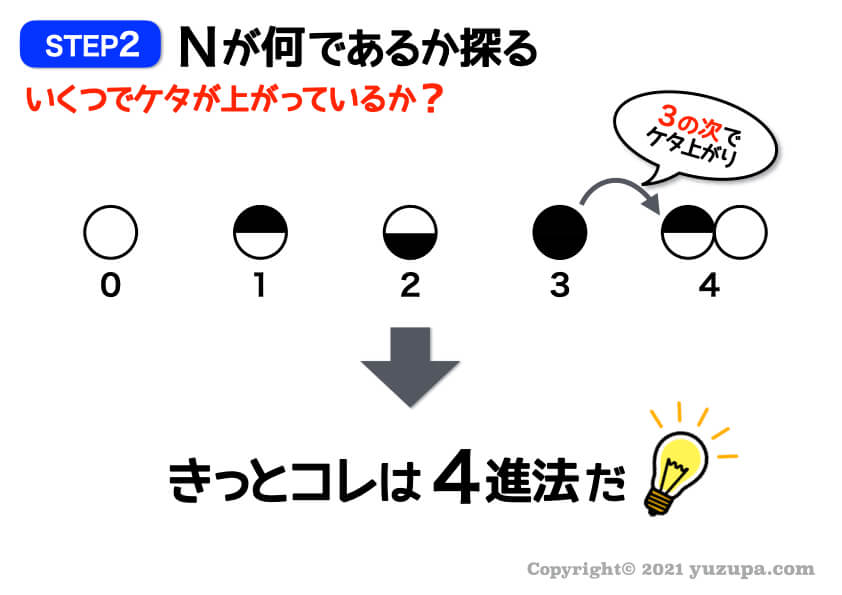
この場合は４進法ですねd(^_^o)

Ｎ進法のＮが何か分かれば次はＮ進法の本質に移ります。４進法と分かれば 各ケタのカタマリも分かりますね。

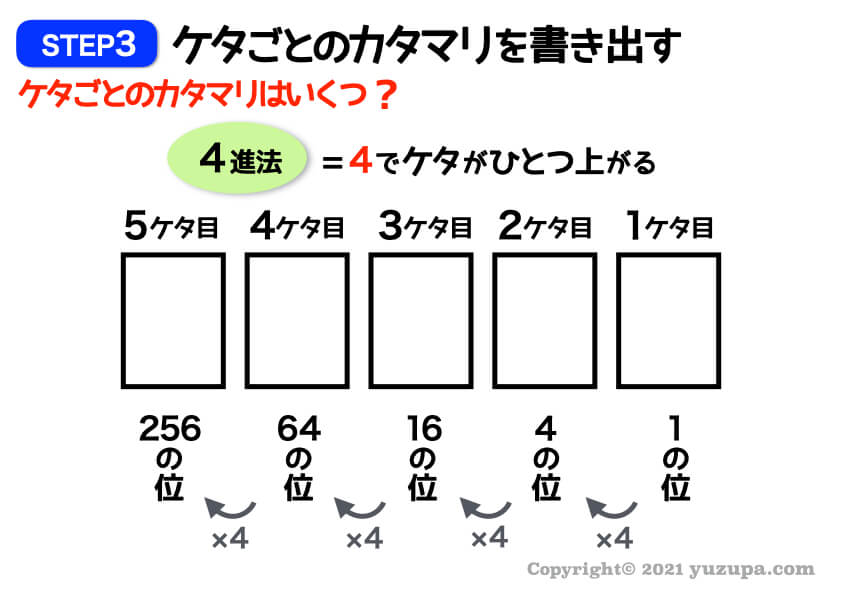
各ケタのカタマリがいくつずつあるのかを考えます。

この問題では１のカタマリが２つ、４のカタマリが３つ、１６のカタマリが１つですねd(^_^o)

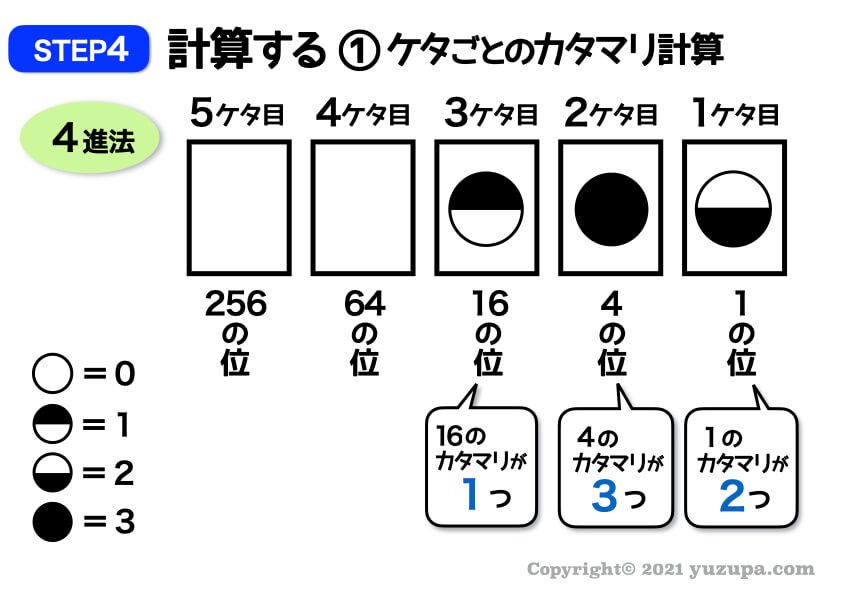
最後は計算です。

答えは ３０ ですd(^_^o)

 

パタン② 図にかきいれなさい

次のはパターン①とは逆のパターンです。今度は数字から図を描きなさいという形の問題 です。

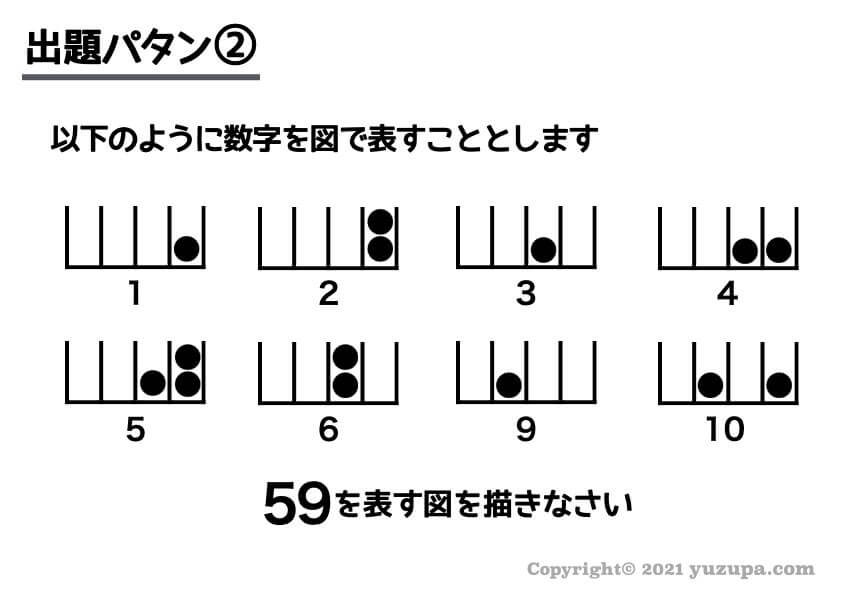
同様にＮ進法のＮが何なのか？探りを入れていきます。

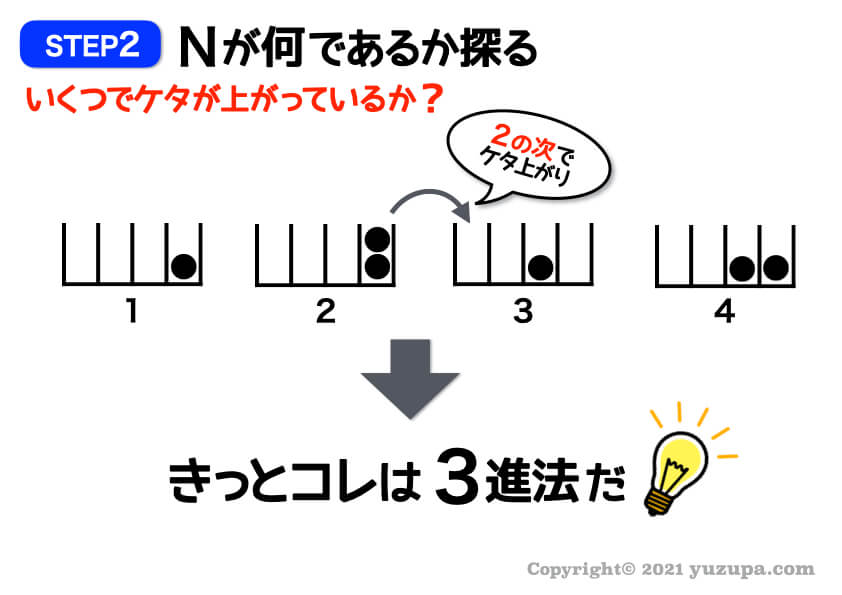
これは ２の次の数字でケタ上がりしているので３進法 だと分かりました。次はカタマリです。

３進法の各ケタのカタマリは以下のようになりますね。

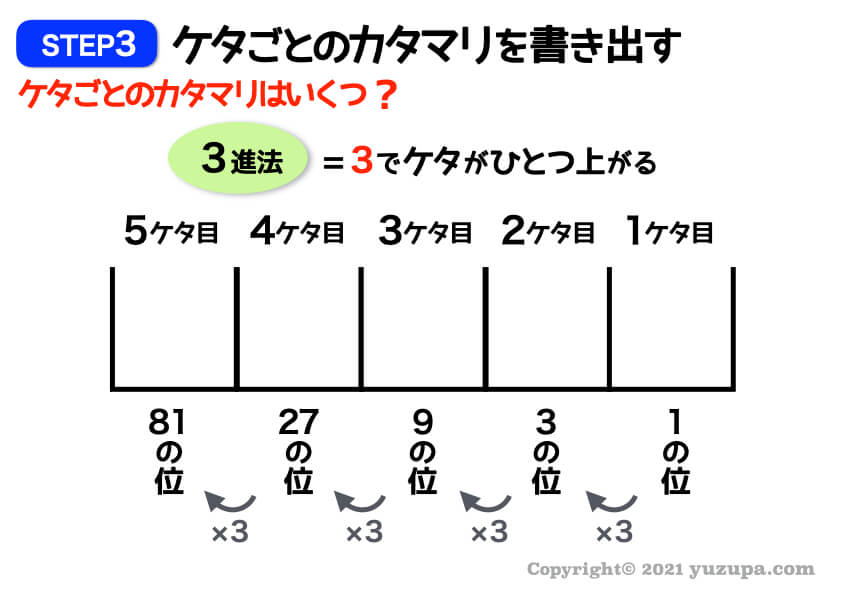
ここからがこのパターンのポイントです。

51という数字を描くために、どのケタにいくつ数字を入れていけば良いかを考えなくてはいけません。

51を分解しながら上から各ケタに数字を入れていきます

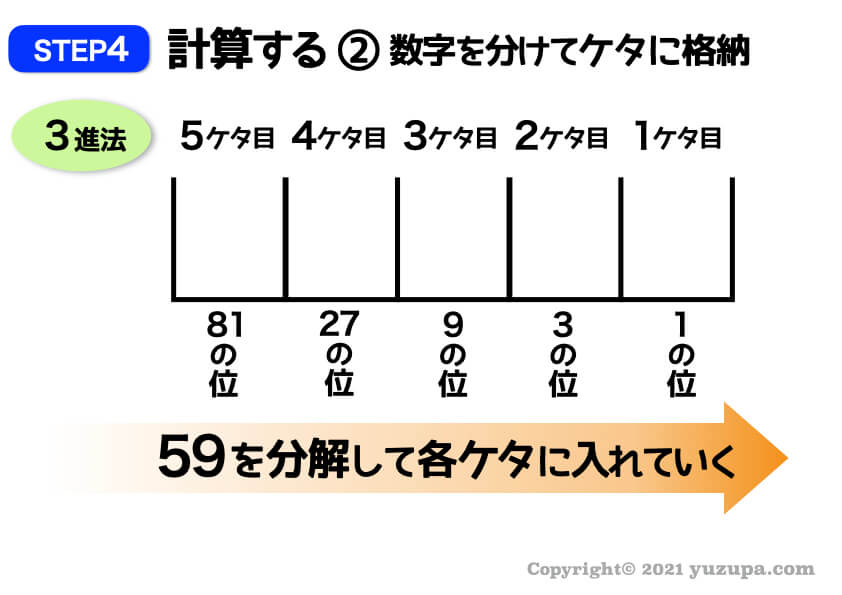
具体的にやってみましょう。

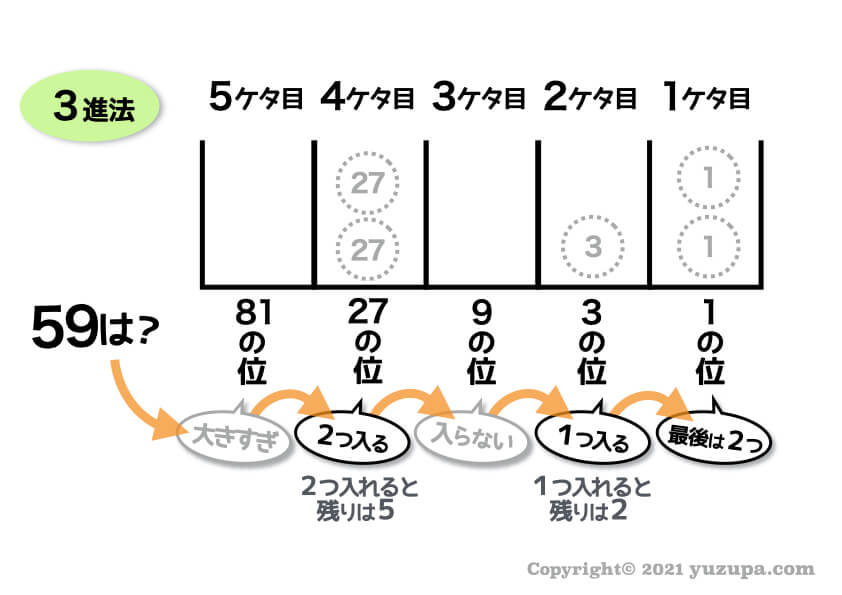
表したい数字は 59 なので５ケタ目は大きすぎます。次の４ケタ目はカタマリの大きさが27なので２つ入りますね。

59から27のカタマリを２つ格納したので残りは５です。

こうやって59が全て格納できれば完成ですo(^-^)o

 

実際に検算してみましょう。

１のカタマリが２つ、３のカタマリが１つ、２７のカタマリが２つ…全部合わせると確かに59になりますね！

 

パタン③ 表現できる範囲は？

最後は表現できる範囲を問う問題です。さっそくですが、まずは例題をごらんください。

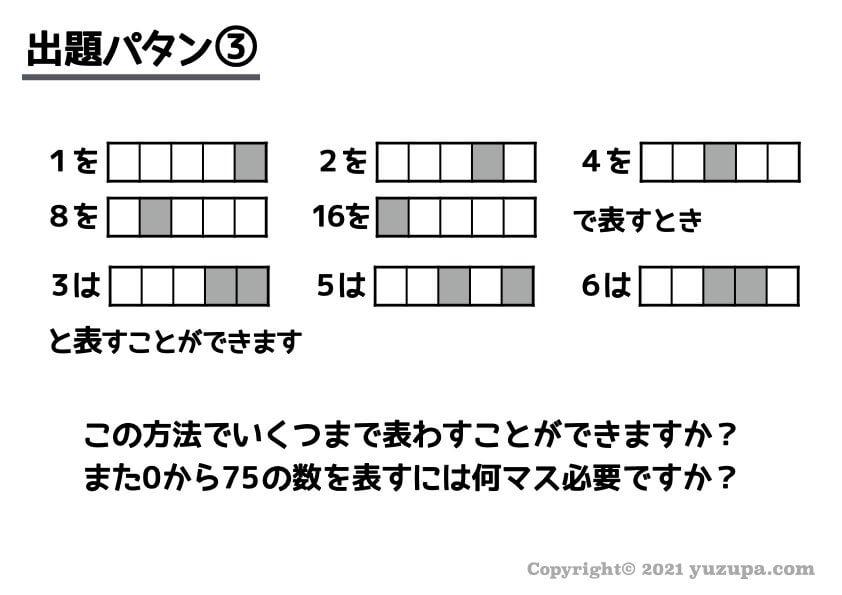
ちょっと難しそうですが…やることはいっしょです。Ｎ進法だと思ったらNがいくつかを探りますd(^_^o)

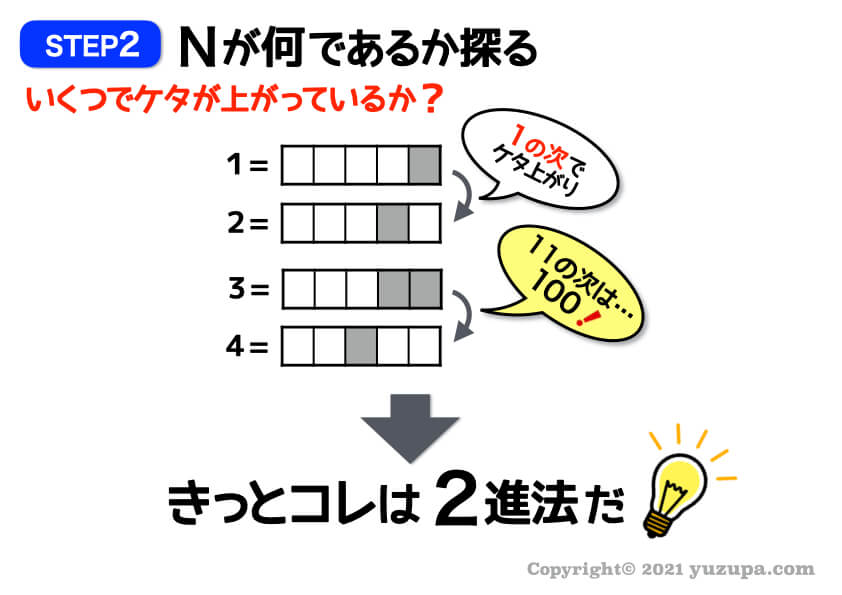
これは２つ目の数字でいきなりケタがあがっているので２進法だということがわかりますね(@_@)

いつもどおり各ケタのカタマリも意識しましょう！

 

設問① いくつまで表せるか？

最初の設問です。

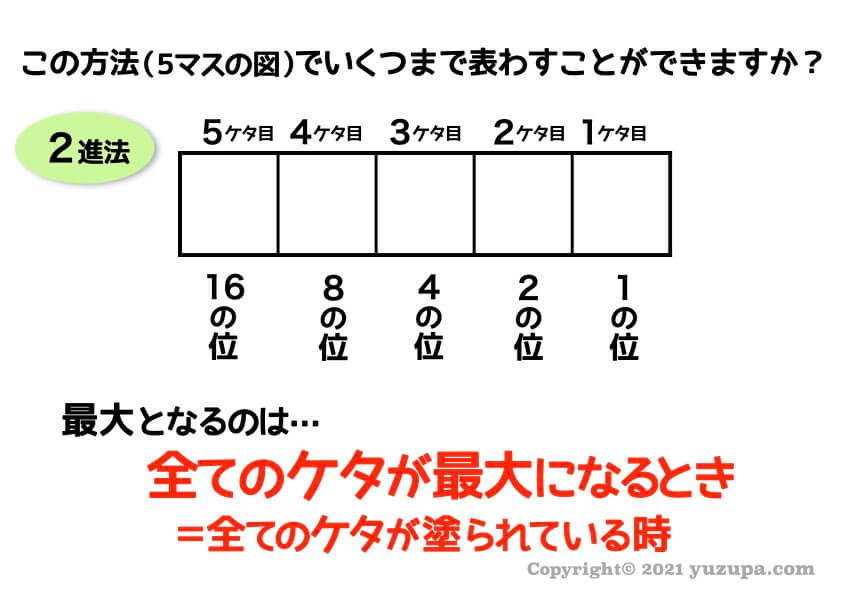
この５つのマスで表せるもっとも大きな数字はいくつでしょうか？最大の数となるのは全てのケタが最大の時です。

そしてその最大の数字がいくつであるか計算します。

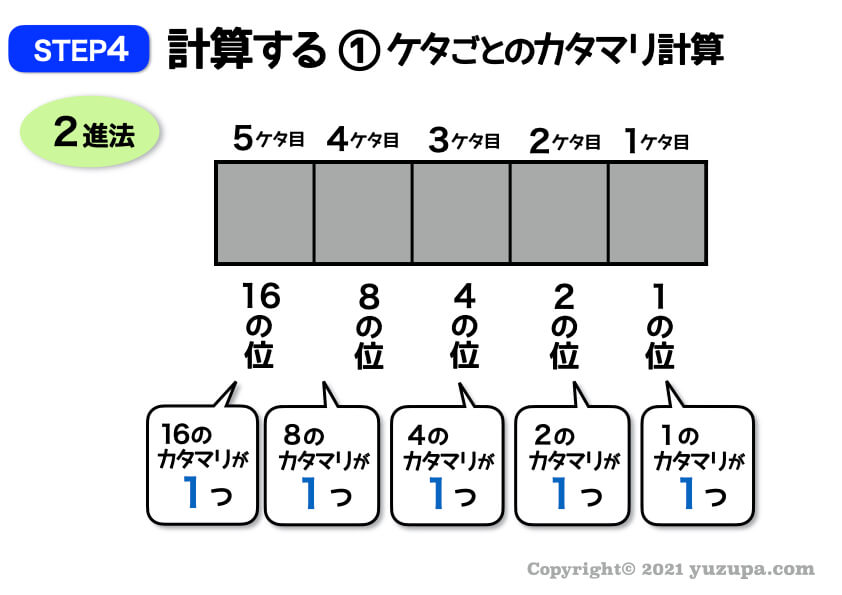
各ケタのカタマリを計算してみましょう。

 

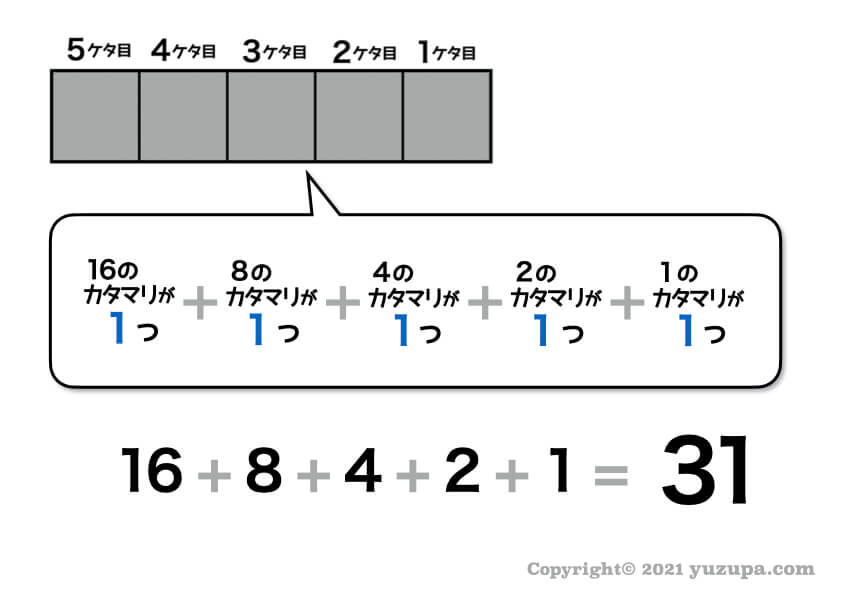
２進法の数字５ケタで表すことができる最大の数字は３１ であるということが分かりましたo(^-^)o

 

設問② 何マス必要か？

２つ目の設問です。

最大である75を表すのには何マス必要なのでしょうか？ 最大である75をこの２進法の表現で書いてみましょうd(^_^o)

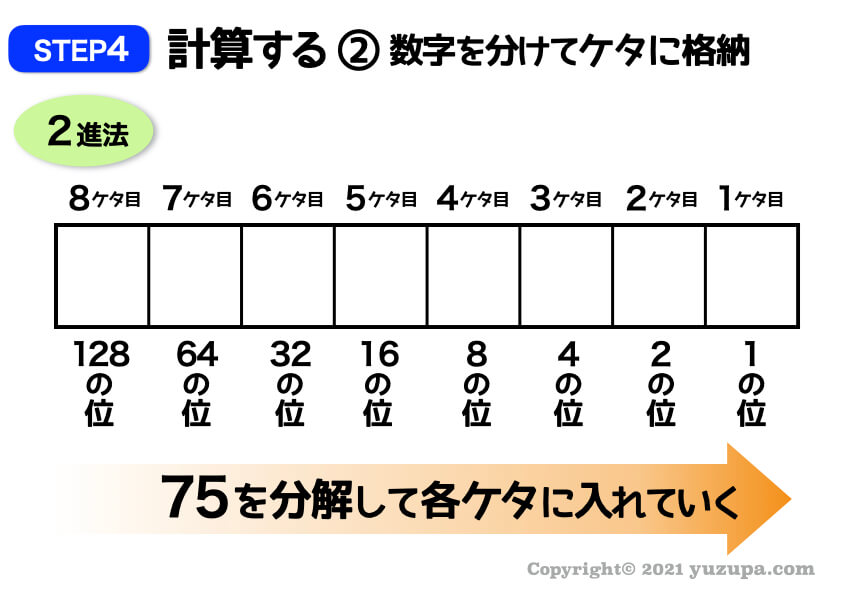
上のケタから75を各ケタに格納していきます…

７ケタ目に１つ、４ケタ目に１つ、２ケタ目に１つ、１ケタ目に１つの数字が入ることが分かります。

そうすると何マス必要なのか分かりますね！

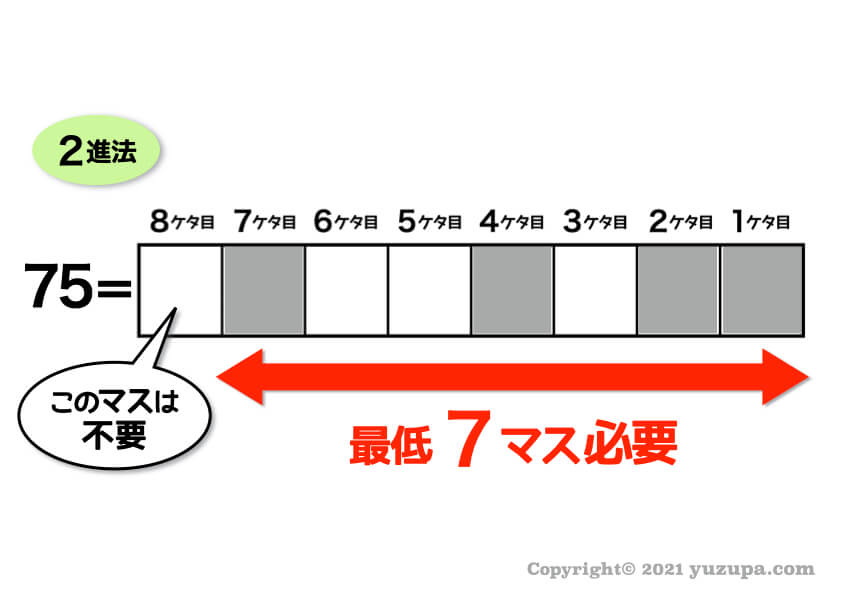
７ケタ目までで75を表すことができますので、８ケタ目より大きケタは不要ですねd(^_^o)

 

まとめ

Ｎ進法… ２進法の数字は暗号にしかみえなかったり、図で示された数字が全く読み取れなかったり… とっつきにくいＮ進法も５つの基本でスッキリ理解できますd(^_^o)

Ｎ進法 ”５つの基本”
　① Ｎ進数は 数字の表現方法
　② 本質は いくつでケタが上がるか
　③ ケタごとのカタマリを意識せよ
　④ 表現方法はあたくさんある
　⑤ N進法の身近な例 

そしてこの５つの基本を使って王道のアプローチをしましょう！

 

これらを理解していれば、Ｎ進法の入試問題も怖くありません o(^-^)o

参考：”素数”の本質の解説はこちら