中学受験:相当算とは?たったひとつのコツ…割合と数字のペアを見つけろ
問題文に”割合”と”数字”が入り乱れたら相当算かも…コツはたったひとつ!
 こんにちは。かるび勉強部屋 ゆずぱ です。
こんにちは。かるび勉強部屋 ゆずぱ です。
相当算という得体の知れない特殊算。特殊算の中でもイチバン雲のようなホワホワした存在 です(-_-;) どうもスッキリしない理由は、問題文をパッと見て”これは相当算を使うんだ”とはならないから。
でも…見分けられなくてOKです
全く問題ありませんd(^_^o)
相当算を使うんだと見分けること自体は本来の目的ではありません。目的は問題の答えにたどり着くこと。そう考えてみると 大事なことが何か見えてきますd(^_^o)
最も大切なこと
それは…
割合と数字が入り乱れて出てきたら、そのペアを見つければ解けるかも…という感覚を持つことですd(^_^o)
それでは、詳細の解説に参りましょう!
目次
相当算とは?割合と数字が出てくる問題
割合と数字が入り乱れる問題
相当算の定義… Wikipediaによると ”比の1と実際の数量との関係で考える” 計算方法 とのこと。想定どおりですが厳密な定義は子供に教えても全く意味がありません(^_^;)
とりあえず…
割合と数字が両方出てきたら相当算かも?
くらいの感覚でよいでしょうd(^_^o)厳密な定義はぶっちゃけどうでもよく、大切なのは 割合と数字が出てきたらそのペアを見つければ解けるかも…という感覚 を持つことです。
百聞は一見にしかず…実際の問題例です
花子さんは、ある小説を1日目に全体の7分の1読み、2日目に44ページ読んだところ、2日目の読み終わり時点で、全体の3分の1がまだ読んでいない状態となりました。この小説の総ページ数は何ページでしょうか?
割合と数字が入り乱れていますねd(^_^o)
ちなみに…中学受験では特殊算と言われる得体の知れない解法が山ほど存在します。が…全く体系化されていません∑(゚Д゚) 同じ問題でも複数の解法で解けたり…… 気にしすぎないように!
線分図の “3つの本質” で解ける!
割合と数字が入り乱れた文章を整理するためにはどうすれば良いでようか? そこで便利なツール線分図ですd(^_^o)
線分図とは…簡単にいうと ”棒グラフ” のこと
線分図の基礎を知りたい方は こちらの記事 こちらの記事 へd(^_^o)
上記の記事でも紹介していますが、線分図には”3つの本質”があります。これが超大切なのでシッカリおさえましょう!

そして相当算ならではの注意があります。割合は丸数字で書くことです。実際の数字と区別するためですねd(^_^o)
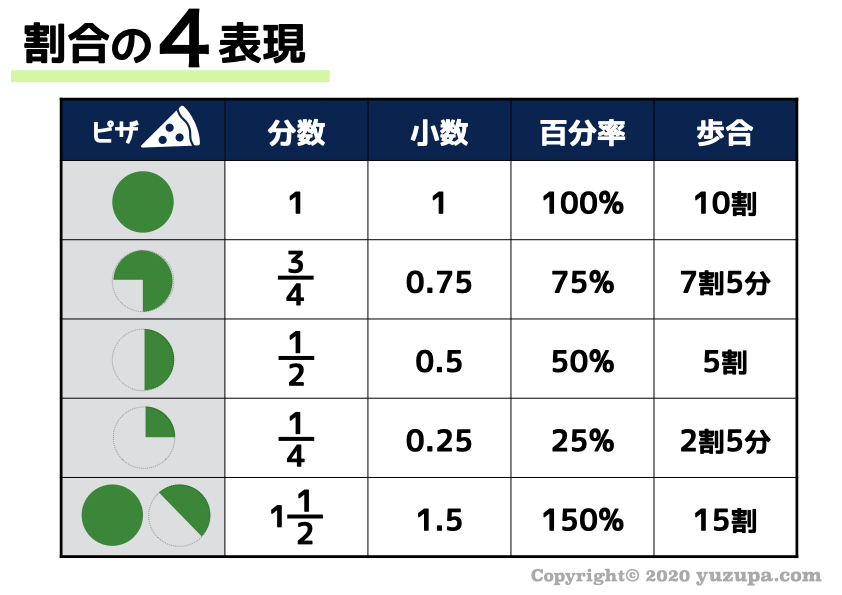
割合には4つの表現があるので注意
相当算とは割合と数字が両方出てきて、ペアを見つけることが本質だとお伝えしましたが、”割合” ってなんでしょう?
”割合”の厳密な定義を覚えることは不要ですが、全体を1とした時の量… 以下の4つの表現 があります_φ(・_・
線分図を書いて割合と数字のペアを見つけろ!
では冒頭の例題を使って実際に解いてみましょうd(^_^o)
花子さんは、ある小説を1日目に全体の7分の1読み、2日目に44ページ読んだところ、2日目の読み終わり時点で、全体の3分の1がまだ読んでいない状態となりました。この小説の総ページ数は何ページでしょうか?
まずは問題を読んで線分図を描く
まずは問題文を読みながら…落ち着いて線分図を書きます。問題文に出てくる数字は全て使いますd(^_^o)
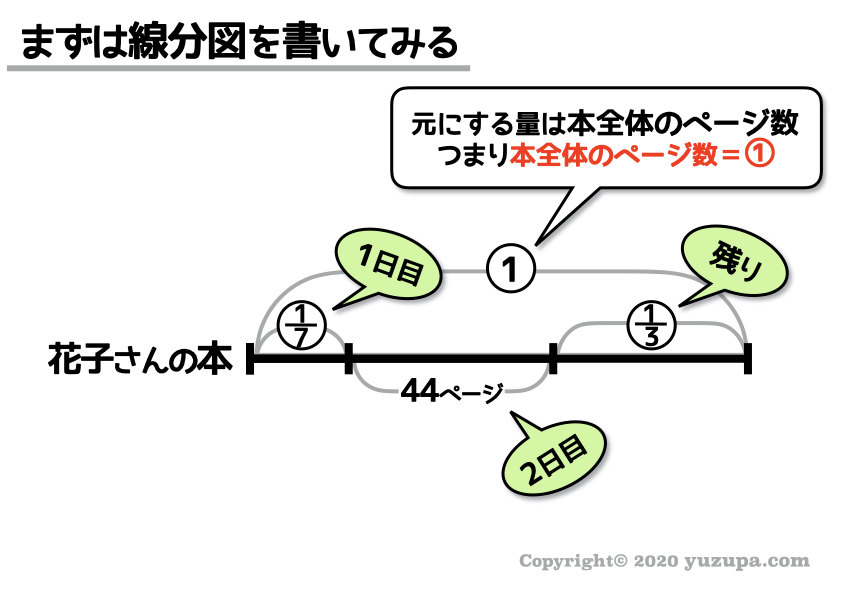
“7分の1”や”3分の1”は割合なので丸数字 ですね。そして”44ページ” は実際の数量なので普通の数字 で書きます。
分かるところをガンガン埋める
次のステップは問題文には直接書いていないものの、線分図を見てわかる数字をガンガンうめていきますd(^_^o)
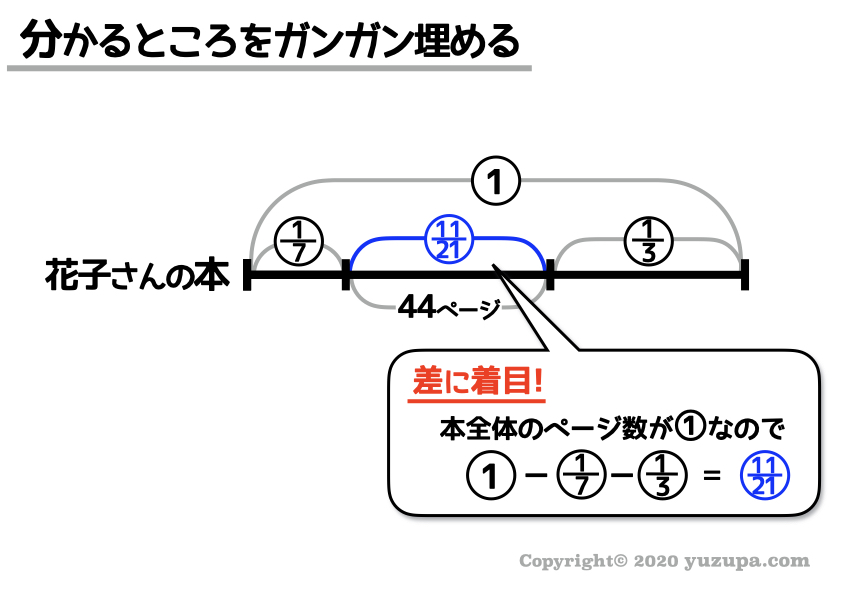
この問題の場合、線分図の本質の”差に着目” すれば、真ん中の部分の割合も分かってしまいますね ∑(゚Д゚)
割合と数字のペアを見つける
分かるところを埋めているうちに、割合と数字のペアを見つけることができたら、もうゴールはスグそこ!d(^_^o)
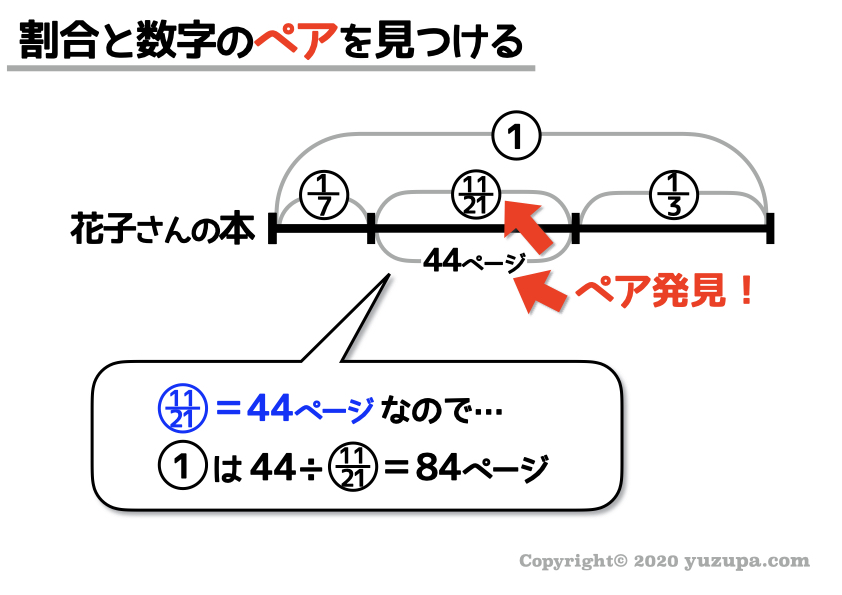
ペアが見つかれば “丸数字1つ分” が計算できます。丸数字は全て実際の数量に変換することができますd(^_^o)
この問題の場合 “丸数字1つ分”=84ページ です。初日に読んだ7分の1は 12ページだと分かりますし、2日目の終わり時点で残っていた3分の1は28ページ だというのも分かりますd(^_^o)
さて…いかがでしたでしょうか?
相当算というかっこいい名前がついていますが、大切なのは 割合と数字が入り乱れていたら… 割合と数字のペアを見つけたら解けるかも… という感覚 ですd(^_^o)
そして1つでもペアを発見できれば、一気にゴールに近づけるということもお分かりかと思います。
では例題を もう2題いってみましょう!
具体的な問題を通してマスターする
例題1
ある中学校の入学試験の結果、合格者は受験者数全体の4分の1より15人多く、不合格者は受験者数全体の5分の3より48人多くなりました。受験者数は何人ですか?
ではさっそく線分図を書いてみましょうd(^_^o)
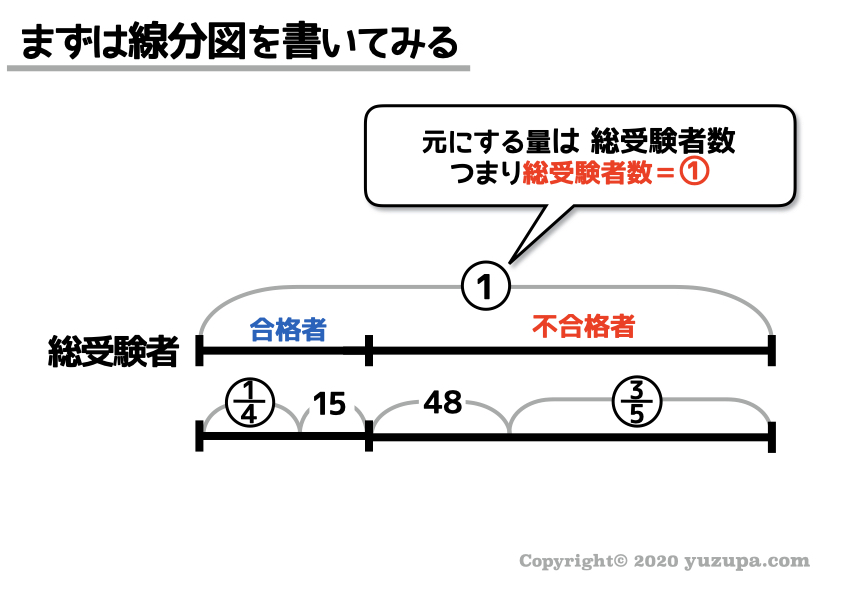
この問題の場合、受験者数全体の人数を①とおくのがよいでしょう。問題文の情報だけでここまでできちゃいます∑(゚Д゚)
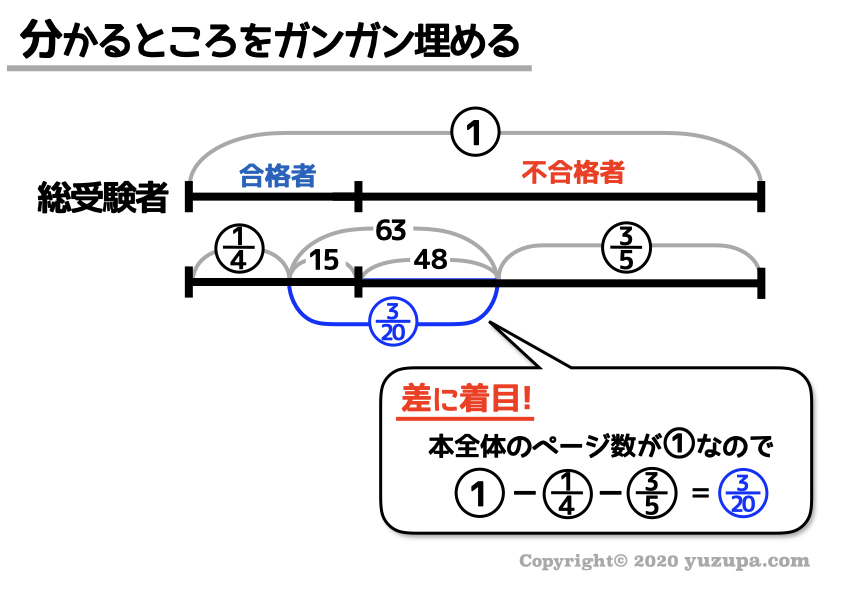
線分図の本質である“差に着目”すると、さらに線分図を埋めていくことができますd(^_^o)
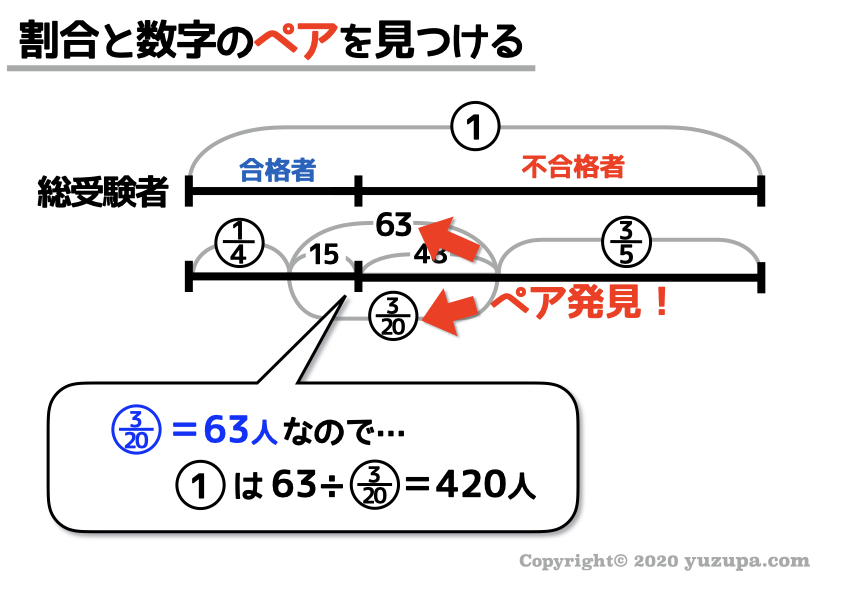
ペアを発見しましたd(^_^o)
計算すると①が420人になりますね。今回の問題で問われているのは“受験者数 全体の人数” ですので答えはそのまま420人になります。
例題2
きよし君はお小遣いをもらいました。もらったお小遣いの5分の3は貯金しました。そして残りのお金の12分の5を使って200円の文房具を買いました。もらったお小遣いはいくらだったか?
ではさっそく線分図を書いてみましょうd(^_^o)
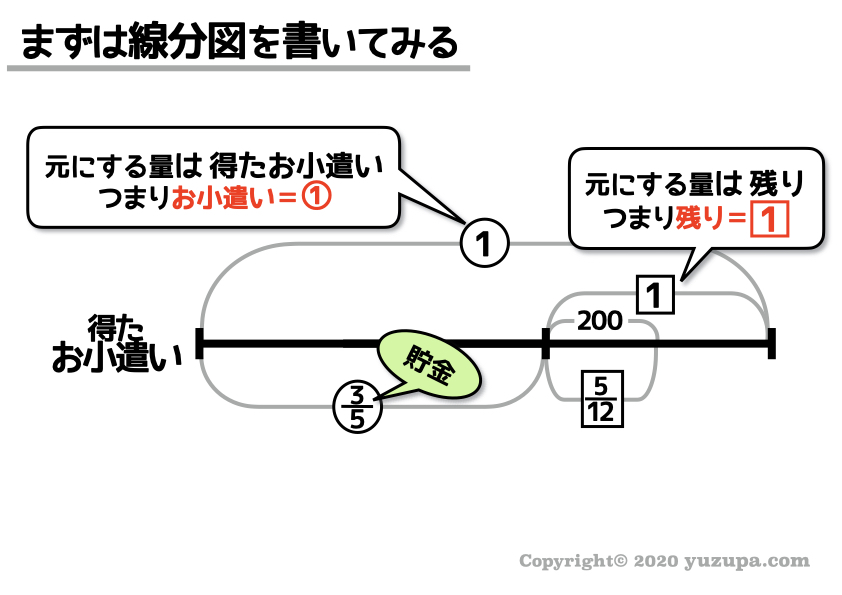
今回注意しなければならないのは いわゆる“元にする量”が2つ登場することです∑(゚Д゚) 元にする量が違うので、丸数字ではなく…四角数字を使います。
この時点で既にペアが見つかっちゃいますが、先にうめられるところをガンガンうめてしまいましょうかね…。
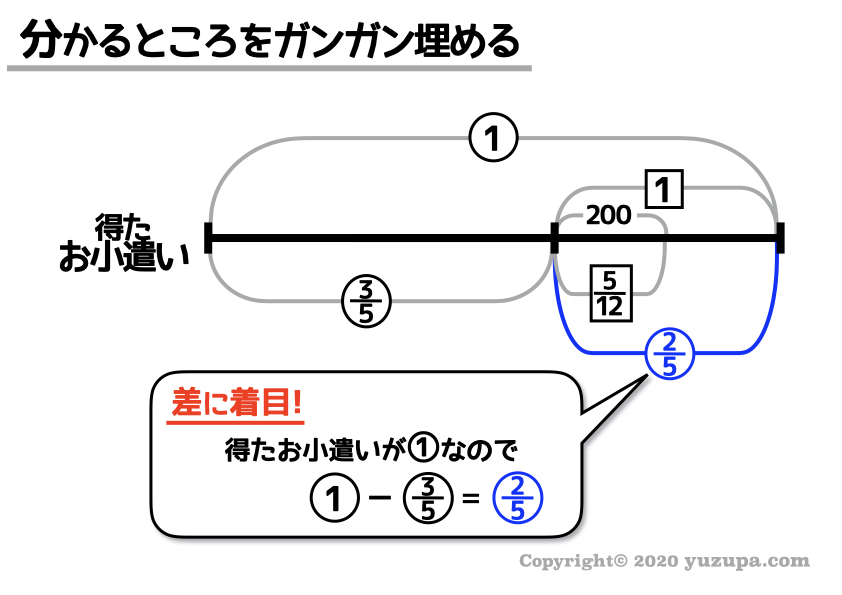
いつものように“差に着目”ですd(^_^o)

四角数字のペアを発見しました!
これで“四角ひとつ分”がわかりますね。計算すると“四角ひとつ分”は480円であることがわかります。
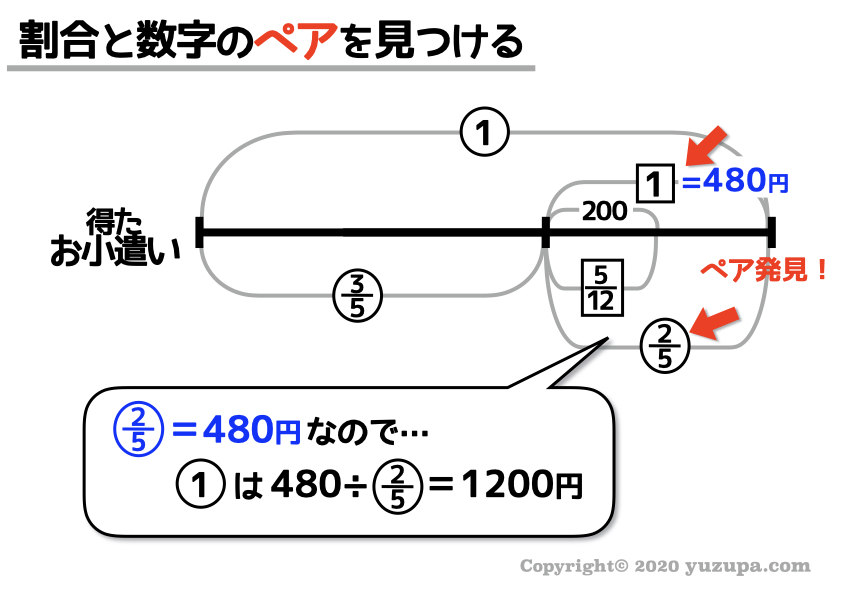
これで、めでたく丸数字の方のペアも発見できましたd(^_^o) “丸数字ひとつ分”は計算すると1200円ですねd(^_^o)
問題で書かれているのは、もらったお小遣いなので、答えは1200円になります。
まとめ
今回は特殊算の中でも、ひときわモヤモヤする存在…”相当算”についてその攻略法を開設しましたd(^_^o)
繰り返しになりますが、問題文を見てすぐに相当算だと気づく必要は全くありません。大事なことは…
割合と数字が入り乱れてたら
ペアを見つければ解けるかも…
という感覚
実際には、旅人算や平均算、図形など多岐にわたる分野と複合的に問題が構成されることも少なくありません_φ(・_・
そして、割合と数字のペアを見つけるという簡単なひとつのコツさえつかんでしまうことが重要ですd(^_^o)











いつもありがとうございます。 毎回 分かりやすい纏め方をしてくださっており助かっています。 6年の息子は今が天王山なのですが、算数で 「比と相似を使った面積の求め方」 と 「数列、規則性、場合の数」 がとても苦手です。
特に数列、規則性は 公式を見るだけで嫌がります。
面積の比は、順番等がごっちゃになってしまっている様子。
何か良い方法やノウハウはおありでしょうか?
このブログの面積図で、息子は面積図へのアレルギーがなくなりました。
とても分かりやすいと。
お手数ですが、お教え下さい
77のpapaさま
コメントを頂きありがとうございます。
6年生の夏とのことでまさに天王山…陰ながら
応援させていただきます!
規則性(数列など)については、
試行錯誤する武器を持っていないのかもしれません
そのような記事はまだ書いていないのですが、
難しい規則性の数列を見た瞬間に分かる子供は少なく
隣同士の数字の差をとってみたり、
商をとってみたり、隣同士の数字を出してみたり、
と試行錯誤している間に、規則性に気づくというものです。
数列に使える道具は他に何があるか…
それをリストアップできれば、試行錯誤の道具を
待つことになります。
といいつつ…
私の中でも整理できていません。
以前から何件か、七つ道具と銘打って、
試行錯誤に使える道具をリスト化する
記事をまとめていますので、規則性に
ついてもリスト化できるか検討してみます!
ゆずぱさん
お忙しい所、ありがとうございます。 規則性は地道な練習から、コツを掴むということでしょうか。 いやなことからか、 どうにも階差数列や三角数、四角数の公式やパターンが理解できないよ様子です。
規則性のリスト化、期待してお待ちしております。