中学受験：ニュートン算とは？ “３つの基本” だけで簡単に解ける！

ニュートン算…実は “たった３つの基本” で頭の中がスッキリする！

かるび勉強部屋の ゆずぱ です o(^-^)o

今回はニュートン算について。苦手意識を持っている小学生も多いかと思います(-_-;) 私の子供達も嫌いでした…。問題の土台になっているのは “仕事算” なので、単位時間あたりの仕事量という考え方で出来るはずなのに…なぜか出来ない (>_<

難しいと感じる理由、それは…
仕事を増やすクセモノが居るから

多くの解説サイトでは、はじめの量が分かっている場合はこうやる… 単位当たりの仕事しか分からない場合はこうやる…という具合に 場合分けで解説しているサイトが多い…∑(ﾟДﾟ)

この手の解法は…複雑な問題になると分からなくなる

賛否はあるかと思いますが、あえて…ニュートン算の本質である ” 仕事を増やす要素がある ” から導かれる “３つの基本” で理解する方法 をご紹介しますd(^_^o)

私の子供たちには好評ですので ニュートン算が苦手なお子様はぜひお試しください！

 

 

ニュートン算とは？ ３つの基本

本質は “仕事を増やす要素”

まず “ニュートン算とはナニモノなのか？” から解説したいと思いますd(^_^o)

土台となっているのは仕事算。つまり１分間にする仕事量を扱う “単位時間あたりの量” の分野。でも１つ大きな特徴があります。それが “仕事を増やす要素” があるというもの_φ(･_･

具体的に見てみましょう。

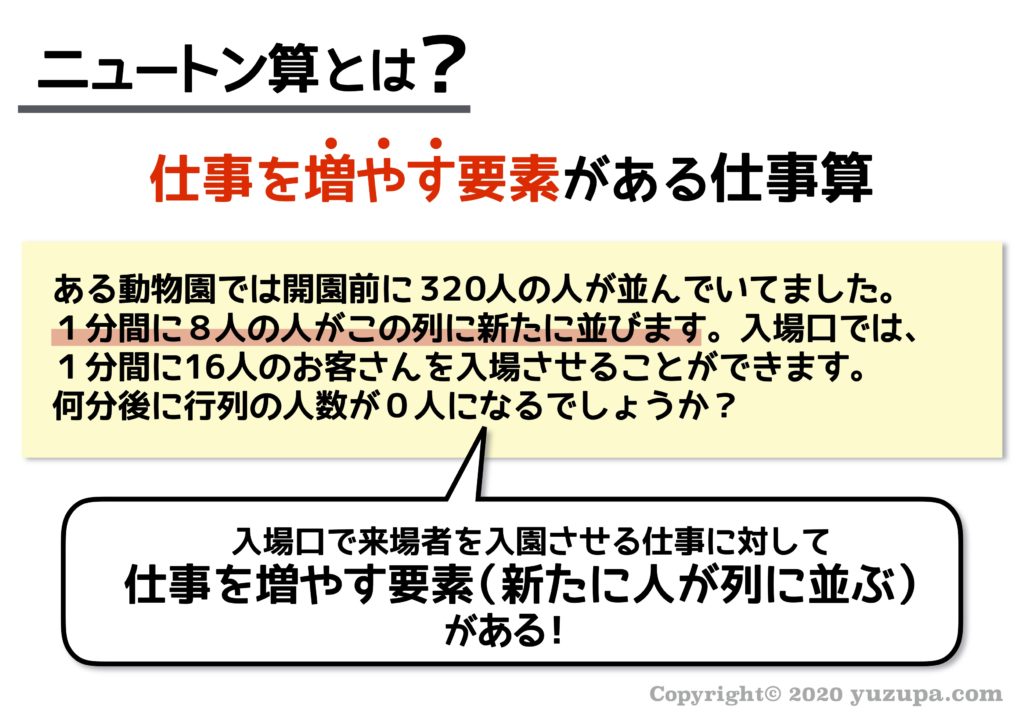
１分間に１６人のお客さんをさばくことができる…ほら、単位時間あたりの仕事量が出てくる “仕事算” ですね。でも、本質は赤いアンダーラインの部分にありますd(^_^o)

ただ単位時間あたりに仕事をさばくのではなく、“仕事を増やす(邪魔者の)要素”があるんです。この問題の場合、仕事をさばいている最中も、新たに人が列に並ぶというもの。

この 本質を理解するため “３つの基本” をご紹介しますd(^_^o)

 

基本① ３つの数字を整理する

ニュートン算で最初にやること…それは 問題文から３つの数字を読み取ること です。その３つの数字とは… 仕事が増える数、仕事のはじめの数、仕事をさばく数 の３つです_φ(･_･

冒頭に紹介した問題の場合… １分間に８人ずつ新たに行列に加わるので “仕事が増える数” は “１分間に８人” ですねd(^_^o) 残り２つの数字も問題文から読むことができます。

基本② 未来予想図を描く

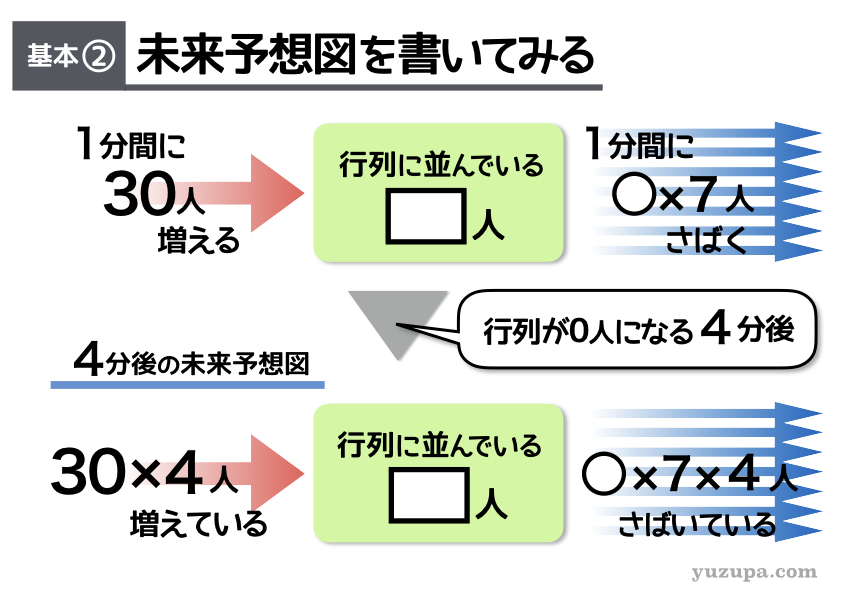
２つ目の基本は、未来予想図を書くという点です。例えば…１０分後の未来予想図を書いてみましょう。１０分後にはどれだけ仕事が増えているでしょう？どれだけ仕事をさばいているでしょう？

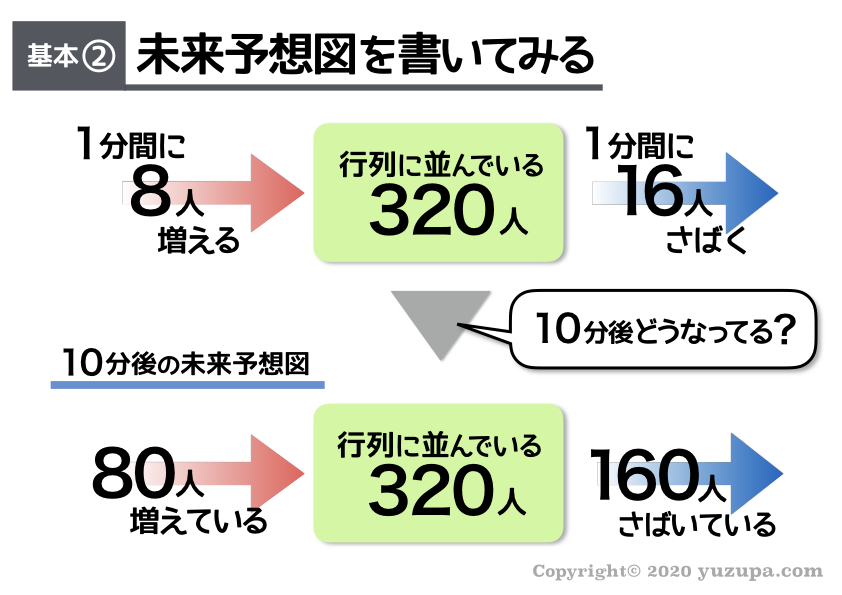
この問題の例の場合、”１分間に８人”ずつ仕事が増えていますので、１０分後には８０人分の仕事が増えているはずです。(ちょっと表現が古い感じですが…) 未来予想図を書くことが大切ですd(^_^o)

もちろん１分間に１６人の仕事をさばいていますので、１０後までに１６０人の仕事が減っているはず です。

基本③ 式を立てる(たまった仕事 と さばいた仕事)

最後の基本③が超大事です！

まさにニュートン算の本質です。さきほど書いた未来予想図で  “80人” と “320人” は10分後の未来までに “たまった仕事” の合計 です。一方 “160人” は10分後の未来までに “さばいた仕事” の合計 です。

そして この２つの数字の関係性が重要 なんですd(^_^o)

描いた未来予想図で、仕事がちょうど無くなったという条件 であれば “たまった仕事”＝”さばいた仕事”という式を立てれば良いでしょう。ほとんどのニュートン算ではこの式をたてますd(^_^o)

描いた未来予想図で、まだ仕事が残っているという条件であれば  “たまった仕事”ー”さばいた仕事” を計算すれば、残っている仕事を求めることができるでしょう。 

“３つの基本” はコレだけです。特に３つ目の基本である式を立てる時の考え方が超重要です∑(ﾟДﾟ) この “３つの基本” だけで全てのニュートン算を解くことができますd(^_^o)

 

ニュートン算は “３つの基本” だけで解ける

実際に具体的な例題で “３つの基本” を体得していきましょう！

例題① まずは基本的な問題

問題文

この問題では “１分間に８人が新たに行列に加わる” という部分が “仕事を増やす要素” ですね。さっそく３つの基本にしたがって、問題文を整理していきましょうd(^_^o)

３つの基本を整理

３つの数字は全て問題文にダイレクトに書かれているので、すぐに整理できるはずですd(^_^o) 問題文を読みながら以下のように数字を整理できましたでしょうか？

次は未来予想図を書いてみましょう。この問題では “行列が０人になる未来予想図” を書く必要 があります。何分後か分からないので以下のように□分後として書きましょうd(^_^o)

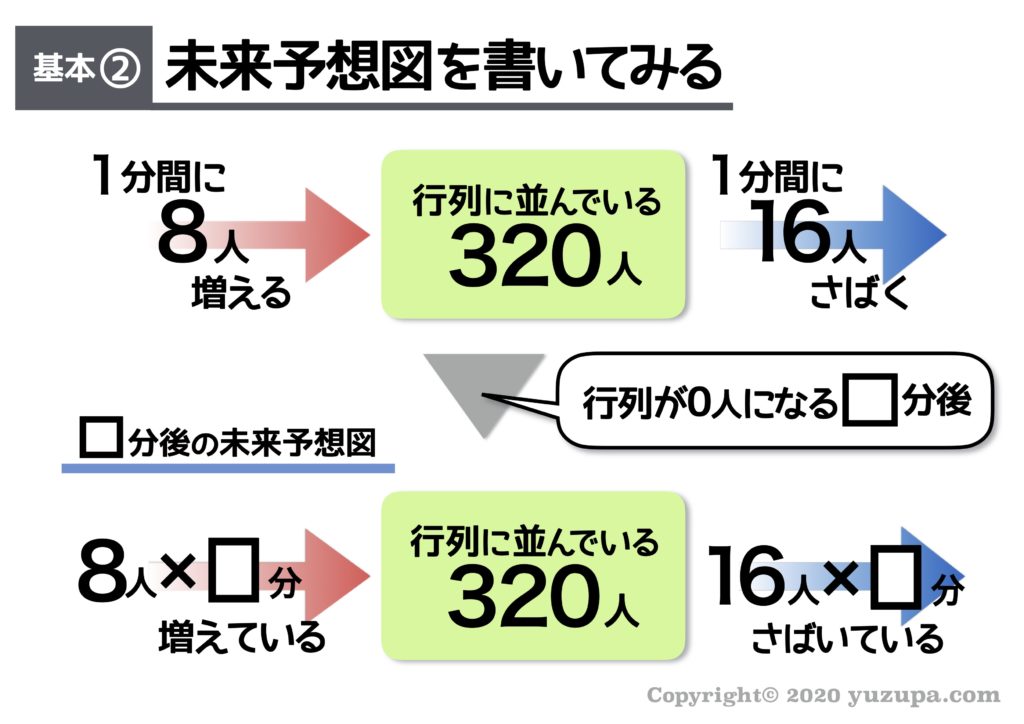
最後は式を立てます。この□分後の未来予想図で ちょうど行列が０人になるので “たまった仕事” = “さばいた仕事”という式 を立てることができれば本質をシッカリとらえることができていますねd(^_^o)

計算する

最後は計算です。□を含む “虫食い算” です。

答えは 40分後 ということになりますd(^_^o)

 

例題② “３つの基本” を２回やる

問題文

この問題の場合は水槽から水をくみ出すという仕事に対して… “１分間に８Ｌの水が入ってくる”という”仕事を増やす要素” がありますねd(^_^o) 赤いアンダーラインの部分です。

３つの基本を整理

ポンプを２つ使って仕事をした場合のことが問題文に書かれているので、ポンプを２つ使った場合の３つの数字整理を行います。以下のように整理できればＯＫです！

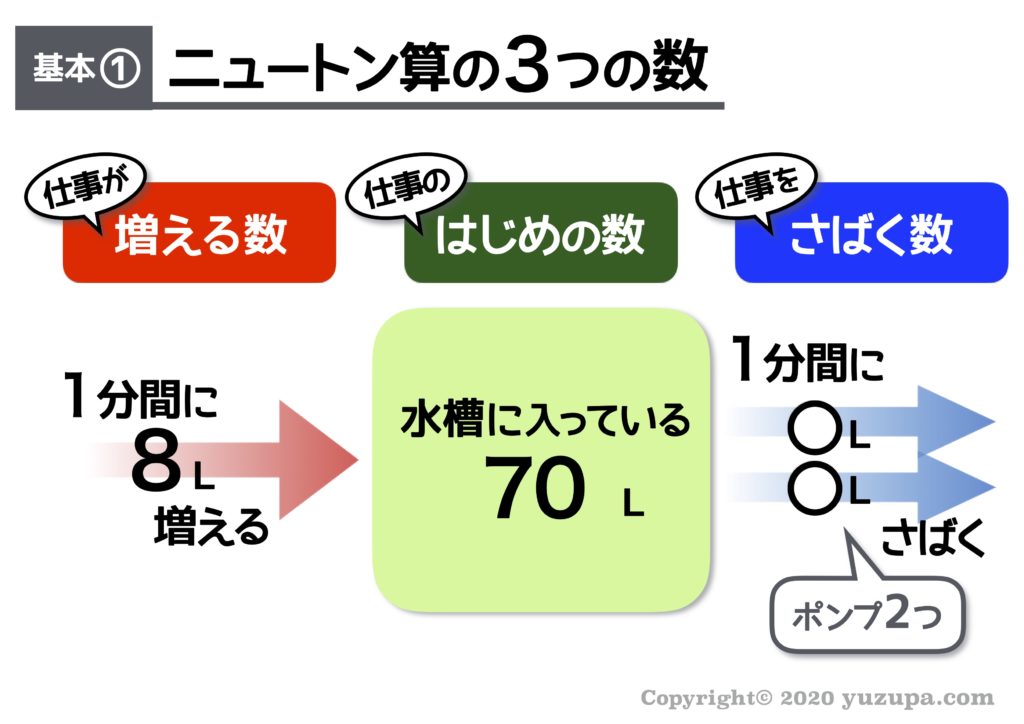
問題文に３５分後に水がなくなった(＝仕事が全部さばけた状態になった)とあるので、書くべき未来予想図は ３５分後の未来の世界 ですねd(^_^o) ３５分後はどうなっているでしょうか？

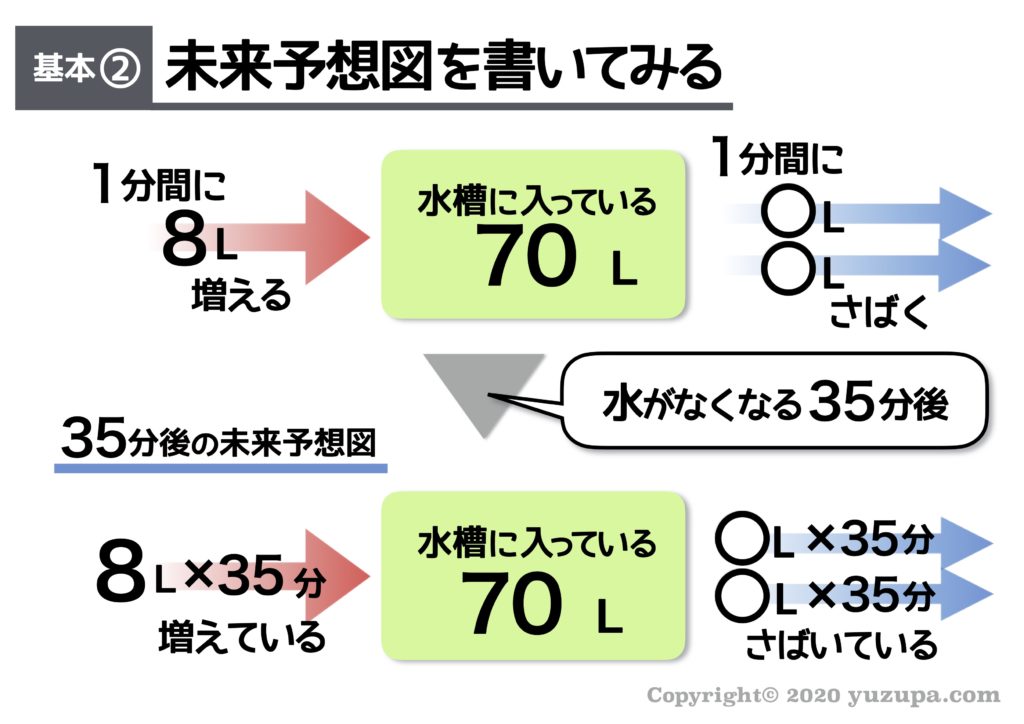
最後は式を立てます。３５分後の未来は “仕事が全てさばけた状態” ですので、”たまった仕事” ＝ “さばいた仕事” という式をたてることになります。

計算する

最後は計算です。○を含む 虫食い算 ですね！

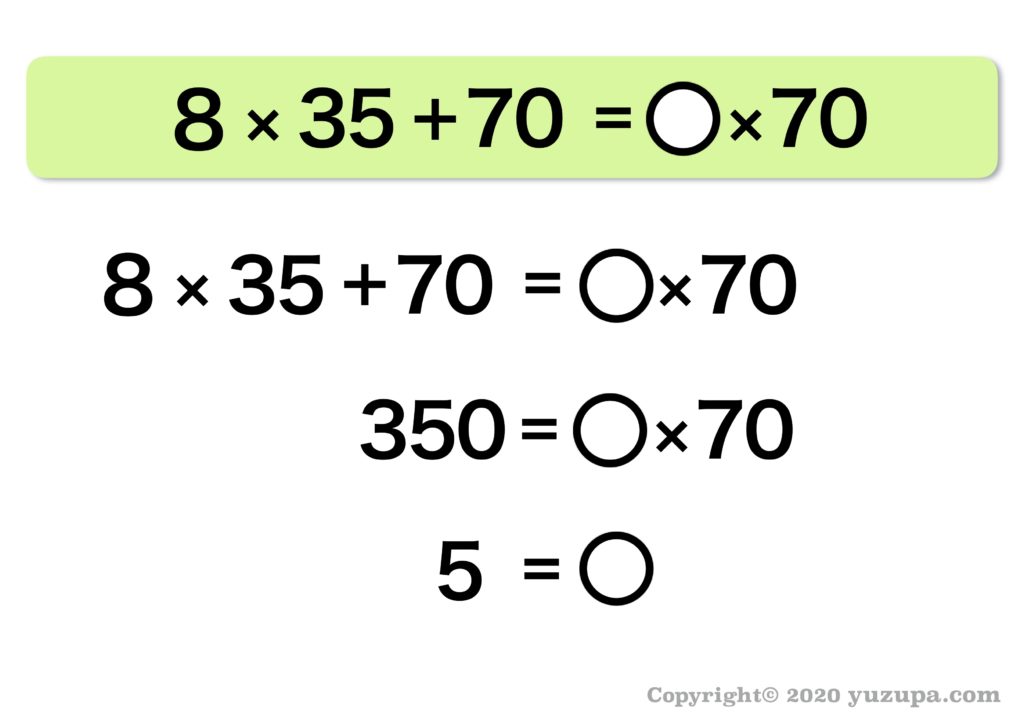
○は５となりました！ これでポンプ１つが１分間にくみ出すことができる水の量は５Ｌ であるということがわかりました。数字が追加でわかりましたので “３つの基本”をあらためて整理 してみましょうd(^_^o)

あらためて ３つの基本を整理

ひとつのポンプは１分間に５Ｌの水をくみ出すという仕事をさばくのが分かったので、あらためてポンプが３つの時の数を整理してみます。

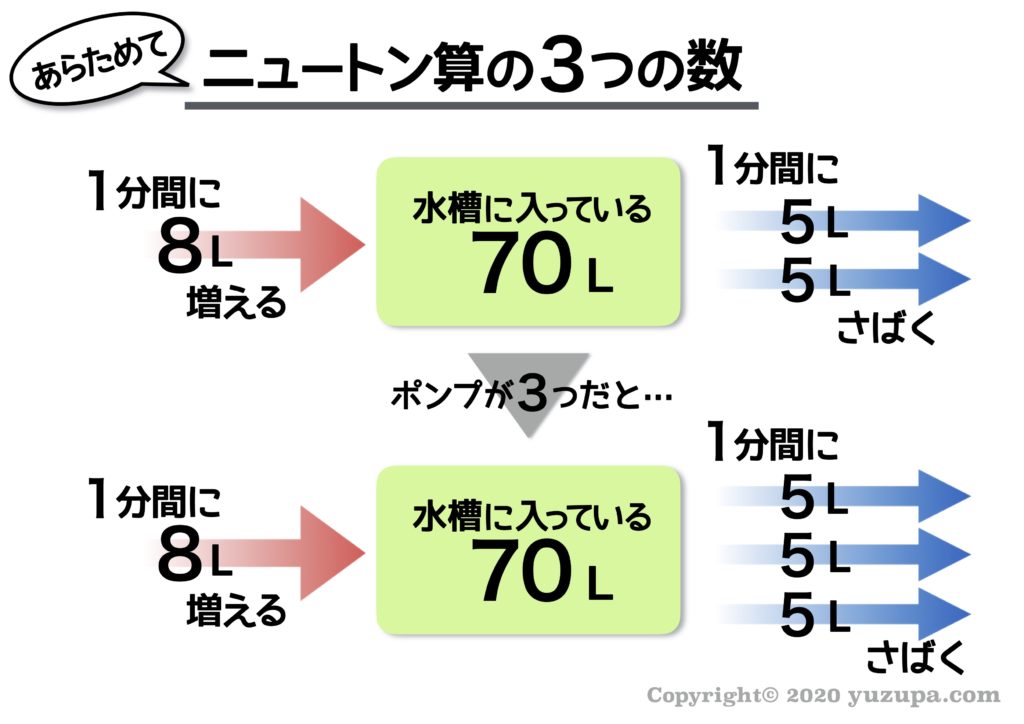
そして水槽から水がなくなる(＝残っている仕事がなくなる)未来予想図を描いてみましょう。ここまで来れば例題①と全く同じです ね ∑(ﾟДﾟ)  □分後の未来予想図を描きましょう。

 

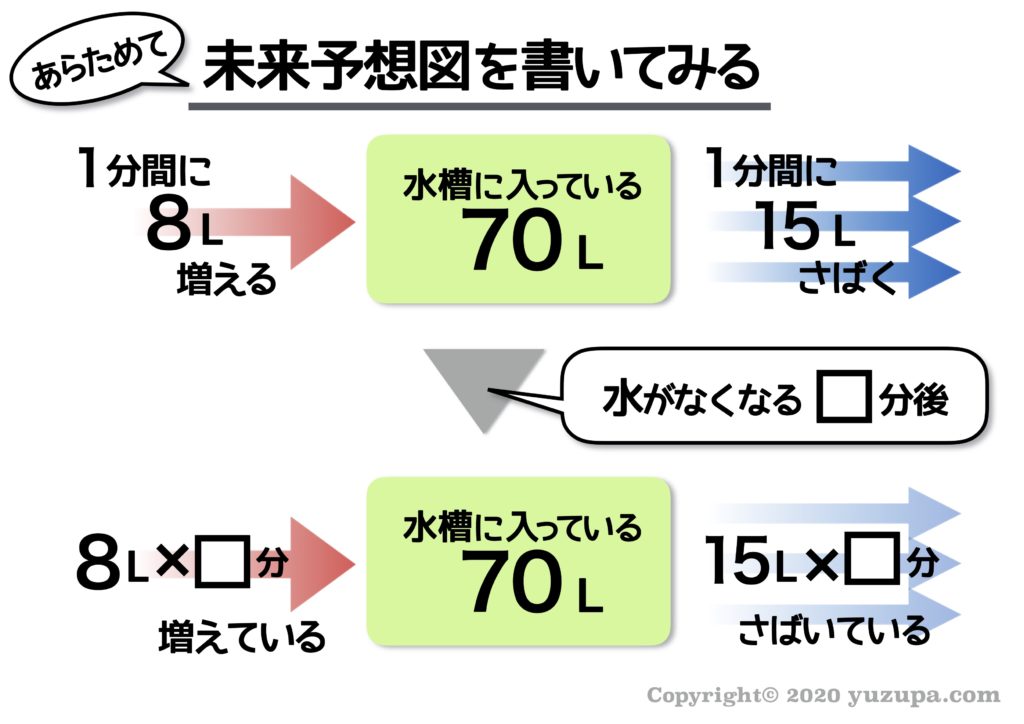
残っている仕事がなくなっている状態なので “たまった仕事” ＝ “さばいた仕事” という式を立てれば良いですねd(^_^o) ２回目なので慣れましたでしょうか？

 

あらためて 計算する

最後は計算です。虫食い算も慣れましたか？

 

答えは１０分後 となりますd(^_^o)

 

例題③ 計算がちょっと難しい

問題文

この問題も行列をさばく系の問題ですね。そしてニュートン算では定番の“１分間に３０人が新たに列に並ぶ” という”仕事を増やす要素” がガッツリ入っていますd(^_^o)

今回は入り口が３つの場合と７つの場合の２つが問題文に書かれているので “３つの基本” も２つの場合でそれぞれ書いてみましょう。さて…どうなるでしょうか？

３つの基本を整理(入り口が３つの時)

最初に行列に並んでいる人数が分からないので□人としています。

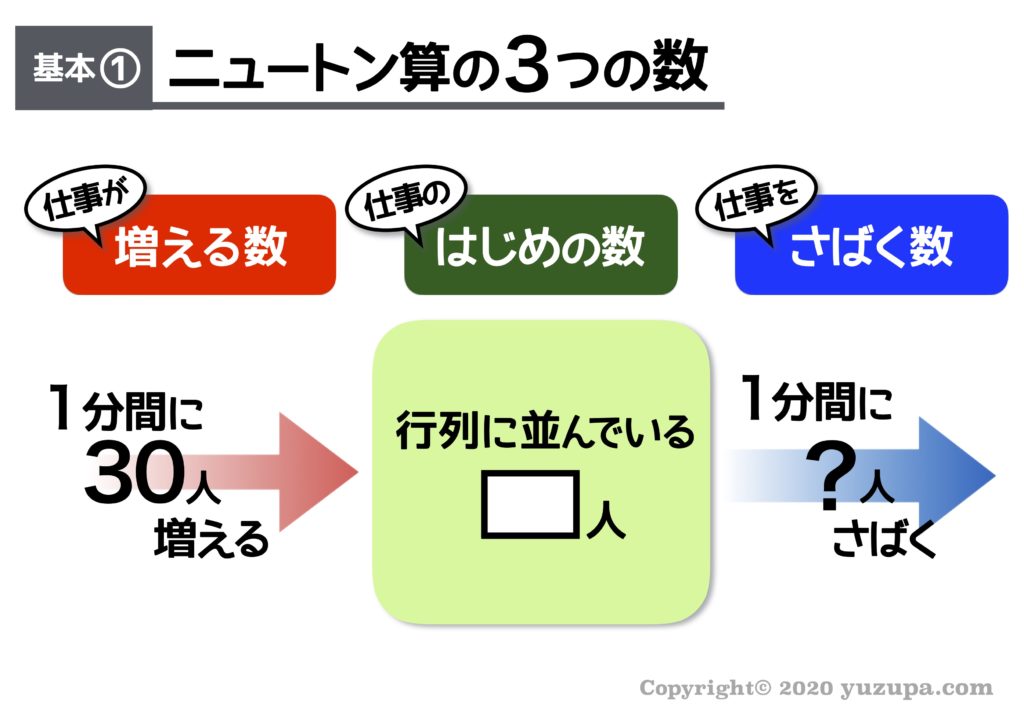
未来予想図は、問題文に “12分後に行列が無くなった” とあるので12分後の未来予想図です。１つの入り口で１分間にさばける人数を○人 としましょう。入り口が３つなら１分間にさばける仕事は “○×３” 人です。

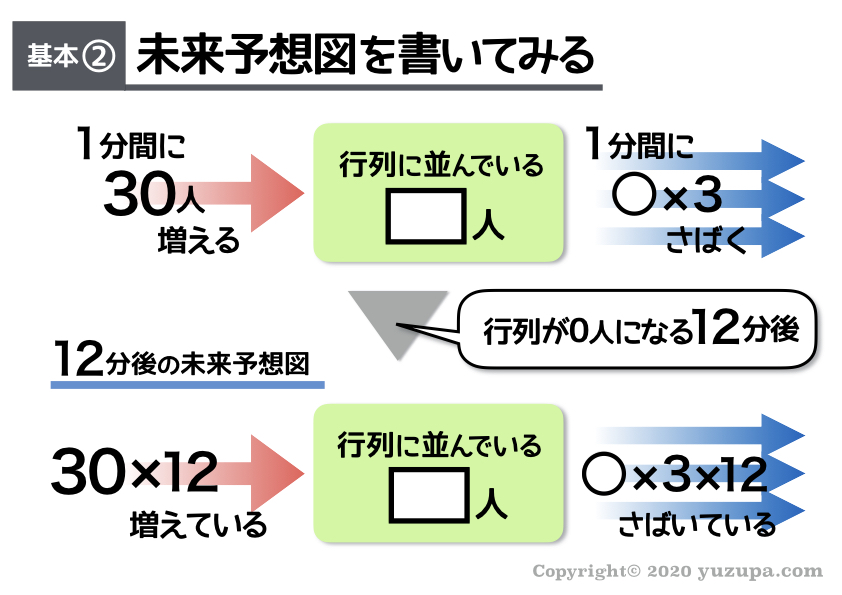
最後は式を立てますが12分後では “行列に人がいなくなる” なので、いつものように “たまった仕事” ＝ “さばいた仕事” という式をたてましょう。もう…お子様も慣れているはずですd(^_^o)

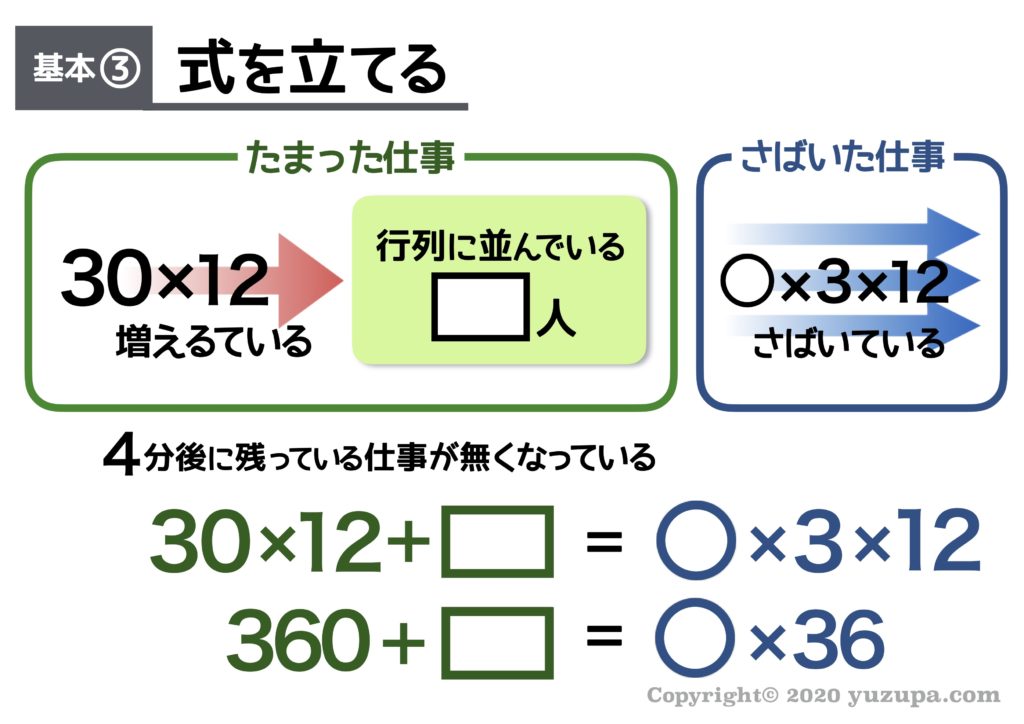
３つの基本を整理(入り口が７つの時)

今回の問題の場合は入り口が７つの場合も書かれているので、こちらの場合でも “３つの基本” をやってみましょう。自信がなくても…分からなくても…”３つの基本”を武器にして試行錯誤することが大切 ですd(^_^o)

入り口が３つの時と同様ですね (･_･;

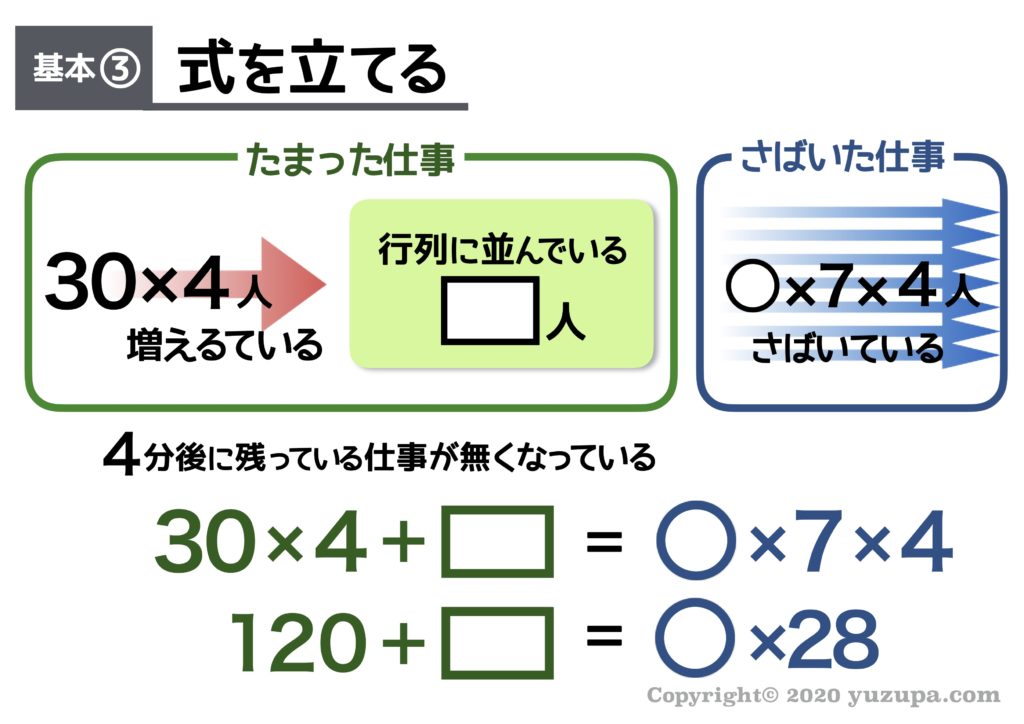
式も定番どおりです。描いた未来予想図は “行列に人がいなくなる” シーンですので、“たまった仕事” ＝ “さばいた仕事” を立てます。慣れてくると式の意味を忘れてしまうので意識することが大切です_φ(･_･

計算する

“３つの基本”をベースに情報を整理したところ式が２つ出来上がりました。そうするとシンプルな消去算がでてきました d(^_^o) いままでの虫食い算とは違いますが計算すれば答えが出ます！

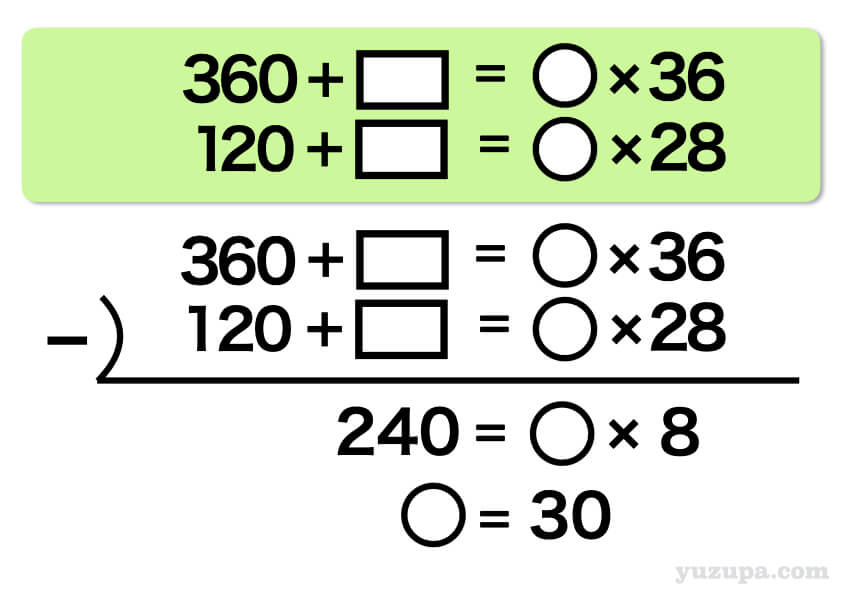
○は30となりました。つまり…１つの入り口が１分間にさばける人数は３０人ということです。答えは３０人ということになりますねd(^_^o)

ちなみに…今回の問題では求める必要はありませんが、最初に行列にいた人数は７２０人になります_φ(･_･

 

まとめ

ニュートン算は “仕事を増やす要素” が出てくる仕事算です。いろいろな解法が紹介されていますが 今回はあえて “３つの基本” という形でまとめてみました_φ(･_･

多くのサイトで紹介されている解法とはちょっと異なりますが “たった３つの基本” で解くことができますので、ニュートン算が苦手なお子様にはぜひお試しくださいd(^_^o)

私の子供達は コレで攻略できました！