中学受験：多角形の内角の和？公式を忘れなくする論理的３ステップ

公式は 論理的なステップ を把握することで忘れなくなる！

こんにちは、かるび勉強部屋 ゆずぱ です。

算数の世界で当たり前のように使っている公式。公式を丸暗記しても問題は解けますが… 応用問題で手詰まりになってしまったり、そもそも公式をすぐ忘れてしまったりします

解決する方法はただひとつ！

公式を単なる文字列ではなく論理的に理解すること… 難しいようですが小学生でも意外と簡単に習得することができます。そして一度やるともう公式を忘れませんd(^_^o)

それでは詳細にまいりましょう！

 

超重要…公式を論理的に理解する

公式よりも論理的３ステップ

算数や数学の世界では公式というものが山ほど登場しますが、複雑な公式は ”使い慣れる” ことに重点が置かれています。二次方程式の解の公式なんかはその色が強いですねd(^_^o)

でも小学生のうちから
公式の丸暗記は超キケン！！

無意識のうちに公式を使いこなせるほど慣れてしまうこと。コレも大切ですが、なぜその公式になっているかを理解していないと、後々、大きなやけどにつながるかもしれません∑(ﾟДﾟ)

多角形の内角の和の公式であれば以下のように理解しますd(^_^o)

 

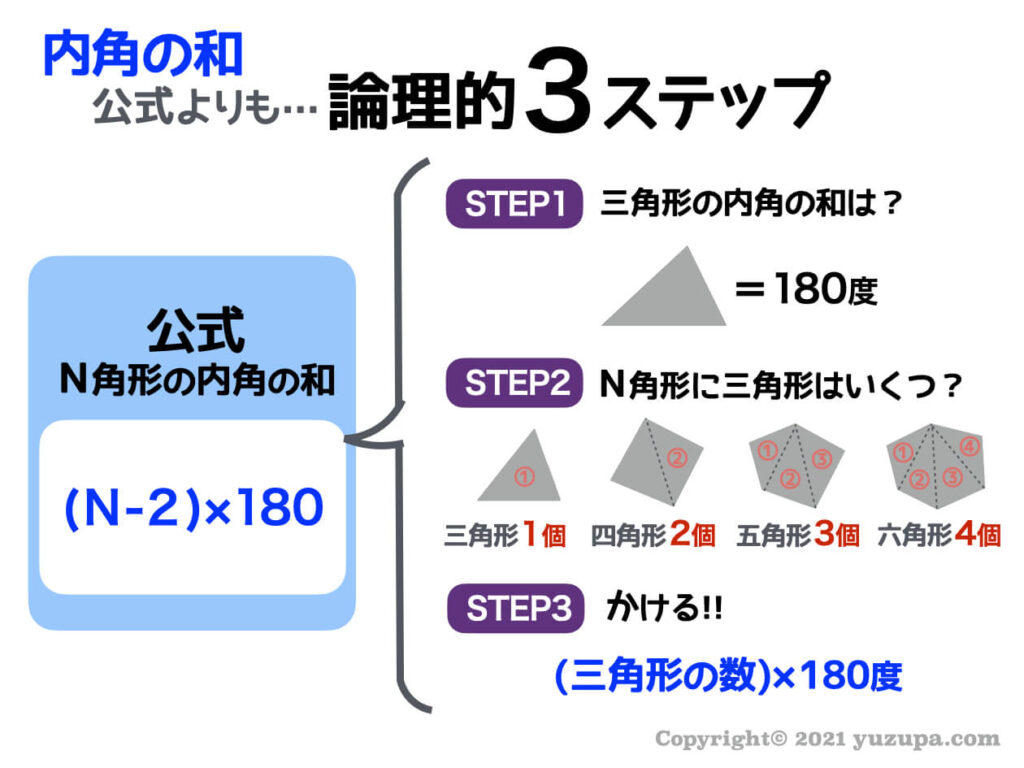
論理的に理解することのメリット

公式を丸暗記することは超キケン！と申し上げましたが…それはなぜでしょうか？公式を単なる文字式ではなく論理的な理解と共に使いこなすことのメリットをご紹介しますd(^_^o)

 

① 結果として忘れなくなる！

ちょっと変な話ですが…結果的に忘れなくなります(^_^;) その公式が導かれる論理的な理解をしようとすること自体が記憶への定着を加速させます∑(ﾟДﾟ)

無機質な文字列は覚えられませんが、
物語は一度覚えると頭から離れにくくなります

 

② 記憶があやしい時も落ちつける

人の脳はものを忘れるように作られています。算数の公式であればアレ…っとなってしまうこともよくあることでしょう。でも論理的に理解していれば、うろ覚えの公式にも確信が持てます。

公式を論理的に理解することは、
記憶があやしい時にも落ち着くことができます

 

③ 応用問題でも太刀打ちできる

論理的に公式を理解することの最も大きなメリットはコレでしょう！応用問題にも対応できるようになります。文字列として公式を暗記していたとしたら応用問題の対応は絶望的ですね (-_-;)

 

 

内角の和の公式…論理的３ステップ

内角の和の公式は３つのステップで論理的に理解することができます。全体像は以下のとおりでとてもシンプルですd(^_^o)

 

STEP1: 三角形の内角の和は？

最初のステップは三角形の内角の和です。 

三角形の内角の和はいくつでしょうか？

これは 図形問題では”超”がつくほどよく使う定理ですので ”180度！”と即答できる でしょうd(^_^o) この定理は本当によく使うので暗記してしまいましょう。

でも本当に三角形の内角は180度になるの？

イキナリ問われると”えっ…と”と戸惑ってしまいそうですが、平行線を１本ひいてあげるだけで簡単に説明可能 です。錯角と同位角が等しいということが条件ですd(^_^o)

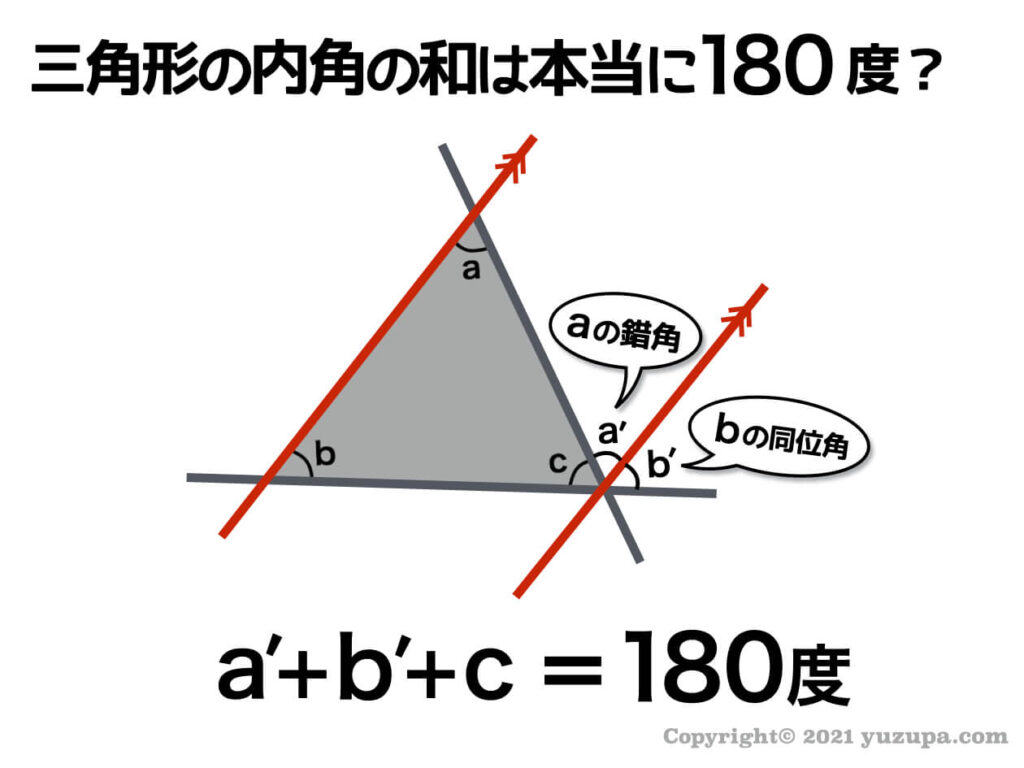
平行線を引いてあげると、aの錯角が現れ、bの同位角が現れます。そして aとbとcの角度が集まると一直線上に∑(ﾟДﾟ)  つまり… aとbとcを足すと180度になるということです。

こうして どんな三角形でも内角の和は180度 なワケですd(^_^o)

 

じゃあ、錯角はなぜ等しいの？同位角はなぜ等しいの？と続きそうですが、これらは ”ユークリッドの第五公準” としてあげられており、公理( 明らかに正しいこと )…。

明らかに等しいのが正しいと最初に決めたということです_φ(･_･

 

STEP2: 図形の中に三角形はいくつある？

次は図形の中にいくつ三角形があるか数えましょう。 

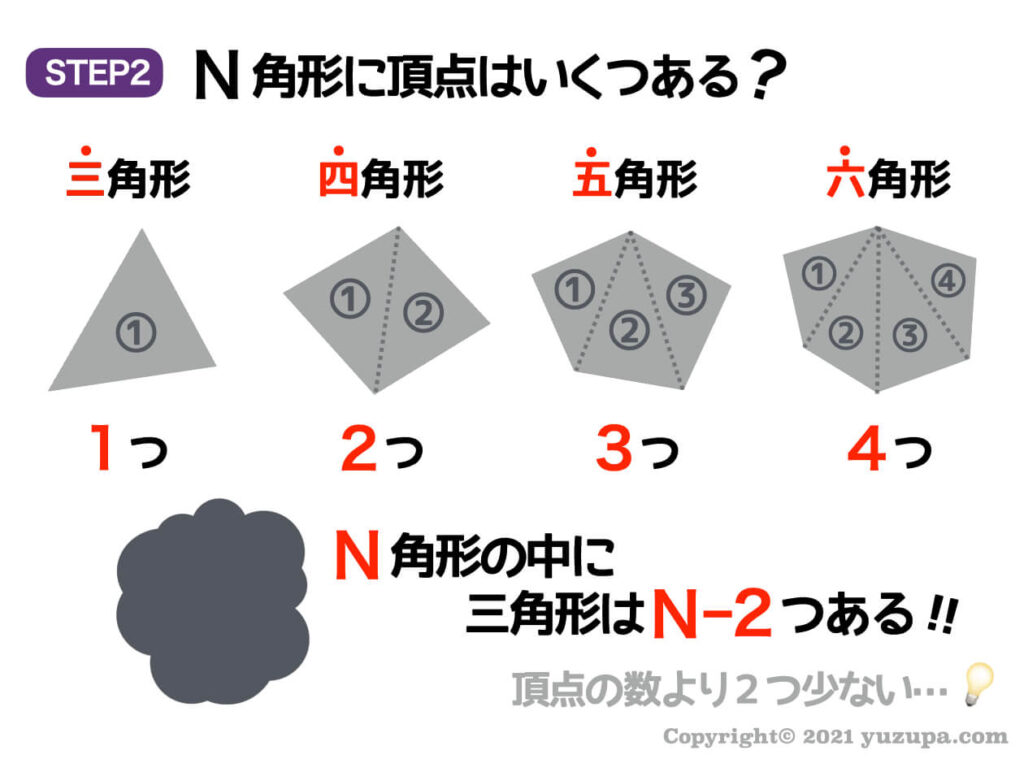
とつぜん考えても分からないかと思います(^_^;)

そんな時は三角形ならばどう？四角形ならばどう？五角形ならばどう？…という感じで具体的に考えるのが王道的アプローチ。

そう考えると、三角形の中には当然ですが三角形は１つ、四角形だと２つ、五角形だと３つ、六角形だと４つありそうです。

つまり、頂点の数より２つ少ない数となりますd(^_^o)

 

STEP3: かけ算をする!

最後は計算です。 

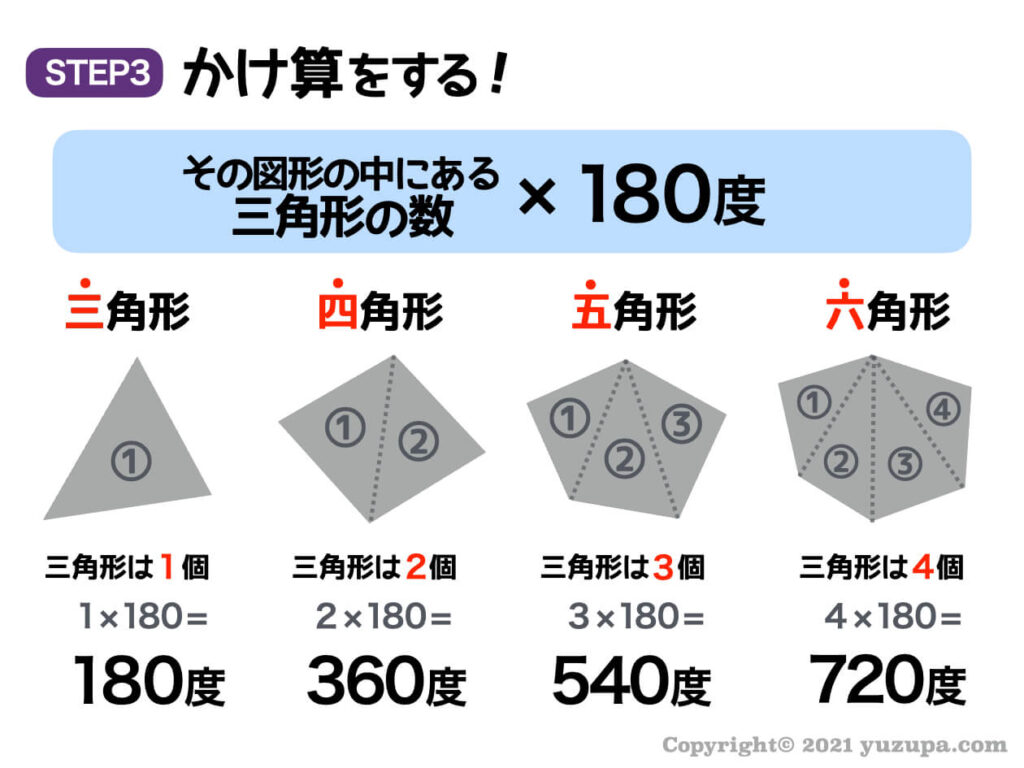
考え方は超シンプルです。

三角形の内角の和は180度なので、その図形の中にある三角形の数に180度をかけ算するだけですね d(^_^o) 

 

論理的３ステップで公式を使ってみる

公式を使う時も論理的な３ステップを意識すると、機械的な作業ではなくなります。コレ…重要ですね_φ(･_･

試しに 五百角形の内角の和を 求めてみましょう！

 

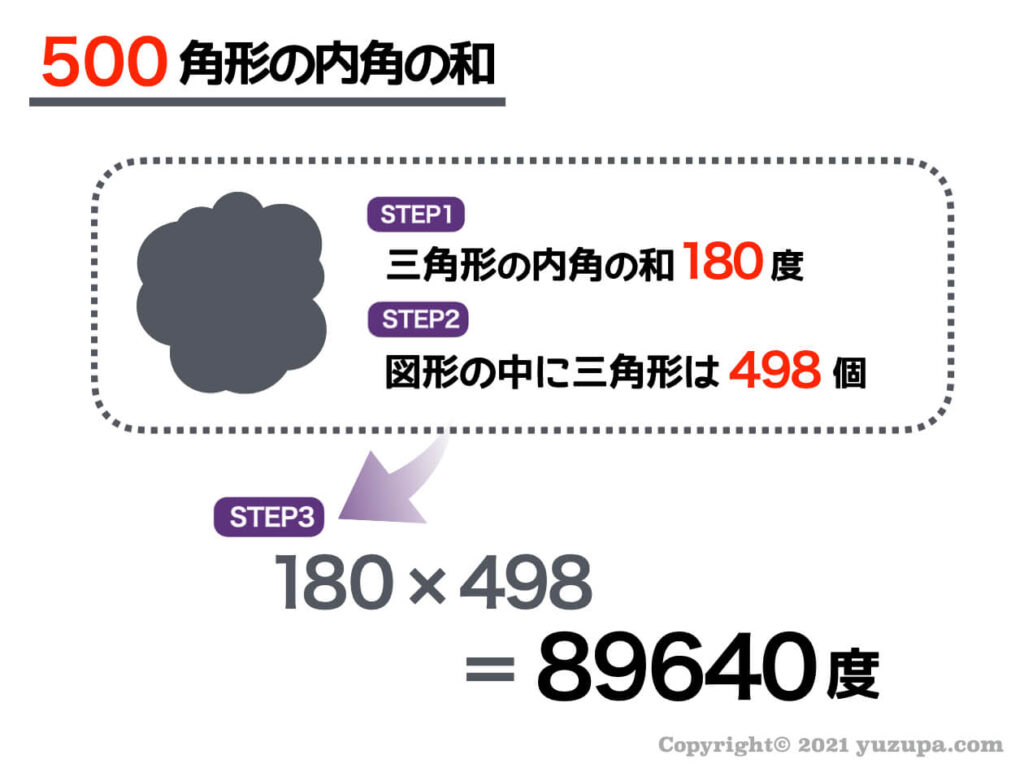
公式を暗記し、無機質に機械的な作業をするのとは、まったく異なる感じがしますd(^_^o)

 

まとめ

今回は多角形の内角の和の公式を論理的に理解するための３ステップをご紹介いたしました。まったく同じ作業であっても、意識するのとしないのとでは大きな差 がありますねd(^_^o)

そして論理的３ステップを一度でも理解できれば、公式はほぼ忘れなくなるという大きなメリットがあります。もし公式をすぐに忘れてしまうなどのお悩みがある小学生は、ぜひお試しを！