中学入試 問題解説：既約分数を扱う問題 2017年駒場東邦

もう約分できない分数 “既約分数” の難問… 素数を使いこなして攻略せよ！

こんにちは。かるび勉強部屋 ゆずぱ です。

今回は読者の現役受験生である 小学６年生の方からリクエスト のあった入試問題の解説に挑戦してみたいと思いますd(^_^o)

当ブログで入試問題の解説は初めての試みです∑(ﾟДﾟ)

今回いどむ問題は 2017年の 駒場東邦中 の入試で出題された算数の問題 … 既約分数に関する問題で、素数を使いこなさないと解くことができません(･_･;

それでは詳細に参りましょう！

 

 

入試問題例

ではさっそく問題を見てみましょうd(^_^o)

いかがでしょうか？

既約分数という難しそうな言葉が出てきますが…それ自体は難しいものではなく普段から皆さんがやっていることですねd(^_^o)

小問１は この言葉の意味が理解できていればスンナリ解くことができます。

難問は小問２と小問３ですね…(>_<)

解説を見るまえに、ぜひ鉛筆を使って試行錯誤してみてください_φ(･_･

 

 

 

解説例１

それでは設問１から解説して参りますd(^_^o)

この問題…実は 普通に約分しまくれば難なく解けてしまいます d(^_^o)

でも これ以上約分できない という言葉から…かけ算の形の最小単位である “素数” に着目 できることが重要です∑(ﾟДﾟ)

素数に着目するとは、登場する数字を 素因数分解してみる ということです_φ(･_･

それぞれの分数を、これ以上分割できない最小単位の数字＝素数 で表すことができます。

そうすると いつもやっている約分が超スッキリ 見えてきます∑(ﾟДﾟ)

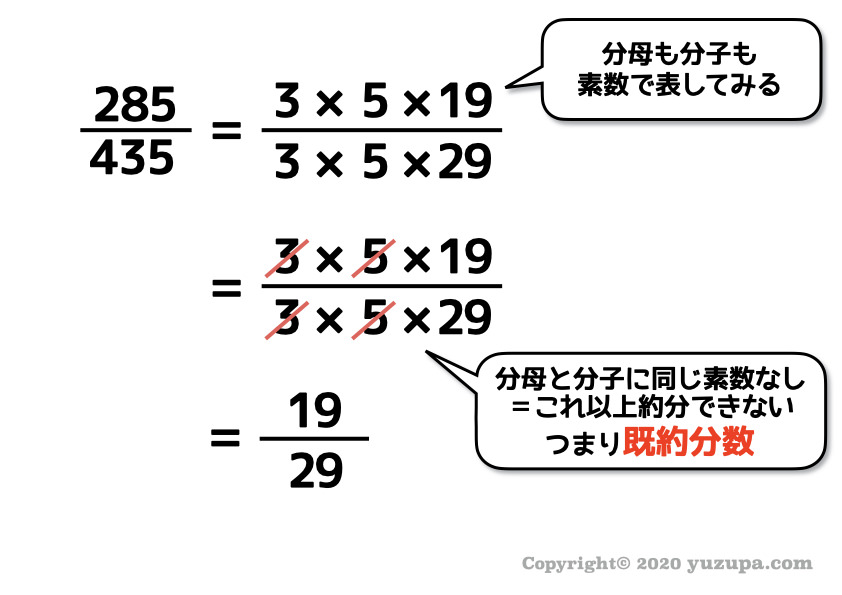
もうひとつの分数も同様ですd(^_^o)

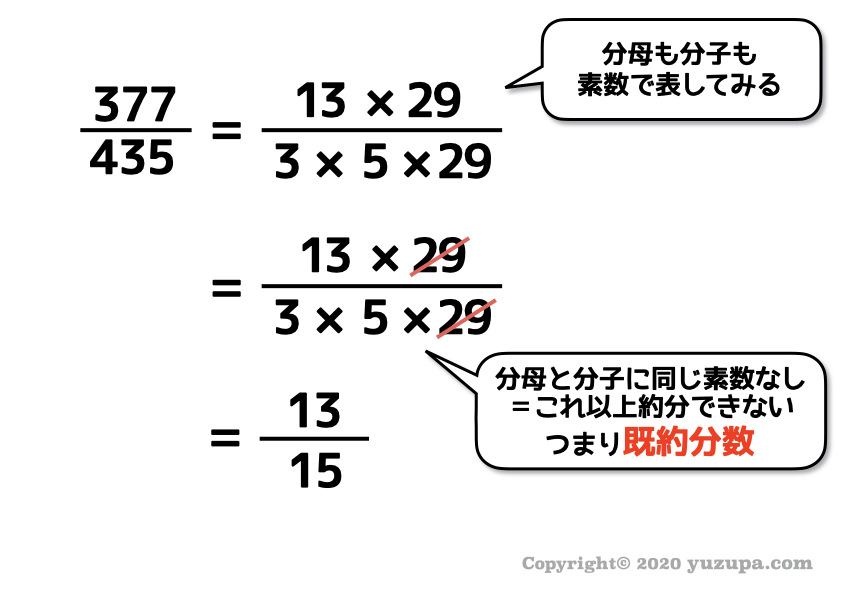
実はコレが約分の本質ですd(^_^o)

分母も分子も素数で表してしまえば、これ以上約分できないということが目に見えて分かる のです！

素数についての 細かい解説は以下の記事で
参考：素数とは？

 

 

 

 

解説例２

次に設問２の解説に参ります。

さて一気に難易度があがりました…が、先ほどのように 分母も分子も素数で表すという意識 をもってのぞみましょう。

分数が既約分数…つまりこれ以上約分できないとはどういうことでしょうか？

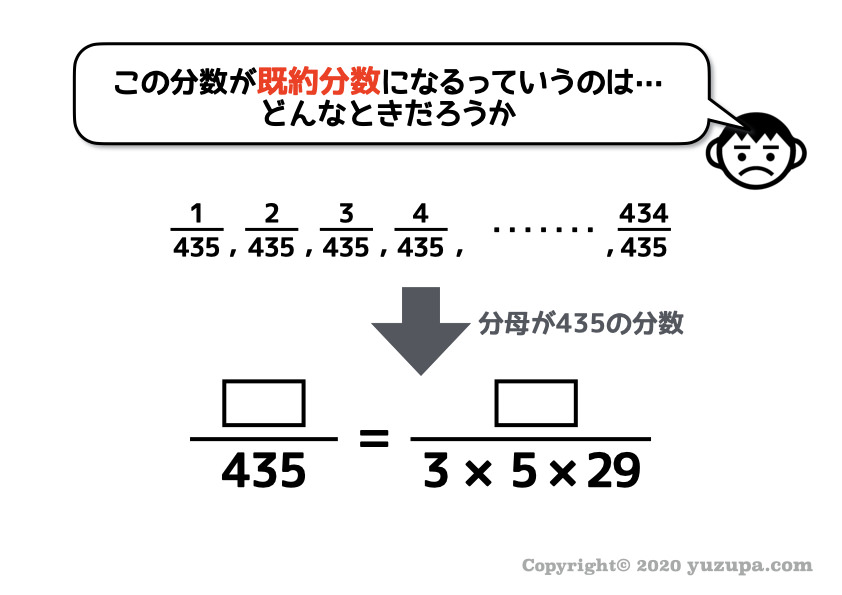
分母が435の分数を、素数で表してみるとこのように分母が 3 x 5 x 29 の分数ですね。

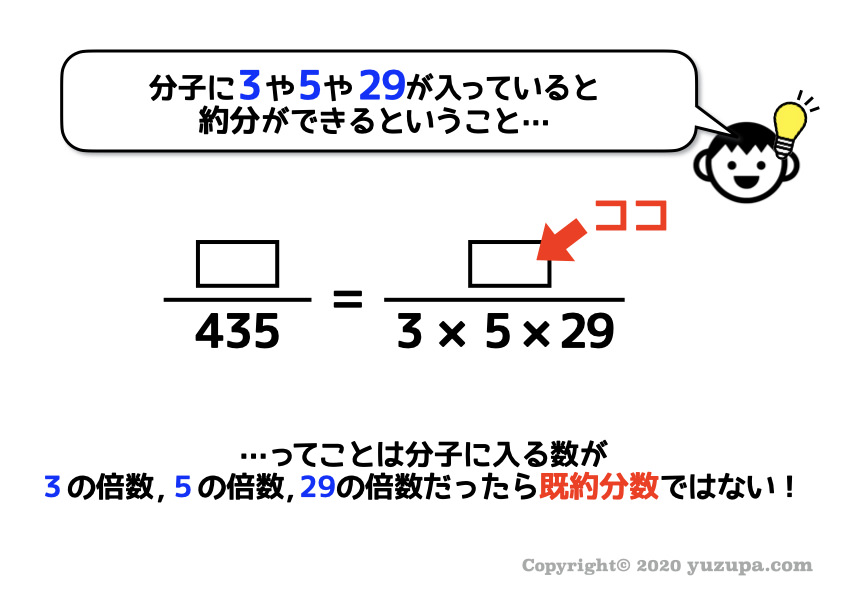
この分数の分子が3や5や29の倍数である場合にはまだ約分できる ということになります。

わからない方のために…具体的に見てみましょうd(^_^o)

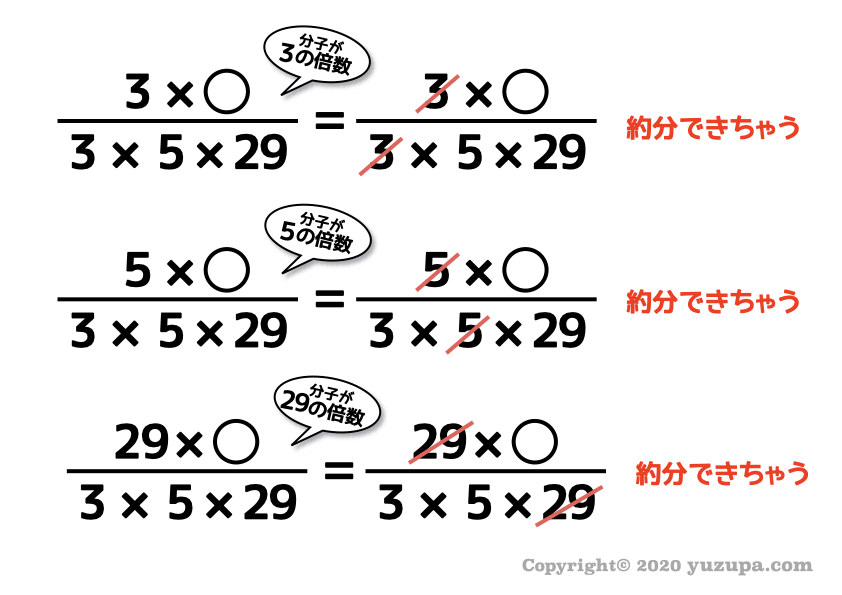
ほら、分子が３の倍数や５の倍数や２９の倍数だと約分できちゃう んです(^_^;)

一方、３の倍数でも５の倍数でも２９の倍数でもない場合はどうでしょうか？

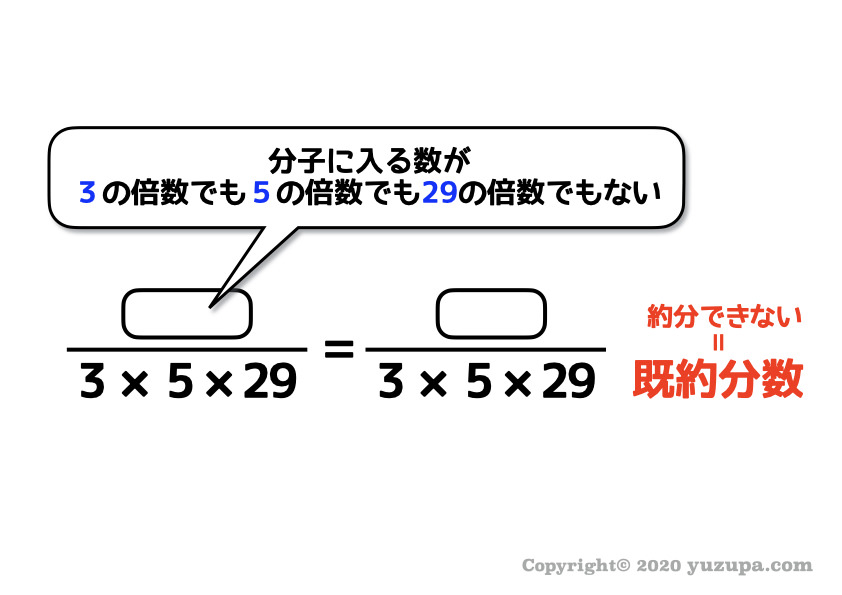
約分することができませんね…つまり既約分数ですd(^_^o)

本題に戻りましょう…それでは既約分数の数を数えるにはどうしたらよい でしょうか？

とてもシンプルですd(^_^o)

既約分数となる分子…つまり、３の倍数でも５の倍数でも２９の倍数でもない数がいくつあるか数えれば良い のです！

数えるには、あのツールを使いますd(^_^o)

ここで登場するのがベン図です∑(ﾟДﾟ)

モノの数に関する問題 … “集合算” と呼んだりしますが、その代表的なツールがベン図です。

では具体的にベン図に３の倍数、５の倍数、２９の倍数を表してみましょう。

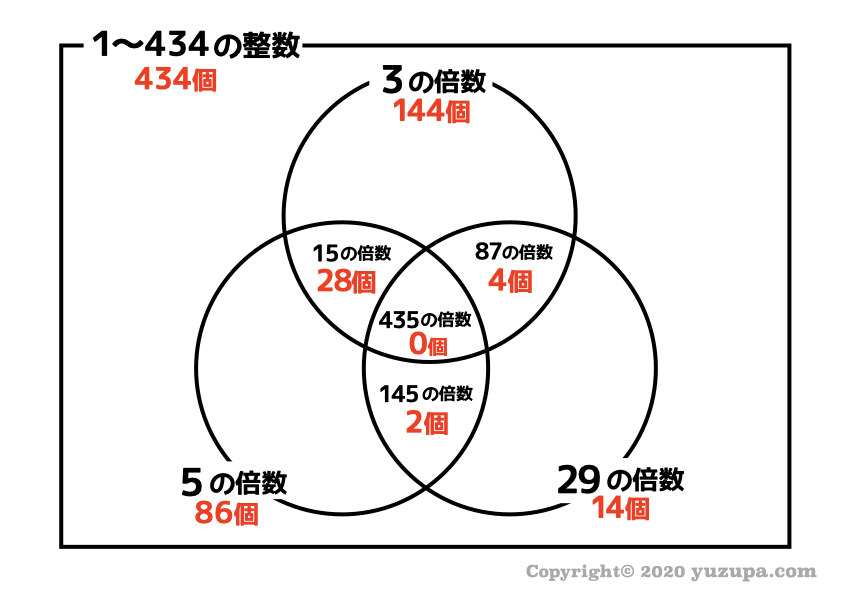
こんな感じになりますd(^_^o)

注意すべきは、３の倍数でありながら５の倍数でもある数字の存在… １５の倍数を忘れてはいけません。

同様に３の倍数でありながら、２９の倍数でもある８７の倍数、

５の倍数でありながら２９の倍数でもある１４５の倍数もですね_φ(･_･

ベン図がかけらたら計算 です。

計算できましたでしょうか？

いくつかポイントをご紹介しておきます。

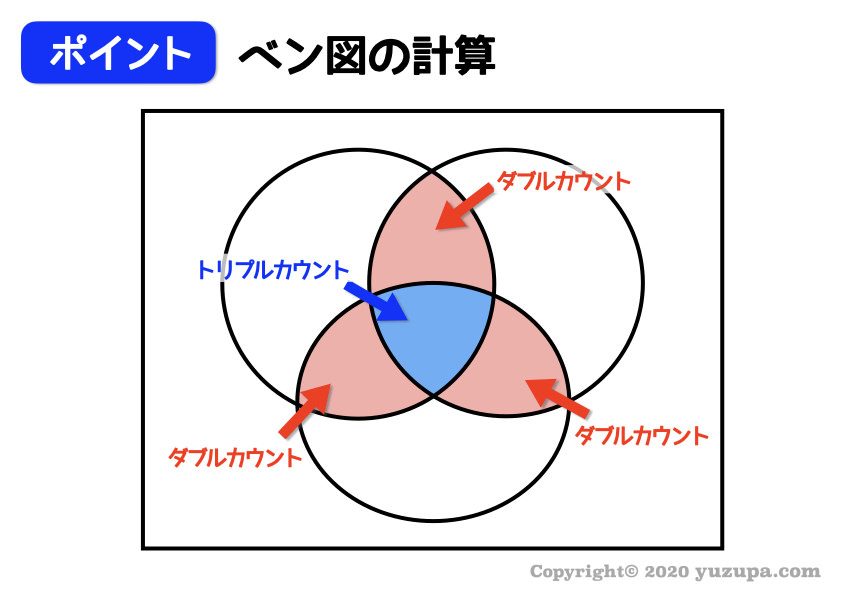
ベン図の計算の基本です。先ほどの例でいう３の倍数の数と５の倍数の数と２９の倍数の数をシンプルに足してしまった場合。

上の図の部分の領域は、ダブルカウントしてしまっている部分や トリプルカウントしてしまっている部分 ことに注意が必要ですねd(^_^o)

この部分はあとから引いてあげる…これがベン図の最重要ポイントですd(^_^o)

 

あともうひとつポイントを。

倍数がいくつあるかを計算でしっかり求めることです。

算数の入試は時間との勝負なので、倍数を１つ１つ書き出すなんてことはしない ようにしましょう_φ(･_･

 

 

解説例３

最後の設問にまいりましょう。

もういちど “既約分数でない分数” がどんなものををオサライ します。

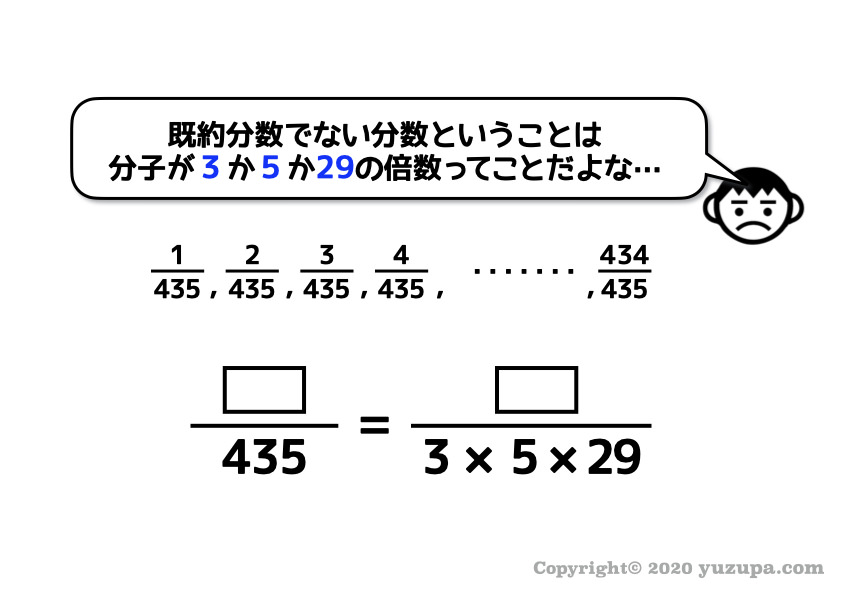
“既約分数でない” ということはまだ約分できる分数ということ なので… 分子が３の倍数か５の倍数か２９の倍数になる分数 ですね。

といっても…それがいくつ連続するかなんてよく分かりません(-_-;)

しょうがないので… ３の倍数、５の倍数、２９の倍数ととりあえず並べてみる！この思考が大事 ですd(^_^o)

並べてみてから…糸口を探します。どれどれ…？ 並べてみたは良いけれどたったの２つしか連続しない なぁ(･_･;

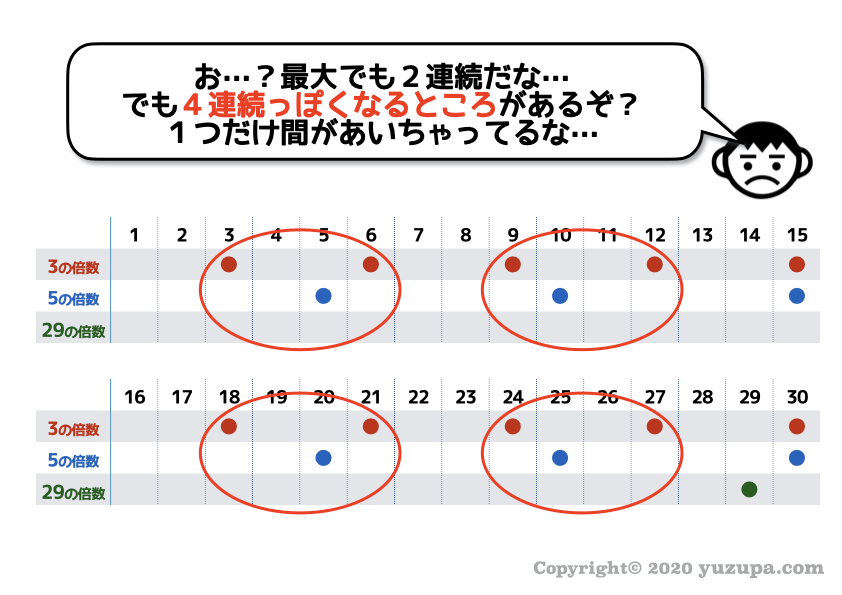
でもよーく見ると…あれ、もう少しで４連続になりそうなところがある ことに気づきます∑(ﾟДﾟ)

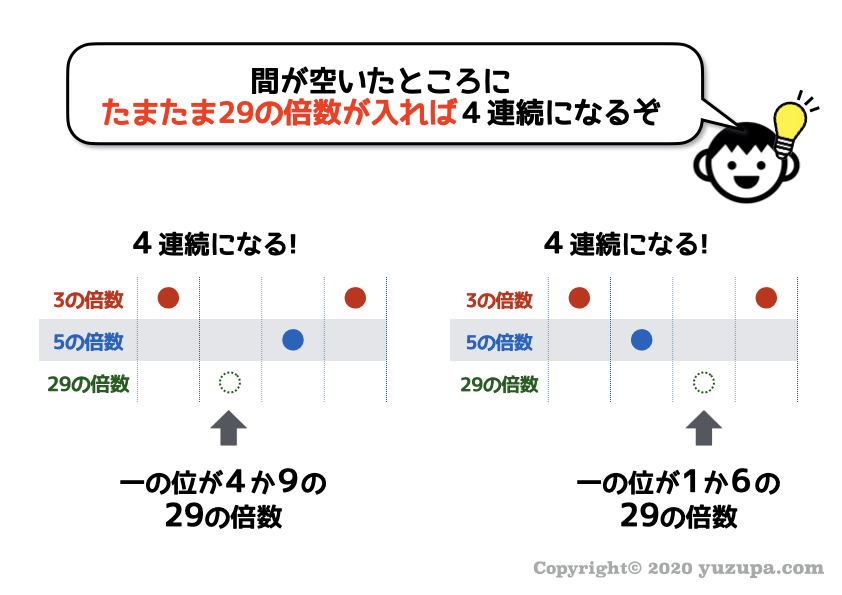
このもう少しで４連続になれそうなところの間に、たまたま２９の倍数が入り込んできたら連続数が４連続に のびますd(^_^o)

そこまでひらめいたらやることは一つですねd(^_^o)

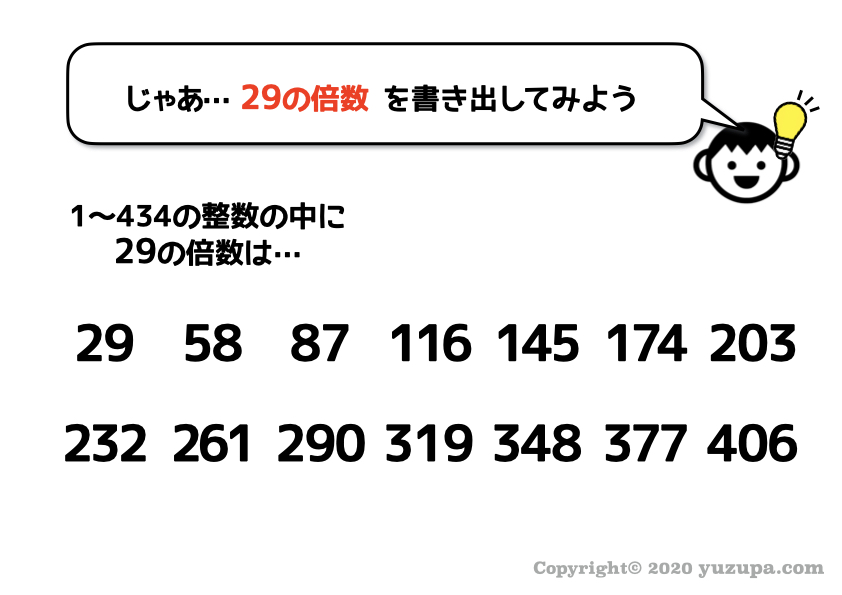
1から434の整数の中には29の倍数は１４個あります。間の空いたところに入れてみましょう。

ただ 全部やっていたら時間がかかるので一の位の数字に着目 して試してみましょうd(^_^o)

29の倍数からピックアップした、319や116を入れてみると４連続にのびました！

ですので 答えは以下のようになりますd(^_^o)

 

ちょっと補足です、一の位が１か６、一の位が４か９の２９の倍数って他にもあった はずです…

はい、たしかにありましたがちょっと見てみましょう。

上記のように４連続にならないんです∑(ﾟДﾟ) しっかり試してみることも大事なんです…d(^_^o)

 

まとめ

今回は、実際の 入試問題を解説するという初の試み をやってみました。リクエストをくれた受験生の方ありがとうございました。

今回のキーポイントはいくつかありましたが以下のとおりです。

・既約分数＝それ以上約分できない分数
・かけ算の形の最小単位の数字＝素数
・数を数える時にベン図を活用する
・素数を理解して…とりあえず並べてみるという行動

ぜひ、お試しくださいd(^_^o)