中学受験：倍数算とは？線分図の３つの本質で解ける…唯一のコツも解説

倍数算は基本的な線分図で解けるが、たった１つだけのコツ”比の結合”が必要

※ 2021年11月13日 記事の最後の図に誤記がございましたので修正しました

こんにちは。かるび勉強部屋 ゆずぱ です。

中学受験の独特の世界観の代表選手… 特殊算と呼ばれる算数の解法たち です。その中で “倍数算” と呼ばれるものがあります。その名前からはどんな解法なのか全く想像できませんが… シンプルに表現すると以下のようになりますd(^_^o)

同じモノに対して
複数の比が出てくる文章題

百聞は一見にしかず。具体的な文章題を見てみましょう。 

兄と弟の所持金という同じモノを扱っているのに、５：４や７：１１とか複数の比が登場しています。これがザックリとした倍数算の概要です。では…なぜ倍数算と呼ぶのでしょうか？

記事の中盤でその名前の由来を明らかにしますd(^_^o) 

 

倍数算とは？

倍数算は “複数の比” が出てくる特殊算

繰り返しになりますが 倍数算 とは中学受験の算数の世界に登場する 特殊算といわれる解法群 の一種です。 

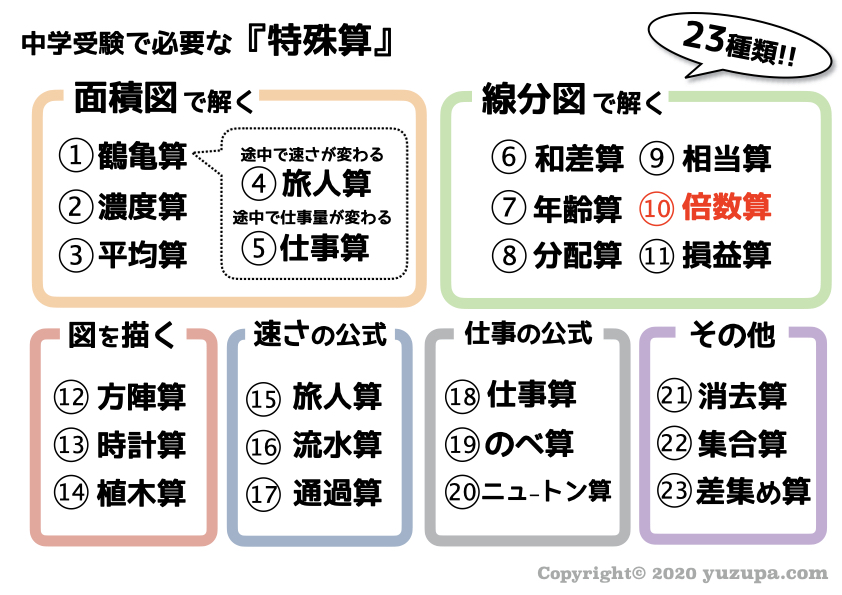
筆者が上記のようにキレイに分類しましたが特殊算自体は、まったく体系化されておらず…好き勝手に発展したもの です_φ(･_･

その中で倍数算とは…

同じモノに対して
複数の比が出てくる文章題

と考えておきましょう d(^_^o)

 

基本は “線分図３つの本質” で解ける

倍数算の解法は これまた中学受験独特の 線分図 ですd(^_^o) そして線分図を使った問題は “３つの本質” をおさえれば解けます。 

線分図について詳しい資料は以下をご参照ください。

参考：線分図はいつ使う？ たった３つの本質で解ける

 

ただ…比に関するコツが１つだけ必要

この倍数算… 同じモノに対して複数の比が登場する文章題であるとお伝えしました。たった１つだけコツが必要 なんです。

複数の比が出てくると何が困る でしょうか？

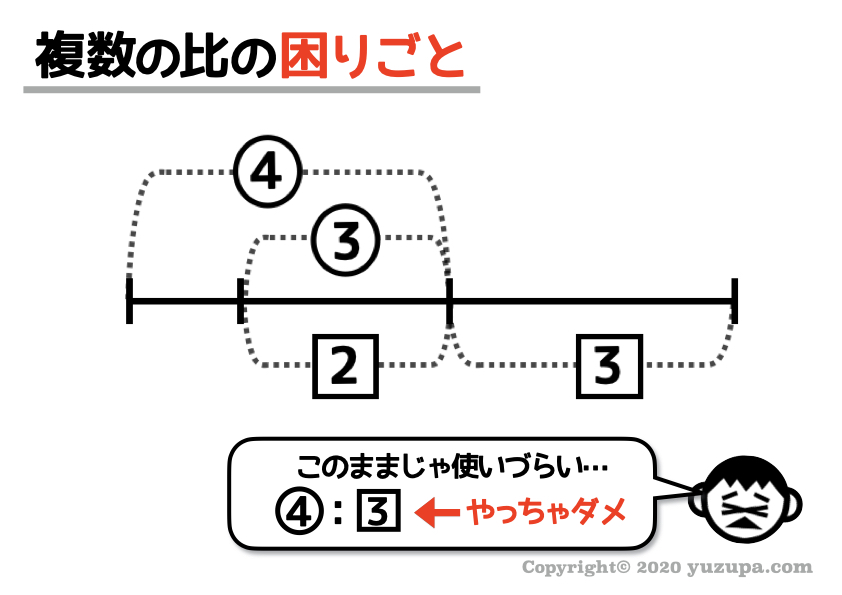
 困りごとはコレですね…

異なる比はいっしょには使えません。丸数字の比 と 四角数字の比 が２つあっても同じ比として扱ってはダメです。

そこでコツの登場…比の結合 ですd(^_^o)

 

比の結合は下記の３ステップで出来ちゃいます。

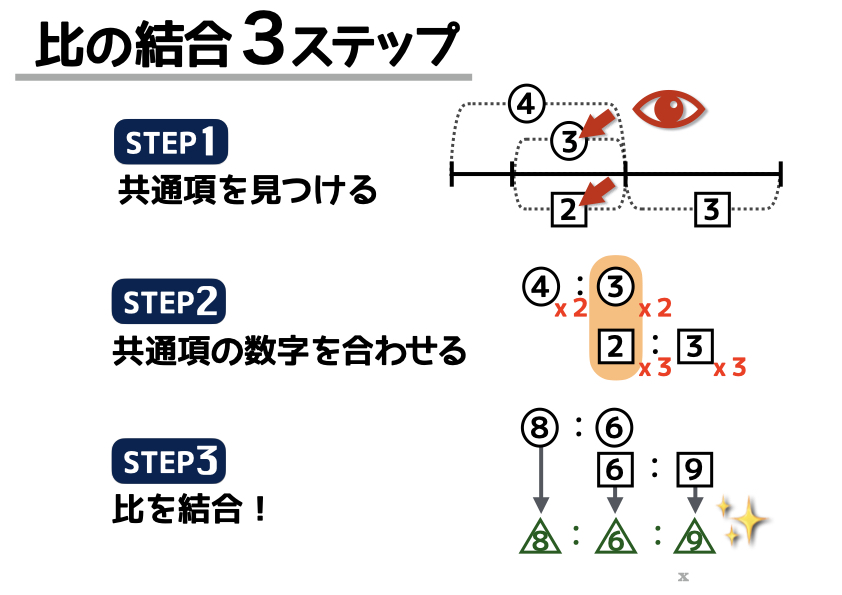
まず共通項を見つけること。上記の例では 線分図の同じ大きさ なのに２つの異なる比がありますねd(^_^o)

次は共通項の数字を合わせます。丸数字の比には２を掛け、四角数字の比には３を掛ければ共通項が６で合わさります。

共通項が合わされば、比の数字をそろえることができますねd(^_^o)

 

ちなみに… 倍数算という名前の根拠はココ にあります。

比を結合するときに 最小公倍数の考え方 を使って数字を合わせますよね。だから倍数算というんです ∑(ﾟДﾟ)

 

実際の問題を３つの本質で解いてみる

手順①：問題文から線分図を描く

それでは実際の問題を解いてみましょうd(^_^o) 

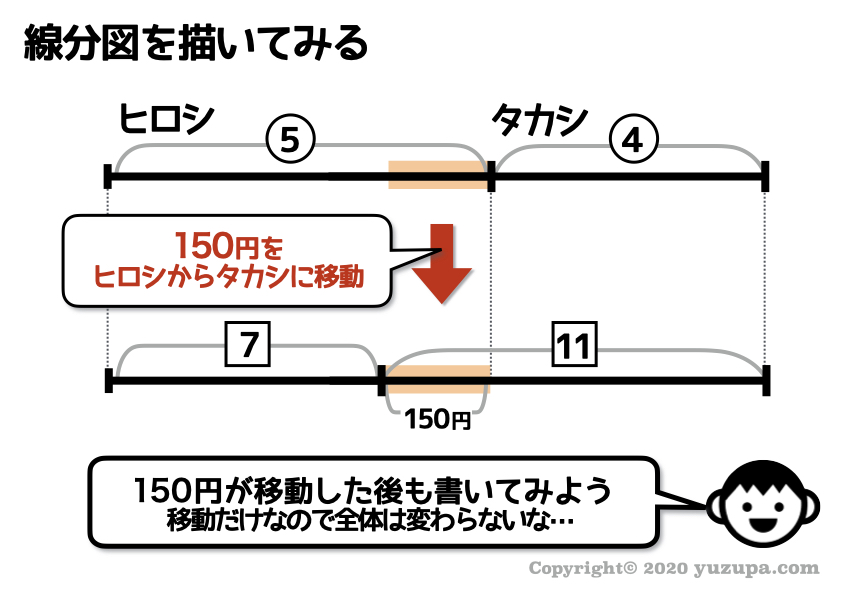
問題文を読みながら丁寧に線分図を書いてみましょう。

ヒロシとタカシを縦に並べて２本の線分図を描くか…それとも横に並べて１本の線分図を描くか… 今回は１本でいってみましょう。

 

 

手順②：複数の比を結合する

まず共通項を探してみましょうd(^_^o) 

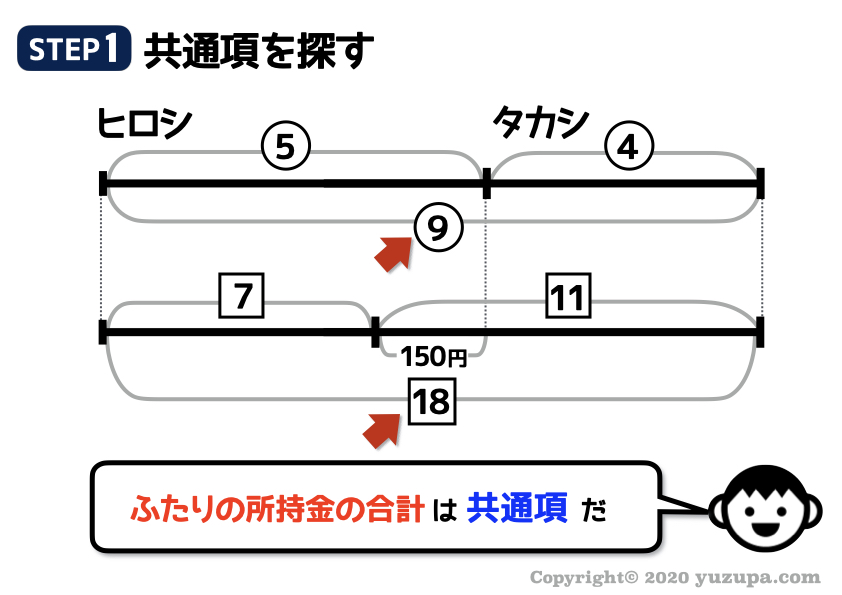
ふたりの所持金の合計は丸数字の比では９。資格数字の比では１８。コレが共通項であることが分かります ねd(^_^o)

共通項が見つかったら数字を合わせる作業です。それぞれの比に数字を掛けて同じにしましょう。何を掛ければよいでしょうか？

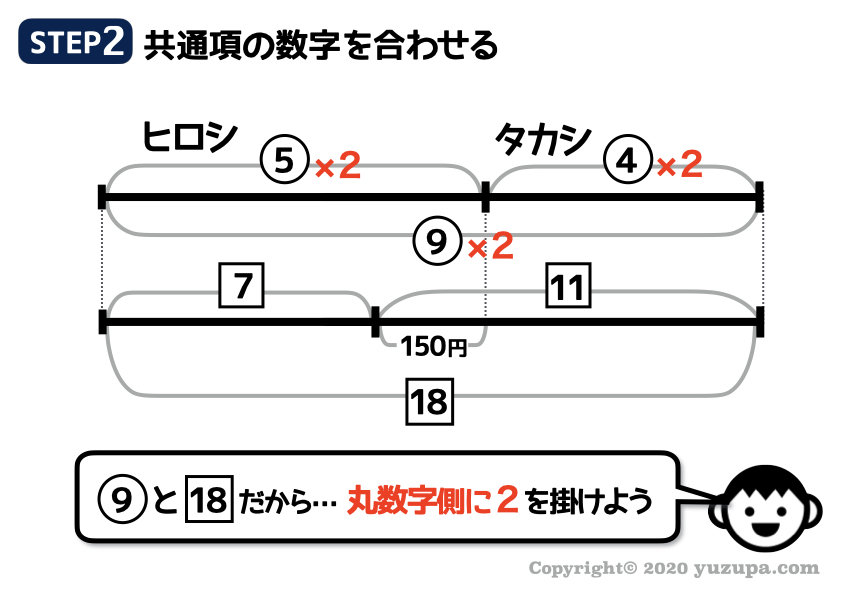
 ９と１８なので 丸数字側に２を掛ければ　数字を合わせることができます。最小公倍数に合わせるのがポイントですd(^_^o) 

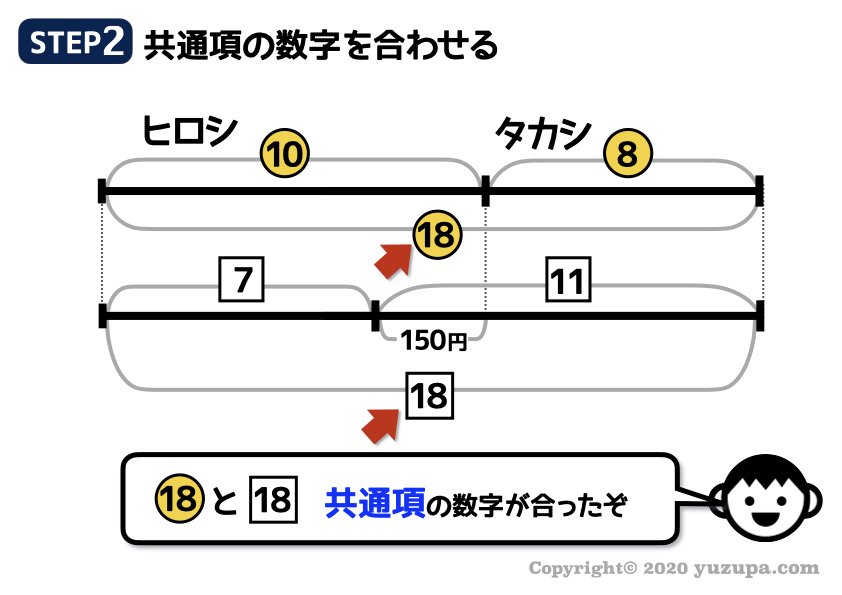
共通項の数字が１８で合いました！ここまでくれば最後の仕上げ です。同じ大きさが同じ比になったのですから 丸数字 も 四角数字 も同じ比です。結合しましょう！  

 

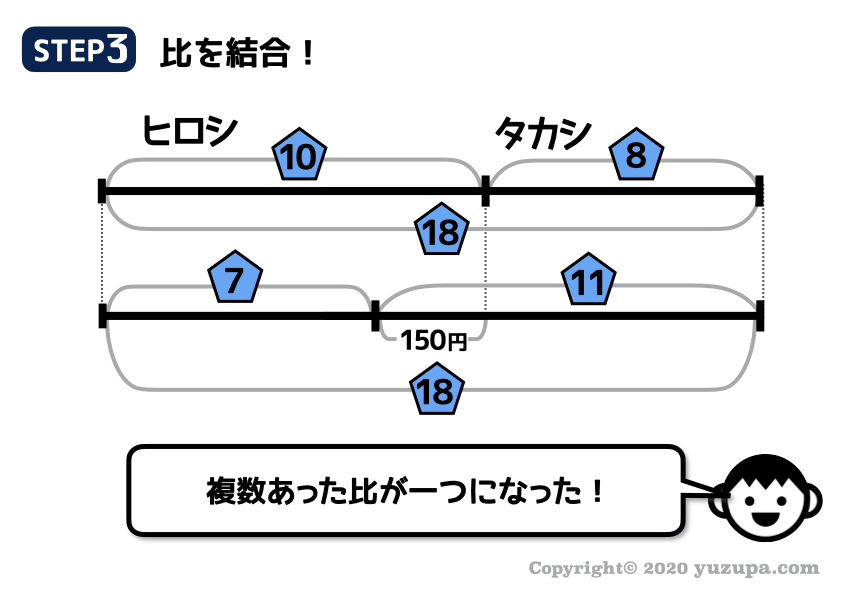
手順③：線分図３つの本質を使う

比がひとつになって扱いやすくなったところで、線分図の３つの本質を使って攻略していきましょうd(^_^o)

改めて 線分図の３つの本質のオサライ です。

ではさっそくまいりましょう。 

線分図をよく観察し３つの本質を使って埋められるところをガンガン埋めます。比であっても差に着目すれば埋まります_φ(･_･

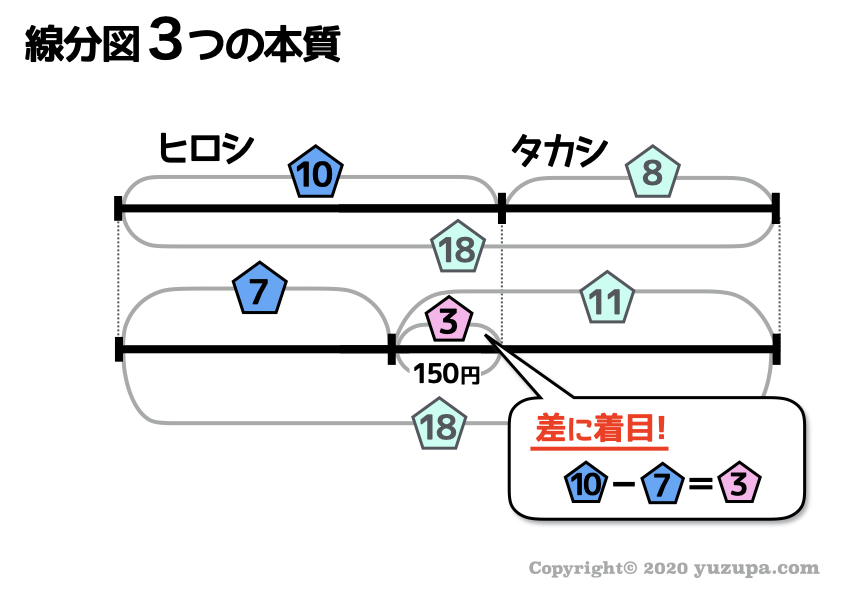
数字を埋めているうちに 数字と割合のペアが見つかればGOOD です。見つけられましたでしょうか？

 

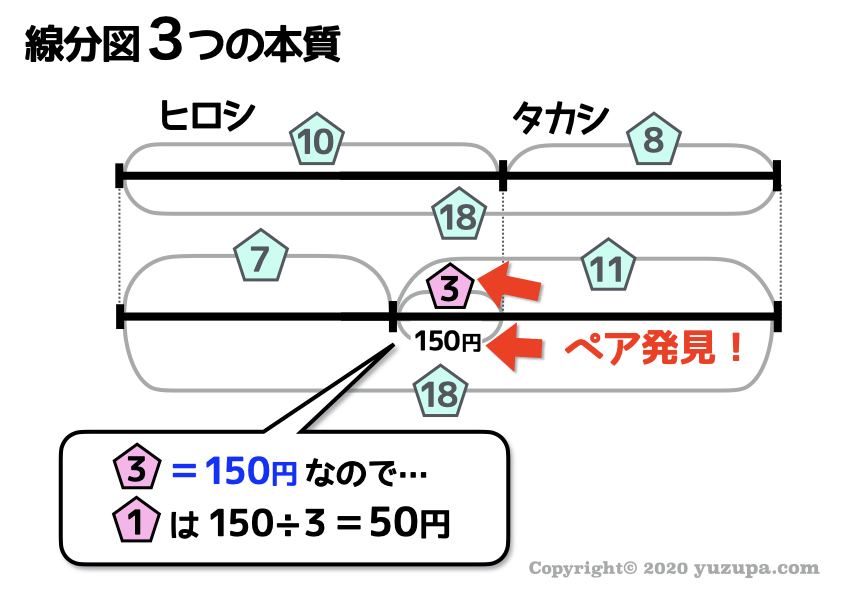
数字と割合のペアを発見できれば、割合１つ分の数量 を求めることができます。そして…ここまで来ればゴールは近い！

  

割合１つ分の数量が分かれば、線分図にある比を次々と実際の数量に書き換えることが できますねd(^_^o)

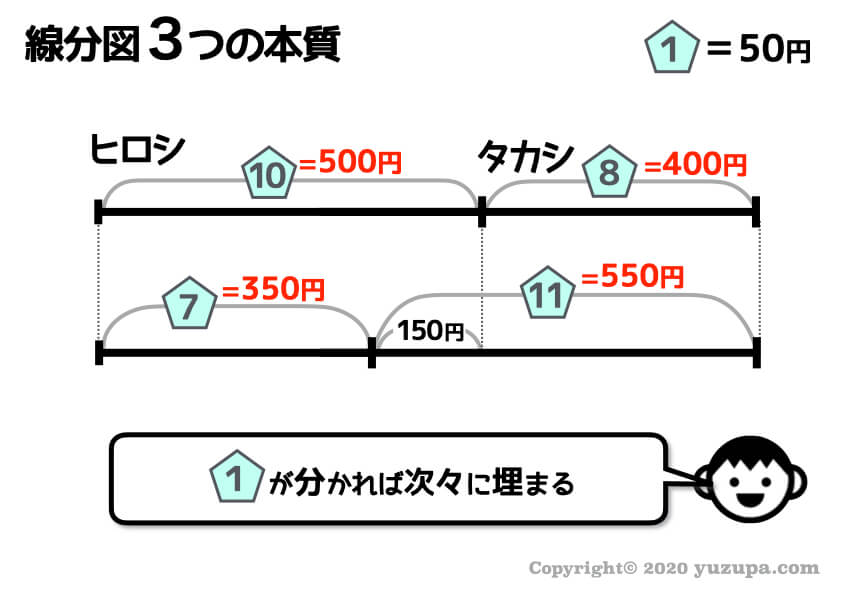
問われているのは この兄弟が最初に持っていた所持金 ですので、兄ヒロシは500円、弟タカシは400円が答え となります。

 

まとめ

中学受験で独特の世界観となる特殊算の世界。倍数算というちょっとマイナーな特殊算を解説しました。

倍数算かなと思うきっかけ
同じモノに複数の比が登場

解き方は線分図を使うのが良いでしょうd(^_^o)

線分図３つの本質
　① 差に着目して数字を埋める
　② 高さをそろえて割る
　③ 数字と割合のペアを見つける

そして倍数算を解くためのたったひとつのコツ。それは比を結合すること！比の結合は３つのステップで！

比の結合３ステップ
　STEP1. 共通項を見つける
　STEP2. 共通項の数字をそろえる
　STEP3. 結合する！