中学受験：振り子の周期は？２つ物理法則を知り余計な数字は無視せよ！

たくさんある “振り子の要素” に惑わされるな…着目点は決まっている！

こんにちは。かるび勉強部屋 ゆずぱ です。

振り子の分野でつまづく子供が多いようです。理由は教科書やテキストを見ればすぐにわかります…。正直、何がポイントなのか全くわかりません(-_-;)

対照実験の様子が書いてあって、結果として ”振幅の大きさはおもりの重さに関係しません” とか “おもりの重さが重いほど箱は遠くへ飛ばされます” とか…

対照実験とその結果考察のオンパレード
こりゃ嫌になります…

小学生における振り子の問題は 大きく分けて２つの物理法則 を使います。”振り子の等時性” と “エネルギー保存法則” です。

どちらの物理法則を使うかによって着目するポイントは決まっています。他の要素は無視してしまって構いません∑(ﾟДﾟ)

それでは詳細にまいりましょう！

ちなみに…”対照実験”そのものは超重要！入試問題も知識から思考へシフトしています。詳細は以下の記事からどうぞ！

参考：対象実験とは？論理的に考えさせる問題が本当によく出る！

 

振り子の問題は ２つの異なるパターンが！

振り子を決める “３つの要素” とは

本題の物理法則に入る前に… まずは振り子の性質を決める “３つの要素” をおさえましょう。

この３つさえ決まれば…
周期も振幅も速さも全てが決まりますd(^_^o)

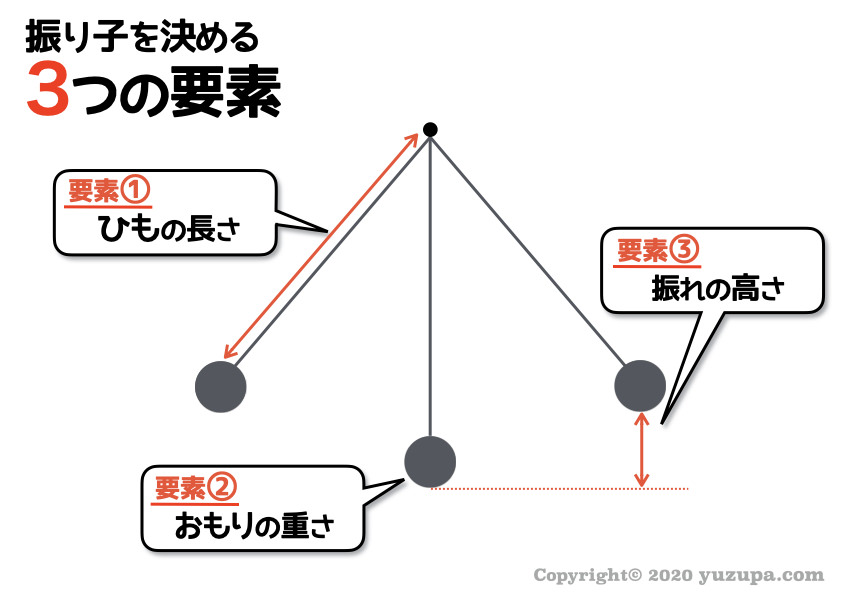
要素の１つ目は ”ひもの長さ” です。理科の世界では ひもの重さも伸縮も無視するのでシンプルに 長さ だけですd(^_^o)

要素の２つ目は “おもりの重さ” です。これも同様に体積は無視することになっているので シンプルに 重さ だけです。

要素の３つ目は “振れの高さ” です。振り子が最も低くなる部分を基準にした高さと理解すればＯＫですd(^_^o)

 

問題は “２種類の法則” を問うもの！

それでは… 中学受験で出題される振り子問題で使う２つの物理法則をご紹介します。どちらの法則を使うかによって着目する要素が違うというところがミソですd(^_^o)

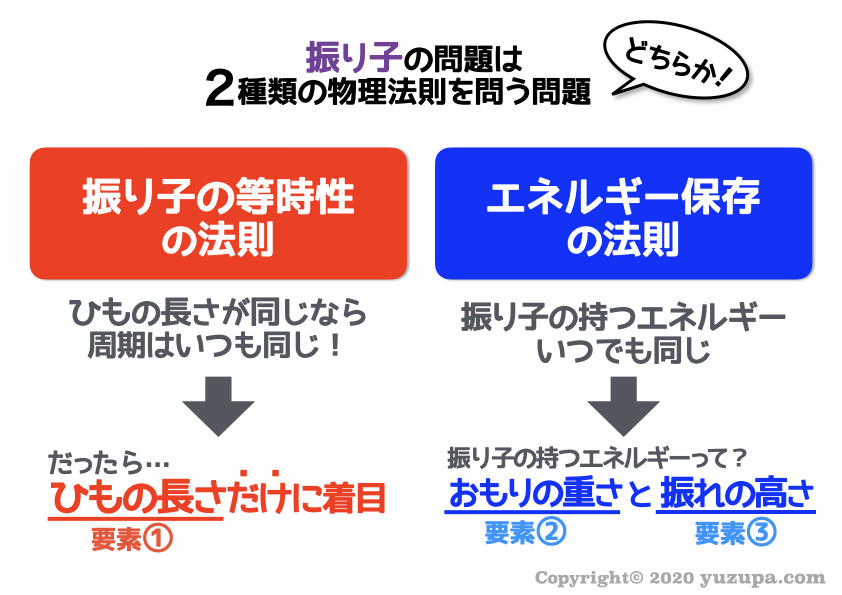
１つ目は “振り子の等時性” を使うもの。振り子の周期はひもの長さのみによって決まるというもの。

２つ目は “エネルギー保存法則” を使うもの。振り子の持つエネルギーはいつでも同じというもの。

 

繰り返しになりますが、どちらの問題かによって着目する要素が決まってくるというがミソですd(^_^o)

 

物理法則① 振り子の等時性の法則

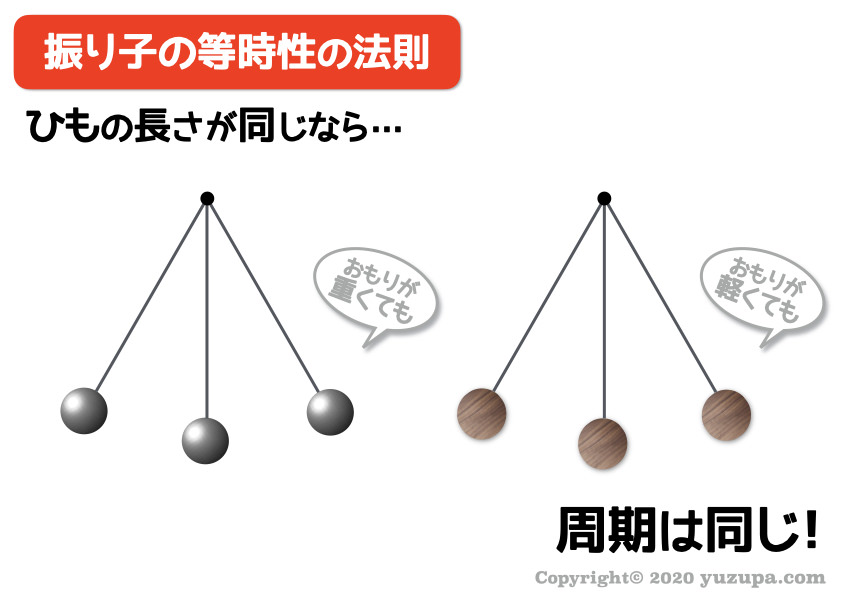
難しい名前ですが内容は超シンプル ですd(^_^o) 読んで字のごとく ひもの長さ が同じなら周期はいつも同じというもの。

おもりの重さが違っても周期は同じ∑(ﾟДﾟ)

振れの高さが違っても周期は同じ∑(ﾟДﾟ)

 

 

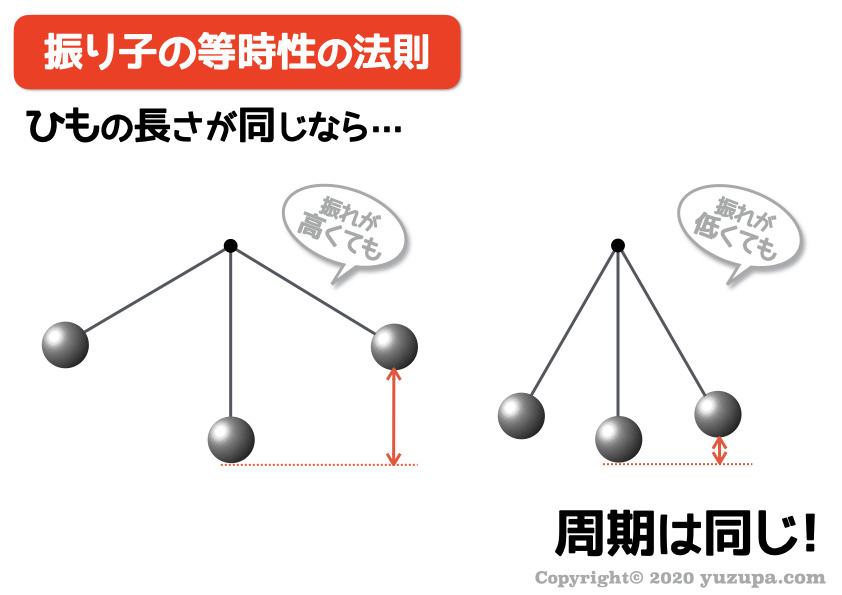
物理法則② エネルギー保存の法則

振り子は いちばん高いところでピタッと止まり ます。そして… イチバン低いところで速さが最大 になります。

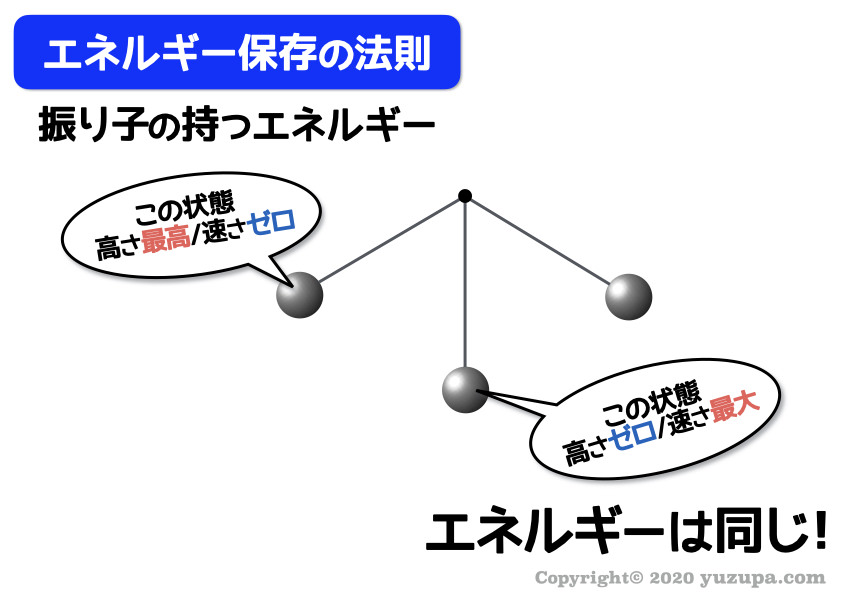
全く異なる状態の振り子ですが、振り子が持っているエネルギーはどちらも同じです∑(ﾟДﾟ)

ところで…エネルギーってナニ？

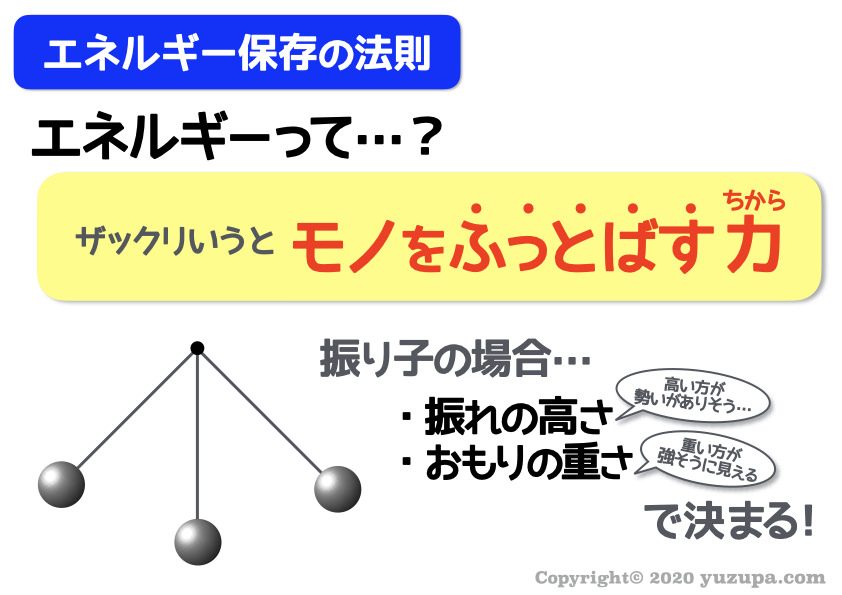
ざっくりと表現すると “モノをふっとばす力” のこと。

中学入試の世界では 振り子を何かにぶつけてふっ飛ばすという問題が多いのでまずは…コレでよいでしょう(^_^;)

エネルギーは振り子の振れが高い方が大きく、おもりの重さが重いほど大きく なります…イメージ通りですねd(^_^o)

 

振り子の等時性は”長さ”に着目せよ

最も振り子の周期が長いのはどれでしょう？

さっそくですが問題です…。以下の４つの振り子のうち、振り子の周期が最も長いのはどの振り子でしょうか？

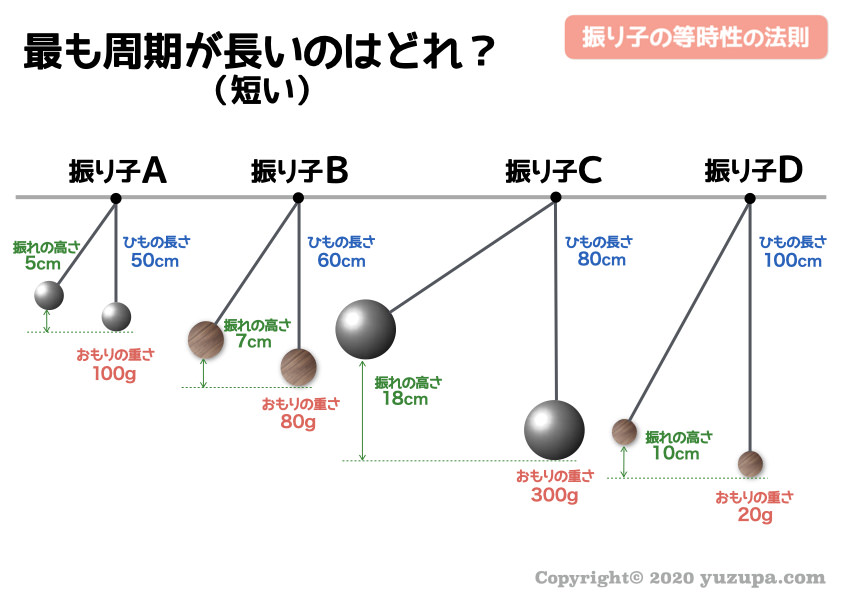
振れが大きかったり小さかったり… おもりが重たい金属だったり軽い木だったり… 難しそうに見えます(-_-;)

が…惑わされてはいけません
着目するのは ”ひもの長さ” だけです

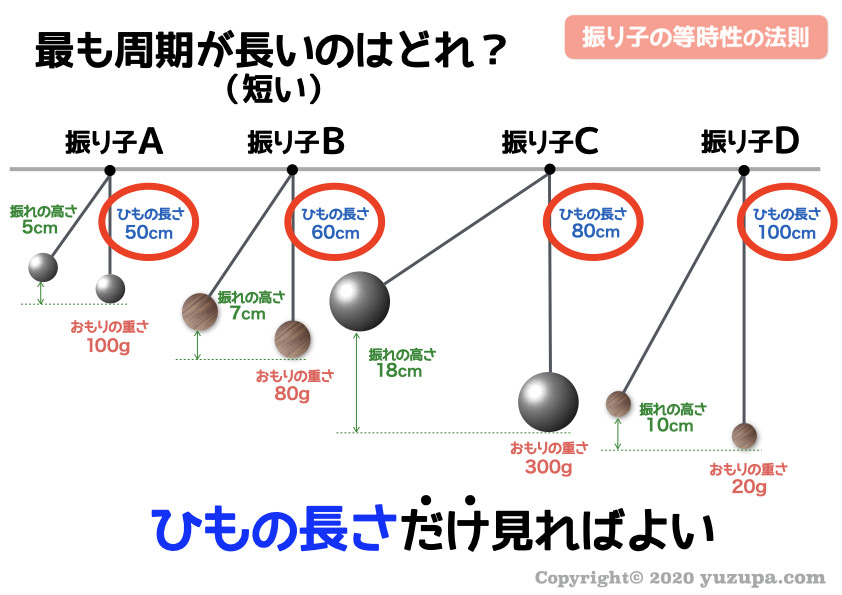
ひもの長さがイチバン短い 振り子Ａの周期が最も短く、紐の長さがイチバン長い 振り子Ｄの周期が最も長くなりますd(^_^o)

 

“ひもの長さ”から”周期”が分かる

ひもの長さから分かるのは 周期の長さの大小だけではありません。”周期”を求めることもできますd(^_^o)

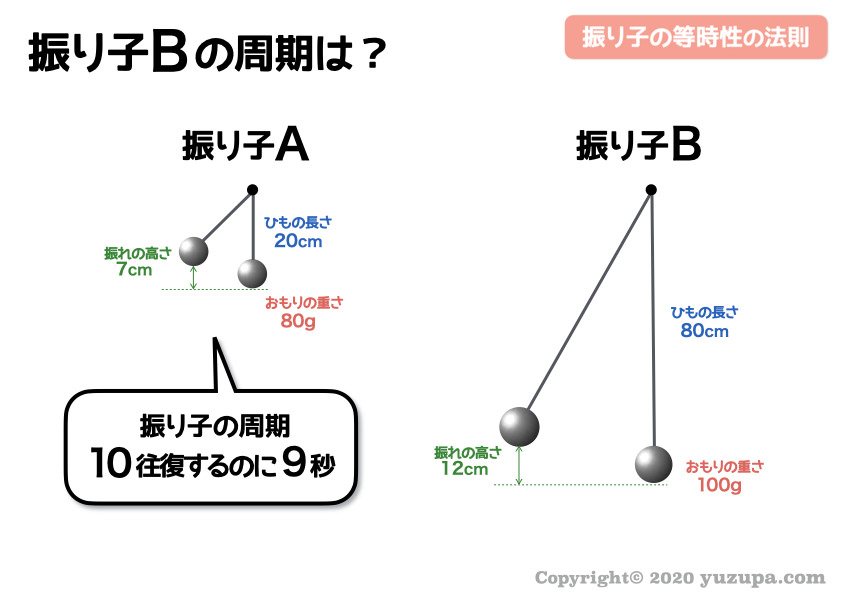
振り子Ｂの周期をもとめてみましょう。振り子の等時性の問題なので もちろん ”ひもの長さ” だけに着目 しますd(^_^o)

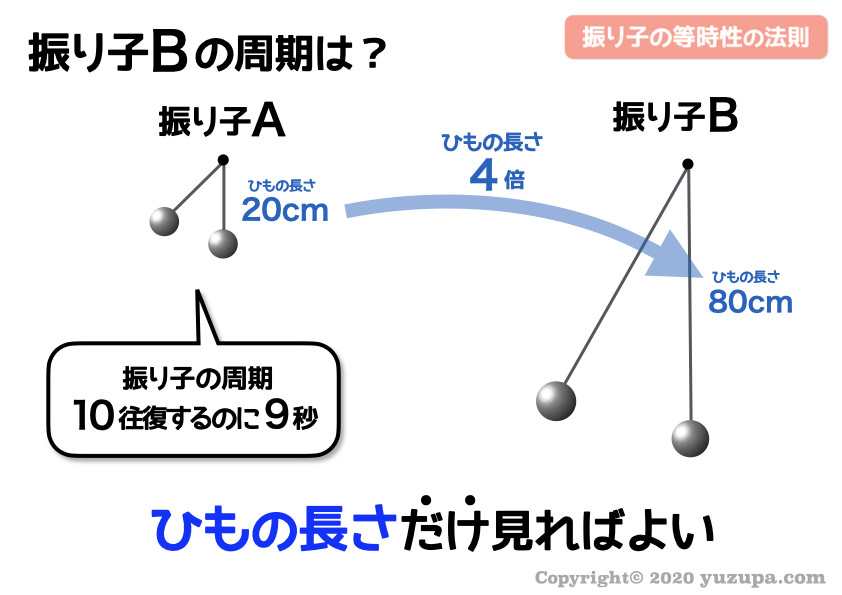
“ひもの長さ”に着目すると 振り子Ａに比べて振り子Ｂは４倍 の長さがありますね… じゃあ周期も４倍でしょうか？

同じでは無いので注意 ∑(ﾟДﾟ)
以下の表のような関係になっています

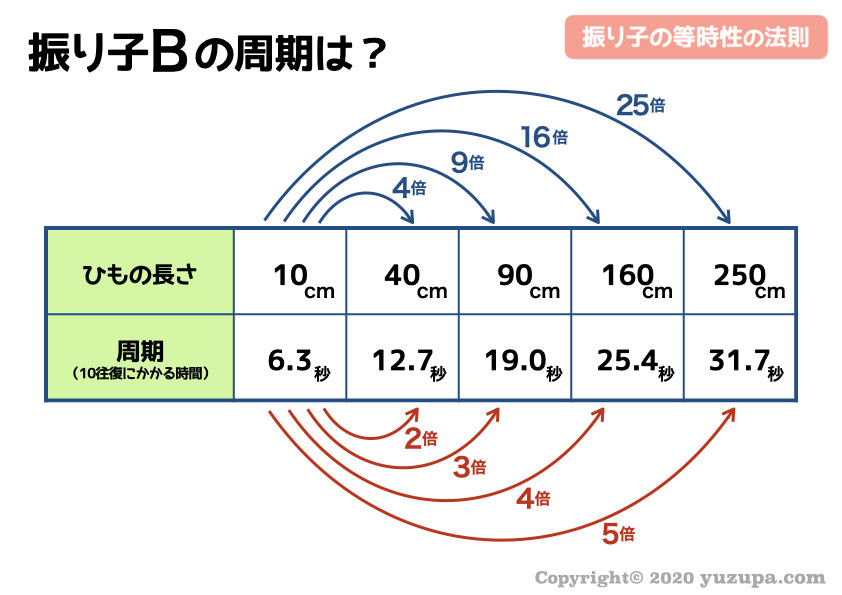
“ひもの長さ”が４倍だったら “周期” は２倍 ですねd(^_^o)

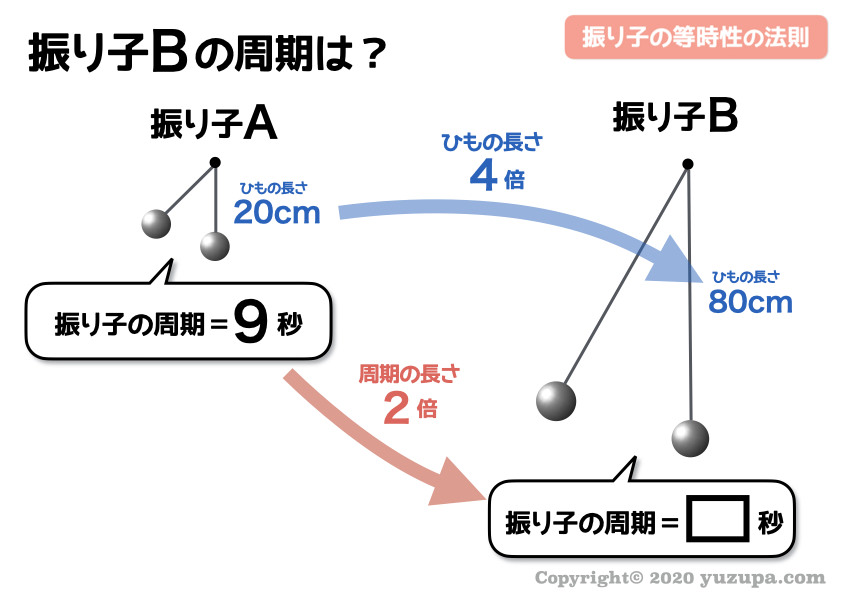
振り子Ｂの周期は １８秒であることがわかりますね。この問題の場合は１０往復するのに掛かる時間です_φ(･_･

 

逆に…”周期”から”ひもの長さ”も分かる

さっきの表の関係があるならば…当然ですが逆に”周期”から”ひもの長さ”を求めることもできちゃいますd(^_^o)

定番中の定番ですが… 振り子の途中にクイを打って、ひもの長さを途中から短くする振り子の問題 ですd(^_^o)

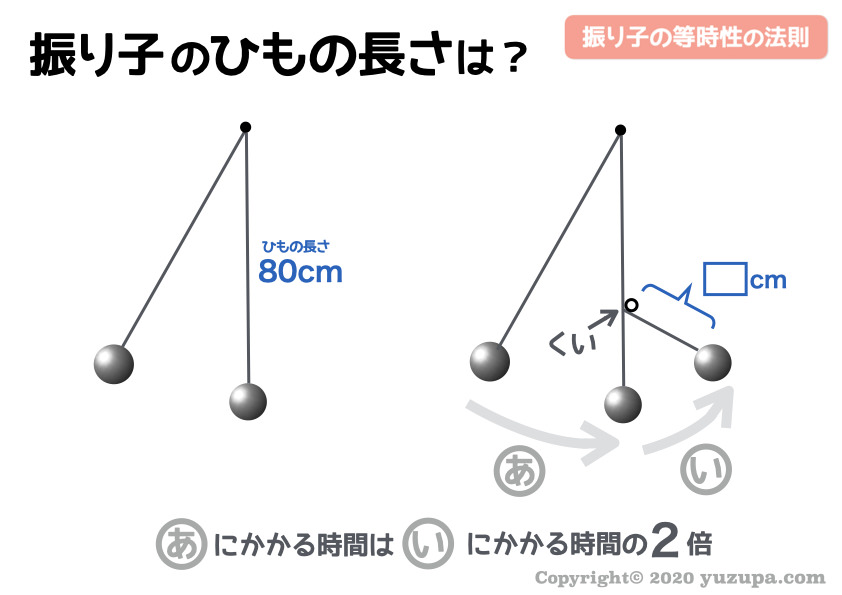
全体の振り子の周期(あ)は、クイを支点とした小さい振り子の周期(い)の２倍であることがわかっていますd(^_^o)

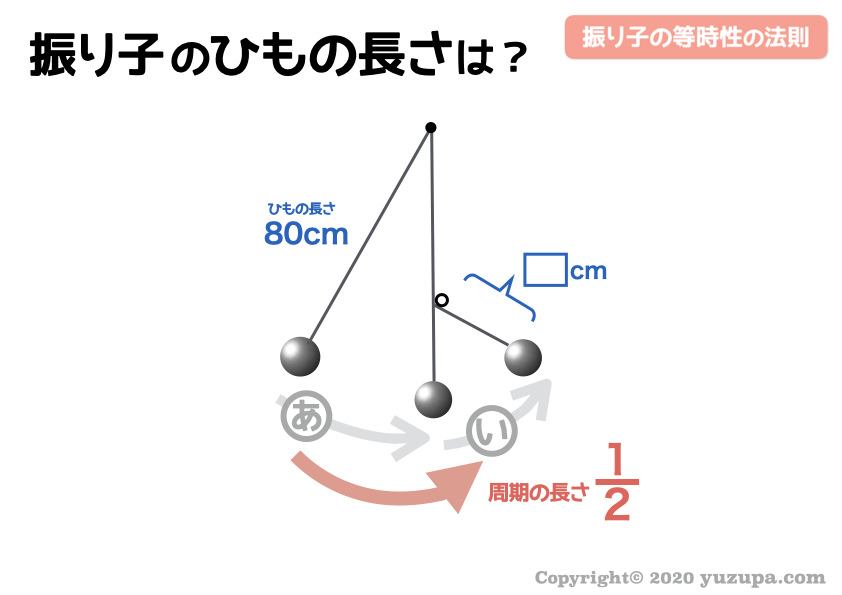
つまり “周期”は２分の１になっていますね_φ(･_･  じゃあ ”ひもの長さ” はどうでしょう？さきほどと同様に２分の１では無いですよ！

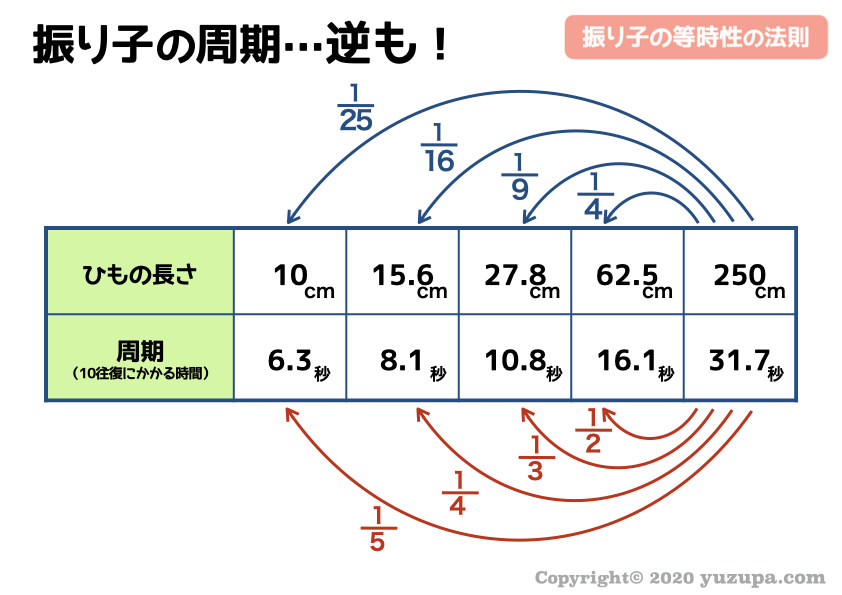
“周期が”が２分の１だったら “ひもの長さ” は４分の１ です。

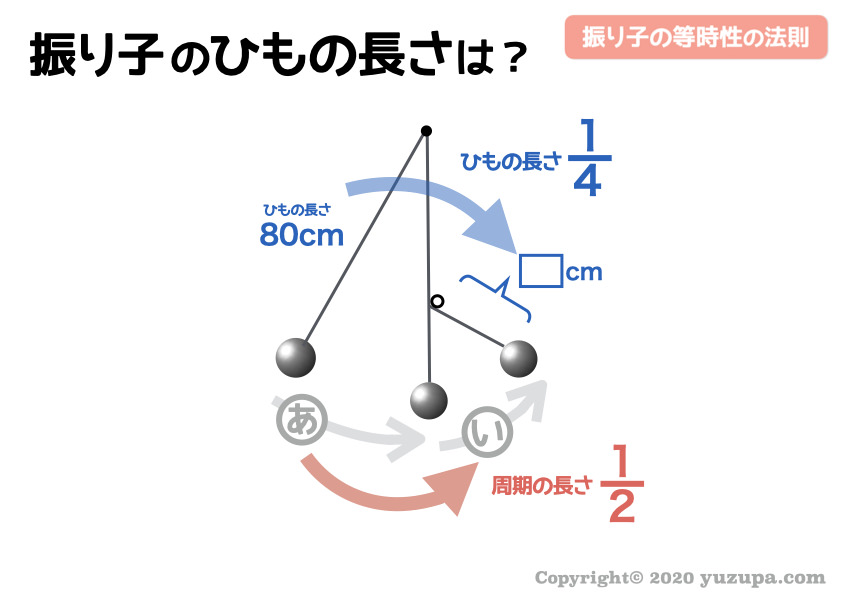
クイを支点とした小さい振り子の “ひもの長さ”は ２０cm であることがわかりますね

以上が ” 振り子の等時性 ” に関する解説でした…。それでは２つ目の物理法則へ参りましょう。

 

エネルギー保存法則は”高さ”と”重さ”に着目せよ

エネルギーを多くもつのはどちら？その１

さっそく問題です…。以下の ２つの振り子のうちエネルギーを多く持つ振り子はどちら の振り子でしょうか？

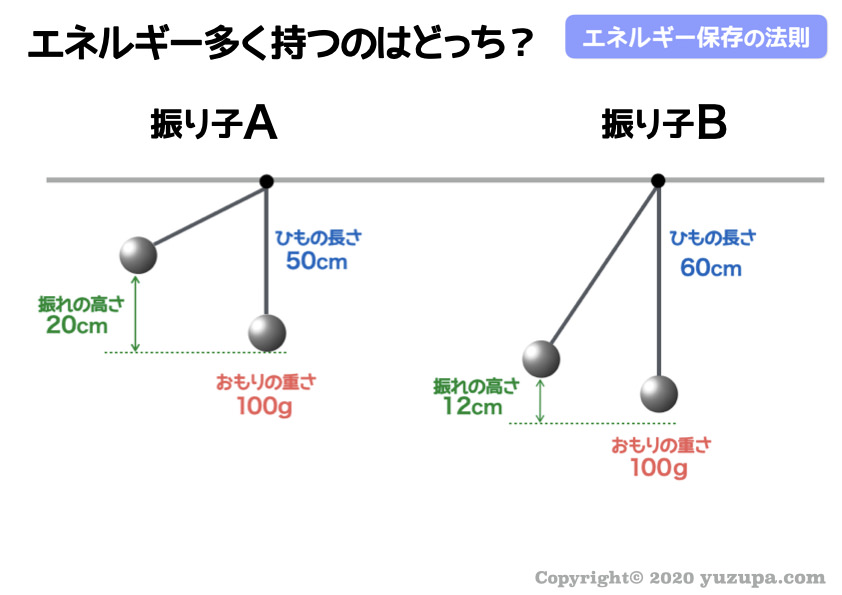
“ひもの長さ”は無視 しましょう。エネルギーを決めるのは”振れの高さ”と”おもりの重さ”ですd(^_^o)

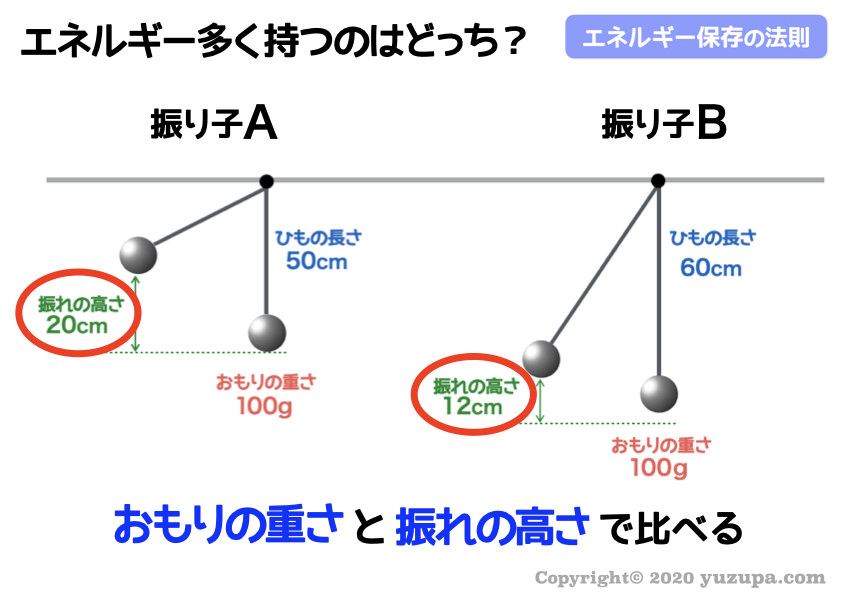
“おもりの重さ” はどちらも100gで同じなので、“振れの高さ” をみればその振り子のもつエネルギーの大小が分かります。

“振れの高さ” が20cmの振り子Ａの方が大きなエネルギーを持っていることになりますd(^_^o)

 

エネルギーを多くもつのはどちら？その２

同じような問題です…。以下の２つの振り子のうちエネルギーを多く持つ振り子はどちらの振り子でしょうか？

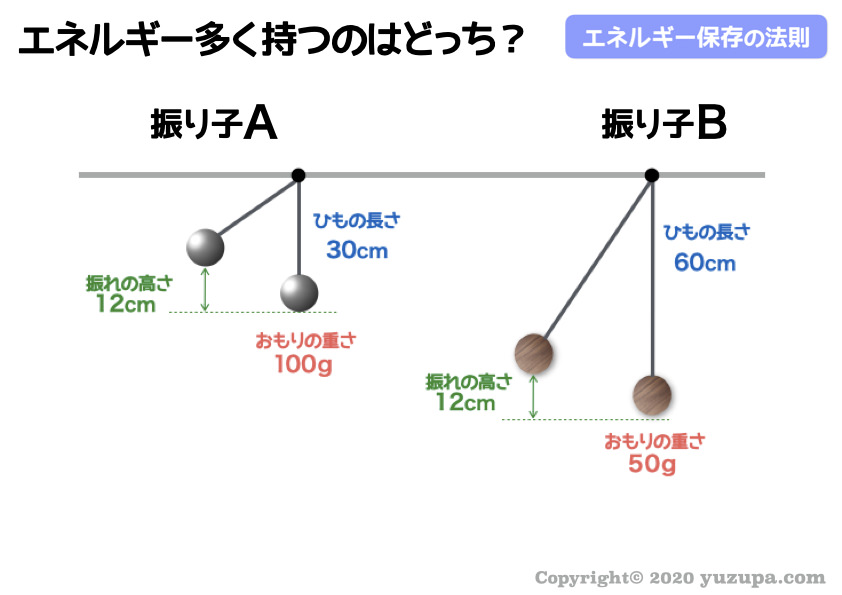
同様に“ひもの長さ”は無視です。エネルギーを決めるのは”振れの高さ”と”おもりの重さ”ですd(^_^o)

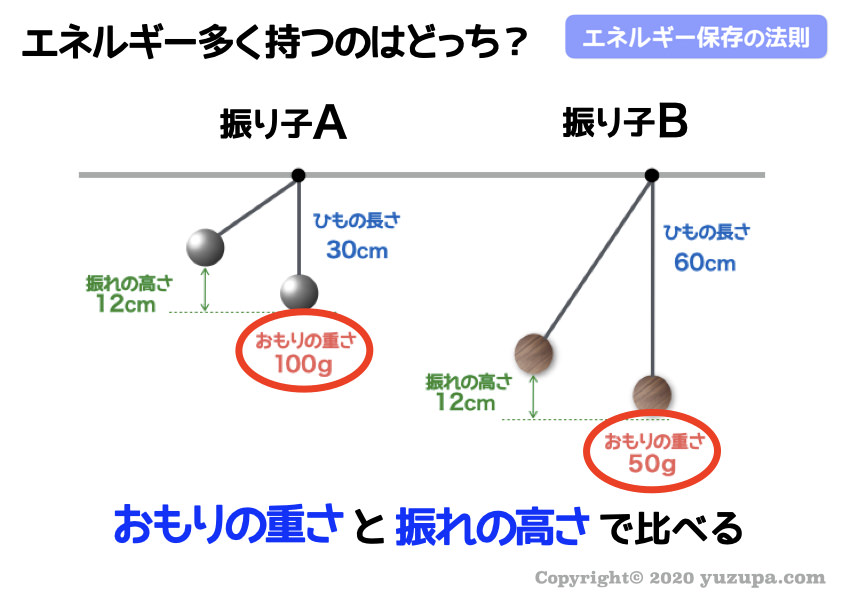
“振れの高さ”はどちらも１２cmで同じなので、おもりの重さをみればその振り子のもつエネルギーの大小が分かります。

おもりの重さが100gの振り子Ａの方が、大きなエネルギーを持っていることになりますd(^_^o)

 

箱が遠くまでふっ飛ぶのはどちら？

エネルギーの大小がわかっただけでは面白くありません。この 振り子を箱にぶつけてふっ飛ばしてみましょうd(^_^o)

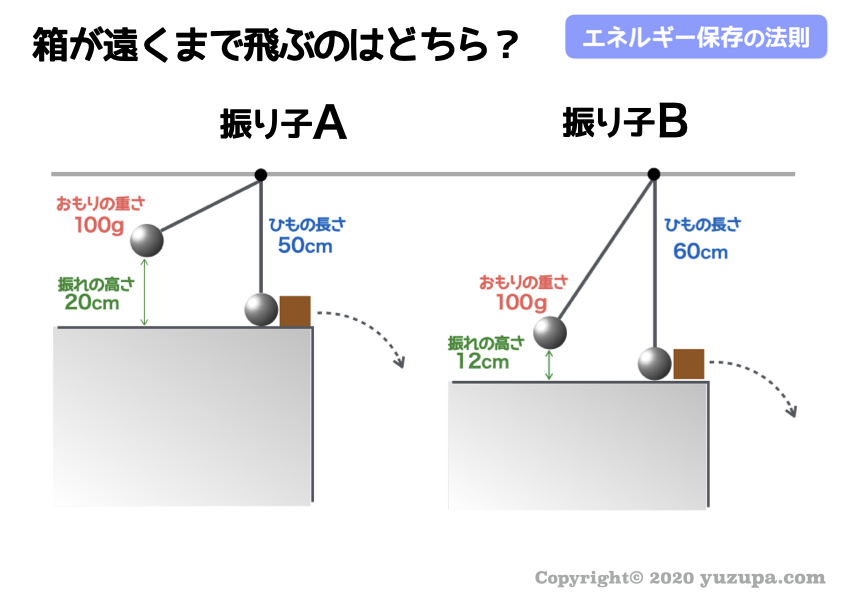
この問題は、箱をふっ飛ばすための エネルギーを多く持っている振り子を選ぶという問題に読み替える ことができます_φ(･_･

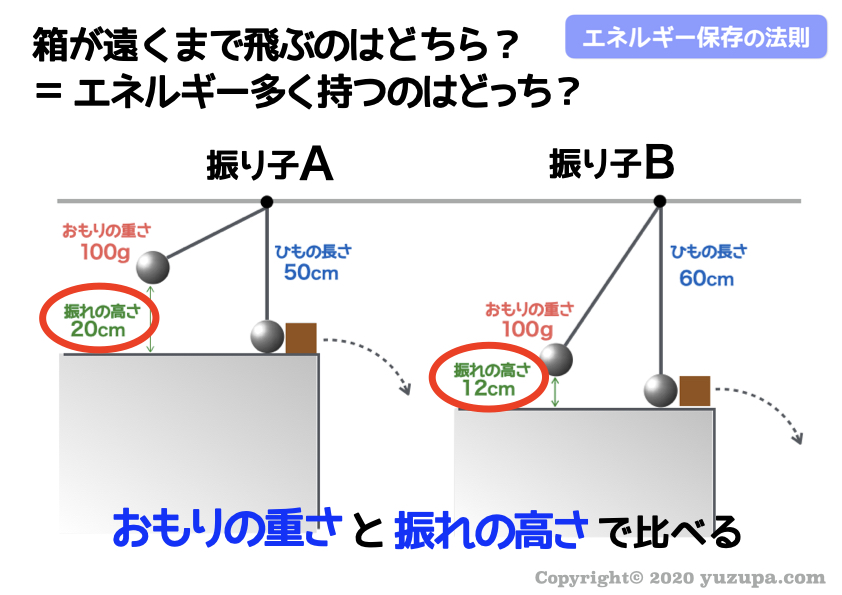
エネルギー保存法則の問題なので “ひもの長さ”は無視 しましょう。着目すべきは ”振れの高さ”と”おもりの重さ” です。

この問題の場合は 振り子Ａの方がエネルギーを多くもっています。つまり箱が遠くまでふっ飛ぶのも振り子Ａの方です。

 

まとめ

今回は ”振り子” についてまとめました。教科書やテキストは対照実験とその結果考察のペアが淡々と説明されており分かりにくい！

２つの物理法則のどちらを使うかで
着目する要素をしぼるのがミソでしたd(^_^o)