中学受験：ばね問題の解き方…単純な問題でも”つり合いの式”を意識せよ

簡単な問題は解けるのに”浮力”や”はかり”が出てくると分からなくなる…

こんにちは。かるび勉強部屋 ゆずぱ です。

理科の力学分野を苦手とする小学生がとても多いようです(-_-;)

我が家の子供も例に漏れず、かなり苦手意識をもっておりました。子供との対話の中で、力学に苦手意識を持つ理由を探索してみたところ、結局は以下のような根本にいきつきました。

どんな時に…どの方向に…どんな大きさの…
力が発生するのかを正しく理解していない

中学受験で登場する力学は高校で学習する物理と異なり、たった５つの力しか登場しません。さらには力の方向も単純な２方向でありベクトルの分解も不要。そして最大の特徴は ほぼ全ての問題で ”力がつり合っている” ということ。

つまり…全ての力を描いて
イコールで結べば解けてしまいます

本記事では小学生における力学の問題を解く手順を中心に据えて、特にばねが絡んでくる問題にフォーカスして解説します。

 

ばね問題を解くための3つの基本知識

力学の問題を解く手順に入る前に、まずはばねが絡む問題を解くために 絶対に必要な３つの基本知識 についておさえましょう！

基本① ばねを伸ばすと弾性力がはたらく

力学の基本は… ズバリ”力を矢印でもれなく正しく描く”こと！

どの方向に、どんな大きさの力がはたらくのかを正確に理解することこそ力学の問題攻略の第一歩です。では…ばねにつながったものにはどんな力がはたらくのでしょうか？

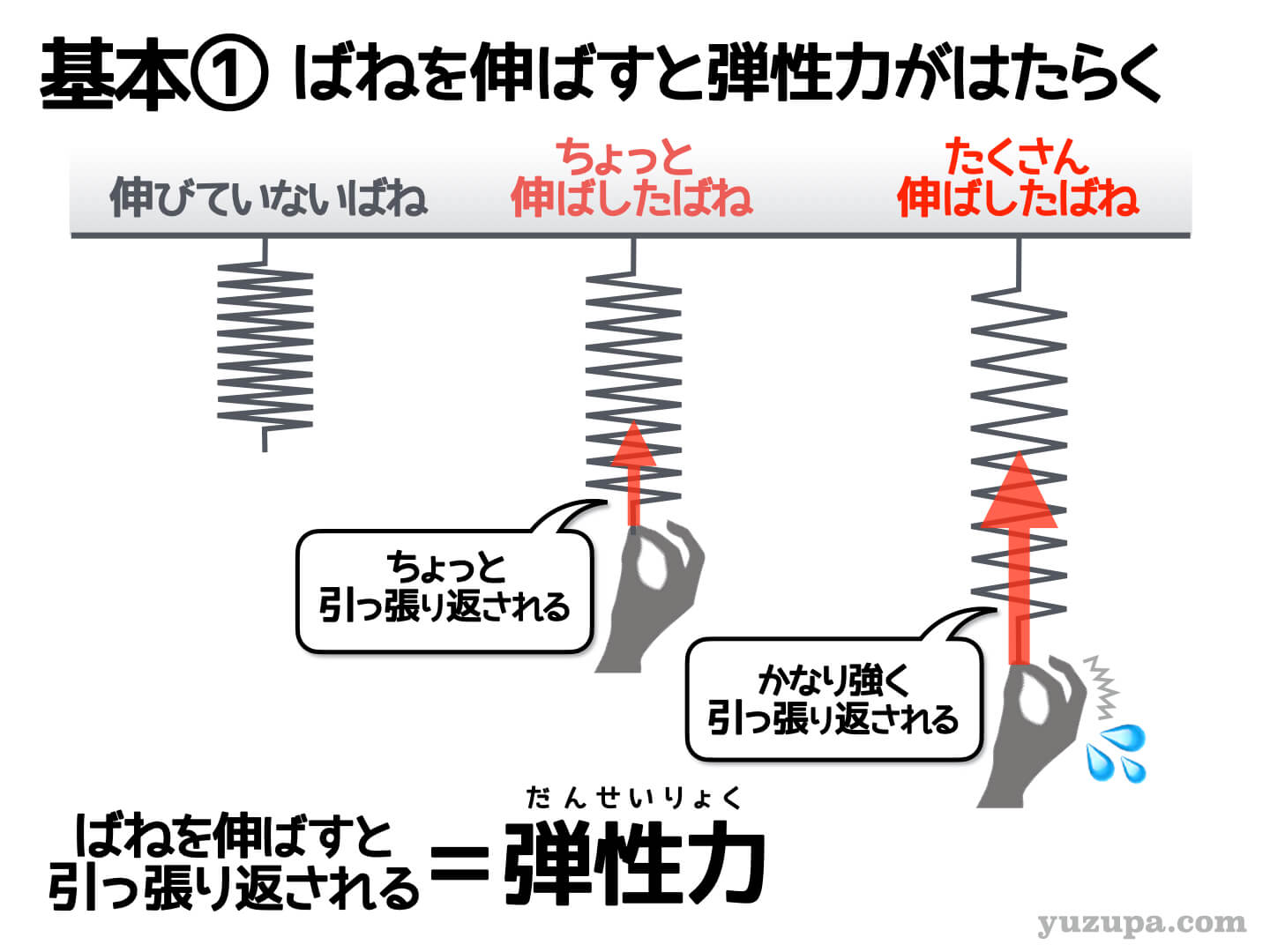
(1) ばねを伸ばすと…引っ張り返される

ばねを手などで伸ばすと… ばねは引っ張り返してきます ね。少し伸ばしただけでは小さな力で引っ張り返されますが、たくさん伸ばすとかなり強く引っ張り返されます。

(2) ばねを押すと…押し戻される

逆にばねを押すとどうでしょうか？ ばねは押し戻してきます。こちらも同様に、少し押しただけでは小さな力で押し戻されますが、たくさん押すと大きな力で押し戻されます。

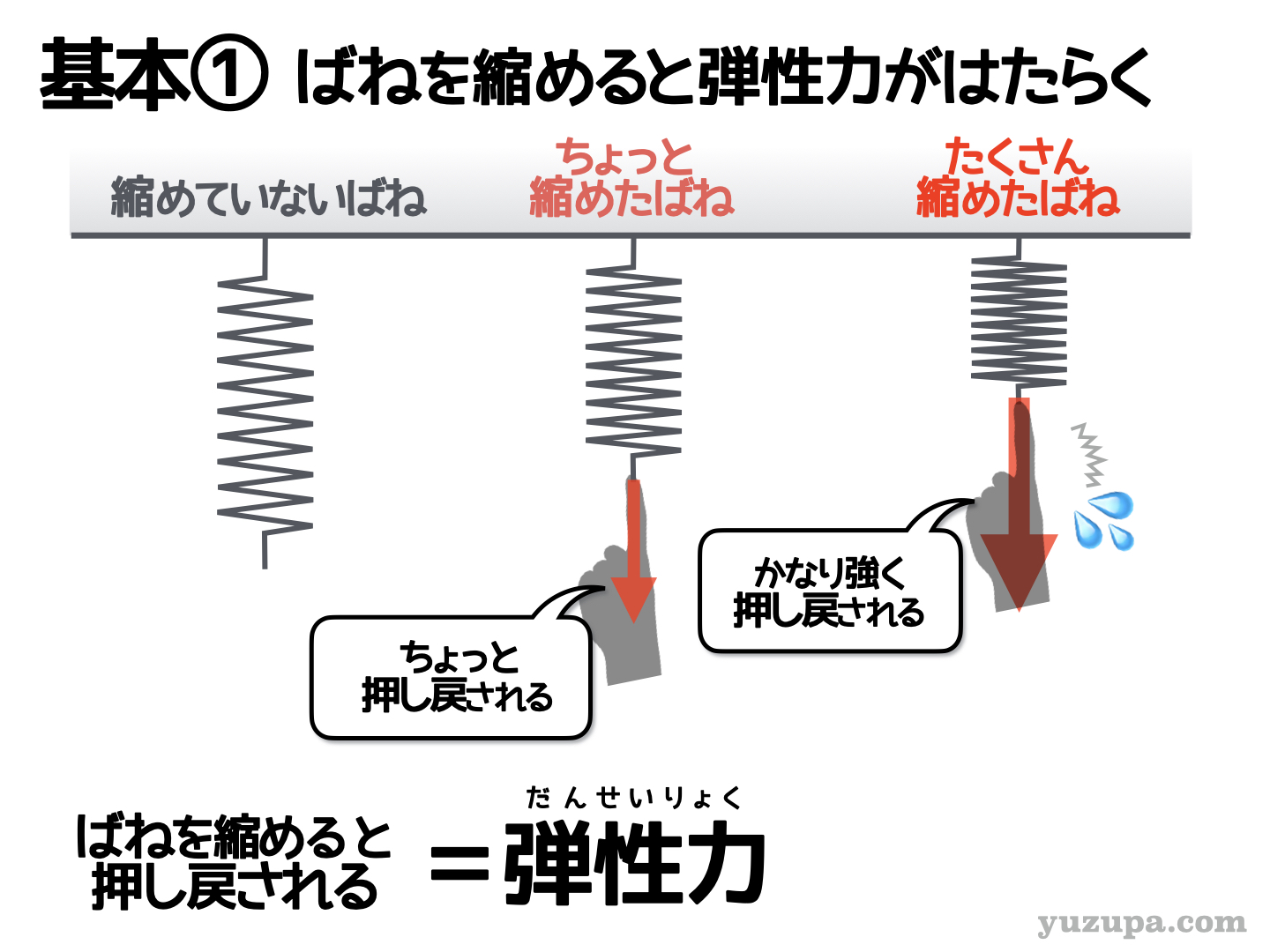
これが ばねの弾性力 です。

 

基本② 弾性力の大きさ＝ばねの伸びに比例

弾性力がどんな時に発生するかを理解したところで、今度は その力の大きさを知る必要 があります。ばねの弾性力の大きさですが…極めてシンプルです。

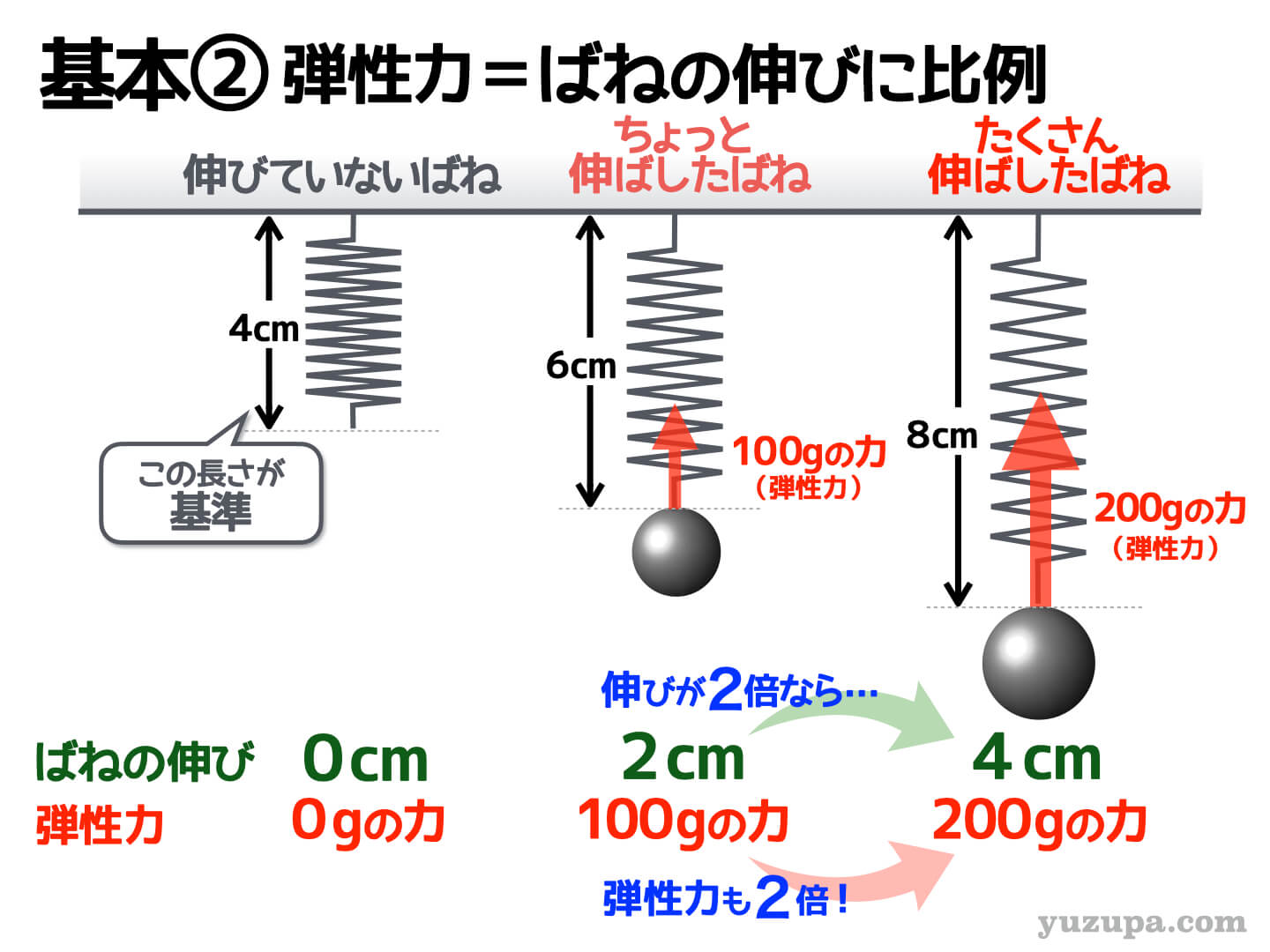
弾性力の 大きさは”ばねの伸び”に比例する ので超簡単です

例えば…力をかけずに伸びていない状態の長さが4ｃｍのばねを、6cmになるまで伸ばしたとき(伸びが2cmのとき)の弾性力が100gの大きさとなるばねがあるとします。

このばねが8cmになった時、弾性力の大きさはいくつでしょう？ 8cmになったときのばねの伸びは4cmですので、伸びが2cmの時の2倍の力…つまり200ｇの大きさとなります。

”ばねの伸び”と“弾性力の大きさ”は比例 するということ

小学生が問題を解いている時に間違ってしまう典型的な例として、”ばねの伸び” と ”ばねの全長” を取り違えてしまう という例。理解不足というよりは、ミスに近い間違えです。

”ばねの伸び”と”ばねの長さ”を意識しないといけないですねd(^_^o)

 

基本③ 弾性力の大きさ＝はかりの値そのまま

ばねの弾性力がはたらくのは “シンプルなばね” だけではありません。“ばねばかり” も “台ばかり” もその正体は “ばね” です！分解すると中には “ばね” が入っています。

ばねが入っているということは…
もちろん伸ばしたり縮めたりすると弾性力がはたらきます

ただ…”ばねばかり” や “台ばかり” は中に入っているばねの伸びや縮みは見えません。ただ “ばねばかり” や “台ばかり”の弾性力は拍子抜けするほど簡単に知ることができます！

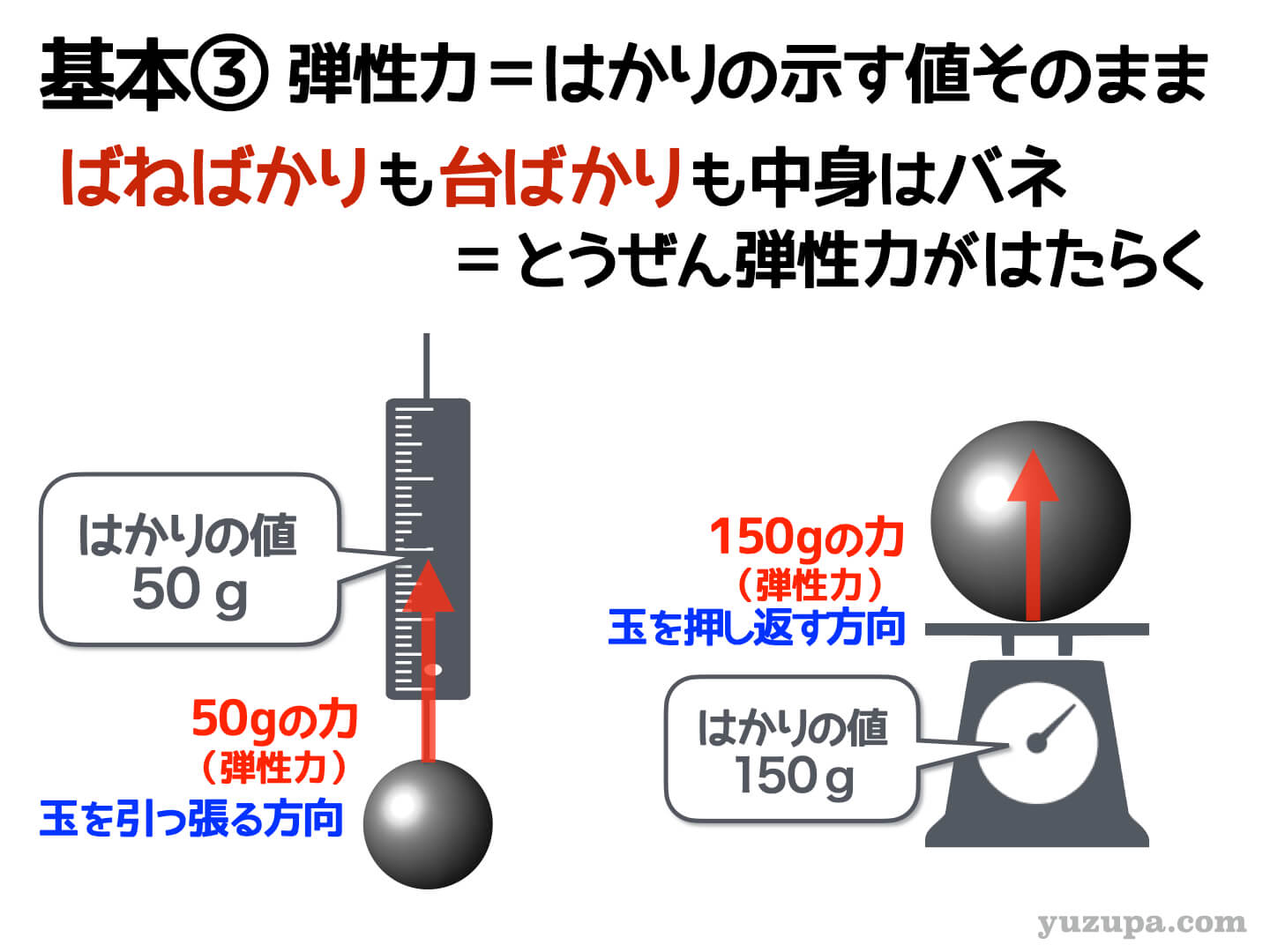
“ばねばかり”は、はかりの示す値と同じ大きさでぶら下がったものを引っ張り返します。”台ばかり”は、はかりの示す値と同じ大きさで、のっかったものを押し返します。

つまり…
弾性力の大きさ＝はかりの示す値 “そのまま”

超シンプルですね！

 

補足①  比例関係の表現方法は２種類

さて…ばねを引っ張ったり、押したりすると、ばねの伸びや縮みに比例した大きさの弾性力が発生します。この 比例の関係を整理する表現方法はメジャーどころで2つ の方法があります。

表とグラフの2種類 です_φ(･_･

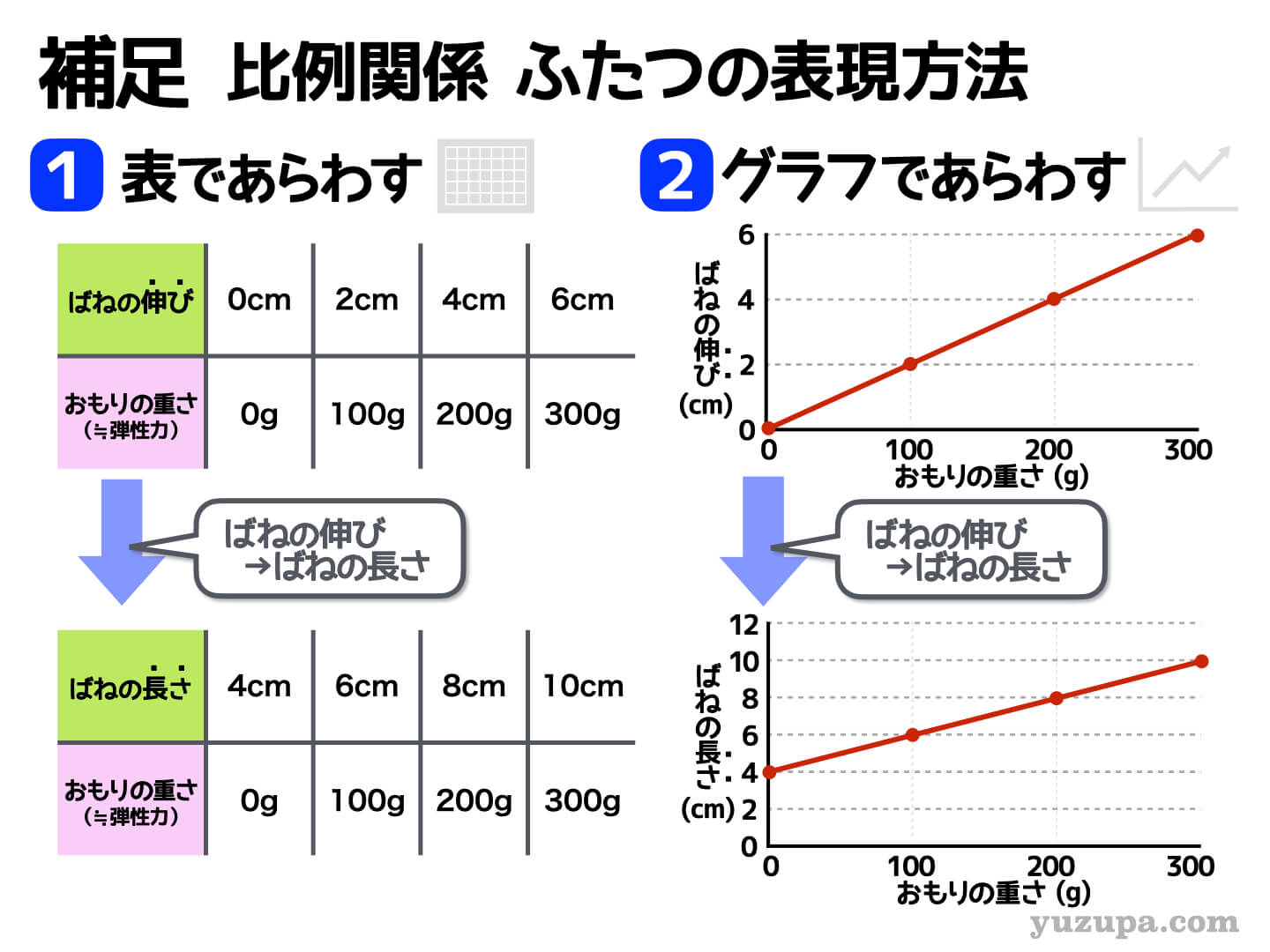
表やグラフを正しく読むことができれば、ばねの伸びと弾性力を相互に変換することができます。試しに表を読み取ってみましょう！

　ばねの伸びが2cmだったら？
　　→ ばねに発生する弾性力は100gの力

　ばねに300gのおもりがぶら下がっていたら？
　　→ ばねの伸びは6cm

もちろん表やグラフにのっていない値でもできますね d(^_^o) 表を読み取ると…このばねは100gで2cm伸びるばね という事がわかりましたね。あとは計算で出すことができます_φ(･_･

　ばねの伸びが8cmだったら？
　　→ ばねに発生する弾性力は400gの力

　ばねに600gのおもりがぶら下がっていたら？
　　→ ばねの伸びは12cm

という具合ですね_φ(･_･

 

！ココに気をつけろ！

表もグラフも単純に ”ばねの伸び” ではなく “ばねの長さ” になっていることがよくあります∑(ﾟДﾟ) ここをウッカリ読み間違えると間違えてしまうので注意しましょう_φ(･_･

 

補足②  おもりの重さと弾性力は同じ？

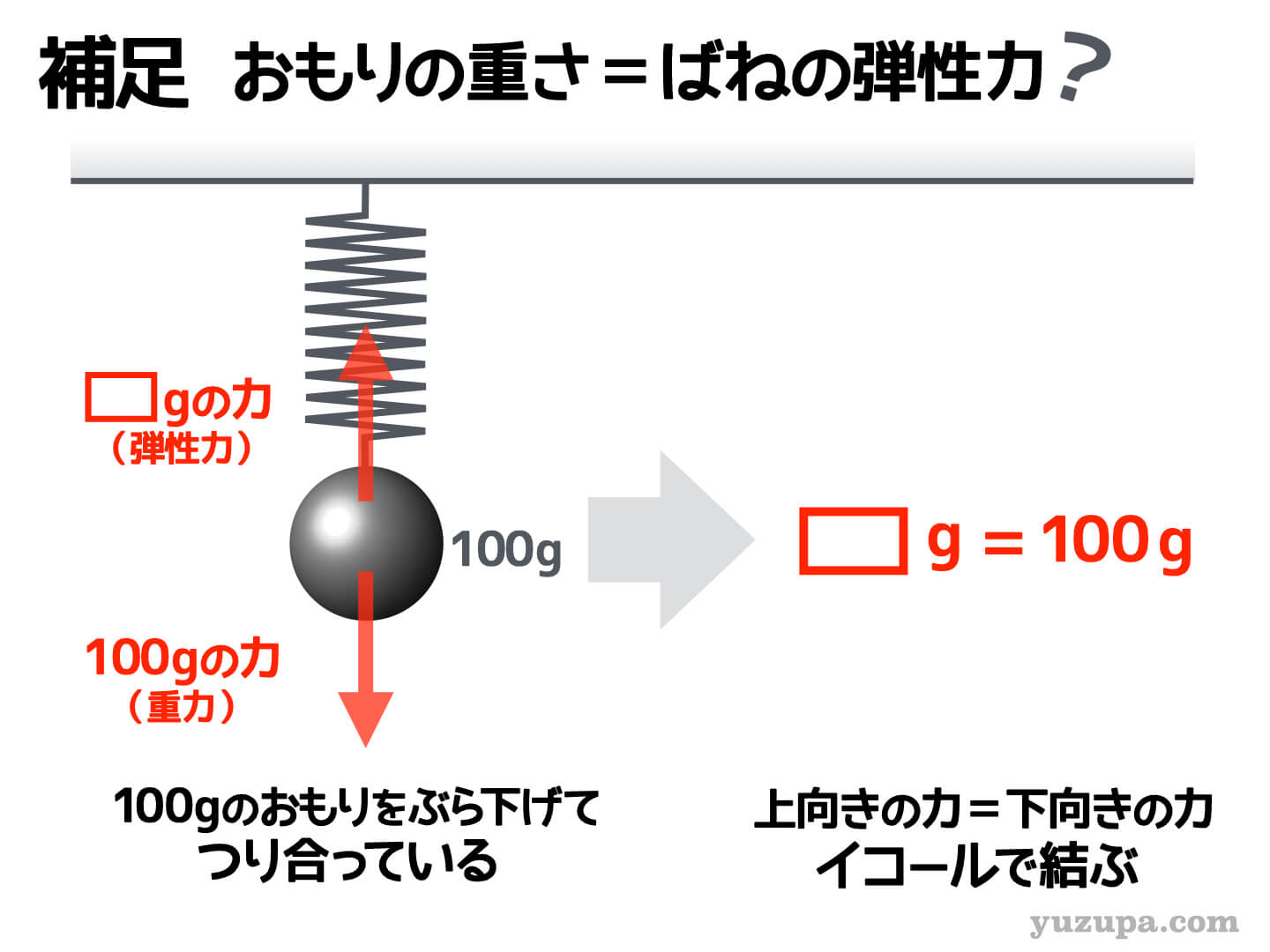
ところで表やグラフには “弾性力”とは書かれていません。”おもりの重さ”と書かれています。それなのにどうしてこれが弾性力の大きさであるといえるのでしょうか？

なぜならば、おもりをぶら下げたときの重力と弾性力がつりあっている状態なので…つり合いの式が成り立ちます。２つの力をイコールで結んでしまいましょう！すると…

おもりにはたらく”重力” ＝ おもりにはたらく”弾性力” 

となるわけです！

 

補足③  弾性力は”ばねの両端”にはたらく

もうひとつ超重要な補足です。天井に吊り下げられたばねに100gの力で弾性力がはたらいているとします。その時、ばねのもう片方はどうなっているのでしょうか？

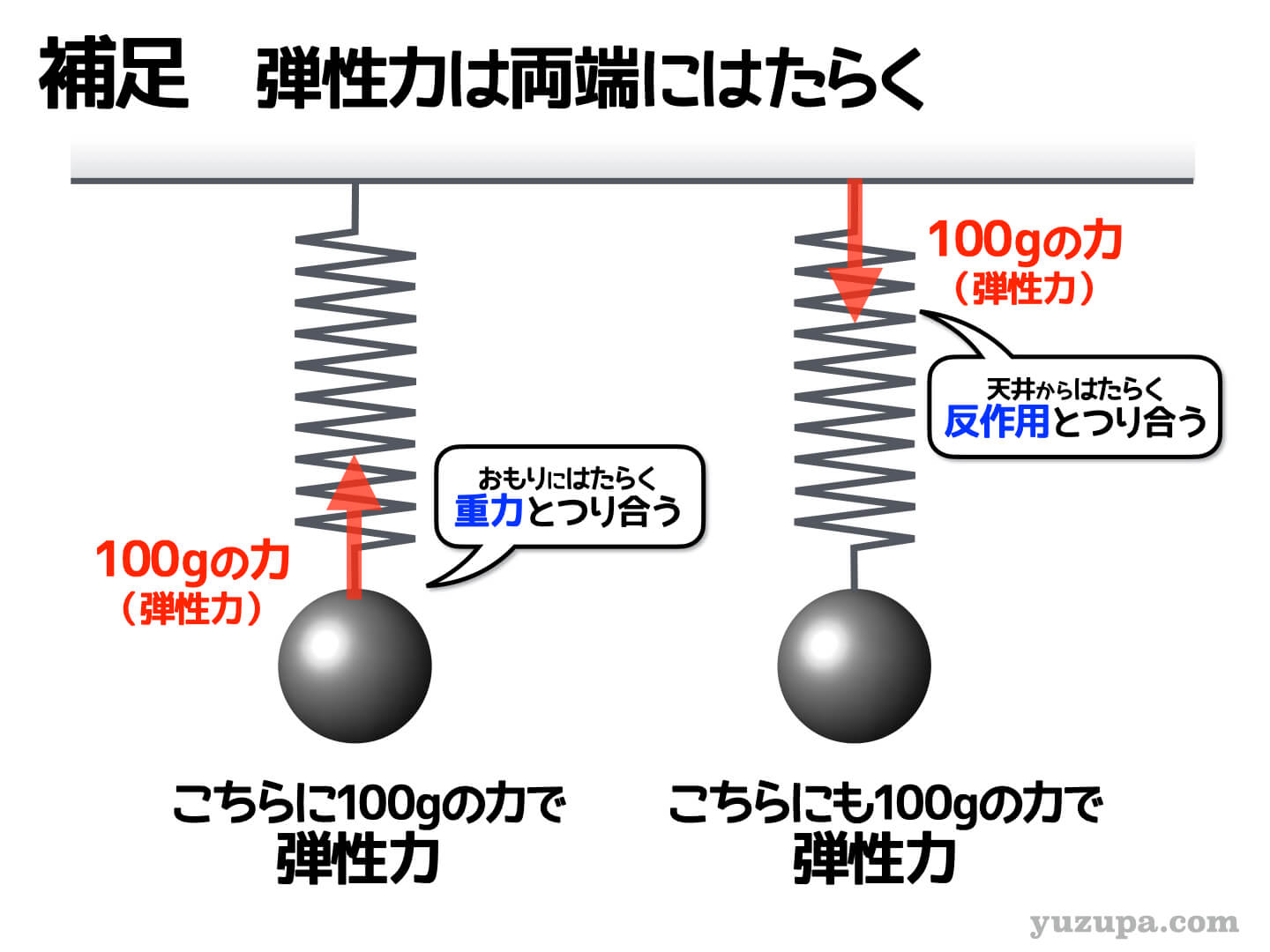
ばねの両端には…
同じ大きさの弾性力がはたらいています_φ(･_･

この図の場合… ばねの下端は おもりの重力とつり合って、ばねの上端は 天井の反作用の力とつり合って います。ばねに弾性力がはたらいていたら… もう片方もはたらいていると考えましょう。

 

力学の王道アプローチ…つりあいの式

全ての力を描いてつりあいの式を立てる

さていよいよ力学の本質にふみこんでまいりましょう。改めて中学受験で出題される力学問題の超限定的な条件を確認してみます。

  中学受験の力学は超限定的
　・たった５種類の力しか登場しない
　・力の向きは単純な２方向（力の分解は不要）
　・必ずと言っていいほど “つり合っている”

つまり…たった５つの力の矢印の描き方をマスターし、イコールで結んであげれば解答に近づくことができますd(^_^o)

 

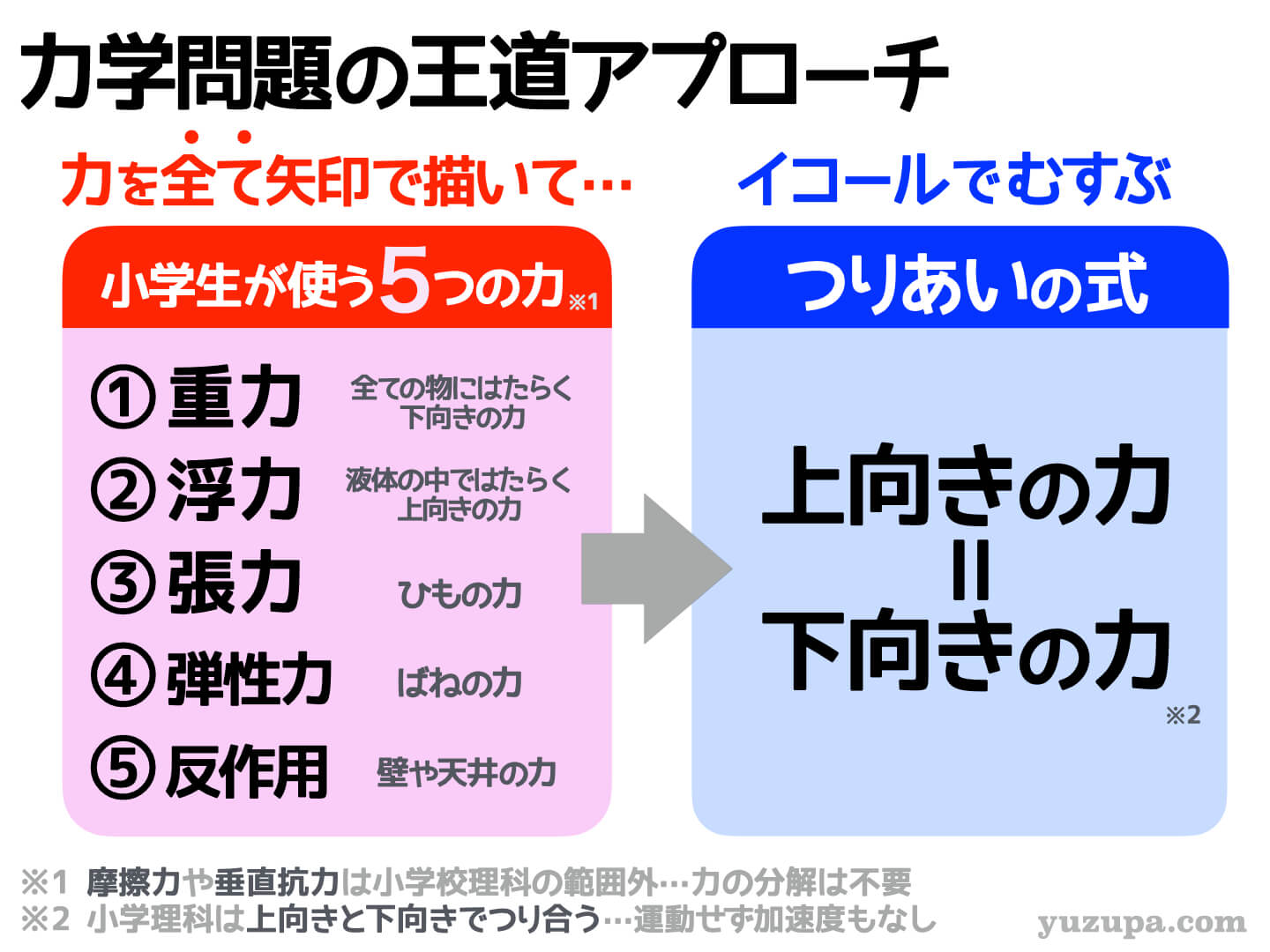
 中学受験で登場する5つの力

“上向きの力”と”下向き”の力をイコールで結ぶ前の大仕事。それはもれなく正しく力の矢印を描くこと ですd(^_^o) 中学受験で登場する５つの力をひとつずつ見ていきましょう！

(1) 重力

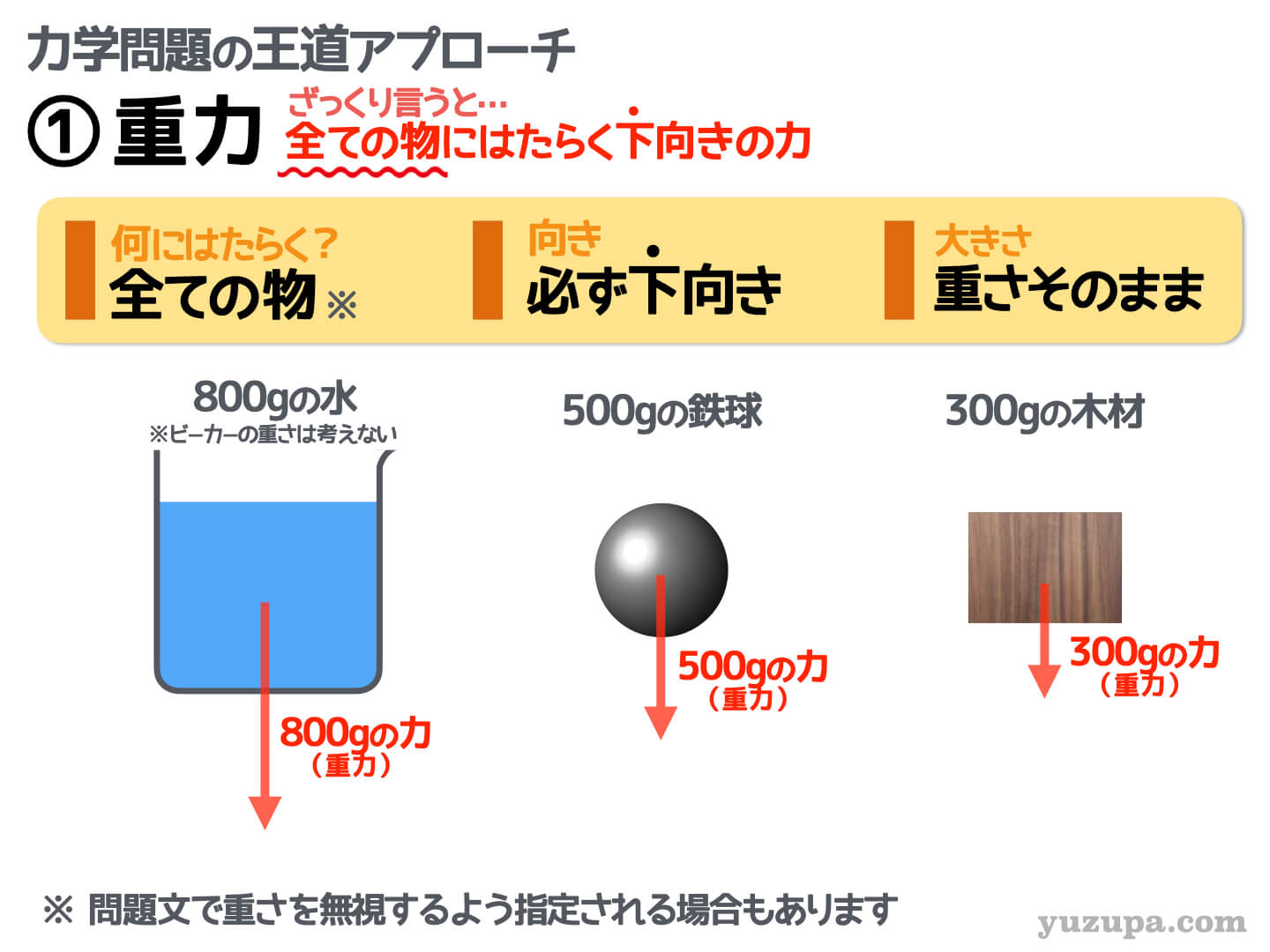
まず最初は 最重要の”重力” です_φ(･_･

最重要といえども…５つの力の中で最もシンプル。地球上にあるもの全てのものにはたらき、必ず下向きの方向、そして力の大きさは重さそのものです。超簡単です ∑(ﾟДﾟ)

ただし理科では…重力を無視しなければならない場合があります。例えば800gの水が入ったビーカー。もちろんビーカーにも重さはありますが問題によっては無視しなくてはいけません∑(ﾟДﾟ)

重さを無視するかどうかは
必ず問題文に書いてあるので注意しましょうd(^_^o)

ばねの重さや、てこに使う棒の重さなんかは…ほぼ重力を無視するよう指定されます。動滑車に使われる滑車は無視することが多いですが、重さを考慮する場合もあります _φ(･_･

 

(2) 浮力

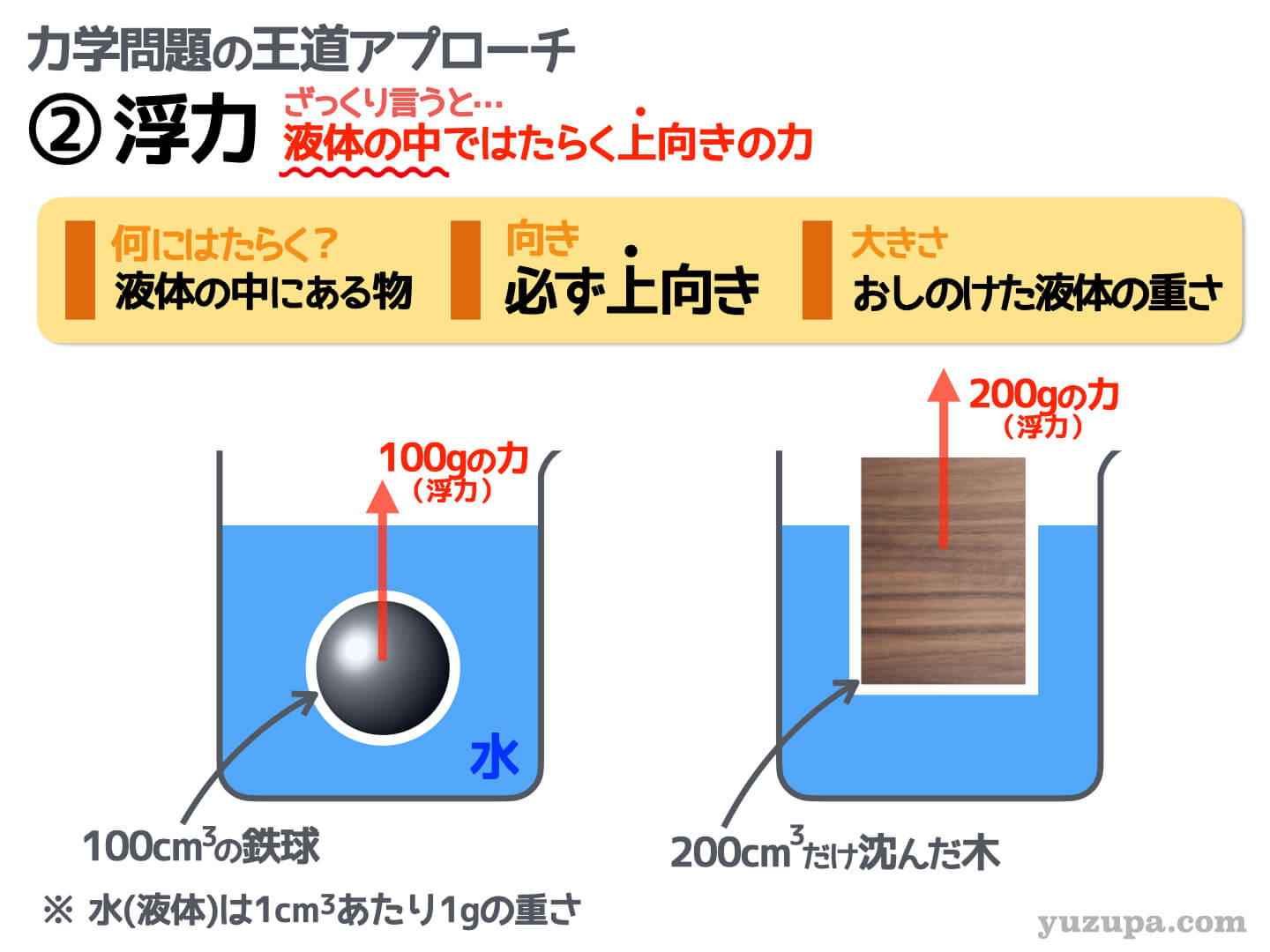
次は とっつきにくい”浮力” です_φ(･_･

ものが液体の中に入っていたら必ず浮力がはたらきます。実際の入試問題ではその液体は ”水” であることがほとんどです。そして力の向きは必ず上向きですねd(^_^o)

力の大きさは ”おしのけた液体の重さと同じ” になります。水であれば１㎤の重さが１gなので水に浸かっている体積が分かれば、力の大きさは簡単ですね_φ(･_･

ちなみに厳密には…気体の中にあるものにも浮力がはたらきます。ただ気体は押しのけたとしても大した重さにはならないので、無視してしまってもあまり影響がありません。そのため、小学校や中学校の理科の授業では無視します_φ(･_･

 

(3) 張力

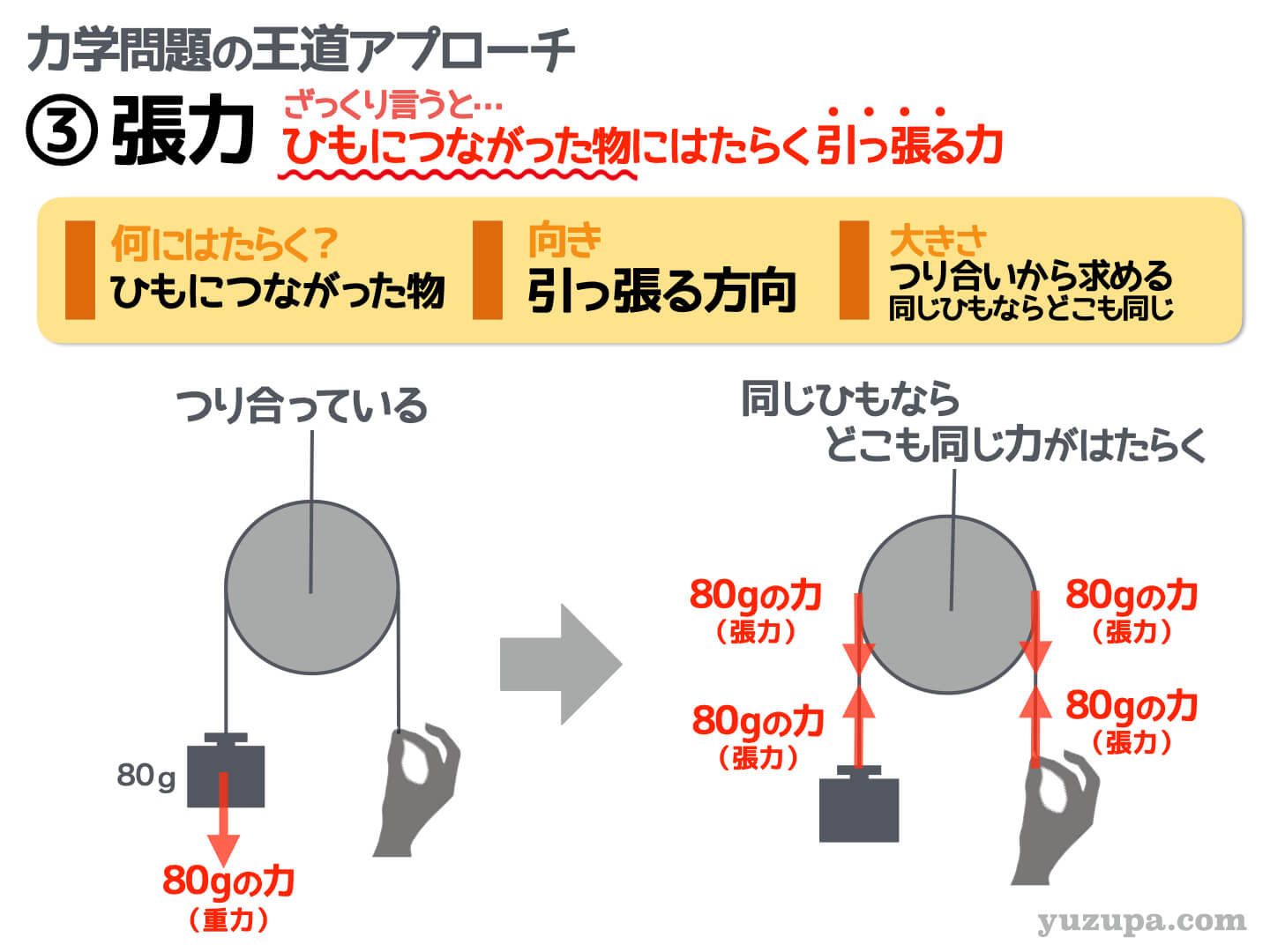
次は 張力 です。

この力はひもがピーンと張った時にはたらく力です。力の向きはひもが引っ張る方向です。力の大きさは、直接的には分からないため ”つりあいの式” から求めることになります。

最大のポイントは…
同じひもであればどの部分にかかる張力も同じ大きさ

ということ！どこか一箇所でも張力の大きさが分かってしまえば、全部わかってしまいます ∑(ﾟДﾟ) おもりにはたらく張力、動滑車にはたらく張力、つまんだ指にはたらく張力…

全部おなじ大きさですd(^_^o)

 

(4) 弾性力

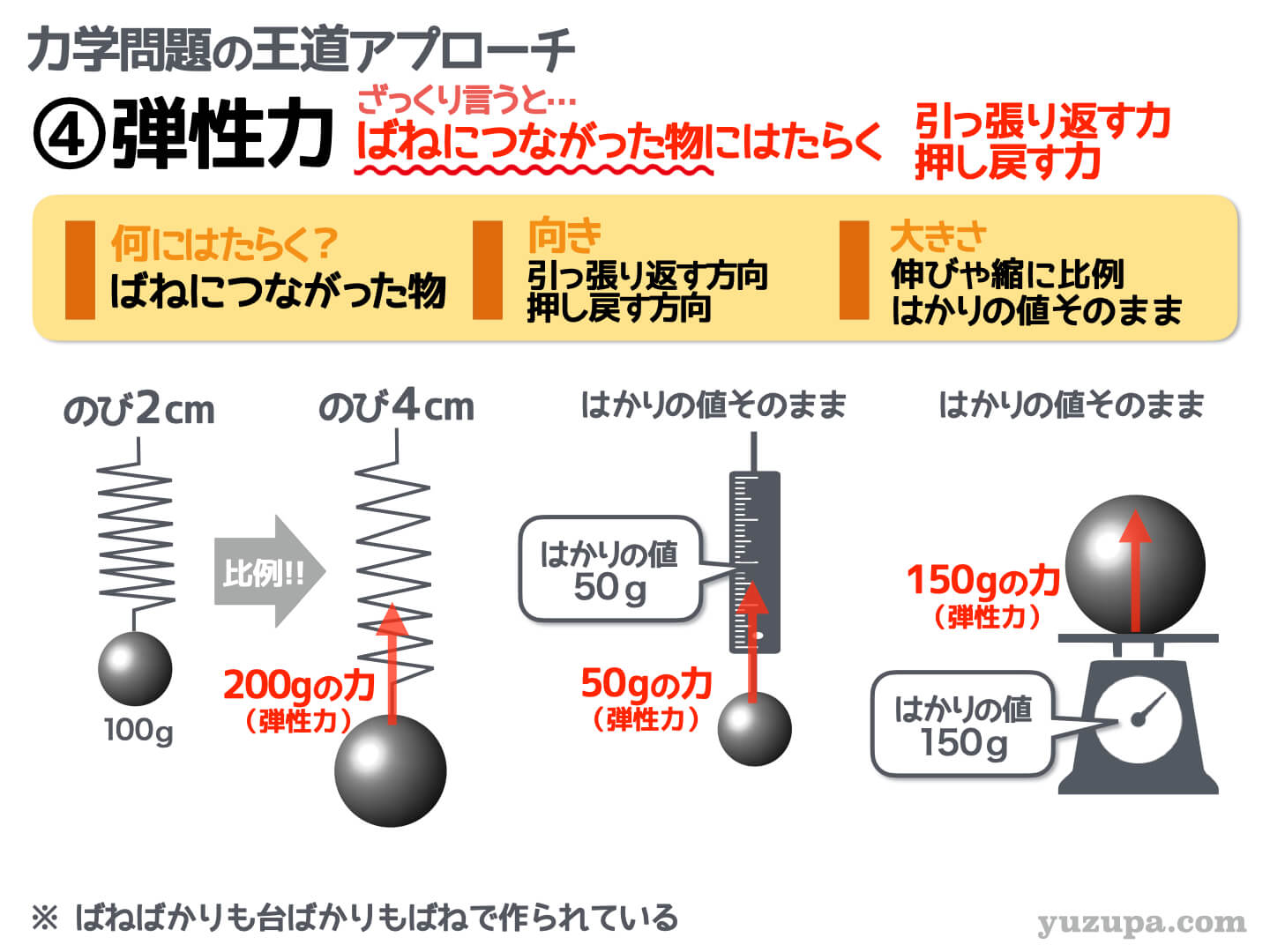
４つ目の力は、今回のメインテーマ…弾性力 です。

前項で説明したとおり…ばねを引っ張れば、引っ張り返す方向に…ばねを押せば押し戻す方向にはたらきます。力の大きさは、ばねの伸びや縮みに比例しますね _φ(･_･

そして… 忘れてはいけないのが 中にばねが入った ”ばねばかり”や”台ばかり”ですね d(^_^o) 

 

(5) 反作用

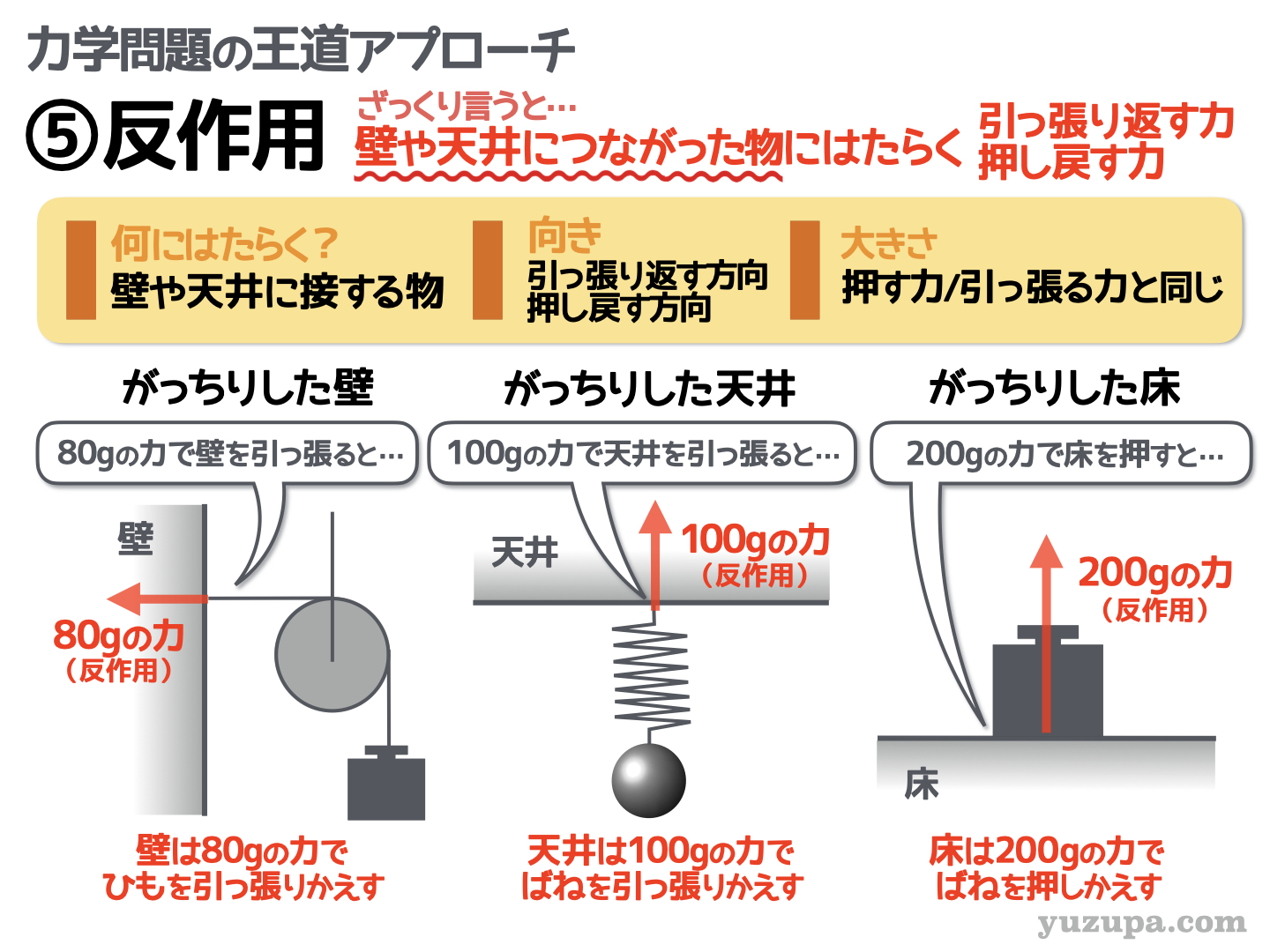
最後は 反作用 です。

正確には 作用・反作用の法則 といいますd(^_^o) 壁とか天井とか床とか ガッチリ動かないもの って引っ張っても押してもビクともしませんよね… それが反作用です。

ガッチリしたものは… 引っ張れば全く同じ大きさで引っ張り返し、押せば全く同じ大きさで押し戻します。作用する力に依存するというわけです。

 

以上が中学受験で登場する５つの力です_φ(･_･ 

 

ばねの弾性力を知る３つのアプローチ

今回のメインテーマである ”ばねの力” についてまとめてみましょう。ザックリいうと３つのアプローチがあります_φ(･_･

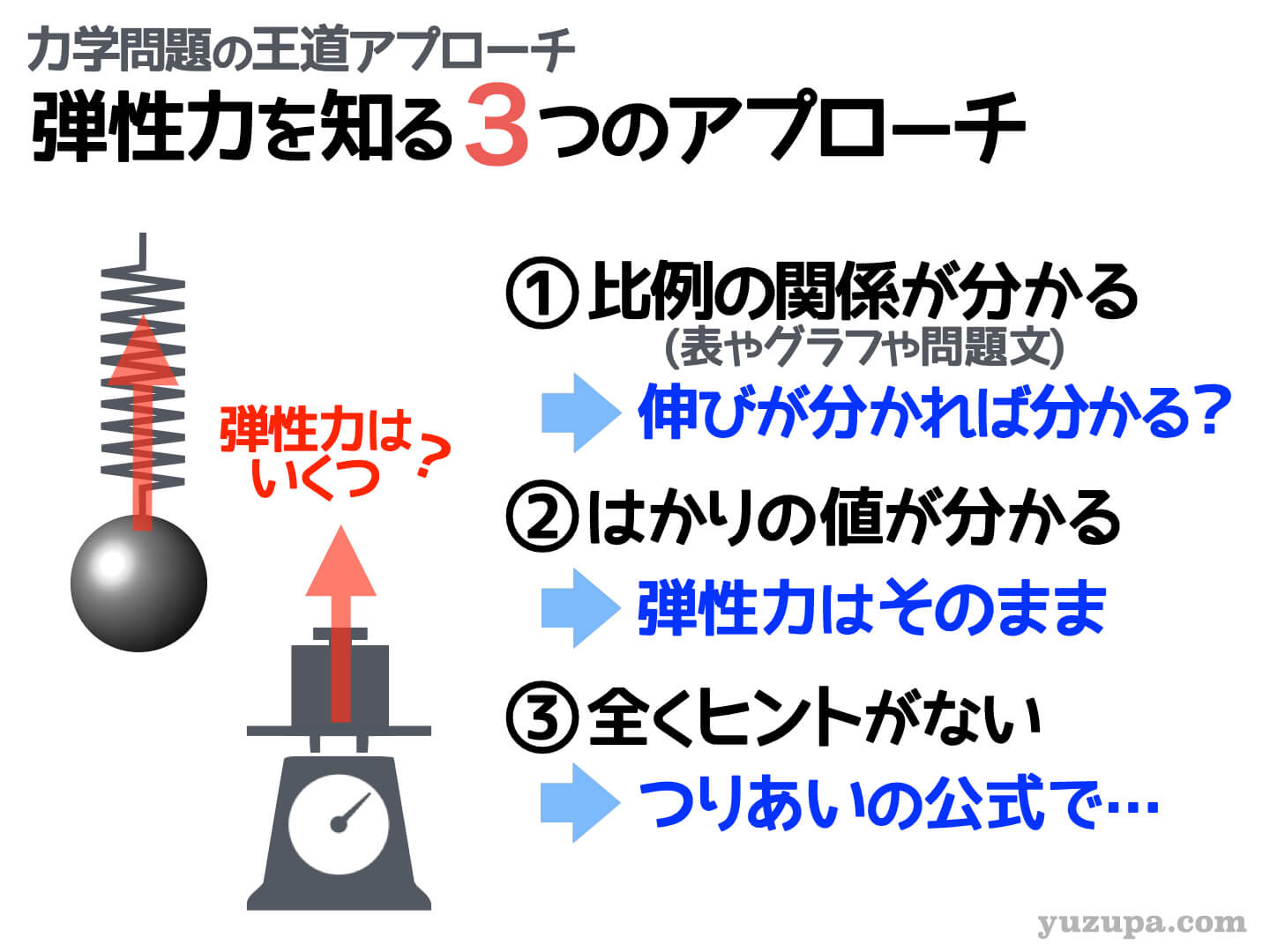
まずは比例の関係を探しまくる。表なのか…グラフなのか…問題文に書かれているのか…。”ばねの伸び”と”弾性力”のペアがひとつでも見つかれば大きなヒントになります_φ(･_･

“ばねばかり”や”台ばかり”があった場合は、その示す値があるかどうかを確認しましょう。はかりの値があればダイレクトに弾性力がわかるのですぐさま図に矢印を描きましょうo(^-^)o

弾性力が比例の関係からも、はかりの示す値からも分からなければ、考えられる力を全て描いてから、つりあいの式をたてましょう。分からない力の値も計算で出せるかもしれません。

それでは、いよいよ具体的な問題へまいりましょう。

 

実際の問題でばねを攻略する

例題① 弾性力をもれなく正しく(1)

まずは…ばねの弾性力をもれなく正しく描くことがポイントとなる例題をみてみましょう_φ(･_･

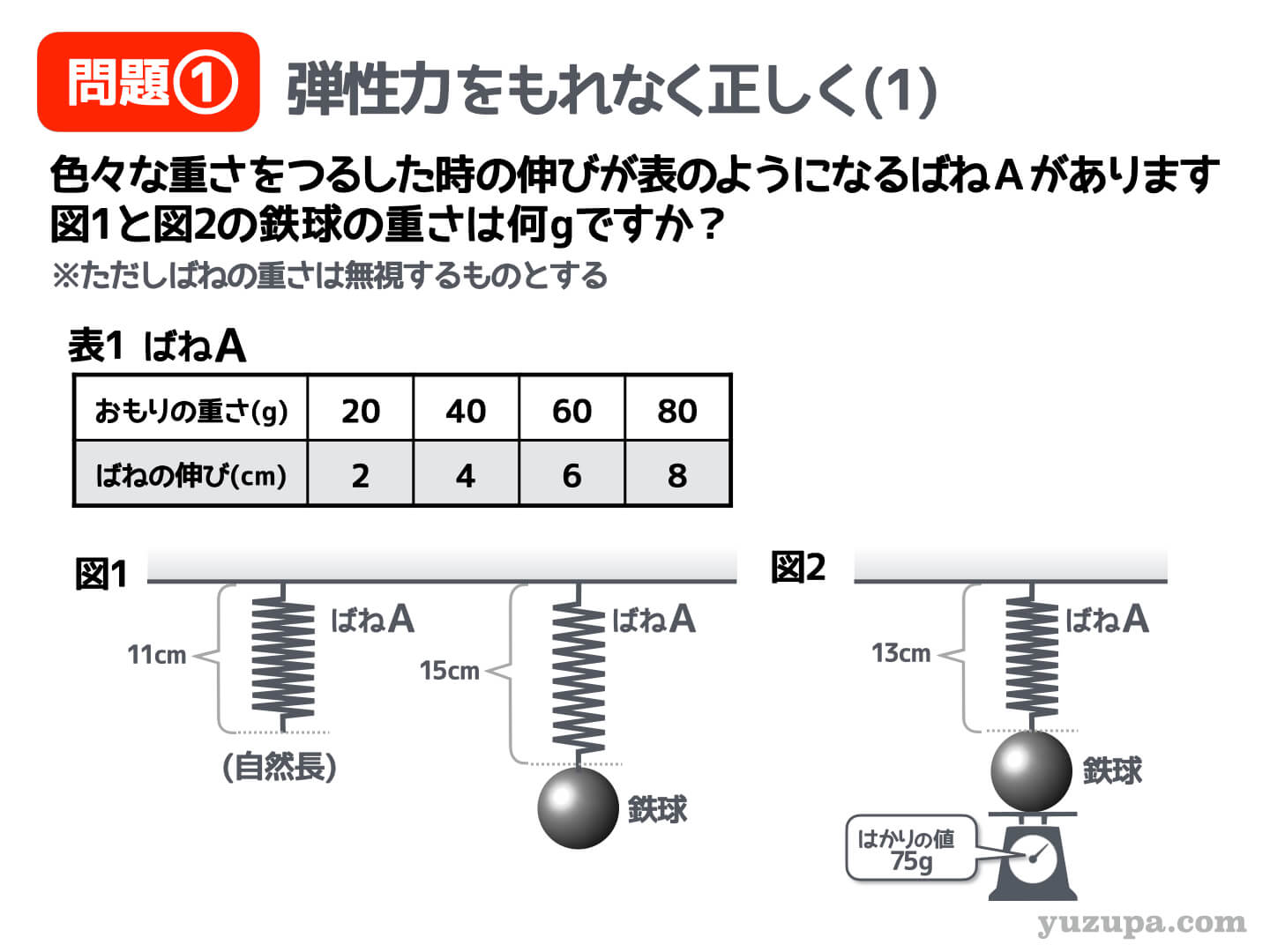
この問題で求めるのは ”ばねにぶら下がった鉄球の重さ” です。

例のとおりつり合っている状態ですので、力学の王道にしたがい、力の矢印をもれなく描いたあとにイコールで結びましょう。

まずは図１から解いてみましょうd(^_^o)

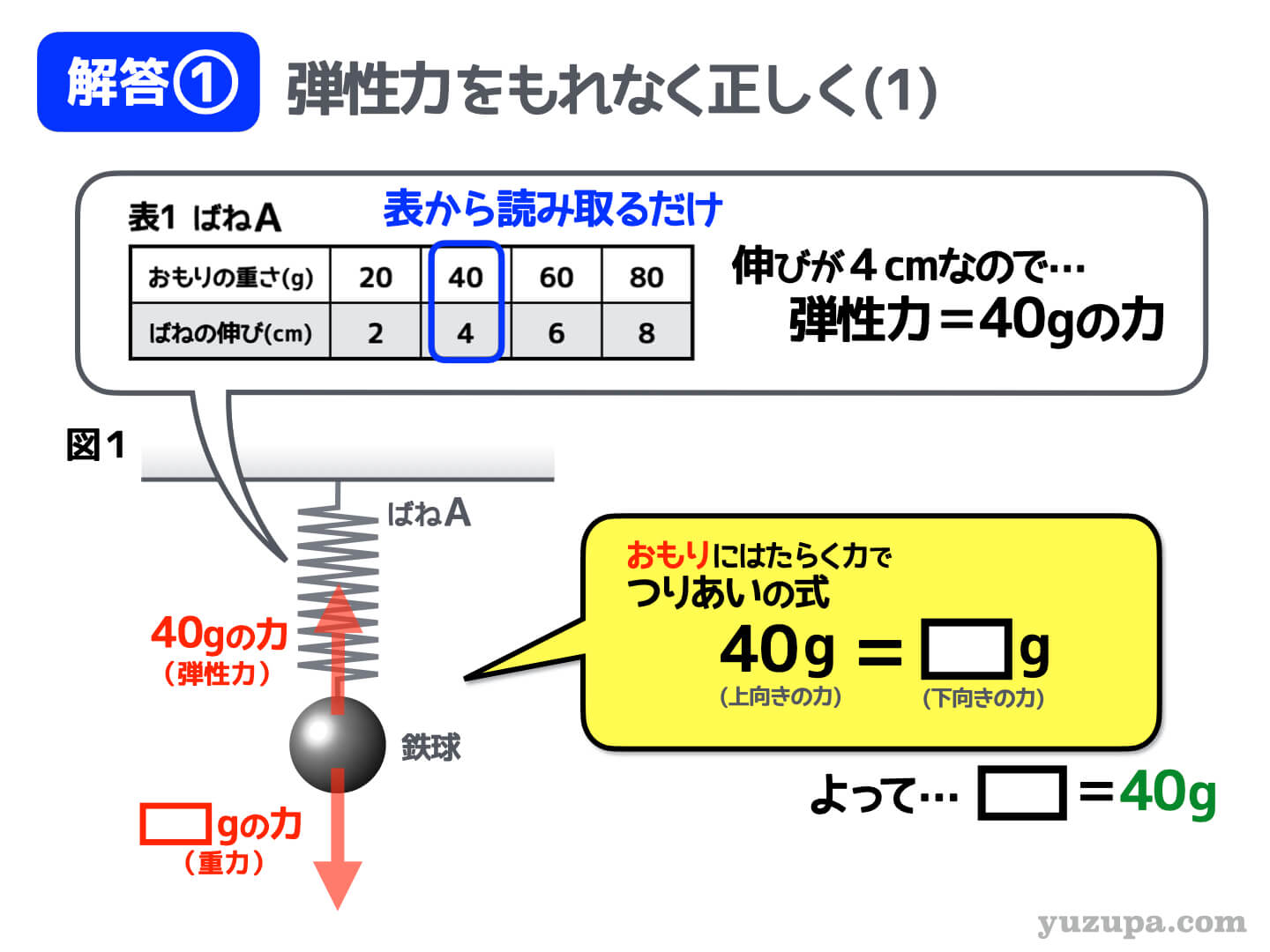
鉄球の重さを知りたいわけですから、鉄球に着目して力の矢印を描いてみましょう。この鉄球にはどんな力がはたいているでしょう？

1-1 . 重力を描く

まずは重力ですね。地球上の全てのものにかかる力ですので、最初にこの力を描くことを考えましょう。

重力は “そのモノの重さそのまんま” ですが、この鉄球の重さは分かりません。しょうがないので “□gの力” としておきましょう。向きはもちろん下向き です d(^_^o)

1-2. 弾性力を描く

鉄球は、ばねにぶら下がっているので弾性力もはたらいているはずですね。本記事のメインテーマですd(^_^o)

ばねにおもりをぶら下げて下に引っ張っている状態ですので、力の向きは ”ばねが引っ張り返す方向”で上向き です。力の大きさは、比例の関係が表で示されているので分かりそうです。

問題から自然長が11cmで図1の状態では15cmになっているので… このばねは4cm伸びている状況 であるということが分かります。表にダイレクトにその値がありますね？

弾性力の大きさは40gです。

2. つりあいの式を立てる

これで鉄球にはたらく力は全て描くことができました。

いよいよ…つり合いの式です。この場合は ”上向きの力” と “下向きの力” をイコールで結んでみます。すると下向きの重力が40gであることが分かりますねd(^_^o)

したがって…鉄球の重さは40g となります。

力学をわかっていれば… イキナリ表から求めてしまって構いません。が…力学の本質はどんな力がはたらいているかを全て書きだして、つり合いの式を立てることです。

ちょっとまどろっこしい解き方をしましたが、本質的にはこう理解することこそ最初にすべきことですd(^_^o)

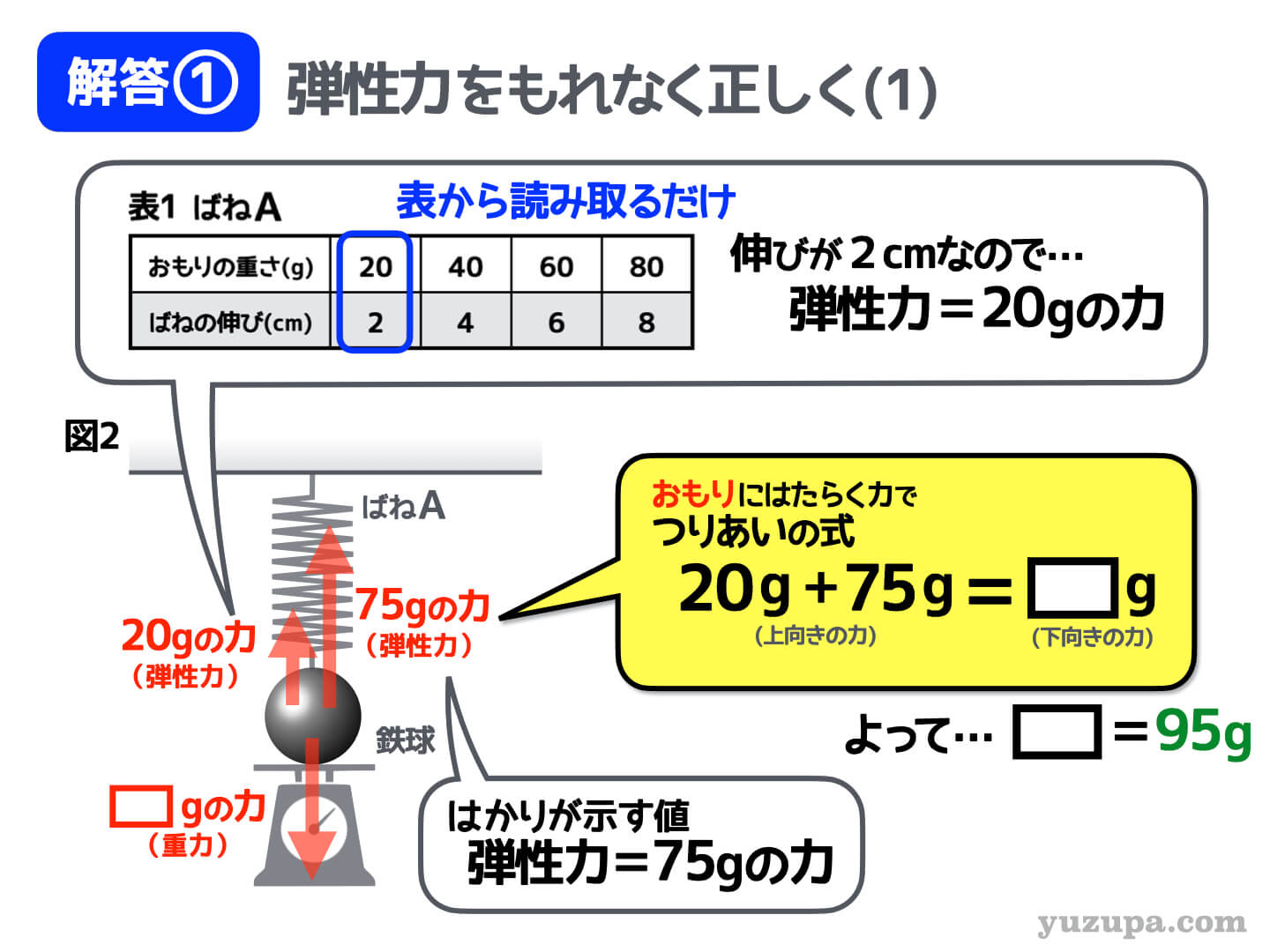
図2も同様におもりの鉄球に着目して全ての力の矢印を描くところからスタートしましょうd(^_^o)

1-1. 重力を描く

最初はやっぱり重力です。図1と同様で、おもりの重さが分からないので□gとしておきましょう。力の向きは…？ もちろん下向きです。重力は必ず下向きでしたねd(^_^o)

1-2. 弾性力(ばね)を描く

これもさきほどの図1と同様で上向きの弾性力がはたらきますが、大きさはどうでしょうか？今回は自然長の11cmから2cm伸びている状態ですので表から20gの力ということが分かります。

1-3. 弾性力(台ばかり)を描く

台ばかりなどの弾性力は “はかりの値が示されていれば超簡単” です。この問題は ”はかりの値” が示されているので簡単ですd(^_^o)

台ばかりですので、力の方向は押し戻す方向で上向き、そして大きさは ”はかりが示す値そのまま” ですので75gの力 です。

2. つり合いの式を立てる

この問題もつり合っている状態ですので、いつも通り “上向きの力” と”下向きの力” をイコールで結びますが、今度は上向きの力が２つあるので間違えないようにしましょう。

上向きの力は “ばねの弾性力” と “台ばかりの弾性力” です。しっかりと２つの力を足して、式をたててあげれば、下向きの重力が95gであることが分かってしましますd(^_^o)

したがって…鉄球の重さは95g となります_φ(･_･

 

この問題は表からシンプルに導きだすことができませんね。力学の問題は応用になると突然解けなくなることが(-_-;) 力学の本質…つり合いの式を立てることを忘れないようにしましょう。

 

例題② 弾性力をもれなく正しく(2)

次の例題も…ばねの弾性力をもれなく正しく描くことがポイントなのですが、先ほどと違い比例に関する情報が乏しい ∑(ﾟДﾟ)

比例の計算がキーポイントとなる問題です_φ(･_･

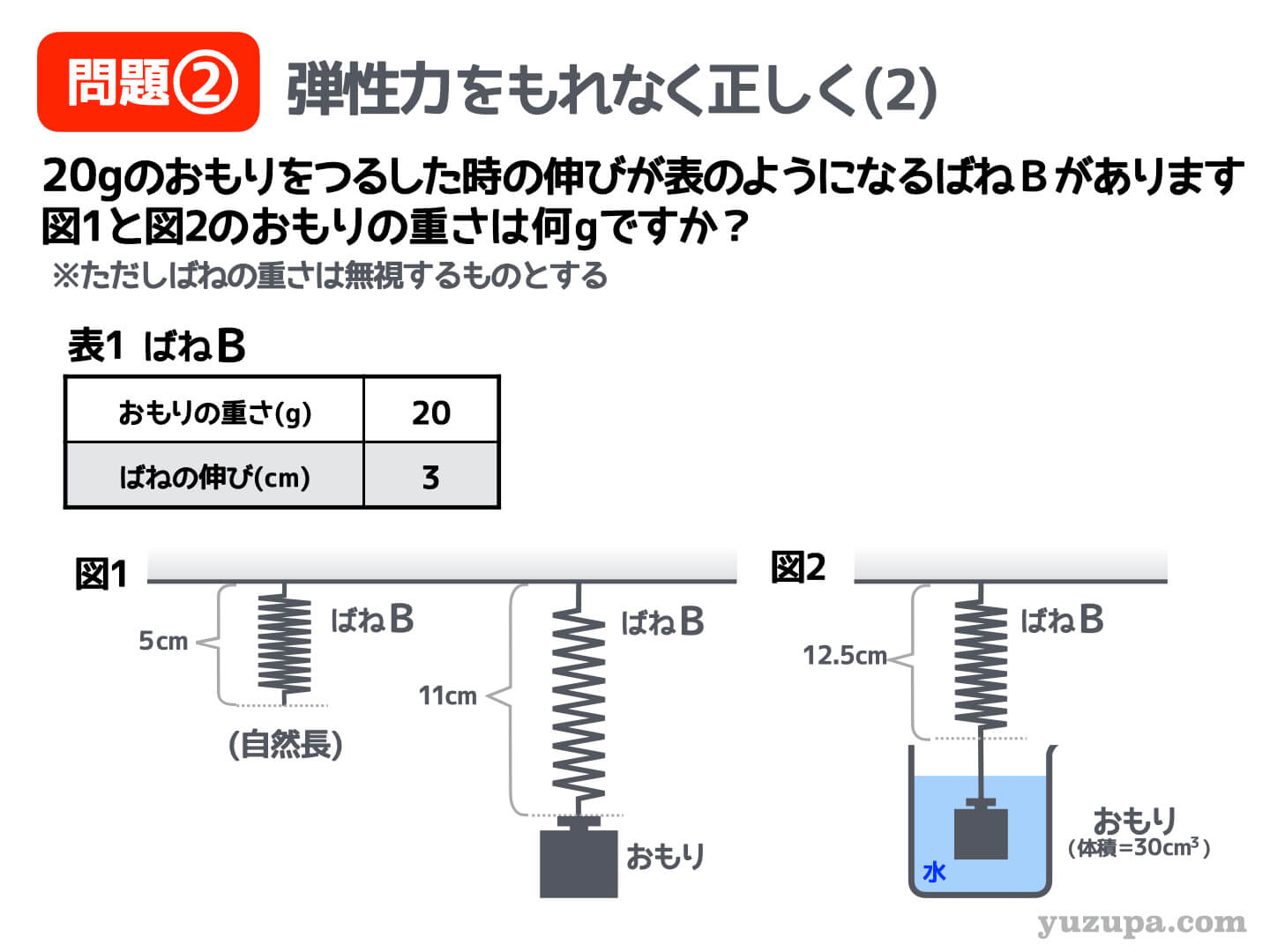
この問題も ”おもりの重さ” を求める問題です。

中学受験の問題はほとんどが…つり合っている状態の問題です。この問題もつり合っているので、力の矢印をもれなく描いたあとにイコールで結ぶという王道のアプローチです。

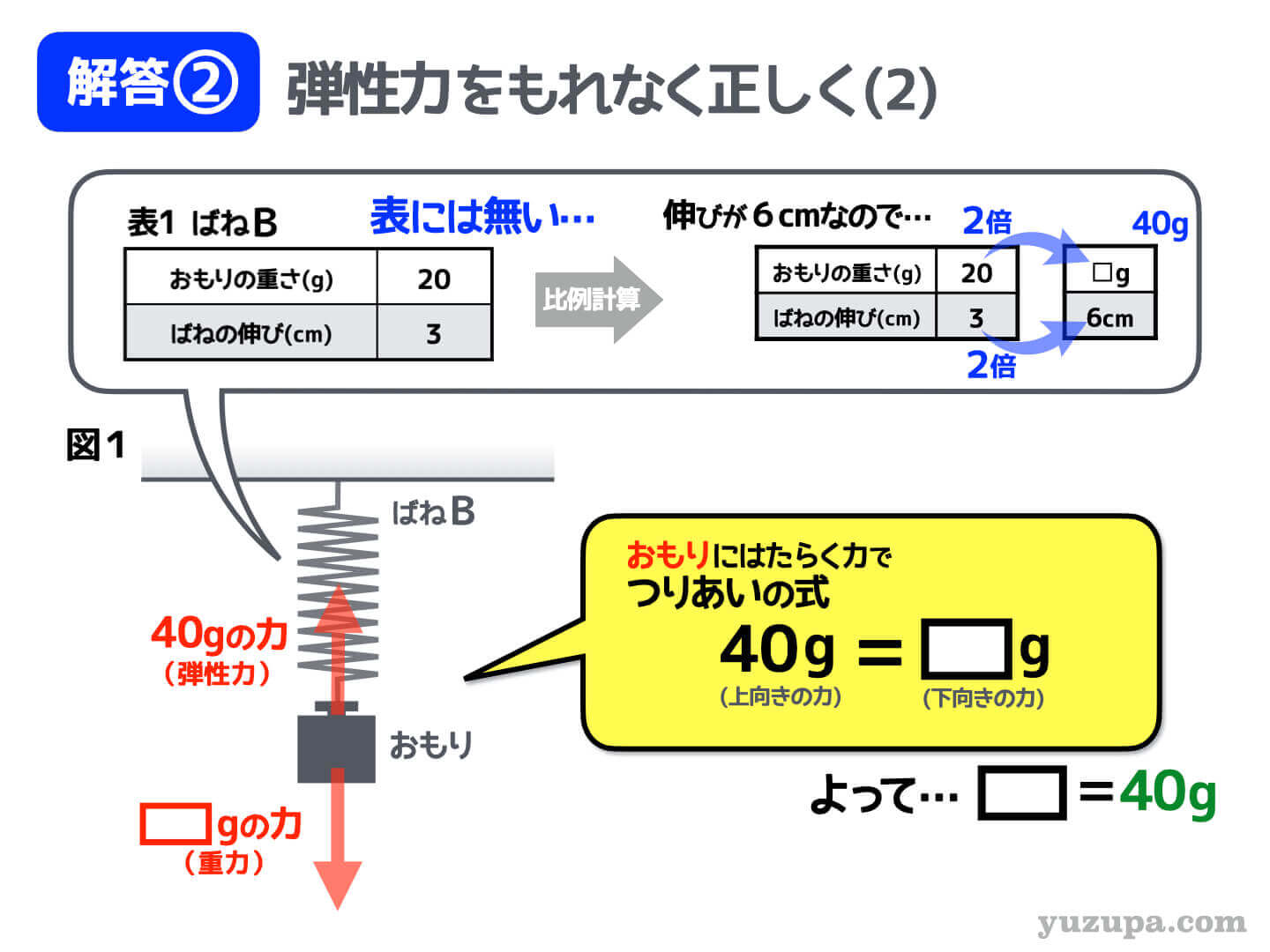
おもりの重さを求めるので、やはり着目すべきは ”おもり” でしょう。おもりにはたらいている力を漏れなく正しく描いていきます。

1-1.  重力を描く

おもりにはたらく重力ですが、分からないので□gとして矢印を描きましょう。向きは重力ですので下向きです。

1-2. 弾性力を描く

弾性力は”引っ張り返す方向”ですので上向きの方向です。大きさ比例の関係が表で示されているので、伸びから出せそうです。このばねの自然長は5cmで、図1は長さが11cmの状態ですので、ばねの伸びは6cm であることが分かります。

ところが…伸び6cmは表にありません∑(ﾟДﾟ)

“ばねの伸び”と”弾性力”は比例関係ですので、１組でも”ばねの伸び”と”弾性力”のペアが分かれば計算で求めることができます。この問題の場合は、それぞれの値を３倍すれば伸び６cmの時の、ばねの弾性力を求めることができますねd(^_^o)

2. つり合いの式を立てる

最後はいつもどおり、つり合いの式を立てます。そうすると下向きの重力が40gであることが分かりますね_φ(･_･

したがって…おもりの重さは40g となります。

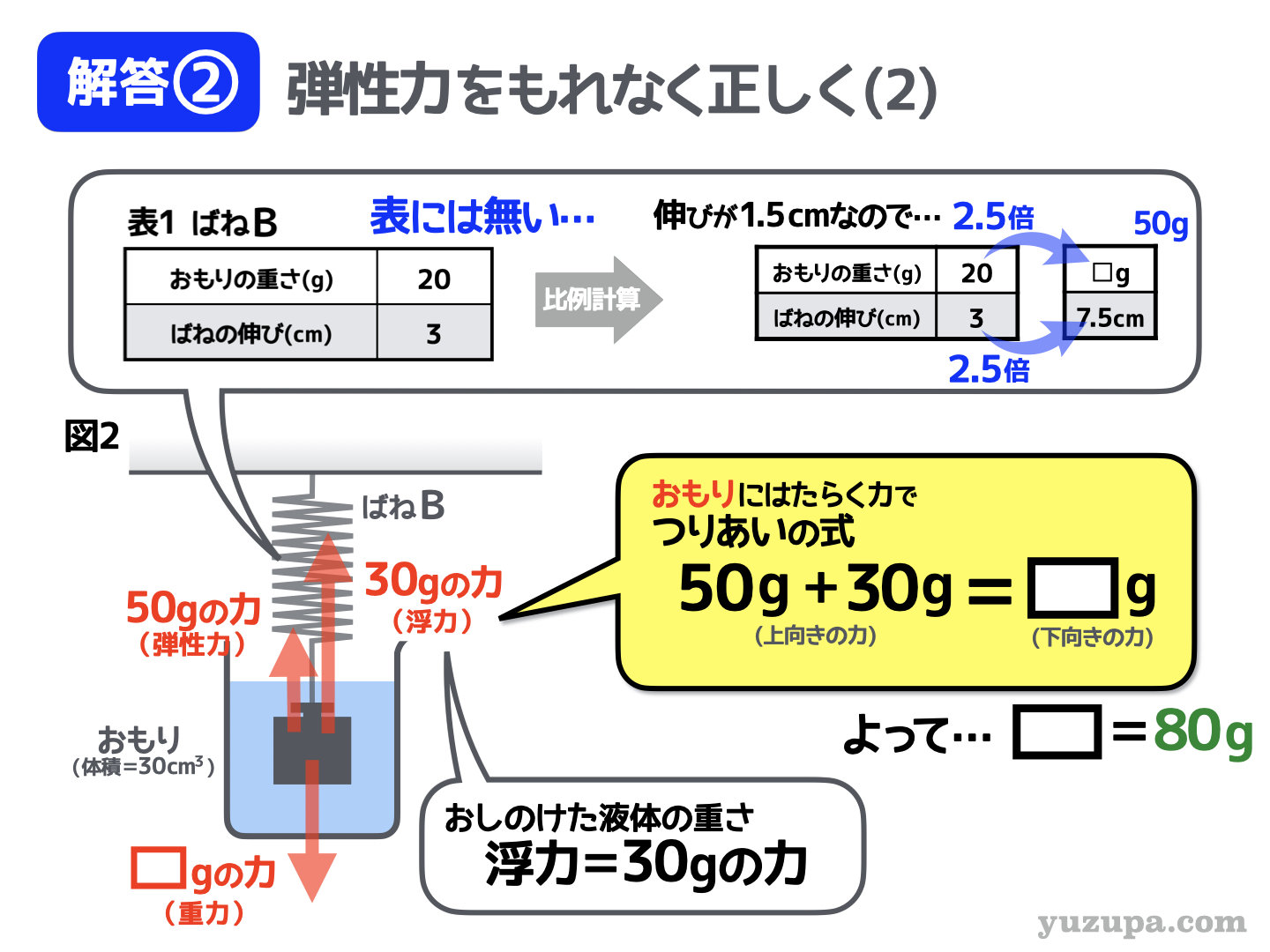
図2にまいりましょう。こんどは何やらおもりが水に浸かっています∑(ﾟДﾟ) それでも慌てる必要はありません。落ち着いて １つずつ力の矢印を書き加えていきましょう！

1-1. 重力を描く

おもりの重さが分かりませんので、重力はいつもどおり□gとして下向きの力として書き加えます。

1-2. 弾性力を描く

ばねの自然長が5cmで、全長12.5cmの状態ですので、ばねの伸びは7.5cmです。例のごとく、表にダイレクトに書かれていませんので、計算で求めることとしましょう。

伸びが3cmの時、20gの弾性力ということが分かっていいますので、それぞれの値を2.5倍にしてあげれば、必要となる情報にたどりつくことができます。この状態の弾性力は50g ですね。

1-3. 浮力を描く

最後はクセモノの浮力です。といいつつ…とてもシンプルです。なぜならば、おもりの体積が明記されているからです。おもりの体積が30㎤ですので、その体積の水を押しのけたことになります。

水は１㎤あたり１gですので、押しのけた液体の重さは30gということになります。浮力の大きさは押し退けた体積の重さになるので浮力は30gの大きさ です。浮力の向きは必ず上向きです。

2. つり合いの式を立てる

“上向きの力”＝“下向きの力” です d(^_^o) 上向きの力は、ばねの弾性力＋浮力ですので合計80gですね。

したがって…おもりの重さは80g となります。

余談ですが…30㎤で80gなので密度は約2.7g/㎤です。これはアルミニウムの密度に近いです。このおもりはアルミかな？くらいまで思えたら最強です(^_^;)

 

例題③ ばねを直列につなぐ　

次は…ばねをつないでみましょう。直列につなぐ場合と、並列につなぐ場合がありますが、まずは直列からです。

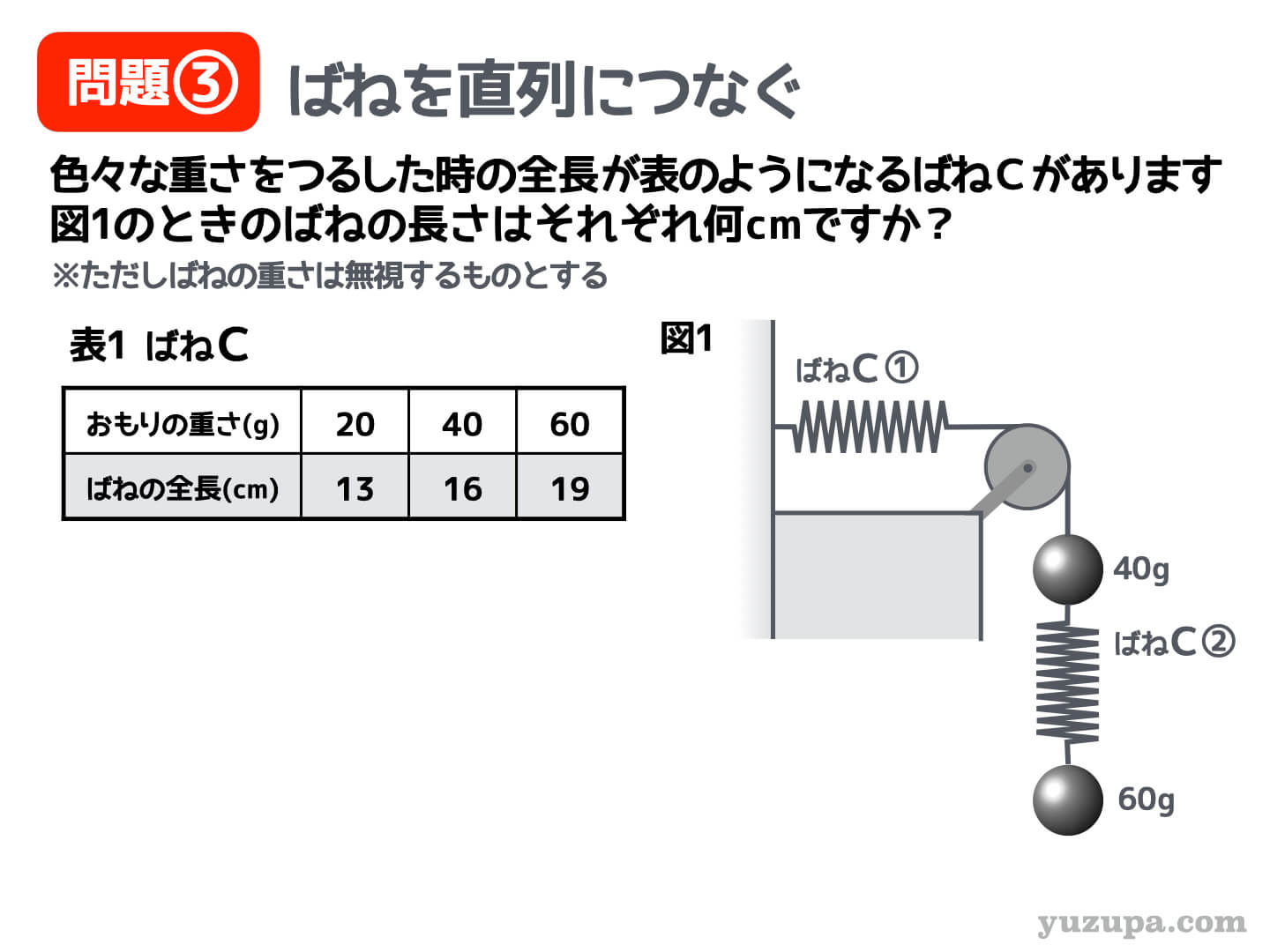
途中に滑車がありますが、ばねが２つ直列につながっていることが分かりますでしょうか？ 図を見ただけで ”お手上げ” 状態になる小学生… 力学の王道アプローチを落ち着いてこなしましょう。

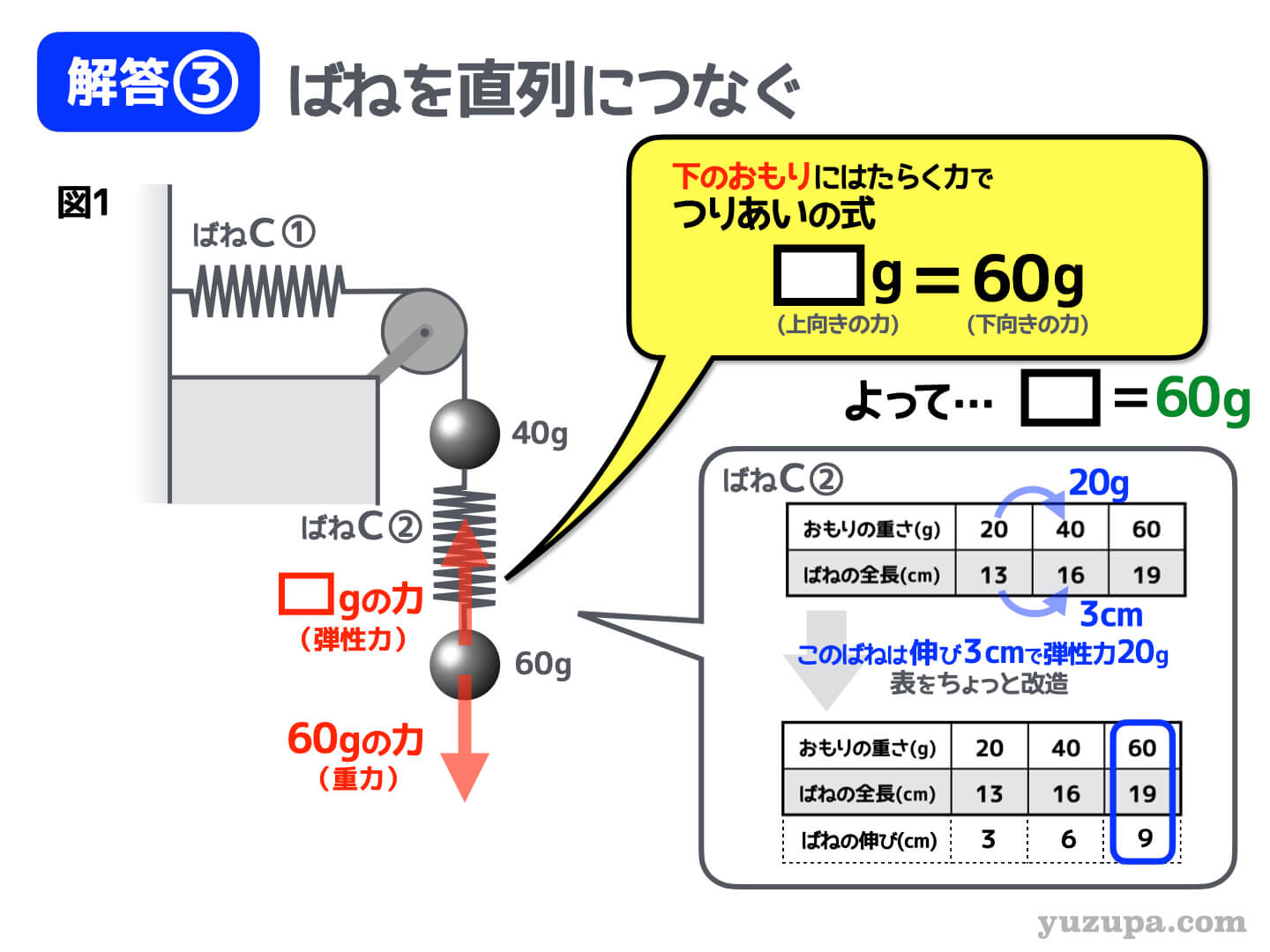それぞれのばねの長さを求める問題ですので、まずは…下にあるおもりに着目 してみましょう。

1-1. 重力を描く

もう慣れましたかね(^_^;) 地球上のどんなものにも重力がはたらきます。このおもりは60gであることが明記されていますので、おもりにかかる重力は 下向き60gの力です！

1-2. 弾性力を描く

この問題の場合、ばねの伸びが分かりません。分からなければ□gで書き加えます。向きは”ばねの引っ張り返す”方向の上向きです。

2. つりあいの式を立てる

図はつり合っている状態ですので “上向きの力”=“下向きの力”の式を立てます。弾性力は60gであることが分かります。

3. ばねの伸びを求める

最後は弾性力60gに対してばねの伸びはいくつかを求めます。ところがこの問題…表にばねの伸びは書かれていません∑(ﾟДﾟ)

そうであれば… 表を拡張して
”ばねの伸び” を書きたしちゃいましょう

表からどうやらこのばねは… 伸び3cmで20gの弾性力が生じる ことが分かります。それが分かれば表を拡張することができます。40gの弾性力であれば伸びはもちろん6cmです。60gの弾性力であれば伸びは9cmですねd(^_^o)

よってこの図の “ばねＣ②”の伸びは９cm です。そして ばねの全長は19cm です。

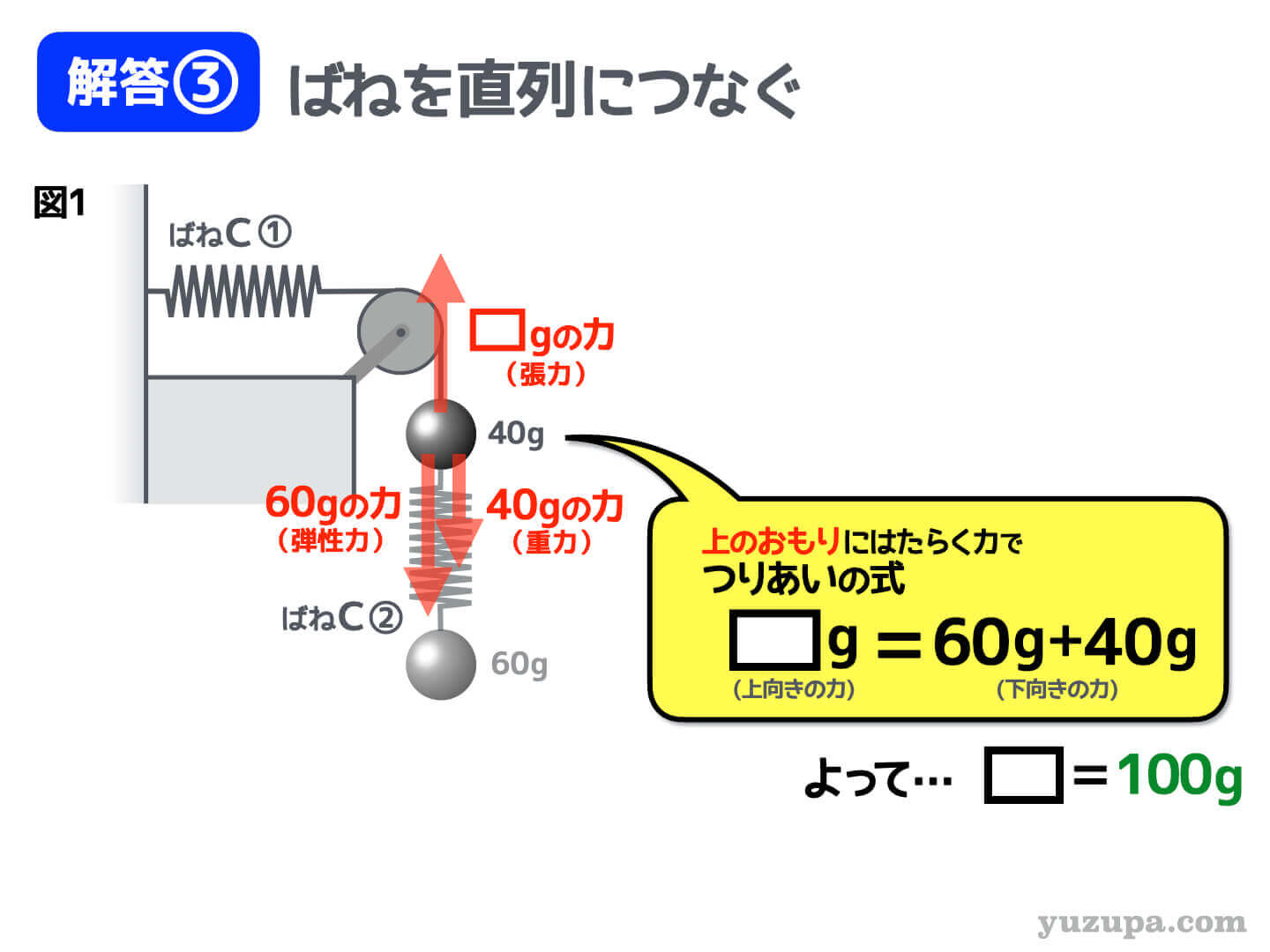
今度は上にある30gのおもりに着目して、はたらく力を全て描いていきましょうd(^_^o)

1-1. 重力を描く

このおもりは40gであることが明記されていますので、おもりにかかる 重力は下向き40gの力 ですね。

1-2. 弾性力を描く

このおもりは下側がばねにつながっています。ばねにつながっているということは弾性力がはたらきます。

その大きさは 下端にはたらく弾性力と同じ です。

つまり…下向き60gの弾性力がはたらいている と考えることができます。ばねの両端には同じ大きさの弾性力がはたらいているという基本を知っていれば簡単ですd(^_^o)

1-3. 張力を描く

このおもりは上側がひもにつながっています。ひもにつながっているということは張力がはたらきます。

張力は 現時点ではよく分かりませんので□gとして 描きましょう。向きは？ ひもの張っている方向ですので上向きです。

2. つり合いの式を立てる

おもりにはたらく力を全て描き終えましたので、つり合いの式を立てます。”上向きの力”＝”下向きの力”ですねd(^_^o)

そうすると… 張力の大きさが100g であることが分かります。

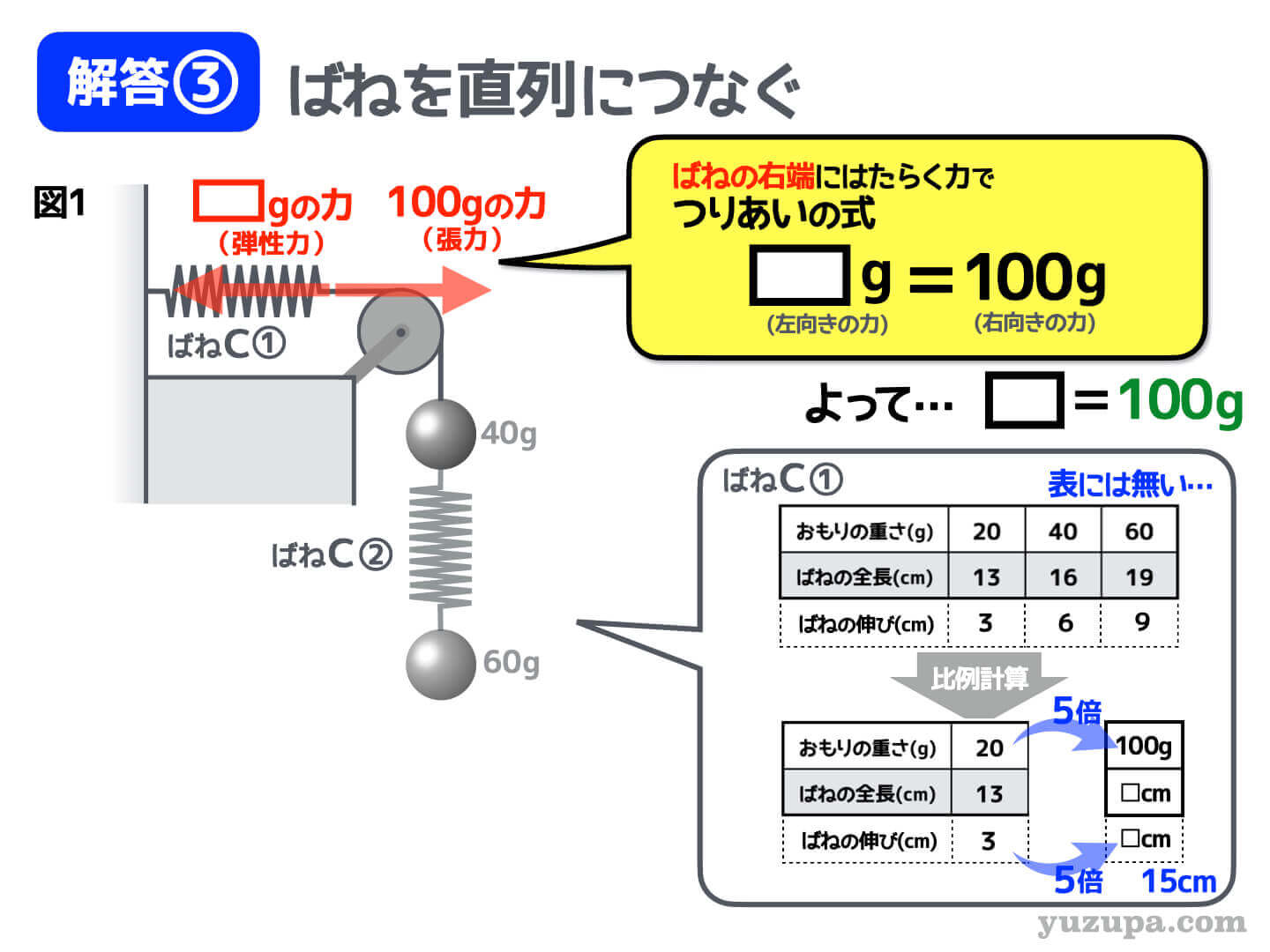
いよいよ仕上げのフェーズですd(^_^o) ラスボス ばねC①の右端に着目して発生する力を描いていきましょう。

1-1. 重力を描く

重力を描きたくなりますが、この問題…ばねの重さは無視するという条件 ですので、重力を描くことは不要になります∑(ﾟДﾟ)

1-2. 張力を描く

このばねは右端がひもにつながっているので張力がはたらきます。その大きさは？ さきほど求めましたね！

ひもにかかる張力はどこも同じ

したがって、このばねの右端にかかる張力も100gの大きさです。方向は 右に引っ張られていますので右方き です。

1-3. 弾性力を描く

最後はこのばねの弾性力です。分からないので□gとしましょう。向きは ばねが引っ張り返す方向ですので左向き です。

2. つり合いの式を立てる

ばねの右端にはたらく力はこれで全てでしょう。それでは、つり合いの式を立てます。”左向きの力”＝”右向きの力” ですね！

そうすると ラスボス ばねＣ①の弾性力が100g と分かります。

3. ばねの伸びを求める

弾性力が分かれば伸びも分かります。さきほど伸びを書き足した表から比例計算をします。100gの弾性力がはたらいている時の ばねの伸びは15cm であることが分かります。

ところで…ばねの自然長はいくつでしょうか？

あたりまえですが ばねの全長ーばねの伸び で求めることができます。表の２段目と３段目の差 ですね d(^_^o)

問題が求めているのは伸びではなく全長ですので、自然長の10cmをたして25cm と間違えないようにかきましょう。

 

例題④ ばねを並列につなぐ

最後はばねを並列につなぐパターンです。並列につなぐとは？ ちょっと説明が難しいので具体的な問題にまいりましょう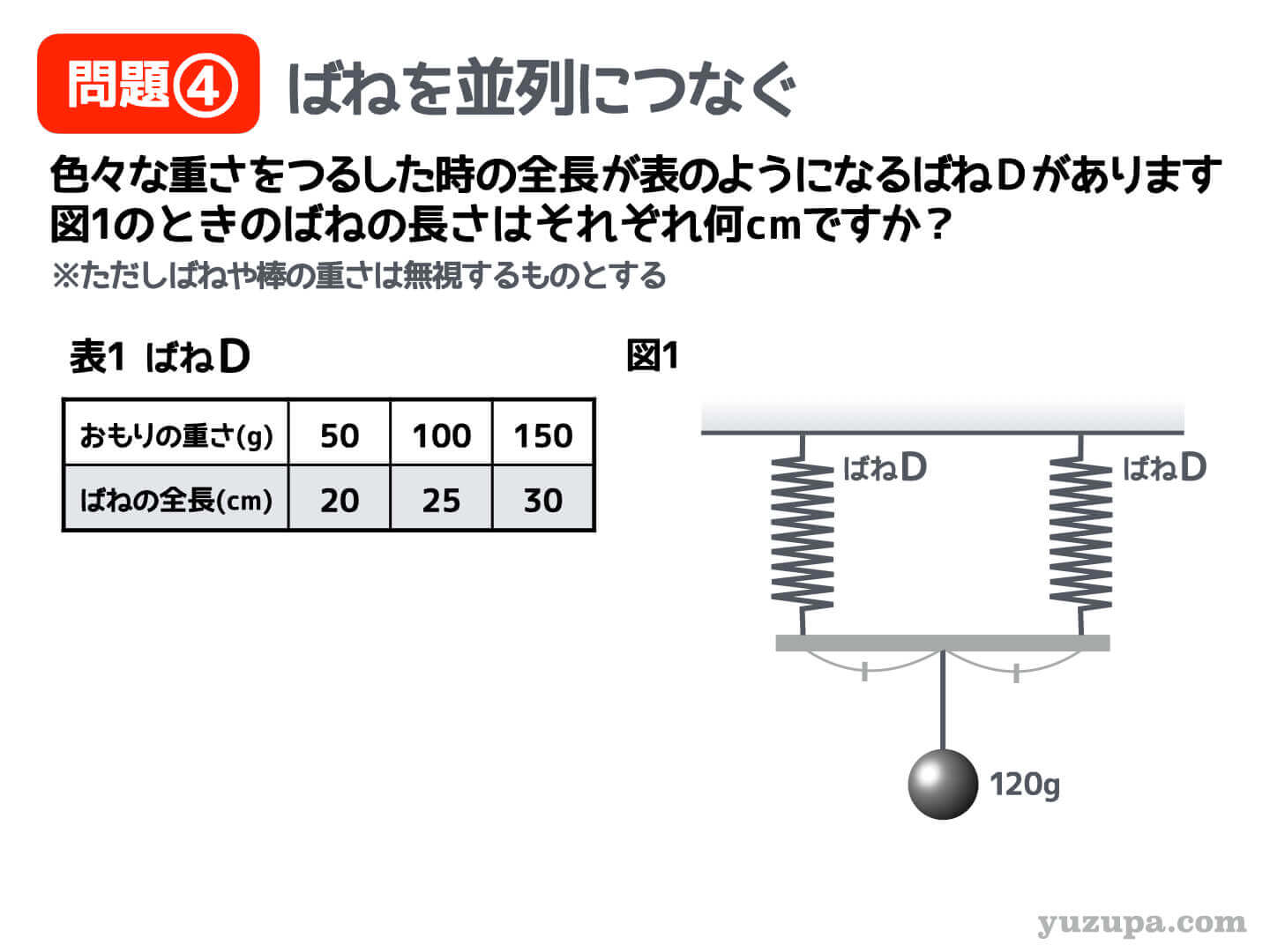！”ばねを並列につなぐ”とは図のように、棒などで２つのばねを連結することを指します。ポイントは ”ばねの下端にどれくらいの大きさの力がかかるか？”です。

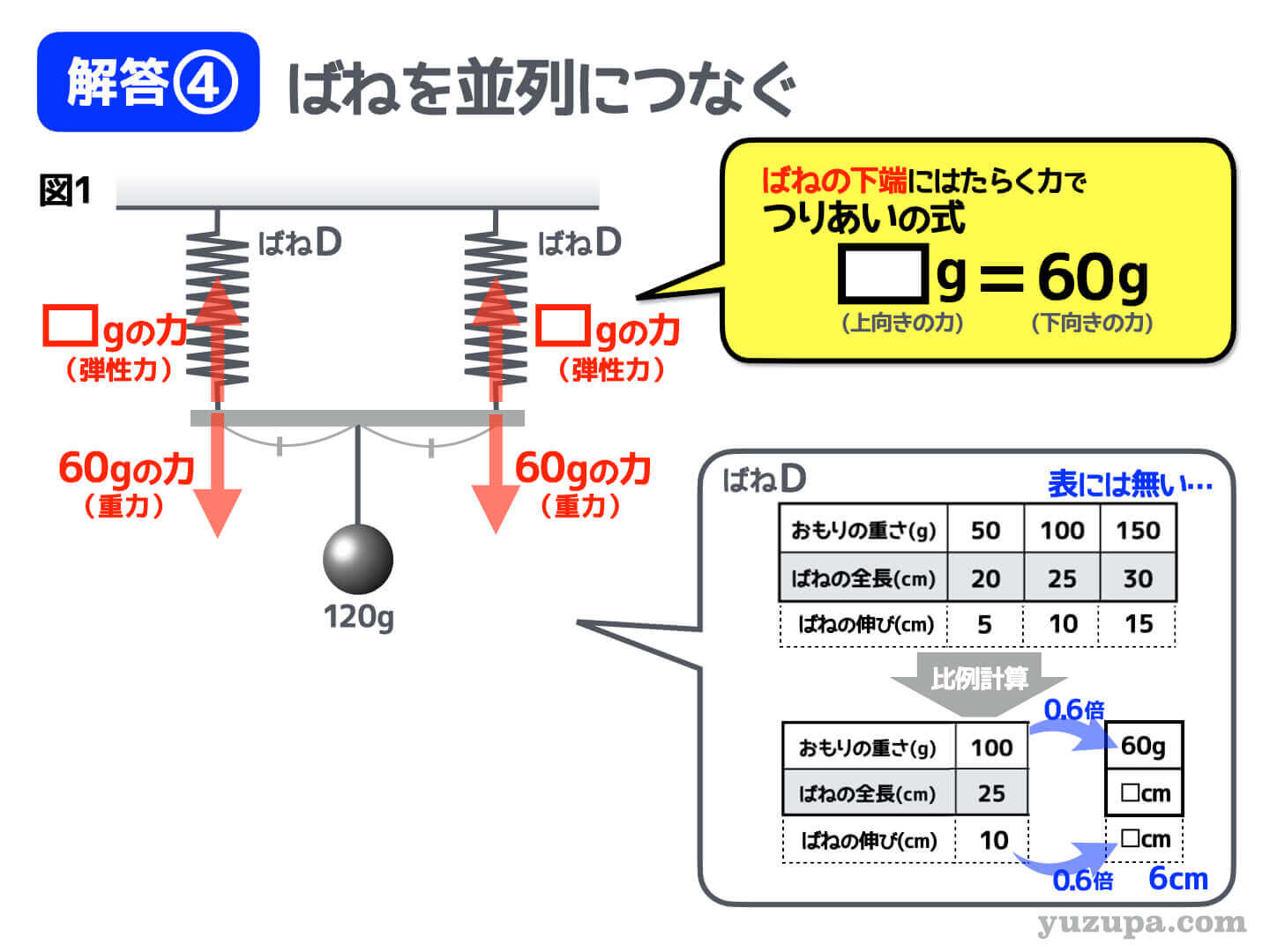
ばねを並列につないで真ん中におもりを吊るすと…２つのばねに半分ずつ下向きの重力がかかります。

1-1. 重力を描く

重力は上記で説明したとおり、120gの重力の半分ずつがばねにはtらくことになります。下向き60gの力ですね。

1-2. 弾性力を描く

弾性力は分かりませんので□gとして上向きで描きます。とても簡単ですね(^_^;)

2. つり合いの式を立てる

“上向きの力”＝”下向きの力”ですね！ 想像どおりの結果かもしれませんがばねの弾性力は60gです。

3. ばねの伸びを求める

この問題もばねの伸びはダイレクトに書かれていないので、表を拡張してあげましょう。このばねは弾性力が50g増えるごとに5cm伸びていることが読み取れればOKですd(^_^o)

あとは60gの弾性力が発生している時のばねの伸びを求めると6cmということが分かります。自然長の15cmをたしてあげて、この時の ばねの長さは21cm となります_φ(･_･

この問題は “棒の真ん中”におもりを吊るすというものでしたが、1:2の位置とか、2:３の位置とかに吊るす問題も出題されることも…

その場合は、おもりの重力の分散が半分ずつではなく1:2になったり2:3になります _φ(･_･

 

まとめ

小学生が苦手意識を持つ力学分野。今回は”ばね”にフォーカスして例題をまじえて解説しました。どんなに単純な問題でも力学の王道を軽視しないということ d(^_^o)

シンプルな問題はできるのに、浮力がでてくると分からなくなる…はかりに乗っかると分からなくなる… もしかすると力学の王道である”つり合いの式を立てる” を軽視した結果かも しれません。

そして今回のメインテーマとなる ”ばねの弾性力” は主に３つのアプローチで求めます。

　・比例関係から求める
　・はかりの示す値から求める
　・つり合いの式から求める

おちついて物体にどんな力がはたらいているかを考え、つりあいの式を立てましょう d(^_^o)