中学受験:音の速さの求め方… 音の速さ問題がややこしいと感じる3つの理由
算数の速さ問題と同じなのに…理科の音の速さ問題がなぜかややこしく感じる
 こんにちは。かるび勉強部屋 ゆずぱ です。
こんにちは。かるび勉強部屋 ゆずぱ です。
音の速さを求める問題。算数で出てくる速さを求める問題はできるのに…理科で出てくる音の速さの問題になるとなぜか分からなくなる(-_-;)
どうやら以下が原因の模様です。
音の速さの問題がややこしい3つの理由
① 速さを求める2つのアプローチがある
② 音源が動いていても音の速さは変わらない
③ 音を聞く人もやたら動く…相対速度の考え方が必要
算数の速さ問題と異なり、音はものすごく速いのでスケールが違うのも1つの要因かもしれませんが、もっとややこしくしているのは上記の3つの理由です。
そうと分かれば…この3つの理由をひとつずつ攻略するまで!それではひとつずつひもといてまいりましょう。
目次
音の速さをややこしくする3つの理由
理由① 音の速さには2つのアプローチがある
人が歩く速さであろうと、自動車の走る速さであろうと、音が伝わる速さであろうと…求めるものは速さなので考えることはひとつです。単位時間あたりに進む距離ですね。

アプローチ① 速さの公式(定義)から求める
速さ、距離、時間の3つの値のうち2つの値が分かれば残ったもう1つの値も計算で求めることができます。よく使われる円形の図を使って問題文から値を読み取って整理してもよいでしょう。
例題
花火がさく裂する場所から1675m離れた場所では
花火が見えてから5秒後に音が聞こえました。
音の速さをもとめましょう。
速さ、距離、時間の3つの値を問題文から読み取って整理していきます。この問題の場合、距離は1675mで時間が5秒ですので、速さを計算して求めることができますね!
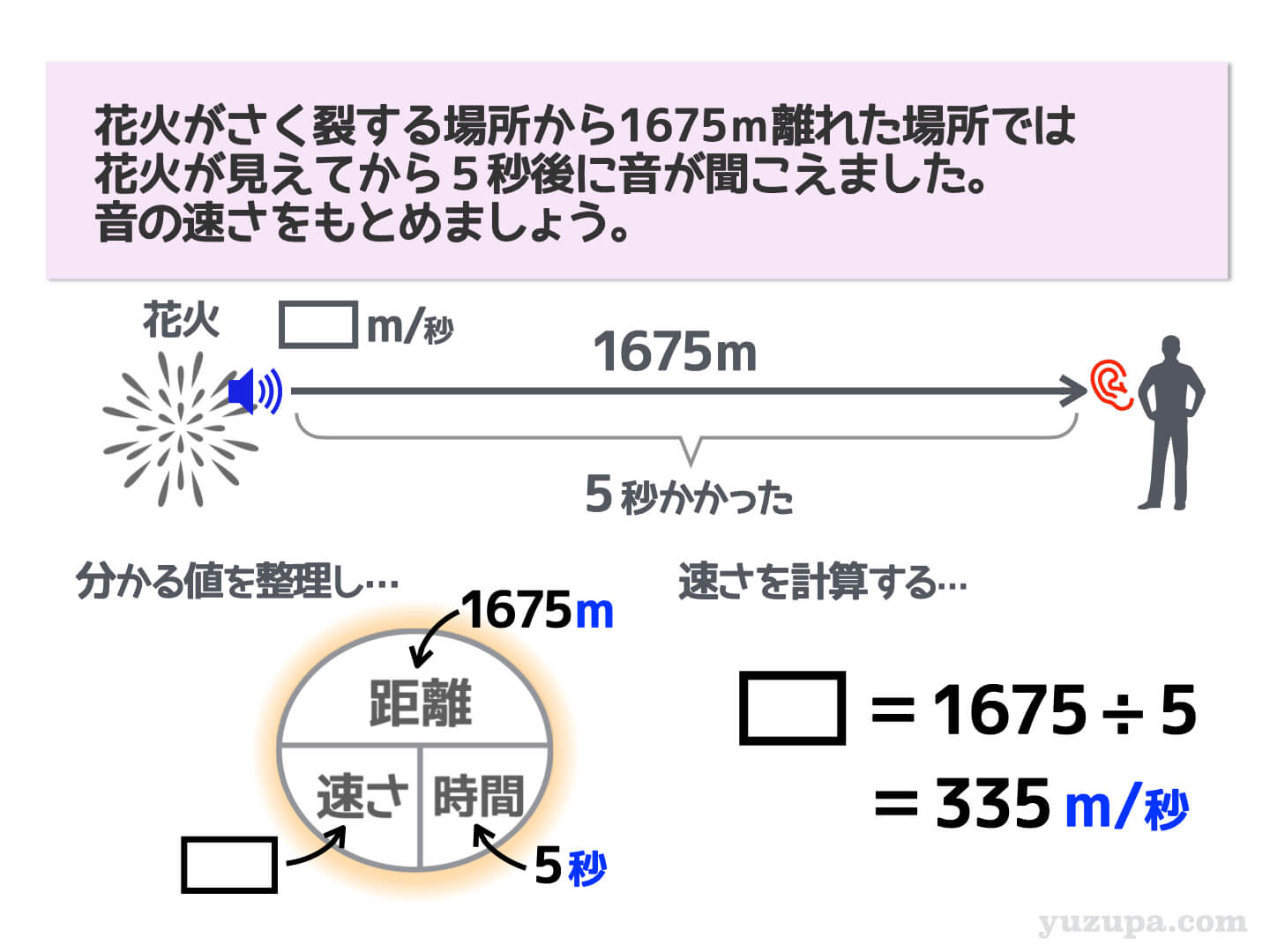
この問題の場合、問題文から距離と時間の2つの値が分かりますので、速さを計算して求めることができます。
アプローチ② 温度など条件から求める
速さの定義からシンプルに求めるアプローチを見てきましたが、音の速さの問題の場合、ちょっと違ったアプローチがあります。それが音が伝わる環境の条件から求める問題です。
百聞は一見にしかず。さっそく具体例をみましょう。
例題
音の速さは気温が0度の時は331m/秒ですが、
気温が1度あがるごとに0.6m/秒ずつ速くなっていきます。
気温が15度の時の音の速さをもとめましょう。
実際の中学入試でもこんな感じで出されるんです。ただ…攻略法は超簡単です。比例関係になっているので計算で求めることができますね。慣れるまでは表を使って整理するのもよいかもしれません。
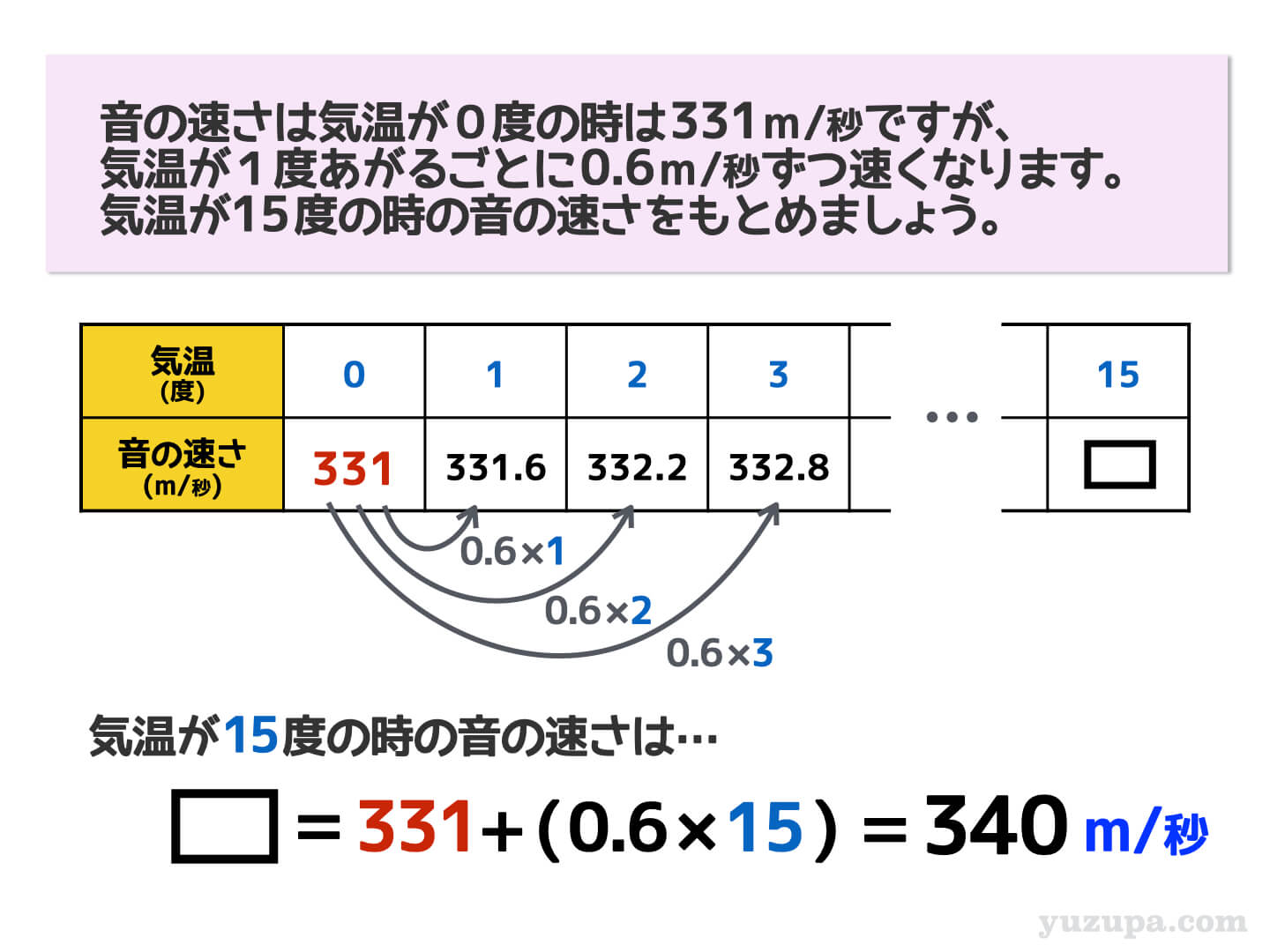
気温が15度ですので、気温が0度の時よりも0.6m/秒 × 15=9m/秒 ほど速くなります。答えは340m/秒ですね!
音の速さを求める2つアプローチ。1つの問題で両方のアプローチを使わないと解けない問題もよく出題されています。意識して使い分けるという気持ちで取り組みましょう!
理由② 音源が動いていても音の速さは変わらない
個人的にはコレが音の速さ問題をややこしくしている代表格のように感じています。音源が動いている場合の音の速さです。まずは、2つの実験を考えてみましょう。
実験(1)
秒速20mで走っている車の中から、進行方向と逆方向に秒速30mでボールを放つとどうなるでしょうか?実験(2)
秒速20mで走っている車の中から、進行方向とは逆方向に秒速340mの音を放ったらどうなるでしょうか?
ボールの場合は車の速さと相殺され、外から見ている人にとっては進行方向と逆方向に秒速10mで飛んでいくように見えます。一方で音の場合は車の速さにまったく影響をうけることなく秒速340mで伝わっていくように見えます。
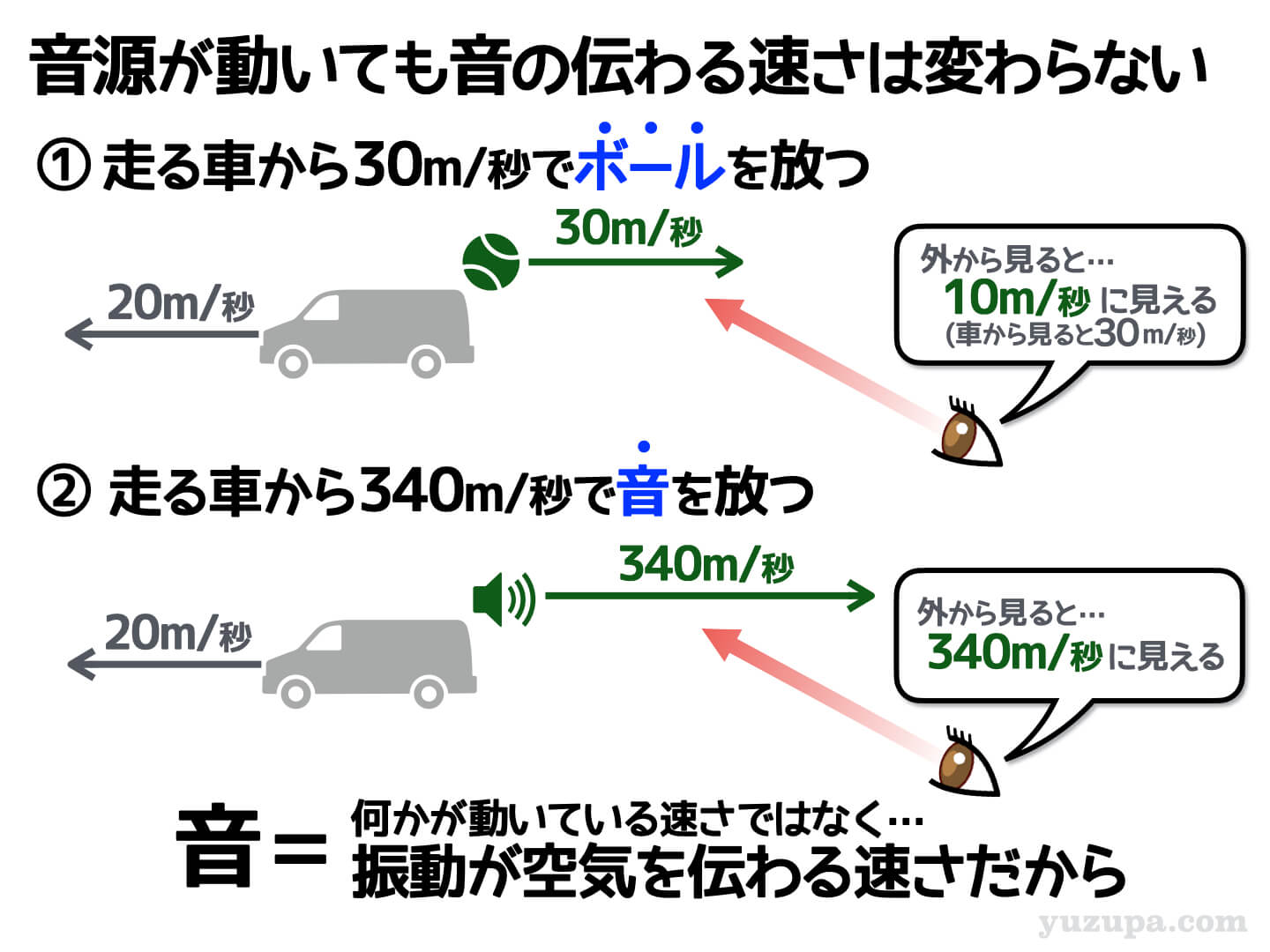
音の速さが変わらない理由
音の速さというのは 正確に表現すると音が ”伝わる” 速さ
音の正体は空気の粒の振動。音が発生すると空気の粒を振動させ、それにつられて隣の空気の粒も振動し、そのまた隣の粒も振動し…と振動が伝わっていくのが音が伝わる仕組みです。
音というナニモノかが動いているわけではないので音源がどんなに動いていようが音が伝わる速さには影響しないというワケです。
理由③ 聞く人が動く場合は”旅人算”を使う
音の問題のややこしいところ。最後は”音を聞く人も”動くという問題がほとんどであること。2つの動くものの速さを扱う単元といえば…? そう算数の単元である旅人算です。
※ 中学受験の世界で ”旅人算” と呼ばれているもの。その正体はシンプルな相対速度のことです…(汗)
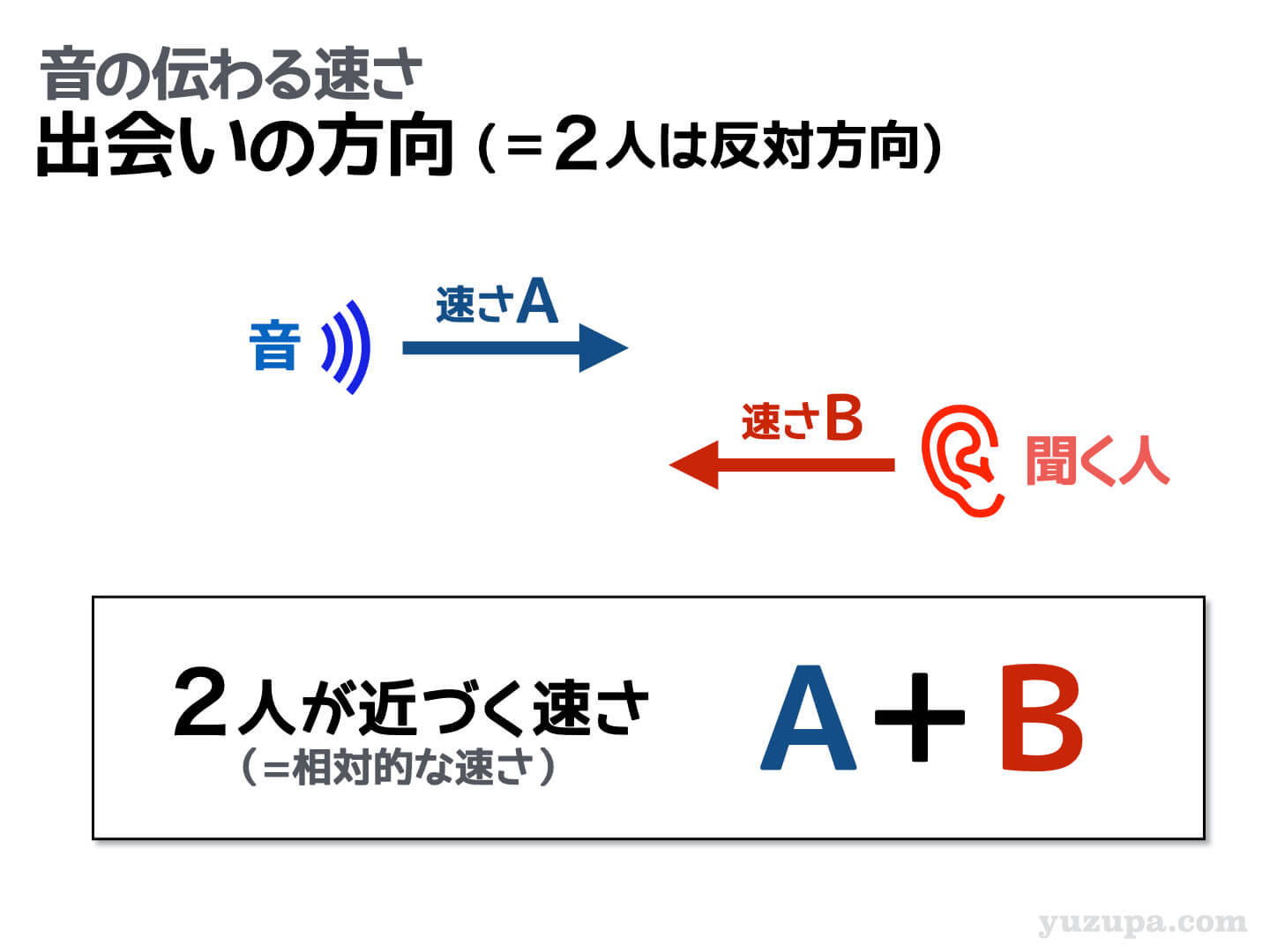
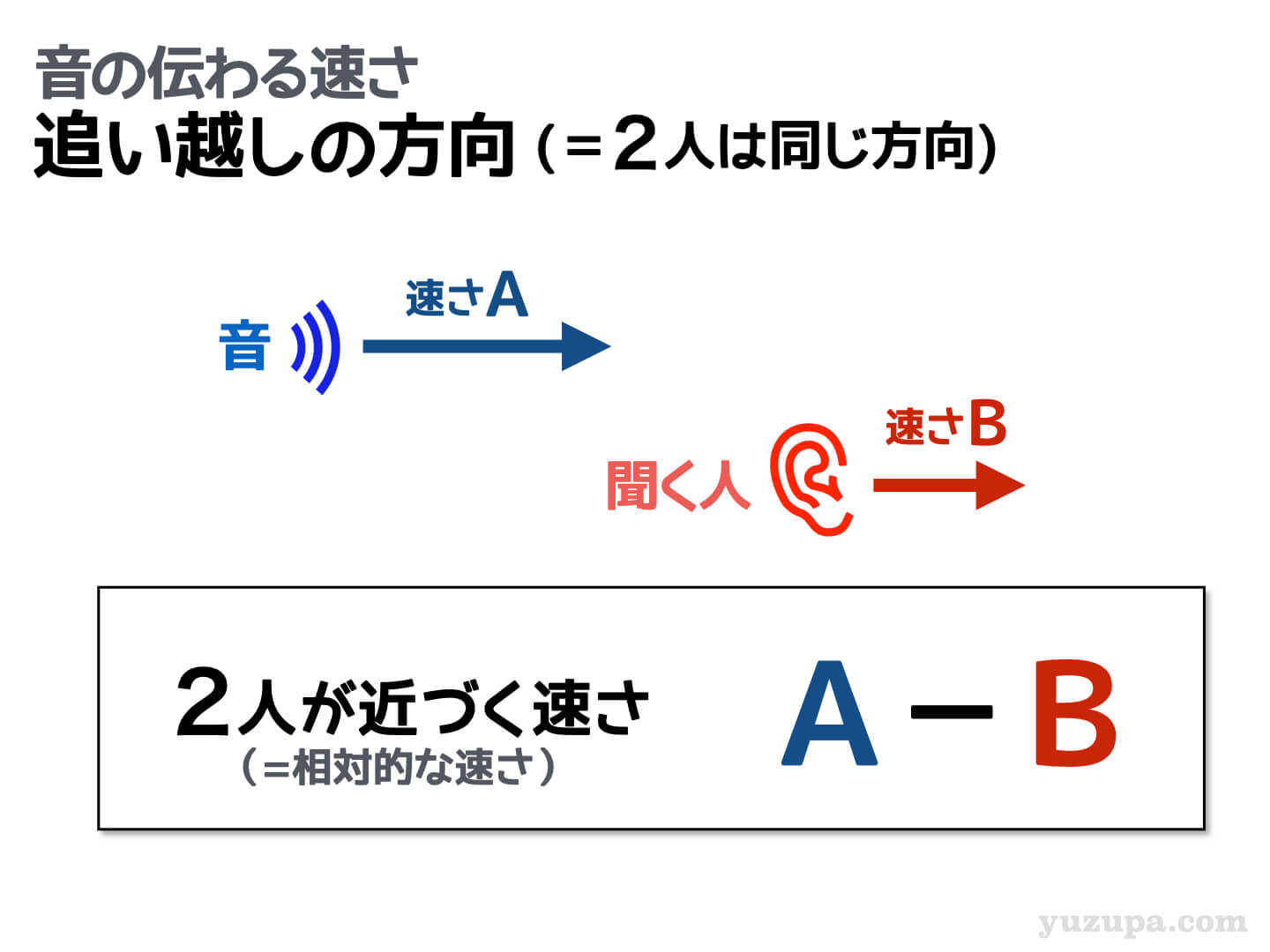
音の進行方向と聞く人の進行方向が同じ方向であれば、2つのものの速さは打消し合います。音の進行方向と聞く人の進行方向が逆の方向であれば、2つのものの速さは合算されます。
音を聞く人が動く場合には、旅人算で解く選択肢も検討しましょう。
実際に入試で出題される問題パターン
音源や聞く人が動かない音の速さの問題

音の速さに関する問題ですので 速さ・距離・時間 の3点セットを問題文から探していきましょうd(^_^o)
(1) 速さ
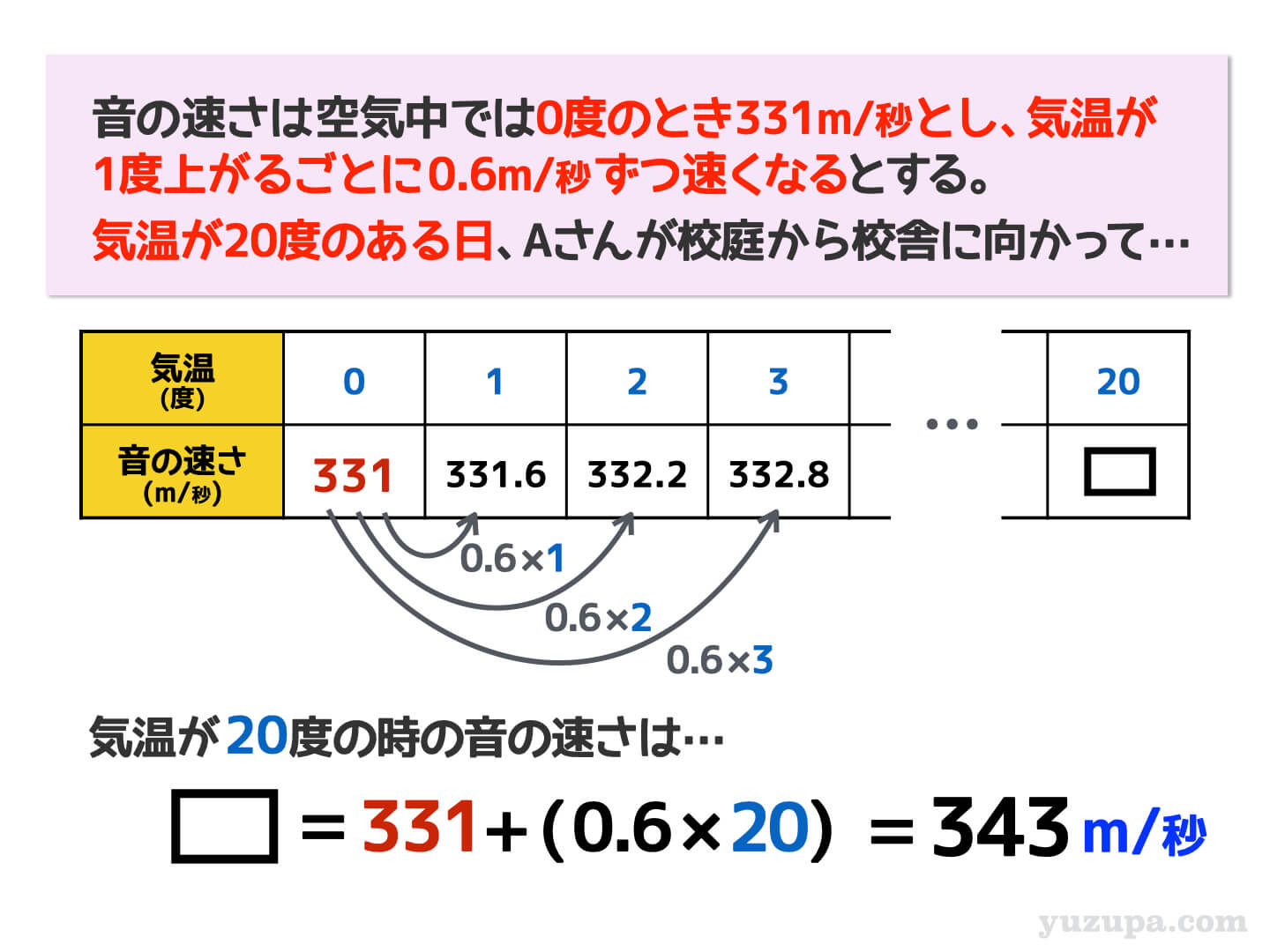
速さは問題文から読み取れそうですが素直に書かれていませんね(^_^;) これは速さを求める2つのアプローチのうちの1つを使って音の速さを求めてみましょう。
以下のように 速さ=秒速 343 m ですね!
(2) 距離
距離はこの問題文が求めている値です。とうぜん問題文に書かれておらず、速さと時間から計算するということになります。
(3) 時間
時間はなんとなく書かれていそうです。太鼓を鳴らしてから太鼓の音が聞こえるまでの 時間=1.6秒 と書かれていますね。
では、速さ・距離・時間の関係を図で書いてみましょう。
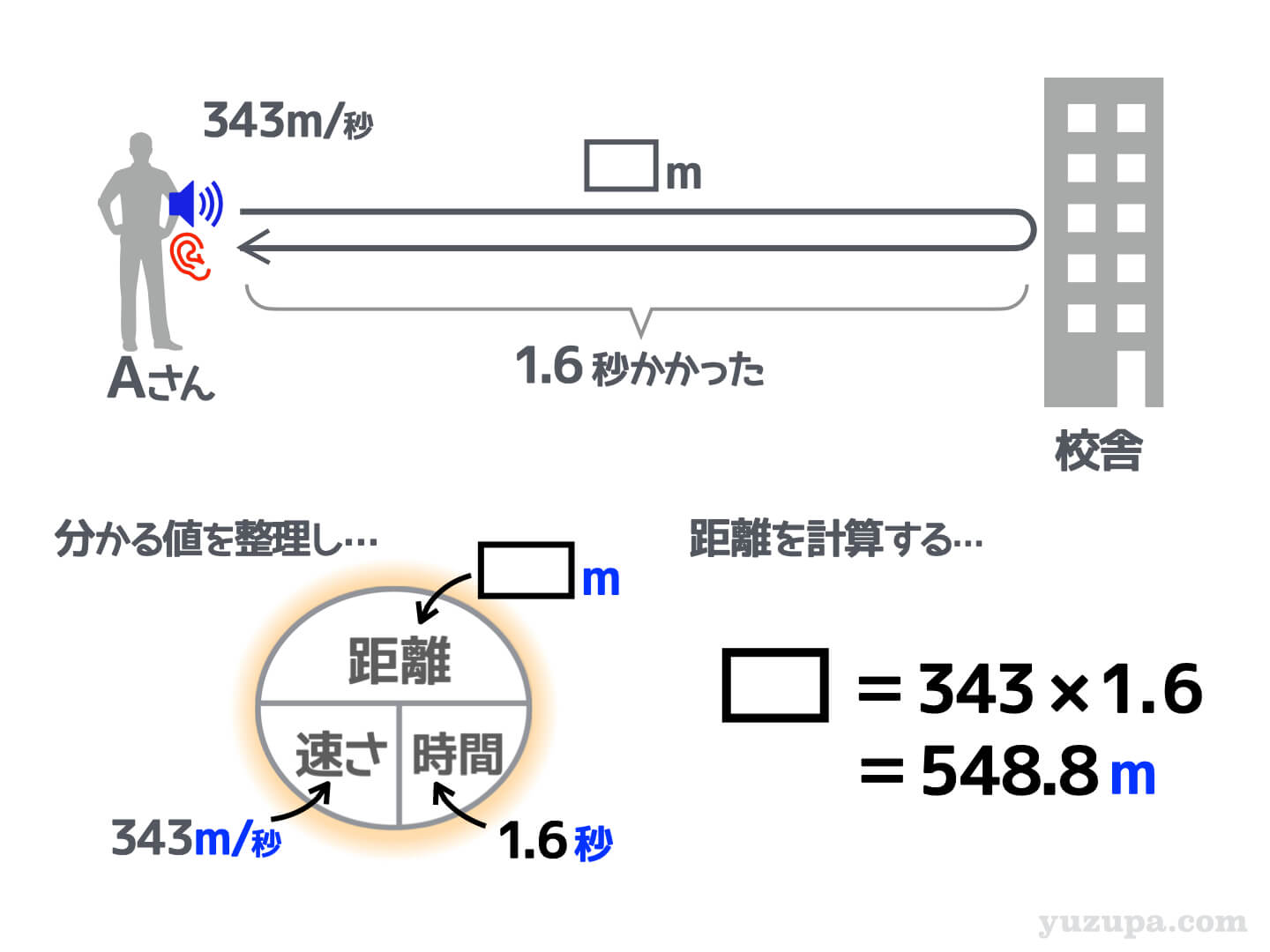
分かる数字を整理して距離を計算します。すると 距離=548.8m になることが分かりました。ただしこの距離は図で示すようにAさんと校舎の往復の距離ですね。
Aさんと校舎の距離はこの半分ですので…274.4mです。
音源や聞く人が動く音の速さの問題

この問題も問題を読めば音の速さに関する問題であるとすぐに分かります。では…3点セットを確認してみましょう!
(1) 速さ
音の速さは問題文にダイレクトに書かれています。音の速さの問題ではこうやって書いてあることも多々ありますので、問題文をしっかり読むようにしましょうd(^_^o)
音の速さ=秒速 340 m です。
もうひとつ速さらしき値が書かれています。船の速さですね。岸壁から遠ざかる方向に秒速10mの速さで航行しているようです。かなりの高速船です…∑(゚Д゚)
船の速さ=秒速 10 m です。
(2) 距離
この問題も距離を求めています。問題文にも書かれていないので、速さと時間から計算するとしましょう。
(3) 時間
汽笛を鳴らしてからその音が聞こえるまで 時間=2秒 と書かれています。これで距離や時間と対応づけてみましょう!
① 旅人算(相対速度)を使ったやり方
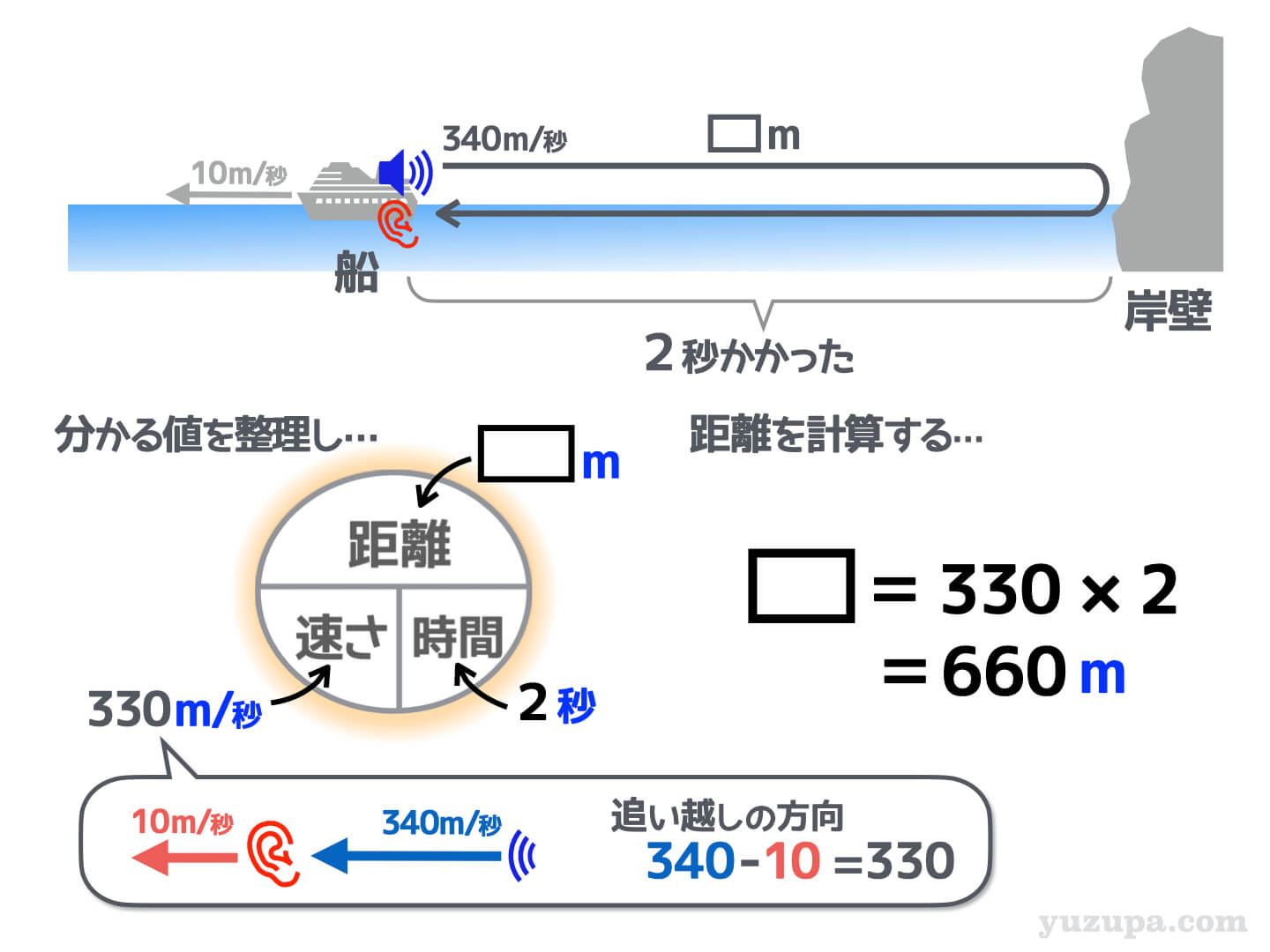
音源も聞く人も同じ船。音源と船の距離は上記のように描くことができます。汽笛が鳴ってから聞こえるまえ2秒なので、音が上記のような距離を進むのにかかった時間が2秒ですね。
注意すべきは速さ です_φ(・_・
音は岸壁での反射を経て船に向かって伝わっていきますが、その船が時速10mの速さで逃げています。これは旅人算(相対速度)では追い越しの方向ですので…
音と船が近づく速さ=秒速330mになります
速さと時間が分かったので距離は計算すれば660mとなります。問題分で求められているのは、汽笛を鳴らした瞬間の船の位置ですので、岸壁から330m離れたところ というのが答えです。
② 旅人算(相対速度)を使わないやり方
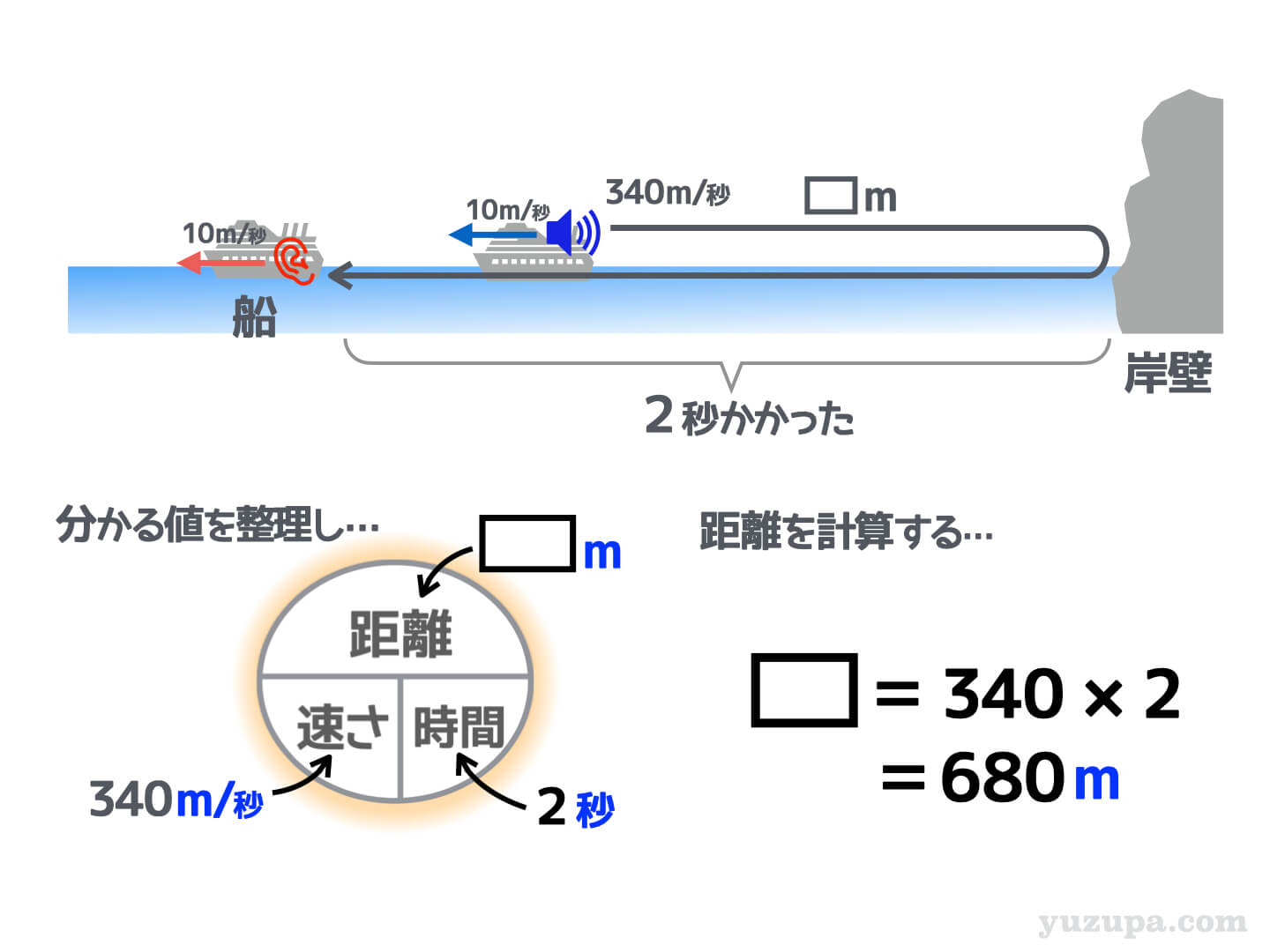
音が伝わる距離は上記のような図になります。汽笛が鳴らされてから船が音を聞くまで2秒。その2秒が経過する間に、とうぜん船も進んでいます。船が進んだ部分もしっかり書く必要があります。
さて速さはどうでしょうか?
この場合は、音源と船が近づく速さではなく、実際に音が伝わる速さですので 秒速340m となります。これで計算をしてみると距離は 680m であることが分かりますねd(^_^o)
さて汽笛が鳴った時の岸壁と船の距離はどうでしょうか?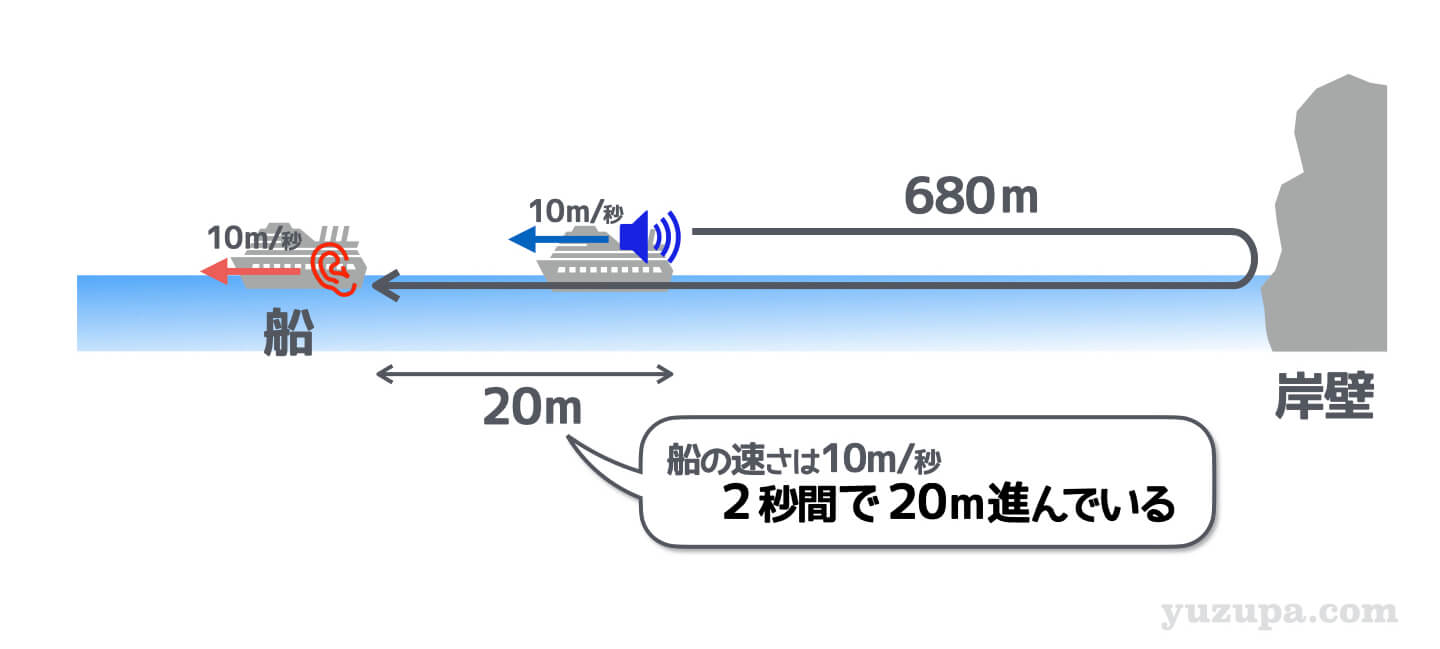
汽笛が鳴らされてから音が聞こえるまでの2秒間に船がどれだけ進んだかを図に書き加えてあげれば、答えが見えてきます_φ(・_・
汽笛が鳴らされた時の船は岸壁から330m の距離ですね!
まとめ
音の速さの問題。算数で出てくる速さの問題はできるのに理科の音の速さの問題となるとなぜかややこしく感じてしまう。その理由は大きく分けて3つあります d(^_^o)
音の速さの問題がややこしい3つの理由
① 速さを求める2つのアプローチがある
② 音源が動いていても音の速さは変わらない
③ 音を聞く人もやたら動く…相対速度の考え方が必要
今回は具体的に入試に出題されるパターンに似せて2つの問題を解いてみました。上記の3つを理解できたのではないでしょうか?
理科で登場する音の速さの問題でも、上記3つの知識を携えて 速さと距離と時間の3点セットを落ち着いて考えることができれば、音の速さ問題も怖くありません o(^-^)o











初めまして。最近、ゆずぱさんを知り参考にさせていただいております。
小1男子母です。
中学受験をぼんやりとですが考えております。
記憶力が良く5回から10回も(日数はまちまちですが)学べば暗記出来てしまいます。
2、3回で覚えてしまう事もあります。
暗記に時間が取られると聞き、都道府県、星座(ゆずぱさんのブログに載っていたもの)、部首を覚えまして今は特産品覚えの段階です。今後は地図記号や植物、また歴史や山地山脈、世界地図などを覚えてみようかと考えております。
暗記を必要する科目でこれもオススメといったものはございますでしょうか?
ブログの内容と関係のない質問となり申し訳ございませんが、宜しくお願い致します。